Как найти ранг тензора

Время на прочтение
10 мин

Количество просмотров 113K

Содержание

1. Что такое тензор и для чего он нужен?
2. Векторные и тензорные операции. Ранги тензоров
3. Криволинейные координаты
4. Динамика точки в тензорном изложении
5. Действия над тензорами и некоторые другие теоретические вопросы
6. Кинематика свободного твердого тела. Природа угловой скорости
7. Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
8. О свертках тензора Леви-Чивиты
9. Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
10. Получаем вектор угловой скорости. Работаем над недочетами
11. Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
12. Параметры Родрига-Гамильтона в кинематике твердого тела
13. СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
14. Нестандартное введение в динамику твердого тела
15. Движение несвободного твердого тела
16. Свойства тензора инерции твердого тела
17. Зарисовка о гайке Джанибекова
18. Математическое моделирование эффекта Джанибекова

Введение

Несказанно рад, что читателям понравилась предыдущая статья. Сразу сделаю оговорку — просто рассказать о таком ёмком понятии как тензор не получится — велик объем информации. Могу обещать, что к концу цикла мозаика сложится.

А в прошлый раз мы остановились на том, что рассмотрев представление вектора в косоугольном базисе, и определив, что он представляется двумя разными (ковариантными и контравариантными) наборами координат, получили общие выражения для скалярного произведения, учитывающие изменение метрики пространства. Таким образом, мы весьма осторожно подошли к понятию тензора

Тензор — математический объект, не изменяющийся при изменении системы координат, представленный набором >своих компонент и правилом преобразования компонент при смене базиса.

Скалярное произведение — это хорошо. Но как же быть с остальными операциями? Как они связываются с геометрией пространства и представимы ли в тензорном виде? Разумеется представимы, ведь векторы — это… тензоры! И скаляры — это тоже тензоры. Привычные нам математические объекты лишь частные примеры более общего понятия, коим является тензор.

Вот об этом мы и поговорим под катом.

1. Геометрический смысл метрического тензора

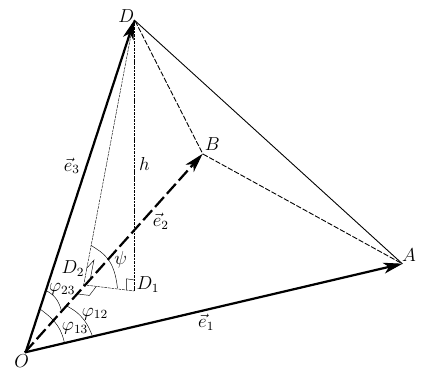
Для наглядности, которая не слишком повлияет на общность рассуждений, ограничимся трехмерным пространством. Докажем следующее утверждение — определитель метрического тензора равен квадрату объема параллелепипеда, натянутого на векторы базиса.

Рис. 1. Соотношения в трехгранном угле, образованном базисом

Рассмотрим произвольный базис

Вычислим объем параллелепипеда, натянутого на базис так, как это принято в стереометрии

где S — площадь основания параллелепипеда; h — высота, проведенная к данному основанию.

Площадь основания вычисляется тривиально — как модуль векторного произведения

С определением высоты придется повозится. Если бы мы знали угол , то легко нашли бы высоту

Угол связан с линейными и двугранными углами трехгранного угла

– первая теорема косинусов для трехгранного угла. Из нее выражаем косинус двугранного угла

Квадрат синуса необходимого нам угла выражаем через полученный косинус

Выполняем последовательные подстановки от (6) до (2), не забывая возвести в квадрат площадь S и высоту h. Выкладки достаточно громоздкие и для их выполнения можно воспользоваться СКА (Maple или Mathematica) и получить квадрат объема параллелепипеда

Теперь вычислим определитель метрического тензора. Им называется определитель матрицы, которая составлена из компонентов тензора. Входящие в нее скалярные произведения векторов базиса выпишем в явном виде

Вычислив его, получим тот же результат, что и для квадрата объема

Таким образом, утверждение (1) верно. Соответственно, объем параллелепипеда, натянутого на базис можно получить извлечением корня из определителя метрического тензора

где для краткости обозначим значение определителя.

Корень (7) часто встречается в литературе по ОТО и альтернативным теориям гравитации типа РТГ. Эта величина имеет фундаментальное значение и пригодится нам чуть позже.

2. Тензорное произведение векторов. Диада. Ранг тензора. Свертка

Обратим внимание на выражение скалятного произведения

Величину

называют тензорным произведением двух векторов или диадой. Тензорным это произведение названо потому что перемножаются тензоры и на выходе получается тензор, в данном случае второго ранга, . Ранг тензора — это количество его индексов. Вектор, внезапно, тоже является тензором, только первого ранга. Да это и понятно — ведь вектор, как геометрическая сущность, не зависит от системы координат, в которой его рассматривают. От выбора системы координат зависят лишь его компоненты.

Тензор второго ранга (8), разумеется, представлен матрицей своих компонент

Используя (8) можно переписать скалярное произведение в виде

это тоже тензорное произведение, называемое сверткой из-за того, что приводит к уменьшению ранга результирующего тензора. Все индексы в (10) «немые», по ним производится двойное суммирование компонент метрического тензора и диады и на выходе получатся число c.

Внимательный читатель скажет, что на выходе должен получится тензор. Так тензор и получается — скаляр, это тоже тензор. Нулевого ранга, так как не имеет индексов и не подлежит преобразованию при смене базиса. Скалярное произведение инвариантно относительно смены базиса, ибо ни длина участвующих в нем векторов ни угол между ними от смены базиса не меняются. Значит скаляр — это тензор нулевого ранга.

Но не любое число есть скаляр. Скаляр — это длина вектора, скалярное произведение векторов, масса материального тела, абсолютная температура и прочие величины, не зависящие от системы координат. Компонента вектора уже не является скаляром — она меняется при смене базиса.

О ранге тензоров и типе из компонент мы поговорим чуть позже, а пока перейдем к следующему животрепещущему вопросу.

3. Векторное произведение. Тензор Леви-Чивиты

Вернемся к нашим векторам и выполним их векторное умножение

За неимением других вариантов, аккуратно раскроем скобки, помня о некоммутативности операции

Разумеется мы хорошо учились в университете и знаем, что векторное произведение вектора самого на себя равно нулю. Но мы не будем сильно спешить с упрощением, ибо кроме этого, несомненно приятного факта, мы видим ещё одну вешь — компоненты диады (9). Но кроме упрощения связанного с нулевым произведением коллинеарных векторов мы больше ничего не наблюдаем. Мы работаем с произвольным базисом в чистом виде.

Применим хитрость — умножим вектор скалярно на первый вектор базиса учтя теперь, что произведения

Коэффициенты в квадратных скобках — смешанные произведения векторов. Если векторы компланарны (лежат в одной плоскости) то такое произведение равно нулю. То есть, если в смешанном произведении повторяется хотя бы один вектор, оно равно нулю. Значит у нас остается только два слагаемых из девяти, в которых не повторяются векторы при смешанном умножении

Так, а теперь вспоминаем, что — ковариантная компонента вектора . Ну и наконец переставим векторы в векторном произведении первого слагаемого, добавив минус как и положено по правилу векторного произведения

Аналогичным образом выделяем остальные компоненты

Выражения (11) — (13) очень напоминают формулы для расчета проекций векторного произведения из курса векторной алгебры, с точностью до множителя со смешанным произведением. Но мы-то работаем не в декартовом базисе, естественно ожидать некоторое отличие. Кстати, а что это за множитель? Ведь смешанное произведение векторов имеет геометрический смысл… Это же… объем параллелепипеда, натянутого на векторы в нем участвующие. А объем параллелепипеда, натянутого на базис это ведь корень из определителя метрического тензора! То есть

Вот она и всплыла на поверхность, метрика используемого пространства. Таким образом, можно построить некий тензор, свертка исходных векторов с которым дает ковариантный вектор, являющийся результатом векторного произведения. Более того, этот тензор связан с метрическим тензором. Таковой тензор третьего ранга носит имя итальянского математика Леви-Чивиты.

Не трудно увидеть, что компоненты тензора Леви-Чивиты определяются соотношением

Их будет 27, но большинство из них, а именно 21 равны нулю. Это те компоненты, индексы которых повторяются хотя бы один раз. Ненулевых компоненты только шесть, они соответствуют не повторяющимся индексам. По модулю они равны , но три из них положительны, другие три отрицательны. В формулах (11) — (13) мы переставили векторы местами и добавили минусы, чтобы сделать коэффициенты при диадах положительными а сами формулы похожими на привычные нам по курсу векторной алгебры. Теперь вернем всё на свои места

Знак смешанных произведений зависит от порядка индексов: в наборах (1,2,3), (2,3,1), (3,1,2) они положительны, в наборах (1,3,2), (2,1,3) и (3,2,1) — отрицательны. Известно, что если векторы заданы в правой системе координат, то их смешанное произведение будет положительно, если они образуют правую тройку векторов. В первых слагаемых (16) — (18) фигурируют правые тройки векторов базиса. Во вторых слагаемых, в смешанном произведении участвуют те же векторы, но взятые как левая тройка.

Как определить, какую тройку дают базисные векторы? Очень просто, ведь они упорядочены, им присвоены номера 1, 2, 3. Если мы соблюдаем порядок следования векторов, мы получаем тройку, соответствующую используемой системе координат, то есть (1,2,3) — правая тройка.

А если первым мы берем вектор 2? То за ним должен следовать вектор 3, по порядку. А какой следующий? А следующий вектор 1, начинаем всё сначала, но не нарушая порядка следования векторов, то есть и (2,3,1) — правая тройка, ну и (3,1,2) — тоже правая тройка. Говоря языком комбинаторики — базисные векторы в упорядоченной тройке образуют четную перестановку (то есть не нарушающую порядок следования элементов). Если порядок следовая векторов в тройке обратный принятому, то их перестановка будет нечетной. Таким образом перестановки (3,2,1), (2,1,3), (1,3,2) — нечетные, а тройки векторов — левые.

Используя всё вышесказанное, введем функцию

и, на основании (14) и (19) наконец выпишем тензор Леви-Чивиты

для правой системы координат

для левой системы координат.

После этого можно выписать выражение для векторного произведения в тензорном виде

Таким образом — векторное произведение, это свертка диады тензором Леви-Чивиты, дающая на выходе ковектор — то есть вектор, заданный ковариантными компонентами.

4. Смешанное (векторно-скалярное) произведение векторов

Вооружившись полученными знаниями рассмотрим теперь такую операцию

Не оперируя векторами, попробуем сразу записать её в тензорном виде. Во-первых, скалярное произведение коммутативно, поэтому

А теперь вспомним, что скалярное произведение можно расписать как тензорное
произведение ковектора на вектор

Векторное произведение, исходя из (21)как раз и дает ковектор, а значит

То есть, окончательно, смешанное произведение в тензорной форме

где снова участвует тензор Леви-Чивиты.

Выражение (22) можно было получить оперируя векторами, выйдя опять на определение тензора Леви-Чивиты, но, как видно, рациональнее использовать тензорную запись.

5. Ранг тензора. Ковариантные и контравариантные компоненты

Итак, в процессе разбора векторных операций мы пришли к выводу, что тензоры — это математические объекты, обобщающие свойства и операции над многими, известными нам математическими объектами. Тензорами являются и скаляры и векторы. Различаются они рангом и количеством ковариантных и контравариантных компонент. Ранг равен общему числу индексов тензора, а обозначается он парой целых чисел в скобках (p, q), где p — число контравариантных индексов, q — число ковариантных индексов. Говорят что тензор — p-раз контравариантный и q-раз ковариантный, ранга p+q.

1. Тензор ранга (0,0) — это скаляр, величина, значение которой может быть выражено одним числом, со значением инвариантным относительно смены системы координат. У скаляра нет индексов, и он вообще не преобразуется при смене базиса. Но, повторимся, не всякое число есть скаляр. Так например, компонент вектора или тензора не есть скаляр, ибо он изменяется при смене базиса.
2. Тензор ранга (1,0) — вектор. Для вектора естественно контравариантное представление, для вычисления скалярного произведения векторов требуется их свертка с метрическим тензором.

   Преобразование компонент вектора производится путем применения к нему линейного оператора, по сути умножением матрицы преобразования на столбец, содержащий компоненты вектора, что в тензорной форме выглядит как

   

3. Тензор ранга (0,1) — ковектор. Если в рассматриваемом пространстве определен невырожденный метрический тензор

   

   то вектор и ковектор — это два разных представления одного и того же геометрического объекта — вектора. В ортогональном базисе (векторы которого взаимно перпендикулярны) контравариантные и ковариантные координаты cовпадают. Переход от одного представления к другому производится сверткой с метрическим тензором

   

   где контрвариантный метрический тензор, компоненты которого — матрица,
   обратная матрице компонент тензора .

   Для скалярного умножения ковектора на вектор не нужно использовать метрический тензор, оно производится прямой сверткой с вектором.

   

   Преобразование компонент ковектора так же производится путем применения к нему линейного оператора, но в отличие от вектора, производится умножение строки, содержащей компоненты ковектора на матрицу преобразования координат

   

4. Тензор ранга (0,2) — билинейная форма, примером которой может служить дважды ковариантный метрический тензор g_ij. Компоненты метрического тензора преобразуются путем двукратного применения к нему линейного оператора преобразования координат, что соответствует умножению транспонированной матрицы преобразования на матрицу метрического тензора и последующему умножению результата на матрицу преобразования

   

5. Тензор ранга (2,0) — примером может служить диада (8). Вообще, все тензоры рангов (k,0) называются поливекторами или полиадами (триады, тетрады и т.д.), и образованы они как линейные комбинации тензорных произведений соответствующего количества векторов. Их компоненты преобразуются соответствующим рангу количеством применения линейных
   операторов, преобразующих исходные векторы.
6. Тензор ранга (1,1) — линейный оператор. Примером может служить матрица поворота или любого другого преобразования координат векторов и ковекторов. Вообще, применение линейного оператора сводится к операции матричного умножения

   

   где — результат преобразования; — исходный вектор; — компоненты матрицы линейного оператора. Рассмотрим процесс преобразования линейного оператора. Пусть S матрица перехода от одно базиса к другому. Тогда, при смене базиса преобразуются оба вектора — и аргумент и результат

   

   Подставляя (24) в (23) получаем

   

   откуда, умножая слева на матрицу получаем

   

   где — компоненты матрицы . С другой стороны, для векторов в новом базисе справедливо

   

   сравнивая (25) и (26), получаем выражение преобразования линейного оператора

   

   Все перечисленные объекты обладают общностью свойств: имеют набор компонент и правило преобразования при смене базиса.

Выводы

Подведем некоторые итоги.

Во-первых, мы выяснили, что векторные операции могут быть сведены к тензорным соотношениям, что избавляет нас от неудобства каждый раз выводить формулы для них при использовании экзотической системы координат или увеличении размерности пространства. Соотношения останутся прежними, изменится только внутренность тензоров, связанных с геометрией пространства и выбором положительного направления вращения в нем. Учитывая, что многие уравнения физики, математики и механики оперируют векторными величинами, использование тензоров позволяет записать уравнения лишь однажды. Кроме того, тензорная запись компактна — это упрощает проведение выкладок.

Во-вторых, мы понимаем, что многие математические объекты — скаляры, векторы, билинейные формы, линейные операторы — всё это частные случаи тензоров, а значит их свойства могут быть обобщены под могучим крылом своего более сложного собрата-тензора.

В дальнейшем мы увидим, как тензорная запись позволяет подходить к весьма прозаичным вопросам с общих позиций, облегчая жизнь исследователю.

Продолжение следует…

Макеты страниц

21

Лекция
№3

Основные алгебраические операции над тензорами План

1. Линейные
   операции над тензорами, разложение по
   тензорным базисам.

2. Скалярное произведение тензоров одинаковых и различных рангов, свойства скалярного умножения, единичный тензор.

3. Тензор как линейный оператор, транспонированный тензор как сопряжённый оператор.

4. Билинейные и квадратичные формы симметричных тензоров.

1. Линейные операции над тензорами.

Рассматриваются две основные линейные
операции – умножение тензоров на числа
и сложение (вычитание) тензоров.

Умножение
на число

определяется как операция, при которой
каждая из компонент тензора умножается
на это число. Из определения следует,
что данная операция инвариантна
относительно изменения базиса. В
результате данной операции ранг тензора
не изменяется.

Для тензоров
одинакового ранга вводится операция
сложения (вычитания).

Тензор

называется суммой (разностью) тензоров

и

,
если его компоненты в некотором базисе
равны сумме (разности) соответствующих
(отнесённых к одной и той же базисной
полиаде) компонент слагаемых тензоров.
Например, для тензоров 2-го ранга,
отнесённых к взаимному базису, связь
между компонентами имеет следующий
вид:

.

В инвариантной
записи операция сложения определяется
по формуле:

(3.1)

Очевидно, что
операция сложения инвариантна относительно
вектора базиса.

Наряду
с операцией сложения тензоров рассмотрим
операцию разложения по тензорным
базисам. Ограничимся случаем тензоров
2-го ранга. Определим тензорный базис в

:
совокупность тензоров

,
где n
9,
образует базис, если

,
не равных одновременно нулю выполняется
следующее условие:

(3.2)

Множество
тензоров

,
представляемое в виде

,
n
9 (3.3)

образует
n-мерное
тензорное подпространство

.
Здесь

–
компоненты тензора

.

Отметим,
что в

базис полного пространства тензоров
2-го ранга состоит по определению из
девяти базисных диад –

.
Выражение (3.3) назовём разложением
тензора

по тензорному базису.

1. Скалярное умножение тензоров.

Ранее была введена операция скалярного
умножения диад и полиад на вектор.
Рассмотрим операцию скалярного умножения
тензора на вектор. Пусть дан тензор 2-го
ранга

(3.4)

Вводятся
операции скалярного умножения тензора

на вектор

слева и справа. При правом умножении
компоненты вектора

скалярно умножаются
на правые векторы базисных диад, входящих
в сумму (3.4). Результат правого умножения
имеет вид

(3.5)

Можно показать,
что правая часть (3.5) есть вектор.
Аналогичным образом определяется
операция левого умножения

(3.6)

Из
определений (3.5) и (3.6) следует, что векторы

и

в общем случае различны.

Отметим,
что при скалярном умножении (3.5) и (3.6)
перемножаются тензоры различных рангов,
так как вектор есть тензор 1-го ранга.
Операция скалярного умножения тензора
ранга m
на вектор определяется указанием номера
векторов в базисных диадах, на которые
скалярно умножаются вектора

.
Результат скалярного умножения тензора
ранга m
на вектор есть тензор ранга m-1.

Определим
операцию скалярного умножения тензоров
2-го ранга. Будем называть тензор

скалярным произведением тензора

на тензор

,
если смешанные компоненты

определяются следующими выражениями:

; (3.7)

; (3.8)

В
диадном базисе представление (3.7)
получается при скалярном умножении
правых векторов взаимного диадного
базиса тензора

с базисными векторами тензора

(3.9)

Представлению
(3.8) соответствует скалярное умножение
правых векторов ковариантного базиса

и левых векторов контравариантного
базиса

,
тогда

(3.10)

Отметим,
что представление одного из сомножителей
в ковариантном, а другого в контравариантном
базисах диктует простой способ записи
конечного результата, так как

.
В общем случае можно относить перемножаемые
тензоры и к другим базисам (основному,
взаимному, смешанному), естественно,
что результат при этом не изменяется.
Например, относя оба вектора к основному
базису, получим

(3.11)

Запись (3.11), в
отличие от (3.9) и (3.10) включает компоненты
метрического тензора.

Основным свойством
скалярного умножения тензоров является
его некоммутативность. То есть в общем
случае

. (3.12)

Условие
некоммутативности (3.12) получается
непосредственно из сравнения компонент
произведения. В частности, из (3.9) следует,
что

.

Фундаментальную
роль играет единичный тензор 2-го ранга
–

,
который определяется из условия

(3.13)

Покажем,
что единичный тензор совпадает с
метрическим тензором. Представим тензоры

и

в смешанных базисах разложениями

;

. (3.14)

Используя (3.14),
условие (3.13) приводит к следующим
уравнениям:

(3.15)

Система (3.15)
тождественно удовлетворяется, если

.

Таким образом, в
смешанном базисе единичный тензор
представляется единичной матрицей и
его диадное разложение имеет вид

(3.16)

Переходя на
основании формул (1.7) и (1.8) к основному
и взаимному базисам, получим

(3.17)

Из (3.17) следует,
что единичный тензор совпадает с
метрическим.

Непосредственной
проверкой убеждаемся, что операция
скалярного произведения ассоциативна
и поэтому имеют место следующие выражения:

,

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Магия тензорной алгебры: Часть 2 — Векторные и тензорные операции. Ранги тензоров +33

Математика

---

Рекомендация: подборка платных и бесплатных курсов PR-менеджеров – https://katalog-kursov.ru/

Содержание

1. Что такое тензор и для чего он нужен?
2. Векторные и тензорные операции. Ранги тензоров
3. Криволинейные координаты
4. Динамика точки в тензорном изложении
5. Действия над тензорами и некоторые другие теоретические вопросы
6. Кинематика свободного твердого тела. Природа угловой скорости
7. Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
8. О свертках тензора Леви-Чивиты
9. Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
10. Получаем вектор угловой скорости. Работаем над недочетами
11. Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
12. Параметры Родрига-Гамильтона в кинематике твердого тела
13. СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
14. Нестандартное введение в динамику твердого тела
15. Движение несвободного твердого тела

Введение

Несказанно рад, что читателям понравилась предыдущая статья. Сразу сделаю оговорку — просто рассказать о таком ёмком понятии как тензор не получится — велик объем информации. Могу обещать, что к концу цикла мозаика сложится.

А в прошлый раз мы остановились на том, что рассмотрев представление вектора в косоугольном базисе, и определив, что он представляется двумя разными (ковариантными и контравариантными) наборами координат, получили общие выражения для скалярного произведения, учитывающие изменение метрики пространства. Таким образом, мы весьма осторожно подошли к понятию тензора

Тензор — математический объект, не изменяющийся при изменении системы координат, представленный набором своих компонент и правилом преобразования компонент при смене базиса.

Скалярное произведение — это хорошо. Но как же быть с остальными операциями? Как они связываются с геометрией пространства и представимы ли в тензорном виде? Разумеется представимы, ведь векторы — это… тензоры! И скаляры — это тоже тензоры. Привычные нам математические объекты лишь частные примеры более общего понятия, коим является тензор.

Вот об этом мы и поговорим под катом.

1. Геометрический смысл метрического тензора

Для наглядности, которая не слишком повлияет на общность рассуждений, ограничимся трехмерным пространством. Докажем следующее утверждение — определитель метрического тензора равен квадрату объема параллелепипеда, натянутого на векторы базиса.

Рис. 1. Соотношения в трехгранном угле, образованном базисом

Рассмотрим произвольный базис . Будем считать, что нам заданы длины его векторов и углы между парами векторов . Векторы базиса образуют трехгранный угол OABD, и углы между векторами являются его линейными углами, в углы между плоскостями, в которых лежат пары векторов будут его двугранными углами (рисунок 1). Будем считать, что углы между векторами удовлетворяют условию .

Вычислим объем параллелепипеда, натянутого на базис так, как это принято в стереометрии

где S — площадь основания параллелепипеда; h — высота, проведенная к данному основанию.

Площадь основания вычисляется тривиально — как модуль векторного произведения

С определением высоты придется повозится. Если бы мы знали угол , то легко нашли бы высоту

Угол связан с линейными и двугранными углами трехгранного угла

— первая теорема косинусов для трехгранного угла. Из нее выражаем косинус двугранного угла

Квадрат синуса необходимого нам угла выражаем через полученный косинус

Выполняем последовательные подстановки от (6) до (2), не забывая возвести в квадрат площадь S и высоту h. Выкладки достаточно громоздкие и для их выполнения можно воспользоваться СКА (Maple или Mathematica) и получить квадрат объема параллелепипеда

Теперь вычислим определитель метрического тензора. Им называется определитель матрицы, которая составлена из компонентов тензора. Входящие в нее скалярные произведения векторов базиса выпишем в явном виде

Вычислив его, получим тот же результат, что и для квадрата объема

Таким образом, утверждение (1) верно. Соответственно, объем параллелепипеда, натянутого на базис можно получить извлечением корня из определителя метрического тензора

где для краткости обозначим значение определителя.

Корень (7) часто встречается в литературе по ОТО и альтернативным теориям гравитации типа РТГ. Эта величина имеет фундаментальное значение и пригодится нам чуть позже.

Обратим внимание на выражение скалятного произведения

Величину

называют тензорным произведением двух векторов или диадой. Тензорным это произведение названо потому что перемножаются тензоры и на выходе получается тензор, в данном случае второго ранга, . Ранг тензора — это количество его индексов. Вектор, внезапно, тоже является тензором, только первого ранга. Да это и понятно — ведь вектор, как геометрическая сущность, не зависит от системы координат, в которой его рассматривают. От выбора системы координат зависят лишь его компоненты.

Тензор второго ранга (8), разумеется, представлен матрицей своих компонент

Используя (8) можно переписать скалярное произведение в виде

это тоже тензорное произведение, называемое сверткой из-за того, что приводит к уменьшению ранга результирующего тензора. Все индексы в (10) «немые», по ним производится двойное суммирование компонент метрического тензора и диады и на выходе получатся число c.

Внимательный читатель скажет, что на выходе должен получится тензор. Так тензор и получается — скаляр, это тоже тензор. Нулевого ранга, так как не имеет индексов и не подлежит преобразованию при смене базиса. Скалярное произведение инвариантно относительно смены базиса, ибо ни длина участвующих в нем векторов ни угол между ними от смены базиса не меняются. Значит скаляр — это тензор нулевого ранга.

Но не любое число есть скаляр. Скаляр — это длина вектора, скалярное произведение векторов, масса материального тела, абсолютная температура и прочие величины, не зависящие от системы координат. Компонента вектора уже не является скаляром — она меняется при смене базиса.

О ранге тензоров и типе из компонент мы поговорим чуть позже, а пока перейдем к следующему животрепещущему вопросу.

3. Векторное произведение. Тензор Леви-Чивиты

Вернемся к нашим векторам и выполним их векторное умножение

За неимением других вариантов, аккуратно раскроем скобки, помня о некоммутативности операции

Разумеется мы хорошо учились в университете и знаем, что векторное произведение вектора самого на себя равно нулю. Но мы не будем сильно спешить с упрощением, ибо кроме этого, несомненно приятного факта, мы видим ещё одну вешь — компоненты диады (9). Но кроме упрощения связанного с нулевым произведением коллинеарных векторов мы больше ничего не наблюдаем. Мы работаем с произвольным базисом в чистом виде.

Применим хитрость — умножим вектор скалярно на первый вектор базиса учтя теперь, что произведения

Коэффициенты в квадратных скобках — смешанные произведения векторов. Если векторы компланарны (лежат в одной плоскости) то такое произведение равно нулю. То есть, если в смешанном произведении повторяется хотя бы один вектор, оно равно нулю. Значит у нас остается только два слагаемых из девяти, в которых не повторяются векторы при смешанном умножении

Так, а теперь вспоминаем, что — ковариантная компонента вектора . Ну и наконец переставим векторы в векторном произведении первого слагаемого, добавив минус как и положено по правилу векторного произведения

Аналогичным образом выделяем остальные компоненты

Выражения (11) — (13) очень напоминают формулы для расчета проекций векторного произведения из курса векторной алгебры, с точностью до множителя со смешанным произведением. Но мы-то работаем не в декартовом базисе, естественно ожидать некоторое отличие. Кстати, а что это за множитель? Ведь смешанное произведение векторов имеет геометрический смысл… Это же… объем параллелепипеда, натянутого на векторы в нем участвующие. А объем параллелепипеда, натянутого на базис это ведь корень из определителя метрического тензора! То есть

Вот она и всплыла на поверхность, метрика используемого пространства. Таким образом, можно построить некий тензор, свертка исходных векторов с которым дает ковариантный вектор, являющийся результатом векторного произведения. Более того, этот тензор связан с метрическим тензором. Таковой тензор третьего ранга носит имя итальянского математика Леви-Чивиты.

Не трудно увидеть, что компоненты тензора Леви-Чивиты определяются соотношением

Их будет 27, но большинство из них, а именно 21 равны нулю. Это те компоненты, индексы которых повторяются хотя бы один раз. Ненулевых компоненты только шесть, они соответствуют не повторяющимся индексам. По модулю они равны , но три из них положительны, другие три отрицательны. В формулах (11) — (13) мы переставили векторы местами и добавили минусы, чтобы сделать коэффициенты при диадах положительными а сами формулы похожими на привычные нам по курсу векторной алгебры. Теперь вернем всё на свои места

Знак смешанных произведений зависит от порядка индексов: в наборах (1,2,3), (2,3,1), (3,1,2) они положительны, в наборах (1,3,2), (2,1,3) и (3,2,1) — отрицательны. Известно, что если векторы заданы в правой системе координат, то их смешанное произведение будет положительно, если они образуют правую тройку векторов. В первых слагаемых (16) — (18) фигурируют правые тройки векторов базиса. Во вторых слагаемых, в смешанном произведении участвуют те же векторы, но взятые как левая тройка.

Как определить, какую тройку дают базисные векторы? Очень просто, ведь они упорядочены, им присвоены номера 1, 2, 3. Если мы соблюдаем порядок следования векторов, мы получаем тройку, соответствующую используемой системе координат, то есть (1,2,3) — правая тройка.

А если первым мы берем вектор 2? То за ним должен следовать вектор 3, по порядку. А какой следующий? А следующий вектор 1, начинаем всё сначала, но не нарушая порядка следования векторов, то есть и (2,3,1) — правая тройка, ну и (3,1,2) — тоже правая тройка. Говоря языком комбинаторики — базисные векторы в упорядоченной тройке образуют четную перестановку (то есть не нарушающую порядок следования элементов). Если порядок следовая векторов в тройке обратный принятому, то их перестановка будет нечетной. Таким образом перестановки (3,2,1), (2,1,3), (1,3,2) — нечетные, а тройки векторов — левые.

Используя всё вышесказанное, введем функцию

и, на основании (14) и (19) наконец выпишем тензор Леви-Чивиты

для правой системы координат

для левой системы координат.

После этого можно выписать выражение для векторного произведения в тензорном виде

Таким образом — векторное произведение, это свертка диады тензором Леви-Чивиты, дающая на выходе ковектор — то есть вектор, заданный ковариантными компонентами.

4. Смешанное (векторно-скалярное) произведение векторов

Вооружившись полученными знаниями рассмотрим теперь такую операцию

Не оперируя векторами, попробуем сразу записать её в тензорном виде. Во-первых, скалярное произведение коммутативно, поэтому

А теперь вспомним, что скалярное произведение можно расписать как тензорное
произведение ковектора на вектор

Векторное произведение, исходя из (21)как раз и дает ковектор, а значит

То есть, окончательно, смешанное произведение в тензорной форме

где снова участвует тензор Леви-Чивиты.

Выражение (22) можно было получить оперируя векторами, выйдя опять на определение тензора Леви-Чивиты, но, как видно, рациональнее использовать тензорную запись.

5. Ранг тензора. Ковариантные и контравариантные компоненты

Итак, в процессе разбора векторных операций мы пришли к выводу, что тензоры — это математические объекты, обобщающие свойства и операции над многими, известными нам математическими объектами. Тензорами являются и скаляры и векторы. Различаются они рангом и количеством ковариантных и контравариантных компонент. Ранг равен общему числу индексов тензора, а обозначается он парой целых чисел в скобках (p, q), где p — число контравариантных индексов, q — число ковариантных индексов. Говорят что тензор — p-раз контравариантный и q-раз ковариантный, ранга p+q.

1. Тензор ранга (0,0) — это скаляр, величина, значение которой может быть выражено одним числом, со значением инвариантным относительно смены системы координат. У скаляра нет индексов, и он вообще не преобразуется при смене базиса. Но, повторимся, не всякое число есть скаляр. Так например, компонент вектора или тензора не есть скаляр, ибо он изменяется при смене базиса.
2. Тензор ранга (1,0) — вектор. Для вектора естественно контравариантное представление, для вычисления скалярного произведения векторов требуется их свертка с метрическим тензором.

   Преобразование компонент вектора производится путем применения к нему линейного оператора, по сути умножением матрицы преобразования на столбец, содержащий компоненты вектора, что в тензорной форме выглядит как

   

3. Тензор ранга (0,1) — ковектор. Если в рассматриваемом пространстве определен невырожденный метрический тензор

   

   то вектор и ковектор — это два разных представления одного и того же геометрического объекта — вектора. В ортогональном базисе (векторы которого взаимно перпендикулярны) контравариантные и ковариантные координаты cовпадают. Переход от одного представления к другому производится сверткой с метрическим тензором

   

   где контрвариантный метрический тензор, компоненты которого — матрица,
   обратная матрице компонент тензора.

   Для скалярного умножения ковектора на вектор не нужно использовать метрический тензор, оно производится прямой сверткой с вектором.

   

   Преобразование компонент ковектора так же производится путем применения к нему линейного оператора, но в отличие от вектора, производится умножение строки, содержащей компоненты ковектора на матрицу преобразования координат

   

4. Тензор ранга (0,2) — билинейная форма, примером которой может служить дважды ковариантный метрический тензор g_ij. Компоненты метрического тензора преобразуются путем двукратного применения к нему линейного оператора преобразования координат, что соответствует умножению транспонированной матрицы преобразования на матрицу метрического тензора и последующему умножению результата на матрицу преобразования

   

5. Тензор ранга (2,0) — примером может служить диада (8). Вообще, все тензоры рангов (k,0) называются поливекторами или полиадами (триады, тетрады и т.д.), и образованы они как линейные комбинации тензорных произведений соответствующего количества векторов. Их компоненты преобразуются соответствующим рангу количеством применения линейных
   операторов, преобразующих исходные векторы.
6. Тензор ранга (1,1) — линейный оператор. Примером может служить матрица поворота или любого другого преобразования координат векторов и ковекторов. Вообще, применение линейного оператора сводится к операции матричного умножения

   

   где — результат преобразования; — исходный вектор; — компоненты матрицы линейного оператора. Рассмотрим процесс преобразования линейного оператора. Пусть S матрица перехода от одно базиса к другому. Тогда, при смене базиса преобразуются оба вектора — и аргумент и результат

   

   Подставляя (24) в (23) получаем

   

   откуда, умножая слева на матрицу получаем

   

   где — компоненты матрицы . С другой стороны, для векторов в новом базисе справедливо

   

   сравнивая (25) и (26), получаем выражение преобразования линейного оператора

   

Все перечисленные объекты обладают общностью свойств: имеют набор компонент и правило преобразования при смене базиса.

Выводы

Подведем некоторые итоги.

Во-первых, мы выяснили, что векторные операции могут быть сведены к тензорным соотношениям, что избавляет нас от неудобства каждый раз выводить формулы для них при использовании экзотической системы координат или увеличении размерности пространства. Соотношения останутся прежними, изменится только внутренность тензоров, связанных с геометрией пространства и выбором положительного направления вращения в нем. Учитывая, что многие уравнения физики, математики и механики оперируют векторными величинами, использование тензоров позволяет записать уравнения лишь однажды. Кроме того, тензорная запись компактна — это упрощает проведение выкладок.

Во-вторых, мы понимаем, что многие математические объекты — скаляры, векторы, билинейные формы, линейные операторы — всё это частные случаи тензоров, а значит их свойства могут быть обобщены под могучим крылом своего более сложного собрата-тензора.

В дальнейшем мы увидим, как тензорная запись позволяет подходить к весьма прозаичным вопросам с общих позиций, облегчая жизнь исследователю.

Продолжение следует…