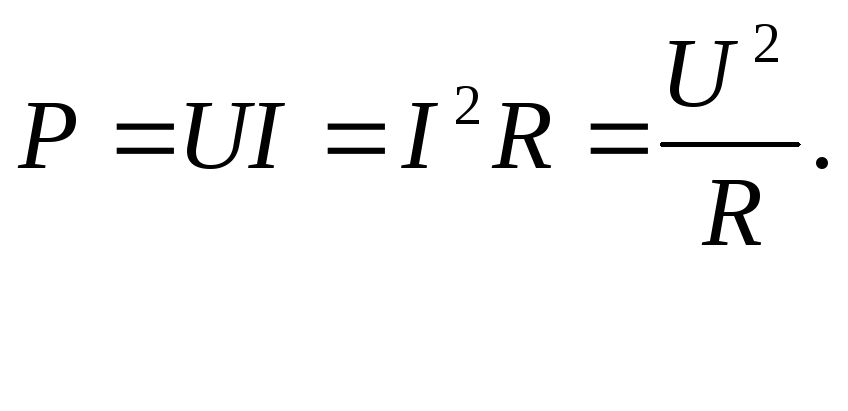Как найти расход электрической энергии цепью

Расчет электрической цепи

Задача 1

От источника постоянного тока получает питание
цепь, состоящая их ряда сопротивлений, включенных смешанно, величины которых
известны. Э.Д.С. источника – Е, внутреннее сопротивление – R₀.

Начертить схему цепи и определить:

1.   эквивалентное сопротивление цепи.

2.      токи и напряжения на каждом
сопротивлении схемы.

.        расход энергии цепью за время t
= 10ч.

Решение проверить составлением баланса
мощностей.

Е, В	100
R0, Ом	0,2
R1, Ом	10
R2, Ом	1
R3, Ом	9
R4, Ом	3
R5, Ом	20
R6, Ом	5
R7, Ом	12
R8, Ом	4
R9, Ом	3
R10,Ом	6

Решение:

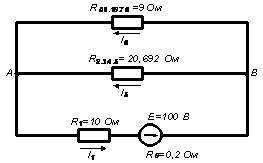
1.      Начертим
схему цепи, обозначим токи и узлы.

2.      Определим
эквивалентное сопротивление цепи Rэкв:

Цепь имеет смешанное соединение.

3.      Начнем
с участка АСВ:

участок АСВ состоит из двух участков: АС и СВ
соединенных последовательно;

на участке АС сопротивления R₂,
R₃
и R₃
включены параллельно, сопротивление R₂₃₄:

;  Ом;

участок АСВ имеет последовательное соединение,
сопротивление на участке АСВ:

 Ом;

4.      Участок
AEDB:

участок ED
имеет параллельное соединение резисторов  и
;

 Ом;

участок АED
имеет последовательное соединение, сопротивление на участке АED:

 Ом;

участок AD
имеет параллельное соединение резисторов  и
;

 Ом;

участок АEDB
имеет последовательное соединение, сопротивление на участке АEDB:

 Ом;

Схема приобретает вид:

5.      Участок
AB:

участок АВ имеет параллельное соединение:

 Ом;

Схема приобретает вид:

6.      Общее
сопротивление цепи :

 Ом;

Схема приобретает вид:

7.      По
закону Ома для замкнутой цепи определим ток I₁:

 А;

8.      По
закону Ома для участка цепи определим напряжение на резисторе R₁:

 В;

9.      Определим
напряжение приложенное к цепи:

сумма падений напряжения на внутреннем
сопротивлении источника тока и на внешней цепи равна ЭДС источника:

;

отсюда:

 В;

10.    По
закону Ома для участка цепи определим напряжение на резисторе :

 В;

11.    Определим
токи  и
:

 А;

 А;

12.    По
первому закону Кирхгофа сделаем проверку в узле А:

 А;

Токи определили верно.

13.    По
закону Ома для участка цепи определим напряжение на резисторе :

 В;

14.    По
закону Ома для участка цепи определим напряжение на резисторе :

 В;

так как резисторы  включены
параллельно, то напряжения приложенные к каждому из них будут одинаковыми:

 В;

15.    Определим
токи ,
:

 А;

 А;

 А;

16.    По
закону Ома для участка цепи определим напряжение на резисторе :

 В;

17.    По
закону Ома для участка цепи определим напряжение на резисторе :

 В;

18.    По
закону Ома для участка цепи определим ток на резисторе :

 А;

19.    По
первому закону Кирхгофа определим ток I₈
из
узла А:

 А;

20.    По
закону Ома для участка цепи определим напряжение на резисторе :

 В;

21.    По
закону Ома для участка цепи определим напряжение на резисторе :

В;

22.    По
закону Ома для участка цепи определим ток на резисторе :

 А;

23.    По
закону Ома для участка цепи определим ток на резисторе :

А;

24.    Определим
расход энергии цепью за время t
= 10ч:

Рассчитаем мощность, потребляемую всей цепью:

 Вт;

Расход энергии за 10 часов работы равен:

 Вт∙час;

25.    Для
проверки решения составим уравнение баланса мощностей:

;

Вт;

1,621 Вт;

Вт;

 Вт;

 Вт;

 Вт;

 Вт;

 Вт;

 Вт;

Вт;

;

,631≈ 599,601;

Неточность допущена при округлениях в расчетах.
Задача решена верно.

Задача 2

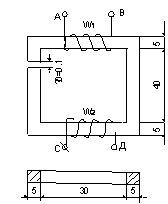
Магнитная цепь, схема которой приведена на
рис.2, состоит из двух вертикальных стержней и двух горизонтальных ярем.
Размеры цепи заданы в сантиметрах. В магнитной цепи предусмотрен зазор 0,1 см.
На ярмах расположены обмотки с числом витков W₁и
W₂.
Зажимы обмоток А, В, С и Д соединены так, как указано в таблице вариантов, при
этом получается согласное или встречное соединение обмоток, что следует
студенту определить самостоятельно.

Найти:

) необходимую силу тока для получения в
сердечнике заданного магнитного потока Ф (или магнитной индукции В);

) абсолютную магнитную проницаемость и магнитную
проницаемость на участке, где расположены обмотки;

)потокосцепление и индуктивность обмоток;

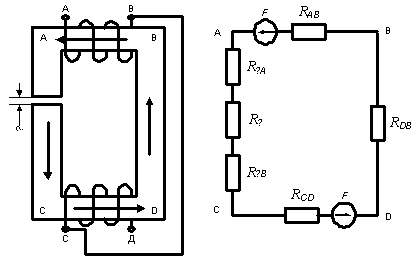
Начертить схему магнитной цепи для своего
варианта.

Магнитный поток, В    –

Магнитная индукция,
Тл      0,8

W₁             200

W₂             900

Обозначения величин

Материал стержней     Чугун

Материал ярем            Э11

Какие зажимы
обмоток соединены вместе – В, С

Индукция, В	Напряженность магнитного поля, А/м
Т	Гс	Электротехническая сталь	Литая сталь	Чугун
		Э 11	Э 42
0,25	2 500	100	25	200	1 050
0,3	3 000	113	29	240	1 220
0,35	3 500	126	33	280	1 430
0,4	4 000	140	37	320	1 640
0,45	4 500	155	42	360	1 910
0,5	5 000	171	48	400	2 200
0,55	5 500	190	55	443	2 550
0,6	6 000	211	63	488	2 940
0,65	6 500	236	73	535	3 420
0,7	7 000	261	84	584	3 920
0,75	7 500	287	96	632	4 600
0,8	8 000	318	110	682	5 400
0,85	8 500	352	125	745	6 300
0,9	9 000	397	140	798	7 360
0,95	9 500	447	160	860	8 600
1,0	10 000	502	185	924	10 100
1,1	11 000	647	260	1 090	14 000
1,2	12 000	843	380	1 290	19 200
1,3	13 000	1 140	680	1 590	26 200
1,4	14 000	1 580	1 450	2 090	34 800
1,5	15 000	2 200	3 100	2 890	47 800
1,6	16 000	4 370	5 600	4 100	–
1,7	17 000	7 780	9 500	–	–
1,8	18 000	12 800	14 600	–	–

Дано:

Магнитная индукция – В = 0,8 Тл

W₁ = 200

W₂
= 900

материал стержней: чугун

материал ярем: Э11

соединены вместе зажимы В, С

Решение:

1.      Размеры магнитопровода по средней
магнитной линии:

Т.к. площадь сечения во всей магнитной цепи
одинаково, то в качестве длины цепи принимаем длину средней магнитной линии
потока. (Среднеарифметическое между наружным и внутренним периметром магнитной
цепи минус воздушный зазор) l = 159,9 см;

длина воздушного зазора l₀ = 0,1 см;

Толщина сердечника 50 мм.

S = 5 ∙ 5 = 25
см² = 25 ∙ 10^-4 м²;

S₀
= 5 ∙ 5 = 25 см² = 25 ∙ 10^-4 м²;

2. Соединение обмоток – согласованное.

.   Магнитный поток в данном магнитопроводе:

Ф = В · S = 0,8 · 25 · 10^-4
= 20 · 10^-4 Вб.

4. Магнитная индукция и воздушном зазоре В₀
= В = 0,8 Тл, т.к. S=S₀.

.   Напряженность магнитного поля для участка из
чугуна находим по табл.2.1: при В = 0,8 Т Н_ч = 54 А/см;

.   Напряженность магнитного поля для участка из
электротехнической стали Э11 находим по табл.2.1: при В = 0,8 Т Н = 3,18 А/см;

.   Напряженность магнитного поля в воздушном
зазоре находим по формуле:

Н₀ = 0,8 ∙ В ∙ 10⁴
= 0,8 ∙ 0,8 ∙ 10⁴ = 6400 М/см

8.      По закону полного тока  находим
ток в обмотках:

А;

.        Определим магнитную проницаемость по
формуле

= μ∙Н

μ = В/Н = 0,8/54 =
0,0148 ;

.        Абсолютная магнитная проницаемость:

μ_а
= В/µ₀ Н = 0,8/1,256·10^-6 ·54 = 0,0118 ·10⁶ ;

.        Относительная магнитная проницаемость:

μ_r
= µ/µ₀ = 0,0148 /0,0118 ·10⁶ = 1,254·10^-6 ;

12.    Определим потокосцепление и индуктивность
обмоток:

Ψ₁
= W∙Ф = 200 ∙ 20 ·
10^-4 = 0,4;

Ψ₁
= W∙Ф = 900 ∙ 20 ·
10^-4 = 1,8;

.        Определим индуктивность обмоток:

L=Ф/I;

L = 20 · 10^-4/3,816
= 5,241· 10^-4 Гн;

Схема магнитной цепи:

Задача 3

К зажимам цепи однофазного переменного тока
приложено напряжение U
(рис. схема а, б). Величины сопротивлений цепи R₁,
R₂,
X_L1,
X_L2,
X_C1,
X_C2 приведены
в таблице вариантов. Начертить схему для своего варианта и определить:

) токи в цепи;

) коэффициент мощности (cosφ)
цепи;

) активную Р, реактивную Q,
полную S мощности цепи,
потребляемые цепью;

) построить в масштабе векторную диаграмму.

Обозначения величин U,
В 36

Схема цепи а

Обозначения величин

R₁,
Ом –

R₂,
Ом 5

X_L1,
Ом 2

X_L2,
Ом –

X_C1,
Ом 4

Схема цепи а).

Решение:

.        Начертим схему цепи:

2.      Определим полное сопротивление цепи Z:

;

X_С
= X_С1
+ X_С2
= 4 + 3 = 7 Ом – арифметическая сумма однотипных индуктивного и емкостного
сопротивлений;

 Ом;

2.      По закону Ома для цепи переменного тока
определим ток цепи I:

= U / Z = 36/7,07= 5,09А;

3.      Из треугольника сопротивлений определим
угол φ:

; угол составит 45º;

4.      Полная мощность цепи:

S = U
∙
I = 36 ∙ 5,09
= 183,24 ВА;

5.      По формуле P
= S ·
Cos φ определим
активную мощность цепи:

Р = 183,24 · 0,707 = 129,55 Вт;

6.      Из формулы треугольника мощностей
определим реактивную мощность Q:

 Вар;

7.      Построение векторной диаграммы:

8.      При построении векторной диаграммы
исходим из следующих условий: Ток одинаков для любого участка цепи, так как
разветлений нет; На каждом сопротивлении при
прохождении тока создается падение напряжения, значение которого определяем по
закону Ома для участка цепи;

9.  Задаемся масштабом: m_u= 4 в/см; m_I=
1А/см;

Для построения векторов напряжений определим
напряжения на активном и индуктивном сопротивлениях:

U_R2 = I ·R₂ = 5,09
· 5 = 25,45 В;_XL1 = I ·X_L1 = 5,09 · 2 = 10,18 В;_XС1 =
I ·X_С1 = 5,09 · 4 = 20,36 В;_XC2 =
I ·X_L2 = 5,09 · 3 = 15,27 В

Определим длины векторов:

_UR2 =
U_R2/m_u = 25,45 /4 = 6,36 см;_UL1 = U_XL1/m_u
= 10,18 /4 = 2,54 см;_UС1 = U_XC1/m_u = 20,36 /4
= 5,09 см;_UC2 = U_XC2/m_u = 15,27 /4 = 3,82 см;_I
= I/m_I = 5,09 /1 = 5,09 см;

Задача 4

электрический магнитный цепь
выпрямитель

В четырехпроводную трехфазную линию с линейным
напряжением U_л
включается треугольником или звездой (согласно варианту) потребитель, в фазах
которого соединяются последовательно активные, индуктивные и емкостные
сопротивления в соответствии с таблицей вариантов. Начертить схему включения
потребителя для своего варианта и определить:

) фазные и линейные токи;

) углы сдвига фаз в каждой фазе;

) построить в масштабе векторную диаграмму и с
ее помощью определить величину тока в нулевом проводе («звезда»), либо линейные
токи («треугольник»);

) определить активную, реактивную и полную
мощности всей цепи.

U_л
= 127 В;

соединение треугольник;

фаза АВ

R = 6 Ом;

X_С
= 8 Ом;

фаза СА

R = 7 Ом;

X_С
= 6 Ом;

фаза ВС

X_С
= 15 Ом;

Решение:

.        При соединении треугольником фазное напряжение
равно линейному, т. е. U_ф
=
U_л =
127 В;

.        Определим полное сопротивление в фазе
СА:

;

 Ом;

3.      Определим ток в фазе СА:

I_CA = U/
Z = 127/9,22
= 13,77 A;

.        Определим полное сопротивление в фазе
АВ:

;

 Ом;

5.      Определим ток в фазе АВ:

I_AB = U/
Z = 127/10
= 12,7 A;

.        Определим полное сопротивление в фазе
ВС:

;

 Ом;

7.      Определим ток в фазе ВС:

I_BC
= U/ Z
= 127/15 = 8,47 A;

.        Определим углы сдвига фаз в каждой
фазе:

в фазе СА:

: угол 40,6º;

в фазе АВ:

; угол 66,4º;

в фазе ВС:

; угол 90º;

9.      определим активную, реактивную и полную
мощности всей цепи:

в фазе СА:

 ВА;

P = S ·
Cos φ;
P = ·
0,759 = 1327,33 Вт:

 Вар;

в фазе АВ:

 ВА;=
S ·
Cos φ;
P =  ·
0,4 = 645,16 Вт:

 Вар;

в фазе ВС:

 ВА;=
S ·
Cos φ;
P = ·
0 = 0 Вт:

 Вар;

Полная мощность всей цепи S:

S =  ВА;

Активная мощность всей цепи Р:

Р = 1327,33 + 645,16 + 0 = 1972,49 Вт;

Реактивная мощность всей цепи Q:

Q =  +
 +
 =
3692,55
Вар;

.        Построение векторной диаграммы:

Задаемся масштабом: по току М_I=2
А/см; по напряжению М_U=20
В/см.

Длина векторов фазных (линейных) напряжений:

L_Uф=

Длина векторов фазных токов:

L_СА=

L_АВ=

L_BС=

При построении векторной диаграммы вначале
откладываем три вектора фазных (линейных) напряжений с углом сдвига фаз
относительно друг друга 120°. Векторы фазных токов отстают от вектора фазных
напряжений, т. к. нагрузка емкостная. В фазе АВ на угол φ=66,4°,
в фазе СА на угол φ=40,6°, в
фазе ВС на угол φ=90°.
Векторы
линейных токов являются геометрической разностью векторов соответствующих
фазных токов:

= –
;
=
–
;
=
–
;

.        По векторной диаграмме определим
линейные токи:

I_A
= 23,8 А;

I_B
= 20 А;

Задача 5

Мостовой выпрямитель должен питать потребитель
постоянным током. Мощность потребителя Р₀, Вт, при напряжении
питания U₀,
В. Следует выбрать один из трех типов полупроводниковых диодов, параметры
которых приведены в табл. 5.11 для схемы выпрямителя, и пояснить, на основании
чего сделан выбор. Начертить схему выпрямителя.

Р₀ = 300 Вт; U₀ = 40 В;

диоды:

Д214; I_доп
= 5 А; U_обр
= 100 В;

Д215Б; I_доп
= 2 А; U_обр
= 200 В;

Д224А; I_доп
= 10 А; U_обр
= 50 В;

Решение:

1. Схема мостового выпрямителя:

2.      Найдем напряжение U_в,
действующее на диод в непроводящий период для мостовой схемы выпрямителя:

;

 В;

.        Определим ток потребителя I_п
из формулы мощности:

;  А;

.        По значениям I₀
=
7,5 А и U_в
= 62,8 В выбираем из табл. 5.1

4.      Из предложенных диодов выбираем диод
Д214, который удовлетворяет условию:

; ;

Условию, ;
,
не удовлетворяет. Для того, чтобы выполнить условие  необходимо
в цепь включить параллельно 2 диода Д214. В этом случае I_обр=I_в
+
I_в =
5 + 5 = 10 A, что удовлетворяет
условию ,
;

5.      Составим схему выпрямителя с двумя
параллельно включенными диодами Д214:

Задача 6

Для транзистора, включенного по
схеме с общим эмиттером, используя входную и выходную характеристики,
определить коэффициент усиления h_21э, величину сопротивления
нагрузки R_k1 и R_k2и мощность
на коллекторе Р_k1и Р_k2, если
известно напряжение на базе U_бэ, напряжение
на коллекторе U_kэ1 и U_kэ2 и напряжение
источника питания Е_k. Данные для
своего варианта взять из табл. 6.1

Номера рисунков	Uбэ, В	Ukэ1, В	Ukэ2, В	Еk, В.
3, 4	0,3	20	30	40

1 Схема:

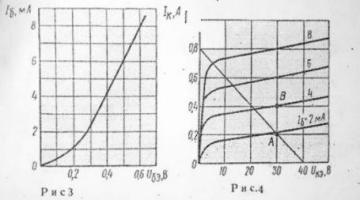
1.      Определяем коэффициент усиления h_21э
по выходным характеристикам:

_21э=ΔI_к/
ΔI_б=(0,4-0,21)/(0,004-0,002)=95

2.      Определяем ток в цепях базы и коллектора
по входным характеристикам: I_б= 4 мА, следовательно для заданных
параметров

I_к=
h_21э· I_б =95·0,004=0,38А.

3.      Определяем сопротивления R_k1
и R_k2:

для R_к1
:

 Ом;

для R_к2
:

 Ом;

4.      Определяем ток на коллекторе I_k1:

 А;

5.      Определяем ток на коллекторе I_k2:

 А;

6.      P_к1=
U_кэ1·
I_к1 =
20·0,38 = 7,6 Вт;

7.      P_к2=
U_кэ2·
I_к2 =
30·0,126 = 3,78 Вт;

Энергия и мощность электрического тока

В любой замкнутой электрической цепи
источник затрачивает электрическую
энергию W_истна
перемещение единицы положительного
заряда по всей цепи: и на внутреннем и
на внешнем участках.

и;

Энергия источника определяется
выражением: W_ист=Eq=EIt=
(U₀+U)It;

Энергия источника (полезная), которая
расходуется на потребителе: W=UIt;

Энергия источника (потери), которая
расходуется на внутреннем сопротивлении
источника: W=U₀It;

Преобразование электрической энергии
в другие виды энергий происходит с
определенной скоростью. Эта скорость
определяет электрическую мощность
элементов электрической цепи:

;

Мощность источника определяется
соотношением:

Мощность потребителя определяется
соотношением:

Коэффициент полезного действияэлектрической цепиηопределяется
отношением мощности потребителя к
мощности источника:

Закон Джоуля – Ленца

Ток, протекая по проводнику, нагревает
его (в этом случае электрическая энергия
преобразуется в тепловую). Количество
выделенного тепла будет определяться
количеством электрической энергии,
затраченной в этом проводнике.

Дж.

(кал).

Коэффициент 0,24 (электротермический
эквивалент) устанавливает зависимость
между электрической и тепловой энергией.

Часть3: Режимы работы электрических цепей

В электрических цепях все основные
элементы делятся на активные и пассивные.
Активными считаются элементы, в которых
преобразование энергии сопровождается
возникновением ЭДС (аккумуляторы,
генераторы). Элементы, в которых ЭДС не
возникает, называются пассивными.

Параметры электрических цепей:

Ток в замкнутой цепи
;

Напряжение на клеммах источника
;

Падение напряжения на сопротивлении
источника
;

Полезная мощность (мощность потребителя)
.

Электрические цепи могут работать в
трех режимах:

• режим холостого хода (цепь разомкнута)
  R=∞:I_хх=0,U=E,
  U₀=0, P=0.

• режим короткого замыкания R=0:

• режим нагрузки R≠0:;;;.

Условие максимальной отдачи мощности:
полезная мощность максимальна, когда
сопротивление потребителя R
станет равным внутреннему сопротивлению
источника R₀.

КПД при максимальной отдаче мощности
равно 50%, к 100% КПД приближается в режиме,
близком к холостому ходу.

Нормальным (рабочим) режимом называют
такой режим работы цепи, при котором
ток, напряжение и мощность не превышают
номинальных значений, заданных
заводом-изготовителем.

Источники тока могут работать в режиме
генератора и в режиме нагрузки. Источники,
ЭДС которых совпадают с направлением
тока в цепи, работают в режиме генератора,
а источники , ЭДС которых не совпадают
с направлением тока, работают в режиме
потребителя.

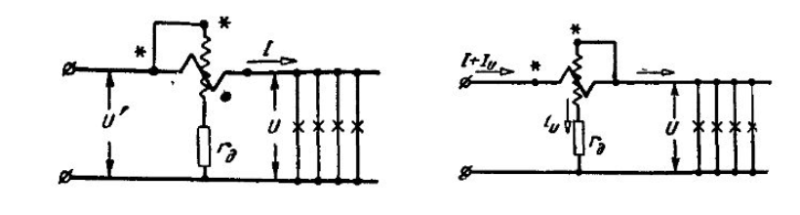
Напряжение источника, работающего в
режиме генератора:
.

Напряжение источника, работающего в
режиме потребителя:
.

Тема 1.3

Расчет электрических цепей постоянного
тока

Основной целью расчета электрической
цепи является нахождение ее параметров:
ток, напряжение, сопротивление, мощность,
КПД. Значения параметров дают возможность
оценить условия и эффективность работы
электротехнического оборудования и
приборов во всех участках электрической
цепи.

Для расчета электрических цепей основой
служат законы Ома и Кирхгофа, Джоуля-Ленца.

Законы Кирхгофа

К характерным элементам электрической
цепи относятся ветвь, узел, контур.

Ветвью электрической цепи называется
ее участок, на всем протяжении которого
величина тока имеет одинаковое значение.
Ветви, которые содержат источники
питания называются активными, а которые
не содержат их – пассивными.

Узлом электрической цепи называется
точка соединения электрических ветвей.

Контуром электрической цепи называют
замкнутое соединение, в которое могут
входить несколько ветвей.

Первый закон Кирхгофа

Сумма токов входящих в узел равна сумме
токов, выходящих из узла. ИЛИ Сумма
токов, сходящихся в узле равна нулю.

∑I=0; – математическое
выражение первого закона Кирхгофа.

Второй закон Кирхгофа

Алгебраическая сумма ЭДС в замкнутом
контуре электрической цепи равна
алгебраической сумме падений напряжений
на всех участках этой цепи.

;
– математическое выражение второго
закона Кирхгофа.

Последовательное соединение
потребителей

Последовательным соединением участков
эй цепи называют соединение, при котором
через все участки цепи проходит один и
тот же ток.

Общее напряжение последовательно
соединенных элементов равно сумме
напряжений на каждом элементе согласно
второму закону Кирхгофа:
;

В соответствии с законом Ома:
;
Из этого соотношения следует:; Таким образом, общее сопротивление
цепи с последовательно соединенными
элементами равно сумме этих сопротивлений.

Параллельное сопротивление
потребителей

Параллельным соединением участков
электрической цепи называется соединение,
при котором все участки цепи присоединяются
к одной паре узлов, то есть находятся
под действием одного и того же напряжения.

Общий ток такого соединения согласно
первому закона Кирхгофа будет равен
сумме токов в отдельных ветвях:
;
В соответствии с законом Ома:;
Если поделить левую и правую части наU, получим:;

Обратная величина общего эквивалентного
сопротивления параллельно включенных
потребителей равна сумме обратных
величин этих потребителей.

Величина, обратная сопротивлению
определяет проводимость потребителя
g. Тогда для параллельно
соединенных потребителей справедливо:;

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Понятие электрической мощности (отдаваемой источником и потребляемой нагрузкой) является одним из самых важных в электротехнике, наряду с напряжением и током. Более того, эта величина объединяет и связывает эти два самых распространенных термина.

Общие понятия электрической мощности

Чтоб понять методы измерения и практического применения этой электрической величины, надо разобраться с теоретическими аспектами.

Определение

При протекании электрического тока по проводнику происходит перенос заряда. В процессе этого переноса электрический ток совершает работу по преодолению взаимодействия носителей заряда с другими частицами вещества. Это взаимодействие проявляется в нагреве проводника, световом излучении, химическом действии тока и т.д.

Чем большую работу производит электрический ток за один и тот же промежуток времени, тем большая электрическая мощность потребовалась для производства этой работы. Отсюда определение мощности – она равна работе электрического тока за промежуток времени, отнесенной к длительности этого промежутка.

Единицы измерения

Единица электрической мощности, принятая в СИ – 1 Ватт. При этой мощности за 1 секунду совершается работа в 1 Джоуль. В различных случаях удобнее применять дольные и кратные единицы:

• киловатт – 1000 ватт;
• мегаватт — 1 миллион ватт;
• милливатт – 0,001 ватт;
• другие единицы с соответствующими приставками.

Для обозначения мощности (как электрической, так и механической, и любой другой) используется латинская буква P.

Раньше для измерения электрической мощности применялись и внесистемные единицы (включая лошадиную силу). На сегодняшний день они практически вышли из употребления.

В цепях переменного тока, помимо активной мощности, измеряемой в ваттах, измеряют и другие виды электрической мощности – полную (в ВА – вольтамперах) и реактивную (в ВАр – вольтамперах реактивных). Их соотношение с активной мощностью зависит от величиныя и знака реактивности у нагрузки.

Формула расчета

Формула расчета следует из определения электрической мощности – надо совершенную током работу (в джоулях) разделить на время (в секундах), в течение которого совершена эта работа: P=A/t.

Если исходить из того, что мощность – это скорость преобразования энергии, можно вычислить искомую величину, как Р=E/t, где:

• E – потребленная (преобразованная) энергия;
• t – промежуток времени, в течение которого происходил расход электрической энергии.

Эта формула на практике применяется нечасто.

Свойства

В практической электротехнике используются некоторые свойства электрической мощности, позволяющие облегчить измерения и упростить измерительные приборы.

Связь электрической мощности с напряжением и силой тока

В реальности формула, использующая отношение работы ко времени ее совершения не используется. Это связано со сложностью непосредственного измерения работы и с неудобством контроля времени. Но если учесть, что работу электрического тока можно вычислить по формуле A=U*I*t, то легко представить формулу для вычисления мощности, как P=U*I*t/t=U*I.

Если известна лишь одна из величин (ток или напряжение), но при этом известно сопротивление нагрузки, формулу легко видоизменить, подставляя в нее низвестную величину, преобразованную по закону Ома (I=U/R). Например, если неизвестен ток, мощность вычисляется, как Р= U*I=U*U/R=U²/R.

Понятие эффективной мощности и ее значение в электротехнике

В электротехнике, как и в механике, существует понятие эффективной мощности. Дело в том, что электрическая мощность подается потребителю не напрямую от сети, а после преобразования (через трансформаторный блок питания, импульсный БП или другое устройство). При преобразовании происходят неизбежные потери мощности, которые зависят от КПД преобразующего устройства.

Естественно, от сети преобразователь потребляет больше, чем отдает в нагрузку, поэтому потребляемая мощность не всегда дает представление о том, возможно ли питание нагрузки от данного преобразователя. Полную информацию дает значение эффективной мощности. Если производитель БП ее не дает, эту величину можно вычислить (или хотя бы оценить) по формуле Рэфф=Pпотр/η, где:

• Рэфф – эффективная мощность, вт;
• Рпотр – мощность, потребляемая из сети, вт;
• η – КПД.

КПД различных преобразующих устройств можно найти в технической литературе.

Влияние электрической мощности на нагрузку

Понятие потребления электрической мощности подразумевает наличие источника этой мощности и ее потребителя. Источник мощности должен как минимум обеспечивать потребление нагрузки плюс потери при транспортировке (нагрев проводов, падение напряжения и т.п.). В противном случае потребитель недополучит электрическую энергию и не сможет произвести работу, которую от него требуется.

Методы измерения электрической мощности

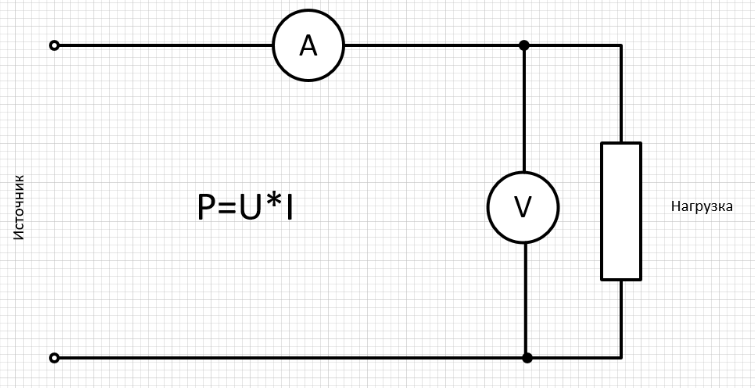
Как показано выше, для вычисления электрической мощности достаточно знать ток и напряжение. Для замеров можно использовать амперметр и вольтметр, перемножив их показания.

А можно использовать специальный прибор – ваттметр, который замеряет обе величины одновременно и перемножает их. Классический ваттметр электродинамической системы состоит из двух катушек, подвижной и неподвижной. Эти катушки включаются на измерение напряжения и тока, соответственно, параллельно и последовательно с нагрузкой.

При прохождении тока и подаче напряжения обе катушки создают магнитные поля, которые взаимодействуют между собой в определенном направлении. Результирующий вращающий момент пропорционален мощности электрического тока (происходит перемножение величин механическим способом), и он ведет к отклонению стрелки, прикреплённой к подвижной катушке, на определенный угол. Этот угол можно считать по шкале, которая обычно градуируется сразу в единицах мощности.

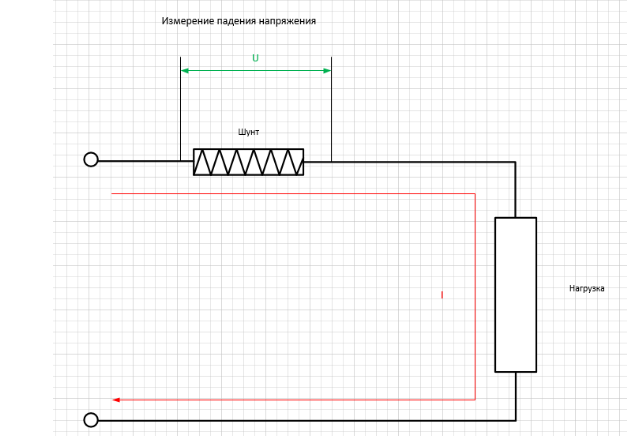
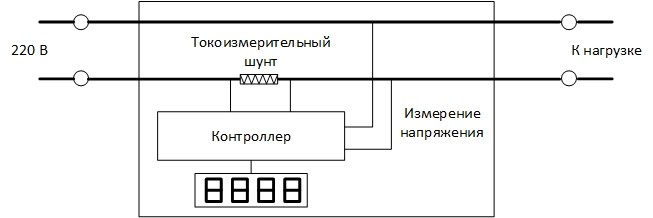
В современных цифровых измерителях мощности используется тот же принцип, только ток измеряется другим способом. Последовательно с нагрузкой включается шунтовой резистор. Он имеет небольшое сопротивление, и на нагрузку практически не влияет. Когда через шунт идет ток, на нем падает небольшое напряжение, которое, как следует из закона Ома, прямо пропорционально протекающему току. Это напряжение измеряется и пересчитывается в ток.

Замеренные ток и напряжение перемножаются, пересчитываются в мощность (при этом учитывается угол сдвига между током и напряжением), масштабируются и выводятся на дисплей в удобной для восприятия форме.

Измерить среднюю потребляемую мощность за определенный промежуток времени можно с помощью счетчика электрической энергии. Для этого надо воспользоваться формулой P=∆E/t. Здесь ∆E – разница в показаниях счетчика за период времени, а t – длительность этого периода.

Таким способом можно измерить электрическую мощность в цепях постоянного тока. В цепях переменного тока подобным методом измеряется так называемая полная мощность (без учета сдвига фаз между током и напряжением), что не всегда информативно.

Рекомендуем прочесть:

• Как замерить ампераж тока мультиметром
• Как найти силу тока по формулам и приборам

Примеры определения мощности тока в электрических системах

Самый тривиальный случай измерения мощности – если у источника электрической энергии (блока питания и т.п.) имеется амперметр и вольтметр. Тогда достаточно перемножить измеренные значения. Например, на фото показан измерительный прибор блока питания. По формуле P=U*I легко определить, что мощность постоянного тока, отдаваемая источником (и потребляемая нагрузкой) равна P=12,4 В х 0,1 А=1,24 ватта.

Если надо постоянно контролировать мощность, лучше установить стационарный ваттметр. С него можно в любое время считать показания и использовать их для анализа и расчетов.

Существуют и бытовые измерители мощности. Они включаются в обычную бытовую розетку 220 вольт, а уже в розетку прибора включается нагрузка. Это может быть компьютер, настольная или напольная лампа – любой бытовой электроприбор.

Ваттметр может собирать статистику замеров за определенный временной период, обрабатывать показания, при необходимости выдавать на дисплей значения других электрических величин (тока, напряжения). С его помощью можно измерить фактическую мощность бытовых электроприборов и оценить их энергопотребление. Проанализировав режимы работы, можно оптимизировать затраты на оплату электрической энергии.

Разобравшись с понятием и сущностью электрической мощности, можно использовать его не только в теории, но и на практике. Например, знание фактической потребляемой мощности потребителей поможет минимизировать платежи за электроэнергию.