Как раскрасить вершины графа
Время на прочтение
4 мин
Количество просмотров 7.1K
В этой небольшой заметке я хочу показать, как с помощью алгебры можно решать классическую задачу о раскраске вершин графа. Об этом сюжете я узнал из книги W.W. Adams, P. Loustanau. An Introduction to Groebner Basis (параграф 2.7).
Введение
Для начала обсудим все необходимые понятия. Пусть — это некоторое множество, а
— множество, состоящее из неупорядоченных пар
элементов множества
. Тогда графом называется пара
При этом
называется множеством вершин графа, а
— множеством рёбер графа. Вершины
называются смежными, если они соединены ребром, то есть
.
Рассмотрим граф, состоящий из трех вершин, которые попарно соединены ребрами. Множество вершин такого графа имеет вид , а множество рёбер —
. Все вершины у графа являются смежными. Удобно представить себе этот граф, изобразив его на плоскости.
Заметим, что при этом мы смогли нарисовать ребра так, что они не пересекаются вне вершин. Графы, для которых удаётся такое сделать, называются планарными или плоскими. Не всякий граф является планарным. Например, граф с пятью вершинами, у которого каждая пара различных вершин является смежной, не будет планарным.
Пусть — множество из
элементов (множество красок). Тогда раскраской вершин графа
с помощью
красок называется отображение
такое, что для любой пары
смежных вершин графа выполняется условие
. Иными словами, каждой вершине мы однозначно сопоставляем один из
цветов таким образом, чтобы соединенные ребром вершины были покрашены в разные цвета. Для простоты мы будем рассматривать только случай трёх красок (
), хотя используемые методы годятся и для любого
. Наш трехвершинный граф без труда можно раскрасить в три цвета.
Итак, мы хотим определять по графу, можно ли раскрасить его вершины в три цвета, так чтобы смежные вершины не были раскрашены в один и тот же.
Алгебра приходит на помощь
Пусть парой множестви
задан граф. Основная идея состоит в том, чтобы сопоставить нашему графу систему алгебраических уравнений. В качестве множества красок будем использовать множество
где Это множество состоит из кубических корней из единицы, то есть таких комплексных чисел, которые при возведении их в третью степень дают
(в общем случае нужно рассматривать множество корней
-ой степени). Будем считать, что каждая вершина
является переменной. При раскраске каждая такая переменная
может принять одно из значений
Мы можем выразить этот факт в алгебраической форме следующим образом: при выборе одного из трех указанных значений переменного
должен занулиться многочлен
Таким образом, мы получаем систему из алгебраических уравнений
Однако пока мы никак не учитываем то, что смежные вершины нельзя покрасить в один и тот же цвет. Пусти
являются смежными вершинами, то есть множество
содержит ребро
Тогда в правой части равенства
первый сомножитель не может обращаться в ноль, так как Следовательно должна зануляться вторая скобка. Таким образом, к уже имеющимся
уравнениям мы должны добавить уравнение вида
для каждого ребра. Теперь вопрос о раскраске вершин графа превратился в вопрос о совместности системы алгебраических уравнений, то есть в вопрос о существовании решения у такой системы. Если у системы нет решений, то граф нельзя раскрасить. Если решения существуют, то каждое даёт способ раскраски вершин графа.
Знакомые с коммутативной алгеброй читатели знают, что этот вопрос о совместности системы алгебраическхи уравнений над алгебраически замкнутым полем решается с помощью так называемой слабой теоремы Гильберта о нулях и теории базисов Гребнера. Мы же в следующем пункте воспользуемся встроенной в модуль SciPy функцией решения систем уравнений для реализации разобранного метода на языке Python.
Реализация на Python
В качестве библиотеки, позволяющей работать с графами, будем использовать igraph.
Тестировать наш скрипт будем на следующем графе из восьми вершин. Отметим, что данный граф является планарным, хотя алгоритм Кавады и Каваи не смог уложить его на плоскость без пересечения ребер вне вершин.
from igraph import *
from sympy import solve, symbols
# Зададим количество вершин
NumberOfVertices = 8
# Перечислим все ребра нашего графа
EdgesList = [(0,1), (0,4), (0,5), (1,7), (1,2), (2,3), (2,7), (1,3), (3,4), (3,6), (4,5), (4,6),(5,6), (6,7)]
# Инициализируем граф, обозначив его вершины с помощью символов x1,...x8
TestGraph = Graph()
TestGraph.add_vertices(NumberOfVertices)
TestGraph.add_edges(EdgesList)
x1, x2, x3, x4, x5, x6, x7, x8 = symbols("x1 x2 x3 x4 x5 x6 x7 x8")
TestGraph.vs["name"] = [x1, x2, x3, x4, x5, x6, x7, x8]
TestGraph.vs["label"] = TestGraph.vs["name"]
# Генерируем уравнения для системы, определяющей раскраску
EquationList=[]
for edge in EdgesList:
EquationList.append("x%d^2 + x%d * x%d + x%d^2"%(edge[0]+1,edge[0]+1,edge[1]+1,edge[1]+1))
for vertice in range(NumberOfVertices):
EquationList.append("x%d^3-1"%(vertice+1))
# Сопоставляем кубическим корням из единицы красную, зеленую и синию краски
Roots = solve(x1**3-1)
RootsToColors = {Roots[0]: "red", Roots[1]: "green", Roots[2]: "blue"}
# Непосредственно решаем систему уравнений
Colorings = solve(EquationList, dict=True)
print("The number of colorings is %d."%len(Colorings))
# Если система совместна, то выводим k-ю раскраску.
# Если нет, то делаем вывод о том, что граф нельзя раскрасить в три цвета.
if(Colorings):
# Раскрашиваем вершины графа
k = 0
RawColors = [Colorings[k][vertice] for vertice in TestGraph.vs["name"]]
ColorDictionary = [RootsToColors[color] for color in RawColors]
TestGraph.vs["color"]=ColorDictionary
# Укладываем граф на плоскость и рисуем
Layout = TestGraph.layout_kamada_kawai()
visual_style = {}
visual_style["vertex_size"] = 40
visual_style["bbox"] = (300, 300)
plot(TestGraph, layout=Layout, **visual_style)
else:
print("The graph is non-colorable.")В результате получаем одну из возможных раскрасок.
Впрочем раскраску для этого графа нетрудно получить без всякой науки, методом проб и ошибок. Однако добавив к графу ребро, соединяющее вершиныи
, мы приходим к графу, который нельзя раскрасить. В этом случае метод проб и ошибок бессилен.
Реберная раскраска
Граф
G называется реберно к –
раскрашиваемым, если его ребра можно раскрасить к красками таким образом, что никакие два смежных
ребра не окажутся одного цвета. Если граф G реберно
к – раскрашиваем, но не является
реберно (к
— 1) -раскрашиваемым, то к называется хроматическим классом или хроматическим индексом, или реберно-хроматическим числом графа G . При этом используется запись Xe(G) = к. На
рисунке изображен граф G , для которого Xe(G) = 4.
Ясно, что если наибольшая из степеней
вершин графа G равна p , то Xe(G)≥ p
. Следующий результат, известный как теорема Визинга, дает точные оценки для
хроматического класса графа G.
Доказательство этой теоремы можно найти у Оре (Ore O. The four–color problem, Academic Press, New York,
1967).
Теорема.(Визинг, 1964) Пусть в графе G, не имеющем петель, наибольшая из степеней вершин равна p; тогда p
≤ Xe(G) ≤ p + 1.
Задача, состоящая в выяснении того,
какие графы имеют хроматический класс p, а какие p + 1,
не решена. Однако в некоторых частных случаях соответствующие результаты
находятся легко. Например, Xe(Cn)= 2 или 3 в
зависимости от того, четно n или
нечетно, а Xe(Wn)= n – 1
, при n≥ 4. Хроматические классы полных графов
и полных двудольных графов вычисляются тоже просто.
Теорема. Xe(Km,n )= p= max(m,n).
Доказательство
Без потери общности можно считать,
что m ≥ n и что граф Km,n изображен так:
n вершин
расположены на горизонтальной линии под m вершинами.
Тогда искомая реберная раскраска получается последовательным окрашиванием
ребер, инцидентных этим та вершинам, с
использованием следующих групп красок: {1,2, …, m};{2,3, …,m, 1}:…: {n, …, m, 1, …, n – 1}:при этом краски
из каждой группы располагаются по часовой стрелке, вокруг соответствующей
вершины.
Теорема. Хe(Кп) — n,
если n нечетно (n ≠1), и Хе(Кn) = n – 1, если n четно.
Доказательство
В случае нечетного п расположим вершины графа Кп в виде правильного n-угольника. Тогда его
ребра можно раскрасить следующим образом: сначала окрашиваем каждую сторону n-угольника в
свой цвет, а затем каждое из оставшихся ребер, диагонали n-угольника, окрашиваем в
тот же цвет, что и параллельная ему сторона.
То, что граф Кп
не является реберно (n— 1) -раскрашиваемым, сразу же следует из того,
что максимально возможное число ребер одного цвета равно (n – 1)/2.
В случае четного n(≥ 4) граф Кп
можно рассматривать как соединение полного (п — 1) — графа Кn-1и отдельной
вершины. Если в Кn-1 окрасить ребра описанным выше способом, то для
каждой вершины останется один неиспользованный цвет, причем все эти
неиспользованные цвета будут различными. Таким образом, чтобы получить реберную
раскраску Кп,
достаточно окрасить оставшиеся ребра в соответствующие “неиспользованные”
цвета.
Свойство 1. Любая вершина полного
графа с шестью или более вершинами и ребрами двух цветов принадлежит, по
меньшей мере, трем ребрам одного цвета.
Свойство 2. В любом полном графе с
шестью или более вершинами и ребрами двух цветов найдется, по меньшей мере,
один треугольник с одноцветными сторонами.
Свойство 3. Если в полном графе с
пятью вершинами и ребрами двух цветов не найдется треугольника с одноцветными
сторонами, то граф можно изобразить в виде “пятиугольника” с красными
сторонами и синими диагоналями.
Свойство 4. В любом полном графе с
шестью или более вершинами и ребрами одного из двух цветов всегда найдутся два
разных треугольника с одноцветными сторонами. Эти два треугольника могут иметь
общую вершину или даже общее ребро.
Если два треугольника имеют общую
вершину или ребро, то их называют сцепленными.
Свойство 5. В полном графе с
семнадцатью или более вершинами и ребрами трех цветов всегда найдется, по
меньшей мере, один треугольник с одноцветными сторонами.
Свойство 6. В полном графе с
восемью вершинами, ребра которого окрашены в два цвета, обязательно найдутся
два треугольника с одноцветными сторонами, которые не являются сцепленными.
Хроматическое число
Рассмотрим задачу: при каких
условиях вершины графа можно раскрасить так, чтобы каждое ребро было инцидентно
вершинам разного цвета? Нас больше всего интересует вопрос, какие графы можно
раскрасить с соблюдением определенных условий, чем вопрос, сколькими способами
можно выполнить это раскрашивание.
Пусть граф G не имеет петель; тогда G называется к –
раскрашиваемым, если каждой его вершине можно приписать один из к цветов таким
образом, чтобы никакие две смежные вершины не оказались одного цвета. Если граф
G является к
-раскрашиваемым, но не является (к – 1) – раскрашиваемым, назовем его к
-хроматическим, а число к назовем хроматическим числом графа G и обозначим через X(G ). На рисунке изображен 4-хроматический (и, следовательно, к
-раскрашиваемый граф при к ≥ 4) граф; цвета обозначены греческими буквами.
Для удобства будем предполагать,
что все графы не содержат петель. Однако будем допускать существование кратных
ребер, так как они не влияют на наши рассуждения.
Ясно, что Х(Кп)=n,
и, следовательно, легко построить графы со сколь угодно большим хроматическим
числом. С другой стороны, нетрудно видеть, что X(G )=1 тогда и только тогда, если G — вполне несвязный граф, и
что
X(G )=2 тогда и только тогда, если G — двудольный граф, отличный от вполне несвязного графа.
Теорема. Если наибольшая из степеней вершин графа G равна
p, то этот граф (р + 1) -раскрашиваем.
Доказательство. Проведем индукцию по числу вершин в G . Пусть G — граф с n вершинами; если
из него удалить произвольную вершину V вместе
с инцидентными ей ребрами, то в оставшемся графе будет n -1 вершин, причем степени вершин по-прежнему не превосходят p. По предположению индукции этот граф (р + 1) – раскрашиваем, отсюда получится (р + 1) -раскладка для G ,
если окрасить вершину V цветом, отличным от
тех, которыми окрашены смежные с ней вершины, а их не более чем Р.
Теорема (Брукса). Пусть G — простой связный граф, не являющийся полным; если
наибольшая из степеней его вершин равна р(р ≥ 3), то он Р -раскрашиваем.
Доказательство. Проведем индукцию по числу вершин графа G . Предположим, что G имеет
n вершин. Если при этом степень какой-нибудь его
вершины меньше Р, дальше можно рассуждать,
как в доказательстве теоремы 1, и все будет закончено. Поэтому без потери
общности можно считать граф G
регулярным степени Р.
Выберем
произвольную вершину V и удалим ее, вместе с
инцидентными ей ребрами. Останется граф с n – 1 вершинами, в котором наибольшая из степеней вершин не превосходит Р. По предположению
индукции этот граф Р-раскрашиваем. Теперь
окрасим вершину V в один из имеющихся Р цветов. Как и
раньше, считаем, что смежные с V вершины V1, …, Vp расположены вокруг V по часовой
стрелке и окрашены в различные цвета Ai,C2,..,Ср.
Определяя
подграфы Hij(i≠j, 1≤i,j ≤ р), когда Vi, Vj
лежат в разных компонентах графа Hij. Таким образом,
можно считать, что при любых данных i,j вершины Vi, Vj связаны простой цепью, целиком
лежащей в Hij
. Обозначим компоненту графа Hij, содержащую
вершины Vi, Vj, через Cij .
Ясно, что
если вершина Vi — смежная более чем с одной вершиной цвета Cj, то существует цвет, отличный от Ci, не приписанный
никакой из вершин, смежных с Vi. Тогда вершину Vi можно окрасить в этот цвет, что, в свою очередь,
позволит окрасить вершину V
в цвет Ci и
закончить на этом доказательство теоремы. Если этот случай не имеет места, то
используем аналогичное рассуждение, чтобы показать, что каждая вершина из Cij (отличная от Vi и от Vj )
должна иметь степень 2. Предположим, что W — первая вершина простой цепи из в Vj,
которая имеет степень больше 2; тогда W можно перекрасить в цвет, отличный от Ci или Cj, нарушая тем самым свойство, что Vi и Vj связаны простой цепью, целиком лежащей в Cij. Поэтому мы
можем считать, что для любых i
и j компонента
Cij состоит только из простой цепи, соединяющей вершину
Vi
с Vj .
Заметим
теперь, что две простые цепи вида Cij
и Cji , где i ≠ I
, можно считать пересекающимися только
в вершине Vj,
так как если W— другая
точка пересечения, то ее можно перекрасить в цвет, отличный от Ci или Cj, или Cl, а это противоречит факту, что Vi и
Vj связаны
простой цепью.
Для завершения доказательства выберем (если это возможно)
две несмежные вершины Vi , Vj и допустим,
что W — вершина цвета Cj, смежная с Vi. Поскольку
Сil — простая цепь (для любого I ≠ j
), можно поменять между собой цвета
вершин в этой цепи, не затрагивая раскраску остальной части графа. Но это
приводит к противоречию, потому что тогда w будет
общей вершиной простых цепей Cij
и Cji. Отсюда следует, что нельзя
выбрать две вершины Vi и Vj несмежными,
и поэтому G должен быть полным графом Kp+1.
А так как это не допускается условием теоремы, то все возможные случаи
рассмотрены.
Гипотеза
о четырех красках
Уже сто с лишним лет математики пытаются
доказать гипотезу четырех красок. В этом направлении был достигнут значительный
прогресс. В печати появилось сообщение (K.Appel, W.Haken, Every planar map is
four colorable, Bull. of Amer. Math. Soc., 82, No,5 (sept. 1976)), что
гипотезу четырех красок удалось обосновать с использованием ЭВМ.
Сформулируем без доказательства несколько
относящихся к этой проблеме результатов:
1. Если гипотеза четырех красок не верна, то любой
опровергающий ее пример будет очень сложным. Известно, например, что всякий
планарный граф, имеющий менее 52 вершин, 4-раскрашиваем.
2. Любой не содержащий треугольников планарный
граф 3-раскрашиваем (теорема Греча).
3. Если попытаться доказать гипотезу четырех
красок, то достаточно доказать ее для гамильтоновых планарных графов (довольно
неожиданный результат Уитни).
Возникновение гипотезы четырех красок
исторически связано с раскрашиванием географических карт. Если имеется карта с
изображением нескольких стран, то интересно узнать, сколько понадобится цветов
для такой раскраски этих стран, чтобы никакие две соседние страны не были
окрашены в один и тот же цвет. Возможно, самая привычная форма гипотезы четырех
красок такова: любую карту можно раскрасить с помощью четырех красок.
Чтобы сделать это утверждение точным, надо
определить, что означает слово “карта”. Поскольку в рассматриваемых
нами задачах о раскраске требуется, чтобы страны, расположенные по обе стороны
ребра, были разного цвета, придется исключить карты, обладающие мостом. Таким
образом, удобно определить карту как связный плоский граф, не содержащий
мостов. Заметим, что при таком определении карты не исключаем петель или
кратных ребер.
Назовем карту k – раскрашиваемой, если ее грани можно
раскрасить k красками так, чтобы никакие две смежные
грани, то есть грани, границы которых имеют общее ребро, не были одного цвета.
Там, где можно запутаться, будем использовать термин вершинно k – раскрашиваемой , имея в виду k -раскрашиваемость в
описанном выше смысле. Например, изображенный ниже граф является
3-раскрашиваемым и вершинно 4-раскрашиваемым.
Теперь сформулируем гипотезу четырех красок для карт: всякая карта 4-раскрашиваема.
Теорема.
Карта G является 2-раскрашиваемой тогда и только тогда, если G представляет собой эйлеров граф.
Доказательство.
Любую вершину V из G должно
окружать четное число граней, так как их можно раскрасить в два цвета. Отсюда
следует, что степень каждой вершины четна, и поэтому G — эйлеров граф.
Жордановой кривой, или жордановой дугой, на
плоскости называется непрерывная кривая, не имеющая самопересечений; замкнутой
жордановой кривой называется жорданова кривая, начало и конец которой
совпадают.
Опишем метод, дающий нужную раскраску
граней графа G. Выберем
произвольную x грань F
и окрасим ее в красный цвет. Проведем жорданову кривую из точки грани F в некоторую точку любой грани, причем
так, чтобы эта кривая не проходила ни через какую вершину графа G. Если на пути от точки x до точки y
грани F‘ наша кривая пересечет четное число
ребер, окрасим грань F‘
в красный цвет; в противном случае — в синий.
Нетрудно показать, что раскрашивание
определено корректно: берем “цикл”, состоящий из двух таких
жордановых кривых (то есть замкнутую жорданову кривую), и показываем, что он
пересекает четное число ребер графа G (надо использовать индукцию по числу вершин, находящихся внутри
цикла, и тот факт, что каждой вершине графа G инцидентно четное число ребер).
Корректная раскраска вершин графа наименьшим набором цветов — тремя.
Раскраска графа — теоретико-графовая конструкция, частный случай разметки графа. При раскраске элементам графа ставятся в соответствие метки с учётом определённых ограничений; эти метки традиционно называются «цветами». В простейшем случае такой способ окраски вершин графа, при котором любым двум смежным вершинам соответствуют разные цвета, называется раскраской вершин. Аналогично раскраска рёбер присваивает цвет каждому ребру так, чтобы любые два смежных ребра имели разные цвета[1]. Наконец, раскраска областей планарного графа назначает цвет каждой области, так, что каждые две области, имеющие общую границу, не могут иметь одинаковый цвет.
Раскраска вершин — главная задача раскраски графов, все остальные задачи в этой области могут быть сведены к ней. Например, раскраска рёбер графа — это раскраска вершин его рёберного графа, а раскраска областей планарного графа — это раскраска вершин его двойственного графа[1]. Тем не менее, другие проблемы раскраски графов часто ставятся и решаются в изначальной постановке. Причина этого частично заключается в том, что это даёт лучшее представление о происходящем и более показательно, а частично из-за того, что некоторые задачи таким образом решать удобнее (например, раскраска рёбер).
Раскраска графов находит применение и во многих практических областях, а не только в теоретических задачах. Помимо классических типов проблем, различные ограничения могут также быть наложены на граф, на способ присвоения цветов или на сами цвета. Этот метод, например, используется в популярной головоломке Судоку. В этой области всё ещё ведутся активные исследования.
История[править | править код]
Первые результаты были получены для плоских графов в задаче раскрашивания карт. Пытаясь раскрасить карту округов Англии, Францис Гутри[en] сформулировал проблему четырёх красок, отметив, что четырёх цветов достаточно, чтобы раскрасить карту так, чтобы любые два смежных региона имели разные цвета. Его брат передал вопрос своему учителю по математике, Огастесу де Моргану, который упомянул о нём в своем письме Уильяму Гамильтону в 1852 году. Артур Кэли поднял эту проблему на встрече Лондонского математического сообщества в 1878 году. В том же году Тэйтом было предложено первое решение этой задачи. Раскраску вершин первоначального графа он свел к раскраске рёбер двойственного графа и предположил, что эта задача всегда имеет решение[2]. В 1880 году Альфред Кемпе[en] опубликовал статью, в которой утверждалось, что ему удалось установить результат, и на десятилетие проблема четырёх цветов считалась решённой. За это достижение Кемпе был избран членом Лондонского Королевского общества и позже — президентом Лондонского математического сообщества[3].
В 1890 году Хивуд нашёл ошибку в доказательстве Кемпе. В этой же статье он доказал теорему пяти красок[en], показав, что любая плоская карта может быть раскрашена не более, чем пятью цветами. При этом он опирался на идеи Кемпе. В следующем столетии было разработано большое количество теорий в попытках уменьшить минимальное число цветов. Теорема четырёх красок была окончательно доказана в 1977 году учеными Кеннетом Аппелем[en] и Вольфгангом Хакеном с использованием компьютерного перебора. Идея доказательства во многом опиралась на идеи Хивуда и Кемпе и игнорировала большинство промежуточных исследований[4]. Доказательство теоремы четырёх красок является одним из первых доказательств, в которых был использован компьютер.
В 1912 году Джордж Дэвид Биркхоф предложил использовать для изучения задач раскраски хроматический многочлен, являющийся важной частью в алгебраической теории графов. Хроматический многочлен впоследствии был обобщён Уильямом Таттом (многочлен Татта). Кемпе в 1879 году уже обращал внимание на общий случай, когда граф не являлся плоским[5]. Много результатов обобщений раскраски плоских графов на поверхности более высоких порядков появилось в начале XX века.
В 1960 году Клод Бердж[en] сформулировал гипотезу о совершенных графах, мотивированное понятием из теории информации, а именно нулевой ошибкой ёмкости графа[6], представленным Шенноном. Утверждение оставалось неподтвержденным на протяжении 40 лет, пока не было доказано как знаменитая строгая теорема о совершенных графах математиками Чудновской[en], Робертсоном[en], Сеймуром и Томасом в 2002 году.
Раскраска графов как алгоритмическая проблема начала изучаться с 1970-х годов: определение хроматического числа — входит в число 21 NP-полных задач Карпа (1972). И примерно в то же время были разработаны разнообразные алгоритмы на базе поиска с возвратом и рекурсивного удаления и стягивания Зыкова[7]. С 1981 года раскраска графа применяется для распределения регистров в компиляторах[8].
Определение и терминология[править | править код]
Раскраска вершин[править | править код]
Этот граф может быть раскрашен 3 цветами 12 способами.
Когда говорят о раскраске графов, почти всегда подразумевают под этим раскраску их вершин, то есть присвоение цветовых меток вершинам графа так, чтобы любые две вершины, имеющие общее ребро, имели разные цвета. Так как графы, в которых есть петли, не могут быть раскрашены таким образом, они не являются предметом обсуждения.
Терминология, в которой метки называются цветами, происходит от раскраски политических карт. Такие метки как красный или синий используются, только когда число цветов мало, обычно же подразумевается, что метки являются целыми числами 
Раскраска с использованием 







Хроматическое число в терминах расстояния Громова-Хаусдорфа[править | править код]
Пусть 













- Теорема (А.О.Иванов, А.А.Тужилин)[9]: Пусть
— наибольшее натуральное число, для которого
(если таких натуральных чисел не существует, то положим
). Тогда
.
Замечание.
Хроматический многочлен[править | править код]
Хроматический многочлен — это функция 


Этот факт был обнаружен Биркгофом и Льюисом при попытке доказать гипотезу четырёх красок[10].
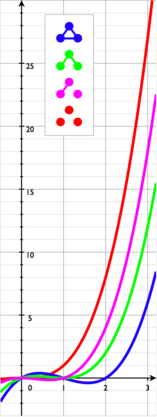
Все не изоморфные графы из 3 вершин и их хроматические многочлены. Пустой граф E3 (красный) допускает раскраску одним цветом, остальные — нет. Зелёный граф может быть раскрашен 3 цветами 12 способами.
Например, граф на изображении справа может быть раскрашен 12 способами с использованием 3 цветов. Двумя цветами он не может быть окрашен в принципе. Используя 4 цвета, мы получаем 24+4*12 = 72 вариантов раскраски: при использовании всех 4 цветов, есть 4! = 24 корректных способа (каждое присвоение 4 цветов для любого графа из 4 вершин является корректным); и для каждых 3 цветов из этих 4 есть 12 способов раскраски. Тогда для графа в примере таблица чисел корректных раскрасок будет начинаться так:
| Доступное число цветов | 1 | 2 | 3 | 4 | … |
| Количество способов раскраски | 0 | 0 | 12 | 72 | … |
Для графа в примере 

Хроматический многочлен содержит по меньшей мере столько же информации о раскрашиваемости 

Треугольный  |

|
Полный граф  |

|
Дерево с  ребрами ребрами |

|
Цикл  |

|
| Граф Петерсена | 
|
Рёберная раскраска[править | править код]
Рёберная раскраска графа подразумевает под собой назначение цветов ребрам так, что никакие два ребра одного цвета не принадлежат одной вершине. Эта задача эквивалентна разделению множества граней на множества независимых граней. Наименьшее число цветов, необходимое для рёберной раскраски графа 

Тотальная раскраска[править | править код]
Тотальная раскраска — это один из видов раскраски вершин и рёбер графа. Под ней подразумевают такое присвоение цветов, что ни соседние вершины, ни смежные ребра, ни вершины и ребра, которые их соединяют, не имеют одинакового цвета. Полное хроматическое число 

Свойства[править | править код]
Свойства хроматического многочлена[править | править код]
- Если
— пустой граф[11],
- Если в
есть петля[11],
Ограничения на хроматическое число[править | править код]
- Назначение всем вершинам разных цветов всегда дает правильную раскраску, так что
- Если
содержит клики размера k, тогда необходимо минимум k цветов для раскраски этой клики, другими словами хроматическое число больше, либо равно кликовому числу:
-
- Для интервальных графов это ограничение точно.
- По теореме о четырёх красках, любой плоский граф может быть раскрашен четырьмя цветами.
- 2-раскрашиваемые графы — это двудольные графы, в том числе и деревья.
- Граф
является двудольным в том и только в том случае, если он не содержит циклов нечетной длины[11].
- Жадная раскраска показывает, что любой граф может быть раскрашен при использовании на один цвет больше, чем его максимальная степень вершины[12],
-
для связанного, простого графа
, если
не является ни полным графом, ни графов-циклом.
Графы с большим хроматическим числом[править | править код]
- Графы с большими кликами имеют большое хроматическое число, но обратное утверждение не всегда верно. Граф Грёча — это пример 4-раскрашиваемого графа без треугольников, и этот пример может быть обобщен на граф Мычельского.
-
- Теорема Мычельского (Александр Зыков 1949, Ян Мычельский,1955): Существуют графы без треугольников со сколь угодно большими хроматическими числами.
- Из теоремы Брукса, графы с большим хроматическим числом должны иметь высокую максимальную степень вершины. Другое локальное условие, из-за которого хроматическое число может быть большим — это наличие большой клики. Но раскрашиваемость графа зависит не только от локальных условий: граф с большим обхватом локально выглядит как дерево, так все циклы длинные, но его хроматическое число не равно 2:
-
- Теорема Эрдёша: Существуют графы со сколь угодно большим обхватом и хроматическим числом[12].
Ограничения на хроматический индекс[править | править код]
- Более того[14],
-
- Теорема Кёнига:
, если
— двудольный.
- Теорема Кёнига:
- В общем случае, связь намного сильнее, чем дает теорема Брукса для раскраски вершин[14]:
-
- Теорема Визинга: Граф с максимальной степенью вершины
имеет рёберное хроматическое число
или
.
- Теорема Визинга: Граф с максимальной степенью вершины
Другие свойства[править | править код]
- Граф является k-хроматическим тогда и только тогда, когда он имеет ациклическую ориентацию, для которой длина наибольшего пути равна k. Это было доказано в теореме Галлаи — Хассе — Роя — Витавера[15].
- Для плоских графов, раскраска вершин эквивалентна нигде не нулевому потоку.
- О бесконечных графах известно намного меньше. Ниже приведены два результата для раскраски бесконечных графов.
- Если все конечные подграфы бесконечного графа
k-хроматические, то и
тоже является k-хроматическим (доказывается при предположении аксиомы выбора). Это — формулировка теоремы де Брёйна — Эрдёша[16].
- Если граф допускает полную n-раскраску для любого
, то он допускает бесконечную полную раскраску[17].
Открытые вопросы[править | править код]
Хроматическое число плоскости, в которой две точки являются смежными, если между ними единичное расстояние, неизвестно. Оно может быть равным 5, 6, или 7. Другие открытые вопросы о хроматическом числе графов включают в себя гипотезу Хадвигера, утверждающую, что любой граф с хроматическим числом k имеет полный граф из k вершин, как его минор, гипотезу Эрдёша-Фабера-Ловаса, которая ограничивает хроматическое число полных графов, которые имеют ровно одну общую вершину для каждой пары графов, и гипотезу Альбертсона о том, что среди k-хроматических графов полными являются те, которые имеют наименьшее число пересечений.
Когда Бирков и Льюис представили хроматический многочлен в их попытке решить теорему четырёх цветов, они утверждали, что для плоских графов 




Алгоритмы раскраски[править | править код]
Полиномиальные алгоритмы[править | править код]
Для двудольного графа задача раскраски вычисляется за линейное время с помощью поиска в ширину. В случае совершенных графов, хроматическое число и соответствующая ему раскраска может быть найдена за полиномиальное время при использовании полуопределённого программирования. Точные формулы для нахождения хроматического числа известны для многих классов графов (леса, циклы, колеса, хордальные графы) и так же могут быть вычислены за полиномиальное время.
Точные алгоритмы[править | править код]
Алгоритм полного перебора для случая k-раскраски рассматривает все 
Используя динамическое программирование и оценку размера наибольшего независимого множества, в графе возможность k-раскраски может быть разрешена за время 


Стягивание[править | править код]
Стягивание вершин — это операция, которая из графа 






Хроматическое число удовлетворяет рекуррентному соотношению

где 





Хроматический полином удовлетворяет рекуррентному соотношению

где 














Выражения, данные выше, приводят к рекурсивной процедуре, названной алгоритм удаления и стягивания, сформировавшей основу для многих алгоритмов раскраски графов. Время работы удовлетворяет такому же рекуррентному соотношению, как и числа Фибоначчи, поэтому в наихудшем случае алгоритм будет работать за время 
Жадная раскраска[править | править код]
Два результата работы жадного алгоритма при выборе разных порядков вершин.
Жадный алгоритм упорядочивает вершины 







Для хордального графа и для его особых случаев (например, интервальный граф) алгоритм жадной раскраски может быть использован для нахождения оптимальной раскраски за полиномиальное время, выбирая порядок вершин обратным к совершенному порядку исключения. Этот алгоритм может быть применен и к более широкому классу графов (вполне упорядочиваемые графы), однако найти такой порядок для таких графов — NP-сложная задача.
Если вершины упорядочены в соответствии с их степенями, алгоритм жадной раскраски использует не более чем 



Параллельные и распределённые алгоритмы[править | править код]
В области распределённых алгоритмов встречается аналогичная задача. Допустим, вершины графа — это компьютеры, которые могут общаться между собой, если они соединены ребром. Задача состоит в том, чтобы каждый компьютер выбрал для себя «цвет», так, чтобы соседние компьютеры выбрали разные цвета. Эта задача тесно связана с проблемой нарушения симметрии[en]. Наиболее развитые вероятностные алгоритмы работают быстрее, чем детерминированные алгоритмы для графов с достаточно большой максимальной степени вершин 
В симметричных графах детерминированные распределённые алгоритмы не могут найти оптимальную раскраску вершин. Нужна дополнительная информация, чтобы избежать симметрии. Делается стандартное предположение, что первоначально каждая вершина имеет уникальный идентификатор, например, из множества 



Простая версия распределённого жадного алгоритма для 

Наиболее простым интересным случаем является n-цикл. Ричард Коул и Узи Вишкин[24] показали, что существует распределённый алгоритм, который уменьшает количество цветов от n до 

Функция 

Техника Коула и Вишкина также может быть применена для произвольного графа с ограниченной степенью вершин, в этом случае время работы составляет 
Проблема раскраски рёбер также изучалась в распределённой модели. Пансонецци и Рицци достигли 

Децентрализованные алгоритмы[править | править код]
Децентрализованными называются алгоритмы, в которых не разрешена внутренняя передача сообщений (в отличие от распределённых алгоритмов, где процессы обмениваются между собой данными). Существуют эффективные децентрализованные алгоритмы, успешно справляющиеся с задачей раскраски графов. Эти алгоритмы работают в предположении, что вершина способна «чувствовать», что какая-либо из её соседних вершин раскрашена в тот же цвет, что и она. Другими словами, есть возможность определить локальный конфликт. Такое условие довольно часто выполняется в реальных прикладных задачах — например, при передаче данных по беспроводному каналу передающая станция, как правило, имеет возможность детектировать, что другая станция пытается передавать одновременно в тот же канал. Способности к получению подобной информации достаточно для того, чтобы алгоритмы, основанные на обучающихся автоматах[en], с вероятностью единица правильно решат задачу раскраски графа[29][30].
Сложность вычислений[править | править код]
Раскраска графа является вычислительно сложной задачей. Узнать, допускает ли граф k-раскраску для заданного k — это NP-полная задача, кроме случаев k = 1 и k = 2. В частности, задача вычисления хроматического числа NP-сложна[31]. Задача о 3-раскраске NP-полная даже для случая планарного графа степени 4[32].
Также NP-сложной задачей является раскраска 3-раскрашиваемого графа 4 цветами[33] и k-раскрашиваемого графа 
Вычисление коэффициентов хроматического полинома #P-сложная задача. Доказано, что не существует ни одного FPRAS-алгоритма для вычисления хроматического полинома ни для какого рационального числа k ≥ 1,5, кроме k = 2, если только не выполнится, что NP = RP[35].
Применение[править | править код]
Планирование[править | править код]
Раскраска вершин моделирует многие проблемы планирования[36]. В своей простейшей постановке заданный набор работ должен быть распределен по временным отрезкам, каждая такая работа занимает один отрезок. Они могут быть выполнены в любом порядке, но две работы могут конфликтовать в том смысле, что не могут быть выполнены одновременно, так как, например, используют общие ресурсы. Соответствующий граф содержит вершину для каждой из работ и ребро для каждой конфликтующей пары. Хроматическое число построенного графа — это минимальное время выполнения всех работ без конфликтов.
Детали проблемы планирования определяют структуру графа. Например, когда идет распределение самолётов по рейсам, результирующий граф конфликтов является интервальным графом, так что проблема раскраски может быть решена эффективно. При распределении радиочастот получается граф единичных кругов конфликтов, и для такой задачи существует 3-аппроксимационный алгоритм.
Распределение регистров[править | править код]
Компилятор — это компьютерная программа, которая переводит один компьютерный язык в другой. Для улучшения времени выполнения результирующего кода одной из техник компиляторной оптимизации, является распределение регистров, в которой наиболее часто используемые переменные компилируемой программы хранятся в быстродействующих регистрах процессора. В идеальном случае переменные хранятся в регистрах так, что они все находятся в регистрах во время их использования.
Стандартный подход к этой задаче состоит в сведении её к задаче раскраски графов[8]. Компилятор строит интерференционный граф, где вершины соответствуют переменным, а грань соединяет две из них, если они нужны в один и тот же момент времени. Если этот граф k-хроматический, то переменные могут храниться в k регистрах.
Цифровые водяные знаки[править | править код]
Технология цифровых водяных знаков (англ. digital watermarking) позволяет вместе с данными (будь то медиафайлы, исполняемые файлы и прочие) передать некое скрытое сообщение («водяной знак», Watermark). Такое скрытое сообщение может быть применено в защите авторских прав для идентификации владельца данных.
Это важно, например, для установления источника их распространения нелегальным образом. Или же для подтверждения прав на данные, например — программное обеспечение систем на кристалле (system-on-chip).
Сообщение можно закодировать в том числе и в способе распределения регистров. Одну из таких техник предложили Qu и Potkonjak[37] (поэтому её иногда называют QP-алгоритмом).
Состоит она вот в чём: пусть 

Извлечь это сообщение можно путём сравнением распределения регистров с исходной раскраской;[38] существуют и способы удостовериться в том, было ли некое сообщение закодировано в программе без использования исходного.
В дальнейшем разные авторы развивали и уточняли идеи Qu и Potkonjak[39].[38][40]
Другие применения[править | править код]
Задача раскраски графов была поставлена во многих других областях применения, включая сопоставление с образцом.
Решение головоломки судоку можно рассматривать как завершение раскраски 9 цветами заданного графа из 81 вершины.
Примечания[править | править код]
- ↑ 1 2 3 (Molloy & Reed 2002, The Basic Definitions)
- ↑ (Донец & Шор 1982, Историческая справка)
- ↑ (Kubale 2004, History of graph coloring)
- ↑ (van Lint & Wilson 2001, Chap. 33)
- ↑ (Jensen & Toft 1995, С. 2)
- ↑ C.E. Shannon, “The zero-error capacity of a noisy channel, ” IEEE Trans. Information Theory, pp. 8-19, 1956.
- ↑ (Зыков 1949)
- ↑ 1 2 (Chaitin 1982)
- ↑ A.O.Ivanov, A.A.Tuzhilin (2019), The Gromov-Hausdorff Distance between Simplexes and Two-Distance Spaces, <https://arxiv.org/pdf/1907.09942.pdf> Архивная копия от 29 июля 2019 на Wayback Machine
- ↑ (Birkhoff & Lewis 1946)
- ↑ 1 2 3 4 (Tutte 1984, Chromatic polynomial)
- ↑ 1 2 3 (Diestel 2005, Colouring vertices)
- ↑ (Brooks & Tutte 1941)
- ↑ 1 2 (Diestel 2005, Colouring edges)
- ↑ (Nešetřil & Ossona de Mendez 2012)
- ↑ (de Bruijn, Erdős 1951)
- ↑ (Fawcett 1978)
- ↑ (Lawler 1976)
- ↑ (Beigel & Eppstein 2005)
- ↑ (Fomin, Gaspers & Saurabh 2007)
- ↑ (Sekine, Imai & Tani 1995)
- ↑ (Welsh & Powell 1967)
- ↑ 1 2 (Schneider 2010)
- ↑ (Cole & Vishkin 1986), см. также (Cormen, Leiserson & Rivest 1990, Section 30.5)
- ↑ 1 2 (Linial 1992)
- ↑ (Goldberg, Plotkin & Shannon 1988)
- ↑ (Schneider 2008)
- ↑ (Panconesi & Rizzi 2001)
- ↑ (Leith & Clifford 2006)
- ↑ (Duffy, O’Connell & Sapozhnikov 2008)
- ↑ (Garey, Johnson & Stockmeyer 1974); (Garey & Johnson 1979).
- ↑ (Dailey 1980)
- ↑ (Guruswami & Khanna 2000)
- ↑ (Khot 2001)
- ↑ (Goldberg & Jerrum 2008)
- ↑ (Marx 2004)
- ↑ (Qu & Potkonjak 1998)
- ↑ 1 2 (Zhu & Thomborson 2006)
- ↑ (Collberg, Thomborson & Townsend 2004)
- ↑ (Myles & Collberg 2003)
Литература[править | править код]
- Донец, Г. А. & Шор, Н. З. (1982), Алгебраический подход к проблеме раскраски плоских графов, Наукова думка, с. 5—7
- Зыков, А. А. (1949), О некоторых свойствах линейных комплексов, Матем. сб. Т. 24(66) (2): 163–188, <http://mi.mathnet.ru/eng/msb5974>
- Beigel, R. & Eppstein, D. (2005), 3-coloring in time O(1.3289n), Journal of Algorithms Т. 54 (2)): 168–204, DOI 10.1016/j.jalgor.2004.06.008
- Birkhoff, G. D. & Lewis, D. C. (1946), Chromatic Polynomials, Trans. Amer. Math. Soc. Т. 60: 355—451, <http://www.ams.org/journals/tran/1946-060-00/S0002-9947-1946-0017288-3/S0002-9947-1946-0017288-3.pdf>
- Brélaz, D. (1979), New methods to color the vertices of a graph, Communications of the ACM Т. 22 (4): 251–256, DOI 10.1145/359094.359101
- Brooks, R. L. & Tutte, W. T. (1941), On colouring the nodes of a network, Proceedings of the Cambridge Philosophical Society Т. 37 (2): 194–197, DOI 10.1017/S030500410002168X
- N. G. de Bruijn, P. Erdős. A colour problem for infinite graphs and a problem in the theory of relations (англ.) // Nederl. Akad. Wetensch. Proc. Ser. A. — 1951. — Т. 54. — С. 371—373. (= Indag. Math. 13)
- Byskov, J.M. (2004), Enumerating maximal independent sets with applications to graph colouring, Operations Research Letters Т. 32 (6): 547–556, DOI 10.1016/j.orl.2004.03.002
- Cormen, T. H.; Leiserson, C. E. & Rivest, R. L. (1990), Introduction to Algorithms (1st ed.), The MIT Press
- Collberg, Christian; Thomborson, Clark & Townsend, Gregg M. (2004), Dynamic Graph-Based Software Watermarking, <ftp://ftp.cs.arizona.edu/reports/2004/TR04-08.pdf>
- Chaitin, G. J. (1982), Register allocation & spilling via graph colouring, Proc. 1982 SIGPLAN Symposium on Compiler Construction, с. 98–105, ISBN 0-89791-074-5, DOI 10.1145/800230.806984
- Cole, R. & Vishkin, U. (1986), Deterministic coin tossing with applications to optimal parallel list ranking, Information and Control Т. 70 (1): 32–53, DOI 10.1016/S0019-9958(86)80023-7
- Dailey, D. P. (1980), Uniqueness of colorability and colorability of planar 4-regular graphs are NP-complete, Discrete Mathematics Т. 30 (3): 289–293, DOI 10.1016/0012-365X(80)90236-8
- Diestel, R. (2005), Graph theory, <http://www.math.ubc.ca/~solymosi/2007/443/GraphTheoryIII.pdf> Архивная копия от 25 ноября 2014 на Wayback Machine
- Duffy, K.; O’Connell, N. & Sapozhnikov, A. (2008), Complexity analysis of a decentralised graph colouring algorithm, Information Processing Letters Т. 107: 60–63, doi:10.1016/j.ipl.2008.01.002, <http://www.hamilton.ie/ken_duffy/Downloads/cfl.pdf>
- Fawcett, B. W. (1978), On infinite full colourings of graphs, Can. J. Math. Т. XXX: 455–457
- Garey, M. R. & Johnson, D. S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 0-7167-1045-5
- Garey, M. R.; Johnson, D. S. & Stockmeyer, L. (1974), Some simplified NP-complete problems, Proceedings of the Sixth Annual ACM Symposium on Theory of Computing, с. 47–63, doi:10.1145/800119.803884, <http://portal.acm.org/citation.cfm?id=803884>
- Goldberg, L. A. & Jerrum, M. (July 2008), Inapproximability of the Tutte polynomial, Information and Computation Т. 206 (7): 908–929, DOI 10.1016/j.ic.2008.04.003
- Goldberg, A. V.; Plotkin, S. A. & Shannon, G. E. (1988), Parallel symmetry-breaking in sparse graphs, SIAM Journal on Discrete Mathematics Т. 1 (4): 434–446, DOI 10.1137/0401044
- Guruswami, V. & Khanna, S. (2000), On the hardness of 4-coloring a 3-colorable graph, Proceedings of the 15th Annual IEEE Conference on Computational Complexity, с. 188–197, ISBN 0-7695-0674-7, DOI 10.1109/CCC.2000.856749
- Jaeger, F.; Vertigan, D. L. & Welsh, D. J. A. (1990), On the computational complexity of the Jones and Tutte polynomials, Mathematical Proceedings of the Cambridge Philosophical Society Т. 108: 35–53, DOI 10.1017/S0305004100068936
- Jensen, Tommy R. & Toft, Bjarne (1995), Graph Coloring Problems, John Wiley & Sons, ISBN 0-471-02865-7
- Khot, S. (2001), Improved inapproximability results for MaxClique, chromatic number and approximate graph coloring, Proc. 42nd Annual Symposium on Foundations of Computer Science, с. 600–609, ISBN 0-7695-1116-3, DOI 10.1109/SFCS.2001.959936
- Kubale, M. (2004), Graph Colorings, American Mathematical Society, ISBN 0-8218-3458-4
- Kuhn, F. (2009), Weak graph colorings: distributed algorithms and applications, Proceedings of the 21st Symposium on Parallelism in Algorithms and Architectures, с. 138–144, ISBN 978-1-60558-606-9, DOI 10.1145/1583991.1584032
- Lawler, E.L. (1976), A note on the complexity of the chromatic number problem, Information Processing Letters Т. 5 (3): 66–67, DOI 10.1016/0020-0190(76)90065-X
- Leith, D.J. & Clifford, P. (2006), A Self-Managed Distributed Channel Selection Algorithm for WLAN, Proc. RAWNET 2006, Boston, MA, <http://www.hamilton.ie/peterc/downloads/rawnet06.pdf>
- Linial, N. (1992), Locality in distributed graph algorithms, SIAM Journal on Computing Т. 21 (1): 193–201, DOI 10.1137/0221015
- van Lint, J. H. & Wilson, R. M. (2001), A Course in Combinatorics (2nd ed.), Cambridge University Press, ISBN 0-521-80340-3
- Molloy, Michael & Reed, Bruce (2002), Graph colouring and the probabilistic method, Springer, ISBN 3-540-42139-4, ISSN 0937-5511
- Marx, Dániel (2004), Graph colouring problems and their applications in scheduling, Periodica Polytechnica, Electrical Engineering, vol. 48, с. 11–16, CiteSeerX:10.1.1.95.4268
- Mycielski, J. (1955), Sur le coloriage des graphes, Colloq. Math. Т. 3: 161–162, <http://matwbn.icm.edu.pl/ksiazki/cm/cm3/cm3119.pdf>.
- Myles, Ginger & Collberg, Christian S. (2003), Software Watermarking Through Register Allocation: Implementation, Analysis, and Attacks, ICISC, с. 274—293, DOI 10.1007/b96249
- Nešetřil, Jaroslav & Ossona de Mendez, Patrice (2012), Theorem 3.13, Sparsity: Graphs, Structures, and Algorithms, vol. 28, Algorithms and Combinatorics, Heidelberg: Springer, с. 42, ISBN 978-3-642-27874-7, DOI 10.1007/978-3-642-27875-4.
- Panconesi, Alessandro & Rizzi, Romeo (2001), Some simple distributed algorithms for sparse networks, Distributed Computing (Berlin, New York: Springer-Verlag) . — Т. 14 (2): 97–100, ISSN 0178-2770, DOI 10.1007/PL00008932
- Panconesi, A. & Srinivasan, A. (1996), On the complexity of distributed network decomposition, Journal of Algorithms, vol. 20
- Qu, Gang & Potkonjak, Miodrag (1998), Analysis of watermarking techniques for graph coloring problem, ICCAD, с. 190—193, DOI 10.1145/288548.288607
- Schneider, J. (2010), A new technique for distributed symmetry breaking, Proceedings of the Symposium on Principles of Distributed Computing, <http://www.dcg.ethz.ch/publications/podcfp107_schneider_188.pdf> Архивная копия от 30 июля 2013 на Wayback Machine
- Schneider, J. (2008), A log-star distributed maximal independent set algorithm for growth-bounded graphs, Proceedings of the Symposium on Principles of Distributed Computing, <http://www.dcg.ethz.ch/publications/podc08SW.pdf> Архивная копия от 30 июля 2013 на Wayback Machine
- Sekine, K.; Imai, H. & Tani, S. (1995), Computing the Tutte polynomial of a graph of moderate size, Proc. 6th International Symposium on Algorithms and Computation (ISAAC 1995), vol. 1004, Lecture Notes in Computer Science, Springer, с. 224–233, ISBN 3-540-60573-8, DOI 10.1007/BFb0015427
- Tutte, W. T. (1984), Graph theory, Encyclopedia of mathematics and applications (Cambridge University Press) . — Т. 21, ISBN 0-521-30241-2
- Welsh, D. J. A. & Powell, M. B. (1967), An upper bound for the chromatic number of a graph and its application to timetabling problems, The Computer Journal Т. 10 (1): 85–86, DOI 10.1093/comjnl/10.1.85
- Wilf, H. S. (1986), Algorithms and Complexity, Prentice–Hall
- Zhu, William & Thomborson, Clark (2006), Recognition in software watermarking, MCPS ’06: Proceedings of the 4th ACM international workshop on Contents protection and security, ACM, с. 29–36, ISBN 1-59593-499-5, DOI 10.1145/1178766.1178776
Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером
Раскрашивание графа
—
Теория графов
В этом уроке мы разберем, что такое раскраска графов и как это относится к цифрам на вершинах. Также покажем примеры раскраски графов разных типов, так как в каждом случае этот процесс немного отличается.
Раскраска графов
Когда мы присваиваем вершинам графа метки — это называется раскраской графов.
Цвета — это целые положительные цифры. Графы нужно раскрашивать так, чтобы соседние вершины имели разные цвета. Еще стоит использовать как можно меньше цветов.
Вот несколько примеров раскраски графа:

Первый пример на схеме выше не совсем верный, потому что соседним вершинам присваивается один и тот же цвет. Вторая раскраска лучше, так как удовлетворяет правилам, но в ней используется больше цветов, чем нужно. Третья раскраска — правильная. Она удовлетворяет правилам и использует как можно меньше цветов.
В этих графах невозможно использовать меньше трех цветов, так как треугольники содержат три вершины, которые являются соседями.
Хроматическое число графа
, которое обозначается
— это минимальное количество цветов, необходимое для правильной раскраски графа.
Чтобы обозначить, о каком графе идет речь, мы будем сокращенно обозначать
как
. Рассмотрим раскраску графов на просто классе графов — путях.
Раскраска путей
Вот несколько оптимальных вариантов раскраски путей:

В общем случае
для каждого
.
Рассмотрим другие примеры:

Четные и нечетные циклы ведут себя по-разному. У нечетных всегда хроматическое число три, а у четных — хроматическое число два.
Теперь рассмотрим, как раскрашивают полные графы.
Раскраска полных графов
У нас есть следующие полные графы с уже помеченными вершинами:

Поскольку в полном графе каждая вершина смежна с любой другой вершиной, мы не можем повторить ни одного цвета. Таким образом,
.
Раскраска двудольных графов
Рассмотрим следующие примеры:

На графиках видно, что соседние вершины раскрашены в один цвет. В случае с двудольными графами такое возможно, так как применяется правило партитного множества — независимое множество, между вершинами которого нет ребер. Поэтому мы можем окрасить все его вершины в один цвет.
Для двух партитных множеств нужно два цвета. И это относится к любому двудольному графу, а не только к полному.
Любой граф с хотя бы одним ребром является двудольным, когда он двухцветный. Поскольку деревья двудольные, мы теперь знаем, что все нетривиальные деревья имеют хроматическое число
.
Объединения и стыковки
Мы пришли к такой формуле:
Это связано с тем, что между копиями
и
в объединении нет ребер. Поэтому мы можем раскрасить каждый граф отдельно, и не беспокоиться:

Мы также имеем
— каждая вершина
смежна с каждой вершиной
. Поэтому ни один цвет, который используется на
, не может быть использован на
и наоборот.
Обратите внимание на второй граф на схеме выше. Чтобы получить правильную раскраску
, мы можем раскрасить
и
отдельно, а затем заменить каждый цвет
из
на
.
Декартово произведение
Декартово произведение немного сложнее. Результат
, что совпадает с результатом для объединения.
Рассмотрим пример:
. Ниже выделена конкретная вершина:

Выделенная вершина — это часть сразу двух графов (
и
). Нам нужно убедиться, что ее раскраска работает в отношении обоих графов. Мы можем представить
и
как состоящий из пяти копий
со связями между копиями, которые определяются связями
.
Нам нужно раскрасить каждую из пяти копий
по-своему и убедиться, что взаимодействия между копиями, которые определяются
, соблюдены. Начнем с оптимальных раскрасок
и
:

Хитрость в том, чтобы для каждой вершины взять ее цвет в
, ее цвет в
и сложить их. При этом нужно уменьшить результат по модулю
и заменить все полученные нули тройками. В итоге раскраски для пяти копий выглядят следующим образом:

Такой способ гарантирует, что соседние вершины никогда не будут иметь одинаковый цвет. Этот же процесс работает и в общем случае:
-
Для графов
и
пусть будет
-
Раскрасим вершину
из
цветом
-
Уточним, что в выражении выше
и
— это цвета в
и
соответственно
Произвольный граф
Вот еще один пример раскраски графа без очевидной структуры:

Может потребоваться некоторое усилие, чтобы придумать ответ к такой неочевидной структуре. Пройдем этот процес по шагам:
-
На графе много треугольников, поэтому нам нужно использовать как минимум три цвета
-
На графе справа выделен
-цикл, для него требуется
цвета
-
Вершина в середине цикла смежна со всем циклом, поэтому мы не можем повторно использовать ни один из цветов цикла
-
Таким образом, требуется
цвета
Раскраска
графов.
Введение
Понятие
«граф» связано с понятием «графический»,
«графика». Действительно, графовые
модели имеют простую и понятную
графическую интерпретацию, позволяющую
с их помощью образно представить самые
разные объекты, в то же время оставаясь
в рамках строгих математических моделей.
Первой
работой теории графов как математической
дисциплины считают статью Эйлера
(1736г.), в которой рассматривалась задача
о Кёнигсбергских мостах. Эйлер показал,
что нельзя обойти семь городских мостов
и вернуться в исходную точку, пройдя по
каждому мосту ровно один раз. Следующий
импульс теория графов получила спустя
почти 100 лет с развитием исследований
по электрическим сетям, кристаллографии,
органической химии и другим наукам.
С
графами, сами того не замечая, мы
сталкиваемся постоянно. Например, графом
является схема линий метрополитена.
Точками на ней представлены станции, а
линиями – пути движения поездов. Исследуя
свою родословную и возводя ее к далекому
предку, мы стоим так называемое
генеалогическое древо. И это древо –
граф.
Методы
теории графов широко применяются в
дискретной математике. Без них невозможно
обойтись при анализе и синтезе различных
дискретных преобразователей: функциональных
блоков компьютеров, комплексов программ
и т.д.
В
настоящее время теория графов охватывает
большой материал и активно развивается.
Графом
называется набор точек (эти точки
называются вершинами), некоторые из
которых объявляются смежными (или
соседними). Считается, что смежные
вершины соединены между собой ребрами
(или дугами).
Таким
образом, ребро определяется парой
вершин. Два ребра, у которых есть общая
вершина, также называются смежными (или
соседними).
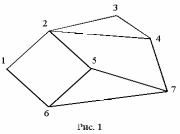
Рис.1
пример графа «звезда».
Граф
называется ориентированным
(или орграфом), если
некоторые ребра имеют направление. Это означает,
что в орграфе некоторая вершина может
быть соединена с другой вершиной, а
обратного соединения нет. Геометрически
граф часто изображают точками плоскости,
причем соседние вершины соединены
дугами (для орграфа некоторые дуги имеют
направление, что обычно отмечают
стрелкой).
Помимо
этого, в теории графов рассматриваются
также мультиграфы
– это
такие графы, в которых могут быть петли (т. е.
некоторая вершина соединена сама с
собой ребром) или некоторые пары вершины
могут быть соединены между собой
несколькими ребрами.
Маршрут в
графе – это последовательность соседних
(смежных) вершин. Ясно, что можно определить
маршрут и как последовательность смежных
ребер (в этом случае ребра
приобретаютнаправление).
Заметим, что в маршруте могут повторяться
вершины, но не ребра. Маршрут
называется циклом,
если в нем первая вершина совпадает с
последней.
Путь в
графе (иногда говорят простой путь) –
это маршрут без повторения вершин (а
значит, и ребер).
Контур
– это
цикл без повторения вершин, за исключением
первой вершины, совпадающей с последней.
Последовательности
вершин (рис. 2): 1–2–3–4–2–5 не простой
путь, а маршрут; последовательности
1–2–3–4–7–5 и 1–2–5 – простые пути;
1–2–3–4–2–5–6–1 –это цикл (но не контур);
1–2–5–6–1 – это контур.
Рис.2
Если
имеется некоторый маршрут из вершины t в
вершину s, заданный
в виде последовательности ребер, которые
в этом случае приобрели направление, и
если в этот маршрут входит ребро,
соединяющее вершины (i, j),
то это ребро по отношению к вершине i называют
иногда прямой
дугой, а
по отношению к вершине j
– обратной дугой (или
обратным ребром).
Граф
называется связным,
если любые две его вершины можно соединить
маршрутом (или путем). На
рис. 2 изображен связный граф.
Ребро,
при удалении которого граф перестает
быть связным, иногда называют мостом или перешейком.
Следующее
определение имеет смысл только для
графов или мультиграфов без петель (но
не для орграфов).
Степень вершины
– это число ребер, входящих в эту вершину.
Вершина называется висячей,
если ее степень равна единице.
2. Раскраска графа
Раскраской вершин
графа называется назначение цветов его
вершинам. Обычно цвета – это числа 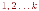
Тогда раскраска является функцией,
определенной на множестве вершин графа
и принимающей значения в множестве 
Раскраску можно также рассматривать
как разбиение множества вершин 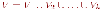
где 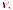
множество вершин цвета 
Множества 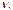
цветными классами. Раскраска
называется правильной,
если каждый цветной класс является
независимым множеством. Иначе говоря,
в правильной раскраске любые две смежные
вершины должны иметь разные цвета.
Задача о раскраске состоит в нахождении
правильной раскраски данного графа 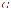
наименьшее число цветов. Это число
называется хроматическим
числом графа
и обозначается 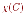
Соседние файлы в папке лекции новые
- #
- #
- #
- #
- #
- #
- #
- #
- #