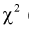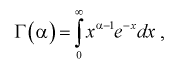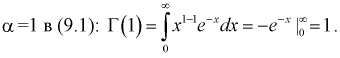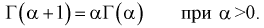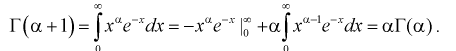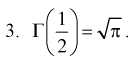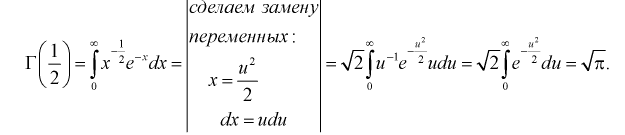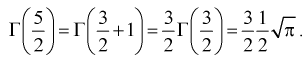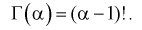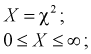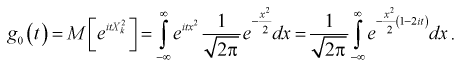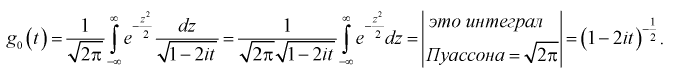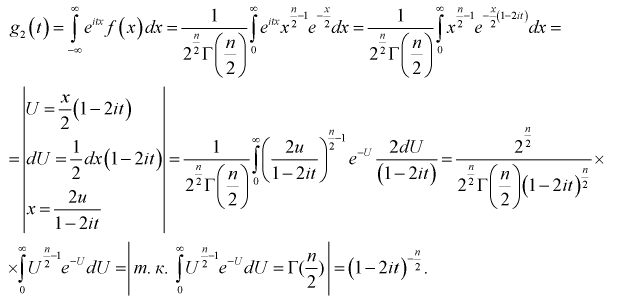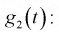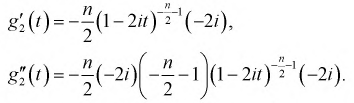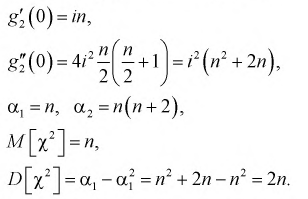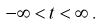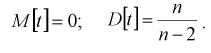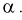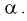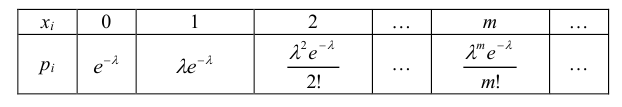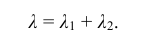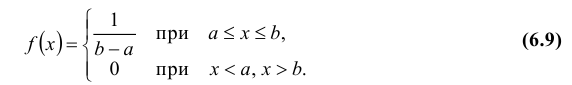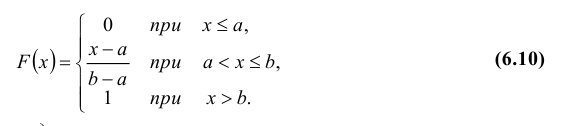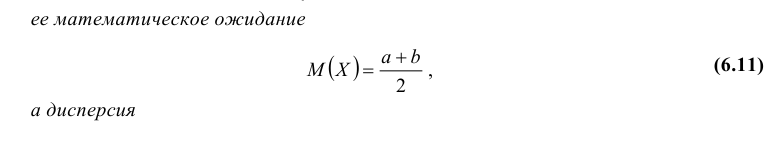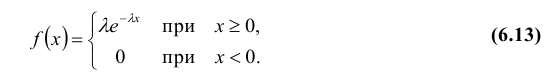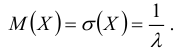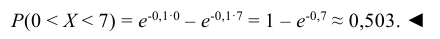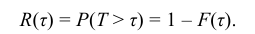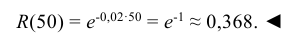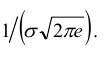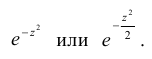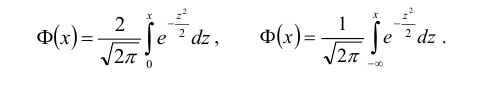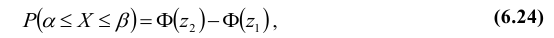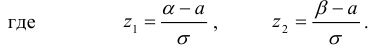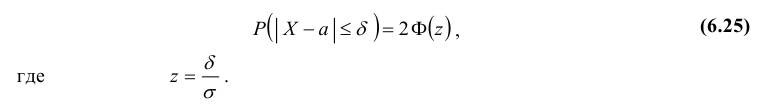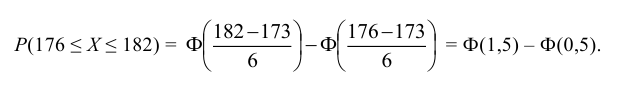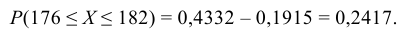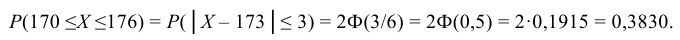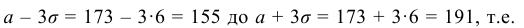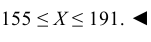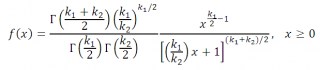| Распределение Фишера (Распределение Снедекора) | |
|---|---|
 Плотность вероятности Плотность вероятности |
|
 Функция распределения Функция распределения |
|
| Обозначение |
 |
| Параметры |
 – числа степеней свободы – числа степеней свободы |
| Носитель |
 |
| Плотность вероятности |
 |
| Функция распределения |
 |
| Математическое ожидание |
 , если , если  |
| Мода |
 , если , если  |
| Дисперсия |
 если если  |
| Коэффициент асимметрии |
 если  |
| Производящая функция моментов | не существует[1] |
Распределе́ние Фи́шера в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений.
Определение[править | править код]
Пусть 


называется распределением Фишера (распределением Снедекора) со степенями свободы
и
. Пишут
.
Моменты[править | править код]
Математическое ожидание и дисперсия случайной величины, имеющей распределение Фишера, имеют вид:
, если
,
, если
.
Свойства распределения Фишера[править | править код]
Связь с другими распределениями[править | править код]
Примечания[править | править код]
- ↑ Johnson N. L., Kotz S., Balakrishnan N. Continuous Univariate Distributions, Volume 2 (Second Edition, Section 27).. — Wiley, 1995. — ISBN 0-471-58494-0.
Ссылки[править | править код]
- Table of critical values of the F-distribution
- Earliest Uses of Some of the Words of Mathematics: entry on F-distribution contains a brief history
- Free calculator for F-testing
Пусть имеем две СВ распределенные по
закону «хи квадрат»
и
со степенями свободы
и
соответственно. Тогда следующая СВ:
(2.46)
называется СВ с F-
распределением (т.е. распределением
Фишера) с
и
степенями свободы (обозначают также
через)
. Как видим, F- отношение
положительная СВ. При больших
и
это распределение приближается к
нормальному (рис.2.6). Заметим, что
(где
– СВ, имеющая распределение Стьюдента
с числом степеней свободы
)
совпадает с F-распределением
со степенями свободы 1,
–
.
Числовые характеристики распределения
Фишера:
,
(2.47)
На графике изображены распределения
Фишера для различных степеней свободы.
Рис. 2.6
Распределение Фишера используется при
проверке статистических гипотез, в
дисперсионном и регрессионном анализах.
В таблице Пр.5. приводятся правосторонние
критические границы
этого распределения для разных значений
степеней свободы:
.
-
Предельные теоремы теории вероятностей. Закон больших чисел.
В этом параграфе приведены основные
сведения о законах больших чисел и
центральной предельной теореме. Законы
больших чисел утверждают, что среднее
арифметическое большого числа независимых
СВ ведет себя как среднее арифметическое
их математических ожиданий.
Согласно центральной предельной
теореме большая сумма малых СВ ведет
себя приближенно как нормальная СВ.
Эти утверждения имеют большое
практическое значение и составляют
теоретическую основу математической
статистики, широко применяющейся для
анализа экономической информации
(результатов наблюдении) с целью выработки
обоснованных управляющих решений.
Анализируя собранную экономическую
информацию и определив закон распределения
СВ, все же нельзя уверенно прогнозировать,
предвидеть ее дальнейшие значения,
потому что на явление (процесс) влияют
многие неучтенные в модели (по причине
наших незнании о их существовании или
нашей неспособности их учета) факторы,
причины. Оказывается, что при достаточно
большого числа случайных величин (СВ),
хоть и каждое из них имеет стохастическое,
хаотическое поведение, суммарное
поведение всего ансамбля почти утрачивает
случайный характер и становится почти
закономерным.
Для практики очень важно знать, при
каких условиях совокупное влияние
большого числа случайных причин (величин)
приводит к результату, почти не зависящему
от случая (от каждого из них), т.е.
позволяет прогнозировать ход явлений.
Эти условия приводятся в виде теорем,
основное из которых теорема Чебышева
(в частном случае теорема Бернулли).
Теоретическую основу законов больших
чисел составляют понятие сходимости
СВ по вероятности и неравенство Чебышева.
Сходимость по вероятности
последовательности СВ
к СВ
означает,
что при
вероятность приближенности
к
стремится к единице:
.
По теореме Чебышева среднее
арифметическое большого числа независимых
СВ (дисперсии которых равномерно
ограничены, т.е. не превышают постоянного
числа С) ведет себя как среднее
арифметическое их математических
ожиданий ( тем точнее, чем больше
независимых « участников» – СВ):
(2.48)
Формулируя теорему Чебышева, предполагали,
что СВ имеют различные мат. ожидания.
На практике часто СВ имеют одинаковые
мат. ожидания – обозначим через
,
следовательно их среднее арифметическое
также равно
.
Для этого частного случая теорема
Чебышева формулируется так:
Если
–
попарно независимые случайные величины,
имеющие одно и то же мат. ожидание
,
и если дисперсии этих величин равномерно
ограничены, то, как бы мало не било число
,
вероятность неравенства
будет как угодно близка к единице,
если число СВ
достаточно велико.
Другими словами будет иметь место
равенство:
(2.49)
Сущность теоремы такова: хотя
отдельные независимые СВ могут принимать
значения, далекие от своих мат. ожиданий,
среднее арифметическое достаточно
большого числа СВ с большой вероятностью
принимает значения, близкие среднему
арифметическому их мат. ожиданий. Иными
словами, отдельные СВ могут иметь
значительный разброс, а их среднее
арифметическое имеет малый разброс.
Таким образом, нельзя уверенно
предсказать, какое возможное значение
примет каждая из СВ, но можно предвидеть,
какое значение примет их среднее
арифметическое.
Среднее арифметическое достаточно
большого числа независимых СВ (дисперсии
которых равномерно ограничено) почти
утрачивает характер СВ. Объясняется
это тем, что отклонения каждой из СВ от
своих мат. ожиданий могут быть как
положительными, так и отрицательными,
а в среднем арифметическом они взаимно
погашаются.
Значение теоремы Чебышева для практики
велико. Широко применяемый в статистике
выборочный метод, суть которого состоит
в том, что по сравнительно небольшой
случайной выборке судят о всей совокупности
исследуемых объектов, основан на теореме
Чебышева.
Например, определение качества зерна
по небольшой его пробе. Число наудачу
отобранных зерен мало сравнительно со
всей массой зерна, но само по себе оно
достаточно велико, чтобы судить о
качестве всей совокупности. Обычно для
измерения некоторой физической величины
производят несколько измерений и в
качестве искомого размера берут их
среднее арифметическое, тем самим
минимизируя случайные отклонения
измеряемой величины. Однако ошибочно
думать, что, увеличивая число измерений,
можно достичь сколь угодно большой
точности. Дело в том, что все измерения
получаются лишь с точностью, не превышающей
точности (чувствительности) прибора.
Пусть производится
независимых испытаний, в каждом из
которых вероятность появления события
А равна
.
Можно ли предвидеть, какова примерно
будет относительная частота появлений
события? Положительный ответ на этот
вопрос дает теорема Якоба Бернулли
(доказана им и опубликована в 1713 г.),
которая получила название «закона
больших чисел» и положила начало теории
вероятностей как науке.
Теорема Бернулли. Если в каждом
из
независимых испытаний вероятность
появления события А постоянна, то как
угодно близка к единице вероятность
того, что отклонение относительной
частоты от вероятности
по абсолютной величине будет сколь
угодно малым, если число испытаний
достаточно велико.
Иными словами имеет место равенство:
(2.50)
Сходимость относительной частоты
к вероятности
отличается от сходимости в смысле
математического анализа.
стремится к
по вероятности при
,
означает, что не для всех значений
(где
большое
число) неуклонно выполняется неравенство
,
т.е. для отдельных значений
неравенство может не выполняться.
Как видим, теорема Бернулли объясняет,
почему относительная частота при
достаточно большом числе испытаний
обладает свойством устойчивости и
оправдывает статистическое определение
вероятности (см. гл. 1.).
Понятие о теореме Ляпунова (центральная
предельная теорема) Известно, что
нормально распределенные СВ широко
распространены. Чем это объясняется?
Ответ на этот вопрос был дан выдающимся
русским математиком А.М. Ляпуновым:
теорема – если СВ Х представляет собой
сумму большого числа взаимно независимых
СВ, влияние каждого из которых на всю
сумму ничтожно мало, то Х имеет
распределение, близкое к нормальному.
На практике эта теорема наиболее часто
используется в том случае, когда члены
суммы имеют одинаковое распределение.
Следствие из теоремы Ляпунова –
Если независимые СВ
имеют одинаковое распределение (),
то функция распределения их
центрированной и нормированной суммы
сходится к функции распределения
стандартной нормальной СВ:
(2.51)
Этим положением пользуются при решении
практических задач: при
распределение соответствующей суммы
заменяют на распределение стандартной
нормальной СВ.
Пример 2.2 Определить вероятность
того, что средняя продолжительность
100 производственных операций окажется
в пределах от 46 до 49 с, если мат. ожидание
одной операции равно 47,4 с, а среднее
квадратичное отклонение – 4,9 с.
Решение – в этой задаче СВ Х это
продолжительность наугад взятой
операции, причем
=47,4
с,
=4,9
с,
,
(=100
) – средняя продолжительность одной
операций и
=47,4
с,
=
.
= Ф(3,265)+ Ф(2,857) = = 0,9984 (воспользовались
таблицей значении функции Лапласа).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
В статистике наиболее часто применяются такие распределения:
- Нормальное (Гауссовское) распределение.
- Распределение Пирсона, распределение
- Распределение Стьюдента (t – распределение).
- Распределение Фишера (F – распределение).
Нормальный закон распределения мы подробно рассмотрели при изучении раздела 6.5 теории вероятностей и здесь рассматриваться не будет.
Отметим, что в законы распределений математической статистики входит гамма-функция, поэтому необходимо познакомиться с этой функцией и рассмотреть ее свойства.
Гамма-функция и ее свойства
Гамма-функцией или интегралом Эйлера второго рода называется функция следующего вида:
где 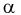
Свойства гамма-функции:
1. Г(1) = Г(2) = 1.
Доказательство:
Подставим
2.
Доказательство:
Вычислим интеграл в (9.1), используя интегрирование по частям:
Доказательство:
Значит, если значение 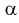
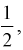
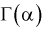
Для целых 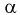
Например,
Г(3) = 2! = 2, Г(4) = 3! = 6, Г(5) = 4! = 24.
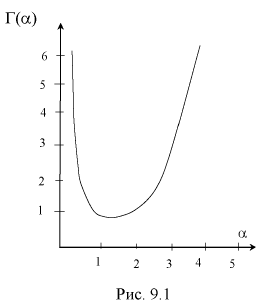
Отметим, что смысл гамма-функции – распространение понятия факториал на нецелые значения. На рис. 9.1 приведен график гамма-функции.
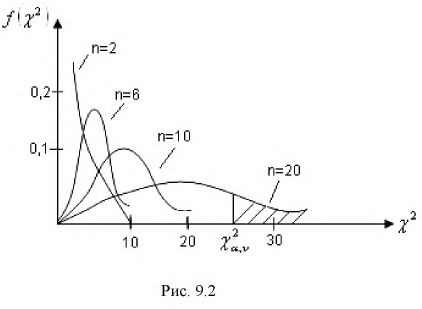
Распределение (хи-квадрат )
Распределение 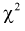
Случайная величина имеет закон распределения 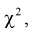
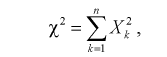
где 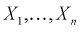
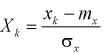
Распределение случайной величины, определенной по формуле (9.2), называется распределением Пирсона.
Покажем, что плотность распределения случайной величины 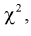
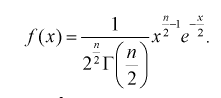
Здесь для краткости записи
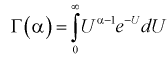
Для доказательства используем аппарат характеристических функций. Найдем характеристическую функцию случайной величины которая входит в формулу (9.2), учитывая, что 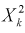
Используем подстановку 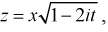
Согласно 5-му свойству характеристической функции (для суммы независимых случайных величин) найдем характеристическую функцию 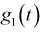
Найдем характеристическую функцию 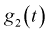
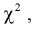
При сравнении правых частей характеристических функций 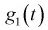
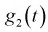
Найдем математическое ожидание и дисперсию случайной величины
Продифференцируем 2 раза
Значения производных при t = 0:
Таким образом, математическое ожидание 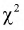
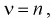
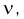
С ростом 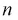
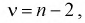
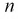
При 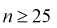
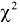
Квантилем 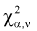
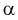
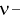
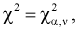
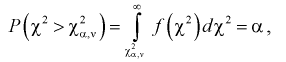
т. е. это то значение 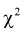
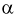
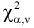
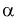
Распределение Стьюдента
Распределение Стьюдента 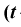
Случайная величина t имеет распределение Стьюдента, если она определяется так.
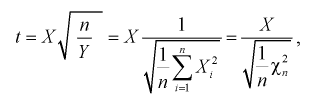
где X – нормированная нормальная случайная величина,
Y – величина 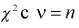
X и Y – независимые случайные величины.
Случайная величина t является функцией нормально распределенных нормированных случайных величин и называется безразмерной дробью Стьюдента. Плотность распределения случайной величины t определяется равенством
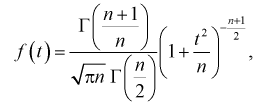
где
Числовые характеристики случайной величины t :
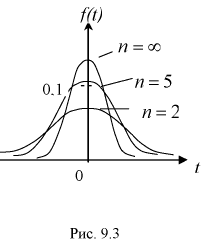
На рис. 9.3 приведены кривые распределения Стьюдента. Кривые на рис. 9.3 качественно напоминают кривые нормального закона распределения с математическим ожиданием, равным нулю, и при 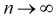
Квантили распределения Стьюдента 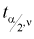
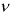
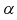
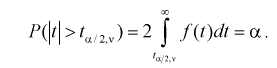
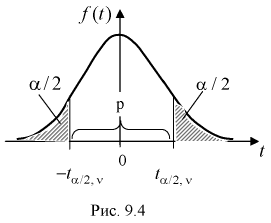
Рис. 9.4 иллюстрирует процесе определения квантилей, т. е. необходимо так выбрать 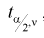
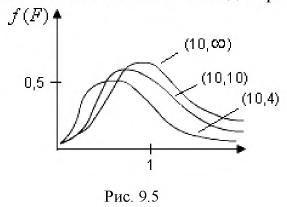
Распределение Фишера (F-распределение)
Случайная величина F имеет распределение Фишера, если она определяется так:
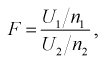
где 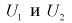
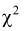
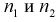
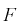
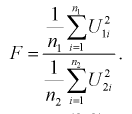
Безразмерная случайная величина F (9.8) имеет плотность распределения, определяемую следующей формулой:
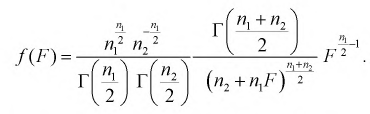
Распределение случайной величины F зависит от двух параметров 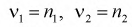
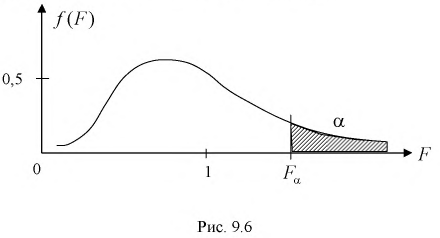
Квантили распределения Фишера 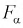
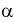
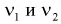
На рис. 9.6 показано, что надо так выбрать 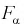
Как правило, квантили 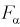
Биноминальный закон распределения
Определение: Дискретная случайная величина Х имеет биноминальный закон распределения, если она принимает значения 0, 1, 2, …, m, …, n с вероятностями 
Как видим, вероятности Р(Х = m) находятся по формуле Бернулли.
Следовательно, биноминальный закон распределения представляет собой закон распределения числа X = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.
Ряд распределения биноминального закона имеет вид:
Теорема. Математическое ожидание случайной величины, распределенной по биноминальному закону 
Следствие. Математическое ожидание частости события в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью, равно 
Биноминальный закон распределения широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и в других областях.
Закон распределения Пуассона
Определение: Дискретная случайная величина Х имеет закон распределения Пуассона, если она принимает значения 0, 1, 2, …, m с вероятностями 
Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е.
При достаточно больших n (вообще при n → ∞) и малых значениях р (р → 0) при условии, что произведение np – постоянная величина (nр → λ = const), закон распределения Пуассона является хорошим приближением биноминального закона. Т.е. при n → ∞, р → 0, nр → λ = const закон распределения Пуассона является предельным случаем биноминального закона. Так как при этом вероятность р события А в каждом испытании мала, то закон распределения Пуассона часто называют законом редких явлений.
По закону Пуассона распределены, например, число сбоев на автоматической линии, число отказов сложной системы в нормальном режиме, число требований на обслуживание в единицу времени в системах массового обслуживания, и т.п.
Отметим еще, что если случайная величина представляет собой сумму двух независимых случайных величин, каждая из которых распределена по закону Пуассона, то она также распределена по закону Пуассона с параметром
Равномерный закон распределения
Определение: Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a; b], если ее плотность вероятности f(x) постоянна на этом отрезке и равна нулю вне его, т.е.
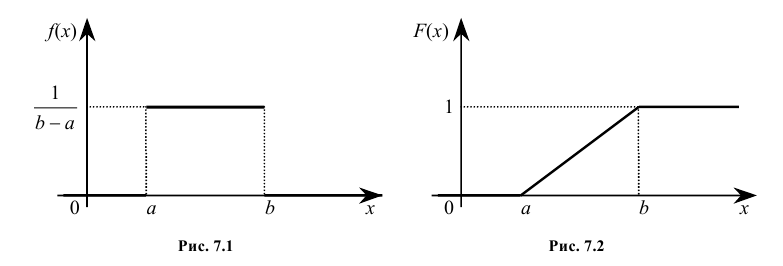
Кривая распределения f(x) и график функции распределения F(x) случайной величины Х приведены соответственно на рис. 7.1 и рис. 7.2.
Теорема. Функция распределения случайной величины Х, распределенной по равномерному закону, есть
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач теории массового обслуживания, при статистическом моделировании наблюдений, подчиненных заданному распределению, и т.д.
Показательный (экспоненциальный) закон распределения
Определение: Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности f(x) имеет вид:
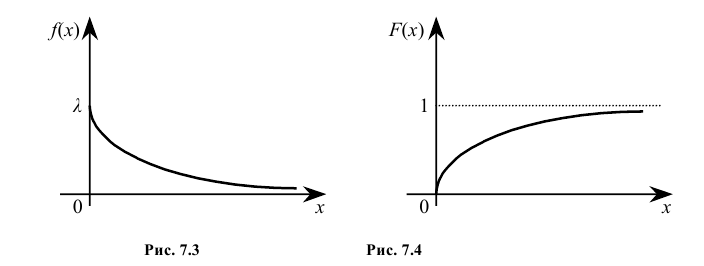
Кривая распределения f(x) и график функции распределения F(x) случайной величины Х приведены соответственно на рис. 7.3 и рис. 7.4.
Теорема. Функция распределения случайной величины Х, распределенной по показательному (экспоненциальному) закону, есть 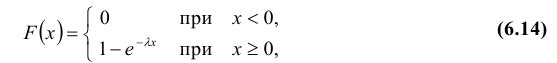

Отсюда следует, что для случайной величины, распределенной по показательному закону, математическое ожидание равно среднему квадратическому отклонению, т.е.
Вероятность попадания в интервал [a; b] непрерывной случайной величины Х, распределенной по показательному закону, находится как
Пример:
Установлено, что время ремонта железнодорожных вагонов есть случайная величина Х, распределенная по показательному закону. Определить вероятность того, что на ремонт вагона потребуется менее 7 дней, если среднее время ремонта вагонов составляет 10 дней.
Решение:
По условию математическое ожидание М(Х) = 1/λ = 10, откуда параметр λ = 0,1. По формуле (6.17) находим вероятность попадания случайной величины Х в интервал [0, 7]:
Показательный закон распределения играет большую роль в теории массового обслуживания. Так например, интервал времени между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром λ – интенсивностью потока. Кроме того, показательное распределение широко применяется в теории надежности, одним из основных понятий которой является функция надежности.
Функция надежности
Будем называть элементом некоторое устройство. Пусть элемент начинает работать в момент времени 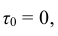
Таким образом, интегральная функция 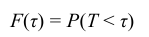
Функцией надежности R(τ), называют функцию, определяющую вероятность безотказной работы элемента за время длительностью τ: 
Широкое использование показательного закона распределения обусловлено тем, что только он обладает следующим важным свойством: Если промежуток времени Т, распределенный по показательному закону, уже длился некоторое время τ, то это никак не влияет на закон распределения оставшейся части 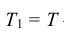
Пример:
Время безотказной работы устройства распределено по показательному закону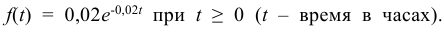
Решение:
По условию постоянная интенсивность отказов λ = 0,02. Используя формулу (6.18), получаем:
Нормальный закон распределения
Нормальный закон распределения наиболее часто встречается на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
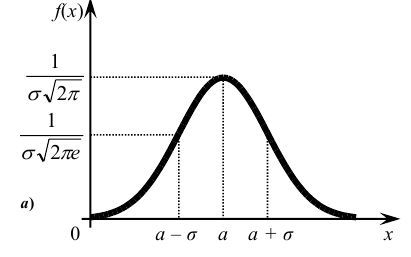
Определение: Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и 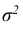
Кривую нормального закона распределения называют нормальной или гауссовой кривой. На рис. 6.5 а), б) показана нормальная кривая с параметрами а и 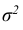
Обратим внимание на то, что нормальная кривая симметрична относительно прямой х = а, имеет максимум в точке х = а, равный 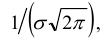
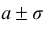
Можно заметить, что в выражении плотности нормального закона параметры распределения обозначены буквами а и 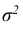
Теорема. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру a этого распределения, т.е. 
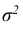
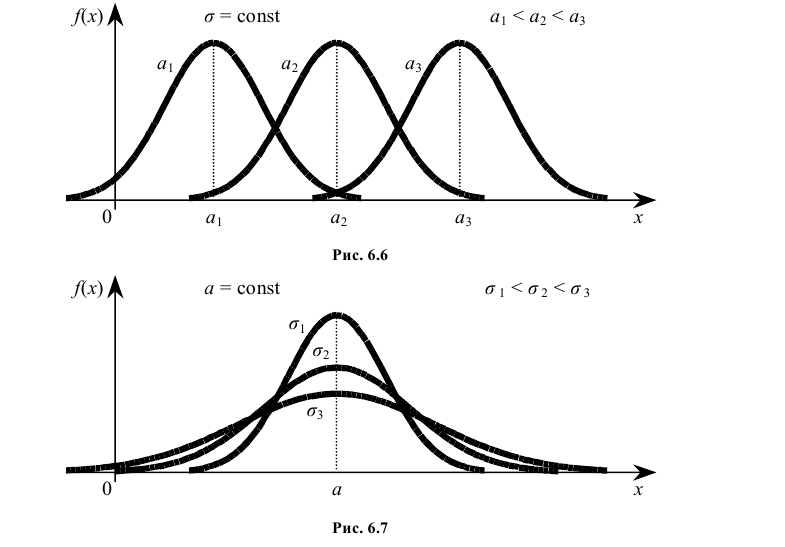
Выясним, как будет меняться нормальная кривая при изменении параметров а и σ. Если σ = const, и меняется параметр a (а1 < а2 < а3), т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (рис. 6.6).
Если а = const и меняется параметр σ, то меняется ордината максимума кривой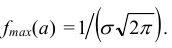
Таким образом, параметр a характеризует положение , а параметр σ – форму нормальной кривой.
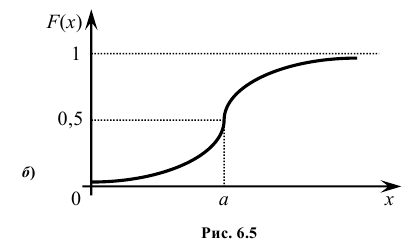
Нормальный закон распределения случайной величины с параметрами a = 0 и σ = 1 называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной. Сложность непосредственного нахождения функции распределения случайной величины, распределенной по нормальному закону, связана с тем, что интеграл от функции нормального распределения не выражается через элементарные функции. Однако его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения
Такую функцию называют функцией Лапласа, для нее составлены таблицы. Существует много разновидностей такой функции, например:
Мы будем использовать функцию:
Для такой функции табличные значения приведены в Приложении 2.
Теорема. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле
Рассмотрим свойства случайной величины, распределенной по нормальному закону.
1. Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал [α, β] равна
2. Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания a не превысит величину δ > 0 (по абсолютной величине), равна
Вычислим по этой формуле вероятности 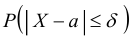
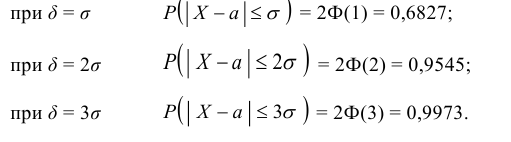
Пример:
Полагая, что рост мужчин определенной возрастной группы есть нормально распределенная случайная величина Х с параметрами а = 173 и 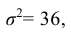
Решение:
1. Находим плотность вероятности 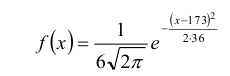
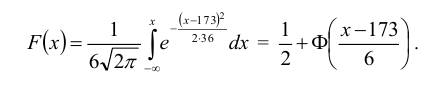
По таблице значений функции Лапласа (Приложение 2) находим:
Окончательно получаем
Долю костюмов 3-го роста (170 – 176 см) можно найти аналогично. Однако проще это сделать, если учесть, что данный интервал симметричен относительно математического ожидания а = 173, т.е. неравенство 170 ≤ Х ≤ 176 равносильно неравенству │Х – 173│≤ 3. Тогда
3. Сформулируем «правило трех сигм» для случайной величины Х: Практически достоверно, что рост мужчин данной возрастной группы заключен в границах от
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Ковариация в теории вероятности
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
- Нормальный закон распределения
Рассмотрим распределение Фишера (F-распределение). С помощью функции
MS
EXCEL
F
.РАСП()
построим графики функции распределения и плотности вероятности, поясним применение этого распределения для целей математической статистики.
F-распределение
(англ. F-distribution)
применяется для целей дисперсионного анализа (ANOVA), при
проверке гипотезы о равенстве дисперсий двух нормальных распределений (F-тест)
и др.
Определение
: Если U
1
и U
2
независимые случайные величины, имеющие
ХИ2-распределение
с k
1
и k
2
степенями свободы
соответственно, то распределение случайной величины:
носит название
F
-распределения
с параметрами k
1
и k
2
.
Плотность
F
-распределения
выражается формулой:
где Г(…) – гамма-функция:
если
альфа
– положительное целое, то Г(
альфа
)=(
альфа
-1)!
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Приведем пример случайной величины, имеющей
F
-распределение.
Пусть имеется 2
нормальных распределения
N(μ
1
;σ
1
) и N(μ
2
; σ
2
), из которых сделаны выборки размером n
1
и n
2
. Если s
1
2
и s
2
2
–
дисперсии этих выборок
, то отношение
имеет
F
-распределение.
Это соотношение нам потребуется при проверке
гипотезы о равенстве дисперсий двух нормальных распределений (F-тест)
.
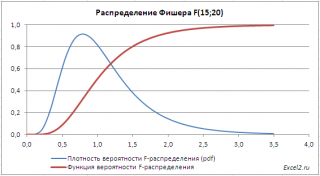
Графики функций
F
-распределение
при небольших параметрах (<50) имеет несимметричную форму, скошенную вправо (длинный правый хвост).
Среднее значение
равно k
2
/(k
2
-2) при k
2
>2,
дисперсия
равна 2*k
2
2
*(k
1
+k
2
-2)/(k
1
*(k
2
-4)*(k
2
-2)
2
) при k
2
>4.
В
файле примера на листе График
приведены
графики плотности распределения
вероятности и
интегральной функции распределения
.
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью
Основные типы диаграмм
.
F-распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для
F-распределения
имеется специальная функция
F.РАСП()
, английское название – F.DIST(), которая позволяет вычислить
плотность вероятности
(см. формулу выше) и
интегральную функцию распределения
(вероятность, что случайная величина Х, имеющая
F
–
распределение
, примет значение меньше или равное х, P(X <= x)).
Примечание
:
Плотность вероятности
можно также вычислить впрямую, с помощью формул (см.
файл примера
).
До MS EXCEL 2010 в EXCEL была функция
FРАСП()
, которая позволяет вычислить
функцию распределения
(точнее – правостороннюю вероятность, т.е. P(X>x)). Функция
FРАСП()
оставлена в MS EXCEL 2010 для совместимости. Аналогом
FРАСП()
является функция
F.РАСП.ПХ()
, появившаяся в MS EXCEL 2010.
Примеры расчетов приведены в
файле примера на листе Функции
.
В MS EXCEL имеется еще одна функция, использующая для расчетов
F-распределение
– это
F.ТЕСТ(массив1;массив2)
. Эта функция возвращает результат
F-теста
: двухстороннюю вероятность того, что разница между дисперсиями выборок “массив1” и “массив2” несущественна. Предполагается, что
выборки
делаются из
нормального распределения
.
Подробнее об использовании этой функции см.
статью про проверку гипотез о равенстве двух дисперсий
.
Обратная функция F-распределения
Обратная функция используется для вычисления
альфа
–
квантилей
, т.е. для вычисления значений
x
при заданной вероятности
альфа
, причем
х
должен удовлетворять выражению P{X<=x}=
альфа
.
В MS EXCEL обратная функция реализована с помощью функции
F.ОБР()
.
Функция
F.ОБР.ПХ()
используется для вычисления
верхнего квантиля
. Т.е. если в качестве аргумента функции указан уровень значимости, например 0,05, то функция вернет такое значение случайной величины х, для которого P(X>x)=0,05. В качестве сравнения: функция
F.ОБР()
вернет такое значение случайной величины х, для которого P(X<=x)=0,05.
В MS EXCEL 2007 и ранее вместо
F.ОБР.ПХ()
использовалась функция
FРАСПОБР()
.
Вышеуказанные функции можно взаимозаменять, т.к. следующие формулы возвращают одинаковый результат:
=F.ОБР(0,05;k1;k2) =F.ОБР.ПХ(1-0,05;k1;k2) = FРАСПОБР (1-0,05;k1;k2)
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
F-распределение является асимметричным и обычно используется в дисперсионном анализе. Такую плотность распределения имеют величины, являющиеся отношением двух величин, имеющих хи-квадрат распределение, при этом соответствующее F-распределение определяется двумя значениями числа степеней свободы. Первый индекс всегда соответствует числу степеней свободы для числителя, и этот порядок является существенным, поскольку F(10,12) не равно F(12,10). В столбце показано число степеней свободы числителя, а в строке — число степеней свободы для знаменателя. В названии таблицы указано значение вероятности. Например, критическое значение F-распределения для вероятности 0.05 и степеней свободы 10 и 12 находится на пересечении столбца со значением 10 (числитель) и строки со значением 12 (знаменатель): F(0.05, 10, 12) = 2.7534.
df1— число степеней свободы большей дисперсии
df2—число степеней свободы меньшей дисперсии
Уровень значимости a =0.05
|
df2/df1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
15 |
20 |
24 |
30 |
40 |
60 |
120 |
INF |
|
1 |
161.4476 |
199.5000 |
215.7073 |
224.5832 |
230.1619 |
233.9860 |
236.7684 |
238.8827 |
240.5433 |
241.8817 |
243.9060 |
245.9499 |
248.0131 |
249.0518 |
250.0951 |
251.1432 |
252.1957 |
253.2529 |
254.3144 |
|
2 |
18.5128 |
19.0000 |
19.1643 |
19.2468 |
19.2964 |
19.3295 |
19.3532 |
19.3710 |
19.3848 |
19.3959 |
19.4125 |
19.4291 |
19.4458 |
19.4541 |
19.4624 |
19.4707 |
19.4791 |
19.4874 |
19.4957 |
|
3 |
10.1280 |
9.5521 |
9.2766 |
9.1172 |
9.0135 |
8.9406 |
8.8867 |
8.8452 |
8.8123 |
8.7855 |
8.7446 |
8.7029 |
8.6602 |
8.6385 |
8.6166 |
8.5944 |
8.5720 |
8.5494 |
8.5264 |
|
4 |
7.7086 |
6.9443 |
6.5914 |
6.3882 |
6.2561 |
6.1631 |
6.0942 |
6.0410 |
5.9988 |
5.9644 |
5.9117 |
5.8578 |
5.8025 |
5.7744 |
5.7459 |
5.7170 |
5.6877 |
5.6581 |
5.6281 |
|
5 |
6.6079 |
5.7861 |
5.4095 |
5.1922 |
5.0503 |
4.9503 |
4.8759 |
4.8183 |
4.7725 |
4.7351 |
4.6777 |
4.6188 |
4.5581 |
4.5272 |
4.4957 |
4.4638 |
4.4314 |
4.3985 |
4.3650 |
|
6 |
5.9874 |
5.1433 |
4.7571 |
4.5337 |
4.3874 |
4.2839 |
4.2067 |
4.1468 |
4.0990 |
4.0600 |
3.9999 |
3.9381 |
3.8742 |
3.8415 |
3.8082 |
3.7743 |
3.7398 |
3.7047 |
3.6689 |
|
7 |
5.5914 |
4.7374 |
4.3468 |
4.1203 |
3.9715 |
3.8660 |
3.7870 |
3.7257 |
3.6767 |
3.6365 |
3.5747 |
3.5107 |
3.4445 |
3.4105 |
3.3758 |
3.3404 |
3.3043 |
3.2674 |
3.2298 |
|
8 |
5.3177 |
4.4590 |
4.0662 |
3.8379 |
3.6875 |
3.5806 |
3.5005 |
3.4381 |
3.3881 |
3.3472 |
3.2839 |
3.2184 |
3.1503 |
3.1152 |
3.0794 |
3.0428 |
3.0053 |
2.9669 |
2.9276 |
|
9 |
5.1174 |
4.2565 |
3.8625 |
3.6331 |
3.4817 |
3.3738 |
3.2927 |
3.2296 |
3.1789 |
3.1373 |
3.0729 |
3.0061 |
2.9365 |
2.9005 |
2.8637 |
2.8259 |
2.7872 |
2.7475 |
2.7067 |
|
10 |
4.9646 |
4.1028 |
3.7083 |
3.4780 |
3.3258 |
3.2172 |
3.1355 |
3.0717 |
3.0204 |
2.9782 |
2.9130 |
2.8450 |
2.7740 |
2.7372 |
2.6996 |
2.6609 |
2.6211 |
2.5801 |
2.5379 |
|
11 |
4.8443 |
3.9823 |
3.5874 |
3.3567 |
3.2039 |
3.0946 |
3.0123 |
2.9480 |
2.8962 |
2.8536 |
2.7876 |
2.7186 |
2.6464 |
2.6090 |
2.5705 |
2.5309 |
2.4901 |
2.4480 |
2.4045 |
|
12 |
4.7472 |
3.8853 |
3.4903 |
3.2592 |
3.1059 |
2.9961 |
2.9134 |
2.8486 |
2.7964 |
2.7534 |
2.6866 |
2.6169 |
2.5436 |
2.5055 |
2.4663 |
2.4259 |
2.3842 |
2.3410 |
2.2962 |
|
13 |
4.6672 |
3.8056 |
3.4105 |
3.1791 |
3.0254 |
2.9153 |
2.8321 |
2.7669 |
2.7144 |
2.6710 |
2.6037 |
2.5331 |
2.4589 |
2.4202 |
2.3803 |
2.3392 |
2.2966 |
2.2524 |
2.2064 |
|
14 |
4.6001 |
3.7389 |
3.3439 |
3.1122 |
2.9582 |
2.8477 |
2.7642 |
2.6987 |
2.6458 |
2.6022 |
2.5342 |
2.4630 |
2.3879 |
2.3487 |
2.3082 |
2.2664 |
2.2229 |
2.1778 |
2.1307 |
|
15 |
4.5431 |
3.6823 |
3.2874 |
3.0556 |
2.9013 |
2.7905 |
2.7066 |
2.6408 |
2.5876 |
2.5437 |
2.4753 |
2.4034 |
2.3275 |
2.2878 |
2.2468 |
2.2043 |
2.1601 |
2.1141 |
2.0658 |
|
16 |
4.4940 |
3.6337 |
3.2389 |
3.0069 |
2.8524 |
2.7413 |
2.6572 |
2.5911 |
2.5377 |
2.4935 |
2.4247 |
2.3522 |
2.2756 |
2.2354 |
2.1938 |
2.1507 |
2.1058 |
2.0589 |
2.0096 |
|
17 |
4.4513 |
3.5915 |
3.1968 |
2.9647 |
2.8100 |
2.6987 |
2.6143 |
2.5480 |
2.4943 |
2.4499 |
2.3807 |
2.3077 |
2.2304 |
2.1898 |
2.1477 |
2.1040 |
2.0584 |
2.0107 |
1.9604 |
|
18 |
4.4139 |
3.5546 |
3.1599 |
2.9277 |
2.7729 |
2.6613 |
2.5767 |
2.5102 |
2.4563 |
2.4117 |
2.3421 |
2.2686 |
2.1906 |
2.1497 |
2.1071 |
2.0629 |
2.0166 |
1.9681 |
1.9168 |
|
19 |
4.3807 |
3.5219 |
3.1274 |
2.8951 |
2.7401 |
2.6283 |
2.5435 |
2.4768 |
2.4227 |
2.3779 |
2.3080 |
2.2341 |
2.1555 |
2.1141 |
2.0712 |
2.0264 |
1.9795 |
1.9302 |
1.8780 |
|
20 |
4.3512 |
3.4928 |
3.0984 |
2.8661 |
2.7109 |
2.5990 |
2.5140 |
2.4471 |
2.3928 |
2.3479 |
2.2776 |
2.2033 |
2.1242 |
2.0825 |
2.0391 |
1.9938 |
1.9464 |
1.8963 |
1.8432 |
|
21 |
4.3248 |
3.4668 |
3.0725 |
2.8401 |
2.6848 |
2.5727 |
2.4876 |
2.4205 |
2.3660 |
2.3210 |
2.2504 |
2.1757 |
2.0960 |
2.0540 |
2.0102 |
1.9645 |
1.9165 |
1.8657 |
1.8117 |
|
22 |
4.3009 |
3.4434 |
3.0491 |
2.8167 |
2.6613 |
2.5491 |
2.4638 |
2.3965 |
2.3419 |
2.2967 |
2.2258 |
2.1508 |
2.0707 |
2.0283 |
1.9842 |
1.9380 |
1.8894 |
1.8380 |
1.7831 |
|
23 |
4.2793 |
3.4221 |
3.0280 |
2.7955 |
2.6400 |
2.5277 |
2.4422 |
2.3748 |
2.3201 |
2.2747 |
2.2036 |
2.1282 |
2.0476 |
2.0050 |
1.9605 |
1.9139 |
1.8648 |
1.8128 |
1.7570 |
|
24 |
4.2597 |
3.4028 |
3.0088 |
2.7763 |
2.6207 |
2.5082 |
2.4226 |
2.3551 |
2.3002 |
2.2547 |
2.1834 |
2.1077 |
2.0267 |
1.9838 |
1.9390 |
1.8920 |
1.8424 |
1.7896 |
1.7330 |
|
25 |
4.2417 |
3.3852 |
2.9912 |
2.7587 |
2.6030 |
2.4904 |
2.4047 |
2.3371 |
2.2821 |
2.2365 |
2.1649 |
2.0889 |
2.0075 |
1.9643 |
1.9192 |
1.8718 |
1.8217 |
1.7684 |
1.7110 |
|
26 |
4.2252 |
3.3690 |
2.9752 |
2.7426 |
2.5868 |
2.4741 |
2.3883 |
2.3205 |
2.2655 |
2.2197 |
2.1479 |
2.0716 |
1.9898 |
1.9464 |
1.9010 |
1.8533 |
1.8027 |
1.7488 |
1.6906 |
|
27 |
4.2100 |
3.3541 |
2.9604 |
2.7278 |
2.5719 |
2.4591 |
2.3732 |
2.3053 |
2.2501 |
2.2043 |
2.1323 |
2.0558 |
1.9736 |
1.9299 |
1.8842 |
1.8361 |
1.7851 |
1.7306 |
1.6717 |
|
28 |
4.1960 |
3.3404 |
2.9467 |
2.7141 |
2.5581 |
2.4453 |
2.3593 |
2.2913 |
2.2360 |
2.1900 |
2.1179 |
2.0411 |
1.9586 |
1.9147 |
1.8687 |
1.8203 |
1.7689 |
1.7138 |
1.6541 |
|
29 |
4.1830 |
3.3277 |
2.9340 |
2.7014 |
2.5454 |
2.4324 |
2.3463 |
2.2783 |
2.2229 |
2.1768 |
2.1045 |
2.0275 |
1.9446 |
1.9005 |
1.8543 |
1.8055 |
1.7537 |
1.6981 |
1.6376 |
|
30 |
4.1709 |
3.3158 |
2.9223 |
2.6896 |
2.5336 |
2.4205 |
2.3343 |
2.2662 |
2.2107 |
2.1646 |
2.0921 |
2.0148 |
1.9317 |
1.8874 |
1.8409 |
1.7918 |
1.7396 |
1.6835 |
1.6223 |
|
40 |
4.0847 |
3.2317 |
2.8387 |
2.6060 |
2.4495 |
2.3359 |
2.2490 |
2.1802 |
2.1240 |
2.0772 |
2.0035 |
1.9245 |
1.8389 |
1.7929 |
1.7444 |
1.6928 |
1.6373 |
1.5766 |
1.5089 |
|
60 |
4.0012 |
3.1504 |
2.7581 |
2.5252 |
2.3683 |
2.2541 |
2.1665 |
2.0970 |
2.0401 |
1.9926 |
1.9174 |
1.8364 |
1.7480 |
1.7001 |
1.6491 |
1.5943 |
1.5343 |
1.4673 |
1.3893 |
|
120 |
3.9201 |
3.0718 |
2.6802 |
2.4472 |
2.2899 |
2.1750 |
2.0868 |
2.0164 |
1.9588 |
1.9105 |
1.8337 |
1.7505 |
1.6587 |
1.6084 |
1.5543 |
1.4952 |
1.4290 |
1.3519 |
1.2539 |
|
inf |
3.8415 |
2.9957 |
2.6049 |
2.3719 |
2.2141 |
2.0986 |
2.0096 |
1.9384 |
1.8799 |
1.8307 |
1.7522 |
1.6664 |
1.5705 |
1.5173 |
1.4591 |
1.3940 |
1.3180 |
1.2214 |
1.0000 |
- F-распределение для alpha=0.01
- F-распределение для alpha=0.025
- F-распределение для alpha=0.10
Вернуться Статистические таблицы




![{mathbb {M}}[F]={frac {d_{2}}{d_{2}-2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b335de762ca25732cc5258f62e0264da8d9bfcb)
![{displaystyle mathrm {D} [F]={frac {2,d_{2}^{2},(d_{1}+d_{2}-2)}{d_{1}(d_{2}-2)^{2}(d_{2}-4)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a39fe175b149f8ee9b19a9f877311160dbbcc7c)