|
|
Макеты страниц
ограничена, то не могут появиться значения 

Обратимся к рис. 2, на котором изображены функции 







Выразим эту же вероятность через исходный закон распределения, связав таким образом 












Нетрудно видеть, что речь идет о процедуре подсчета вероятностей, сходной с той, которая приводит к биномиальному закону распределения.
Вероятность для исходной случайной величины принять значение, близкое к 

Вероятность расположения выборки вокруг значения 



Но именно эта вероятность и определяется выражением 

Если при переходе от плотности 

Последнее выражение показывает, что плотность распределения порядковой статистики зависит от исходного распределения и ранга 


Крайний справа максимальный член имеет функцию распределения 






среднего члена

и максимального


Рис. 3
Эти плотности изображены на рис. 3. В полном согласии с интуитивными представлениями плотность центрального члена выборки симметрична относительно медианы исходного распределения, а плотности крайних ограничены тем же интервалом, что и 
Продемонстрируем на этом же примере еще одно любопытное свойство распределений порядковых статистик. Сложим плотности 

на отрезке [0, 1].
Сумма (нормированная) плотностей порядковых статистик оказалась равной исходной плотности 

Оглавление
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА
Утверждение 4.8.
Пусть
– выборка из распределения
,
тогда функция распределения
-ой
порядковой статистики
:
Доказательство:
Выберем произвольным образом и зафиксируем
значение
,
определим на основе выборки
вектор бинарных случайных величин
:

Случайные величины
независимы в совокупности (поскольку
случайные величины
независимы в совокупности) и имеют
одинаковое распределение
(поскольку случайные величины
имеют одинаковую функцию распределения)
:
,
.
Пусть
–
-ая
порядковая статистика, по определению
функция распределения
:
.
Порядковая статистика
меньше величины
тогда и только тогда, когда среди величин
выборки
()
величин меньше
и
величин не меньше
,
то есть тогда и только тогда, когда в
векторе бинарных случайных величин
величин равны 1 и
величин равны 0, что эквивалентно тому,
что случайная величина
больше или равна
.
Поскольку все
независимы и одинаково распределены,
то случайная величина
имеет распределение Бернулли с параметрами
и
,
тогда:
|
|
(4.13) |
Заметим, что полученное равенство
справедливо для любого
,
поскольку величина
была выбрана произвольным образом.
При
из (4.13) получим:
.
При
из (4.13) получим:
.
Утверждение доказано.
Утверждение 4.9
Пусть выполнены условия утверждения
4.8 и функция распределения
дифференцируема при всех
и
,
тогда плотность вероятности
-ой
порядковой статистики
:
,
где
– плотность вероятности.
Доказательство:
Действительно, для того, чтобы получить
выражение для плотности вероятности
достаточно продифференцировать функцию
распределения
:
При
получим:
.
При
получим:
.
При
получим (для краткости опускаем аргумент
функций):
.
Утверждение доказано.
Порядковые статистики используются
для построения оценок квантилей
распределений и параметров.
Определение 4.10.
Пусть
– функция распределения,
–квантиль
(квантиль уровня
)
функции распределения
есть число
такое, что:
.
(если существует несколько значений
,
удовлетворяющих условию
,
то в качестве
-квантили
принимают наименьшее из этих значений).
Если распределение, соответствующее
имеет название, то обычно говорят,
например, «квантиль уровня
нормального распределения с параметрами
0 и 1» или «квантиль уровня
распределения хи-квадрат с
степенями свободы».
Предположим, что функция распределения
зависит от неизвестного параметра
,
тогда
-квантиль
является функцией параметра
и является неизвестной величиной. Для
построения оценки
-квантили
функцию распределения
заменяют эмпирической функцией
распределения
.
Определение 4.11.
Пусть
– эмпирическая функция распределения
выборки
и
– реализация выборки
,
число
называется выборочной
-квантилью,
если:
.
Поскольку реализации эмпирической
функции распределения являются
кусочно-постоянными функциями, то для
(где
– целое число,
)
существует бесконечно много значений
,
удовлетворяющих условию
,
а для
,
вообще говоря, нет ни одного значения
,
удовлетворяющего условию
.
В таком случае в качестве оценки
-квантили
используют порядковую статистику
«наиболее близкую» к выборочной
-квантили
,
для этого, как нетрудно убедиться,
достаточно положить
(где
– целая часть числа). Таким образом, в
качестве оценки
-квантили
следует взять величину:
.
Теорема 4.12. (Крамер)
Пусть
– выборка из распределения
,
–
-квантиль
распределения
и в некоторой окрестности точки
плотность вероятности
непрерывно дифференцируема и положительна,
,
тогда статистика
имеет асимптотически нормальное
распределение:

при
.
Следствие
При выполнении условий теоремы 4.12
статистика
является состоятельной оценкой
-квантиля
,
поскольку математическое ожидание
и дисперсия
при
.
Пусть функция распределения
зависит от неизвестного параметра
,
для построения оценки величины
с помощью порядковых статистик достаточно
выразить величину
через квантили функции распределения
:
.
Использование вместо квантилей
,
…,
их оценок, полученных с помощью порядковых
статистик,
,
…,
,
приводит к статистике:
,
которая используется в качестве оценки
.
При некоторых условиях статистики
являются состоятельными оценками
квантилей
,
то есть имеет место сходимость по
вероятности
при
,
если функция
непрерывна в точке
,
тогда по свойству сходимости по
вероятности статистика
сходится по вероятности к величине
:
,
при
,
тогда по определению статистика
является состоятельной оценкой
.
Оценки, полученные методом порядковых
статистик, как правило, имеют дисперсию
больше, чем дисперсии оценок, полученные
другими методами. Тем не менее, оценки,
полученные методом порядковых статистик,
могут обладать дополнительными
положительными свойствами, например,
устойчивостью к «засорению» выборки
(«засорение» выборки означает наличие
в выборке ошибочных значений, полученных
в результате неверного измерения и
т.п.)
54
Соседние файлы в папке Лекции_2
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Поря́дковые стати́стики в математической статистике — это упорядоченная по неубыванию выборка одинаково распределённых независимых случайных величин и её элементы, занимающие строго определенное место в ранжированной совокупности.
Содержание
- 1 Определение
- 2 Замечания
- 3 Порядковые статистики абсолютно непрерывного распределения
- 4 Пример
- 5 См. также
- 6 Примечания
Определение[править | править код]
Пусть 





.
Эта последовательность называется вариационным рядом. Вариационный ряд и его члены являются порядковыми статистиками. Случайная величина 

Замечания[править | править код]
Очевидно из определения:
;
.
Порядковые статистики абсолютно непрерывного распределения[править | править код]
.
.
Пример[править | править код]
Плотности стандартного непрерывного равномерного распределения и его порядковых статистик для случая n=5.
Пусть ![{displaystyle U_{1},ldots ,U_{n}sim mathrm {U} [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1abbcc02676fef51d5ffafa6be2c9d62d57d80dd)
,
то есть 

;
.
См. также[править | править код]
- Статистика (функция выборки)
- Алгоритм выбора
Примечания[править | править код]
- ↑ Математический энциклопедический словарь. — М.: «Сов. энциклопедия », 1988. — С. 847.
- ↑ Доказательство Архивная копия от 27 февраля 2012 на Wayback Machine, с. 12, з. 1.18
|
|
Для улучшения этой статьи по математике желательно:
После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки. |




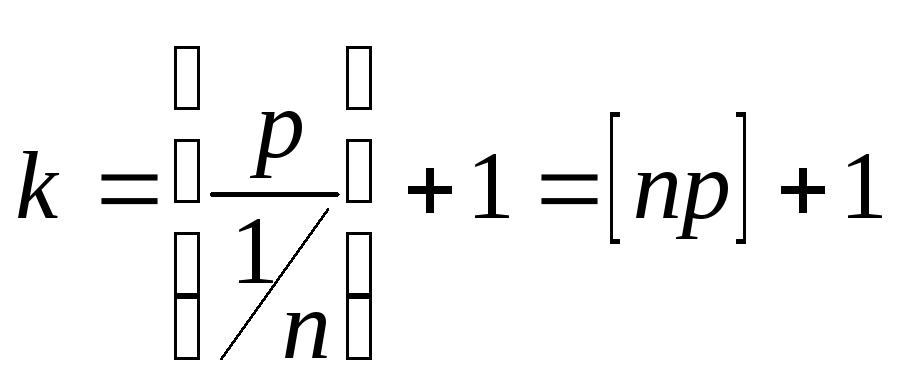



![{displaystyle f_{X_{(k)}}(x)={frac {n!}{(n-k)!(k-1)!}}[F_{X}(x)]^{k-1}[1-F_{X}(x)]^{n-k}f_{X}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c79fa3072fbffaa19b8025e0e5d1beaa74cd229)
![{displaystyle f_{X_{(j)},X_{(k)}}(x_{j},x_{k})=left{{begin{matrix}{frac {n!}{(j-1)!(k-j-1)!(n-k)!}}[F_{X}(x_{j})]^{j-1}[F_{X}(x_{k})-F_{X}(x_{j})]^{k-j-1}[1-F_{X}(x_{k})]^{n-k}f_{X}(x_{j})f_{X}(x_{k}),&x_{j}leq x_{k}\0,&x_{j}>x_{k}end{matrix}}right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39ded13ac10474e555f92e2d6703c968636d91c)

![{displaystyle f_{U_{(k)}}(u)={frac {n!}{(n-k)!(k-1)!}}u^{k-1}[1-u]^{n-k},quad uin [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bca300a4b9065ddf85f41ec8d9f155e53276063)
![{displaystyle f_{U_{(j)},U_{(k)}}(u_{j},u_{k})={frac {n!}{(j-1)!(k-j-1)!(n-k)!}}u_{j}^{j-1}[u_{k}-u_{j}]^{k-j-1}[1-u_{k}]^{n-k},quad j<k,quad 0leq u_{j}leq u_{k}leq 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/914aaae9a3ee8d7ea79ac461828b1bf0c9b843e6)

