Алгоритм решения
задач по физике для расчета характеристик электрической цепи.
Малкова Анастасия Викторовна, ГБОУ школа №
258 Колпинского района Санкт-Петербурга
Цель: систематизация знаний учащихся по теме «Электрический
ток», применение полученных знаний для решения задач на расчет характеристик
электрической цепи в случае смешанного соединения проводников
Характеристиками электрической цепи являются значения
сопротивления элементов ее составляющих, сила тока и напряжение на них, а также
работа и мощность.
Основополагающим для школьников среднего звена при
изучении электрического тока является закон Ома для участка цепи:
I = U / R
Также необходимо не забывать о правилах при вычислении
тех или иных характеристик цепи при разных типах соединения проводников. Для
удобства восприятия все необходимые для вычисления формулы можно
систематизировать в таблице:
|
Сила тока I (А) |
Сопротивление R (Ом) |
Напряжение U (В) |
Работа А (Дж) |
Мощность Р (Вт) |
|
|
Определение |
I = q/t |
R = U / I |
U = A / q |
A = UIt |
P = UI |
|
Последовательное соединение |
I = I1 = I2 |
R= R1 + R2 |
U = U1 + U2 |
A = I2Rt |
P = I2R |
|
Параллельное соединение |
I = I1 + I2 |
1/R = 1/R1 + 1/R2 |
U = U1 = U2 |
A = U2t / R |
P = U2 / R |
При
рассмотрении задач на смешанное соединение проводников необходимо делить их на
небольшие задачки, в каждой из которых рассматривать уже только один тип
соединения.
Рассмотрим
задачу:
Найдите
распределение сил токов и напряжений в цепи, общее сопротивление элементов
цепи, если амперметр показывает 3 А, а R1=2 Ом, R2=4 Ом, R3=3 Ом, R4=1 Ом, R5=12Ом. 
|
Дано: Ia= R1=2Ом R2=4Ом R3=3Ом R4=1Ом R5=12Ом |
Решение: Задача представляет из себя пример смешанного соединение проводников. I этап. Нахождение общего сопротивления цепи. Рассмотрим 1 и 2 резисторы, они между собой связаны последовательным R12 = R1 + R2
|
|
Найти: Rобщ – ? I1 , I2 ,I3 ,I4 ,I5 – ? U1 , U2 ,U3 ,U4 ,U5 – ? |

Резисторы
R12 и R5 соединены в цепь последовательно.
Преобразовываем схему и применяем формулу
![]() =
= ![]() +
+ ![]()
Приводим
формулу и рассчитываем R125
 R125 =
R125 = ![]()
R125 = ![]() = 4 Ом
= 4 Ом
Элементы
R3, R4, R125 последовательно соединены. Делаем последнее преобразование цепи и
применяя формулы для расчеты сопротивления проводников при последовательном
соединении , находим значение R общ
Rобщ = R3 + R4 + R125
Rобщ = 3 Ом + 4 Ом + 1 Ом
= 8 Ом
II этап. Нахождение распределения сил токов и
напряжений на элементах электрической цепи.
Для
наиболее наглядного представления результатов вычислений рекомендуется
использовать таблицу. По данным задачи мы можем внести в нее значение
сопротивлений всех элементов цепи и общее значение силы тока (поскольку именно
это значение измеряется при данном подключении амперметра). Также мы можем
заполнить ячейку с ранее вычисленным общим значением сопротивления цепи.
|
1 |
2 |
3 |
4 |
5 |
общее |
|
|
Сила тока I (А) |
3 |
|||||
|
Напряжение U (В) |
||||||
|
Сопротивление R (Ом) |
2 |
4 |
3 |
1 |
12 |
8 |
Исходя
из данных таблицы найдем значение напряжения по закону Ома для участка цепи:
Uобщ = Iобщ * Rобщ
Uобщ = 3А * 8 Ом = 24 В
По
правилу распределения тока в цепи Iа = I3 = I3 = I125 = 3А
Можем
воспользовавшись законом Ома для участка цепи определить напряжения на 3-ем и
4-ом проводниках:
U3 = I3 * R3
U3 = 3А * 3Ом = 9 В
U4 = I4 * R4
U4
= 3А * 1 Ом = 3
В
Рассмотрим
элемент, состоящий из 1го, 2го и 5го проводников. Поскольку между 5м и 1-2м
параллельное соединение, то воcпользуемся формулой:
U125 = U12 = U5 = 12 В
Зная
значение напряжения на 5м проводнике и его сопротивление, найдем значение силы
тока на нем:
I5 =
U5 / R5
I5 = 12 / 12 = 1 А
Для
нахождения тока на 1-2 резисторах воспользуемся правилом (т к 1-2 и 5
проводники соединены параллельно) :
I125
= I12 + I5
Следовательно,
I12 = I125 – I5 = 3А – 1А = 2А
Т
к проводники между собой соединены последовательно , то и значение сил токов на
них совпадают, а значит
I1 =I2 = I12 = 2А
Осталось
по закону Ома для участка цепи вычислить значение напряжений на этих резисторах
U1 =
I1 * R1
U1 = 2А * 2Ом = 4 В
U2 = I2 * R2
U2 = 2А * 4 Ом = 8 В
Все
полученные результаты вычислений были занесены в таблицу.
|
1 |
2 |
3 |
4 |
5 |
общее |
|
|
Сила тока I (А) |
2 |
2 |
3 |
3 |
1 |
3 |
|
Напряжение U (В) |
4 |
8 |
9 |
3 |
12 |
24 |
|
Сопротивление R (Ом) |
2 |
4 |
3 |
1 |
12 |
8 |
Таким
образом сложную задачу удалось решить методом последовательного упрощения
электрической схемы или рассмотрения отдельных элементов этой цепи.
Задача для самостоятельной работы:
Найдите
распределение сил токов и напряжений в цепи, общее сопротивление элементов
цепи, если вольтметр показывает 68 В, а R1=2 Ом, R2=8 Ом, R3=3 Ом, R4=6 Ом, R5=3,4 Ом.

Ответы
к задаче:
|
1 |
2 |
3 |
4 |
5 |
общее |
|
|
Сила тока I (А) |
16 |
4 |
13,3 |
6,6 |
20 |
20 |
|
Напряжение U (В) |
32 |
32 |
40 |
40 |
68 |
140 |
|
Сопротивление R (Ом) |
2 |
8 |
3 |
6 |
3,4 |
7 |
Задачи, решенные в классе
№ 1123
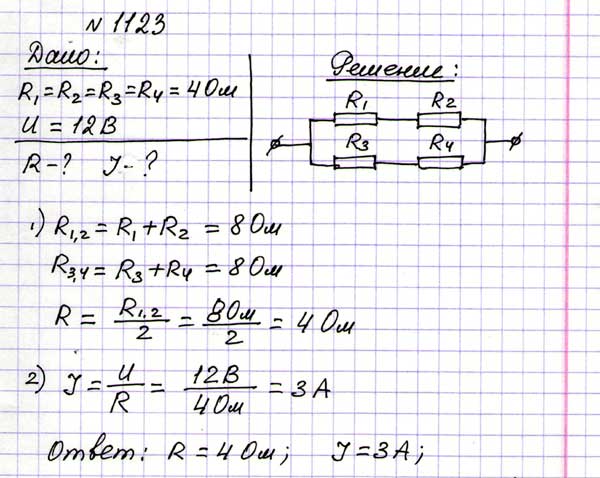
№ 1125
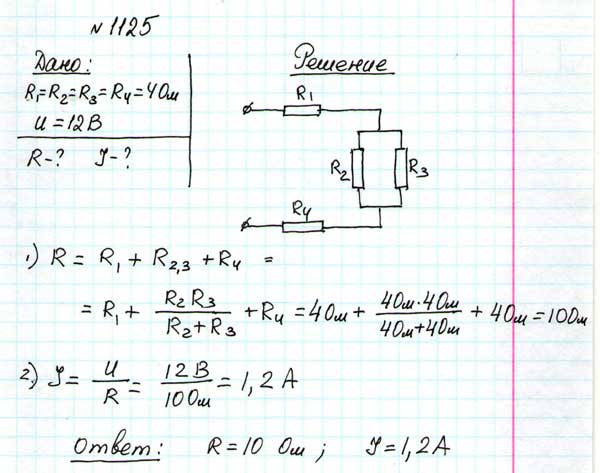
№ 1127

Задачи. заданные на дом
№ 1124
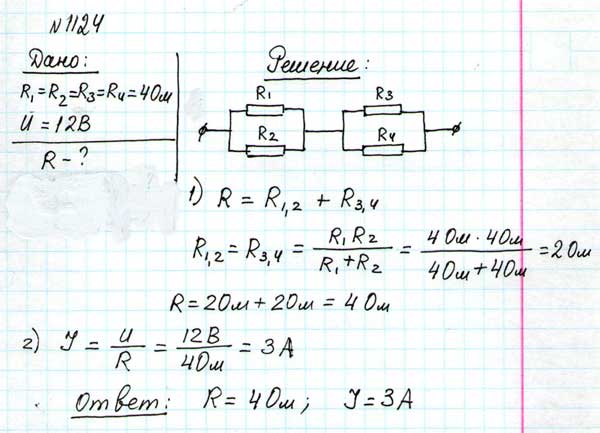
№ 1126
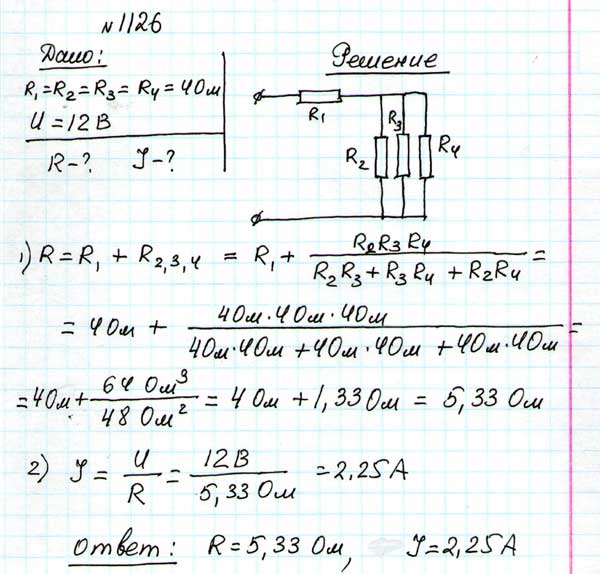
№ 1128

№ 1129
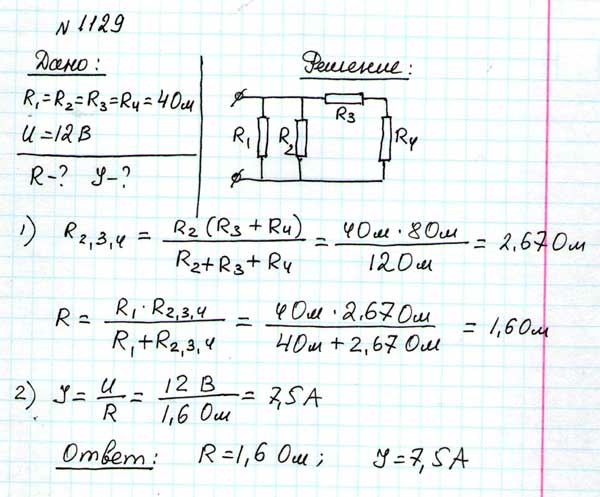
Постарайтесь решить приведенные ниже задачи
самостоятельно. Если возникнут трудности,
разберитесь в приведенных готовых решениях.
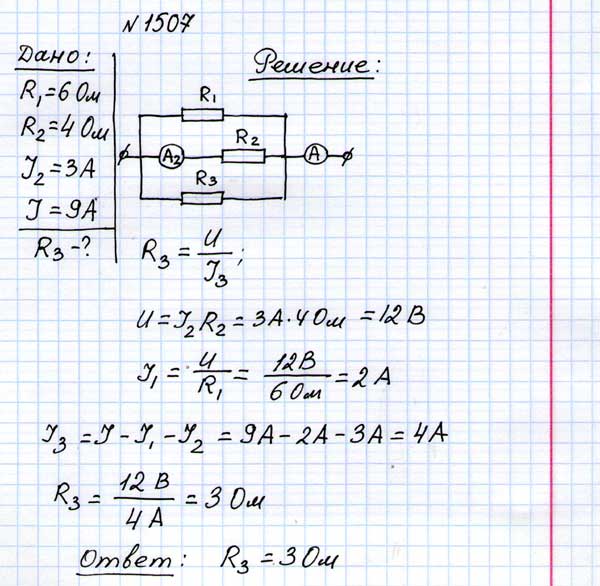
№ 1507
Вычислите величину сопротивления R =4 Ом
=4 Ом
(рис.168), если I =3А, I=9А.
=3А, I=9А.
№ 1519
Найдите распределение сил токов и напряжений в цепи, изображенной на рис.175, если R =3 Ом, R
=3 Ом, R
=2 Ом,
R =4 Ом, а амперметр показывает 6А.
=4 Ом, а амперметр показывает 6А.

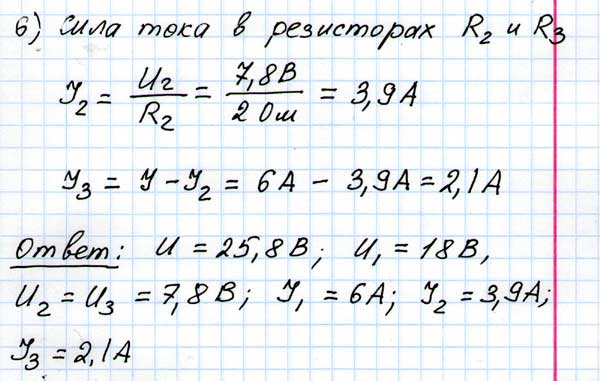
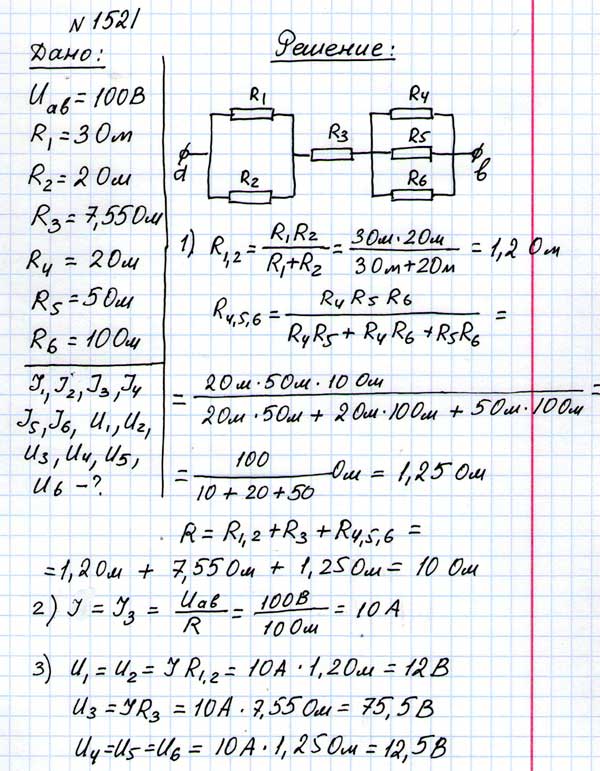
Найдите распределение сил токов и напряжений в цепи, изображенной на рис.177, если U
 =100 В,
=100 В,R
 =3 Ом,
=3 Ом, R
 =2 Ом, R
=2 Ом, R =7,55 Ом, R
=7,55 Ом, R =2 Ом,
=2 Ом,R
 =5 Ом, R
=5 Ом, R =10 Ом.
=10 Ом.
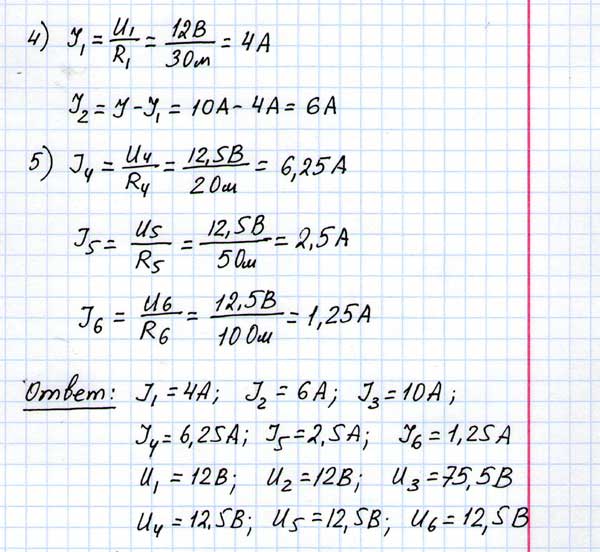
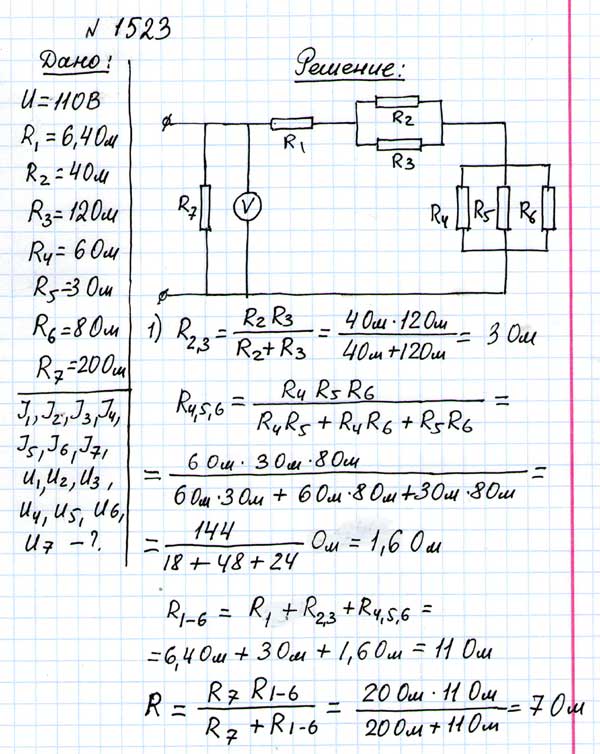
№ 1523
Найдите распределение сил токов и напряжений в цепи, изображенной на рис.179, если вольтметр показывает 110В, а
R =6,4 Ом, R
=6,4 Ом, R =4 Ом, R
=4 Ом, R =12 Ом, R
=12 Ом, R =6 Ом,
=6 Ом,
R =3 Ом, R
=3 Ом, R =8 Ом, R
=8 Ом, R =20 Ом.
=20 Ом.
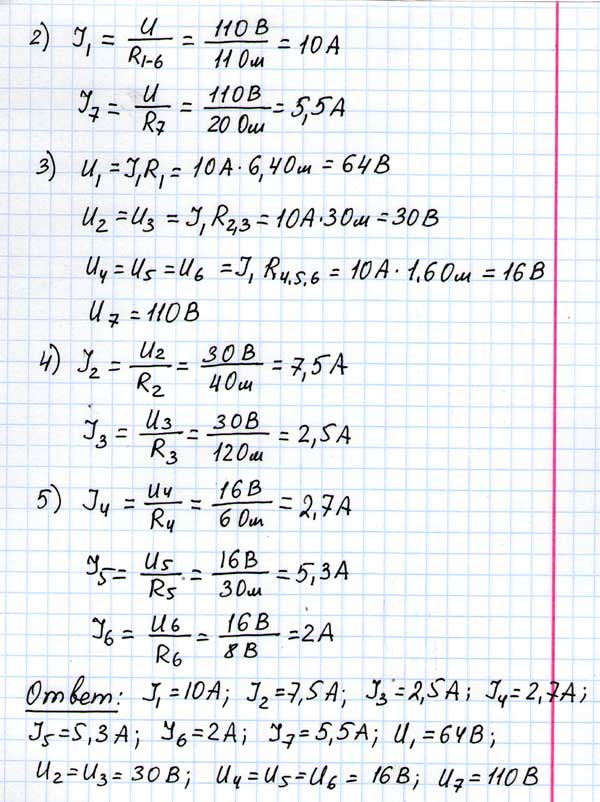
Конспект урока: Решение задач. Смешанное соединение проводников. Электрические цепи. Измерение токов и напряжений в цепи
Постоянный электрический ток
Решение задач. Смешанное соединение проводников
План урока
- Смешанное соединение проводников. Метод эквивалентных преобразований
- Примеры решения задач
Цели урока
- Знать понятие смешанного соединения проводников; метод эквивалентных преобразований
- Уметь рассчитывать электрические схемы со смешанным соединением проводников
Разминка
- Как найти общее напряжение при последовательном соединении проводников?
- Как найти общее сопротивление при последовательном соединении проводников?
- Как найти общее сопротивление при параллельном соединении проводников?
Смешанное соединение проводников. Метод эквивалентных преобразований
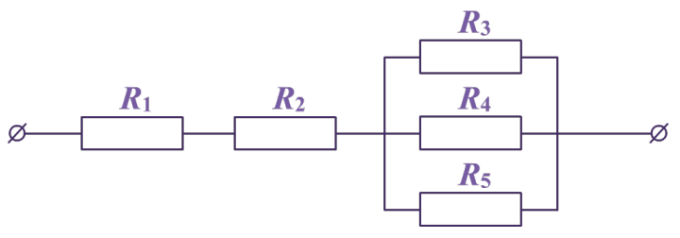
Рис. 1. Смешанное соединение проводников
Рассмотрим схему, представленную на рисунке 1.
Резисторы с сопротивлениями R1 и R2 соединены между собой последовательно, резисторы R3, R4 и R5 – параллельно.
Если в электрической цепи одновременно присутствуют и последовательное, и параллельное соединения проводников, такое соединение называют
смешанным
.
Для расчета электрической цепи, содержащей смешанное соединение, используют метод эквивалентных преобразований. Суть данного метода заключается в том, что исходную электрическую цепь заменяют на более простую электрическую цепь, при этом распределение сил токов и напряжений в непреобразованной части цепи остается прежним.
Например, в изображенной на рисунке 1 схеме проводники с сопротивлениями R3, R4 и R5 можно заменить на один проводник, сопротивление которого R345 равно общему сопротивлению трех данных резисторов:
1R345=1R3+1R4+1R5.

Рис. 2. Эквивалентная схема
Тогда исходную электрическую цепь можно заменить на эквивалентную схему, состоящую из трех последовательно соединенных проводников с сопротивлениями R1, R2 и R345 (рис. 2).
При этом распределение сил токов и напряжений на резисторах R1 и R2 останется таким же, каким было до преобразования электрической цепи.
Примеры решения задач
Пример 1
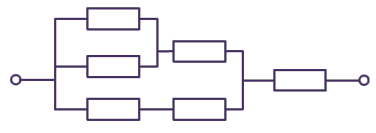
Рис. 3. Иллюстрация к примеру 1
Найти общее сопротивление участка цепи, представленного на рисунке 3, если сопротивления всех резисторов одинаковы и равны R = 2 Ом.
Решение
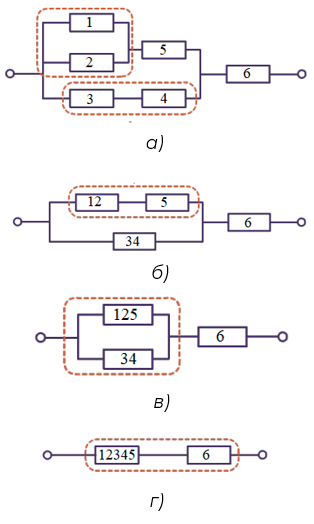
Рис. 4. Эквивалентные схемы сложной цепи
Пронумеруем резисторы (рис. 4, а). Проводники 1 и 2 соединены параллельно, найдем их общее сопротивление R12:
1R12=1R1+1R2=12+12=1;
R12=1 Ом.
Проводники 3 и 4 соединены последовательно, найдем их общее сопротивление R34:
R34=R3+R4=2+2=4 Ом.
Проводники 1 и 2 можно заменить на один проводник сопротивлением R12, проводники 3 и 4 – на проводник R34. В результате получаем упрощенную, эквивалентную схему, представленную на рисунке 4, б.
Из рисунка 4, б видно, что проводники 12 и 5 соединены последовательно, найдем их общее сопротивление R125:
R125=R12+R5=1+2=3 Ом.
Заменяем два проводника 12 и 5 на один проводник сопротивлением R125, получаем эквивалентную схему, состоящую из трех резисторов (рис. 4, в). Находим общее сопротивление проводников 125 и 34:
1R12345=1R125+1R34=13+14=4+312=712;
R12345=127≈1,7 Ом.
В результате преобразований получаем схему, состоящую из двух последовательно соединенных проводников с сопротивлениями R12345 и R6 (рис. 4. г).
R123456=R12345+R6=1,7+2=3,7 Ом.
Ответ: R123456=3,7 Ом.
Пример 2
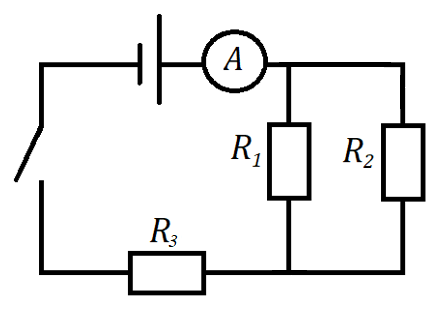
Рис. 5. Иллюстрация к примеру 2
Рассчитайте электрическую цепь, изображенную на рисунке 5. Амперметр показывает силу тока 2 А. Сопротивления первого, второго и третьего резисторов равны 4, 6 и 0,6 Ом соответственно.
Решение
Прежде всего, рассчитаем общее сопротивление цепи. Резисторы 1 и 2 соединены параллельно, найдем их общее сопротивление:
1R12=1R1+1R2=14+16=1024;
R12=2410=2,4 Ом.
Исходной схеме эквивалента схема из двух проводников сопротивлениями R12 и R3, соединенных последовательно. Тогда общее сопротивление данной цепи равно:
R=R12+R3=2,4+0,6=3 Ом.
Амперметр находится в неразветвленной части цепи, следовательно, он показывает общую силу тока в цепи, одинаковую на проводниках, соединенных последовательно:
I=I12=I3=2 А.
Найдем общее напряжение, а также напряжение на проводниках 12 и 3, используя закон Ома:
U=I·R=2·3=6 В;
U12=I12·R12=2·2,4=4,8 В;
U3=I3·R3=2·0,6=1,2 В.
Осталось найти распределение сил токов и напряжений на проводниках 1 и 2. Данные резисторы соединены параллельно, следовательно, напряжения на данных резисторах одинаковы и равны общему напряжению на данном участке цепи:
U1=U2=U12=4,8 В.
Сопротивления резисторов 1 и 2 известны, находим силы токов на данных проводниках по закону Ома:
I1=U1R1=4,84=1,2 А;
I2=U2R2=4,86=0,8 А.
Ответ: I=2 А; I1=1,2 А; I2=0,8 А; U=6 В; U1=4,8 В; U2=4,8 В; U3=1,2 В.
Пример 3
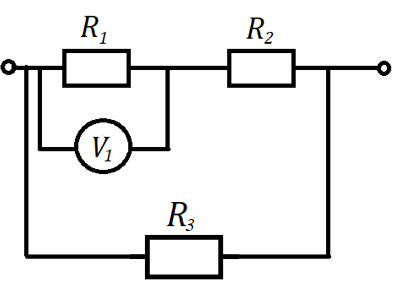
Рис. 6. Иллюстрация к примеру 3
Найти общую силу тока в электрической цепи, изображенной на рисунке 6. Вольтметр показывает напряжение 21 В. Сопротивления первого, второго и третьего резисторов равны 3, 2 и 5 Ом соответственно.
Решение
Из условия задачи известны сопротивление и напряжение на первом резисторе, найдем силу тока на данном проводнике:
I1=U1R1=213=7 А.
Так как проводники 1 и 2 соединены последовательно, сила тока на них одинакова:
I12=I1=I2=7 А.
Используя закон Ома, найдем напряжение на втором резисторе:
U2=I2·R2=7·2=14 В.
Так как проводники 1 и 2 соединены последовательно, общее напряжение на данном участке равно сумме напряжений на данных резисторах:
U12=U1+U2=21+14=35 В.
Участок цепи, изображенный на рисунке 6 можно представить в виде упрощенной схемы, состоящей из двух параллельно соединенных проводников с сопротивлениями R12 и R3. Тогда напряжение на данных резисторах одинаково и равно общему напряжению на данном участке:
U12=U3=U=35 В.
Найдем силу тока на третьем резисторе:
I3=U3R3=355=7 А.
Общая сила тока равна сумме сил тока на проводниках 12 и 3:
I=I12+I3=7+7=14 А.
Ответ: I=14 А.
Упражнение 1
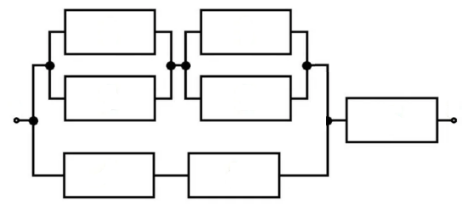
Рис. 7
1. Рассчитайте общее сопротивление участка цепи, представленного на рисунке 7, если сопротивления всех резисторов одинаковы и равны R = 2 Ом.
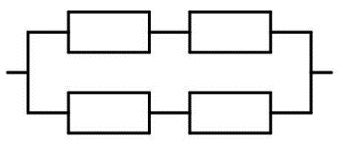
Рис. 8
2. Рассчитайте электрическую цепь, представленную на рисунке 8, если сопротивления всех резисторов одинаковы и равны 4 Ом. Сила тока в неразветвленной части цепи равна 50 А.
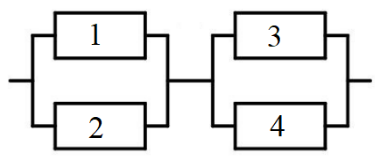
Рис. 9
3. Сопротивления резисторов 1, 2, 3 и 4 равны 2, 3, 7 и 3 Ом соответственно
(рис. 9). Известно, что напряжение на резисторе 1 составляет 20 В. Найти распределение сил токов и напряжений на данном участке цепи.
Ответы
Упражнение 1
1. R = 3,3 Ом.
2. I1 = I2 = I3 = I4 = 25 А; U = 200 В; U1 = U2 = U3 = U4 = 100 В.
3. I = 16,7 А; I1 = 10 А; I2 = 6,7 А; I3 = 5 А; I4 = 11,7 А; U = 55,07 В;
U2 = 20 В; U3 = U4 = 35,07 В.
Предыдущий урок
Работа и мощность электрического тока. Закон Джоуля — Ленца. Электрические нагревательные приборы
Постоянный электрический ток
Следующий урок
Источники тока
Постоянный электрический ток
Постоянный ток: законы Кирхгофа
При решении задач на законы Кирхгофа лучше придерживаться определенного алгоритма: 1. определить число неизвестных токов – столько уравнений должно быть в системе ; 2. определить количество узлов – уравнений по первому закону тогда нужно составить на одно меньше; 3. проложить контуры и записать для них уравнения по второму закону. Кто хочет разобраться досконально – есть видео.
Задача 1. Два элемента с В и
В соединены по схеме, показанной на рисунке . Сопротивление
Ом. Внутреннее сопротивление элементов одинаково
Ом. Определить силу тока, идущего через сопротивление
.

К задаче 1
Обозначим токи в ветвях произвольно. По первому закону Кирхгофа сумма токов, сходящихся в узле, равна 0:
Будем обходить верхний контур против часовой стрелки. По второму закону Кирхгофа сумма падений напряжений в контуре равна сумме ЭДС:
Будем обходить второй контур по часовой стрелке:
Неизвестных токов – три, мы составили три уравнения. Этого достаточно, чтобы найти токи:
Выразим из второго уравнения, а
– из третьего:
Подставим эти выражения в первое уравнение:
Тогда токи и
Ответ: A,
A,
A.
Задача 2.
Найти силу тока на всех участках цепи‚ если В,
В‚
В,
Ом‚
Ом‚
Ом‚
Ом‚
Ом,
Ом.

К задаче 2
Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас два узла, поэтому уравнение будет одно.
Затем, обходя контуры, составим два уравнения по второму закону: их нужно составить два, так как неизвестных токов в цепи три.
Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора): ,
,
.
Ответ: ,
,
.
Задача 3.
В схеме, показанной на рисунке, найти силу тока через гальванометр, если В,
кОм;
В,
кОм. Сопротивлением гальванометра пренебречь.

К задаче 3
Нам неизвестно сопротивление гальванометра, запишем для напряжения на нем два уравнения:
Приравнивая, получим
Заметим, что, если , то равенство будет выполнено. Таким образом, ток через гальванометр не течет.
Ответ: .
Задача 4.
В цепи В‚
В,
Ом,
Ом. Найти распределение токов в цепи. Внутреннее сопротивление источников тока не учитывать.

К задаче 4
Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас три узла, поэтому уравнений будет два. Затем, обходя контуры, составим три уравнения по второму закону: их нужно составить именно три, так как неизвестных токов в цепи шесть.
Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора): ,
,
,
,
,
.
Ответ: ,
,
,
,
,
.
Задача 5.
Какую силу тока покажет амперметр в схеме, изображенной на рисунке? Сопротивлением амперметра пренебречь.

К задаче 5
Обозначим токи в цепи произвольно. Обозначим направления обхода контуров. Запишем систему уравнений: составим три уравнения по первому закону (на одно меньше, чем количество узлов) и три уравнения по второму закону, так как неизвестных токов шесть и система должна состоять из шести уравнений.
Чтобы воспользоваться калькулятором, я задала Ом и
В. В итоге получилось:
,
,
,
,
,
.
Минусы свидетельствуют о противоположном направлении тока в этой ветви тому, что мы нарисовали.
Распределение сил токов
Ученик
(201),
на голосовании
13 лет назад
Голосование за лучший ответ
Леонид Зарубин
Гуру
(3011)
13 лет назад
параллельное соединение R4,R5,R6 дает эквивалентное сопротивление 1,6 ом (1/общее = 1/R4+1/R5+1/R6) при напряжении 8 вольт, ток – 8/1.6 = 5А. Параллельное соединение R2, R3 – 1/общее = 1/R2+1/R3 дает 3 ома, при токе 5А – падение напряжения – 3*5=15V. Падение напряжения на R1 – 6.4*5=32V. Напряжение на входе цепи – 8+15+32=55V. Ток через R7 = 55/20=2.75A. Вроде, все. А вообще это все просто.
ЗЫ: ток через R4 = 8/6= 1.333333A, через R5=8/3=2.666666A, через R6=8/8=1A, через R2=15/4=3.75A, через R3=15/12=1.25A, через R1 – 5A. Вроде все. Удачи!
 R
R