Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.
При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:
Формула перемещения
Пример №1. По графику определить перемещение тела в момент времени t=3 с.
Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:
Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
v = v0 ± at
В итоге получается формула:
Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает вид:
Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:
Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.
Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
t1 = t – t2
Когда тело тормозит, через некоторое время t1 оно останавливается. Поэтому скорость в момент времени t1 равна 0:
0 = v01 – at1
При торможении перемещение s1 равно:
Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
t2 = t – t1
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
v = at2
При разгоне перемещение s2 равно:
При этом модуль перемещения в течение всего времени движения равен:
s = |s1 – s2|
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
l = s1 + s2
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с2. Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:
Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
v02 = v01 + a1t1 = a1t1 (так как v01 = 0)
Подставляем выраженные величины в формулу:
Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:
За первую секунду тело переместится на расстояние, равное:
За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:
За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:
Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:
Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду
Пример №4. Автомобиль разгоняется с ускорением 3 м/с2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:
Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:
где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с2. Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:
Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:
График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:
Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.
Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:
Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:
График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.
В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.
Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.
При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:
Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:
Задание EF18553

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные и перевести их единицы измерения величин в СИ.
2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.
3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.
4.Определить перемещение тела и его кинетическую энергию.
5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x(t)=x0+v0t+at22
Теперь мы можем выделить кинематические характеристики движения тела:
• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).
Перемещение тела определяется формулой:
s=v0t+at22
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x(t)=v0t+at22=5t−3t2
Кинетическая энергия тела определяется формулой:
Ek=mv22
Скорость при прямолинейном равноускоренном движении равна:
v=v0+at=5−6t
Поэтому кинетическая энергия тела равна:
Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2
Следовательно, правильная последовательность цифр в ответе будет: 34.
Ответ: 34
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18774
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18831
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1 и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1 и s2, а затем сложим их:
s1 + s2 = 100 + 100 = 200 (м)
Ответ: 200
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 25.2k
Равномерно ускоренное движение без начальной скорости
Перемещение выраженное через скорость и время
Тело начинает двигаться равноускоренно из состояния покоя.
|
На графике скорости перемещение равно площади треугольника
[s = frac{ut}{2}] Здесь: |
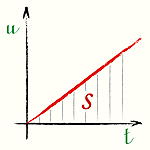 График скорости – Равномерно ускоренное движение без начальной скорости |
Скорость выраженная через ускорение и время
|
Поскольку движение начинается из состояния покоя, то изменение скорости равно величине скорости, достигнутой к моменту времени t, и скорость вычисляется по следующей формуле:
[u = at] |
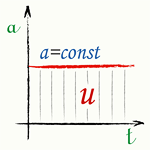 График ускорения – Равномерно ускоренное движение без начальной скорости |
Перемещение выраженное через ускорение и время
|
Из формул (1) и (2) получается следующая формула пройденного пути:
[s = frac{at^2}{2}] Здесь: |
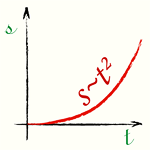 График перемещения – Равномерно ускоренное движение без начальной скорости |
Равномерно ускоренное движение без начальной скорости |
стр. 399 |
|---|
Мы с вами продолжаем рассматривать прямолинейное
равноускоренное движение тела. Теперь давайте рассмотрим, как определить
проекцию вектора перемещения тела при его равноускоренном движении без
начальной скорости. В этом случае уравнение проекции перемещения будет иметь
вид:
Для простоты дальнейших рассуждений будем считать, что
направление векторов перемещения и ускорения тела совпадают. Тогда записанное
нами уравнение мы можем переписать, подставив в него вместо проекций векторов
ускорения и перемещения их модули:
Так как ускорение тела является величиной постоянной, то из
формулы следует, что при прямолинейном равноускоренном движении модуль
вектора перемещения прямо пропорционален квадрату времени, в течение которого
это перемещение совершено.
Например, если тело за некоторый промежуток времени t1 совершило
перемещение s1,
то за вдвое большее время оно совершит в четыре раза большее перемещение. Если
промежуток времени увеличится в 3 раза, по сравнению с первоначальным, то
перемещение тела увеличится уже в 9 раз, по сравнению с первоначальным. Логично
предположить, что в случае увеличения промежутка времени в k раз, перемещение увеличится в k2 раз. Только
помним, что число k
должно быть натуральным:
Данную закономерность можно представить графически в виде
последовательных отрезков перемещений:
Или с помощью графика скорости для равноускоренного движения
без начальной скорости:
Из рисунков хорошо видно, что в случае увеличения
промежутков времени, отсчитываемых от начала движения, в целое число раз,
модули соответствующих векторов перемещений возрастают как ряд квадратов
последовательных натуральных чисел:
Теперь давайте найдём отношения модулей перемещений,
проходимых телом за равные последовательные промежутки времени. Получим, что модули
векторов перемещений, совершаемых телом за равные последовательные промежутки
времени при прямолинейном равноускоренном движении без начальной скорости,
относятся как ряд нечётных чисел:
Полученными закономерностями обладает только равноускоренное
движение. Поэтому ими можно пользоваться в случае, когда требуется определить,
как движется тело — с ускорением или без него.
Например, пусть нам требуется определить, является ли
движение гусеницы равноускоренным, если она за первые 10 секунд движения
переместилась на 5 сантиметров, за вторые 10 секунд — на 15 сантиметров, а за
третьи 10 секунд — на 25 сантиметров.
Для этого найдём отношения перемещений, совершённых за второй
и третий промежутки времени, к перемещению гусеницы на первом отрезке времени:
Таким образом видим, что полученные отношения представляют
собой последовательный ряд нечётных чисел. Значит, движение гусеницы было
равноускоренным.
Закрепление материала. В течение восьми равных
промежутков времени от начала движения тело, двигаясь равноускорено,
переместилось на 160 метров. Какой путь прошло это тело в течение двух первых
таких же промежутков времени?
Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в (XVI) веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении модуль перемещения совпадает по своему значению с пройденным путём. Формула выглядит следующим образом:
, где (а) — это ускорение.
Сравним графики равномерного и равноускоренного движения.
Графики прямолинейного равномерного движения
Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость (a(t)) — прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Скорость со временем не изменяется, график (v(t)) — прямая линия, параллельная оси времени.
Правило определения пути по графику (v(t)): численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.
Зависимость пути от времени. График (s(t)) — наклонная линия.
Рис. (1). График зависимости скорости от времени при равномерном прямолинейном движении
Рис. (2). График зависимости пути от времени при равномерном прямолинейном движении
Графики равноускоренного движения
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график (a(t)) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. Скорость изменяется согласно линейной зависимости.
Зависимость пути от времени. При равноускоренном движении путь изменяется согласно квадратной зависимости:
s=v0t+at22
. В координатах зависимость имеет вид:
x=x0+v0xt+axt22
.
Графиком является ветка параболы.
Рис. (3). График зависимости пути от времени при равноускоренном движении
Источники:
Рис. 1. График зависимости скорости от времени при равномерном прямолинейном движении. © ЯКласс.
Рис. 2. График зависимости пути от времени при равномерном прямолинейном движении. © ЯКласс.
Рис. 3. График зависимости пути от времени при равноускоренном движении. © ЯКласс.
Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в XVI веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении модуль перемещения совпадает по своему значению с пройденным путем. Формула выглядит следующим образом:
S=Vot+ at2/2,
где а – это ускорение.
Случай равномерного движения
Первый, самый простой случай, это ситуация, когда ускорение равно нулю. Это означает, что уравнение, приведенное выше, превратится в уравнение: S = V0t. Это уравнение дает возможность найти пройденный путь равномерного движения. S, в данном случае, является модулем вектора. Его можно определить как разность координат: конечная координата х минус начальная координата х0. Если подставить это выражение в формулу, то получается зависимость координаты от времени.
Случай движения без начальной скорости
Рассмотрим вторую ситуацию. При V0 = 0 начальная скорость равна 0, это значит, что движение начинается из состояния покоя. Тело покоилось, затем начинает приобретать и увеличивать скорость. Движение из состояния покоя будет записываться без начальной скорости: S = at2/2. Если S – модуль перемещения (или пройденный путь) обозначить как разность начальной и конечной координаты (из конечной координаты вычитаем начальную), то получится уравнение движения, которое дает возможность определить координату тела для любого момента времени: х = х0 + at2/2.
Проекция ускорения может быть, как отрицательной, так и положительной, поэтому можно говорить о координате тела, которая может как увеличиваться, так и уменьшаться.
Пропорциональность пути квадрату времени
Важные закономерности уравнений без начальной скорости, т.е. когда тело начинает свое движение из состояния покоя:
Sx – пройденный путь, он пропорционален t2, т.е. квадрату времени. Если рассматривать равные промежутки времени – t1, 2t1, 3t1, то можно заметить следующие соотношения:
Sx ~ t2
S1 ~ 1 S1 = a/2*t12
S2 ~ 4 S2 = a/2*(2t1)2
S3 ~ 9 S3 = a/2*(3t1)2
Если продолжить, закономерность сохранится.
Перемещения за последовательные промежутки времени
Можно сделать следующее заключение: пройденные расстояния увеличиваются пропорционально квадрату увеличения промежутков времени. Если был один промежуток времени, например 1 с, значит, пройденный путь будет пропорционален 12. Если второй отрезок 2 с, то пройденное расстояние будет пропорционально 22, т.е. = 4.
Если за единицу времени выбираем некий промежуток, то полные расстояния, пройденные телом за последующие равные промежутки времени, будут относиться как квадраты целых чисел.
Иными словами, перемещения, совершенные телом за каждую последующую секунду, будут относиться как нечетные числа:
S1:S2:S3:…:Sn=1:3:5:…:(2n-1)
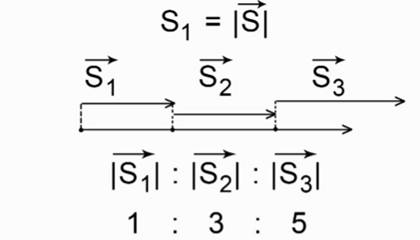
Рис. 1. Перемещения за каждую секунду относятся как нечетные числа
Рассмотренные закономерности на примере задачи
Исследованные два очень важных заключения свойственны только прямолинейному равноускоренному движению без начальной скорости.
Задача: автомобиль начинает двигаться от остановки, т.е. из состояния покоя, и за 4 с своего движения проходит 7 м. Определите ускорение тела и мгновенную скорость через 6 с после начала движения.
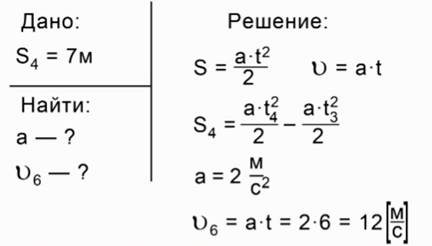
Рис. 2. Решение задачи
Решение: автомобиль начинает движение из состояния покоя, следовательно, путь, который проходит автомобиль, рассчитывается по формуле: S = at2/2. Мгновенная скорость определяется как V = at. S4 = 7 м, расстояние, которое автомобиль прошел за 4 с своего движения. Его можно выразить как разность полного пути, пройденного телом за 4 с, и пути, пройденного телом за 3 с. Используя это, получаем ускорение а = 2 м/с2, т.е. движение ускоренное, прямолинейное. Чтобы определить мгновенную скорость, т.е. скорость в конце 6 с, следует ускорение умножить на время, т.е. на 6 с, во время которых тело которое продолжало двигаться. Получаем скорость v(6с) = 12 м/с.
Ответ: модуль ускорения равен 2 м/с2; мгновенная скорость в конце 6 с равна 12 м/с.








































