Версия для печати и копирования в MS Word
Найдите расстояние между противоположными углами (диагональ) участка в метрах.
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м2 гравием, требуется 0,2 м3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Спрятать решение
Решение.
Найдём расстояние между противоположными углами участка по теореме Пифагора:
м.
Ответ: 40.
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Жилой дом | Репа | Капуста | Кукуруза |
|---|---|---|---|---|
| Цифры |
2
Гравий продаётся в больших мешках по 2 м3. Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между полями?
3
Найдите площадь территории, которая не занята постройками и полями. Ответ дайте в квадратных метрах.
4
Владимир планирует купить трактор для обслуживания полей. Он рассматривает два варианта: трактор с бензиновым двигателем и трактор с дизельным двигателем. Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице.
| Цена трактора |
Средний расход топлива |
Стоимость топлива руб. за л |
|
|---|---|---|---|
| Дизельный двигатель | 990 000 | 5,5 л/ч | 47 |
| Бензиновый двигатель | 900 000 | 7 л/ч | 53 |
Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?
Приветствую на своём канале, сегодня разберём тренировочный вариант № 40064136, с 1-ого по 5-е задание включительно по ОГЭ – тема “Участок”.
Задание 1. Прочитав текст, можно расставить в таблице названия с цифрами. У меня получилось так: 5426
Задание 2. Гравий продаётся в больших мешках по 2 кубических метра. Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между полями?
Пояснение: Сначала рассчитаем площадь пространства между полями, учитывая, что сторона клетки – 2 м. В тексте к рисунку сказано, что, чтобы засыпать 4 квадратных метра требуется 0,2 кубических метра. Поэтому площадь, которая получилась, делим на 4, а затем умножаем на 0,2, получается 4,8 кубических метров, и умножаем на 2, приблизительно получается 3 мешка.
Задание 3. Найдите площадь территории, которая не занята постройками и полями. Ответ дайте в квадратных метрах.
Пояснение: Площадь между полями мы уже знаем из второго задания, она = 96 квадратных метров. Далее я посчитала оставшуюся площадь и вычла площади гаража и жилого дома.
Задание 4. Найдите расстояние между противоположными углами (диагональ) участка в метрах.
Пояснение: Когда проведём диагональ из одного угла в другой, то получается прямоугольный треугольник, а диагональ – гипотенуза и можно найти по теореме Пифагора. Квадрат одного катета + квадрат другого катета и далее из полученного числа вывести корень.
Задание 5. Владимир планирует купить трактор для обслуживания полей. Он рассматривает два вариант: трактор с бензиновым двигателем и трактор с дизельным двигателем. Цены на покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице. Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?
Пояснение: Вычитаем стоимости тракторов – из большего меньший. Затем считаем расход топлива для каждого вида двигателя. И так же вычитаем из большего меньшее. Далее разность в цене делим на разность в расходе топлива, и получаем ответ.
Благодарю за внимание. В следующих статьях разберём следующие задания из варианта, не пропустите. Вопросы или записаться на индивидуальные занятия, заказать решение заданий можете, написав на почту: KasFrangolc@yandex.ru.
Так же можете предложить интересную Вам тему для разбора в комментариях.
Вначале определим, под какими цифрами зашифрованы какие комнаты.
Жилой дом расположен сразу перед воротами. Он обозначен цифрой 5.
За домом гараж под цифрой 1.
3 – поле с морковью.
2 – поле, около гаража под капусту.
Наибольшее поле отведено под картофель. Это номер 7.
Соседнее поле 6 отведено под кукурузу.
Оставшееся поле 4 засевается репой.
В ответе необходимо указать последовательность цифр: 5426.
_________________
Пустое пространство на участке засыпано гравием.
Длина стороны каждой клетки равна 2 м.
Для начала найдем площадь пространства между полями.
S = 2 * 12 = 24 клетки2 или 24 * 2 * 2 = 96 м2.
На 4 м2 требуется 0.2 мешка гравия.
Количество мешков гравия равны: 96 /0,4 * 0.2 = 4.8 гравия. Округляем в большую сторону. Получается 5 мешков.
Далее найдем оставшуюся большую площадь и из нее вычтем площади жилого дома и гаража.
Площадь большого пространства равна: 4 * 12 = 48 клетки2.
Площадь дома: 2 * 3 = 6 клетки2.
Площадь гаража: 2 * 2 = 4 клетки2.
Искомая площадь: 48 – 6 – 4 = 38 клетки2.
Площадь, засыпанная гравием равна: 38 + 24 = 62 клетки2. или 62 * 4 = 248 м2.
Длина участка – 16 клеток или 16 * 2 = 32 метра.
Ширина – 12 клеток или 12 * 2 = 24 метра.
Диагональ необходимо найти по теореме Пифагора.
L = 40 метров.
Владимир выбрал дизель. Узнаем, через сколько стоимость покупки скомпенсируется.
Найдем разность в стоимости между дизелем и бензиновым двигателем.
990000 – 900000 = 90 000 рублей.
Использую дизельный двигатель, расходы на топливо составят
5.5 * 47 = 258.5 рублей.
Рассчитаем расходы при бензиновом двигателе: 7 * 53 = 371 рублей.
Разность равна: 371 – 258.5 = 112.5 рублей.
Срок окпаемости равен: 90000 / 112.5 = 800 часов.
![]()
12
Найдите расстояние между противоположными углами участка (длину диагонали) в метрах.
P.S: ответ должен быть 40.
1 ответ:
![]()
0
0
Ответ:
40 метров.
Объяснение:
Участок прямоугольный, значит, диагональ разделит его на два равных прямоугольных треугольника, в каждом из которых будет являться гипотенузой.
1 клетка = 2 метра.
Ширина = 12 клеток = 24 метра.
Длина = 16 клеток = 32 метра.
А теперь теорема Пифагора:
Диагональ = метров.
Читайте также
![]()
это табличные значения
![]()
Хоспади левую и правую часть в квадрат и погнала
х²-5х+1=х-4
х²-6х+5=0
D=16
х₁=(6-4)2=1
х₂=102=5. Много писать все типовые задания, только в третьем уравнении левую часть в квадрат и правую, но там уже квадрат суммы.
![]()
3x ≥ √(730),
x ≥ √(730)/3.
Множество целых чисел не ограничено сверху, поэтому требуемого значения не существует, даже если мы выберем такое целое x, всегда можно взять (x+1)>x≥√(730)/3.
![]()
{ 4x – 4b <= 6 – 3x
{ -5x <= b
В 1 переносим х налево, остальное направо.
{ 7x <= 6 + 4b
{ -5x <= b
Складываем неравенства
2x <= 6 + 5b
x <= 3 + 2,5*b
Но из 2 неравенства
x >= -b/5
Собственно, это и есть решение при любом b.
Никаких ограничений по области определения ни для b, ни для х,
я не вижу.
![]()
Умножив обе части на sin(x), получим уравнение 3+2*sin(x)=2*sin²(x)-sin(x), или 2*sin²(x)-3*sin(x)-3=0. Пусть sin(x)=t, тогда получаем квадратное уравнение 2*t²-3*t-3=0. Дискриминант D=9-4*2*(-3)=33,
t1=sin(x1)=(3+√33)/4, t2=sin(x2)=(3-√33)/4. Но так как √33>√25=5, то t1>(3+5)/4=2. А так как /sin(x)/≤1, то уравнение sin(x1)=(3+√33)/4 не имеет решений. Так как √33<√36=6, то 0>(3-√33)/4>-1, то есть уравнение sin(x)=(3-√33)/4 имеет решение. Но так как (3-√33)/4<0, а на промежутке [0;π] sin(x)≥0, то это решение не принадлежит промежутку [0;π]. Значит, на этом промежутке уравнение решений не имеет.
Ответ: решений нет.
Задание 16115
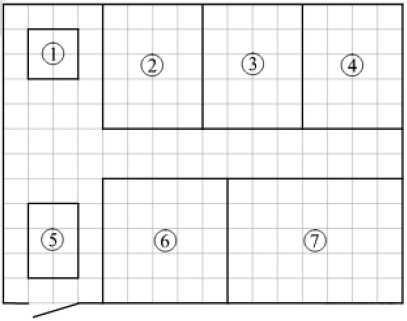
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки соответствует 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м2 гравием, требуется 0,2 м3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов, запятых и других разделительных символов.
| Объекты | Жилой дом | Репа | Капуста | Кукуруза |
|---|---|---|---|---|
| Цифры |
2. Гравий продаётся в больших мешках по 2м3. Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между полями?
3. Найдите площадь территории, которая не занята постройками и полями. Ответ дайте в квадратных метрах.
4. Найдите расстояние между противоположными углами (диагональ) участка в метрах.
5. Владимир планирует купить трактор для обслуживания полей. Он рассматривает два варианта: трактор с бензиновым двигателем и трактор с дизельным двигателем. Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице (см. ниже).
Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?
| Двигатель | Дизельный | Бензиновый |
|---|---|---|
| Цена трактора (тыс. руб.) | 900 | 990 |
| Средний расход топлива (л/ч) | 5,5 | 7 |
| Стоимость топлива (руб./л) | 47 | 53 |
Ответ: 1) 5426 2) 3 3) 248 4) 40 5) 800
Скрыть
Прямо перед воротами предполагается построить жилой дом. Значит, дом отмечен цифрой 5.
Капустой планируется засеять поле, ближайшее к гаражу, значит, поле с капустой отмечено цифрой 2.
На поле рядом с картофелем планируется посеять кукурузу, следовательно, поле с кукурузой отмечено цифрой 6.
Оставшееся поле с репой отмечено цифрой 4.
Скрыть
Площадь одной клетки равна 2 · 2 = 4 м2. Значит, площадь пространства, которую необходимо засыпать гравием, равна
$$2cdot12cdot4=96$$ м2.
Чтобы засыпать 4 м2 гравием, требуется 0,2 м3 материала. Следовательно, понадобится $$frac{96}{4}cdot0,2=4,8$$ м3 гравия.
Значит, придётся купить 3 мешка с гравием.
Скрыть
Площадь всего участка равна
$$12cdot16cdot4=768$$ м2.
Площадь гаража равна
$$2cdot2cdot4=16$$ м2.
Площадь жилого дома равна
$$3cdot2cdot4=24$$ м2.
Площадь полей, засеянных капустой, морковью и репой, равна
$$5cdot12cdot4=240$$ м2.
Площадь полей, засеянных кукурузой и картофелем, равна
$$5cdot12cdot4=240$$ м2.
Таким образом, площадь территории, которая не занята постройками или полями, равна
$$786-16-24-240-240=248$$ м2.
Скрыть
Найдём расстояние между противоположными углами участка по теореме Пифагора:
$$sqrt{24^2+32^2}=sqrt{576+1024}=sqrt{1600}=40$$ м.
Скрыть
Разность в стоимости тракторов равна 990 000 − 900 000 = 90 000 руб. Стоимость топлива за час работы трактора с дизельным двигателем равна 47 · 5,5 = 258,5 руб. Стоимость топлива за час работы трактора с бензиновым двигателем равна 53 · 7 = 371 руб. Следовательно, за час работы трактора Владимир экономит 371 − 258,5 = 112,5 руб. Таким образом, Владимир компенсирует разницу в стоимости между тракторами с разными двигателями через
$$frac{90000}{112,5}=800$$ часов.





