Как найти расстояние между изображениями в зеркалах?
Источник
света находится между двумя плоскими зеркалами, образующими двугранный угол 600
. Изображение в зеркалах находятся на расстояниях 12 и 16 см от источника.
Определите расстояние между изображениями.
Решение.
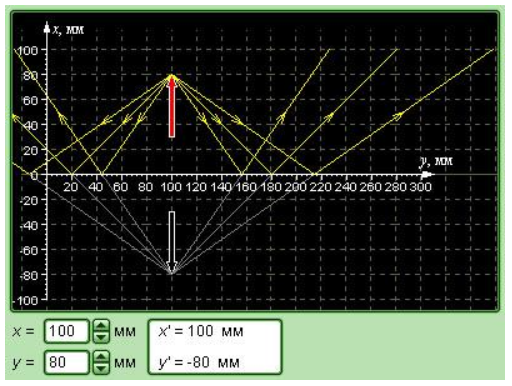
Положение
источника света и его изображений представлено на рисунке выше, где SS1 = a = 12 см, SS2 = b = 16 см, S1S2 = c. Поскольку в четырехугольнике OASB углы OBS и OAS прямые, то угол при вершине S β = 1800 –
α. Тогда применяем теорему косинусов к треугольнику SS1S2 .
Подставляем
численные значение величин и находим c = 12 см.
Ответ:
c
= 12 см.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
Плоское зеркало представляет собой простейшее способное создавать изображение предмета оптическое устройство. Получаемое с помощью него изображение некоторого объекта формируется за счет отражаемых от зеркальной поверхности лучей.
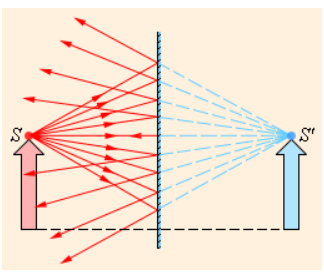
По причине его образования вследствие пересечения «мнимых» продолжений, а не непосредственно самих лучей подобные изображения носят название мнимых (рис 3.2.1).
Рисунок 3.2.1. Ход лучей при отражении от плоского зеркала. Точка S’ является мнимым изображением точки S.
Мнимое изображение предмета расположено симметрично относительно плоскости зеркальной поверхности вследствие закона отражения света. Размер изображения эквивалентен размеру отражаемого объекта.
Виды зеркал
Обладающую формой сферического сегмента зеркально отражающую поверхность называют сферическим зеркалом.
Оптическим центром зеркала называют использованный в процессе вырезания в качестве необходимого материала центр сферы.
Полюсом является вершина сферического сегмента.
Проходящая через оптический центр и полюс зеркала прямая, называется главной оптической осью сферического зеркала.
Главная оптическая ось выделена из всех других проходящих через оптический центр прямых только тем, что она является осью симметрии зеркала.
Сферические зеркала делятся на вогнутые и выпуклые.
Если на вогнутое сферическое зеркало падает параллельный главной оптической оси пучок лучей, то, отразившись от зеркала, лучи пересекутся в точке, которая носит название главного фокуса F зеркала.
Типы изображений в зеркалах
Расстояние от фокуса до полюса зеркала называют фокусным расстоянием. Оно, как главный фокус, обозначается буквой F.
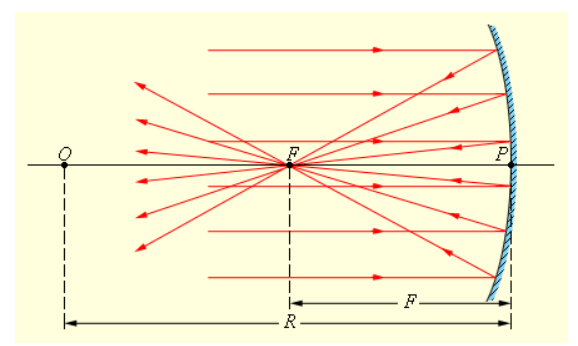
У вогнутого сферического зеркала главный фокус является действительным. Он расположен в середине между центром и полюсом зеркала, как это проиллюстрировано на рисунке зеркала 3.2.2.
Рисунок 3.2.2. Отражение параллельного пучка лучей от вогнутого сферического зеркала. Точки O – оптический центр, P – полюс, F – главный фокус зеркала; OP – главная оптическая ось, R – радиус кривизны зеркала.
Стоит учитывать, что отраженные лучи пересекаются примерно в одной точке только тогда, когда падающий параллельный пучок, так называемый параксиальный пучок, достаточно узок.
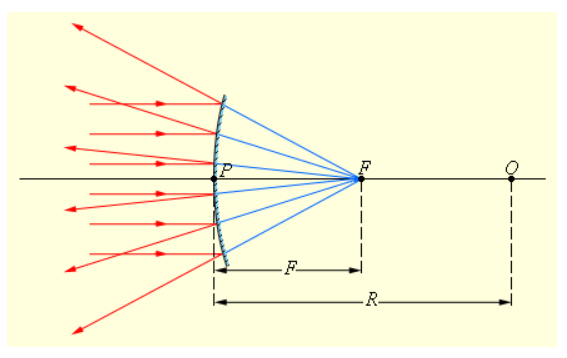
Главный фокус выпуклого зеркала мнимый. В случае, если на выпуклое зеркало падает параллельный главной оптической оси пучок лучей, то, отразившись в фокусе, пересекаются продолжения лучей (рисунок 3.2.3).
Рисунок 3.2.3. Отражение параллельного пучка лучей от выпуклого зеркала. F – мнимый фокус зеркала, O – оптический центр, OP – главная оптическая ось.
Фокусные расстояния сферических зеркал характеризуются определенным знаком: в случае вогнутого зеркала F=R2, выпуклого же – F=-R2, где R представляет собой радиус кривизны зеркала.
Изображение каждой конкретной точки A предмета в сферическом зеркале может быть построено благодаря любой паре стандартных лучей:
- Луч AOC, который проходит сквозь оптический центр зеркала. Отраженный луч COA идет по этой же прямой;
- Луч AFD, проходящий через фокус зеркала. Отраженный луч параллелен главной оптической оси;
- Луч AP, падающий на полюс зеркала. Отраженный луч относительно главной оптической оси симметричен с падающим.
- Параллельный главной оптической оси луч AE. Отраженный луч EFA1 проходит через принадлежащий зеркалу фокус.
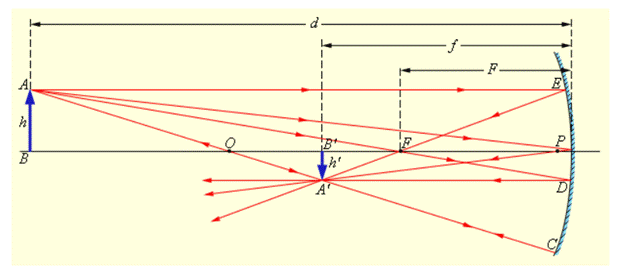
Приведенные в списке выше стандартные лучи на рисунке 3.2.4 проиллюстрированы для случая вогнутого зеркала. Данные лучи проходят через являющуюся изображением точки A точку A’. Оставшиеся отраженные лучи тоже проходят через точку A’.
Такой ход лучей, при котором все вышедшие из одной точки лучи пересекаются в другой точке, называется стигматическим.
Отрезок A’B’ представляет собой изображение объекта AB. Аналогичны построения и для случая с выпуклым зеркалом.
Рисунок 3.2.4. Построение изображения в вогнутом сферическом зеркале.
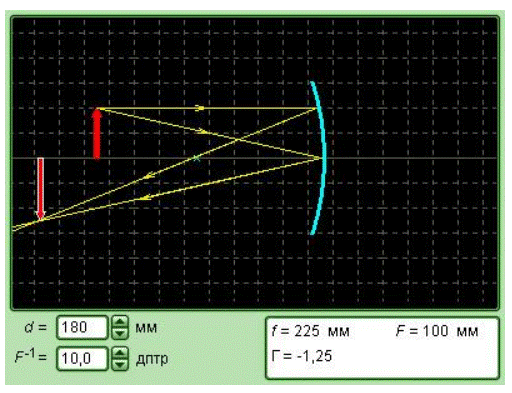
С помощью формулы сферического зеркала могут быть определены размер и положение изображения объекта:
1d+1f=1F.
В данном соотношении d играет роль расстояния от предмета до зеркала, а f представляет собой расстояние от зеркала до изображения. Величины d и f подчиняются определенному правилу знаков:
- d>0 и f>0 – для действительных изображений и предметов;
- d<0 и f<0 – для мнимых изображений и предметов.
Для проиллюстрированного на рисунке 3.2.4 случая мы имеем: F>0, то есть зеркало вогнутое; d=3F>0 (действительный предмет).
Из формулы сферического зеркала получаем: f=32F>0, соответственно, изображение является действительным.
Если вместо вогнутого зеркала взять выпуклое, с аналогичным по модулю фокусным расстоянием, мы получим приведенный ниже результат:
F<0, d=–3F>0, f=34F<0 – изображение мнимое.
Величина линейного увеличения, принадлежащая сферическому зеркалу, может быть определена в виде отношения линейных размеров предмета h и изображения h’.
В зависимости от того, является ли изображение перевернутым или прямым, h’ приписывают определенный знак, (h'<0) минус в первом случае и плюс во втором (h’>0). Величина h всегда считается положительной. В случае подобного определения линейное увеличение сферического зеркала выражается в виде формулы, легко получаемой из рисунка 3.2.4:
Г=h’h=-fd.
В первом из рассмотренных ранее примеров Г=-12<0 – соответственно, изображение является перевернутым, уменьшенным в 2 раза. Во втором Г=14>0 – то есть изображение прямое и уменьшенное в 4 раза.
Рисунок 3.2.5. Модель изображения в плоском зеркале.
Рисунок 3.2.6. Модель сферического зеркала.
Вы уже ознакомились с уроками «Отражение света» и «Плоское зеркало«. На этих уроках мы рассматривали природу такого явления, как отражения света, и получение изображения в плоском зеркале.
На данном уроке вы познакомитесь с примерами задач на отражение света от плоского зеркала и их решениями.
Задача №1
Плоское зеркало повернули на угол $varphi = 16 degree$ вокруг оси, лежащей в плоскости зеркала. На какой угол $eta$ повернется отраженный зеркалом луч, если направление падающего луча осталось неизменным?
Построим к задаче чертеж (рисунок 1). Обозначим плоское зеркало в начальном положении, как $AB$. Проведем перпендикуляр к его поверхности — $CO$. Отметим угол $varphi$, на который зеркало повернули, и обозначим его новое положение, как $A_1B_1$. Перпендикуляр поворачивается вместе с зеркалом на угол $varphi$ — $OC_1$.
Также обозначим на рисунке падающий луч $DO$ и угол падения $alpha$. После поворота зеркала падающий луч не меняет своего направления. Луч $OE$ отражается от зеркала под углом отражения $beta$. После поворота зеркала угол отражения отклонится от прежнего положения на угол $eta$.
Показать решение и ответ
Скрыть
Решение:
Рассмотрим углы падения и отражения после поворота зеркала. Из рисунка видно, что новый угол падения составляют изначальный угол падения $alpha$ и угол поворота зеркала $varphi$ (так как перпендикуляр повернулся на тот же угол):
$angle DOC_1 = alpha + varphi$.
Теперь рассмотрим новый угол падения:
$angle C_1OE_1 = (beta — varphi) + eta$.
По закону отражения света: $beta = alpha$.
Тогда мы можем записать:
$angle C_1OE_1 = alpha — varphi + eta$.
Закон преломления действует и после поворота зеркала. Значит,
$angle DOC_1 = angle C_1OE_1$.
Подставим выражения полученные выше:
$alpha + varphi = alpha — varphi + eta$.
Выразим отсюда угол, на который отклонился отраженный луч:
$eta = alpha + varphi — alpha + varphi = 2 varphi$.
Рассчитаем этот угол:
$eta = 2 cdot 16 degree = 32 degree$.
Ответ: $eta = 32 degree$.
Задача №2
Угол между плоским зеркалом и падающим на него лучом составляет $30 degree$. Чему равны углы падения и отражения луча?
Сделаем чертеж (рисунок 2). Опустим на поверхность зеркала $MN$ перпендикуляр $CO$. Обозначим падающий луч как $AO$, а отраженный луч — $OB$. Отметим угол падения $alpha$ и угол отражения $beta$. Угол между зеркалом и падающим лучом обозначим буквой $varphi$.
Показать решение и ответ
Скрыть
Решение:
Сделав правильный чертеж, решить такую задачу очень просто. Из него видно, что:
$alpha = 90 degree — varphi = 90 degree — 30 degree = 60 degree$.
По закону отражения света:
$beta = alpha = 60 degree$.
Ответ: $alpha = beta = 60 degree$.
Задача №3
На стене вертикально висит зеркало, как показано на рисунке 3. Не смотря на то, что зеркало не достает до пола, динозаврик может видеть свое отражение в полный рост. Какая длина у зеркала? Рост динозавра 152 см, а расстояние от его глаз до верхней части головы 10 см.
Показать решение и ответ
Скрыть
Решение:
Как вам известно, изображение в плоском зеркале любого предмета образуется от поверхности зеркала на том же расстоянии, что и сам предмет. При этом размеры изображения предмета равны по размеру самому предмету. Видим мы это изображение, когда световые лучи попадают нам в глаз.
Используя эту информацию, сделаем чертеж для решения этой задачи (рисунок 4).
- Точка $A$ — это глаз динозавра, в который попадает изображение в зеркале
- $EG$ — плоское зеркало
- $AB$ — световой луч, попадающий в глаз, от верхней точки головы динозавра
- $AD$ — световой луч, попадающий в глаз, от нижней точки ног динозавра
- $AC$ — световой луч, соединяющий глаз динозавра и его изображение в плоском зеркале. Он будет проходить перпендикулярно зеркалу.
Отрезок $BD$ равен росту динозавра. Он состоит из двух отрезков: $BC$ и $CD$.
$BC = 10 space см$ — расстояние от верхней точки головы до глаз.
$CD = 152 space см — 10 space см = 142 space см$ — расстояние от глаз до нижнего края ног.
Сначала рассмотрим треугольники $AEF$ и $ABC$. Они будут подобны друг другу по двум углам: $angle EFA = angle BCA = 90 degree$ и $angle EAF = angle BAC$ (это один и тот же угол для двух треугольников).
Определим коэффициент подобия:
$AF = k cdot AC$.
Расстояния от предмета до зеркала и его изображения до зеркала равны. Поэтому $AC = 2AF$.
Тогда, $AF = k cdot 2AF$.
Значит, $k = frac{1}{2}$.
Зная коэффициент подобия $k$, запишем соотношение для других сходственных сторон:
$EF = k cdot BC = frac{1}{2} cdot 10 space см = 5 space см$,
т. к. по условия расстояние от глаза до верхней точки головы составляет $10 space см$. Это утверждение справедливо и для изображения динозавра.
Теперь рассмотрим треугольники $AFG$ и $ACD$. Они также будут подобны по двум углам, и коэффициент подобия будет равен $k = frac{1}{2}$.
Тогда, $FG = k cdot CD = frac{1}{2} cdot 142 space см = 71 space см$.
Теперь мы можем найти длину зеркала:
$EG = h = EF + FG = 5 space см + 71 space см = 76 space см$.
Ответ: $h = 76 space см$.
Задача №4
Две лампочки находятся в точках $A$ и $B$, как показано на рисунке 5. Постройте такое положение глаза человека перед зеркалом, при котором он увидит изображения лампочек совмещенными.
Показать построение и пояснения
Скрыть
Построение:
Изначально нам необходимо построить изображения этих светящихся точек (лампочек).
Из точки $A$ опустим перпендикуляр на плоское зеркало и продолжим его за зеркало. Отложим на нем расстояние по другую сторону зеркала, равное расстоянию от точки $A$ до зеркала. Получим изображение светящейся точки $A_1$.
То же самое проделаем для точки $B$ и получим ее изображение $B_1$ (рисунок 6).
В условии задачи сказано, что изображения этих точек совпадут друг с другом. Мы же видим изображения, когда нам в глаз попадают световые лучи от этих точек. Это означает, что луч должен быть один сразу для обоих точек.
Соединим точки $A_1$ и $B_1$ друг с другом и продолжим эту прямую. Со стороны от зеркала, где находятся лампочки, мы можем поставить точку на этой прямой на любом расстоянии от зеркала. Так мы получили точку $E$ — положение глаза наблюдателя, при котором он увидит лампочки совмещенными друг с другом.
Задача №5
Солнечные лучи образуют с поверхностью стола угол $varphi = 50 degree$ (рисунок 7). Под каким углом к поверхности стола надо расположить зеркало, чтобы направить солнечный зайчик в горизонтальном направлении?
Показать решение и ответ
Скрыть
Решение:
Условие задачи говорит, что отраженный луч (солнечный зайчик) должен идти горизонтально. В таком случае у него может быть два направления: горизонтально влево и горизонтально вправо. Решим задачу для обоих случаев.
- Сначала рассмотрим ситуацию, где отраженный луч пойдет горизонтально вправо. Сделаем чертеж (рисунок 8).
- $MN$ — поверхность стола
- $AB$ — плоское зеркало
- $DO$ — падающий луч
- $alpha$ — угол падения
- $varphi$ — угол, образованный падающим лучом и поверхностью стола. Мы обозначили его, используя продолжение отраженного стола, параллельному столу. В этом случае продолжение отраженного луча и поверхность стола — две параллельные прямые, а падающий луч — секущая. Соответственные углы равны
- $OE$ — отраженный луч
- $beta$ — угол отражения
- $OC$ — перпендикуляр, опущенный в точку падения луча на поверхность зеркала
- $eta$ — искомый луч наклона зеркала
Из чертежа видно, что:
$varphi + alpha + beta = 180 degree$.
По закону отражения света: $alpha = beta$. Тогда,
$varphi + 2 alpha = 180 degree$,
$alpha = frac{180 degree — 50 degree}{2} = 65 degree$.
Снова рассматривая $AB$ как секущую двух параллельных прямых, мы можем сказать, что $angle EOB = eta$.
Тогда, $eta = angle EOB = 90 degree — beta = 90 degree — alpha = 90 degree — 65 degree = 25 degree$.
- Рассмотрим второй случай, когда отраженный луч пойдет горизонтально влево. Так же сделаем чертеж (рисунок 9).
- $MN$ — поверхность стола
- $AB$ — плоское зеркало
- $DO$ — падающий луч
- $alpha$ — угол падения
- $varphi$ — угол, образованный падающим лучом и поверхностью стола. Мы обозначили его, используя продолжение отраженного стола, параллельному столу. В этом случае продолжение отраженного луча и поверхность стола — две параллельные прямые, а падающий луч — секущая. Соответственные углы равны
- $OE$ — отраженный луч
- $beta$ — угол отражения
- $OC$ — перпендикуляр, опущенный в точку падения луча на поверхность зеркала
- $eta$ — искомый луч наклона зеркала
Рассмотрим $angle COA$. Это прямой угол, образованный перпендикуляром $OC$ и поверхностью зеркала $AB$. Он состоит из двух углов: $beta$ и $angle EOA$. Угол $eta$ и $angle EOA$ равны друг другу, т .к. это накрест лежащие углы, образованные секущей и двумя параллельными прямыми.
По закону отражения света: $alpha = beta$.
Из чертежа: $varphi = alpha + beta = 2 alpha$. Т.е., $alpha = frac{varphi}{2}$.
Тогда,
$eta = angle EOA = angle COA — beta = angle COA — alpha = angle COA — frac{varphi}{2} = 90 degree — frac{50}{2} = 65 degree$.
Ответ: $eta_1 = 25 degree$, $eta_2 = 65 degree$.
|
На каком расстоянии находится мнимое изображение предмета в зеркале?Aomine 8 лет назад
габбас 8 лет назад На таком же, что и предмет от зеркала. Если имеется в виду расстояние между предметом и изображением, то это будет два раза больше расстояния до зеркала. Например Вы находитесь на расстояние 2 м, то и Ваше изображение будет находиться на расстояние 2 м от зеркала. А расстояние между Вами и Вашим зеркальным двойником будет 4 м. Все это верно только для плоского зеркала. автор вопроса выбрал этот ответ лучшим комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Зеркала и изображение в плоском зеркале:
Каждый день по нескольку раз вы смотрите в зеркало и видите в нем свое изображение (рис. 237). Попробуем ответить на ряд вопросов. Где и на каком расстоянии от зеркала находится изображение? Каковы его размеры по сравнению с размерами самого предмета? Как образуется изображение?
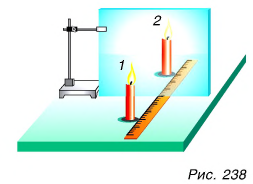
Проведем опыт. На столе расположим вертикально стеклянную пластинку и зажженную свечу 1, как показано на рисунке 238.
Стеклянная пластинка будет выполнять роль плоского зеркала. В стекле хорошо видно изображение свечи. Заглянув за пластинку, мы, конечно же, не обнаружим этой свечи.
Такую же по размерам, но незажженную свечу 2 будем перемещать с другой стороны пластинки до тех пор, пока она не совместится с изображением (не будет казаться зажженной). По линейке определим расстояние 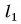
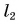
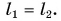
Продолжим опыт. Передвинем свечу 1 ближе к стеклянной пластинке. Ее изображение тоже приблизится, причем ровно на столько же, в чем легко убедиться с помощью линейки.
Положение изображения не изменится, если вместо стеклянной пластинки использовать плоское зеркало.
Из проведенных опытов следует, что в плоском зеркале глаз видит изображение таких же размеров, что и предмет, и на таком же расстоянии за зеркалом. Но что означает: «Глаз видит изображение»? Как глаз определяет местоположение предмета или его изображения?
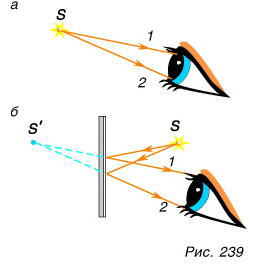
Рассмотрим лучи 1 и 2, попадающие в глаз (рис. 239, а). Эти лучи идут от светящейся точки S. А если лучи попадут в глаз не от самой светящейся точки, а отразившись от зеркала (рис. 239, б)? Глазу безразлично, как эти лучи идут до того момента, как попадают в него. Он будет фиксировать положение источника лучей (точки S) на пересечении продолжений попадающих в него лучей — в точке S’. Глаз увидит, что светящаяся точка находится именно там. Это мнимое изображение светящейся точки S, от которой в глаз попадают лучи 1 и 2.
Значит, глаз видит и сам предмет (светящуюся точку), и его мнимое изображение только тогда, когда в него попадают лучи, идущие от предмета непосредственно или после отражения от зеркала и несущие световую энергию. Если таких лучей нет, то и изображение в глазу не создается.
Поясним еще раз, почему изображение S’ в плоском зеркале называют мнимым. Мы можем увидеть это изображение. Но если мы поместим в точку S’ устройства, чувствительные к световой энергии (фотопленку или просто белый экран), то ничего там не обнаружим. В эту точку энергия света не поступает.
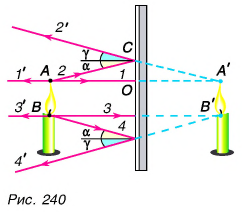
Построим теперь изображение протяженного предмета (пламени свечи) в плоском зеркале.
- Заказать решение задач по физике
Найдем изображение двух крайних точек А и В.
Для построения изображения каждой точки можно использовать два любых луча (рис. 240).
Пусть луч 1 падает на зеркало в точку О перпендикулярно плоскости зеркала 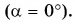
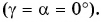
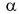
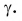
Итак, из опыта и построения следует: изображение предмета в плоском зеркале является мнимым, прямым, по размерам равным предмету и находится на таком же расстоянии за зеркалом, на котором расположен предмет перед зеркалом.
Для любознательных:
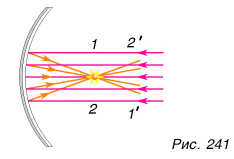
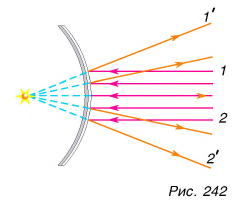
Важную роль играют зеркала, отражающие поверхности которых являются кривыми: вогнутыми (рис. 241) или выпуклыми (рис. 242). Если зеркало вогнутое, оно может параллельно падающие лучи после отражения собрать в одну точку, т. е. сконцентрировать световую энергию. Выпуклое зеркало, наоборот, после отражения дает расходящийся пучок света.
Зеркала применяются в различных сферах жизнедеятельности человека: в быту, медицине (рис. 243), транспорте, для оформления помещений и т. д.
Для любознательных:
Выпуклые зеркала используются в автомобилях (рис. 244), на станциях метро (рис. 245), на перекрестках улиц для обзора окрестности. Они обеспечивают гораздо более широкий обзор, чем плоские. Вогнутые зеркала используются там, где необходимо сконцентрировать световую энергию, например в зеркальном телескопе (рис. 246). С его помощью можно наблюдать даже неяркие далекие звезды.
Главные выводы:
- Световые лучи, падающие на зеркало, отражаются и за зеркало не попадают.
- Изображением светящейся точки в плоском зеркале является точка пересечения продолжения лучей, отраженных от поверхности зеркала.
- Плоское зеркало дает мнимое, прямое изображение предмета, равных с ним размеров и на таком же расстоянии, что и предмет, от зеркала.
- Световой луч и световой пучок
- Разложение белого света на цвета и образование цветов
- Давление света в физике
- Химическое действие света
- Скорость света
- Отражение света
- Спектральный состав естественного света
- Фотоны в физике