Как найти расстояние до небесных тел

Секция:
АСТРОНОМИЯ

Тема
исследования:

«Определение расстояния до
небесных тел»

Исполнитель: 
Каров Астемир,  ученик 9 класса

МКОУ
«Гимназия №1 г. Майского»

Руководитель: 
Биттирова Зухра Исмаиловна,

учитель
физики

высшей
квалификационной категории

Содержание

1.  Введение …………………………………………………………………3

2.  Методы
определения расстояний

2.1  
Понятие астрономической единицы, парсек, световой год…..5

2.2   Метод лазерной локации и радиолокации……………………..6

2.3   Уникальные стандартные свечи…………………………….…..7

2.4   Метод стандартных свечей……………………………………….7

2.5  
Метод тригонометрического параллакса………………………..8

2.6  
Метод триангуляции…………………………………………….10

2.7 
Фотометрический
метод определения расстояний……………..11

2.8   
Определение расстояния по относительным скоростям…..….11

2.9 
Определение расстояния до тел Солнечной системы, зная периоды обращений и
одно из расстояний. III закон Кеплера…………………….…12

3.  Заключение………………………………………………………………….12

4. Список
литературы………………………………………………………….15

5. Интернет-ресурсы. ………………………………………………………..15

6. Приложение ……………………………………………………………….16

1.  Введение

На Земле определение расстояний
обычно не составляет особого труда, но когда дело касается масштабов, в
миллионы раз превышающих земные, обычные способы не годятся. За долгие годы
развития астрономии появилось несколько способов определения расстояний до
небесных тел, но универсальный так и не был выработан, поэтому определённый
метод выбирают, обычно исходя из условий.

Задача определения расстояний до
различных небесных тел и их размеров была поставлена уже в древности. Первое из
документальных подтверждений подобных попыток относится к 360 году до нашей эры
– однако тогда Аристотелю не удалось достигнуть особой точности. В 125 г. до
нашей эры Гиппарху удалось довольно точно определить радиус Земли, а Николаю
Копернику в начале XVI века – расстояние от Земли до Солнца и других планет
Солнечной системы.

Цель:  рассмотреть
различные способы определения расстояния до тел Солнечной системы, далеких
галактик. Изучить  и выпустить наглядное пособие – диаграмму Герцшрунга –
Рассела, установить взаимосвязь между характеристиками звёзд и расстояниями.

Задачи:  1. Ввести понятия
геометрического (параллактического), «радиолокационного» и «лазерного» методов
определения расстояний до тел Солнечной системы, далеких галактик.

2.
Раскрыть,  что современная наука располагает различными методами определения
расстояний до небесных тел и их размеров для получения достоверные сведения о
масштабах Солнечной системы и размерах входящих в нее небесных тел,
содействовать формированию мировоззренческой идеи о познаваемости мира.

3.
Показать, что на первый взгляд неразрешимая проблема определения расстояний до
небесных тел и радиусов небесных тел в настоящее время решается различными
методами.

4.
Установить взаимосвязи между физическими характеристиками звёзд; убедиться в
наличии разных групп звёзд, принадлежность к которым обусловлена их физическими
характеристиками.

Объектом исследования являются небесные тела, а
конкретным предметом – звезды.

Методы:  изучение
литературы и других источников информации сети «Интернет»;
обобщение полученных данных; изготовление
наглядного пособия.

Актуальность  данной темы,  считаю
недостаток внимания у многих учащихся к интересным фактам окружающего мира. И
действительно, если задуматься насколько далеки от нас звезды, планеты…, глядя
ночью на звёздное небо, человек может видеть множество других неизведанных
миров далеких и близких.

Проблема: можно ли применить
способы измерения расстояний до недоступных точек, не используя измерительные
приборы?

Новизна: возможно, обнаружение очень молодой
галактики, представляющая собой единый очаг звездообразования. Полученные
результаты могут служить основой для дальнейших исследований этих близких
галактик в оптическом и радиодиапазоне, таких как изучение состава звездного
населения, различных стадий эволюции галактик, изучение процессов
звездообразования. Измеренные расстояния необходимы при определении
принадлежности галактик к близким группам и скоплениям, при изучении кинематики
близкой вселенной. Полученные снимки близких карликовых галактик с разрешенным
ярчайшим звездным населением используются при построении карт распределения
нейтрального водорода в этих галактиках.

2. 
Содержание

2.1   Понятие астрономической единицы, парсек,
световой год

Космические
просторы, как известно, довольно масштабны, а потому астрономы не используют
для их измерения метрическую систему, привычную для нас. В случае с расстоянием
до Луны (~384 000 км) километры еще могут быть применимы, однако если выразить
в этих единицах расстояние до Плутона, то получится 4 250 000 000 км, что уже
менее удобно для записи и вычислений. По этой причине у астрономов в ходу иные
единицы измерения расстояния. Наименьшей из таких единиц является
астрономическая единица (а.е.). Исторически так сложилось, что одна
астрономическая единица равняется радиусу орбиты Земли вокруг Солнца, иначе –
среднее расстояние от поверхности нашей планеты до Солнца. Данный метод
измерения был наиболее подходящим для изучения структуры Солнечной системы в
XVII веке. Ее точное значение 149 597 870 700 метра. Сегодня астрономическая
единица используется в расчетах с относительно малыми длинами. То есть при
исследовании расстояний в пределах Солнечной системы или других планетных
систем.

Несколько большей единицей измерения длины в астрономии является
световой год. Он равен расстоянию, которое проходит свет в вакууме за
один земной, юлианский год. Подразумевается также нулевое влияние
гравитационных сил на его траекторию. Один световой год составляет около 9 460
730 472 580 км или 63 241 а.е. Данная единица измерения длины
используется лишь в научно-популярной литературе по той причине, что световой
год позволяет читателю получить примерное представление о расстояниях в
галактическом масштабе. Однако из-за своей неточности и неудобности световой
год практически не используется в научных работах.

Наиболее практичной и
удобной для астрономических вычислений является такая единица измерения
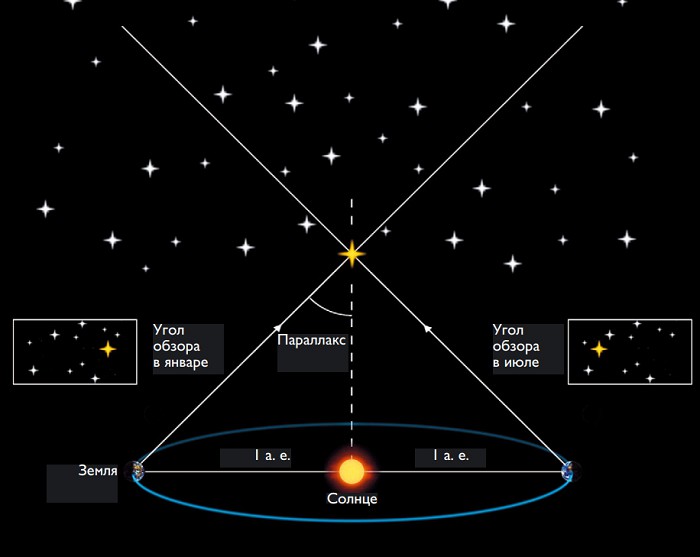
расстояния как парсек. Чтобы понять ее физический смысл, следует
рассмотреть такое явление как параллакс. Его суть состоит в том,
что при движении наблюдателя относительно двух отдаленных друг от друга тел,
видимое расстояние между этими телами также меняется. В случае со звездами
происходит следующее. При движении Земли по своей орбите вокруг Солнца
визуальное положение близких к нам звезд несколько меняется, в то время как
дальние звезды, выступающие в роли фона, остаются на тех же местах. Изменение
положения звезды при смещении Земли на один радиус ее орбиты, называется годичный
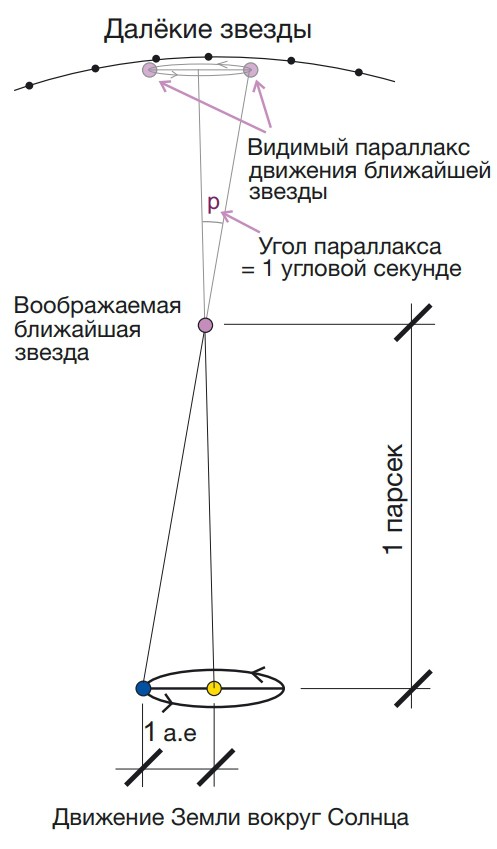
параллакс, который измеряется в угловых секундах. Тогда один парсек
равен расстоянию до звезды, годичный параллакс которой равен одной угловой
секунде – единице измерения угла в астрономии. Отсюда и название «парсек»,
совмещенное из двух слов: «параллакс» и «секунда». Точное значение парсека
равняется 3,0856776·1016 метра или 3,2616 светового года. 1 парсек
равен примерно 206 264,8 а. е.

2.2   Метод лазерной
локации и радиолокации

Эти два современных метода служат для определения точного
расстояния до объекта в пределах Солнечной системы. Он производится следующим
образом. При помощи мощного радиопередатчика посылается направленный
радиосигнал в сторону предмета наблюдения. После чего тело отбивает полученный
сигнал и возвращает на Землю. Время, потраченное сигналом на преодоление пути,
определяет расстояние до объекта. Точность радиолокации – всего несколько
километров. В случае с лазерной локацией, вместо радиосигнала лазером
посылается световой луч, который позволяет аналогичными расчетами определить
расстояние до объекта. Точность лазерной локации достигается вплоть до долей
сантиметра.

         Основные
антенны для радиолокации планет:

– Евпатория, Крым,
радиолокационная установка центра дальней космической связи имеет антенну с
диаметром главного зеркала 70 м и оборудована передатчиком мощностью несколько
сотен кВт на волне  = 39 см;

– Аресибо, Пуэрто Рико,
диаметр зеркала 305 м, на волне  = 12,6 см;

– Голдстоун, Калифорния,
диаметр зеркала 64 м, на волне  = 3,5 и 12,6 см.

2.3   Уникальные
стандартные свечи

Цефеиды – наиболее используемые стандартные свечи, представляющие собой
переменные пульсирующие звезды. Изучив физические особенности
этих объектов, астрономы узнали, что цефеиды обладают дополнительной характеристикой
– периодом пульсации, который легко можно измерить и который соответствует
определенной светимости.

В
результате наблюдений ученым удается измерить яркость и период пульсации таких
переменных звезд, а значит и светимость, что позволяет высчитать расстояние до
них. Нахождение цефеиды в иной галактике дает возможность относительно точно и
просто определить расстояние до самой галактики. Поэтому данный тип звезд часто
именуется «маяками Вселенной».
Несмотря на то, что метод цефеид является наиболее точным на расстояниях до 10
000 000 пк, его погрешность может достигать 30%. Для повышения точности
потребуется как можно больше цефеид в одной галактике, но и в таком случае
погрешность сводится не менее чем к 10%. Причиной тому служит неточность зависимости
период-светимость.

Кроме
цефеид в качестве стандартных свечей могут использоваться и другие переменные
звезды с известными зависимостями период-светимость, а также для наибольших
расстояний — сверхновые с известной светимостью. Близким по точности к методу
цефеид является метод, с красными гигантами в роли стандартных свеч. Как
выяснилось, ярчайшие красные гиганты имеют абсолютную звездную величину в
достаточно узком диапазоне, которая позволяет посчитать светимость.

2.4   Метод стандартных
свечей

Для
определения расстояний до звезд в других галактиках и расстояний до самих этих
галактик используется метод стандартных свечей. Как известно, чем дальше от
наблюдателя расположен источник света, тем более тусклым он кажется
наблюдателю. Т.е. освещенность лампочки на расстоянии 2 м будет в 4 раза
меньше, чем на расстоянии 1 метр. Это и есть принцип, по которому измеряется
расстояние до объектов методом стандартных свечей. Таким образом, проводя
аналогию между лампочкой и звездой, можно сравнивать расстояния до источников
света с известными мощностями.

В качестве
стандартных свечей в астрономии выступают объекты, светимость (аналог мощности
источника) которых известна. Это может быть любого рода звезда. Для определения
ее светимости астрономы измеряют температуру поверхности, опираясь на частоту
ее электромагнитного излучения. После чего, зная температуру, позволяющую
определить спектральный класс звезды, выясняют ее светимость при помощи
диаграммы Герцшпрунга-Рассела. Затем, имея значения светимости и измерив
яркость (видимую величину) звезды, можно посчитать расстояние до нее. Такая
стандартная свеча позволяет получить общее представление о расстоянии до
галактики, в которой она находится. Однако данный метод достаточно трудоемкий и
не отличается высокой точностью. Поэтому астрономам удобнее использовать в
качестве стандартных свечей космические тела с уникальными особенностями, для
которых светимость известна изначально.

2.5   Метод
тригонометрического параллакса

Используя
третий закон Кеплера, среднее расстояние всех планет от Солнца можно выразить
через среднее расстояние Земли от Солнца. Определив его в километрах, можно
найти в этих единицах все расстояния в Солнечной системе.  Классическим
способом определения расстояний был и остается угломерный геометрический способ
(рис. 1) Им определяют расстояния и до далеких звезд, к которым метод
радиолокации неприменим. Геометрический способ основан на явлении
параллактического смещения. Параллактическим смещением  называется
изменение направления на предмет при перемещении наблюдателя. Посмотрите на
вертикально поставленный карандаш сначала одним глазом, затем другим. Вы
увидите, как он при этом переменил положение на фоне далеких предметов,
направление на него изменилось. Чем дальше вы отодвинете карандаш, тем меньше
будет параллактическое смещение. Но чем дальше отстоят друг от друга точки
наблюдения, т. е. чем больше базис, тем больше параллактическое смешение при
той же удаленности предмета. В нашем примере базисом было расстояние между
глазами. Принцип параллактического смещения широко используется в военном деле
при определении расстояния до цели посредством дальномера. В дальномере базисом
является расстояние между объективами. Для измерения расстояний до тел
Солнечной системы за базис берут радиус Земли. Наблюдают положение светила,
например Луны, на фоне далеких звезд одновременно из двух обсерваторий.
Расстояние между
обсерваториями должно быть как можно больше, а соединяющий их отрезок должен
составлять угол, по возможности близкий к прямому с направлением на светило,
чтобы параллактическое смещение было максимальным. Определив из двух точек А и
В направления на наблюдаемый объект, несложно вычислить (рис. 2)  угол р,
под которым с этого объекта был бы виден отрезок, равный радиусу Земли.  Угол,
под которым со светила виден радиус Земли, перпендикулярный к лучу зрения,
называется горизонтальным параллаксом. Параллакс
Луны составляет 57′. Все планеты и Солнце гораздо дальше, и их параллаксы
составляют секунды. Параллакс Солнца, например, рс = 8,8″. Параллаксу
Солнца соответствует среднее расстояние Земли от Солнца, примерно равное 150
000 000 км. Это расстояние принимается за одну астрономическую
единицу (1 а. е.). В астрономических единицах часто измеряют
расстояния между телами Солнечной системы.

Рис. 3. Определение линейных размеров небесных светил по их
угловым размерам.

При малых углах sin р = p, если угол р выражен в радианах. Если р
выражен в секундах дуги, то вводится множительгде
206265 — число секунд в одном радиане.

Тогда   Знание этих соотношений
упрощает вычисление расстояния по известному параллаксу:      

2.6   Метод триангуляции

Зная базу – расстояние ℓ между двумя телескопами,
расположенными в точках А и В на Земле, и углы, под которыми они направлены на
Луну, можно найти расстояния АС и ВС:

  

Рисунок 4

Горизонтальный экваториальный параллакс светила –  угол ρ,
под которым со светила, находящегося на горизонте виден экваториальный радиус
Земли R⊕ = 6378 км, перпендикулярный лучу зрения. Пусть К –
местонахождение наблюдателя, из которого светило видно на горизонте. Из
прямоугольного  КОС гипотенуза  . Если выразить
величину угла p в радианах и учитывать, что угол выражен в секундах дуги, то

Рисунок 5                              

                                                           1
рад =57,3⁰ = 3438’=206265″.

2.7 
Фотометрический
метод определения расстояний

Освещенности,
создаваемые одинаковыми по мощности источниками света, обратно пропорциональны
квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.
е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной
лучам света) может служить мерой расстояния до них. Выражение освещенностей в
звездных величинах (m–видимая звездная величина, М–абсолютная
звездная величина) приводит к следующей основной формуле фотометрических
расстояний – r_ф:      r_ф = 0,2(m – M) +
1.    При определении r_ф по вышеназванной формуле
погрешность составляет ~30%.

Для
светил, у которых известны тригонометрические параллаксы, можно, определив М по
этой же формуле, сопоставить физические свойства с абсолютными звездными
величинами. Это сопоставление показало, что абсолютные звездные величины многих
классов светил (звезд, галактик и др.) можно оценивать по ряду их физических
свойств. Зная расстояния до некоторого числа звезд, вычисленные методом
параллакса, можно было вычислить светимости и сопоставить их со спектром тех же
звезд.  Из диаграммы видно, что каждому определенному подклассу звезд (например
A) соответствует определенная светимость, таким образом, достаточно точно
определить спектральный класс и можно выяснить ее светимость, а следовательно,
и расстояние.  Иногда определенному классу соответствует другая
светимость, но в этом случае и спектр у них несколько другой. Спектры карликов
и гигантов различаются интенсивностью определенных линий или их пар, причем это
отличие можно выяснить, исследуя близко находящиеся звезды. Это отличие связано
с тем, что атмосферы гигантов обширнее и разреженнее. Точность определения
расстояния таким способом составляет ~20%.

2.8    Определение расстояния по относительным скоростям

Косвенным
показателем расстояния до звезд являются их относительные скорости: как
правило, чем ближе звезда, тем больше смещается она по небесной сфере.
Определить таким способом расстояние, конечно нельзя, но этот способ дает
возможность “вылавливать” близкие звезды.  Также существует другой метод
определения расстояний по скоростям, применимый для звездных скоплений. Он
основан на том, что все звезды, принадлежащие одному скоплению, движутся в
одном и том же направлении по параллельным траекториям. Измерив лучевую
скорость звезд с помощью эффекта Доплера, а также скорость, с которой эти
звезды смещаются относительно очень удаленных, то есть условно неподвижных
звезд, можно определить расстояние до интересующего нас скопления.

2.9  Определение
расстояния до тел Солнечной системы, зная периоды обращений и одно из
расстояний.  III закон Кеплера

Квадраты сидерических периодов
планет, умноженные на сумму масс Солнца и планеты, относятся как кубы больших
полуосей орбит планет:

3.  Заключение

Наши
знания о Вселенной тесно связаны со способностью человека определять расстояния
в пространстве. С незапамятных времен вопрос «как далеко?» играл первостепенную
роль для астронома в его попытках познать свойства Вселенной, в которой он
живет. Но как бы ни было велико стремление человека к познанию, оно не могло
быть осуществлено до тех пор, пока в распоряжении людей не оказались
высокочувствительные и совершенные инструменты. Таким образом, хотя на
протяжении веков представления о физическом мире непрерывно развивались,
завесы, скрывавшие верстовые столбы пространства, оставались нетронутыми. Во
все века философы и астрономы размышляли о космических расстояниях и усердно
искали способы их измерения. Но все было напрасно, так как необходимые для
этого инструменты не могли быть изготовлены. И, наконец, после того как
телескопы уже в течение многих лет использовались астрономами и первые гении
посвятили свой талант изучению богатств, добытых этими телескопами, настало
время союза точной механики и совершенной оптики, который позволил создать
инструмент, способный разрешить проблему расстояний. Барьеры были устранены, и
многие астрономы объединили свои знания, мастерство и интуицию с целью
определить те колоссальные расстояния, которые отделяют от нас звездные миры.

В
1838 году три астронома (в разных частях света) успешно измерили расстояния до
некоторых звезд. Фридрих Вильгельм Бессель в Германии определил расстояние до
звезды Лебедь 61. Выдающийся русский астроном Василий Струве установил
расстояние до звезды Веги. На мысе Доброй Надежды в Южной Африке Томас
Гендерсон измерил расстояние до ближайшей к Солнцу звезды – альфа Центавра. Во
всех названных случаях астрономы измеряли невообразимо малое угловое
расстояние, чтобы определить так называемый параллакс. Их успех был обусловлен
тем, что звезды, до которых они измеряли расстояния, находились относительно
близко к Земле.

Порой возникают такие ситуации, когда важно запомнить
не только какие-либо сведения, но и их правильный порядок. Почти все
школьники знают мнемоническую фразу для запоминания порядка цветов
в радуге про охотника…

Спектральные классы звёзд в зависимости от
температуры делятся на классы: O, B, A, F, G, K, M, L, T. Кроме того,
выделяют три дополнительных класса R, N, S, которые отражают химический состав
звезд. Для запоминания этих классов астрономы используют мнемоническую фразу: «Один
Бритый Англичанин Финики Жует, Как Морковь», её приписывают автору
школьного учебника по астрономии профессору Б.А. Воронцову-Вельяминову.

К сожалению, фраза не кодирует классы L и T,
т. к. она была придумана задолго до того, как эти классы были открыты.

  Я решил предложить свою
версию:

a)     Одиссей – Безупречный Аптекарь, Фантазер, Живописец, Как Маг Летит Творить;

b)    Огонь Бесценный Амазонки Философ  Жора  Классно Мчал Легко Торжественно;

с) Отважный Бодрый Айболит Фаршировал  Жгучий Кактус Медом Ломая Трактор.

         Был
проведен опрос на лучшую  мою мнемоническую
фразу, результаты которой представлены в диаграмме; в опросе участвовали в
основном учащиеся 8-11 классов и учителя гимназии.

Результаты опроса представлены в диаграмме (всего
103 респондентов):

Опрос показал, что все  3 мнемонические  фразы  оказались удачными и  с  небольшим
отрывом победила «Отважный Бодрый Айболит
Фаршировал Жгучий Кактус Медом Летит Творить».

 

 

 

 

4. Список литературы

1.                
Астрономия 11 класс,  Б.А
Воронцов-Вельяминов, Е.К Страут;  Дрофа; 2017-2020г

2.                
Радость познания. Популярная энциклопедия
в 4-х томах. Т. 1. Наука и вселенная: пер. с англ. – М.: Мир, 1983 – 295 с.

3.                
Энциклопедический словарь юного астронома
/ Сост. Н. П. Ерпылев. – М.: Педагогика, 1986. – 336 с.

4.                
CD
“Библиотека электронных наглядных пособий “Астрономия, 9-10
классы”. – М.: ООО “ФИЗИКОН”, 2003.

5.                
CD
“Открытая астрономия 2.5”. – М.: ООО “ФИЗИКОН”, 2002.

6.                
Мухин Л. М. Мир астрономии. Москва, изд.
«Молодая гвардия», 1987 г.

7.                
Левитт И. За пределами известного мира: от
белых карликов до квазаров. Москва, изд. «Мир», 1978 г.

5.
Интернет- ресурсы:

1.                
https://cyberleninka.ru/article/n/ponyatie-rasstoyaniya-i-svyazannye-s-nim-zadachi-na-optimizatsiyu-v-shkolnom-kurse-stereometrii

2.                
https://www.bibliofond.ru/view.aspx?id=48016

3.                
https://spacegid.com/rasstoyaniya-v-kosmose.html

4.                
ОТКРЫТАЯ АСТРОНОМИЯ 2.6

     http://college.ru/astronomy/course/content/content.html#.WfDgQuVLuZY

5.                
http://4book.org/uchebniki–rossiya/7-klass/56-geometriya-7-9-klassy–atanasyan–l–s–i–dr

6.  Приложение

1. Расстояния в цифрах
1 а.е. от Земли до Солнца = 500 св. секунд или 8,3 св. минуты

30 а. е. от Солнца до Нептуна = 4,15 световых часа

132 а.е. от Солнца – таково расстояние до космического аппарата
«Вояджер-1», было отмечено 28 июля 2015 года. Данный объект является самым
отдаленным из тех, что были сконструированы человеком.

Расстояния в Млечном Пути и за его пределами:
1,3 парсека (268144 а.е. или 4,24 св. года) от Солнца до Проксима Центавра –
ближайшей к нам звезды

8 000 парсек (26 тыс. св. лет) – расстояние от Солнца до центра
Млечного Пути
3

0 000 парсек (97 тыс. св. лет) – примерный диаметр Млечного
Пути

770 000 парсек (2,5 млн. св. лет) – расстояние до ближайшей
большой галактики – туманность Андромеды

300 000 000 пк — масштабы в которых Вселенная практически
однородна

4 000 000 000 пк (4 гигапарсек) – край
наблюдаемой Вселенной. Это расстояние прошел свет, регистрируемый на Земле.
Сегодня объекты, излучившие его, с учетом расширения Вселенной,
расположены на расстоянии 14 гигапарсек (45,6 млрд. световых лет).

3.  Двадцать
ближайших звезд.

№№ п. п.	Название звезды	Параллакс в секундах дуги	Расстояние, пс	Видимая звездная величина, m	Абсолютная звездная величина, М	Спек-траль-ный класс
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20	Солнце.  .  .  .  .  .  .  .  . Проксима Центавра   . α Центавра А  .  .  .  .  . α Центавра В  .  .  .  .  . Звезда Барнарда   .  .  . Лаланд 21185 .  .  .  .  . Вольф 359 .  .  .  .  .  .  . +36˚2147   .  .  .  .  .  .  . Сириус   .  .  .  .  .  .  .  . Спутник Сириуса   .  .  Росс 154 .  .  .  .  .  .  .  .  Росс 248 .  .  .  .  .  .  .  . Лейтен 7896   .  .  .  .  .  ε Эридана .  .  .  .  .  .  . Процион   .  .  .  .  .  .  .  Спутник Проциона .  . 61 Лебедя .  .  .  .  .  .  . Спутник 61 Лебедя .  . τ Кита  .  .  .  .  .  .  .  .  . ε Индейца .  .  .  .  .  .	–– 0,762 0,756 0,756 0,543 0,407 0,403 0,388 0,376 0,376 0,350 0,334 0,328 0,303 0,297 0,297 0,296 0,296 0,294 0,288	1/206256 1,31 1,32 1,32 1,84 2,46 2,48 2,58 2,66 2,66 2,86 2,99 3,05 3,30 3,37 3,37 3,38 3,38 3,40 3,47	–26,7 +11,3 +0,3 +1,7 +9,5 +10,7 +13,5 +7,5 –1,5 +8,5 +10,5 +12,2 +12,3 +3,8 +0,5 +10,8 +5,4 +6,1 +3,7 +4,7	+4,9 +15,7 +4,7 +6,1 +13,1 +13,7 +16,5 +10,4 +1,4 +11,4 +13,2 +14,7 +14,9 +6,2 +2,8 +13,1 +7,7 +8,4 +6,0 +7,0	G4 M G4 K1 M5 M2 M8 M2 A1 A5 M5 M6 M6 K2 G4 K3 K5 G5 K5

1. Определение размеров Земли. Первый известный науке метод определения размеров Земли применил греческий учёный Эратосфен. Он выбрал два города, лежащих на одном и том же географическом меридиане земного шара, — Александрию (0₁) и Сиену (0₂) (рис. 41). Из рисунка видно, что если обозначить длину дуги меридиана 0₁0₂ через l, а её угловое значение через n (в градусах), то длина дуги 1° меридиана l₀ будет равна:

а длина всей окружности меридиана:

где R — радиус земного шара. Отсюда

Длина дуги меридиана между выбранными на земной поверхности точками 0₁ и 0₂ в градусах равна разности географических широт этих точек, т. е. n = Δφ = φ₁ — φ₂.

Рисунок 41 — Вычисление радиуса Земли

Длина дуги l — расстояние между Александрией и Сиеной — была хорошо известна. Угол n Эратосфен измерил, используя то обстоятельство, что Сиена лежит на тропике Рака и в день летнего солнцестояния Солнце в полдень здесь наблюдалось в зените. А в Александрии Солнце до зенита не доходило и шест, врытый перпендикулярно в землю, отбрасывал тень. Измерив длину этой тени, Эратосфен получил значение n = 7,2° и длину окружности L примерно 45 тыс. км (современное значение 40 тыс. км).

Современная геодезия располагает точными методами для измерения расстояний на земной поверхности. Определение расстояния l между точками 0₁ и 0₂ (см. рис. 41) затруднено из-за естественных препятствий (гор, рек, лесов и т. п.).

Рисунок 42 — Метод триангуляции

Поэтому длина дуги l определяется путём вычислений, требующих измерения только сравнительно небольшого расстояния — базиса и ряда углов.

Этот метод разработан в геодезии и называется триангуляцией (лат. triangulum — треугольник).

Суть его состоит в следующем. По обе стороны дуги O₁О₂, длину которой необходимо определить, выбирается несколько точек А, В, С, … на взаимных расстояниях до 50 км с таким расчётом, чтобы из каждой точки были видны по меньшей мере две другие точки (рис. 42).

Геодезическая вышка. На ее вершине укреплен цилиндр, на который при измерениях наводят теодолит для измерения углов.

Длину базиса очень тщательно измеряют специальными мерными лентами. Измеренные углы в треугольниках и длина базиса позволяют по тригонометрическим формулам вычислить стороны треугольников, а по ним — длину дуги O₁О₂ с учётом её кривизны.

В России с 1816 по 1855 г. под руководством В. Я. Струве была измерена дуга меридиана длиной 2800 км. В 30-е гг. ХХ в. высокоточные градусные измерения были проведены в СССР под руководством профессора Ф. Н. Красовского.

Триангуляционные измерения показали, что длина дуги 1° меридиана не одинакова под разными широтами: около экватора она равна 110,6 км, а около полюсов — 111,7 км, т. е. увеличивается к полюсам.
Истинная форма Земли не может быть представлена ни одним из известных геометрических тел. Поэтому в геодезии и гравиметрии форму Земли считают геоидом, т. е. телом с поверхностью, близкой к поверхности спокойного океана и продолженной под материками.

В настоящее время созданы триангуляционные сети со сложной радиолокационной аппаратурой, установленной на наземных пунктах, и с отражателями на геодезических искусственных спутниках Земли, что позволяет точно вычислять расстояния между пунктами. Значительный вклад в развитие космической геодезии внёс уроженец Беларуси — известный геодезист, гидрограф и астроном И. Д. Жонголович. На основе изучения динамики движения искусственных спутников Земли он уточнил сжатие нашей планеты и несимметричность Северного и Южного полушарий.

Рисунок 43 — Горизонтальный параллакс светила

2. Определение расстояний методом горизонтального параллакса. Кажущееся смещение светила, обусловленное перемещением наблюдателя, называется параллактическим смещением или параллаксом светила. Параллактические смещения светила тем больше, чем ближе оно к наблюдателю и чем больше перемещение наблюдателя.

Определение расстояний до тел Солнечной системы основано на измерении их горизонтальных параллаксов. Угол р, под которым со светила виден радиус Земли, перпендикулярный к лучу зрения, называется горизонтальным параллаксом (рис. 43). Чем больше расстояние до светила, тем меньше угол р.

Зная горизонтальный параллакс светила, можно определить его расстояние D = SO от центра Земли. Расстояние до светила

( D=frac{R_oplus}{sin p} ), где R_Е — радиус Земли. Приняв R_Е за единицу, можно выразить расстояние до светила в земных радиусах.

Например, параллакс Солнца р_¤ = 8,794″. Параллаксу Солнца соответствует среднее расстояние от Земли до Солнца, примерно равное 149,6 млн км. Это расстояние принимается за одну астрономическую единицу (1 а. е.). В астрономических единицах удобно измерять расстояния между телами Солнечной системы.

При малых углах sin p » p, если угол р выражен в радианах. Если угол р выражен в секундах дуги, то вводится множитель

где 206 265 — число секунд в одном радиане. Тогда

Эта формула значительно упрощает вычисление расстояния D до светила по известному параллаксу p.

3. Радиолокационный метод. Для определения расстояний до тел Солнечной системы используются наиболее точные методы измерений — радиолокационные измерения. Измерив время t, необходимое для того, чтобы радиолокационный импульс достиг небесного тела, отразился и вернулся на Землю, вычисляют расстояние D до этого тела по формуле:

где с — скорость света, равная примерно 3·10⁸ м/с.

С помощью радиолокации определены наиболее точные значения расстояний до тел Солнечной системы, уточнены расстояния между материками Земли, более точно определена астрономическая единица (1 а. е. = 149 597 870 ± 2 км).

Методы лазерной локации (использующие, например, специальные уголковые отражатели, доставленные на Луну) позволили измерить расстояния от Земли до Луны с точностью до нескольких сантиметров.

Рисунок 44 — Определение линейных размеров тел Солнечной системы

4. Определение размеров тел Солнечной системы. При наблюдениях небесных тел Солнечной системы можно измерить угол, под которым они видны наблюдателю с Земли. Зная угловой радиус светила р (рис. 44) и расстояние D до светила, можно вычислить линейный радиус R этого светила по формуле R = D ⋅ sin ρ.

По определению горизонтального параллакса, радиус Земли R_Å виден со светила под углом р, тогда получим:

Так как значения углов r и р малы, окончательно имеем:

Определение размеров небесных тел таким способом возможно только тогда, когда видны их диски.

Главные выводы

1. В основу метода определения размеров Земли положены градусные измерения (триангуляция) длин дуг на её поверхности.
2. Определение расстояний до тел Солнечной системы основано на измерении малых углов (параллаксов). В настоящее время для этого используются методы лазерной локации и радиолокации.
3. Для измерения расстояний между телами Солнечной системы используется астрономическая единица (1 а. е.), равная примерно 149,6 млн км.
4. Определение размеров тел Солнечной системы основано на измерении угловых радиусов и расстояний до них.

Контрольные вопросы и задания
1. Каким образом греческий ученый Эратосфен определил размеры Земли?
2. Как определяют длину дуги меридиана триангуляционным методом?
3. Что понимают под горизонтальным параллаксом?
4. Как определить расстояние до светила, зная его горизонтальный параллакс?
5. Что такое астрономическая единица?
6. В чем состоит радиолокационный метод определения расстояний до небесных тел?
7. На каком расстоянии от Земли находится небесное тело, если его горизонтальный параллакс равен 1ʹ?
8. Определите линейный радиус Луны, если в ходе наблюдений стало известно, что ее горизонтальный параллакс в это время равен 57’, а угловой радиус — 15,5ʹ. Радиус Земли принять равным 6400 км.
9. Оцените расстояние от Солнца до Меркурия, если его наибольшая элонгация равна 28°.
10. Определите диаметр Меркурия, если при прохождении по диску Солнца его угловой диаметр оказался 11,0″, а горизонтальный параллакс в этот момент равен 14,3″.

Проверь себя

Выбор тем

Измерение расстояния до Луны

Способы, применяемые астрономами для определения расстояния до близких к нам небесных тел, в принципе те же самые, которые применяют геодезисты при съемочных работах, землемеры, саперы, артиллеристы и т. д.

Как измерить расстояние до предмета, подойти к которому нельзя, например, до дерева на противоположной стороне реки (рис. 1)?

Топограф или землемер поступит просто. Он отложит на «своем» берегу линию АВ и измерит ее длину. Затем, став на один конец линии в точку А, измерит угол CAB — между направлением своей линии и направлением на предмет С. Перейдя в точку В он измерит угол СВА. А дальше можно поступить двумя способами: можно отложить на бумаге линию АВ в масштабе и построить на ее концах углы CAB и СВА, пересечение сторон которых и дает на плане точку С. Расстояние ее от точек А и В (да и от любой другой точки, отмеченной на плане) представит соответствующее действительное расстояние в том же самом масштабе, в котором изображена линия АВ. Или же можно по формулам тригонометрии, зная одну сторону треугольника и два его угла, вычислить все другие его линии, в том числе и высоту СН — расстояние точки С — далекого дерева до проведенной землемером линии АВ.

Точно так же поступили и астрономы, определяя расстояние до Луны. Если в один и тот же момент два наблюдателя сфотографируют небо с Луной из двух далеких друг от друга мест А и В (рис. 2) и затем сравнят свои снимки, они увидят, что положение Луны относительно звезд несколько различно. Например, звезда Е на снимке наблюдателя А будет видна к северу от Луны, а у наблюдателя В — к югу.

Измеряя снимки или, что проще, определяя положение Луны на небе в двух местах с помощью специальных телескопов, снабженных угломерными приспособлениями, можно по видимому смещению Луны найти и ее расстояние до Земли. Вспомним одну простую теорему из геометрии — сумма углов в четырехугольнике равна 360° — и применим ее к Земле и Луне.

Измерения дадут величину углов z₁ и z₂ — углов между вертикальным направлением в обоих местах и направлением на Луну. Предположим, для простоты, что места А и В лежат на одном меридиане, т. е. на круге, проходящем через оба полюса Земли. ЕЕ — земной экватор и утлы φ ₁ и φ₂ —географические широты обоих мест.

Применяя теорему к четырехугольнику OALB, где О — центр Земли, найдем, что

[(180° — z₁)+φ ₁ + φ ₁₂+ (180°—z₂)[+] p]= 360°

или

р = (z₁+ z₂) — (φ₁+ φ₂)

По известным углам найдем угол р, под которым из центра Луны видна линия АВ. Длина линии АВ известна, так как известен радиус Земли и положение мест наблюдения А и В. По длине этой линии и углу р, так же как и в случае недоступного предмета, можно вычислить расстояние до Луны.

Угол, под которым из центра Луны или другого небесного тела видна линия, длиной равная радиусу Земли, называется параллаксом этого небесного светила. Измерив угол р для любой линии АВ, можно вычислить и параллакс Луны.

Такие измерения были сделаны еще древними греками. Современные точные намерения дают для параллакса Луны на ее среднем расстоянии от Земли величину немного меньше градуса — 57′ 2″,7, т. е. Земля видна с Луны как диск диаметром почти в 2° (в 4 раза больше диаметра видимого нами диска Луны).

Отсюда следует между прочим тесьма интересный вывод: жители Луны (если бы они были там) с большим правом смогли бы сказать, что Земля служит для освещения Луны, чем мы говорим обратное. В самом деле: диск Земли, видимый с Луны, по площади в 14 раз больше видимого нами диска Луны; а так как каждый участок поверхности диска Земли отражает в 6 раз больше света (из-за наличия атмосферы), чем такой же участок диска Луны, то Земля посылает на Луну в 80 раз больше света, чем Луна на Землю (при одинаковых фазах).

По параллаксу Луны сейчас же находим, что расстояние до нее в 60,267 раз больше радиуса Земли или равно 384 400 км.

Однако — это среднее расстояние: путь Луны не точный круг, и Луна, обращаясь вокруг Земли, то подходит к ней на 363000 км, то удаляется на 405 000 км.

Так решается первая, самая простая задача — измерение расстояния до самого близкого к нам небесного тела. Это сравнительно не трудно, потому что видимое смещение Луны велико, и его можно было измерить с помощью даже тех примитивных приборов, которыми пользовались древние астрономы.

Чему равно расстояние до Солнца

Казалось бы, можно применить тот же самый способ и для измерения расстояния: до Солнца — произвести одновременные наблюдения в двух местах, вычислить углы четырехугольников и треугольников, и задача решена. На деле, однако, обнаружилось весьма много трудностей.

Уже древние греки установили, что Солнце во много раз дальше Луны, но во сколько именно — установить не смогли.

Древнегреческий астроном Аристарх нашел, что Солнце в 20 раз дальше Луны; это измерение было неверно. В 1650—1675 гг. голландские и французские астрономы показали, что Солнце дальше Луны примерно в 400 раз. Стало понятным, почему не удавались попытки обнаружить видимое смещение Солнца, как это удалось сделать для Луны. Ведь параллакс Солнца в 400 раз меньше параллакса Луны, всего около 1/400 градуса, или 9 сек. дуги. А это значит, что даже при наблюдении с двух мест Земли, лежащих на противоположных концах диаметра Земли, например с северного и южного полюсов, видимое смещение Солнца было бы равно видимой толщине проволоки в 0,1 мм (человеческий волос) при рассматривании ее с расстояния в 1,5 м. Величина ничтожная, и заметить ее трудно, хотя и возможно с помощью точного угломерного прибора.

Но возникают большие добавочные трудности. Луну наблюдают ночью и ее положение сравнивают с положениями соседних звезд. Днем звезд не видно, и сравнивать положение Солнца не с чем, приходится целиком полагаться на разделенные круги самого прибора. Прибор нагревается лучами Солнца, различные части его деформируются, вызывая появление новых ошибок. Да и сам воздух, нагретый лучами Солнца, неспокоен, край Солнца кажется волнующимся, дрожащим, по небу как бы бегут волны. Погрешности наблюдений будут больше той величины, которую необходимо измерить. От самого простого метода пришлось отказаться и пойти обходными путями.

Наблюдения видимых движений планет производились еще в глубокой древности. Из сравнения этих наблюдений с современными удалось с очень большой точностью определить время обращения планет вокруг Солнца. Так например, мы знаем что Марс совершает свой оборот в 1,8808 земных года. Но третий закон Кеплера говорит: «Квадраты времен обращения планет относятся, как кубы их средних расстояний от Солнца». Отсюда, принимая за единицу среднее расстояние Земли от Солнца, можно вычислить, что среднее расстояние Марса равно 1,5237. Таким путем можно построить точный «план» солнечной системы, нанести орбиты планет, Земли, комет, но у плана будет не хватать «мелочи» — масштаба. Мы сможем уверенно сказать, что Венера в 1,38 раза ближе к Солнцу, чем Земля, а Марс в 1,52 раз дальше, но ничего не будем знать о том, сколько же километров от Венеры или Земли до Солнца. Достаточно, однако, найти хотя бы одно из расстояний в километрах: мы получим в свои руки масштаб и, пользуясь им, сможем измерить любое расстояние на плане.

Именно этот способ был применен для измерения расстояния от Солнца до Земли. Меркурий и Венера находятся ближе к Солнцу, чем Земля. Может оказаться, что когда Земля и Венера будут находиться по одну сторону от Солнца, — центры Солнца и обеих планет окажутся на одной “прямой линии (рис. 3). Венера будет видна с Земли на диске Солнца. Расстояние от Земли до Венеры будет почти в 4 раза меньше расстояния до Солнца, а параллакс ее почти в 4 раза больше параллакса Солнца. Кроме того, нужно будет определить положение Венеры относительно центра Солнца, что можно сделать гораздо точнее, чем определение видимого положения Солнца (ошибки, присущие инструменту, влияют значительно меньше при определении относительного положения двух небесных тел).

Если бы движение Земли и Венеры происходило в одной и той же плоскости, то «прохождения Венеры по диску Солнца» наблюдались бы каждый раз, когда Венера, движущаяся быстрее Земли, обгоняет ее, т. е. примерно раз в 1 год и 7 мес. Но плоскости путей Земли и Венеры наклонены друг к другу. Обгоняя Землю, Венера проходит выше или ниже Солнца и не может быть наблюдаема, так как она повернута к Земле темной, не освещенной Солнцем стороной. Мы увидим ее на диске Солнца лишь в том случае, если и «обгон» будет происходить вблизи линии пересечения плоскостей орбит обеих планет.

Такое «счастливое совпадение» случается не часто. После одного прохождения второе следует через 8 лет, но зато следующее — лишь через 105—120 лет. Впервые явление наблюдали в 1639 г. Следующие прохождения — 1761, 1769, 1874 и 1882 гг. наблюдались уже весьма тщательно для определения точного расстояния до Солнца. Для наблюдения последних двух прохождений было снаряжено большое число специальных экспедиций. Наблюдатели в далеко расположенных пунктах с наибольшей доступной точностью наблюдали моменты начала и конца явления, а также положение Венеры на диске Солнца. При наблюдениях последних прохождений применялось уже фотографирование Солнца. Видимый путь Венеры по диску Солнца будет несколько смещен у обоих наблюдателей (рис. 3). Из величины смещения можно вычислить расстояние от Земли до Венеры, т. е. найти тот ключ, масштаб, которого недоставало в построенном плане солнечной системы. Наблюдений прохождений Венеры дали для параллакса Солнца величину 8″,86 и для расстояния Солнца — 148 000 000 км.

Два ближайших прохождения Венеры по диску Солнца будут наблюдаться 8 июня 2004 г. и 6 июня 2012 г.

Могут наблюдаться и прохождения по диску Солнца ближайшей к Солнцу планеты — Меркурия. Они бывают значительно чаще, чем прохождения Венеры, но представляют несравненно меньше интереса для определения расстояния до Солнца: в момент прохождения расстояние от Земли до Меркурия составляет около 90 млн. км, и параллакс его лишь в 1,5 раза больше параллакса Солнца.

Другое удобное расположение планет бывает тогда, когда Земля, двигаясь быстрее Марса, перегоняет его (рис. 4). В это время Марс виден на ночном небе в противоположном от Солнца направлении, почему такие положения его и называются противостояниями. Расстояние между Землей и Марсом уменьшается в среднем до 78 млн. км. Однако орбита Марса сильно отлична от круга, и если сближение Марса и Земли происходит в августе — сентябре, расстояние до Марса может быть всего 56 млн. км. Марс виден всю ночь, и его положение можно очень точно определить, пользуясь как опорными точками близкими звездами.

Наблюдения из двух пунктов дадут параллакс Марса, а отсюда можно вычислить его расстояние и по нему — масштаб к плану солнечной системы. Приближения Марса и Земли — противостояния Марса — повторяются приблизительно через 2 года и 2 мес., а так называемые «великие противостояния», когда Марс ближе всего к Земле, — раз в 15 —17 лет. Последнее «великое противостояние» было 24 августа 1924 г., а следующее будет 23 июля 1939 г. Каждое противостояние используется не только для определения расстояния, но и для физических наблюдений самого Марса.

Еще ближе к Земле может подойти Эрос, одна из семейства малых планет, орбиты большинства которых лежат между орбитам Марса и Юпитера. Орбита Эроса очень сильно отлична от круга, и значительная часть ее лежит даже внутри орбиты Марса (рис. 5). В некоторых случаях расстояние между Землей и Эросом может уменьшаться до 22 млн. км, т. е. до 1/7 расстояния Солнца, довольно близко Эрос подходил к Земле в 1900—1901 гг. (на 48 млн. км) и в 1930— 1931 гг. (на 26 млн. км). Эрос наблюдался в это время, как звездочка, положение которой среди других звезд может быть определено весьма точно.

Нужно заметить, что для определения параллакса по наблюдениям Эроса не нужно обязательно производить наблюдения из двух далеких пунктов. Вращение Земли вокруг оси уносит с собой наблюдателя и, если он находится на экваторе, за 12 час. вращение Земли перенесет его на расстояние, равное диаметру Земли, или 12,7 тыс. км. Наблюдатель, расположенный к северу или к югу от экватора, переместится меньше. И если снимки Эроса произведены в начале и в конце ночи, — они равносильны снимкам, сделанным на большом расстоянии друг от друга. Нужно, конечно, принять во внимание движение Земли и Эроса по орбитам за время между снимками.

Существуют ещё другие способы измерения расстояния до Солнца, но они не являются основными, и рассматривать их мы не имеем возможности. Между прочим такой же метод использовался древними и для определения параллакса Луны.

Сопоставление всех наиболее точных определений дает для параллакса Солнца величину 8″,803 с возможной ошибкой в 0″,001, а отсюда — среднее расстояние Земли равно 149 450 000 км с возможной ошибкой в 17 000 км.

Среднее расстояние Солнца—Земля является основным для выражения других расстояний в солнечной системе и названо «астрономической единицей». Но действительное расстояние до Солнца может отличаться от среднего, так как путь Земли около Солнца — не круг, а эллипс. В июле расстояние до Солнца на 2,5 млн. км больше среднего, а в январе на столько же меньше.

Астрономическая единица есть та мера, которой мы измеряем «не только все расстояния до тел солнечной системы, но и расстояния самых далеких звезд, туманностей и звездных скоплений. Словом, это та мера, при помощи которой мы определяем масштаб строения вселенной. Поэтому на определения ее потрачено много усилий, и известна она современной науке с большой точностью.

Может показаться, что указанная выше ошибка в 17 000 км велика; но не надо забывать, что эта ошибка составляет лишь немногим больше 0,0001 всей астрономической единицы. Представим себе, что мы измерили длину комнаты в 9 м и при этом измерении ошиблись всего лишь на 1 мм. По сравнению с длиной комнаты эта ошибка соответствует точности, с которой известно среднее расстояние Земли от Солнца. Но если попробовать на самом деле измерить длину в 9 м с ошибкой в 1 мм, — это окажется совсем не так просто: потребуется большое внимание и хорошие измерительные инструменты, чтобы обеспечить такую точность при обыкновенном измерении по гладкому полу, во всех точках доступному измерителю. Тем более нужно отдать должное точности, с которой произведено измерение через межпланетное пространство расстояния до Солнца, к которому ни один человек ее приближался ближе чем на 147 млн. км, — расстояние, которое пушечное ядро сможет пролететь, двигаясь со скоростью 1000 м/сек, только в 4,5 года.

Обновлено: 15.05.2023

Определение расстояния в Космосе является неотъемлемой частью развития астрономии. Для астрономов вопрос точности измерения стоит в первых рядах.

Например, человечество узнало, что несколько миллиардов лет назад Вселенная расширялась гораздо медленнее, чем сейчас. Тем самым, выяснив, что воздействие темной энергии постепенно возрастает.

Да и к тому же важно знать своё место во Вселенной. Ради улучшения способов учёные со всего света слетаются каждое десятилетие.

1. Метод локации

Метод локации эффективен для измерения расстояний до объектов, расположенных в пределах Солнечной системы. Суть в следующем: лазер излучает свет в сторону нужного космического объекта.

На этом объекте, к примеру Луна, установлены специальные уголковые отражатели, благодаря которым падающий луч света отражается точно в сторону источника излучения. Зная скорость света, а также время полёта, простой формулой определяется расстояние.

Благодаря этому способу человечество узнало удалённость Земли от Луны с погрешностью до одной десятой сантиметра. Уголковые отражатели на Луне были доставлены как советскими луноходами, так и американскими астронавтами миссии “Аполлон”.

Впоследствии учёные определили, что каждый год Луна отдаляется от Земли на 3 – 4 сантиметра именно с помощью метода лазерной локации. Стоит учесть, излучение необязательно должно быть в световом (видимом) диапазоне.

Теоретически, этим способом можно точно измерить расстояние между Землёй и Плутоном. Свету потребуется всего лишь 11 часов, чтобы долететь до карликовой планеты и вернуться назад.

Конечно, вряд ли там когда-нибудь установят отражатели. Да и ни к чему они, так как для этого существуют космические аппараты, которые, пролетая мимо планет, отправляют снимки со скоростью света в родную гавань.

К примеру, в июле 2015-го космический аппарат “Новые горизонты”, во время пролёта, максимально сблизился с Плутоном на расстоянии в 12500 км, отправив впечатляющие снимки карликовой планеты Земле.

Как указано выше, у этого метода есть предел. Если ближайшая звезда к Земле, (не считая Солнца), Проксима Центавра удалена на расстоянии в 4.22 светового года, то самому быстрому аппарату “Вояджер-1”, скорость которого составляет 17 км/с относительно Солнца, понадобится 75 000 лет.

Да и чем дальше объект, тем сложнее идентифицировать то самое отражённое излучение. Поэтому метод лазерной локации подходит только для Солнечной системы. Значит пора перейти ко второму.

2. Метод годичного параллакса

( в ролике нагляднее — прим. автора )

Этот метод дает обширные возможности для определения расстояния до звёзд. Сначала разберёмся со словом параллакс. Параллакс — смещение близкого объекта относительно удалённого при наблюдении с разного местоположения. Чем больше смещение, тем ближе объект.

С явлением параллакс мы встречаемся повседневно и в обычной жизни. Например, когда мы смотрим в окно при передвижении на поезде, то замечаем, что более близкие деревья или кустарники смещаются гораздо быстрее по сравнению с удалёнными.

Так как звёзды находятся слишком далеко, то эффект параллакса на Земле незаметен. Но здесь на помощь приходит естественное движение планеты вокруг Солнца. Тут уже можно наблюдать необходимую звезду в пределах 300 миллионов км.

Сам годичный параллакс представляет собой угол, вершиной которого является звезда (не Солнце). Угол образован между двумя сторонами. Чем меньше угол, тем дальше объект.

Первая сторона: расстояние между необходимой звездой и Солнцем. Вторая: расстояние между той же звездой и Землёй. Получается треугольник, у которого третья сторона не что иное, как радиус земной орбиты, равный 1 астрономической единице.

По сути, для определения угла до нужной звезды достаточно годовое наблюдение, так как Земля совершает полный оборот за это время. Отсюда и пошло название годичного параллакса.

Другой причиной круглогодичного непрерывного наблюдения является корректировка движения удалённых звёзд и самого Солнца вокруг центра Млечного Пути. Ведь всё движется во Вселенной.

Для определения расстояния обычно используют прямоугольный треугольник. Причём прямой угол может быть как у Земли, так и у Солнца. В основном это зависит от расположения наблюдаемой звезды относительно Солнечной системы.

Если звезда ближе к эклиптике, то прямой угол берётся у Земли. Если ближе к перпендикуляру Солнечной системы, то у Солнца. Всё же треугольник необязательно должен быть прямоугольным.

В случае с обычным треугольником расстояние от Земли до звезды определяется теоремой синусов, где стороны любого треугольника пропорциональны синусам противолежащих углов. В общем, метод годичного параллакса — обычная тригонометрия.

Но и здесь есть ограничения. Дело в том, что даже Проксима Центавра находится на расстоянии, годичный параллакс которого равен 0,75 угловой секунды.

Немного об угловой секунде. Представим 1 угловой градус. Этот градус состоит из 60-ти угловых минут, а минута из 60-ти угловых секунд. То есть 1 угловая секунда — это всё равно что смотреть на человеческий волос с расстояния в 20 метров, толщина которого 0,1 мм.

Мы не способны видеть объекты при таком разрешении. Астрономы даже придумали термин, состоящий из двух слов: параллакс + секунда = парсек , который обозначает расстояние до объекта, годичный параллакс которого равен одной угловой секунде.

Даже ближайшие звёзды расположены дальше 1 парсека, не говоря уж об отдалённых. Благодаря современным приборам человечество научилось измерять расстояния до звёзд этим методом. Но учёные пошли дальше.

В конце 2013 года Европейское Космическое Агентство запустило космический аппарат “Gaia”, который движется по орбите вокруг Солнца в полутора миллионов км от Земли. Точность аппарата составляет 25 микросекунд дуги . Это всё равно что разглядеть с Земли двухрублёвую монету на Луне.

В общем, “Gaia” способен определять расстояния практически до любых звёзд нашего Млечного Пути. Но здесь наступает предел. Расстояния до других галактик измеряются следующим способом.

3. Метод звёздных маяков

Для удобства измерения выбирают звёзды цефеиды. Их ещё называют звёздными маяками. Цефеиды — переменные звёзды, в которых происходит изменение светимости строго с определённым периодом. Период обычно составляет от 1 до 50 суток. Светимость меняется из-за изменения размера Цефеиды.

В 20-м веке в Гарвардской обсерватории состоялось прорывное открытие. Установлена связь между периодом изменения яркости Цефеиды и абсолютной звёздной величиной.

Астрономами было установлено, что абсолютная звёздная величина соответствует видимой на расстоянии в 10 парсек или 32.6 светового года. Величину на таком расстоянии измеряли годичным параллаксом различных ближайших переменных звёзд. То есть предыдущий метод является также калибровочным, благодаря которому установили абсолютную звёздную величину.

У Солнца, например, абсолютная звёздная величина +4.8, у Веги 0,5. Всё что выше + 6, недоступно человеческому глазу с расстояния в 10 парсек.

Зная период пульсаций Цефеиды, определяется абсолютная звёздная величина, с помощью которой, в сравнении с видимой, измеряется расстояние.

С помощью цефеид человечество узнало удалённость миллионов галактик. Но чтобы измерить расстояние до галактик, расположенных в миллиардах световых годах, астрономы полагаются на более яркий метод.

4. Вспышка Сверхновой звезды

Между яркостью и расстоянием есть определённая зависимость. К примеру, возьмём обычную свечу. Если первый объект находится в 2 раза дальше второго от источника освещения, то светового потока будет приходиться на первый объект в 4 раза меньше. То есть зависимость между яркостью и расстоянием обратно квадратичная.

Чем дальше объект, тем сложнее обнаружить его светимость. Но Вселенная часто помогает вспышками сверхновых звёзд, которые рождаются в среднем 1 раз в 100 лет в галактике. В настоящее время считается, что в Наблюдаемой Вселенной около 2 триллионов галактик. Конечно, на самом деле их больше, но пока столько.

Значит, теоретически, каждую секунду вспыхивают 634 сверхновые звёзды. Когда взрывается сверхновая, она выделяет энергию, сопоставимую с энергией 10-миллиардного жизненного цикла Солнца.

То есть Солнце прожило полжизни. За 5 миллиардов лет выделило в космическое пространство энергию аналогичную половине энергии вспышки Сверхновой. Вспышки Сверхновых — это подарок Вселенной для измерения расстояний.

Заключение

Стоит отметить, что чем дальше объект, тем труднее точно измерить расстояние. Дело в том, что расчёты неидеальны, так как для этого нужен 100%-й вакуум в космическом пространстве, которого нигде нет, а Вселенная должна оставаться неподвижной.

Также излучение удалённого объекта рассеивается не только космической пылью, но и тёмной материей, которую учёным пока что обнаружить не удалось, хоть и доказано, что она существует.

Ещё отклонение в расчётах вызывают массивные объекты, которые согласно Общей Теорией Относительности Эйнштейна искривляют траекторию излучения.

Однако учёные не останавливаются на достигнутом, продолжают встречаться и изобретать более совершенные методы и приборы.

Начнем с того, что километры астрономов обычно не интересуют. Разве что в окрестностях Солнца. Если написать, что до Луны , то это еще число удобоваримое. Но расписывать, что , пожалуй, уже излишне. Внутри Солнечной системы для измерения расстояний часто используют в буквальном смысле астрономическую единицу . Одна астрономическая единица равна длине большой полуоси орбиты Земли. Это . Так, до Урана (а. е.). Астрономическая единица удобна тем, что, измеряя расстояния в них, мы одновременно сравниваем эти расстояния с удаленностью Земли от Солнца.

На практике из наблюдений можно узнать период обращения небесного тела вокруг Солнца. А дальше очень просто из третьего закона Кеплера высчитать длину большой полуоси орбиты небесного тела.

Прямое (ну или почти) измерение расстояний подвластно астрономам на дистанциях в несколько астрономических единиц при помощи радиолокации. Это очень точный способ. Однако, при его использовании необходимо учитывать движение Земли и исследуемого тела, а также знать скорость света. Посланный радиотелескопом сигнал отражается от поверхности небесного тела и снова принимается на Земле. Радиолуч проходит двойное расстояние (туда-обратно), зная время, которое затратил сигнал на преодоление пути, можно высчитать само расстояние. Остается учесть взаимные перемещения тел за время движения сигнала, но это также дело сравнительно нетрудное.

Если смотреть на один и тот же предмет с разных мест, то он будет менять свое расположение на фоне более удаленных предметов. Если эти неблизкие предметы далеки настолько, что их видимым перемещением при перемещении наблюдателя можно пренебречь, то из геометрических соображений совсем нетрудно узнать расстояние до близкого предмета.

Для измерения расстояний до объектов внутри Солнечной системы точно отмечают на небе положение этого объекта относительно звезд, которые достаточно удалены. Наблюдения одновременно проводят из двух разнесенных на большое расстояние мест земной поверхности (сотни, тысячи километров). При этом, положение объекта относительно звезд для каждого места наблюдения будет своим. Зная расстояние между точками наблюдения, зная угловое расстояние между положениями объекта для каждой точки, нет ничего проще, чем узнать расстояние до объекта. Такой способ определения расстояний называют методом горизонтального параллакса . Параллакс – это смещение, то самое смещение объекта на фоне звезд при смене места наблюдения.

Определенное любым способом расстояние до небесного тела делает простым выяснение его размеров. Для этого кроме самого расстояния нужно знать угловые размеры тела. Чистая геометрия, никакой астрономии.

Если тело настолько мало, что угловых размеров выяснить не удается, приходится строить догадки об отражательной способности поверхности тела ( альбедо ). Тела, находящиеся на одном удалении, с одним и тем же альбедо, но разных размеров, будут сиять тем ярче, чем они больше. Поэтому, примерные размеры малых небесных тел, в основном, астероидов, узнать тоже можно, учитывая расстояния до тел и альбедо их поверхности.

До звезд – рукой подать

Попробуйте осознать число 40700000000000 км. Пока вы считали знаки и разбивали их на тройки, можно было выпить чаю. Астрономы не любят заниматься такой работой, как разгребание нулей в астрономических числах. Они сделали все возможное для того, чтобы эти числа сделать земными. Расстояние до ближайшей звезды (именно его вы пытались постигнуть) можно примерно записать . Тоже немалое число, . Астрономы пошли дальше. Они записывают это же число или . Изменение единиц измерения делает звезды не такими далекими.

Световой год – это не время. Это расстояние, проходимое за время. Световой год – путь, проходимый светом за один год. Из самых удаленных уголков Вселенной свет до нас добирается более . Чтобы представить себе чудовищность такого расстояния, лучше записать его в привычных километрах:

95 000 000 000 000 000 000 000. 95 миллиардов триллионов километров.

Световой год – не практическая единица. Из наблюдений расстояния в световых годах не получают. Наблюдательная единица – парсек (пс).

Расстояние до не слишком далеких звезд (десятки световых лет) определяют с помощью известного нампараллакса. Только в случае звезд в этом методе кое-что изменяется. Вспомним, что положение тел Солнечной системы отмечают относительно звезд. Теперь нам нужно увидеть перемещение самих звезд. Для этого используют в качестве ориентиров далекие по сравнению со звездами галактики.

Перемещение наблюдателя по поверхности ограничено скромными по космическим меркам размерами нашего голубого шарика. Для звезд эти размеры до смешного малы. Поэтому, чтобы увидеть перемещение звезд на фоне галактик, наблюдения производят из разных точек земной орбиты. Для этого не надо запускать космические аппараты. Можно подождать, пока Земля сама пройдет положенный ей путь и окажется через несколько месяцев в нужной точке. Так узнают угловое перемещение звезды. Зная расстояние между точками на орбите, из все тех же геометрических соотношений узнают расстояние.

Наблюдения будут наиболее продуктивны, если проводить их с промежутком в полгода: Земля перенесется за это время в противоположную точку своей орбиты, и расстояние между пунктами наблюдения будет максимальным. Кроме того, лучше всего выбирать моменты для наблюдений так, чтобы линия, соединяющая точки наблюдения, была перепендикулярна направлению на звезду.

Расстояние в один парсек соответствует смещению звезды на фоне далеких объектов на 1” при перемещении наблюдателя на 1 радиус земной орбиты. Парсек – сокращение слов параллакс и секунда. . При подобных измерениях приходится учитывать взаимное перемещение звезды и Земли за промежуток времени между наблюдениями. Эта величина узнается из наблюдений. Также астрономы учитывают неравномерности вращения Земли вокруг оси, из-за которых постоянно меняется ее направление.

Смещение звезд при таких наблюдениях называют . Чем меньше параллакс, тем больше до звезды парсеков.

Даже орбита Земли мала по сравнению с теми расстояниями, с которыми астрономам приходится работать. Годичный параллакс бессилен для объектов вне крохотной части нашей Галактики поблизости от Солнца. Астрономы нашли еще несколько, способов. Правда, надо отметить, что эти способы уже несравнимы по точности с точностью метода параллакса.

Существуют звезды, которые с правильным периодом меняют свои размеры и, следовательно, яркость. Звезды, меняющие свою яркость, называют переменными. Есть несколько типов переменных звезд. Но некоторые из этих разновидностей имеют для измерения расстояний особое значение. Среди тех переменных звезд, расстояние до которых определимы с помощью метода годичного параллакса, выявили тип звезд с очень интересной особенностью. Период колебания их яркости зависит от массы звезды. Массой определяется средняя светимость звезды, поэтому, выявив период колебания блеска, всегда можно узнать и светимость. А раз мы знаем светимость, мы можем сопоставить ее с яркостью звезды на небе и высчитать расстояние.

Представьте себе ряд одинаковых фонарей. Если все их погасить, а оставить какой-то один, то Вы сможете по тому, насколько ярко выглядит фонарь, сказать, далеко фонарь или близко. Астрономы обладают точными приборами, поэтому они определяют и то, насколько далеко или близко расположена звезда.

Столь полезный тип переменных звезд называют (по имени первой открытой звезде такого рода из созвездия Цефея). Цефеиды вдвойне полезны тем, что это – очень яркие звезды. Их по отдельности замечают не только в пределах нашей Галактики, но и в других близких звездных системах. Самая известная цефеида – Полярная звезда. Правда, обычно об этом никто не знает. Видимо обидевшись, эта звезда в последние года перестала проявлять себя в этом качестве, то есть перестала менять свой блеск

Если бы то, что вынесено в заголовок этого абзаца, имело место, работа криминалистов заметно усложнилась бы. Астрономы, напротив, любят одинаковые признаки, их удобно выявлять на далеких расстояниях. В разделе о звездах сказано, что масса, цвет и яркость всех звезд главной последовательности взаимосвязаны. Это обстоятельство иногда помогает астрономам высчитывать расстояние. Здесь очень важно убедиться в том, что звезда и впрямь принадлежит главной последовательности. Это делается при изучении спектра звезды. Если принадлежность выявлена, то дальше все просто: цвет звезды определяется ее массой, массой определяется светимость. Сопоставляем яркость и светимость и находим расстояние. К сожалению, этот способ весьма грубо определяет искомую нами на этой странице величину.

Все ярче и ярче

В далеких звездных системах, там, где яркости цефеид не хватает, необходимо найти еще какие-нибудь более яркие объекты, которые вели бы себя одинаково. Таким свойством обладают вспышки сверхновых звезд в двойных системах. Спад их яркости после самой вспышки идет во всех случаях одинаково, так как в двойных системах всегда взрываются звезды одинаковой массы. Одинаковы, конечно, и светимости вспышек. Сверхновая – объект, сравнимый по яркости с самой галактикой, поэтому их находят очень далеко от Земли. Исследуя то, как сверхновая ведет себя после вспышки, определяют, принадлежит ли взорвавшаяся звезда двойной системе. Если так, то все идет по тому же сценарию. Сравнивают известную светимость с яркостью и находят расстояние.

Там, где не видны никакие звезды

Всему, видимо, есть предел. На некотором расстоянии от нашей планеты нельзя рассмотреть никаких звезд даже в очень хорошие телескопы. Как определять расстояния до далеких галактик? Нашелся способ и для этого. Связав скорость удаления относительно близких галактик с расстоянием до них, определенным по цефеидам и сверхновым, удалось найти примерное значение коэффициента пропорциональности между этими величинами.

Скорость галактик определяют по красному смещению линий в их спектрах. Согласно эффекту Доплера, свет от удаляющегося объекта краснеет. По величине этого покраснения и находят скорость галактики. Сейчас значение коэффициента пропорциональности между скоростью и расстоянием (постоянная Хаббла) считается примерно на каждый Мегапарсек. Постоянная Хаббла задает скорость расширения Вселенной. Зная скорость расширения Вселенной, мы можем судить о ее возрасте, как, зная скорость движения и маршрут поезда, мы можем примерно сказать, когда он покинул станцию отправления. Значение скорости расширения Вселенной также немаловажно для понимания ее будущего. Чем быстрее расширяется Вселенная, тем с меньшей вероятностью это расширение сменится затем сжатием. О других сторонах этой проблемы читайте здесь.

Никакие объекты не могут двигаться быстрее, чем свет. Самое большое расстояние, на которое мы можем заглянуть равно произведению скорости света и возраста Вселенной, так как свет просто не успел дойти из более дальних областей. Так вот взаимосвязаны время и пространство.

Лестница в небо

Вселенная так велика, что привычные на Земле единицы длины, например километр (км), неудобны для измерения космических расстояний. Для масштабов Земли вполне подходят километры, но когда мы говорим, что до ближайшей к нам галактики в созвездии Андромеды 14,4 квинтиллиона км — 14 400 000 000 000 000 000 км, — то число оказывается настолько большим, что становится бесполезным. Поэтому в километрах обычно выражают лишь размеры планет и в отдельных случаях — расстояния в пределах Солнечной системы. Полезной мерой длины для нашей Солнечной системы является астрономическая единица (а. е.) — среднее расстояние от Земли до Солнца, равное 149 597 870,610 км. Так, расстояние от Меркурия до Солнца равно 1/3 а. е., а среднее расстояние от Плутона до Солнца — 40 а. е.

Расстояние до далеких и недоступных нам звезд можно определить из геометрии, измерив направления на этот предмет с двух концов известного отрезка (базиса), а затем рассчитав размеры треугольника, образованного концами отрезка и удаленным предметом. В качестве базиса используется расстояние между двумя точками земной орбиты, которые наша планета проходит с интервалом в несколько месяцев. При перемещении Земли направление на звезду изменится, она немного сместится на фоне более далеких звезд. Такое смещение более близкой звезды на фоне более далеких называется параллаксом.

Существуют и другие методы, с помощью которых расстояние до звезды можно получить косвенным путем, используя различные астрофизические или статистические соотношения.

Астрономы, изучающие небесные тела и астрономические объекты, находящиеся за пределами Солнечной системы, в качестве единицы расстояний в своей работе используют парсек (пк) — внесистемную единицу расстояний в астрономии, равную расстоянию до космического объекта, с которого радиус орбиты Земли виден под углом 1”. Средний радиус земной орбиты 149 597 870 690м, и парсек, основанный на орбите Земли, равен 30 856 775 813 057 300 м.

Небесное тело, расположенное на расстоянии всего в один парсек, как раз и имеет годичный параллакс в одну угловую секунду (1/1800 диаметра Луны, который приблизительно равен 3476 км).

В научно-популярной литературе обычно используется другая внесистемная единица измерения астрономических расстояний — световой год. Световым годом называется расстояние, которое свет (электромагнитные волны) проходит в вакууме за один т. н. юлианский год, состоящий из 365,25 дней по 86 400 секунд каждый. Скорость света составляет 299 792 км в секунду, и ничто во Вселенной не движется быстрее. Двигаясь со скоростью около 300 000 км в секунду, свет может семь раз обогнуть Землю буквально за одно мгновение. Один световой год приблизительно равен 9,46 триллионов километров (9,46 · 10 12 км).

1 парсек ≈ 3,26 св. года ≈ 206 000 а. е.

Ближайшая к нашей Солнечной системе звезда Проксима Центавра (Кентавра) удалена от нас на расстояние 4,2 световых года (для сравнения, свет Солнца достигает Земли за 8,5 минут, то есть мы всегда видим то, что происходило на Солнце 8,5 минут ранее). Проксима Центавра — это светило, которое в 7 раз меньше Солнца и довольно тусклое, мы видим его лишь потому, что оно расположено очень близко от нас. Более яркие объекты мы сможем увидеть с более далекого расстояния.

Например, гораздо ярче звезд гигантские звездные системы — галактики. Одна из наших ближайших соседок по космосу, галактика Андромеды, удалена от нас на 2,5 млн световых лет. Одной из самых далеких звездных систем в настоящее время является галактика EGS8p7. Ее свету понадобилось 13,24 млрд лет, чтобы долететь до Земли. Мы видим эту галактику лишь потому, что на луче зрения в направлении нее практически отсутствует нейтральный газ, хорошо поглощающий свет. С улучшением астрономических методов и приборов мы будем заглядывать все дальше и дальше вглубь Вселенной, так что EGS8p7 не самая далекая звездная система, которую разглядит человечество.

Чтобы оценить масштабы расстояний в космосе (и то, почему для их измерений используется столько различных единиц), сравним расстояния от Земли до разных объектов:

Выстраивая нашу лестницу к окраинам Вселенной, мы умалчивали о фундаменте, на котором она покоится. Между тем метод параллаксов дает расстояние не в эталонных метрах, а в астрономических единицах, то есть в радиусах земной орбиты, величину которой тоже удалось определить далеко не сразу. Так что оглянемся назад и спустимся по лестнице космических расстояний на Землю.

Вероятно, первым удаленность Солнца попытался определить Аристарх Самосский, предложивший гелиоцентрическую систему мира за полторы тысячи лет до Коперника. У него получилось, что Солнце находится в 20 раз дальше от нас, чем Луна. Эта оценка, как мы теперь знаем, заниженная в 20 раз, продержалась вплоть до эпохи Кеплера. Тот хотя сам и не измерил астрономическую единицу, но уже отметил, что Солнце должно быть гораздо дальше, чем считал Аристарх (а за ним и все остальные астрономы).

Первую более или менее приемлемую оценку расстояния от Земли до Солнца получили Жан Доминик Кассини и Жан Рише. В 1672 году, во время противостояния Марса, они измерили его положение на фоне звезд одновременно из Парижа (Кассини) и Кайенны (Рише). Расстояние от Франции до Французской Гвианы послужило базой параллактического треугольника, из которого они определили расстояние до Марса, а затем по уравнениям небесной механики вычислили астрономическую единицу, получив значение 140 миллионов километров.

На протяжении следующих двух веков главным инструментом для определения масштабов Солнечной системы стали прохождения Венеры по диску Солнца. Наблюдая их одновременно из разных точек земного шара, можно вычислить расстояние от Земли до Венеры, а отсюда и все остальные расстояния в Солнечной системе. В XVIII–XIX веках это явление наблюдалось четырежды: в 1761, 1769, 1874 и 1882 годах. Эти наблюдения стали одними из первых международных научных проектов. Снаряжались масштабные экспедиции (английской экспедицией 1769 года руководил знаменитый Джеймс Кук), создавались специальные наблюдательные станции… И если в конце XVIII века Россия лишь предоставила французским ученым возможность наблюдать прохождение со своей территории (из Тобольска), то в 1874 и 1882 годах российские ученые уже принимали активное участие в исследованиях. К сожалению, исключительная сложность наблюдений привела к значительному разнобою в оценках астрономической единицы – примерно от 147 до 153 миллионов километров. Более надежное значение – 149,5 миллиона километров – было получено только на рубеже XIX–XX веков по наблюдениям астероидов. И, наконец, нужно учитывать, что результаты всех этих измерений опирались на знание длины базы, в роли которой при измерении астрономической единицы выступал радиус Земли. Так что в конечном итоге фундамент лестницы космических расстояний был заложен геодезистами.
Только во второй половине XX века в распоряжении ученых появились принципиально новые способы определения космических расстояний – лазерная и радиолокация. Они позволили в сотни тысяч раз повысить точность измерений в Солнечной системе. Погрешность радиолокации для Марса и Венеры составляет несколько метров, а расстояние до уголковых отражателей, установленных на Луне, измеряется с точностью до сантиметров. Принятое же на сегодня значение астрономической единицы составляет 149 597 870 691 метр.

Как измеряется расстояние до звезд и что такое световой год?

Расстояния между звездами настолько велики, что измерять их километрами или милями – занятие с бесконечными нолями. Привычную систему измерений применяют для обозначения расстояний в одной системе. К примеру называют, что минимальное расстояние от Земли до Марса – 55,76 миллионов километров. Со звездами всё сложнее, и здесь обычно используют понятия светового года и парсека.

Астрономическая единица – принятая в астрономии единица измерения объектов Солнечной системы и ближайших к ней объектов Вселенной. Астрономическая единица равна 149 598 100 км (+- ~750 км), что приблизительно равняется среднему расстоянию Земли от Солнца. Современные наблюдения зафиксировали постепенно увеличение значения на 15 см ежегодно, что объясняется, возможной потерей Солнцем массы, последствия солнечного ветра.

Световой год – расстояние, которое свет проходит за один год, в метрах это 9 460 730 472 580 800. На самом деле свет звезд, который мы видим в безоблачную ночь, шёл до нашей планеты многие столетия, а некоторые из них вообще больше не существуют.

Интересно то, что в научно-популярной и фантастической литературе принято использовать понятие светового года, а парсеками обычно пользуются только в профессиональных трудах и исследованиях.

(Галактика UDFj-39546284 – самая далекая от Земли галактика (13,3 миллиардов световых лет от Земли), на снимке, сделанным телескопом Хаббл выглядит, как красная точка )

Ближайшая к нам звезда – это Альфа Центавра, которая находится от Земли на расстоянии в 4,37 световых лет. А вот до самой удалённой галактики (по состоянию на декабрь 2012 года) от Земли целых 13,3 миллиардов световых лет!. Получается, когда солнце этой самой галактики (известной под индексом UDFj-39546284) потухнет, человечество об этом узнает еще не скоро.

Расстояния в цифрах

• Меркурий– ближайшая к Солнцу планета, среднее расстояние от Солнца 0,387 а. е (58 млн. км), а расстояние до Земли колеблется от 82 до 217 млн. км. Меркурий движется вокруг Солнца по сильно вытянутой эллиптической орбите, плоскость которой наклонена к плоскости эклиптики под углом 7°.
• Венера– вторая по удаленности от Солнца планета, среднее расстояние от Солнца 0,72 а.е. (108,2 млн. км). Средний радиус планеты составляет 6051 км, масса – 4,9 на 10 в 24 степени кг (0,82 массы Земли), средняя плотность 5,24 г/см3.
• Земля– третья от Солнца планета Солнечной системы, среднее расстояние от Солнца 1 а.е. (149,6 млн. км), средний радиус 6371,160 км (экваториальный 6378, 160 км, полярный 6356,777 км), масса – 6 на 10 в 24 степени кг.
• Марс– четвертая планета от Солнца, среднее расстояние от Солнца составляет 1,5 а.е. (227,9 млн. км). Минимальное расстояние от Марса до Земли составляет 55,75 млн. км, максимальное – около 401 млн. км.
• Юпитер– пятая по счету от Солнца, а также крупнейшая планета Солнечной системы, среднее расстояние от Солнца 5,2 а.е.(778 млн. км), экваториальный радиус равен 71,4 тыс. км, полярный – около 67 тысяч км, масса 1,9 на 10 в 27 степени кг (317,8 массы Земли), средняя скорость обращения вокруг Солнца – 13,06 км/с.
• Сатурн– шестая планета от Солнца и вторая по размерам планета в Солнечной системе после Юпитера. Среднее расстояние Сатурна от Солнца 9,54 а.е. (1,427 млрд. км), средний экваториальный радиус около 60,3 тысяч км, полярный – около 54 тысяч км, масса 5,68 на 10 в 26 степени кг (95,1 массы Земли).
• Уран– седьмая от Солнца планета Солнечной системы. Планета была открыта в 1781 году английским астрономом Уильямом Гершелем и названа в честь греческого бога неба Урана. Среднее расстояние от Солнца 19,18 а.е. (2871 млн. км), средний радиус 25560 км, масса 8,69 на 10 в 25 степени (14,54 массы Земли), средняя плотность – 1,27 г/см3.
• Нептун– восьмая планета от Солнца и четвертая по размеру среди планет. Нептун открыт в Берлинской обсерватории 23 сентября 1846 года немецким астрономом Иоганном Галле на основании предсказаний, сделанных независимо математиком Джоном Адамсом в Англии и астрономом Урбеном Леверрье во Франции. Среднее расстояние планеты Нептун от Солнца 30,1 а.е. (4497 млн. км), средний радиус около 25 тысяч км, масса 1,02 на 10 в 26 степени кг (17,2 массы Земли), плотность 1,64 г/см3.
• Плутоном– в честь древнеримского бога подземного царства. В тот момент предполагали, что его масса сравнима с массой Земли, но позже было установлено, что масса Плутона почти в 500 раз меньше земной, даже меньше массы Луны. Масса Плутона 1,2 на 10 в22 степени кг (0,22 массы Земли). Среднее расстояние Плутона от Солнца 39,44 а.е. (5,9 на 10 в12 степени км), радиус около 1,65 тысяч км.

Методы исследования расстояний между звездами?

Метод лазерной локации и радиолокации

Эти два современных метода служат для определения точного расстояния до объекта в пределах Солнечной системы. Он производится следующим образом. При помощи мощного радиопередатчика посылается направленный радиосигнал в сторону предмета наблюдения. После чего тело отбивает полученный сигнал и возвращает на Землю. Время, потраченное сигналом на преодоление пути, определяет расстояние до объекта. Точность радиолокации – всего несколько километров. В случае с лазерной локацией, вместо радиосигнала лазером посылается световой луч, который позволяет аналогичными расчетами определить расстояние до объекта. Точность лазерной локации достигается вплоть до долей сантиметра.

Метод тригонометрического параллакса

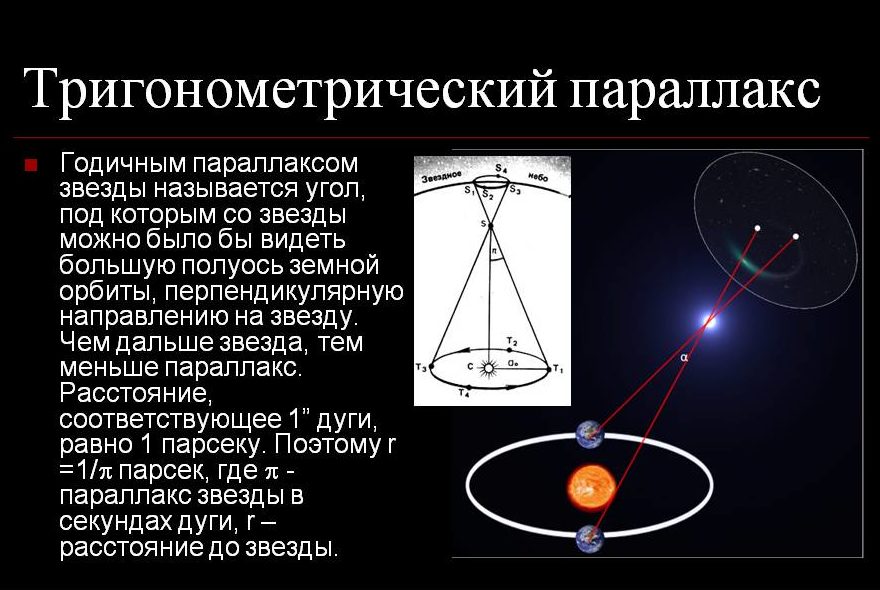
Наиболее простым методом измерения расстояния до удаленных космических объектов является метод тригонометрического параллакса. Он основывается на школьной геометрии и состоит в следующем. Проведем отрезок (базис) между двумя точками на земной поверхности. Выберем на небосводе объект, расстояние до которого мы намерены измерить, и определим его как вершину получившегося треугольника. Далее измеряем углы между базисом и прямыми, проведенными от выбранных точек до тела на небосводе. А зная сторону и два прилежащих к ней угла треугольника, можно найти и все другие его элементы.

Величина выбранного базиса определяет точность измерения. Ведь если звезда расположена на очень большом расстоянии от нас, то измеряемые углы будут почти перпендикулярны базису и погрешность в их измерении может значительно повлиять на точность посчитанного расстояния до объекта. Поэтому следует выбирать в качестве базиса максимально отдаленные точки на Земле. Изначально в роли базиса выступал радиус Земли. То есть наблюдатели располагались в разных точках земного шара и измеряли упомянутые углы, а угол, расположенный напротив базиса назывался горизонтальным параллаксом. Однако позже в качестве базиса стали брать большее расстояние – средний радиус орбиты Земли (астрономическая единица), что позволило измерять расстояние до более отдаленных объектов. В таком случае, угол, лежащий напротив базиса, называется годичным параллаксом.

Данный метод не очень практичен для исследований с Земли по той причине, что из-за помех земной атмосферы, определить годичный параллакс объектов, расположенных более чем на расстоянии в 100 парсек – не удается.

Однако в 1989 год Европейским космическим агентством был запущен космический телескоп Hipparcos, который позволил определить звезды на расстоянии до 1000 парсек. В результате полученных данных ученые смогли составить трехмерную карту распределения этих звезд вокруг Солнца. В 2013 году ЕКА запустило следующий спутник – Gaia, точность измерения которого в 100 раз лучше, что позволяет наблюдать все звезды Млечного Пути. Если бы человеческие глаза обладали точностью телескопа Gaia, то мы имели бы возможность видеть диаметр человеческого волоса с расстояния 2 000 км.

Метод стандартных свечей

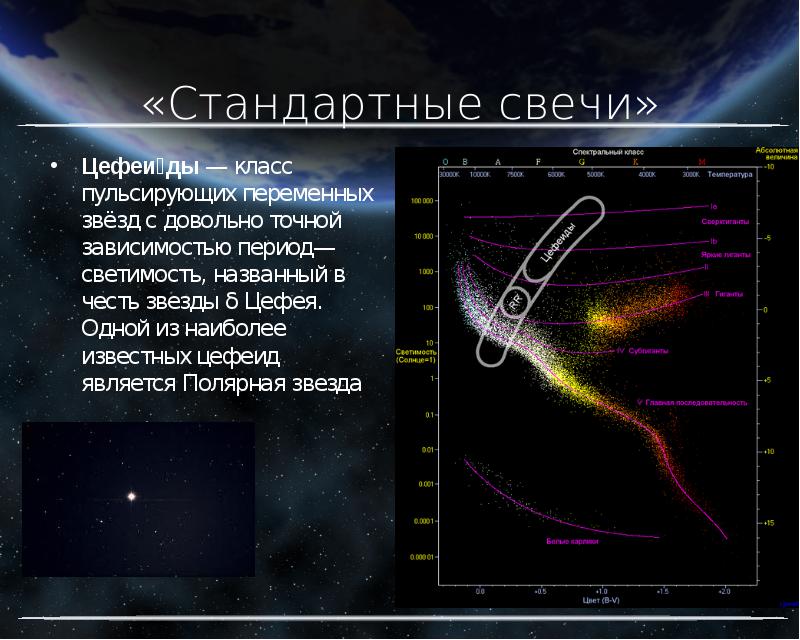
Для определения расстояний до звезд в других галактиках и расстояний до самих этих галактик используется метод стандартных свечей. Как известно, чем дальше от наблюдателя расположен источник света, тем более тусклым он кажется наблюдателю. Т.е. освещенность лампочки на расстоянии 2 м будет в 4 раза меньше, чем на расстоянии 1 метр. Это и есть принцип, по которому измеряется расстояние до объектов методом стандартных свечей. Таким образом, проводя аналогию между лампочкой и звездой, можно сравнивать расстояния до источников света с известными мощностями.

В качестве стандартных свечей в астрономии выступают объекты, светимость (аналог мощности источника) которых известна. Это может быть любого рода звезда. Для определения ее светимости астрономы измеряют температуру поверхности, опираясь на частоту ее электромагнитного излучения. После чего, зная температуру, позволяющую определить спектральный класс звезды, выясняют ее светимость при помощи диаграммы Герцшпрунга-Рассела. Затем, имея значения светимости и измерив, яркость (видимую величину) звезды, можно посчитать расстояние до нее. Такая стандартная свеча позволяет получить общее представление о расстоянии до галактики, в которой она находится.

Однако данный метод достаточно трудоемкий и не отличается высокой точностью. Поэтому астрономам удобнее использовать в качестве стандартных свечей космические тела с уникальными особенностями, для которых светимость известна изначально.

Красные смещения

Самый “дальнобойный” способ. Измеряя красные смещения, можно определить расстояния до самых дальних уголков Вселенной.

Эдвину Хабблу, в честь которого назван известный космический телескоп, удалось из этого сложить общую картину и показать, сопоставив спектры галактик с расстояниями до них, что скорость удаления галактики пропорциональна расстоянию до нее.

Образование космологического красного смещения можно представить так: рассмотрим свет – электромагнитную волну, идущую от далёкой галактики. В то время как свет летит через космос, пространство расширяется. Вместе с ним расширяется и волна. Соответственно, изменяется и длина волны. Если за время полёта света пространство расширилось в два раза, то и длина волны увеличивается в два раза.

Тот же Хаббл благодаря красному смещению доказал расширение Вселенной. Поэтому чем больше человечество ждет с межзвездными перелетами, тем дальше придется лететь в будущем.

Как объясняют Пфайль и его коллеги, сегодня астрономы вычисляют расстояние до далеких от нас светил при помощи так называемого параллакса – того, насколько интересующая их звезда смещается относительно расположенных за ней объектов по мере того, как Земля вращается вокруг Солнца и движется по орбите.

Подобная методика очень точна, однако она работает только для относительно близких к нам светил, расположенных на расстоянии примерно в 1-2 тысячи световых лет от Земли. По этой причине астрономы знают точное расстояние только для 100 тысяч из 100 миллиардов звезд Млечного Пути.

Измерение расстояний до более далеких светил возможно, однако все существующие методики, по мнению Пфайля, опираются на различные статистические модели и допущения о температуре звезды или ее химическом составе, что может вносить существенные искажения в замеры.

В ближайшее время Пфайль и его коллеги планируют составить каталог пар звезд-двойников, а также попытаются вычислить точные размеры Галактики, от одного ее края и до противоположной стороны.

Читайте также:

  

• Концепция развития кадетской школы

  

• Мексика внутренняя политика кратко

  

• Декада гуманитарных наук в школе мероприятия

  

• Курсовая школы стратегического планирования

  

• Тесты на координационные способности для детей младшего школьного возраста