На границе раздела двух различных сред, если эта граница раздела значительно превышает длину волны, происходит изменение направления распространения света: часть световой энергии возвращается в первую среду, то есть отражается, а часть проникает во вторую среду и при этом преломляется. Луч АО носит название падающий луч, а луч OD – отраженный луч (см. рис. 1.3). Взаимное расположение этих лучей определяют законы отражения и преломления света.
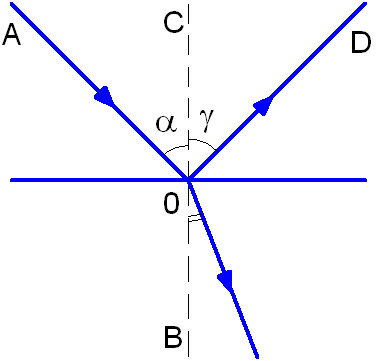
Рис. 1.3. Отражение и преломление света.
Угол α между падающим лучом и перпендикуляром к границе раздела, восстановленным к поверхности в точке падения луча, носит название угол падения.
Угол γ между отражённым лучом и тем же перпендикуляром, носит название угол отражения.
Каждая среда в определённой степени (то есть по своему) отражает и поглощает световое излучение. Величина, которая характеризует отражательную способность поверхности вещества, называется коэффициент отражения. Коэффициент отражения показывает, какую часть принесённой излучением на поверхность тела энергии составляет энергия, унесённая от этой поверхности отражённым излучением. Этот коэффициент зависит от многих причин, например, от состава излучения и от угла падения. Свет полностью отражается от тонкой плёнки серебра или жидкой ртути, нанесённой на лист стекла.
Законы отражения света
| 1 | Падающий луч, отражающий луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. |
| 2 | Угол отражения γ равен углу падения α:
γ = α |
Законы отражения света были найдены экспериментально ещё в 3 веке до нашей эры древнегреческим учёным Евклидом. Также эти законы могут быть получены как следствие принципа Гюйгенса, согласно которому каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Волновая поверхность (фронт волны) в следующий момент представляет собой касательную поверхность ко всем вторичным волнам. Принцип Гюйгенса является чисто геометрическим.
На гладкую отражательную поверхность КМ (рис. 1.4) падает плоская волна, то есть волна, волновые поверхности которой представляют собой полоски.
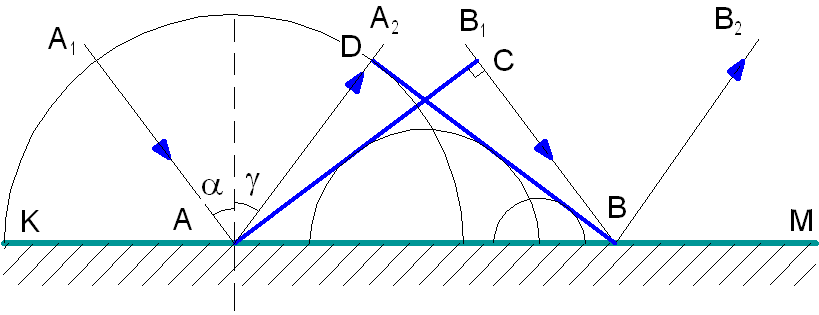
Рис. 1.4. Построение Гюйгенса.
А1А и В1В – лучи падающей волны, АС – волновая поверхность этой волны (или фронт волны).
Пока фронт волны из точки С переместится за время t в точку В, из точки А распространится вторичная волна по полусфере на расстояние AD = CB, так как AD = vt и CB = vt, где v – скорость распространения волны.
Волновая поверхность отражённой волны – это прямая BD, касательная к полусферам. Дальше волновая поверхность будет двигаться параллельно самой себе по направлению отражённых лучей АА2 и ВВ2.
Прямоугольные треугольники ΔАСВ и ΔADB имеют общую гипотенузу АВ и равные катеты AD = CB. Следовательно, они равны.
Углы САВ = = α и DBA = = γ равны, потому что это углы со взаимно перпендикулярными сторонами. А из равенства треугольников следует, что α = γ.
Из построения Гюйгенса также следует, что падающий и отражённый лучи лежат в одной плоскости с перпендикуляром к поверхности, восстановленным в точке падения луча.
Законы отражения справедливы при обратном направлении хода световых лучей. В следствие обратимости хода световых лучей имеем, что луч, распространяющийся по пути отражённого, отражается по пути падающего.
Большинство тел лишь отражают падающее на них излучение, не являясь при этом источником света. Освещённые предметы видны со всех сторон, так как от их поверхности свет отражается в разных направлениях, рассеиваясь. Это явление называется диффузное отражение или рассеянное отражение. Диффузное отражение света (рис. 1.5) происходит от всех шероховатых поверхностей. Для определения хода отражённого луча такой поверхности в точке падения луча проводится плоскость, касательная к поверхности, и по отношению к этой плоскости строятся углы падения и отражения.
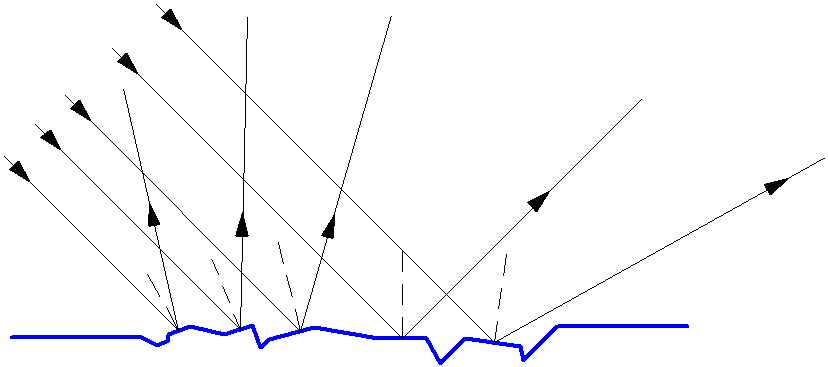
Рис. 1.5. Диффузное отражение света.
Например, 85% белого света отражается от поверхности снега, 75% — от белой бумаги, 0,5% — от чёрного бархата. Диффузное отражение света не вызывает неприятных ощущений в глазу человека, в отличие от зеркального.
Зеркальное отражение света – это когда падающие на гладкую поверхность под определённым углом лучи света отражаются преимущественно в одном направлении (рис. 1.6). Отражающая поверхность в этом случае называется зеркало (или зеркальная поверхность). Зеркальные поверхности можно считать оптически гладкими, если размеры неровностей и неоднородностей на них не превышают длины световой волны (меньше 1 мкм). Для таких поверхностей выполняется закон отражения света.
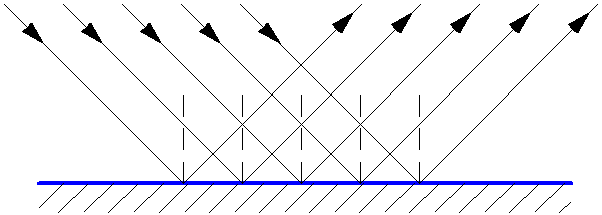
Рис. 1.6. Зеркальное отражение света.
Плоское зеркало – это зеркало, отражающая поверхность которого представляет собой плоскость. Плоское зеркало даёт возможность видеть предметы, находящиеся перед ним, причём эти предметы кажутся расположенными за зеркальной плоскостью. В геометрической оптике каждая точка источника света S считается центром расходящегося пучка лучей (рис. 1.7). Такой пучок лучей называется гомоцентрическим. Изображением точки S в оптическом устройстве называется центр S’ гомоцентрического отражённого и преломлённого пучка лучей в различных средах. Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь от него, падает в глаз наблюдателя, то в зеркале видны изображения этих тел.
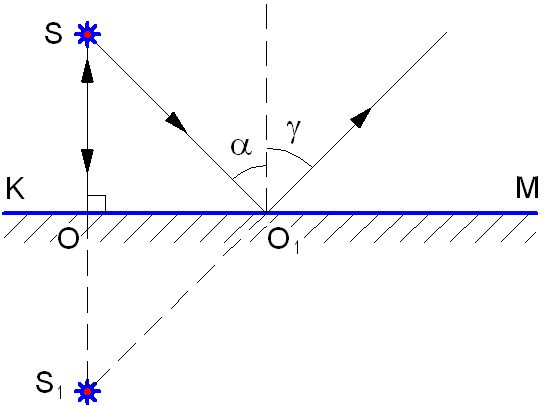
Рис. 1.7. Изображение, возникающее с помощью плоского зеркала.
Изображение S’ называется действительным, если в точке S’ пересекаются сами отражённые (преломлённые) лучи пучка. Изображение S’ называется мнимым, если в ней пересекаются не сами отражённые (преломлённые) лучи, а их продолжения. Световая энергия в эту точку не поступает. На рис. 1.7 представлено изображение светящейся точки S, возникающее с помощью плоского зеркала.
Луч SO падает на зеркало КМ под углом 0°, следовательно, угол отражения равен 0°, и данный луч после отражения идёт по пути OS. Из всего множества попадающих из точки S лучей на плоское зеркало выделим луч SO1.
Луч SO1 падает на зеркало под углом α и отражается под углом γ (α = γ). Если продолжить отражённые лучи за зеркало, то они сойдутся в точке S1, которая является мнимым изображением точки S в плоском зеркале. Таким образом, человеку кажется, что лучи выходят из точки S1, хотя на самом деле лучей, выходящих их этой точки и попадающих в глаз, не существует. Изображение точки S1расположено симметрично самой светящейся точке S относительно зеркала КМ. Докажем это.
Луч SB, падающий на зеркало под углом 2 (рис. 1.8), согласно закону отражения света отражается под углом 1 = 2.
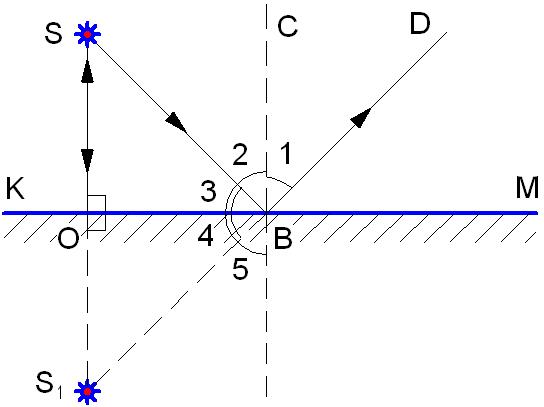
Рис. 1.8. Отражение от плоского зеркала.
Из рис. 1.8 видно, что углы 1 и 5 равны – как вертикальные. Суммы углов 2 + 3 = 5 + 4 = 90°. Следовательно, углы 3 = 4 и 2 = 5.
Прямоугольные треугольники ΔSOB и ΔS1OB имеют общий катет ОВ и равные острые углы 3 и 4, следовательно, эти треугольники равны по стороне и двум прилежащим к катету углам. Это означает, что SO = OS1, то есть точка S1 расположена симметрично точке S относительно зеркала.
Для того чтобы найти изображение предмета АВ в плоском зеркале, достаточно опустить перпендикуляры из крайних точек предмета на зеркало и, продолжив их за пределы зеркала, отложить за ним расстояние, равное расстоянию от зеркала до крайней точки предмета (рис. 1.9). Это изображение будет мнимым и в натуральную величину. Размеры и взаимное расположение предметов сохраняются, но при этом в зеркале левая и правая стороны у изображения меняются местами по сравнению с самим предметом. Параллельность падающих на плоское зеркало световых лучей после отражения также не нарушается.
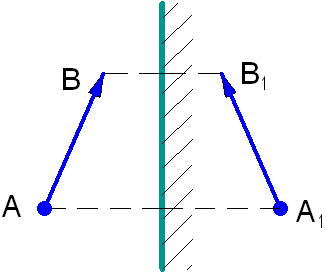
Рис. 1.9. Изображение предмета в плоском зеркале.
В технике часто применяют зеркала со сложной кривой отражающей поверхностью, например, сферические зеркала. Сферическое зеркало – это поверхность тела, имеющая форму сферического сегмента и зеркально отражающая свет. Параллельность лучей при отражении от таких поверхностей нарушается. Зеркало называют вогнутым, если лучи отражаются от внутренней поверхности сферического сегмента. Параллельные световые лучи после отражения от такой поверхности собираются в одну точку, поэтому вогнутое зеркало называют собирающим. Если лучи отражаются от наружной поверхности зеркала, то оно будет выпуклым. Параллельные световые лучи рассеиваются в разные стороны, поэтому выпуклое зеркало называют рассеивающим.
Из прошлых уроков вы уже знаете, что свет распространяется прямолинейно в однородной среде, а при столкновении с какой-либо поверхностью — отражается.
Один из видов отражения называется зеркальным. При слове «зеркало» мы представляем себе плоское стекло, на одну сторону которого нанесено специальное покрытие, содержащее серебро. Но в физике зеркалом может считаться любой предмет, имеющий гладкую плоскую поверхность.
У зеркал есть одна интересная особенность, которая нас и будет интересовать в этом уроке. Мы видим в зеркале отражения — себя и окружающих нас предметов.
Мы же видим предметы благодаря свету, но предметы в зеркале — ненастоящие. Что происходит на самом деле? Как это объясняет физика? На данном уроке вы узнаете много нового и интересного о, казалось бы, такой простой и привычной вещи, как зеркало.
Изображение в плоском зеркале
Плоское зеркало — это плоская поверхность, зеркально отражающая свет.
Рассмотрим изображение, которые мы получаем с помощью него.
Возьмем плоское зеркало $MN$ (рисунок 1). У нас есть источник света $S$, от которого идет расходящийся пучок света. Мы изобразим его с помощью расходящихся лучей $SO$, $SO_1$ и $SO_2$.
Рассмотрим все лучи по очереди:
- Луч $SO$
Луч достигает зеркала и отражается. Угол падения равен $0 degree$, значит (по закону отражения света) угол отражения тоже будет равен $0 degree$. Отраженный луч $OS$ совпадает с лучом $SO$, но имеет другое направление
- Луч $SO_1$
Этот луч падает на зеркало под углом $alpha_1$ и отражается под углом $beta_1$. По закону отражения: $angle beta_1 = angle alpha_1$
- Луч $SO_2$
Данный луч падает на плоское зеркало под углом $alpha_2$ и отражается под углом $beta_2$ ($angle beta_2 = angle alpha_2$)
Мы видим, что в глаз попадет расходящийся пучок света, который определяют лучи $SO_1$ и $SO_2$.
А теперь продолжим все отраженные лучи за зеркало. Они сойдутся в точке $S_1$. Эта точка называется мнимым изображением точки $S$.
Изображение в плоском зеркале называют мнимым, так как оно получается в результате пересечения не реальных лучей света, а их воображаемых продолжений.
В итоге, получается, что в глаз попадает расходящийся пучок света, исходящий как будто бы из точки $S_1$. Но в этой точке сходятся не сами лучи, а только их продолжения. В действительности изображения в этой точке нет: нам только кажется, что из этой точки исходят лучи.
Построение мнимого изображения светящейся точки
Источник света, подобный тому, что мы рассмотрели выше, принято называть светящейся точкой (точка $S$ на рисунке 1). Построить мнимое изображение такой точки очень просто.
На рисунке 1 мы описали пучок света с помощью трех лучей, чтобы обратить ваше внимание на то изображение, которое попадает в глаза. Для построения такого изображения на чертеже нам хватит выделить всего два луча:
1. Луч, перпендикулярный зеркалу
2. Луч, падающий под углом
Второй луч мы выбираем удобным для нас образом, чтобы он попадал на зеркало под каким-то углом падения $alpha$.
Итак, возьмем светящуюся точку $S$ и плоское зеркало $MN$ (рисунок 2).
Из точки $S$ опустим перпендикуляр на зеркало. Мы отметили первый луч $SA$. Отраженный луч будет совпадать с ним, но иметь обратное направление — $AS$.
Отметим второй луч — $SB$, он падает на поверхность зеркала под углом $alpha$. Опустим на поверхность зеркала перпендикуляр $BC$ и отложим от него угол $beta$, по закону отражения света равный углу $alpha$. Мы получили отражённый луч $CD$.
Теперь необходимо продолжить лучи $AS$ и $CD$ за зеркало до их пересечения. Точка их пересечения $S_1$ — это мнимое изображение светящейся точки $S$.
Расположение и размеры предмета и его мнимого изображения относительно зеркала
Используя признаки равенства треугольников на рисунке 1, мы можем доказать, что $S_1O = OS$. То же самое можно проделать и с отрезками $AS$ и $AS_1$ на рисунке 2. Значит, изображение предмета находится на таком же расстоянии за зеркалом, на каком предмет расположен перед зеркалом.
Подтвердим этот факт простым, но очень показательным опытом. Возьмем обычную линейку и вертикально укрепим на ней кусок плоского стекла, как на рисунке 3.
Стекло будет являться полупрозрачным зеркалом. С одной его стороны мы видим зеркальное отражение предметов, а с другой — то, что происходит за этим стеклом.
Также у нас имеются две одинаковые свечи. Одну поставим на расстоянии 3 см от зеркала и зажжем. Мы видим ее отражение в зеркале. Кажется, что оно находится позади стекла.
Наша задача — разместить вторую свечу с другой стороны зеркала так, чтобы она тоже казалась зажженой. Передвигая ее, найдем это положение.
Что мы получили? Незажженная свеча находится именно в том месте, где наблюдается изображение горящей свечи (рисунок 3, а). А теперь взгляните на линейку — за зеркалом свеча находится тоже на 3 см от него. Расстояние от свечи до стекла и от ее изображения до стекла одинаковы.
Итак, мы подошли к интересному выводу.
Мнимое изображение предмета в плоском зеркале находится на том же расстоянии от зеркала, на каком находится сам предмет.
Из этого опыта также очевидно, что высота изображения свечи равна высоте самой свечи (рисунок 3, б). Ведь, передвигая свечу за зеркалом, мы добились того, что она полностью совпала с изображением зажженной свечи.
Размеры изображения предмета в плоском зеркале равны реальным размерам предмета.
Из своего жизненного опыта каждый из нас знает, что когда мы смотрим на изображение предмета в зеркале, мы видим его симметричную форму (рисунок 4).
Это означает, что в зеркале «право» и «лево» меняются местами. Например, зеркальное изображение левой руки представляет для нас как бы правую руку.
Давайте подведем итоги.
Изображение предмета в плоском зеркале:
- Мнимое (находится на пересечении продолжений лучей, а не самих лучей)
- Прямое (не перевернутое)
- Равное по размеру самому предмету
- Находится за зеркалом на таком же расстоянии, как и предмет перед ним
- Симметричное предмету
Построение мнимого изображения предмета
Вы уже узнали определение плоского зеркала и установили его свойства. Теперь давайте рассмотрим, как самостоятельно построить мнимое изображение любого предмета в зеркале.
На чертеже у нас есть плоское зеркало и предмет $AB$ (рисунок 5).
Начнем построение изображения. Для этого опустим из точки $A$ перпендикуляр $АС$ на плоское зеркало. Теперь измерим и зафиксируем длину этого отрезка ($AC$).
Продлим отрезок $AC$ за зеркало и отложим расстояние, равное его длине. Так мы получили точку $A_1$ — мнимое изображение точки $A$.
Проделаем то же самое с точкой $B$. Опустим перпендикуляр на зеркало, продолжим и на определенном расстоянии отметим точку $B_1$.
Теперь осталось только соединить две полученные точки. Так мы получили мнимое изображение $A_1B_1$ предмета $AB$.
Пример задачи
Солнечные лучи при падении образуют с горизонтом угол $varphi = 40 degree$. Под каким углом к горизонту нужно расположить плоское зеркало, чтобы отраженные лучи пошли вертикально вверх?
Дано:
$varphi = 40 degree$
$eta — ?$
Для решения задачи нам понадобится рисунок 6.
Как мы получили такую картинку? Давайте разберемся.
Первым делом проводим линию горизонта $MN$ и отмечаем наш источник света ($S$). Солнечные лучи представим в виде одного падающего луча $SO$. Отмечаем угол между падающим лучом и линией горизонта — угол $varphi$.
Теперь нарисуем отраженный луч $OD$. По условию задачи $OD perp MN$.
По закону отражения света угол падения равен углу отражения. Поэтому мы разделим угол, образованный на картинке падающим и отраженными лучами, пополам — проведем биссектрису $OC$. Отметим угол падения $alpha$ и угол отражения $beta$.
Теперь вспомните, как мы строим отражённый луч. Для этого мы проводим перпендикуляр к отражающей поверхности. В нашем случае, эта поверхность — это зеркало, а перпендикуляр у нас уже есть — $OC$. Значит, поверхность зеркала должна располагаться перпендикулярно этому отрезку.
Таким образом изобразим на рисунке зеркало и отметим искомый угол $eta$.
Теперь можно приступать к решению задачи.
Посмотреть решение и ответ
Скрыть
Решение:
Из условия задачи $OD perp MN$, $angle MOD = 90 degree$.
Из рисунка мы видим, что $angle MOD$ составляют два угла: $angle MOS$ и $angle SOD$.
Значит, $angle SOD = 90 degree — varphi$.
$angle SOD = 90 degree — 40 degree = 50 degree$.
По закону отражения света $angle alpha = angle beta$. Именно эти два угла и составляют $angle SOD$. Выразим этот угол через углы падения и отражения:
$angle SOD = alpha + beta = 2alpha$.
Теперь мы можем найти угол $alpha$:
$alpha = frac{angle SOD}{2} = frac{50 degree}{2} = 25 degree$.
Рассмотрим прямоугольный треугольник $OCA$.
$angle COA = 90 degree$.
С другой стороны:
$angle COA = eta + varphi + alpha$.
Отсюда найдем угол $eta$:
$eta = angle COA — varphi — alpha = 90 degree — 40 degree — 25 degree = 25 degree$.
Ответ: $eta = 25 degree$.
Применение плоских зеркал
В повседневной жизни нас окружает множество плоских зеркал. Они нашли очень широкое применение как в быту, так и в технике.
Например, плоские зеркала используют в фарах различных автомобилей, прожекторов. И помимо этого, мы можем упомянуть и о дорожных и автомобильных зеркалах (боковых и заднего вида). Многие оптические приборы содержат в своем устройстве одно или несколько зеркал: объективы фотоаппаратов, лазеры, телескопы, перископы).
Перископ — это специальный прибор для наблюдения за поверхностью моря с подводной лодки, идущей на небольшой глубине (рисунок 7).
Простейший перископ представляет собой трубу, в углах которой расположены зеркала. Они наклонены относительно трубы на $45 degree$. Сделано это для изменения хода световых лучей. Благодаря этому человек, находящийся у нижнего края трубы может видеть то, что находится у ее верхнего края.
Также в настоящее время зеркала используются в дизайне интерьеров. С их помощью создается иллюзия пространства — большой объем в небольших помещениях.
Интересный прием с зеркалами используют в магазинах. Один предмет помещают между несколькими зеркальным поверхностями, и создается впечатление, что предмет не один, а их много. Это возможно, если установить зеркала под определенным углом $alpha$ друг к другу. Здесь работает формула, позволяющая рассчитать количество изображений $n$: $n = frac{360 degree — alpha}{alpha}$.
Содержание:
Геометрическая оптика – это раздел оптики, в котором изучаются законы распространения световой энергии в прозрачных средах на основе представления о световом луче. Световой луч – это линия, имеющая направление, вдоль которого распространяется энергия световых волн.
Закон отражения света с точки зрения корпускулярной и волновой теории
Если луч света состоит из частиц, как утверждал И. Ньютон, то можно полагать, что они отражаются от поверхности, как упругие мячи (рис. 149) в соответствии с законом отражения, изученным в геометрической оптике.
К такому же выводу приводит и волновая теория, основанная на принципе Х. Гюйгенса: каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Огибающая фронты вторичных волн является фронтом результирующей волны (§ 11).
Рассмотрим отражение плоской волны от поверхности MN (рис. 150). Лучи 
Поскольку рассматриваемые треугольники равны, то углы  равны, лучи лежат в одной плоскости, выполняется закон отражения света.
равны, лучи лежат в одной плоскости, выполняется закон отражения света.
Запомните! Закон отражения: Угол падения равен углу отражения 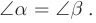 Луч падающий, луч отраженный и перпендикуляр, восстановленный в точку падения луча к границе раздела двух сред, лежат в одной плоскости.
Луч падающий, луч отраженный и перпендикуляр, восстановленный в точку падения луча к границе раздела двух сред, лежат в одной плоскости.
На основе волновой теории можно объяснить, почему свет почти не отражается от поверхности толстого стекла и практически полностью отражается от тончайшей металлической фольги. Стекло – диэлектрик, в нем нет свободных заряженных частиц, он прозрачен для электромагнитных волн. В металлах свободные электроны под действием световой волны совершают колебательные движения, созданное ими поле отражает световую волну.
Применение закона отражения
Закон отражения получил применение в различных устройствах и аттракционах.
На транспорте применяется угловой отражатель – катафот, изготовленный из стекла или пластмассы. Сзади велосипеда укрепляют красный, впереди – белый, на спицах колес – оранжевый. Светоотражатель направляет луч света обратно к освещающему его источнику независимо от угла падения света на поверхность. Ими оборудуются все транспортные средства и опасные участки дорог. Светосигнальные приборы европейского образца появились на автодорогах республиканского значения, их установили на участках «Алматы – Ташкент – Термез», «Новый обход перевала Куюк» в Жамбылской области (рис. 151). Приборы заряжаются солнечными лучами, и они освещают осевую линию дороги в темное время суток. Установлены сигнальные столбики с надписью «Kazautozhol» на автомобильных дорогах, где нет искусственного освещения.
Светоотражающие материалы используются для пошива спецодежды – костюмов для работников пожарных, медицинских, военных и других видов служб. Существует два вида светоотражателей: на текстильной и основе ПВХ. Светоотражатели на текстильной основе производят с использованием стеклянных микрошариков с алюминиевым слоем отражателя, которые наносятся на рабочую поверхность материал полимерным клеем. Светоотражатели на основе ПВХ производят с использованием микропирамидок. Они превосходят светоотражатели на текстильной основе в износостойкости, поскольку микропирамидки находятся изнутри пленки.
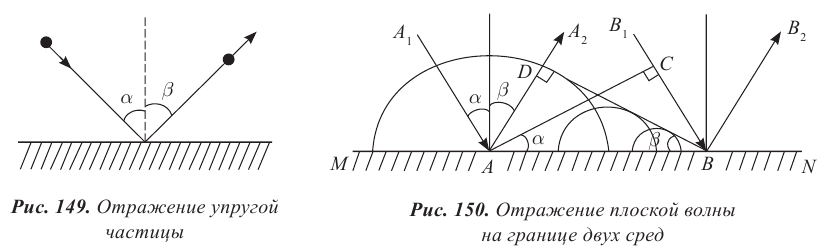
Формула плоского зеркала
Запишем формулу плоского зеркала в соответствии с изображением, полученным на рисунке 158:

где d − расстояние от предмета до зеркала; 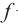 − расстояние от зеркала до изображения. Знак минус свидетельствует о том, что изображение мнимое.
− расстояние от зеркала до изображения. Знак минус свидетельствует о том, что изображение мнимое.
Изображение в двух плоских зеркалах
С помощью двух плоских зеркал можно получить несколько изображений, число которых определяется углом между отражающими поверхностями зеркал 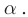 При построении необходимо помнить, что изображение первого зеркала становится предметом для второго зеркала, и наоборот, изображение второго зеркала – предметом первого. Последнее полученное изображение находится за отражающей поверхностью двух зеркал (рис. 159). Для определения числа изображений необходимо от числа секторов, на которые угол a делит полный угол, равный 360°, отнять один, в котором находится сам предмет:
При построении необходимо помнить, что изображение первого зеркала становится предметом для второго зеркала, и наоборот, изображение второго зеркала – предметом первого. Последнее полученное изображение находится за отражающей поверхностью двух зеркал (рис. 159). Для определения числа изображений необходимо от числа секторов, на которые угол a делит полный угол, равный 360°, отнять один, в котором находится сам предмет:
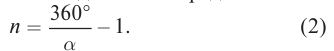
Например, при 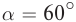 число изображений в зеркалах равно:
число изображений в зеркалах равно: 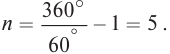
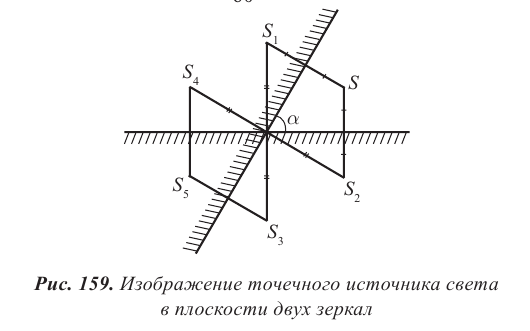
Сферические зеркала. Основные точки и линии зеркал
Зеркала, отражающая поверхность которых представляет собой часть сферы, называют сферическими.
Основные точки и линии зеркал: вершина зеркала – точка O; центр кривизны – точка C; главная оптическая ось (ГОО) − прямая, проходящая через вершину и центр зеркала; фокус зеркала – точка F, в которой фокусируются все лучи, падающие на плоскость зеркала параллельно ГОО (рис. 160). Фокус выпуклого зеркала мнимый, он находится за плоскостью зеркала.
Введем еще несколько основных точек и линий для сферических зеркал. Побочная оптическая ось (ПОО) – прямая, проходящая через центр кривизны зеркала С. Фокус побочной оптической оси F1 находится в точке пересечения ПОО с фокальной плоскостью (ФП). Через эту точку проходят лучи, параллельные ПОО. Фокальная плоскость – это плоскость, перпендикулярная главной оптической оси и проходящая через ее фокус. МК – главная плоскость сферического зеркала – это плоскость, перпендикулярная ГОО и проходящая через вершину зеркала.
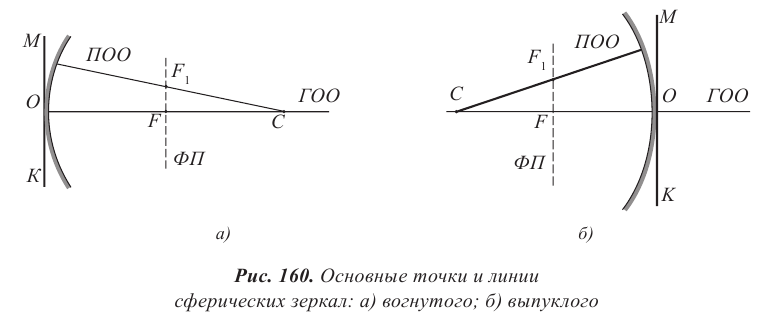
Формула вогнутого сферического зеркала
Формула вогнутого сферического зеркала справедлива для параксиальных лучей, которые составляют с главной оптической осью малые углы. При таком условии фокальная плоскость перпендикулярна главной оптической оси. На рисунке 161 изображен луч источника света S, он отражается от точки A поверхности вогнутого зеркала.
KM − касательная в точке А, перпендикулярная радиусу AC или побочной оптической оси. Для параксиальных лучей можно считать, что: 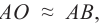 следовательно, расстояние от зеркала до предмета
следовательно, расстояние от зеркала до предмета 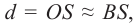 расстояние от зеркала до изображения
расстояние от зеркала до изображения 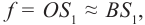 радиус кривизны
радиус кривизны 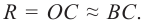 Выразим
Выразим  через катет AB треугольников
через катет AB треугольников  полученных в результате построения:
полученных в результате построения:
Установим связь между углами треугольников. Угол 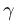 является внешним для треугольника
является внешним для треугольника 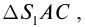 угол
угол 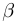 − внешним для треугольника
− внешним для треугольника 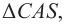 следовательно:
следовательно:

Из (5) выразим 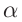 и, подставив в (4), получим:
и, подставив в (4), получим:
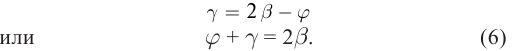
Тангенсы малых углов равны значениям углов в радианной мере. Выразим тангенсы из уравнений (3) и, подставив в уравнение (6), получим формулу сферического зеркала: 
Построение изображения предмета в сферическом зеркале
Для построения изображения в сферическом зеркале достаточно использовать два луча из тех, ход которых известен (рис. 162):
- луч, параллельный оптической оси, после отражения проходит через ее фокус;
- луч, прошедший через фокус зеркала, отражается параллельно оптической оси;
- луч, падающий в точку вершины зеркала, отражается под тем же углом;
- луч, прошедший через центр кривизны зеркала, отражается вдоль линии падения в обратном направлении.
Алгоритм построения изображения точечного источника света
1. Провести ПОО, указать в точке пересечения с ФП фокус проведенной оси (рис. 163).
2. От источника света S построить луч, параллельный ПОО, до главной плоскости зеркала. Провести отраженный луч через фокус побочной оси.
3. Указать в точке пересечения с лучом, направленным вдоль ГОО, полученное изображение 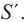
Вспомните! Изображение мнимое, если пересекаются не сами отраженные лучи, а их продолжения. Изображение предмета действительное, если пересекаются лучи.
Линейное увеличение
Рассчитать изменение линейных размеров тела можно из подобия треугольников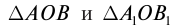 (рис. 162):
(рис. 162):

где H − высота изображения; h − высота предмета; 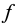 − расстояние от изображения до вершины зеркала; d − расстояние от предмета до вершины зеркала; Г − увеличение.
− расстояние от изображения до вершины зеркала; d − расстояние от предмета до вершины зеркала; Г − увеличение.
Физическую величину, равную отношению высоты изображения к высоте предмета, называют линейным увеличением зеркала.
Если 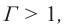 то размеры изображения тела увеличиваются; если
то размеры изображения тела увеличиваются; если 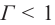 − уменьшаются. Лучи обратимы, следовательно, если считать, что на рисунке 162 предметом является отрезок
− уменьшаются. Лучи обратимы, следовательно, если считать, что на рисунке 162 предметом является отрезок 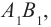 то его изображением станет отрезок AB.
то его изображением станет отрезок AB.
Закон преломления света с точки зрения волновой теории
Закон преломления света открыт экспериментально голландским математиком В. Снеллиусом в начале XVII в.
Произведение абсолютного показателя преломления на синус угла падения остается постоянной величиной, являясь «оптическим инвариантом» при переходе света из одной среды в другую.
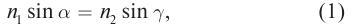
где 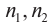 – абсолютные показатели сред,
– абсолютные показатели сред,  – угол падения,
– угол падения, 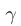 – угол преломления.
– угол преломления.
Рассмотрим преломление двух лучей 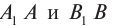 плоской волны на границе двух сред MN на основе принципа Гюйгенса (рис. 165). Фронт падающей волны в момент, когда луч
плоской волны на границе двух сред MN на основе принципа Гюйгенса (рис. 165). Фронт падающей волны в момент, когда луч 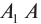 достигает границы сред MN, обозначен на рисунке отрезком AC. Показатель преломления второй среды больше, чем первой среды
достигает границы сред MN, обозначен на рисунке отрезком AC. Показатель преломления второй среды больше, чем первой среды  Фронт вторичной волны, созданной во второй среде в момент падения луча
Фронт вторичной волны, созданной во второй среде в момент падения луча  на границу MN, обозначен отрезком DB. В результате построения получены прямоугольные треугольники
на границу MN, обозначен отрезком DB. В результате построения получены прямоугольные треугольники 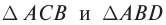 с общей стороной AB. В треугольниках угол
с общей стороной AB. В треугольниках угол 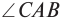 равен углу падения
равен углу падения 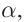 угол
угол 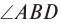 равен углу преломления
равен углу преломления 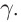 Выразим сторону AB через отрезки AD и CB, пройденные лучами за один и тот же промежуток времени, получим:
Выразим сторону AB через отрезки AD и CB, пройденные лучами за один и тот же промежуток времени, получим:
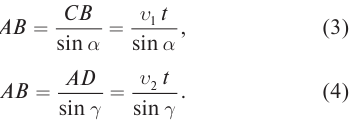
Из формул (3) и (4) следует, что: 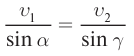
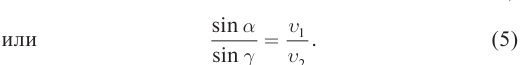
Выразим скорость света в средах через абсолютный показатель преломления: 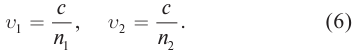
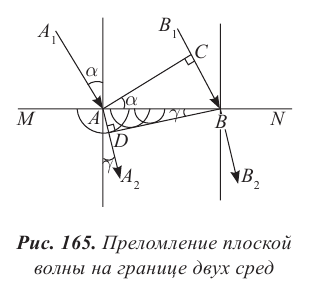
Вспомните! Абсолютный показатель преломления – это физическая величина, показывающая, во сколько раз скорость распространения света в вакууме больше скорости распространения света в данной среде: 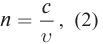 где n − абсолютный показатель преломления среды, с − скорость света в вакууме,
где n − абсолютный показатель преломления среды, с − скорость света в вакууме, 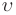 − скорость света в среде. Оптически менее плотная среда обладает меньшим абсолютным показателем преломления.
− скорость света в среде. Оптически менее плотная среда обладает меньшим абсолютным показателем преломления.
Подставив формулы (6) в (5), получим:
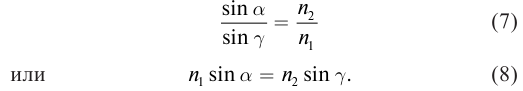
На основе волновой теории Гюйгенса получен закон преломления Снеллиуса.
Вспомните! Относительный показатель преломления – это физическая величина, которая показывает во сколько раз скорость распространения света в первой среде больше скорости распространения света во второй среде. 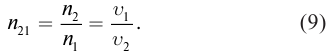
Заменим в уравнении (7) отношение абсолютных показателей преломления относительным показателем, получим: 
Полное внутреннее отражение света
Если направить луч света из оптически более плотной среды в менее плотную среду, то угол преломления больше угла падения. Наибольшему значению угла преломления, равному 90º, соответствует угол падения 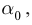 он назван предельным углом полного внутреннего отражения.
он назван предельным углом полного внутреннего отражения.
При падении луча на границу сред под углом, превышающим предельный угол полного внутреннего отражения 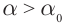 преломленный луч исчезает, происходит полное отражение света (рис. 166).
преломленный луч исчезает, происходит полное отражение света (рис. 166).
Закон преломления для предельного угла примет вид:

Из полученного равенства следует, что предельный угол полного отражения определяется показателем преломления среды в том случае, если второй средой является вакуум или воздух: 
Запомните! Закон преломления света:
Отношение синуса угла падения к синусу угла преломления для двух сред есть величина постоянная. Она равна относительному показателю преломления второй среды относительно первой.
Луч падающий, луч преломленный и перпендикуляр восстановленный в точку падения луча к границе раздела двух сред, лежат в одной плоскости.
Преимущества оптоволоконной технологии при передаче световых сигналов
Простейшая оптоволоконная система передачи информации между двумя точками состоит из трех основных элементов: оптического передатчика, оптоволоконного кабеля и оптического приемника.
Оптический передатчик преобразует электрический сигнал в модулированный световой поток, предназначенный для передачи по оптоволокну. В качестве источника света используются светодиоды и полупроводниковые лазеры. Длина волны излучения выбрана с учетом максимальной прозрачности материала волокна и наивысшей чувствительности фотодиодов. Оптические передатчики работают в диапазоне инфракрасных лучей с длиной волны 850, 1300 и 1550 нм.
Оптический приемник преобразует световой сигнал в копию исходного электрического сигнала. В качестве чувствительного элемента оптического приемника используется фотодиод.
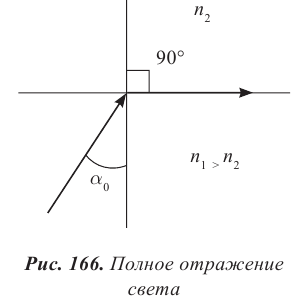
Световод (оптоволоконный кабель) − закрытое устройство для направленной передачи света.
Оптоволоконный кабель состоит из одного или нескольких стеклянных волокон со ступенчатым или плавным изменением показателя преломления вдоль радиуса (рис. 167 а). Волокно со ступенчатым профилем показателя преломления состоит из сердцевины, изготовленной из стекла с малыми оптическими потерями, окруженной стеклянной оболочкой с более низким показателем преломления (рис. 167 б). Оптоволокно с плавным профилем состоит из стекла только одного сорта, но оно обработано так, что его показатель преломления плавно уменьшается от центра к поверхности волокна. Такой световод постоянно отклоняет распространяющийся по нему свет к центру (рис. 167 в).
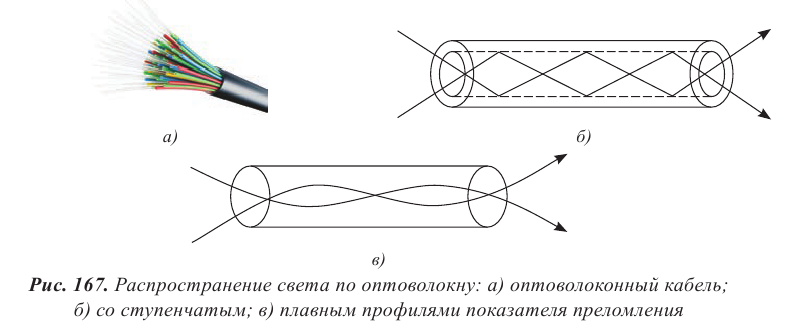
В зависимости от числа волокон различают кабели одножильные, многожильные и многомодовые, которые позволяют распространяться световым волнам по нескольким различным путям, которые называют модами.
В многомодовых волокнах каждая световая волна распространяются под своим углом. Волны по-разному отражаются от оболочки и поступают в приемник в разное время. В одном многомодовом кабеле может быть порядка 80–100 мод. В многожильных кабелях возможно использование нескольких отдельных волокон, диаметр которых колеблется от 8 мкм до 10 мкм, соответствует диаметру одножильных кабелей. Многомодовые и многожильные кабели в сравнении с одножильными кабелями обеспечивают большую пропускную способность на малые расстояния, около 2 метров, на больших дистанциях возникают помехи. Одножильное оптоволокно чаще всего применяется в телекоммуникационных системах большой протяженности.
Оптические кабели имеют ряд преимуществ над обычными проводами и кабелями:
- могут с высокой скоростью передать значительно большее количество информации;
- тоньше и легче медных кабелей с такой же пропускной способностью;
- не подвержены внешним помехам, включая грозовые разряды;
- практически не взаимодействуют с агрессивными химическими веществами, вызывающими коррозию;
- не проводят электричество, могут находиться в прямом контакте с высоковольтным электрооборудованием, не несут опасности поражения электрическим током при ремонте;
- не создают вокруг себя электромагнитного излучения;
- обеспечивают защиту передаваемой информации, несанкционированное подключение к кабелю легко обнаруживается.
Интересно знать! В настоящее время используются оптоволоконные кабели, позволяющие передавать данные на большие расстояния с пропускной способностью до 100 Гбит/с. Максимальная пропускная способность оптоволоконного кабеля со спектральным уплотнением каналов WDM достигает 9,6 Тбит/с, так как он способен передать данные одновременно по 96 каналам.
Построение изображения в системе линз. Формула тонкой линзы
I. Собирающая и рассеивающая линзы
Линза представляет собой прозрачное тело, ограниченное с двух сторон сферическими поверхностями: 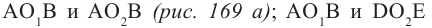 (рис. 170 а). Одна из поверхностей может быть плоской, ее можно рассматривать как сферическую поверхность большого радиуса.
(рис. 170 а). Одна из поверхностей может быть плоской, ее можно рассматривать как сферическую поверхность большого радиуса.
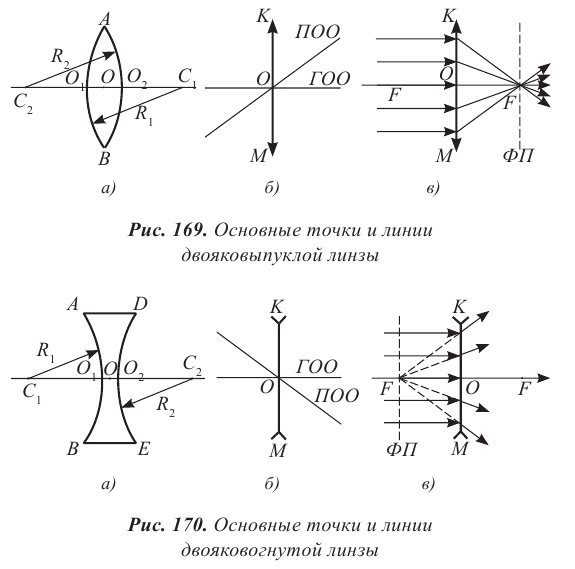
Обратите внимание! Если показатель преломления линзы больше показателя преломления среды, то выпуклые линзы фокусируют падающие на них лучи, вогнутые линзы – рассеивают.
II. Ход лучей в собирающей и рассеивающей линзах
Луч 1, параллельный главной оптической оси, проходит через задний фокус линзы (рис. 171);
Луч 2, прошедший через центр линзы, не преломляется (рис. 171);
Луч 3, прошедший через передний фокус линзы, становится параллельным главной оптической оси (рис. 171);
Луч 4, прошедший через центр кривизны одной из сферической поверхностей, проходит через центр кривизны другой поверхности (рис. 171).
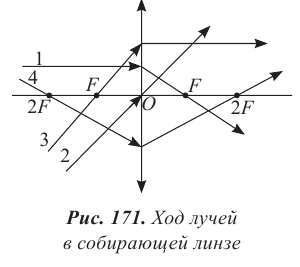
Обратите внимание! Зеркала дают изображение в отраженных лучах, а линзы – в проходящих.
III. Побочные оси. Построение лучей с использование побочных осей
Фокусы побочных оптических осей F1 также принадлежат фокальной плоскости и находятся в точках пересечения ПОО с ФП (рис. 175 а). Лучи, падающие на собирающую линзу параллельно побочной оси, проходят через фокус ПОО (рис. 175 б). В рассеивающей линзе в фокусе побочной оси пересекаются продолжения лучей (рис. 175 в).

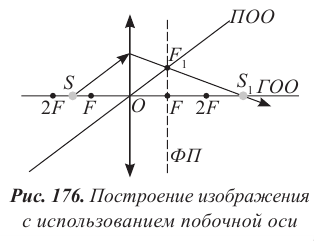
В том случае, когда предмет представляет собой точечный источник света, находящийся на главной оптической оси, для построения изображения используют побочную ось. На рисунке 176 изображен ход лучей при условии  использован луч, параллельный ПОО, и луч, проходящий через центр линзы О. Полученное изображение действительное, находится по другую сторону линзы за двойным фокусом.
использован луч, параллельный ПОО, и луч, проходящий через центр линзы О. Полученное изображение действительное, находится по другую сторону линзы за двойным фокусом.
Запомните! Побочную ось необходимо ввести для лучей, падающих на линзу под произвольным углом. Она проводится параллельно падающему лучу. В этом случае преломленный луч пройдет через задний фокус побочной оси собирающей линзы (рис. 176). Для рассеивающей линзы необходимо провести преломленный луч таким образом, чтобы его продолжение прошло через передний фокус побочной оси.
IV. Формула тонкой линзы. Оптическая сила линзы. Увеличение линзы
Формула тонкой линзы вам известна из курса физики 8 класса:
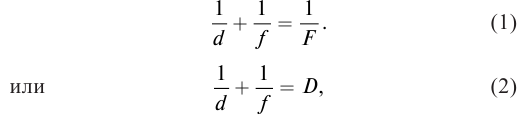
где D – оптическая сила линзы. Для собирающей линзы фокус линзы положительный F > 0, для рассеивающей линзы – отрицательный F < 0.
Физическую величину, равную отношению высоты изображения к высоте предмета, называют увеличением линзы.
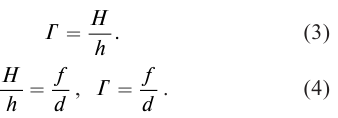
Если изображение предмета увеличенное, то увеличение больше единицы Г > 1, если изображение уменьшенное, то Г < 1.
Оптическая сила линзы – это физическая величина, равная обратной величине фокусного расстояния линзы.

Оптическую силу измеряют в диоптриях: 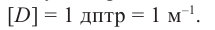
V. Зависимость преломляющих свойств линзы от показателя преломления и радиусов кривизны линзы
Рассмотрим ход луча от точечного источника, находящегося на главной оптической оси (рис. 179). Угол отклонения луча 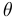 является внешним углом треугольника
является внешним углом треугольника  он равен сумме внутренних углов не смежных с ним:
он равен сумме внутренних углов не смежных с ним:

Для параксиальных лучей углы имеют малые значения, в радианной мере они равны тангенсам углов:
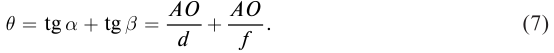
Запомните! Для действительного предмета d > 0, для мнимого предмета d < 0. Если в расчетах получено  то изображение действительное. Если
то изображение действительное. Если 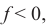 то изображение мнимое.
то изображение мнимое.
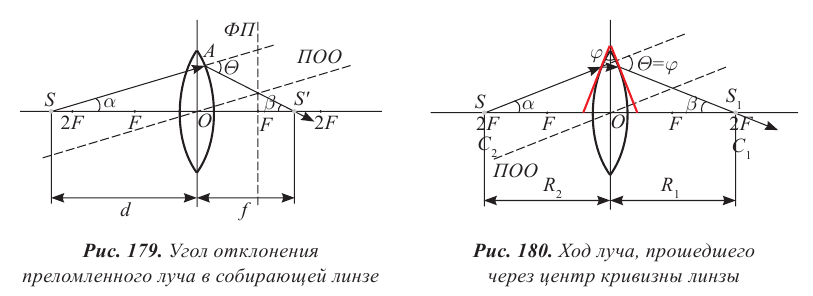
Переместим источник в точку 2F, которая является центром кривизны линзы, тогда в точке преломления луч станет перпендикулярным касательной к сферической поверхности (рис. 180). Угол, образовавшийся в результате пересечения касательных, обозначим  и рассмотрим линзу как тонкую призму. Угол отклонения луча равен преломляющему углу призмы, поскольку стороны углов взаимно перпендикулярны. Расстояние от предмета и изображения до линзы равны радиусам кривизны поверхности.
и рассмотрим линзу как тонкую призму. Угол отклонения луча равен преломляющему углу призмы, поскольку стороны углов взаимно перпендикулярны. Расстояние от предмета и изображения до линзы равны радиусам кривизны поверхности.
Соотношение углов (6) примет вид:
Подставив (7) и (8) в формулу тонкой призмы (9), получим:
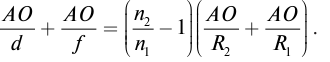
Сократим на АО, получим
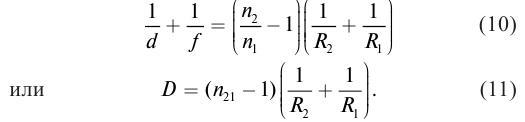
Полученные выражения (10), (11) являются формулами тонкой линзы.
Чем больше относительный показатель преломления вещества линзы и меньше радиус кривизны сферических поверхностей, тем больше оптическая сила линзы.
В случае 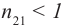 двояковыпуклая линза рассеивает лучи, ее оптическая сила при этом условии имеет отрицательное значение.
двояковыпуклая линза рассеивает лучи, ее оптическая сила при этом условии имеет отрицательное значение.
Кусочки науки:
Луч света, падающий на призму, дважды преломляется при прохождении на гранях ОА и ОВ. Если призма сделана из материала оптически более плотного, чем окружающая среда, то луч света отклоняется на угол  к основанию призмы:
к основанию призмы: 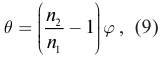
где 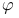 – преломляющий угол призмы (рис. 181).
– преломляющий угол призмы (рис. 181).
Оптические приборы
I. Угловое увеличение оптического прибора
Основное назначение лупы, микроскопа и телескопа − увеличение угла зрения на рассматриваемые объекты.
Угловое увеличение оптического прибора – это отношение тангенса угла зрения при рассмотрении предмета через оптический прибор к тангенсу угла зрения при рассмотрении предмета невооруженным глазом на расстоянии наилучшего зрения.

Разрешающей способностью оптической системы называют наименьшее расстояние между элементами наблюдаемого объекта, при котором эти элементы еще могут быть отличены один от другого.
Оптический прибор и глаз наблюдателя составляют единую оптическую систему. Оптическая сила системы определяется суммой оптических сил приборов, входящих в систему.
II. Глаз, как оптический прибор
Нормальный глаз в спокойном состоянии дает изображение удаленных предметов. При приближении предметов к глазу наблюдателя кривизна хрусталика увеличивается, фокусное расстояние уменьшается, возрастает угол зрения – угол 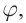 под которым виден предмет. Для нормального глаза благоприятным расстоянием является
под которым виден предмет. Для нормального глаза благоприятным расстоянием является 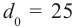 см. Угол зрения невооруженного глаза определяется расстоянием наилучшего зрения (рис. 182 а):
см. Угол зрения невооруженного глаза определяется расстоянием наилучшего зрения (рис. 182 а):

Способность глаза к аккомодации ограничена, поэтому приблизить предмет непосредственно к глазу невозможно, в таком случае используют оптические приборы.
Вспомните! Изображение, полученное на сетчатке глаза, всегда действительное, уменьшенное, перевернутое. Роль собирающей линзы выполняет хрусталик. Резкость изображения обеспечивается способностью глаза к аккомодации – изменению кривизны поверхностей хрусталика.
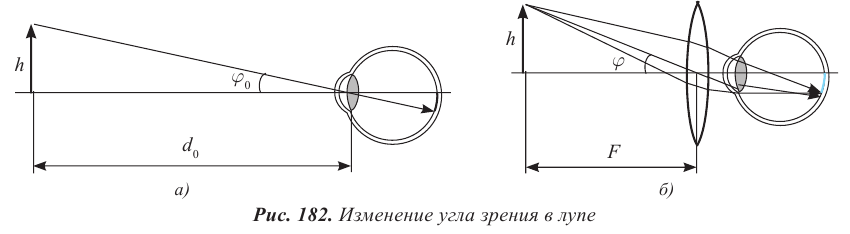
III. Лупа
Если предмет расположить в фокусе линзы 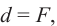 то после прохождения через нее лучи попадают в глаз человека параллельным пучком. При таком условии нормальный глаз сводит пучок в точку на сетчатке без аккомодации, глаз не утомляется. При этом изображение на сетчатке и угол зрения
то после прохождения через нее лучи попадают в глаз человека параллельным пучком. При таком условии нормальный глаз сводит пучок в точку на сетчатке без аккомодации, глаз не утомляется. При этом изображение на сетчатке и угол зрения 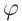 увеличатся, угол зрения станет равным (рис. 182 б):
увеличатся, угол зрения станет равным (рис. 182 б):

Подставим (2) и (3) в формулу (1). Тогда формула углового увеличения лупы примет вид:
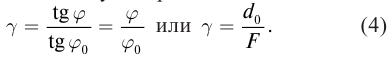
Угловое увеличение лупы определяется отношением расстояния наилучшего зрения к фокусу линзы.
IV. Микроскоп
Оптическая система микроскопа состоит из объектива  и окуляра
и окуляра  (рис. 183). Наиболее благоприятное условие для нормального глаза осуществляется в том случае, когда промежуточное изображение
(рис. 183). Наиболее благоприятное условие для нормального глаза осуществляется в том случае, когда промежуточное изображение  находится в передней фокальной плоскости окуляра
находится в передней фокальной плоскости окуляра 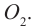 В этом случае изображение предмета удаляется в бесконечность, глаз фокусирует лучи на сетчатке без аккомодации.
В этом случае изображение предмета удаляется в бесконечность, глаз фокусирует лучи на сетчатке без аккомодации.
Определим угловое увеличение по известной формуле:

где  – угол зрения для невооруженного глаза,
– угол зрения для невооруженного глаза,  – угол зрения через микроскоп при условии, что изображение объектива лежит в фокальной плоскости окуляра. Подставим (6) и (7) в (5), получим:
– угол зрения через микроскоп при условии, что изображение объектива лежит в фокальной плоскости окуляра. Подставим (6) и (7) в (5), получим:

Интересно знать! Оптический микроскоп дает возможность различать структуры с расстоянием между элементами до 0,20 мкм, т.е. разрешающая способность такого микроскопа составляет около 0,20 мкм или 200 нм. Предельная разрешающая способность микроскопа имеет предел, обусловленный волновыми свойствами света, она достигается при тысячекратном линейном увеличении.
В формуле (8) отношение является линейным увеличением объектива, представим его как отношение расстояний от линзы до изображения и предмета:

где L − расстояние между фокусами объектива и окуляра.
Поскольку в микроскопах объектив короткофокусный, то 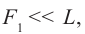 формула (9) примет вид:
формула (9) примет вид:

Подставив (10) в (8), получим:

где 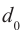 − расстояние наилучшего видения;
− расстояние наилучшего видения;
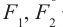 − фокусные расстояния объектива и окуляра;
− фокусные расстояния объектива и окуляра;
L − расстояние между фокусами объектива и окуляра – оптическая длина тубуса микроскопа.
Из формулы (11) с учетом (10) и (4) получим: 
Угловое увеличение оптического микроскопа определяется произведением линейных увеличений объектива и окуляра.
Несложно доказать, что линейное увеличение микроскопа также равно произведению линейных увеличений окуляра и объектива:
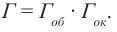
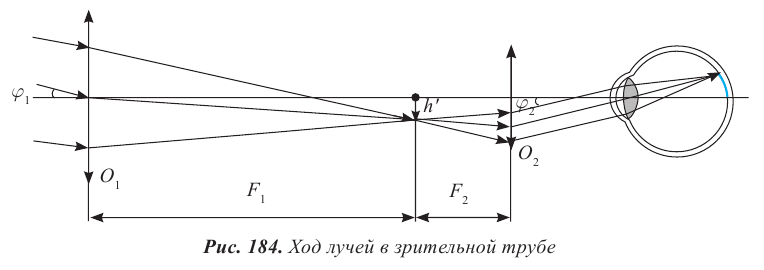
V. Телескоп
Телескоп – это зрительная труба, предназначенная для наблюдения небесных тел. Телескоп, изготовленный из линз, называют рефрактором. Телескоп, в котором объектив заменен на вогнутое зеркало, называют рефлектором.
Зрительная труба – это оптический прибор, предназначенный для рассмотрения удаленных предметов.
Объектив и окуляр прибора располагаются в тубусе таким образом, чтобы задний фокус объектива 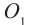 совпадал с передним фокусом окуляра
совпадал с передним фокусом окуляра 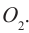 При совмещении фокусов лучи из окуляра выходят параллельным пучком, что позволяет наблюдать за объектом без аккомодации, т.е. без напряжения глазных мышц (рис. 184). Объектив дает уменьшенное изображение удаленного предмета
При совмещении фокусов лучи из окуляра выходят параллельным пучком, что позволяет наблюдать за объектом без аккомодации, т.е. без напряжения глазных мышц (рис. 184). Объектив дает уменьшенное изображение удаленного предмета 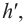 который рассматривают через окуляр, как в лупу.
который рассматривают через окуляр, как в лупу.
Интересно знать! Все звезды в телескоп видны как светящиеся точки, но благодаря угловому увеличению они отдаляются друг от друга, что позволяет обнаружить двойные, тройные звезды или скопление звезд. Телескоп с диаметром объектива 12,5 см может различить две звезды, находящиеся на угловом расстоянии 1″, полуметровый объектив телескопа позволяет различать две звезды, отстоящие на угловом расстоянии 0,25″.
Угол 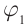 можно считать равным углу зрения невооруженного глаза ввиду значительной удаленности предмета. Выразим углы зрения
можно считать равным углу зрения невооруженного глаза ввиду значительной удаленности предмета. Выразим углы зрения  через высоту изображения объектива
через высоту изображения объектива 
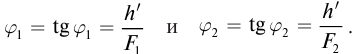
Угловое увеличение оптического прибора определяется отношением тангенса угла зрения через оптический прибор к тангенсу угла зрения невооруженного глаза:
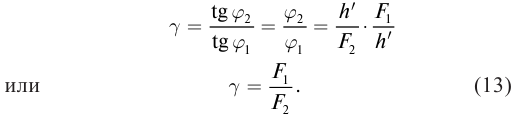
Угловое увеличение зрительной трубы равно отношению фокусных расстояний объектива и окуляра.
Пример решения задачи:
Мальчик, сняв очки, читает книгу, держа ее на расстоянии d = 16 см от глаз. Какова оптическая сила его очков?
Дано:
d = 16 см
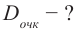
СИ 0,16 м
Решение: Для невооруженного глаза
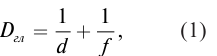
где ƒ − расстояние от хрусталика глаза до сетчатки.
Если надеть очки, то 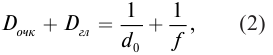
где d0 = 25 см − расстояние наилучшего зрения.
Решая совместно уравнения (1) и (2) для оптической силы очков получим: 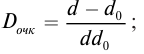
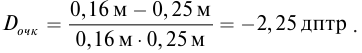
Ответ: Dочк = – 2,25 дптр.
Итоги
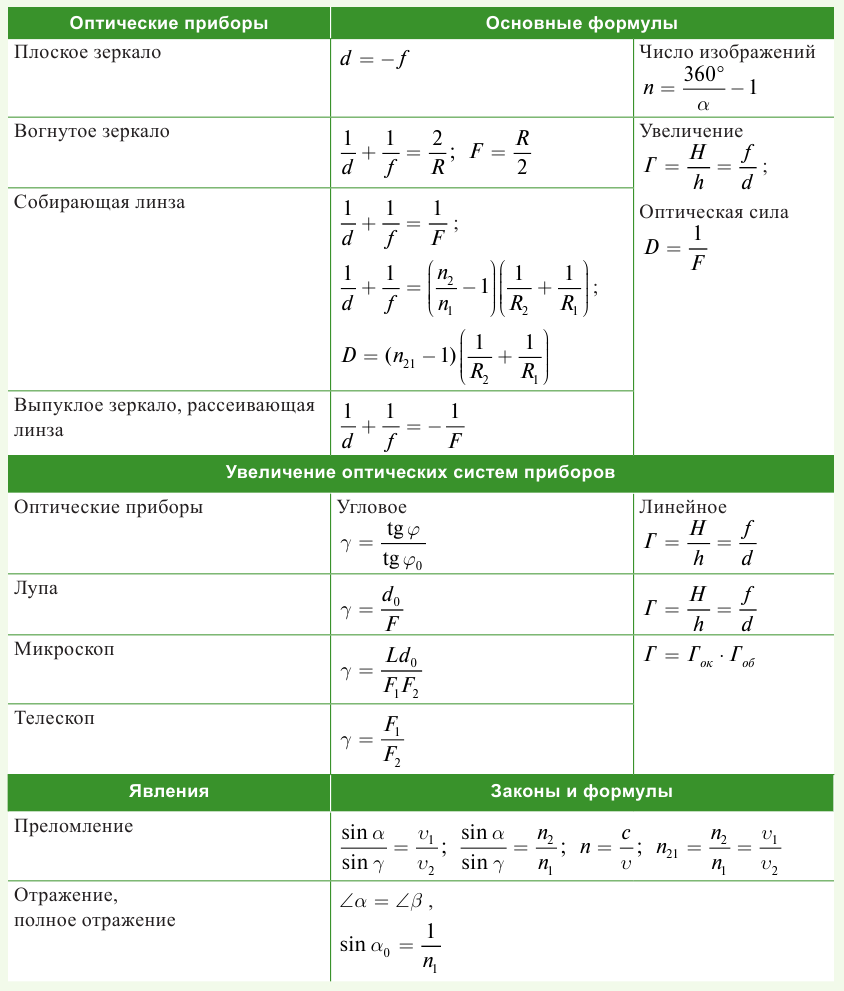
Закон отражения:
Угол падения равен углу отражения  Луч падающий, луч отраженный и перпендикуляр, восстановленный в точку падения луча к границе раздела двух сред, лежат в одной плоскости.
Луч падающий, луч отраженный и перпендикуляр, восстановленный в точку падения луча к границе раздела двух сред, лежат в одной плоскости.
Закон преломления:
Отношение синуса угла падения к синусу угла преломления для двух сред есть величина постоянная. Она равна относительному показателю преломления второй среды относительно первой. Луч падающий, луч преломленный и перпендикуляр, восстановленный в точку падения луча к границе раздела двух сред, лежат в одной плоскости.
Глоссарий
Абсолютный показатель преломления – физическая величина, равная отношению скорости распространения света в вакууме к скорости распространения света в данной среде.
Главная оптическая ось линзы – прямая, проходящая через центры кривизны поверхностей линзы.
Оптический центр линзы – точка пересечения главной оптической оси с плоскостью линзы.
Оптическая длина тубуса микроскопа – расстояние между фокусами объектива и окуляра.
Относительный показатель преломления – физическая величина, равная отношению скорости распространения света в первой среде к скорости распространения света во второй среде.
Побочная оптическая ось линзы – любая прямая, проведенная через оптический центр линзы.
Телескоп – прибор, предназначенный для наблюдения небесных тел.
Увеличение линейное – физическая величина, равная отношению высоты изображения к высоте предмета.
Угловое увеличение оптического прибора – отношение тангенса угла зрения при рассмотрении предмета через оптический прибор к тангенсу угла зрения, при рассмотрении предмета невооруженным глазом на расстоянии наилучшего зрения.
Прямолинейное распространение света
Геометрической оптикой называют раздел оптики, в котором изучаются за-
коны распространения света в прозрачных средах на основе представления о нем как о совокупности световых лучей. Под лучом понимают линию, вдоль которой переносится энергия электромагнитной волны. Условимся изображать оптические лучи графически с помощью геометрических лучей со стрелками. В геометрической оптике волновая природа света не учитывается.
Уже в начальные периоды оптических исследований были экспериментально
установлены четыре основных закона геометрической оптики:
- закон прямолинейного распространения света;
- закон независимости световых лучей;
- закон отражения световых лучей;
- закон преломления световых лучей.
Впервые закон прямолинейного распространения света, составляющий основу геометрической оптики, был сформулирован в III в. до н. э. в труде Евклида «Оптика и катооптика». Закон утверждает, что:
- свет в прозрачной однородной среде распространяется прямолинейно.
Доказательством закона служит образование полной тени и полутени, геометрически подобных препятствиям. Источник дает полную тень (рис. 265), если его размеры значительно меньше расстояния до препятствия, отбрасывающего тень.
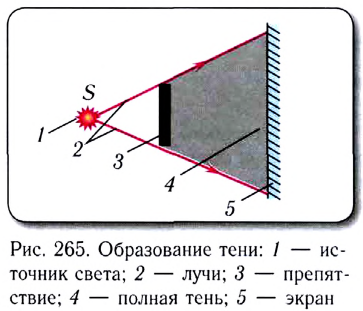
Такой источник принято называть точечным. Подчеркнем, что точечный источник света является идеализацией, подобно материальной точке в механике.
Несколько источников света, или неточечный (протяженный) источник помимо области полной тени, создают также и область полутени (рис. 266).
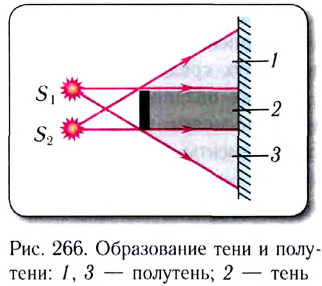
В этих законах использовались понятия световой пучок или световой луч, т. е. предполагалось, что пучок и луч бесконечно тонкие.
Световые пучки получают при пропускании излучения, идущего от удаленного источника, через отверстие (диафрагму) в экране 1 (рис. 267).
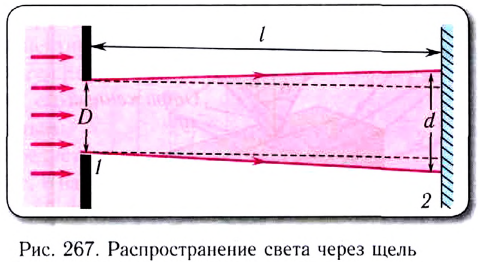
Эксперименты показывают, что если диаметр отверстия D гораздо больше длины световой волны 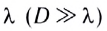 и расстояние l от отверстия до экрана 2 не очень велико, то выходящий из диафрагмы пучок можно считать параллельным.
и расстояние l от отверстия до экрана 2 не очень велико, то выходящий из диафрагмы пучок можно считать параллельным.
Если же диаметр диафрагмы оказывается справедливо сравним с длиной световой волны, то выходящий световой пучок становится расходящимся, свет проникает в область геометрической тени, происходит дифракция света (d > D), т. е. проявляется волновой характер светового излучения. Следует отметить, что дифракция будет наблюдаться на очень больших расстояниях от экрана 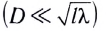 даже при диаметре диафрагмы
даже при диаметре диафрагмы 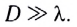
Таким образом, луч — чисто геометрическое понятие. Луч указывает направление, перпендикулярное фронту волны, в котором опа переносит энергию.
Лучи, выходящие из одной точки, называют расходящимися, а собирающиеся в одной точке — сходящимися. Примером расходящихся лучей может служить любой точечный источник света, а примером сходящихся — совокупность лучей, попадающих в зрачок нашего глаза от различных предметов.
Пересекающиеся световые лучи не взаимодействуют друг с другом в рамках геометрической оптики, т. е. «исказить» изображение с помощью других лучей невозможно. Факт независимости распространения световых лучей от наличия (или отсутствия) других лучей устанавливается в следующем законе геометрической оптики.
Закон независимости световых лучей:
- световые лучи распространяются независимо друг от друга.
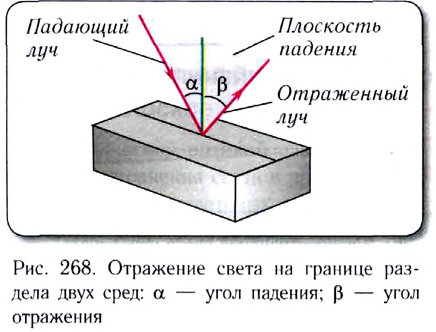
Целый ряд оптических явлений (отражение облаков в воде, отражение предметов в зеркальной или любой полированной поверхности и т. д.) способствовали открытию следующего закона геометрической оптики — закона отражения света (рис. 268):
- угол отражения равен углу падения
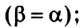
- луч падающий, луч отраженный и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости.
Эксперименты показывают, что существуют два вида отражения света: зеркальное и рассеянное. Поверхность, размеры неровностей которой меньше длины световой волны, называют зеркальной. Лучи света, падающие на такую плоскую поверхность параллельным пучком, после отражения остаются параллельными. Такое отражение называют зеркальным (рис. 269).
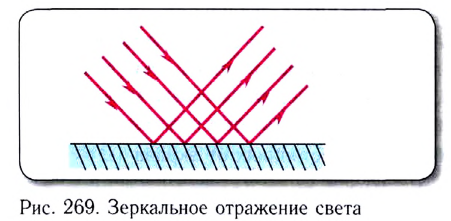
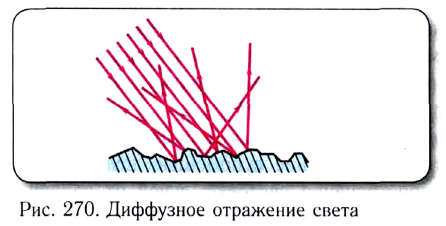
Поверхность, размеры неровностей которой больше длины световой волны, отражает лучи света по всевозможным направлениям и называется шероховатой, а отраженный свет — рассеянным или диффузным (рис. 270).
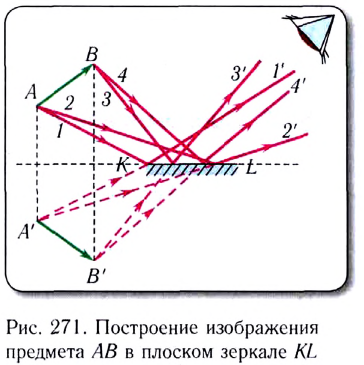
Используя закон отражения света, можно построить изображение предмета АВ в плоском зеркале (рис. 271), представляющем собой плоскую отражающую поверхность. Построив ход лучей 1 и 2 от точки А после отражения от зеркала KL, продолжим их до пересечения в точке А’. Аналогичные построения
сделаем для точки В, найдем ее изображение — точку В’. Глазу наблюдателя будет казаться, что лучи вышли из точек А’ и В’, т. е. оттуда, где будет находиться мнимое изображение А’В’ предмета АВ.
- Заказать решение задач по физике
В оптике изображение называется действительным, если оно образовано самими лучами (т. е. в данную точку поступает световая энергия), если же изображение образовано не самими лучами, а их продолжениями, то говорят, что изображение мнимое (световая энергия не поступает в данную точку).
Изображение называется прямым, если верх и низ изображения ориентированы аналогично самому предмету. Если же изображение перевернуто, то его называют обратным или перевернутым.
Таким образом, изображение предмета в плоском зеркале — мнимое прямое, в натуральную величину. Оно симметрично предмету относительно плоскости зеркала и находится на таком же расстоянии за плоскостью зеркала, как и сам предмет (см. рис. 271).
Преломление света
Изменение направления распространения луча света при прохождении через границу раздела двух сред называется преломлением света.
Для наблюдения данного явления достаточно поместить карандаш в стакан с водой и посмотреть на него со стороны — карандаш будет казаться «надломленным» (преломленным) (рис. 273), оставаясь при этом совершенно целым.

Первые упоминания о преломлении света в воде и стекле встречаются в труде Клавдия Птолемея «Оптика», вышедшего в свет во II в. нашей эры.
Закон преломления света был экспериментально установлен в 1621 г. голландским ученым Виллебродом Снеллиусом и независимо от него теоретически обоснован в 1637 г. Рене Декартом.
Закон преломления световых лучей:
- отношение синуса угла падения
 к синусу угла преломления
к синусу угла преломления 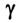 есть величина постоянная для двух данных сред;
есть величина постоянная для двух данных сред; - падающий и преломленный лучи лежат в одной плоскости с перпендикуляром, проведенным в точке падения луча к плоскости границы раздела двух сред
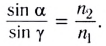
Здесь 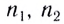 — абсолютные показатели преломления сред.
— абсолютные показатели преломления сред.
Рассмотрим луч, падающий на плоскую границу раздела двух прозрачных сред под некоторым углом 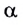 (рис. 274).
(рис. 274).
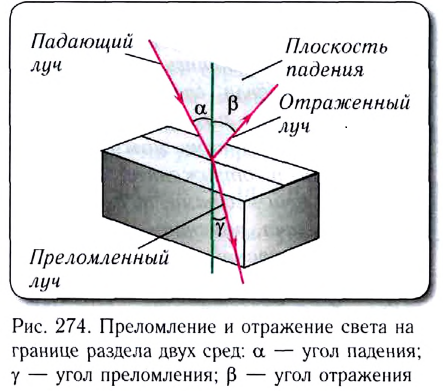
При этом наряду с отраженным лучом будет существовать и преломленный луч. Он распространяется во второй среде под некоторым углом у в соответствии с законом преломления.
Принцип Ферма
Хотя законы геометрической оптики были открыты экспериментально, однако все они (за исключением закона независимости световых лучей) являются следствием принципа «кратчайшего пути» или «минимального времени», сформулированного в 1679 г. французским математиком Пьером Ферма:
распространение света из одной точки среды в другую происходит по траектории, которой соответствует минимальное время по сравнению с другими возможными траекториями.
При помощи этого принципа Ферма вывел закон преломления света. Из этого принципа также следуют законы прямолинейного распространения и отражения света, т. е. принцип Ферма является наиболее общим принципом геометрической оптики.
Действительно, в однородной прозрачной среде, где скорость света постоянна 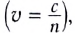 минимальному времени распространения света между двумя точками соответствует движение по прямой, т. е. приходим к закону прямолинейного распространения света.
минимальному времени распространения света между двумя точками соответствует движение по прямой, т. е. приходим к закону прямолинейного распространения света.
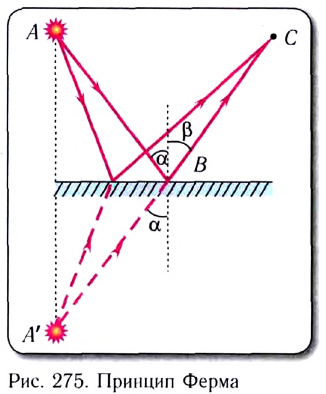
При отражении от плоского зеркала в силу симметрии можем сказать, что сумма |АВ| + |ВС| (рис. 275) будет минимальна в случае, когда 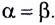 Это как раз и соответствует закону отражения света.
Это как раз и соответствует закону отражения света.
Впервые данный факт геометрически доказал Герон Александрийский (II в. н. э.) задолго до появления принципа Ферма.
Анализируя время распространения луча между двумя точками при преломлении света, можно показать, что принцип Ферма выполняется и в этом случае, т. е. при движении по «траектории» преломления свету потребуется наименьшее время но сравнению с любой другой возможной «траекторией».
Для законов отражения и преломления выполняется принцип обратимости световых лучей:
- луч света, распространяющийся по пути отраженного (преломленного) луча, отразившись в точке О от границы раздела сред, распространяется дальше по пути падающего луча. Иными словами можно менять падающий и отраженный (преломленный) лучи местами, т. е., не изменяя хода луча, поменять направление его распространения.
На границе раздела двух прозрачных сред обычно одновременно с преломлением наблюдается отражение волн.
Согласно закону сохранения энергии сумма энергий отраженной 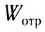 и преломленной
и преломленной 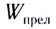 волн равна энергии падающей волны
волн равна энергии падающей волны 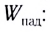
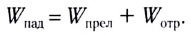
Примерный баланс энергий между отраженной и преломленной волнами приведен на рисунке 276.
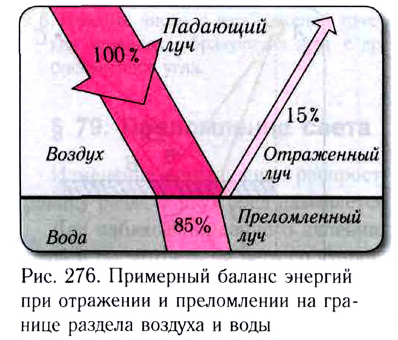
Как следует из закона преломления, при переходе света из оптически более плотной среды I (с большим абсолютным показателем преломления 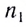 ) в оптически менее плотную среду II (с меньшим показателем преломления
) в оптически менее плотную среду II (с меньшим показателем преломления 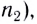 угол преломления
угол преломления 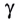 становится больше угла падения
становится больше угла падения 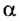 (рис. 277).
(рис. 277).
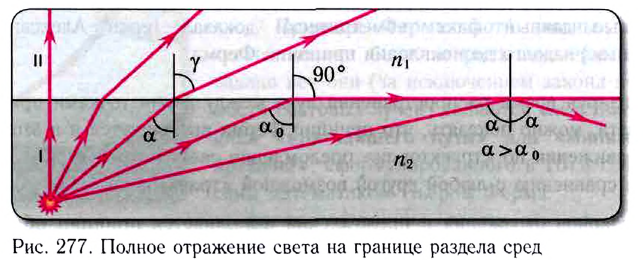
По мере увеличения угла падения, при некотором его значении 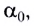 угол преломления станет
угол преломления станет 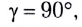 т. е. свет не будет попадать во вторую среду.
т. е. свет не будет попадать во вторую среду.
Энергия преломленной волны при этом станет равной нулю, а энергия отраженной волны будет равна энергии падающей. Следовательно, начиная с этого угла падения вся световая энергия отражается от границы раздела этих сред в среду I.
Это явление называется полным отражением (см. рис. 277). Угол 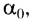 при котором начинается полное отражение, называется предельным углом полного отражения. Он определяется из закона преломления при условии, что угол преломления
при котором начинается полное отражение, называется предельным углом полного отражения. Он определяется из закона преломления при условии, что угол преломления 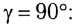
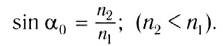
Таким образом, при углах падения, больших 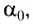 преломленный луч отсутствует.
преломленный луч отсутствует.
Закон преломления света позволяет определять ход лучей в различных оптических системах.
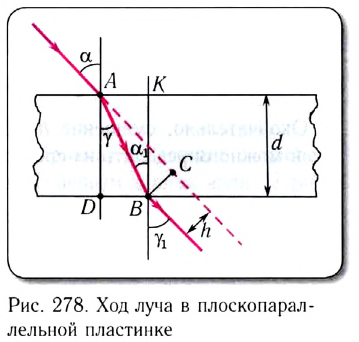
На рисунке 278 показан ход светового луча в плоскопараллельной пластинке толщиной d, находящейся в воздухе. Согласно закону преломления на первой и второй границах раздела для луча, падающего под углом 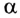 на первую границу,
на первую границу, 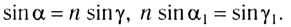
Здесь 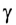 — угол преломления на первой границе,
— угол преломления на первой границе, 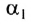 — угол падения луча на вторую границу,
— угол падения луча на вторую границу, 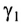 — угол преломления на второй границе, n — показатель преломления вещества пластинки.
— угол преломления на второй границе, n — показатель преломления вещества пластинки.
Накрест лежащие углы 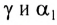 при параллельных прямых AD и ВК — перпендикулярах к первой и второй параллельным границам — равны, т. е.
при параллельных прямых AD и ВК — перпендикулярах к первой и второй параллельным границам — равны, т. е. 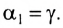 Следовательно,
Следовательно, 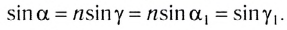 Откуда следует, что
Откуда следует, что 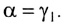
Таким образом, луч света, проходя через плоскопараллельную пластинку, с обеих сторон которой находится одна и та же среда, смещается параллельно своему начальному направлению. Поэтому все предметы, если смотреть на них сквозь прозрачную плоскопараллельную пластинку под углом, не равным нулю, будут казаться смещенными на некоторое расстояние h. Найдем, от каких параметров пластинки зависит это смещение.
Из треугольника АВС следует, что
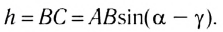
Из треугольника ABD находим
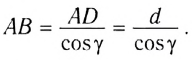
Из этих двух соотношений получаем
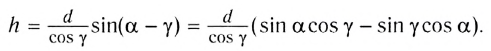
С учетом закона преломления 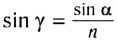 и тригонометрического тождества
и тригонометрического тождества 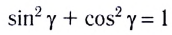 находим
находим 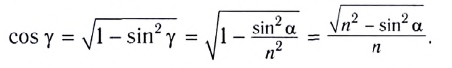
Окончательно, смещение h между направлениями входящего и выходящего лучей можно определить из соотношения
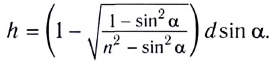
Откуда видно, что h при данном угле падения 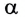 зависит от толщины d пластинки и ее показателя преломления n.
зависит от толщины d пластинки и ее показателя преломления n.
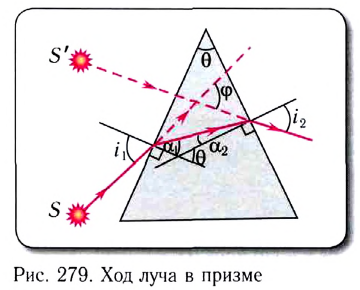
На рисунке 279 показан ход луча через стеклянную призму, находящуюся в воздухе. Грани, через которые проходит луч, называются преломляющими гранями; их ребро — преломляющим ребром, а угол 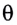 между ними — преломляющим углом призмы. Угол
между ними — преломляющим углом призмы. Угол 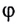 между направлениями входящего и выходящего лучей называется углом отклонения:
между направлениями входящего и выходящего лучей называется углом отклонения:
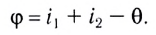
Если угол падения 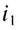 на грань призмы и преломляющий угол призмы
на грань призмы и преломляющий угол призмы 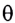 малы, то малыми будут и углы
малы, то малыми будут и углы 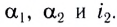 Поэтому в законах преломления отношение синусов можно заменить отношением углов, выраженных в радианах, т. е.
Поэтому в законах преломления отношение синусов можно заменить отношением углов, выраженных в радианах, т. е. 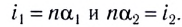 Из геометрических соотношений следует равенство
Из геометрических соотношений следует равенство 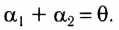 Используя эти соотношения для угла отклонения, находим
Используя эти соотношения для угла отклонения, находим
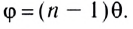
Из последнего равенства следует, что, во-первых, чем больше преломляющий угол 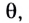 тем больше угол отклонения
тем больше угол отклонения 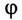 лучей призмой; во-вторых, угол отклонения лучей зависит от показателя преломления вещества призмы. А так как показатель преломления зависит от частоты волны n(v), то при падении на призму белого света он будет разлагаться в спектр.
лучей призмой; во-вторых, угол отклонения лучей зависит от показателя преломления вещества призмы. А так как показатель преломления зависит от частоты волны n(v), то при падении на призму белого света он будет разлагаться в спектр.
Знание наименьшего угла отклонения лучей призмой  позволяет определить показатель преломления вещества, из которого она изготовлена:
позволяет определить показатель преломления вещества, из которого она изготовлена:
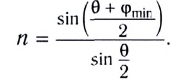
Направив пучок лучей белого света на призму, мы обнаружим его сложную структуру: на экране за призмой появится радужная полоска — спектр (рис. 280).

Образование спектра обусловлено тем, что призма, вследствие дисперсии, по-разному преломляет лучи, соответствующие различным длинам волн. Порядок следования лучей в спектре легко запомнить с помощью известной фразы:
- красный — 770—630 нм каждый
- oранжевый — 630—590 нм охотник
- желтый — 590—570 нм желает
- зеленый — 570—495 нм знать.
- голубой, синий — 495—435 нм где сидят
- фиолетовый — 435—390 нм фазаны
Явление дисперсии совместно с полным отражением приводит к образованию радуги, вследствие преломления солнечных лучей на мельчайших водяных капельках во время дождя, к нежелательному «окрашиванию» изображений в оптических системах (хроматическая аберрация) и т. д.
Линза. Построение изображения в линзах
Линза называется собирающей, если после преломления в ней параллель-ный пучок становится сходящимся. Если же после преломления в линзе параллельный пучок становится расходящимся, то линза называется рассеивающей.
Как известно, плоское зеркало даст мнимое изображение предмета в натуральную величину. Однако для практических нужд чаще необходимы изображения увеличенные или уменьшенные. Эта задача решается с помощью линз (или криволинейных зеркал).
Линза представляет собой прозрачное тело, ограниченное с двух сторон криволинейными поверхностями. Чаще всего применяются линзы с поверхностями, имеющими сферическую форму (сферические сегменты).
По форме ограничивающих поверхностей различают шесть типов линз. На рисунке 281, а. б показаны условные обозначения линз и типы линз.
Отметим условия, при одновременном выполнении которых линза является собирающей:
- толщина в центре больше толщины у краев;
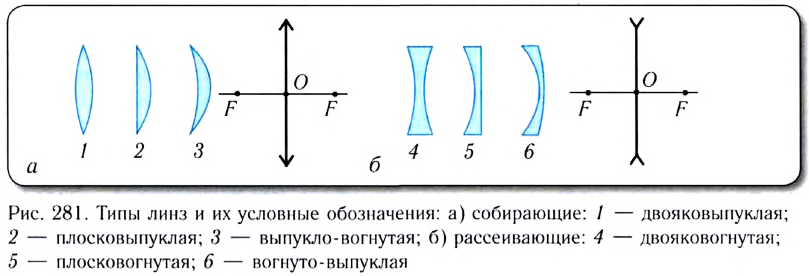
- ее показатель преломления больше показателя преломления окружающей среды.
При невыполнении (или выполнении) только одного из этих условий линза является рассеивающей.
Линза считается тонкой, если ее толщина в центре намного меньше радиусов ограничивающих ее поверхностей. Тонкая линза дает неискаженное изображение только в том случае, если свет монохроматический и предмет достаточно мал, следовательно, лучи распространяются вблизи главной оптической оси. Такие лучи получили название параксиальных.
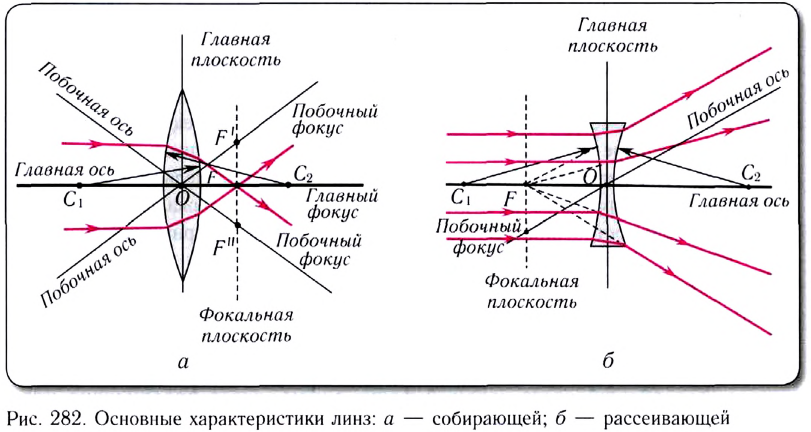
Рассмотрим основные характеристики линзы (рис. 282, а, б).
Прямая линия, на которой лежат центры 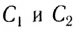 обеих сферических поверхностей линзы, называется главной оптической осью.
обеих сферических поверхностей линзы, называется главной оптической осью.
Точка О линзы, проходя через которую луч не преломляется, называется оптическим центром.
Прямая линия, проходящая через оптический центр линзы, не совпадающая с главной оптической осью, называется побочной оптической осью. Каждая линза имеет только одну главную оптическую ось и бесконечно много побочных осей.
Плоскость, проходящая через оптический центр тонкой линзы перпендикулярно главной оптической оси, называют главной плоскостью линзы.
Точка, в которую собирается параксиальный пучок света после преломления в линзе, распространяющийся параллельно главной оптической оси, называется главным фокусом F линзы. Расстояние OF от оптического центра линзы до се главного фокуса называется фокусным расстоянием линзы.
Плоскость, проходящая через главный фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. Фокальная плоскость собирающей линзы является геометрическим местом точек, в которых пересекаются параллельные лучи, падающие на линзу под любым углом к главной оптической оси.
Пучок света, направленный на собирающую линзу параллельно побочной оптической оси, собирается в побочном фокусе, лежащем в фокальной плоскости.
Обычно для построений в линзах используют три характерных (стандартных) луча (рис. 283, а, б):
- луч, идущий через оптический центр О линзы, не испытывает преломления;
- луч, параллельный главной оптической оси линзы, после преломления проходит через ее главный фокус;
- луч, проходящий через главный фокус линзы, после преломления идет параллельно главной оптической оси.
Для построения изображения в линзе достаточно построить ход двух лучей от каждой точки предмета. Изображение находится в месте пересечения лучей после преломления на поверхностях линзы (действительное изображение) или в месте пересечения продолжений лучей (мнимое изображение).
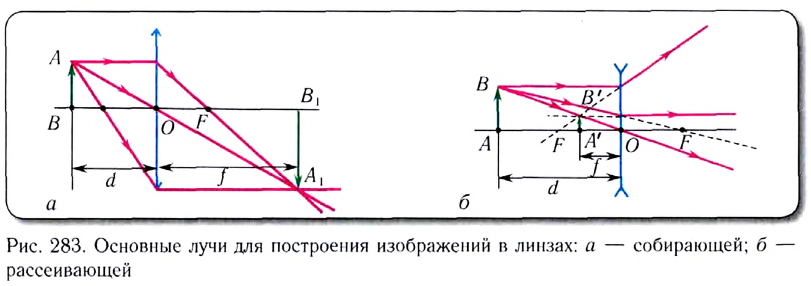
В зависимости от типа линзы и расстояния до нее можно получать изображения: увеличенные и уменьшенные, прямые и обратные (перевернутые), действительные и мнимые (рис. 284).
Все приведенные примеры построений относились к предметам, которые имели определенные размеры. А как найти построением положение изображения точечного источника света, находящегося на главной оптической оси?
Для этого необходимы два любых луча, один из которых — самый простой, — проходящий не преломляясь через оптический центр линзы. Для построения хода другого пользуются побочной оптической осью. Рассмотрим точечный источник, находящийся на главной оптической оси собирающей линзы (рис. 285). Проведем из точки S произвольный луч SA. Для того чтобы найти ход луча после преломления в линзе, проведем побочную оптическую ось 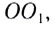 параллельную лучу SA. Нарисуем сечение KL фокальной плоскости линзы.
параллельную лучу SA. Нарисуем сечение KL фокальной плоскости линзы.
Точка пересечения побочной оптической оси 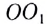 с фокальной плоскостью KL является побочным фокусом
с фокальной плоскостью KL является побочным фокусом 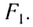 Следовательно, луч SA, преломившись в линзе, должен пройти через побочный фокус
Следовательно, луч SA, преломившись в линзе, должен пройти через побочный фокус 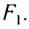 Продлевая прямую
Продлевая прямую  до пересечения с главной оптической осью, находим точку
до пересечения с главной оптической осью, находим точку  которая является изображением точечного источника S.
которая является изображением точечного источника S.
Положение изображения точечного источника, находящегося на главной оптической оси рассеивающей линзы, найдите построением самостоятельно.
Формула тонкой линзы
Между расстояниями от предмета до линзы и от линзы до изображения существует определенная зависимость от фокусного расстояния линзы, называемая формулой линзы.
Выведем формулу тонкой линзы из геометрических соображений, рассматривая ход характерных лучей (рис. 289).
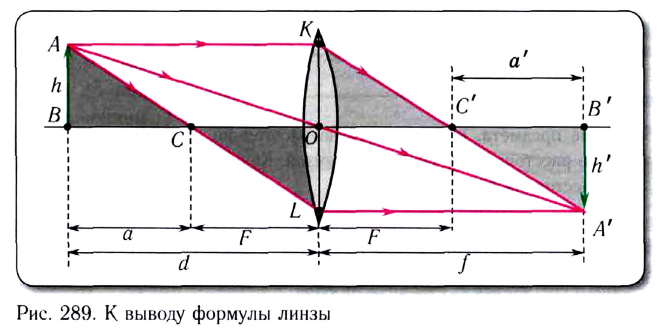
Пусть расстояние от предмета АВ до линзы d, расстояние от линзы до изображения АВ f, фокусное расстояние линзы F, расстояние от предмета до левого фокуса а, расстояние от изображения до правого фокуса а’.
Из рисунка видно, что 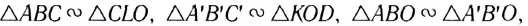 следовательно,
следовательно,
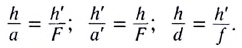
Поперечным увеличением Г называется отношение линейного размера изображения h’ к линейному размеру предмета h:

Из соотношения (I) следует формула Ньютона: 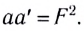
С учетом того, что 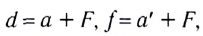 получаем формулу линзы:
получаем формулу линзы:

В 1604 г. в исследовании «Дополнения к Вителло» Кеплер изучал прелом-ление света в линзах различной конфигурации и для малых углов падения пришел к формуле линзы.
Для практического использования формулы линзы следует твердо запомнить правило знаков:
в случае собирающей линзы действительных источника и изображения величины F, d, f считают положительными; в случае рассеивающей линзы мнимых источника и изображения величины F, d, f считают отрицательными.
Заметим, что предмет или источник является мнимым только в том случае, если на линзу падает пучок сходящихся лучей.
Таким образом, линза с F>0 является собирающей (положительной), а с F<0 — рассеивающей (отрицательной).
Величина, обратная фокусному расстоянию линзы, выраженному в метрах, называется ее оптической силой:

Единица оптической силы — диоптрия (1 дптр).
Одна диоптрия соответствует оптической силе линзы с фокусным расстоянием один метр: 1 дптр= 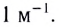
Оптическая сила линзы зависит от свойств окружающей среды (вспомните, как плохо мы видим под водой без плавательных очков).
Современные оптические приборы для улучшения качества изображений используют системы линз. Оптическая сила D системы тонких линз, сложенных вплотную, равна сумме их оптических сил 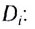
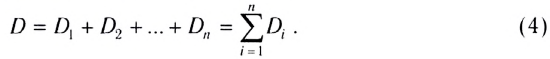
Оптические приборы: лупа, мультимедийный проектор, фотоаппарат
Познакомимся с простейшими оптическими приборами, широко используемыми человеком.
Лупа — оптический прибор (собирающая линза), позволяющий увеличить угол зрения (т. е. увеличить мелкие детали предметов).
Лупа представляет собой короткофокусную линзу (F от 10 мм до 100 мм), которая располагается между глазом и предметом (рис. 290).
Мнимое увеличенное изображение предмета получается на расстоянии наилучшего зрения — 25 см для нормального глаза (или на бесконечности). Таким образом, изображение предмета рассматривается глазом практически без напряжения.
Видимое увеличение, даваемое лупой:
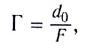 где
где 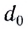 — расстояние наилучшего зрения, F — фокусное расстояние лупы.
— расстояние наилучшего зрения, F — фокусное расстояние лупы.
Вследствие того, что 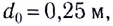 м, лупы имеют увеличение от 2,5 до 25 раз (рис. 291).
м, лупы имеют увеличение от 2,5 до 25 раз (рис. 291).
Лупы с увеличением Г > 40 не применяются из-за сильных искажений изображения или малости обзора.

Мультимедийный (лазерный) проектор (рис. 292) — оптическое устройство, с помощью которого на экране получают действительное (прямое или обратное) увеличенное изображение, «снятое» с экрана компьютера, телевизора или других источников видеосигнала.
Для формирования изображения в мультимедиа-проекторах используются различные базовые технологии: жидкокристаллическая технология, технология цифровой обработки света или технология формирования цифровых изображений методом отражения.
При формировании цифрового изображения методом отражения источник света 1 при помощи разделяющих призм 2 освещает оптическую матрицу с изображением 3 и при помощи системы проекционных линз 4 передает увеличенное изображение на экран 5 (рис. 293).
Популярность мультимедийных проекторов обусловлен их универсальностью, поскольку помимо компьютерного изображения они поддерживают практически вес существующие стандарты видеозаписей, а также полностью совместимы с форматом телевидения высокой четкости.
Мультимедиа-проекторы активно работают на научных конференциях, вы-
семинарах и т. д., поскольку по размерам изображения и по возможностям его настройки с ними не способны конкурировать ни телевизоры, ни плазменные панели.
Так, например, мультимедиа-проекторы позволяют осуществить обратную проекцию или проекцию изображения на просветный экран, при которой зрители и проекционное оборудование находятся по разные стороны экрана. При такой установке проектора докладчик может находиться непосредственно перед экраном, не заслоняя собой проекцию, а освещение в помещении не так сильно влияет на качество изображения.
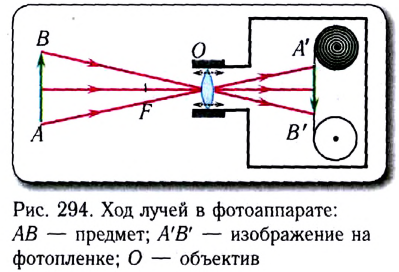
Фотоаппарат (рис. 294) — прибор, предназначенный для получения действительных уменьшенных обратных изображений предметов на фотопленке. При этом предметы могут быть расположены на различном удалении от точки съемки.
Фотоаппарат состоит из закрытой светонепроницаемой камеры и системы линз, называемых объективом (О). С помощью перемещения объектива добиваются наводки на резкость, при которой изображение предмета АВ формируется на фотопленке. В противном случае изображение А’В’ получается нечетким (размытым). Количество световой энергии, поступающей на пленку, определяется размерами диафрагмы и временем открытия затвора (выдержкой).
Сегодня на смену пленочным приходят электронные (цифровые) фотокамеры, в которых изображение записывается не на фотопленку, а на специальный чувствительный элемент (матрицу), с которого информация считывается и хранится в электронном (цифровом) виде, как в памяти компьютера. К достоинствам электронных камер можно отнести возможность «мгновенного» просмотра сделанной фотографии, восстановление ресурсов памяти после переписывания информации в компьютер, высокий темп съемки (10 и более кадров в секунду).
Зрение человека не в состоянии фиксировать очень быстрые и очень медленные изменения положения объекта. Фотоаппарат благодаря возможности фотографировать с различными выдержками от тысячных долей секунды до нескольких секунд позволяет хронометрировать события, визуально «неулавливаемые».
Глаз, очки
Основную часть информации (примерно 90 %) об окружающем мире мы получаем с помощью органов зрения.
Глаз представляет собой сложную оптическую систему, подобную фотоаппарату (рис. 295).
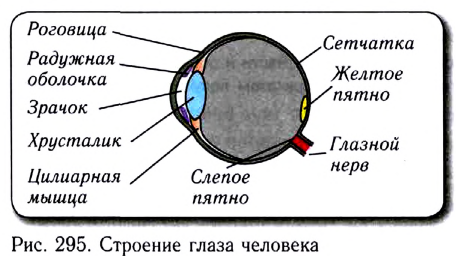
Преломляющая система глаза подобна объективу фотоаппарата, а сетчатка — фоточувствительному слою фотопленки.
У глаза имеется радужная оболочка (окрашенная часть глаза), которая играет роль диафрагмы и автоматически регулирует количество попадающего в глаз света. Зрачок — отверстие в радужной оболочке, через которое проходит свет.
Сетчатка играет роль светочувствительной пленки, находится на задней поверхности глаза. Она состоит из «палочек» (нервные волокна) и «колбочек»
(рецепторы), которые преобразуют световую энергию в электрические сигналы, распространяющиеся по нервным волокнам. Днем свет воспринимается колбочками, а ночью — палочками. Днем мы отчетливо видим мелкие предметы и различаем их цвет. Слабо освещенные предметы (например, ночью) мы видим только в черно-белых тонах (бесцветными). Недаром говорят, что «ночью все кошки серы». Желтое пятно — область диаметром около 0,25 мм — находится в центре сетчатой оболочки, в которой достигается особая острота зрения и наиболее четко различаются цвета. Слепое пятно — место входа глазного нерва — это область сетчатки, которая не участвует в формировании изображения. Роговица — служит предохранительным покрытием и является первой поверхностью, преломляющей свет. Хрусталик — это эластичное линзоподобное тело, которое осуществляет настройку нашего зрения на различные расстояния. В оптической системе глаза фокусировка изображения на сетчатку называется аккомодацией (от латинского слова commodus — удобный). У человека аккомодация происходит за счет увеличения или уменьшения выпуклости хрусталика, которое осуществляется с помощью цилиарных мышц. При этом изменяется оптическая сила глаза.
Точка, видимая глазом при расслабленной цилиарной мышце, называется дальней точкой, а точка, видимая при максимальном напряжении этой мышцы, — ближней точкой.
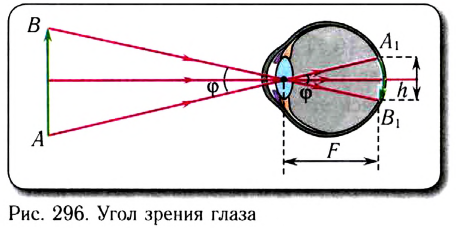
Расстояние наилучшего зрения — это расстояние от предмета до глаза, при котором глаз не устает и угол зрения достаточно велик. Размер изображения на сетчатке (рис. 296) определяется углом зрения 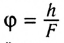 с вершиной в оптическом центре глаза и лучами, направленными на крайние точки предмета.
с вершиной в оптическом центре глаза и лучами, направленными на крайние точки предмета.
От бесконечно удаленного предмета в глаз попадает пучок параллельных лучей. В этом случае 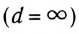 аккомодации не требуется. Если предмет приближается, то лучи становятся расходящимися. Для того чтобы сделать их снова параллельными, необходимо изменить оптическую силу глаза так, чтобы его фокусное расстояние совпало с расстоянием до предмета, т. е. F=d. В этом случае оптическая система глаза соберет параллельные лучи на сетчатке.
аккомодации не требуется. Если предмет приближается, то лучи становятся расходящимися. Для того чтобы сделать их снова параллельными, необходимо изменить оптическую силу глаза так, чтобы его фокусное расстояние совпало с расстоянием до предмета, т. е. F=d. В этом случае оптическая система глаза соберет параллельные лучи на сетчатке.
Оптическую силу аккомодационной добавки или аккомодации найдем из условия
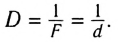
Зрение человека с нормальным зрением характеризуется понятием «нормальный глаз», т. е. расстояние наилучшего зрения около 25 см, а предел зрения (дальняя точка) находится на бесконечности.
Для нормального глаза преломляющая сила хрусталика без аккомодации D= 19,11 дптр, а при максимальной аккомодации —  = 33,06 дптр; оптическая сила всего глаза, соответственно, D = 58,64 дптр и
= 33,06 дптр; оптическая сила всего глаза, соответственно, D = 58,64 дптр и  = 70,57 дптр. Пользуясь этими данными, можно определить минимальное расстояние, на котором нормальный глаз еще может ясно видеть предмет. Максимально возможная аккомодация обеспечивает изменение оптической силы нормального глаза на
= 70,57 дптр. Пользуясь этими данными, можно определить минимальное расстояние, на котором нормальный глаз еще может ясно видеть предмет. Максимально возможная аккомодация обеспечивает изменение оптической силы нормального глаза на 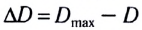 = 11,93 дптр. Этому изменению оптической силы соответствует минимальное расстояние
= 11,93 дптр. Этому изменению оптической силы соответствует минимальное расстояние 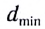 = 8,4 см. Следует отметить, что такая аккомодация возможна только в молодости (до 20 лет).
= 8,4 см. Следует отметить, что такая аккомодация возможна только в молодости (до 20 лет).
С возрастом возможность аккомодации быстро уменьшается в основном из-за уплотнения хрусталика, теряющего способность достаточно сжиматься. Пожилой человек не может отчетливо видеть близкие предметы, а также различать буквы в газетах и книгах. К пятидесяти годам расстояние наилучшего зрения увеличивается в среднем до 50 см.
С возрастом, по болезни или при несоблюдении гигиены могут появиться дефекты зрения. Два наиболее распространенных дефекта — близорукость и дальнозоркость.
Близорукость (миопия) — дефект зрения, при котором глаз видит удаленные предметы не резко, а расплывчато (предел зрения не равен бесконечности). Изображения предметов при этом не попадают на сетчатку глаза, а фокусируются перед ней (точка М на рис. 297, а). Для исправления этого дефекта зрения используют очки с рассеивающими линзами (рис. 297, б). Поскольку оптическая сила этих линз отрицательна, то в повседневной жизни такие очки называют отрицательными.
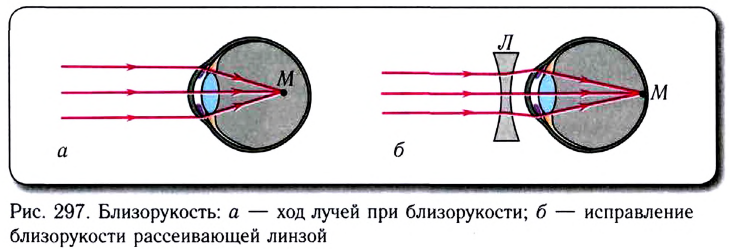
Дальнозоркость (гиперопия) — дефект зрения, при котором глаз не в состоянии видеть резко близкие объекты, хотя удаленные предметы он видит хорошо. Изображения предметов при дальнозоркости получаются за сетчаткой (точка Р на рис. 298, а), и для коррекции зрения необходимо применять собирающие линзы (рис. 298, б), оптическая сила которых положительна (положительные очки).
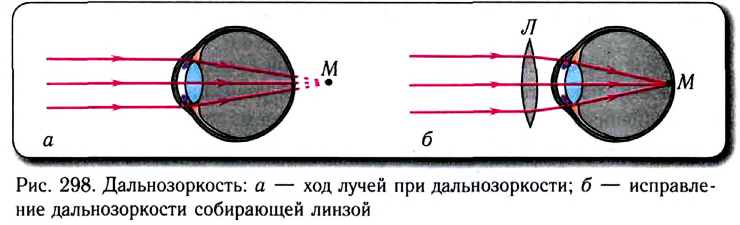
Оптические явления в атмосфере
Атмосфера нашей планеты представляет собой достаточно интересную оптическую систему, показатель преломления которой уменьшается с высотой вследствие уменьшения плотности воздуха. Таким образом, земную атмосферу можно рассматривать как «линзу» гигантских размеров, повторяющую форму Земли и имеющую монотонно изменяющийся показатель преломления.
Это обстоятельство приводит к появлению целого ряда оптических явлений в атмосфере, обусловленных преломлением (рефракцией) и отражением (реф-лекцией) лучей в ней.
Рассмотрим некоторые наиболее существенные оптические явления в атмосфере.
Атмосферная рефракция — явление искривления световых лучей при прохождении света через атмосферу.
С высотой плотность воздуха (значит, и показатель преломления) убывает. Представим себе, что атмосфера состоит из оптически однородных горизонтальных слоев, показатель преломления в которых меняется от слоя к слою (рис. 299).
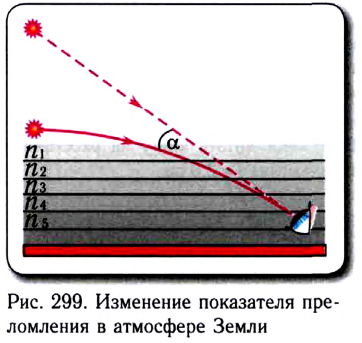
При распространении светового луча в такой системе он будет в соответствии с законом преломления «прижиматься» к перпендикуляру к границе слоя. Но плотность атмосферы уменьшается не скачками, а непрерывно, что приводит к плавному искривлению и повороту луча на угол а при прохождении атмосферы.
В результате атмосферной рефракции мы видим Луну, Солнце и другие звезды несколько выше того места, где они находятся на самом деле.
По этой же причине увеличивается продолжительность дня (в наших широтах на 10—12 мин), сжимаются диски Луны и Солнца у горизонта. Интересно, что максимальный угол рефракции составляет 35′ (для объектов у линии горизонта), что превышает видимый угловой размер Солнца (32′).
Из этого факта следует: в тот момент, когда мы видим, что нижний край светила коснулся линии горизонта, на самом деле солнечный диск находится уже под горизонтом (рис. 300).
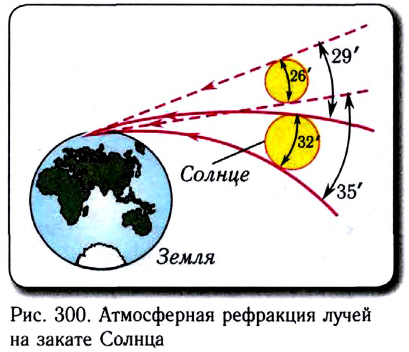
Мерцание звезд также связано с астрономической рефракцией света. Давно было подмечено, что мерцание наиболее заметно у звезд, находящихся вблизи линии горизонта. Воздушные потоки в атмосфере изменяют плотность воздуха с течением времени, что приводит к кажущемуся мерцанию небесного светила. Космонавты, находящиеся на орбите, никакого мерцания не наблюдают.
В жарких пустынных или степных районах и в полярных областях сильный прогрев или охлаждение воздуха у земной поверхности приводит к появлению миражей: благодаря искривлению лучей становятся видимыми и кажутся близко расположенными предметы, которые на самом деле расположены далеко за горизонтом.
Иногда подобное явление называется земной рефракцией. Возникновение миражей объясняется зависимостью показателя преломления воздуха от температуры. Различают нижние и верхние миражи.
Нижние миражи можно увидеть в жаркий летний день на хорошо прогретой асфальтовой дороге: нам кажется, что впереди на ней есть лужи, которых на самом деле нет. В данном случае мы принимаем за «лужи» зеркальное отражение лучей от неоднородно разогретых слоев воздуха, находящихся в непосредственной близости от «раскаленного» асфальта.
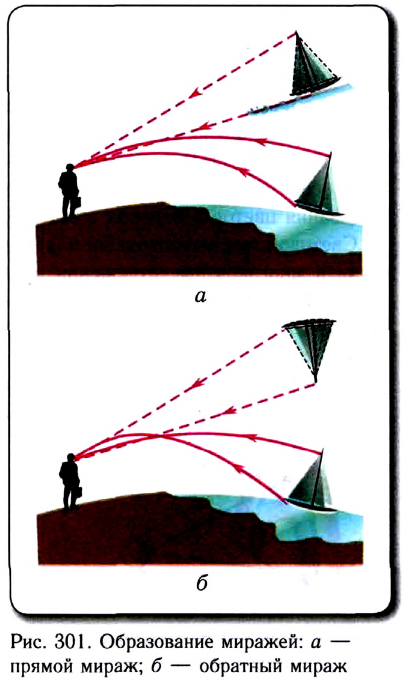
Верхние миражи отличаются значительным разнообразием: в одних случаях они дают прямое изображение (рис. 301, а), в других — перевернутое (рис. 301, б), могут быть двойными и даже тройными. Эти особенности связаны с различными зависимостями температуры воздуха и показателя преломления от высоты.
Атмосферные осадки приводят к появлению в атмосфере эффектных оптических явлений. Так, во время дождя удивительным и незабываемым зрелищем является образование радуги, которое объясняется явлением различного преломления (дисперсии) и отражения солнечных лучей на мельчайших капельках в атмосфере (рис. 302).
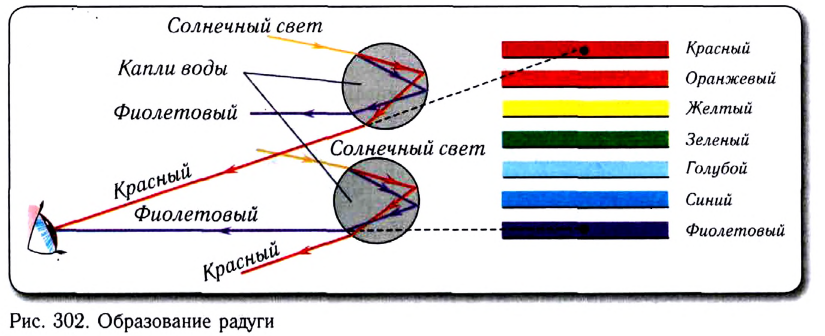
В особо удачных случаях мы можем увидеть сразу несколько радуг, порядок следования цветов в которых взаимообратен.
Световой луч, участвующий в формировании радуги, испытывает два преломления и многократные отражения в каждой дождевой капле. В данном случае, несколько упрощая механизм образования радуги, можем сказать, что сферические дождевые капельки играют роль призмы в опыте Ньютона по разложению света в спектр.
Вследствие пространственной симметрии радуга видна в виде полуокружности с углом раствора около 42°, при этом наблюдатель (рис. 303) должен находиться между Солнцем и каплями дождя, спиной к Солнцу.
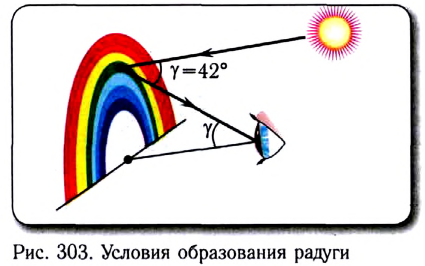
Преломление света в кристалликах льда, сопровождающееся разложением в спектр, приводит к появлению сравнительно редкого и не менее красивого оптического явления гало (рис. 304).

Гало проявляется в виде кругов (иногда столбов, крестов) вокруг Солнца и Луны. Для появления яркого гало необходимо достаточное количество ледяных кристаллов правильной формы.
Разнообразие цветов в атмосфере объясняется закономерностями рассеяния света на частичках различных размеров. Вследствие того, что синий цвет рассеивается сильнее, чем красный, — днем, когда Солнце находится высоко над горизонтом, мы видим небо голубым. По этой же причине вблизи линии горизонта становится красным и не таким ярким, как в зените. Появление цветных облаков также связано с рассеянием света на частичках различных размеров в облаке.
Основные формулы в геометрической оптике
Предельный угол полного отражения:
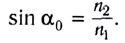
Формула тонкой линзы:
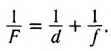
Оптическая сила линзы:
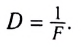
Поперечное увеличение:
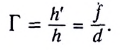
- Фотометрия и световой поток
- Освещенность в физике
- Закон прямолинейного распространения света
- Законы отражения света
- Оптические приборы в физике
- Оптика в физике
- Волновая оптика в физике
- Квантовая оптика в физике
В
данной теме будет рассмотрен один из важнейших законов геометрической оптики –
закон отражения света.
Задача
1.
Два луча падают на зеркало. Угол падения первого луча равен 40º, а угол
падения второго луча равен 60º. Найдите соответствующие углы отражения и
постройте чертёж для каждого случая.
|
ДАНО: |
РЕШЕНИЕ Согласно |
|
|
Задача
2.
Солнечные
лучи составляют угол 32º с горизонтом. На рисунке указан колодец и
зеркало. Под каким углом к вертикали нужно расположить зеркало, чтобы солнечный
луч попал на дно колодца?
|
ДАНО: |
РЕШЕНИЕ Из Угол Закон |
|
|
Ответ:
29º.
Задача
3. Когда
плоское зеркало повернули на некоторый угол вокруг оси, лежащей в плоскости
зеркала, отражённый луч повернулся на 40º. На какой угол повернули
зеркало, если известно, что направление падающего луча не изменилось?
|
ДАНО: |
РЕШЕНИЕ Пусть По Допустим, По Из А По Тогда |
|
|
Ответ:
20º.
Задача
4.
Два луча падают на плоское зеркало в точках A
и B. Угол падения первого
луча равен 45º, а угол падения второго луча равен 60º. Известно, что
расстояние между точками A
и B составляет 10 см.
Найдите расстояние от точки A
до точки пересечения отражённых лучей.
|
ДАНО: |
РЕШЕНИЕ Возможно Первый Из Рассмотрим Из Рассмотрим По Тогда |
|
|
Ответ:
27,3
см.
Закон отражения света: определение, формула, применение
Определение.
Закон отражения света имеет следующее определение: угол отражения равен углу падения. Падающий и отраженный лучи и перпендикуляр к поверхности зеркала в точке падения лежат в одной плоскости. Более подробно о физическом смысле закона и о том на базе чего он был сформулирован читайте далее в этой статье.
Небольшое вступление.
Если вы не знаете, что находится по ту сторону зеркала, спросите физика! Он скажет вам, что вы найдете там не перевернутую копию нашего мира, а другой, столь же загадочный мир физики. Он произнесет множество благозвучных физических названий, таких как видимый образ, закон отражения и луч света.
Хотя сегодня мы не можем представить себе жизнь без зеркал, или плоских стеклянных зеркал, их история не особенно длинна. Однако само явление отражения, благодаря которому зеркала могут существовать и работать, известно уже много веков и не менее увлекательно, чем они сами.
Явление отражения света
Проведите наблюдение, которое позволит вам понять механизм формирования изображения при отражении световых лучей, как вы это наблюдаете на поверхности зеркала или поверхности воды.
Что вам понадобится?
- зеркало без рамы;
- фонарик с сильным светом (он может быть встроенным в телефон);
- расчёска;
- лист бумаги;
- линейка;
- карандаш;
- широкий пластырь или серебристая изоляционная лента.
Инструкция.
- Нанесите ленту на зубья расчески так, чтобы в середине остались один или два зазора.
- На листе бумаги проведите линию, перпендикулярную длинному краю бумаги.
- На тот же край листа бумаги, лежащего на столе, вертикально положите отражающую сторону зеркала.
- Положите расческу на стол вдоль длинного края бумаги напротив зеркала так, чтобы кончики зубцов были перпендикулярны столешнице.
- Осветите расческу, чтобы один или два луча света прошли через незапечатанные щели.
- Осветите зеркало так, чтобы свет фонарика падал на точку, где нарисованная линия пересекается с поверхностью зеркала.
- Изменяйте угол освещения зеркала, располагая расческу под разными углами к листу бумаги — всегда держите фонарик так, чтобы свет падал на расческу перпендикулярно.
- Что происходит с лучом света, отраженным от зеркала?
Подведём итог эксперимента.
Для того чтобы избежать двусмысленности в описании наблюдаемого нами явления, следует сначала выучить определения нескольких терминов.
В физике все гладкие поверхности, отражающие свет, называются зеркалами. Линия, перпендикулярная поверхности зеркала, называется нормалью. Свет фонаря падал в точку, где перпендикуляр (нормаль) пересекался с поверхностью зеркала. Угол между падающим лучом и перпендикуляром называется углом падения. Падающий луч отражается от поверхности зеркала, и получается отраженный луч. Угол между отраженным лучом и перпендикуляром называется углом отражения.
Наблюдения показали, что изменение угла, под которым свет фонаря падает на зеркало после прохождения через расчёску, влечет за собой изменение угла, под которым отражается падающий свет. Когда угол падения увеличивается, угол его отражения также увеличивается; когда он уменьшается, угол отражения также уменьшается.
Закона отражения света
Изменяя угол падения, мы одновременно изменяем угол отражения. Угол падения и угол отражения вместе с перпендикуляром лежат в одной плоскости и равны друг другу.
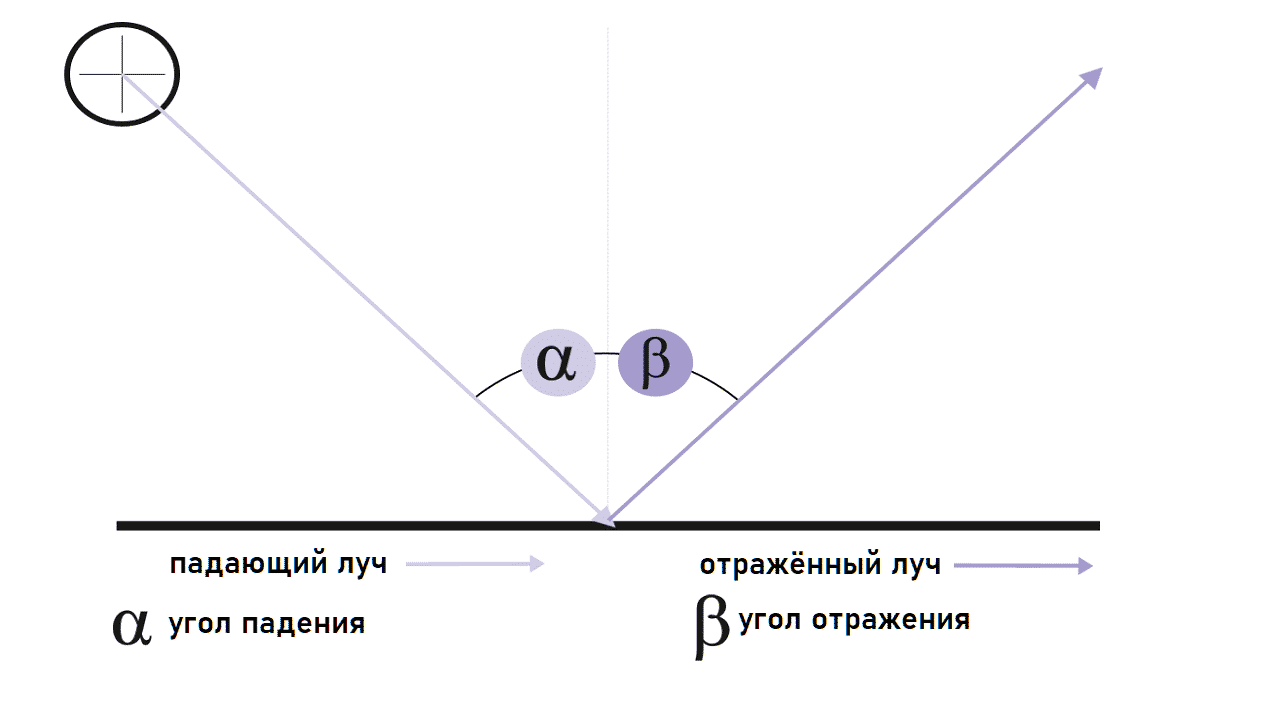 Иллюстрация закона отражения света
Иллюстрация закона отражения света
Формулировка закона и его формула.
Закон отражения света гласит так: угол отражения равен углу падения. Падающий и отраженный лучи и перпендикуляр к поверхности зеркала в точке падения лежат в одной плоскости.
В виде формулы закон отражения света записывается следующим образом: ∠ α = ∠ β.
Применение
Закон отражения используется во многих оптических системах. Повседневное значение имеют применения, описанные ниже.
Закон отражения используется для всех типов зеркал (плоские зеркала, вогнутые зеркала, выпуклые зеркала, параболические зеркала) и их применения (например, фары, фонари, косметические зеркала).
Он также используется для светоотражателей, которые должны быть установлены, например, на велосипедах. Они имеют гладкие стеклянные или пластиковые поверхности снаружи и множество маленьких призм внутри, на которых свет отражается таким образом, что выходит в том же направлении, откуда вошел. Поэтому велосипеды, находящиеся точно по направлению движения автомобиля, могут быть распознаны в темноте гораздо раньше, чем это было бы возможно без дополнительного оснащения светоотражателями.
Также закон отражения должен соблюдаться и в других местах. Гладкая поверхность воды отражает свет. И в тоже время, отражение тел видно на поверхности воды.
В помещениях, освещаемых сфокусированными прожекторами — например, на сцене театра — установка больших стеклопакетов может быть запрещена строительными нормами. Это связано с тем, что стекла воспринимаются только в том случае, если глаз смотрит на отраженный луч света. Для всех остальных людей существует опасность столкнуться со стеклом. В музеях, где много стеклянных витрин с точечным освещением, можно неоднократно наблюдать, как гости ударяются головой о стеклянную обшивку, потому что не заметили само стекло. Поэтому комнаты с большим количеством стеклянных витрин должны иметь рассеянное освещение.
Обратимость световых лучей
Световые пути обычно обратимы. Что это значит, показано на двух рисунках на рис. 2 на простом примере.
В левом изображении на рис. 2 свет исходит слева и отражается от зеркала. Читая угловую шкалу, можно увидеть, что закон отражения выполняется.
В правом изображении на рис. 2 луч света падает на зеркало точно с того направления, в котором луч света был отражен ранее. Вы видите, что теперь отраженный луч света проходит точно там же, где раньше проходил луч падающего света: поэтому путь света является обратимым.
Обратимость светового пути является важным основным принципом геометрической оптики, а также применима к гораздо более сложным явлениям, например, к преломлению света на воде.
Законы отражения света
На границе раздела двух различных сред, если эта граница раздела значительно превышает длину волны, происходит изменение направления распространения света: часть световой энергии возвращается в первую среду, то есть отражается, а часть проникает во вторую среду и при этом преломляется. Луч АО носит название падающий луч, а луч OD – отраженный луч (см. рис. 1.3). Взаимное расположение этих лучей определяют законы отражения и преломления света.
Рис. 1.3. Отражение и преломление света.
Угол α между падающим лучом и перпендикуляром к границе раздела, восстановленным к поверхности в точке падения луча, носит название угол падения.
Угол γ между отражённым лучом и тем же перпендикуляром, носит название угол отражения.
Каждая среда в определённой степени (то есть по своему) отражает и поглощает световое излучение. Величина, которая характеризует отражательную способность поверхности вещества, называется коэффициент отражения. Коэффициент отражения показывает, какую часть принесённой излучением на поверхность тела энергии составляет энергия, унесённая от этой поверхности отражённым излучением. Этот коэффициент зависит от многих причин, например, от состава излучения и от угла падения. Свет полностью отражается от тонкой плёнки серебра или жидкой ртути, нанесённой на лист стекла.
Законы отражения света
| 1 | Падающий луч, отражающий луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. |
| 2 | Угол отражения γ равен углу падения α : |
Законы отражения света были найдены экспериментально ещё в 3 веке до нашей эры древнегреческим учёным Евклидом. Также эти законы могут быть получены как следствие принципа Гюйгенса, согласно которому каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Волновая поверхность (фронт волны) в следующий момент представляет собой касательную поверхность ко всем вторичным волнам. Принцип Гюйгенса является чисто геометрическим.
На гладкую отражательную поверхность КМ (рис. 1.4) падает плоская волна, то есть волна, волновые поверхности которой представляют собой полоски.
Рис. 1.4. Построение Гюйгенса.
А1А и В1В – лучи падающей волны, АС – волновая поверхность этой волны (или фронт волны).
Пока фронт волны из точки С переместится за время t в точку В, из точки А распространится вторичная волна по полусфере на расстояние AD = CB, так как AD = vt и CB = vt, где v – скорость распространения волны.
Волновая поверхность отражённой волны – это прямая BD, касательная к полусферам. Дальше волновая поверхность будет двигаться параллельно самой себе по направлению отражённых лучей АА2 и ВВ2.
Прямоугольные треугольники ΔАСВ и ΔADB имеют общую гипотенузу АВ и равные катеты AD = CB. Следовательно, они равны.
Углы САВ = = α и DBA = = γ равны, потому что это углы со взаимно перпендикулярными сторонами. А из равенства треугольников следует, что α = γ .
Из построения Гюйгенса также следует, что падающий и отражённый лучи лежат в одной плоскости с перпендикуляром к поверхности, восстановленным в точке падения луча.
Законы отражения справедливы при обратном направлении хода световых лучей. В следствие обратимости хода световых лучей имеем, что луч, распространяющийся по пути отражённого, отражается по пути падающего.
Большинство тел лишь отражают падающее на них излучение, не являясь при этом источником света. Освещённые предметы видны со всех сторон, так как от их поверхности свет отражается в разных направлениях, рассеиваясь. Это явление называется диффузное отражение или рассеянное отражение. Диффузное отражение света (рис. 1.5) происходит от всех шероховатых поверхностей. Для определения хода отражённого луча такой поверхности в точке падения луча проводится плоскость, касательная к поверхности, и по отношению к этой плоскости строятся углы падения и отражения.
Рис. 1.5. Диффузное отражение света.
Например, 85% белого света отражается от поверхности снега, 75% — от белой бумаги, 0,5% — от чёрного бархата. Диффузное отражение света не вызывает неприятных ощущений в глазу человека, в отличие от зеркального.
Зеркальное отражение света – это когда падающие на гладкую поверхность под определённым углом лучи света отражаются преимущественно в одном направлении (рис. 1.6). Отражающая поверхность в этом случае называется зеркало (или зеркальная поверхность). Зеркальные поверхности можно считать оптически гладкими, если размеры неровностей и неоднородностей на них не превышают длины световой волны (меньше 1 мкм). Для таких поверхностей выполняется закон отражения света.
Рис. 1.6. Зеркальное отражение света.
Плоское зеркало – это зеркало, отражающая поверхность которого представляет собой плоскость. Плоское зеркало даёт возможность видеть предметы, находящиеся перед ним, причём эти предметы кажутся расположенными за зеркальной плоскостью. В геометрической оптике каждая точка источника света S считается центром расходящегося пучка лучей (рис. 1.7). Такой пучок лучей называется гомоцентрическим. Изображением точки S в оптическом устройстве называется центр S’ гомоцентрического отражённого и преломлённого пучка лучей в различных средах. Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь от него, падает в глаз наблюдателя, то в зеркале видны изображения этих тел.
Рис. 1.7. Изображение, возникающее с помощью плоского зеркала.
Изображение S’ называется действительным, если в точке S’ пересекаются сами отражённые (преломлённые) лучи пучка. Изображение S’ называется мнимым, если в ней пересекаются не сами отражённые (преломлённые) лучи, а их продолжения. Световая энергия в эту точку не поступает. На рис. 1.7 представлено изображение светящейся точки S, возникающее с помощью плоского зеркала.
Луч SO падает на зеркало КМ под углом 0°, следовательно, угол отражения равен 0°, и данный луч после отражения идёт по пути OS. Из всего множества попадающих из точки S лучей на плоское зеркало выделим луч SO1.
Луч SO1 падает на зеркало под углом α и отражается под углом γ ( α = γ ). Если продолжить отражённые лучи за зеркало, то они сойдутся в точке S1, которая является мнимым изображением точки S в плоском зеркале. Таким образом, человеку кажется, что лучи выходят из точки S1, хотя на самом деле лучей, выходящих их этой точки и попадающих в глаз, не существует. Изображение точки S1расположено симметрично самой светящейся точке S относительно зеркала КМ. Докажем это.
Луч SB, падающий на зеркало под углом 2 (рис. 1.8), согласно закону отражения света отражается под углом 1 = 2.
Рис. 1.8. Отражение от плоского зеркала.
Из рис. 1.8 видно, что углы 1 и 5 равны – как вертикальные. Суммы углов 2 + 3 = 5 + 4 = 90°. Следовательно, углы 3 = 4 и 2 = 5.
Прямоугольные треугольники ΔSOB и ΔS1OB имеют общий катет ОВ и равные острые углы 3 и 4, следовательно, эти треугольники равны по стороне и двум прилежащим к катету углам. Это означает, что SO = OS1, то есть точка S1 расположена симметрично точке S относительно зеркала.
Для того чтобы найти изображение предмета АВ в плоском зеркале, достаточно опустить перпендикуляры из крайних точек предмета на зеркало и, продолжив их за пределы зеркала, отложить за ним расстояние, равное расстоянию от зеркала до крайней точки предмета (рис. 1.9). Это изображение будет мнимым и в натуральную величину. Размеры и взаимное расположение предметов сохраняются, но при этом в зеркале левая и правая стороны у изображения меняются местами по сравнению с самим предметом. Параллельность падающих на плоское зеркало световых лучей после отражения также не нарушается.
Рис. 1.9. Изображение предмета в плоском зеркале.
В технике часто применяют зеркала со сложной кривой отражающей поверхностью, например, сферические зеркала. Сферическое зеркало – это поверхность тела, имеющая форму сферического сегмента и зеркально отражающая свет. Параллельность лучей при отражении от таких поверхностей нарушается. Зеркало называют вогнутым, если лучи отражаются от внутренней поверхности сферического сегмента. Параллельные световые лучи после отражения от такой поверхности собираются в одну точку, поэтому вогнутое зеркало называют собирающим. Если лучи отражаются от наружной поверхности зеркала, то оно будет выпуклым. Параллельные световые лучи рассеиваются в разные стороны, поэтому выпуклое зеркало называют рассеивающим.
Отражение и преломление света
Содержание:
Преломление света – явление изменения направления распространения света при прохождении через границу раздела сред с разными оптическими свойствами. Закон прямолинейного распространения света: в однородной оптической среде свет распространяется прямолинейно. Закон отражения света: луч падающий, луч отражённый и нормаль к отражающей поверхности в точке падения лежат в одной плоскости.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Отражение и преломление света
Отражение света — это изменение направления световой волны при падении на границу раздела двух сред, в результате чего волна продолжает распространяться в первой среде.
Преломление света – это явление при котором лучи света меняют свое направление и расположение. Такое явление можно наблюдать поместив карандаш или любой продолговатый объект в стакан наполненный водой.
Световой луч и световой пучок
Световым лучом называется то направление, по которому распространяется свет. Так как светящаяся точка испускает свет по всем направлениям, то любая прямая, проведённая из этой точки, представляет световой луч.
Из нашего определения ясно, что световой луч есть понятие чисто геометрическое.
На практике свет всегда распространяется внутри прямолинейно ограниченного конуса, в виде светового пучка.

На рисунке 254 световой пучок изображён тремя лучами: осевым SO и лучами SА и SB, ограничивающими пучок.
Пучок света в чистом воздухе невидим; но если воздух содержит мелкие частички — пылинки, дым или мелкие капельки воды (туман), то благодаря освещённым частичкам пучок света становится видимым. 
Во всяком действительном опыте, как уже указывалось, мы имеем дело не со световым лучом, а со световым пучком. Смотря по тому, как он ограничен, мы различаем параллельный, расходящийся и сходящийся пучки (рис. 255).
При помощи диафрагм ширина пучка может быть сделана малой, но не произвольно малой. При уменьшении размеров отверстия диафрагмы, через которое проходит пучок лучей, прямолинейность лучей постепенно нарушается—свет начинает заходить в область тени (на это же указывалось в § 127).
Наш глаз обычно воспринимает расходящиеся пучки лучей, и в месте пересечения этих лучей мы видим светящуюся точку. При этом возможны два случая: 1) точка пересечения лучей действительно существует; тогда видимую светящуюся точку называют действительной; 2) расходящийся пучок лучей не имеет действительной точки пересечения, но глазу она представляется существующей в месте пересечения воображаемых продолжений расходящихся лучей; такая точка называется мнимой. Однако ничего мнимого здесь нет. Где-то существует реальная светящаяся точка, из которой вышли лучи, попавшие в наш глаз. Но не всегда мы видим её там, где на самом деле она находится, и в этом смысле употребляется термин «мнимая точка».
Отдел учения о свете, в котором явления распространения света рассматриваются на основе представлений о световом луче, называется геометрической или лучевой оптикой.
Явления, происходящие при падении света на тела
Когда свет падает на какое-нибудь тело, то, во-первых, часть падающего света отражается от поверхности тела. Такое явление называется отражением света.
Во-вторых, часть света проникает внутрь тела и может распространяться в нём дальше. При этом на поверхности тела эта часть света может изменить первоначальное направление и дальше в теле распространяться по другому направлению. Это явление называется преломлением света.
Если сложить отражённый и преломлённый световые потоки, то их сумма будет равна величине полного светового потока, падающего на тело. Но в процессе распространения света внутри тела интенсивность света постепенно уменьшается вследствие поглощения его средой. При этом световая энергия превращается в другие виды энергии, в частности, она может перейти во внутреннюю энергию тела. Хорошо известно, например, что под действием света тела нагреваются.
Относительная величина отражённого и преломлённого света определяется рядом факторов: веществом тела, состоянием его поверхности, составом самого света, углом падения и др.
Поглощение также зависит от вещества тела и от состава светового потока.
Итак, при падении света на поверхность тела можно наблюдать явления отражения и преломления, а при прохождении его в теле — явление поглощения света.
Законы отражения света
Познакомимся с законами отражения света на опыте.
Установим плоское зеркальце РР в центре кругового диска, разделённого на градусы, так, чтобы лучи падали к основанию перпендикуляра CN, восставленного к плоскости зеркальца (рис. 256). Пусть SC — падающий луч, a  — отражённый луч. Точка С — точка падения луча. Угол SCN между падающим лучом SC и перпендикуляром CN называется углом падения. Угол
— отражённый луч. Точка С — точка падения луча. Угол SCN между падающим лучом SC и перпендикуляром CN называется углом падения. Угол  между отражённым лучом
между отражённым лучом  и тем же перпендикуляром CN называется углом отражения.
и тем же перпендикуляром CN называется углом отражения.
Из опыта видно, что луч падающий и луч отражённый лежат в одной плоскости с перпендикуляром к зеркалу, проведённым из точки падения луча.
Вращая диск, будем менять угол, под которым падает луч на зеркальце, мы заметим, что при этом меняется и угол отражения.
Измеряя каждый раз угол падения и соответствующий ему угол отражения, можно установить, что они равны друг другу.
Таким образом, отражение света происходит по следующим законам:
- Отражённый луч лежит в той же плоскости, в которой лежат падающий луч и перпендикуляр к отражающей поверхности, восставленный в точке падения луча.
- Угол отражения равен углу падения.
Если падающий луч идёт по направлению  , то, строя ход отражённого луча согласно сформулированным выше законам отражения, найдём, что отражённый луч пойдёт по
, то, строя ход отражённого луча согласно сформулированным выше законам отражения, найдём, что отражённый луч пойдёт по  Следовательно, падающий и отражённый лучи света взаимообратимы.
Следовательно, падающий и отражённый лучи света взаимообратимы.
Диффузное и зеркальное отражения
Громадное большинство видимых нами тел не являются источниками света и видимы только в том случае, если на них попадает свет от какого-либо источника. Но видеть предметы мы можем только тогда, когда к нам в глаз попадают лучи света. Таким образом, мы приходим к тому выводу, что освещённые тела отражают свет. При этом следует различать рассеянное (диффузное) отражение от зеркального отражения. 
При рассеянном отражении отражённые от предмета лучи распространяются во все стороны, вследствие чего предмет мы видим со всех сторон. Диффузно отражает свет, например, обычный лист бумаги (рис. 257).
Диффузно отражающую поверхность можно представить в виде элементарных плоскостей, различно расположенных и пересекающихся под различными углами. Но если падающий на тело параллельный пучок лучей света отражается в одном определённом направлении, то в этом случае мы говорим о зеркальном отражении (рис. 258). Зеркально отражают свет, например, тщательно отполированные металлы.
Плоское зеркало
Плоским зеркалом называют плоскую поверхность, зеркально отражающую свет.
Пусть MN (рис. 259) — плоское зеркало, S — светящаяся точка, находящаяся перед зеркалом. Из этой точки лучи выходят по разным направлениям:  и т. д. От поверхности зеркала эти лучи отражаются и идут по направлениям AD, BE, CF и т. д.
и т. д. От поверхности зеркала эти лучи отражаются и идут по направлениям AD, BE, CF и т. д. 
расходящимся пучком. Если такой расходящийся пучок лучей попадёт в глаз, то нам будет казаться, что эти лучи выходят из точки  , находящейся на пересечении продолжения этих лучей за зеркалом. Нетрудно доказать из равенства прямоугольных треугольников
, находящейся на пересечении продолжения этих лучей за зеркалом. Нетрудно доказать из равенства прямоугольных треугольников  , что точка
, что точка  находится за зеркалом на таком же расстоянии от него, на каком точка S находится перед зеркалом.
находится за зеркалом на таком же расстоянии от него, на каком точка S находится перед зеркалом.
Две точки  называются симметричными по отношению к плоскости зеркала, причём точка
называются симметричными по отношению к плоскости зеркала, причём точка  называется мнимым изображением светящейся точки S.
называется мнимым изображением светящейся точки S.
Зная, как строится изображение светящейся точки, легко построить изображение предмета. Пусть АВ — лицо (рис. 260), находящееся перед зеркалом MN. Все точки этого лица дадут симметричные мнимые изображения за зеркалом. Так, например, изображением точки А будет точка  точки В — точка
точки В — точка  и т.д. Изображение всего лица АВ в зеркале будет иметь ту же величину, что и само лицо, и будет расположено симметрично ему.
и т.д. Изображение всего лица АВ в зеркале будет иметь ту же величину, что и само лицо, и будет расположено симметрично ему.
Изображение предмета в плоском зеркале, так же как и изображение точки, будет мнимым.
Вогнутое сферическое зеркало
Сферическое зеркало представляет собой тщательно отполированную поверхность шарового сегмента. Сферические зеркала бывают вогнутыми и выпуклыми. Центр шаровой поверхности С называется оптическим центром зеркала (рис. 261); вершима шарового сегмента О — полюсом зеркала.

Всякая прямая, проходящая через оптический центр зеркала С, называется оптической осью зеркала. Оптическая ось СО, проходящая через центр сферы С и полюс зеркала О, называется главной оптической осью.
Угол  , образуемый двумя лежащими в одной плоскости с осью радиусами, проведёнными к краям зеркала, называется угловым отверстием зеркала или апертурой.
, образуемый двумя лежащими в одной плоскости с осью радиусами, проведёнными к краям зеркала, называется угловым отверстием зеркала или апертурой.
Лучи, идущие вблизи главной оптической оси, называются осевыми или центральными лучами. Все наши дальнейшие выводы будут относиться именно к таким лучам.
Если на вогнутое зеркало пустить пучок лучей, параллельных главной оптической оси, то лучи эти, отразившись от зеркала, сойдутся в небольшой области пространства, лежащей на оси приблизительно на середине радиуса.
Если такой опыт произвести с солнечными лучами и поместить в то место, в котором сходятся отражённые от зеркала лучи, какое-нибудь тело, то оно будет сильно освещено и даже нагреется, а легко воспламеняющееся вещество может даже загореться.
По этой причине вогнутые зеркала называются собирающими.

Фокус вогнутого сферического зеркала
Пусть на вогнутое зеркало падает осевой луч SA параллельно главной оптической оси зеркала ОС (рис 262). Проведём из центра С сферической поверхности зеркала перпендикуляр СА и построим отражённый луч АВ. Этот луч пересечёт оптическую ось в точке F. Легко показать, что эта точка расположена на половине расстояния ОС, т. е.
 — радиус сферической поверхности зеркала.
— радиус сферической поверхности зеркала.
В самом деле,  как внутренние накрест лежащие углы. Но
как внутренние накрест лежащие углы. Но  есть угол падения луча, следовательно, и угол отражения луча
есть угол падения луча, следовательно, и угол отражения луча  В треугольнике CFA CF=AF, но так как луч SA— центральный луч, то точки A и О близки друг другу, а это значит, что OF=AF; отсюда
В треугольнике CFA CF=AF, но так как луч SA— центральный луч, то точки A и О близки друг другу, а это значит, что OF=AF; отсюда  что и требовалось доказать.
что и требовалось доказать.
Точка F, в которой центральный луч. параллельный главной оптической оси зеркала, после отражения пересекает эту ось зеркала, называется фокусом зеркала.
Расстояние OF от вершины зеркала до фокуса называется фокусным расстоянием. Для краткости оно обозначается одной буквой F.

В фокусе собирается после отражения от зеркала весь центральный пучок лучей, падающий на зеркало параллельно главной оптической оси зеркала (рис. 263).
Плоскость, проходящая через фокус перпендикулярно глазной оптической оси, называется фокальной плоскостью.
На рисунке 264 светящаяся точка S расположена перед вогнутым зеркалом. Проведём от неё к зеркалу три центральных луча

и, согласно законам отражения, построим отражённые лучи. Все три отражённых луча пересеклись в одной точке  . Так как мы взяли три произвольных центральных луча, то и все прочие центральные лучи, исходящие из точки S, тоже пересекутся в точке
. Так как мы взяли три произвольных центральных луча, то и все прочие центральные лучи, исходящие из точки S, тоже пересекутся в точке  . В таком случае
. В таком случае  будет изображением точки S. Если расположить глаз так, как показано на рисунке 264, то мы увидим в точке
будет изображением точки S. Если расположить глаз так, как показано на рисунке 264, то мы увидим в точке  светящуюся точку. Следовательно, после отражения от зеркала центральные лучи, исходящие из различных точек предмета, должны пересечься в соответствующих точках и совокупность их — образовать изображение предмета. Проверим это на опыте.
светящуюся точку. Следовательно, после отражения от зеркала центральные лучи, исходящие из различных точек предмета, должны пересечься в соответствующих точках и совокупность их — образовать изображение предмета. Проверим это на опыте.
Установив зажжённую свечу перед зеркалом примерно так, как показано на рисунке 265, и расположив соответствующим образом глаз, мы действительно увидим перед зеркалом (при данном расположении свечи относительно зеркала) уменьшенное и обратное изображение свечи. Если там, где мы увидели изображение, поместить лист белой бумаги, то на нём получится изображение пламени свечи, видное со всех сторон, так как белый лист бумаги отражает свет диффузно.
Таким образом, опыт подтверждает наше предположение, что все центральные лучи, исходящие из одной точки, после отражения от вогнутого зеркала пересекаются тоже в одной точке. 
Построение изображений в вогнутом зеркале
Мы видели, что все центральные лучи, исходящие из светящейся точки после отражения от сферического зеркала, пересекаются в одной точке, т. е. после отражения от зеркала «точечный» источник света даёт точечное изображение.
Поэтому для изображения точки достаточно знать направление распространения только двух лучей, выходящих из этой точки: их точка пересечения будет точкой пересечения и других лучей, исходящих из данной точки. Лучи эти могут быть выбраны совершенно произвольно, но удобнее всего пользоваться определёнными лучами, направление распространения которых после отражения заранее известно. Изображение предмета складывается из совокупности изображений отдельных точек этого предмета.
Допустим, что нам нужно построить изображение предмета AВ в вогнутом зеркале (рис. 266а).
Проводим из точки А два луча: один — параллельно главной оптической оси, второй — через оптический центр С, после отражения от зеркала первый пройдёт через фокус F, второй — обратно по тому же направлению. Через точку пересечения этих лучей  пройдут и все остальные лучи, выходящие из точки А и отразившиеся от зеркала: точка
пройдут и все остальные лучи, выходящие из точки А и отразившиеся от зеркала: точка  будет изображением точки А. Таким же образом построим и изображение точки В, это будет точка
будет изображением точки А. Таким же образом построим и изображение точки В, это будет точка  . Изображения остальных точек предмета АВ расположатся между точками
. Изображения остальных точек предмета АВ расположатся между точками  и
и  и, следовательно,
и, следовательно,  будет изображением предмета АВ.
будет изображением предмета АВ.
На рисунке 266 б предмет АВ находится между фокусом и зеркалом. Изображение предмета  — увеличенное и мнимое.
— увеличенное и мнимое.

В зависимости от положения предмета по отношению к зеркалу его изображения могут быть действительные и мнимые, прямые и обратные, увеличенные и уменьшённые. На рисунке 267 показана установка для получения изображений лампочки в вогнутом зеркале. 
Применение вогнутых зеркал
Вогнутые зеркала находят весьма широкое применение в науке и технике. Например, вогнутыми зеркалами пользуются в тех случаях, когда нужно направить в какое-либо место концентрированный пучок света. Так устраиваются осветители в автомобильных, проекционных и карманных фонарях. В каждом из них за источником света помещается вогнутое зеркало. Примером может служить автомобильная фара, изображённая на рисунке 268.

Вогнутые зеркала (параболические) находят чрезвычайно важное применение при устройстве прожекторов. Прожектор состоит из двух главных частей: мощного источника света (электрической дуги) и большого вогнутого зеркала, помещаемого сзади источника света так, чтобы источник света оказался в фокусе зеркала.
Прожектор как осветитель применяется при киносъёмках, при освещении строительных площадок, стадионов, площадей.
В военном деле прожекторы употребляются для освещения и сигнализации.
Вогнутые зеркала находят весьма важное применение при устройстве телескопов-рефлекторов.
Выпуклое зеркало
Пусть MN — выпуклое зеркало (рис. 269). Поместим перед ним светящуюся точку S и построим её изображение. 
Лучи от этой точки после отражения идут расходящимся пучком. Вершина этого пучка лежит за зеркалом в точке пересечения продолжения расходящихся лучей  . В этой точке, как было уже указано в § 135, мы и увидим мнимое изображение светящейся точки S. Где бы предмет ни находился относительно выпуклого зеркала, его изображение в зеркале всегда мнимое и уменьшенное. Построение изображения предмета в выпуклом зеркале показано на рисунке 270; здесь АВ —предмет, а
. В этой точке, как было уже указано в § 135, мы и увидим мнимое изображение светящейся точки S. Где бы предмет ни находился относительно выпуклого зеркала, его изображение в зеркале всегда мнимое и уменьшенное. Построение изображения предмета в выпуклом зеркале показано на рисунке 270; здесь АВ —предмет, а  — его изображение.
— его изображение.

Законы преломления света
Когда луч света падает на гладкую поверхность прозрачной среды, то образуется не один только отражённый луч. Из точки падения луча выходит ещё второй луч, распространяющийся во второй прозрачной среде, его называют преломлённым лучом. Направление преломлённого луча не совпадает с направлением падающего луча, однако между ними существует определённая г связь, которую можно установить на опыте.

На рисунке 271а пучок света падает на полированную поверхность стеклянной пластинки. На границе, разделяющей стекло и воздух, этот пучок раздваивается на два пучка; один из них отражается от поверхности стекла, другой же переходит в стекло, резко изменив своё направление. SO — осевой луч падающего пучка света;  — отражённого и
— отражённого и  — преломлённого пучка.
— преломлённого пучка.
Сравнив направление преломлённого луча с направлением перпендикуляра On, проведённого к границе в точке падения, мы увидим, что преломлённый луч  лежит по ту же сторону перпендикуляра, где находится и луч отражённый
лежит по ту же сторону перпендикуляра, где находится и луч отражённый  . Угол
. Угол  — угол падения луча; обозначим его буквой
— угол падения луча; обозначим его буквой  ; угол
; угол  между преломлённым лучом
между преломлённым лучом  и перпендикуляром On называется углом преломления; обозначим его буквой
и перпендикуляром On называется углом преломления; обозначим его буквой  . При изменении угла падения меняется и угол преломления. Угол преломления равен нулю, когда угол падения равен нулю; с увеличением же угла падения увеличивается и угол преломления; однако всё время угол преломления остаётся меньше угла падения.
. При изменении угла падения меняется и угол преломления. Угол преломления равен нулю, когда угол падения равен нулю; с увеличением же угла падения увеличивается и угол преломления; однако всё время угол преломления остаётся меньше угла падения.
На рисунке 271 б изображена установка для наблюдения явления преломления света при переходе из воздуха в воду и из воды в воздух.
Возьмём стеклянную пластинку, нижняя грань которой параллельна верхней и покрыта тонким слоем серебра (рис. 272). Пустим на пластинку луч света под углом  и проследим ход его из стекла в воздух. Мы заметим, что в этом случае угол преломления всегда больше угла падения. Упав на нижнюю грань под углом
и проследим ход его из стекла в воздух. Мы заметим, что в этом случае угол преломления всегда больше угла падения. Упав на нижнюю грань под углом  , луч отразится от неё и, встретив под этим углом верхнюю грань, выйдет в воздух под некоторым углом
, луч отразится от неё и, встретив под этим углом верхнюю грань, выйдет в воздух под некоторым углом  . Измерив углы
. Измерив углы  можно убедиться, что они равны:
можно убедиться, что они равны:  Если падающий луч будет пущен по направлению преломлённого луча, то луч преломлённый пойдёт по линии луча падающего, т. е. луч падающий и луч преломлённый взаимообратимы.
Если падающий луч будет пущен по направлению преломлённого луча, то луч преломлённый пойдёт по линии луча падающего, т. е. луч падающий и луч преломлённый взаимообратимы.

На основании опытов были установлены следующие законы преломления света:
- 1. Преломлённый луч лежит в той же плоскости, в которой лежат падающий луч и перпендикуляр, восставленный в точке падения луча к границе раздела двух сред.
- 2. При всех изменениях углов падения и преломления отношение синуса угла падения ксинусу угла преломления для данных двух сред есть величина постоянная, называемая показателем преломления второй среды относительно первой.
Математически этот закон можно написать в виде следующей формулы:

где  — угол падения,
— угол падения,  — угол преломления и п — показатель преломления.
— угол преломления и п — показатель преломления.

Показатель преломления данного вещества по отношению к вакууму называется абсолютным показателем преломления этого вещества.
Практически показатель преломления определяется обычно относительно воздуха, а не относительно вакуума. Чтобы получить показатель преломления данного вещества относительно вакуума, надо значение показателя преломления этого вещества относительно воздуха умножить на абсолютный показатель преломления воздуха, равный 1,0003.
Величина показателя преломления для данного вещества зависит от цветности лучей света.
Несколько значений показателей преломления для красного света даны в нижеследующей таблице.

При сравнении двух веществ то из них, которое имеет больший показатель преломления, называется оптически более плотным.
Понятие показателя преломления имеет глубокое физическое содержание. Абсолютный показатель преломления (п) указывает, во сколько раз скорость света в вакууме (с) больше скорости света ( ) в данном веществе, т. е.
) в данном веществе, т. е. 
Этот важный вывод вытекает из волновой теории распространения света, основы которой будут изложены в главе IX.
Полное отражение света
Рассмотрим подробнее случай перехода света из оптически более плотной среды в менее плотную.
Пусть на границу MN стекло — воздух из стекла падает расходящийся пучок света. Определим его тремя лучами — двумя крайними I и III и осевым II (рис. 273,а). У границы часть пучка отразится в стекло, часть перейдёт в воздух. Будем постепенно увеличивать угол падения. Мы заметим, что по мере возрастания угла падения яркость отражённого пучка будет возрастать, а преломлённого уменьшаться. При некотором угле падения  луч I будет скользить по поверхности раздела (рис. 273,6). При увеличении угла падения то же произойдёт и с осевым лучом // и, наконец, с лучом ///. При дальнейшем увеличении угла падения луча /// преломлённого пучка уже не будет, весь падающий пучок отразится в стекло (рис. 273, е). Такое явление называется полным отражением.
луч I будет скользить по поверхности раздела (рис. 273,6). При увеличении угла падения то же произойдёт и с осевым лучом // и, наконец, с лучом ///. При дальнейшем увеличении угла падения луча /// преломлённого пучка уже не будет, весь падающий пучок отразится в стекло (рис. 273, е). Такое явление называется полным отражением.
Наименьший угол падения, при котором наступает полное отражение, называется предельным углом полного отражения.
Таким образом, полное отражение наблюдается при переходе света из оптически более плотной среды в менее плотную в том случае, если все лучи заданного пучка падают под углом, большим предельного.
Предельному углу падения  соответствует угол преломления, равный 90°. Пусть показатель преломления стекла относительно воздуха — п; тогда на основании закона преломления света и свойства обратимости луча можно написать:
соответствует угол преломления, равный 90°. Пусть показатель преломления стекла относительно воздуха — п; тогда на основании закона преломления света и свойства обратимости луча можно написать:

отсюда 


Из полученного соотношения вычисляется предельный угол полного отражения. Для воды (n=1,33) этот угол равен 48°,5, для стекла (n=1,51) 42°, а для алмаза (п = 2,4) предельный угол равен 24°,5.
Полное отражение широко используется в различных оптических приборах, например в полевых биноклях, перископах и т. д.
Полным отражением объясняется целый ряд явлений, например блеск капель росы при солнечном свете, светящиеся фонтаны, блеск («игра») бриллиантов, образование миражей и т. д.
Изменение светового потока при отражении и преломлении
Допустим, что свет, падающий на границу раздела двух сред, не поглощается второй средой. Часть светового потока  отражается от поверхности раздела сред, другая же часть
отражается от поверхности раздела сред, другая же часть  проникает во вторую среду и распространяется в ней. При таких условиях
проникает во вторую среду и распространяется в ней. При таких условиях

Из этого равенства следует, что как отражённая, так и преломлённая части потока света в отдельности не равны падающему потоку света; это легко можно заметить и в наших опытах (рис. 273). Кроме того, опыт показывает, что при малых углах падения преломлённый поток света значительно больше отражённого. По мере же увеличения угла падения увеличивается и отражённый поток, между тем как преломлённый поток уменьшается.
Кроме того, отражённый поток света зависит от оптических свойств тех двух сред, граница между которыми отражает свет. Оказывается, чем больше разница между показателями преломления обеих сред, тем больший поток отражается. Если показатели преломления обеих сред одинаковы, то свет вообще не отражается.
Так, например, показатель преломления кедрового масла весьма близок к показателю преломления стекла; поэтому стеклянная палочка, погружённая в кедровое масло, невидима (несветящиеся тела мы видим благодаря отражённому свету). Этим свойством веществ пользуются для склеивания стёкол в оптических приборах, подбирая такие склеивающие вещества, показатель преломления которых близок к показателю преломления стекла.
Прохождение света через прозрачную пластинку с параллельными гранями
Практически большое значение имеет случай, когда свет переходит из одной среды в другую и затем снова выходит в первую, т. е. свет проходит через какое-либо оптически прозрачное тело. Поверхности раздела могут быть при этом самыми разнообразными. Мы прежде всего разберём случай, когда свет проходит через пластинку, ограниченную параллельными плоскостями.
Пусть  — плоско-параллельная пластинка (рис. 274). Легко показать, что луч SO пучка света, падающего на пластинку, после двух преломлений выйдет наружу по направлению
— плоско-параллельная пластинка (рис. 274). Легко показать, что луч SO пучка света, падающего на пластинку, после двух преломлений выйдет наружу по направлению  , параллельному SO.
, параллельному SO.
Обозначим угол падения луча SO через  , а угол преломления через
, а угол преломления через  . Вследствие параллельности плоскостей
. Вследствие параллельности плоскостей  луч, пройдя стекло, встретит плоскость пластинки под углом
луч, пройдя стекло, встретит плоскость пластинки под углом  и, следовательно, выйдет из неё под углом
и, следовательно, выйдет из неё под углом  Таким образом, при прохождении через плоско-параллельную пластинку луч света не изменяет своего направления, он только смещается. Чем толще пластинка, тем значительнее будет это смещение. Если рассматривать предмет через плоско-параллельное стекло, то он будет казаться нам сдвинутым относительно своего истинного положения.
Таким образом, при прохождении через плоско-параллельную пластинку луч света не изменяет своего направления, он только смещается. Чем толще пластинка, тем значительнее будет это смещение. Если рассматривать предмет через плоско-параллельное стекло, то он будет казаться нам сдвинутым относительно своего истинного положения.

Прохождение света через прозрачную треугольную призму
На рисунке 275а АВ и АС — плоские поверхности призмы, ограничивающие её преломляющий угол  . Плоскость чертежа
. Плоскость чертежа

перпендикулярна к обеим преломляющим поверхностям призмы и представляет собой сечение призмы. Пусть на грань АВ этой призмы падает какой-нибудь одноцветный, например красный, пучок лучей света (на рис. 275а показан только осевой луч DE этого пучка). В точке Е луч DE преломится и пойдёт внутри призмы по направлению EF. У грани АС этот луч ещё раз преломится, отклоняясь к грани ВС. Вышедший из призмы луч света после двукратного преломления отклонится на угол  . Величина угла отклонения
. Величина угла отклонения  зависит от преломляющего угла призмы
зависит от преломляющего угла призмы  и показателя преломления вещества призмы п. Если рассматривать какой-либо предмет через треугольную призму, то предмет покажется смещённым к вершине угла, образованного плоскостями, через которые проходят лучи от источника (рис. 275 б).
и показателя преломления вещества призмы п. Если рассматривать какой-либо предмет через треугольную призму, то предмет покажется смещённым к вершине угла, образованного плоскостями, через которые проходят лучи от источника (рис. 275 б).

Если пропускать пучок лучей на одну из граней стеклянной равнобедренной прямоугольной призмы ABC (рис. 276), то внутри призмы лучи отразятся от грани призмы АС, испытав полное отражение, так как в этом случае угол падения лучей на грань АС больше 42°, т. е. больше предельного угла для стекла. Прямоугольная призма ABC в положениях, показанных на рисунке, может быть использована для поворота светового пучка на 90° и для обращения какого-либо изображения, получающегося в оптическом приборе. В последнем случае нижние лучи, отразившись внутри призмы от грани АС, по выходе из призмы становятся верхними, а верхние — нижними. Такая призма называется оборотной и применяется во многих оптических приборах, в частности в призматическом бинокле.

Линзы
Прозрачные для света тела, ограниченные с двух сторон сферическими или иными кривыми поверхностями (одна из двух поверхностей может быть плоской), называются оптическими стёклами или линзами. 
По форме ограничивающих поверхностей линзы могут быть сферическими, цилиндрическими и другими (в дальнейшем будут рассматриваться только сферические линзы).

Линзы, у которых середина толще, чем края, называются выпуклыми; те же линзы, у которых края толще середины, называются вогнутыми.
На рисунке 277 изображены в поперечном разрезе различные виды сферических линз: 1, 2, 3 — выпуклые линзы; 4, 5, 6—вогнутые линзы.
Пустим параллельный пучок лучей света на выпуклую линзу, а за линзой поместим экран. Перемещая экран относительно линзы, мы получим на нём небольшое светлое пятно. Выпуклая линза, преломляя падающие на неё лучи, собирает их. Поэтому такая линза называется собирающей. Вогнутая же линза, преломляя свет, рассеивает его в стороны. Такая линза называется рассеивающей.
Рисунок 278 поясняет действие собирающих и рассеивающих линз. Собирающую линзу можно представить в виде совокупности большого числа призм, расширяющихся к середине линзы, а рассеивающую — как совокупность большого числа призм, расширяющихся к краям.

Известно, что каждая призма отклоняет лучи света к грани, лежащей против преломляющего угла; величина отклонения зависит от величины отклоняющего угла. Понятно, что линзы с утолщением на середине отклоняют лучи к середине, собирая их, линзы же с утолщением по краям отклоняют лучи к краям, т. е.

рассеивают их. Середина линзы действует как плоско-параллельная пластинка.
Мы будем рассматривать только очень тонкие линзы, в которых расстояние между краями  очень мало по сравнению с расстояниями
очень мало по сравнению с расстояниями  (рис. 279). В таких линзах практически точки
(рис. 279). В таких линзах практически точки  можно считать сливающимися в одной точке О. Эту точку О называют оптическим центром линзы.
можно считать сливающимися в одной точке О. Эту точку О называют оптическим центром линзы.
Всякая прямая, проходящая через оптический центр, называется оптической осью линзы. Оптическая ось, проходящая через центры сферических преломляющих поверхностей  , образующих линзу, называется главной оптической осью линзы (рис. 279), другие — побочными осями.
, образующих линзу, называется главной оптической осью линзы (рис. 279), другие — побочными осями.
Луч света, идущий по какой-либо из оптических осей, проходит тонкую линзу, не меняя своего направления.
Фокус линзы
Если направить на собирающую линзу осевой луч SE, параллельный её оси (рис. 280), то, пройдя линзу, этот луч пересечёт ось на определённом расстоянии от линзы —

в точке F. Расстояние OF называется фокусным расстоянием линзы, а самая точка F называется фокусом линзы. У всякой линзы два фокуса, по обе стороны её.

Основываясь на законах преломления света, можно теоретически доказать, что все осевые лучи, т. е. лучи, идущие вблизи главной оптической оси, падающие на тонкую собирающую линзу параллельно её оси, сходятся в фокусе. Опыт подтверждает это теоретическое доказательство (рис. 281).
Пустив пучок осевых лучей параллельно главной оптической оси на тонкую двояковогнутую линзу (рис. 282), мы заметим, что из линзы лучи выйдут расходящимся пучком. Если такой расходящийся пучок попадёт в наш глаз, то нам будет казаться, что лучи выходят из одной точки F. Эта точка называется мнимым фокусом двояковогнутой линзы.
Плоскость MN, проведённая через фокус линзы перпендикулярно к главной оптической оси, называется фокальной плоскостью линзы (рис. 283). Фокальных плоскостей у линзы две, и расположены они по обе стороны линзы.

Когда на линзу падает пучок лучей, параллельных какой-либо побочной оптической оси, то после преломления в линзе он сходится на соответствующей побочной оптической оси в месте её пересечения с фокальной плоскостью (рис. 283).
Оптическая сила линзы
Величина, обратная фокусному расстоянию линзы F, называется оптической силой D линзы:

За единицу оптической силы линзы принимается оптическая сила такой линзы, фокусное расстояние которой равно 1 м; такая единица называется диоптрией.
У выпуклых линз оптическая сила положительна, у вогнутых — отрицательна.
Пример. Чему равна оптическая сила очковой выпуклой линзы, фокусное расстояние которой F=50 см? 
Величина фокусного расстояния линзы, а следовательно, и её оптическая сила определяются показателем преломления вещества линзы и радиусами сферических поверхностей, её ограничивающих.
Теория даёт формулу, по которой можно рассчитать оптическую силу линзы:

В этой формуле п — показатель преломления вещества линзы,  — радиусы кривизны поверхностей линзы. Радиусы выпуклых поверхностей считаются положительными, вогнутых — отрицательными.
— радиусы кривизны поверхностей линзы. Радиусы выпуклых поверхностей считаются положительными, вогнутых — отрицательными.
Изображение точки в собирающей линзе
Теория показывает и опыт подтверждает, что осевые лучи, вышедшие из одной светящейся точки, после прохождения через линзу сходятся также в одной точке, которая называется изображением первой точки.

Этим важным положением можно воспользоваться для нахождения изображения светящейся точки в собирающей линзе путём геометрического построения хода центральных (осевых) лучей.
Так как все центральные лучи, выходящие из одной точки, пройдя через собирающую линзу, сходятся в одной точке, то для построения изображения её достаточно найти точку пересечения каких-либо двух лучей.
Построим, например, изображение светящейся точки (рис. 284а). Проще всего это можно выполнить при помощи лучей, указанных на этом рисунке. Один из них — луч SC, параллельный главной оптической оси, преломившись в линзе, пройдёт через фокус линзы F; другой луч SD, идущий из точки S через фокус F, за линзой пойдёт параллельно оси линзы. Третий луч SO пройдёт через оптический центр линзы, не преломляясь. Ход всякого иного луча, выходящего из точки S, нужно было бы строить, применяя законы преломления света, что значительно сложнее. Но в этом нет никакой необходимости, так как все центральные (осевые) лучи, выходящие из точки S, преломившись в линзе, обязательно пройдут через точку  .
.
Построим изображение точки S, лежащей на оптической оси линзы (рис. 2846). Для этого проведём из точки S на линзу какой-нибудь луч. Параллельно этому лучу проведём побочную оптическую ось ВС, которая пересечёт фокальную плоскость MN в точке С. После преломления в линзе через точку С пройдёт весь

пучок света, параллельный побочной оптической оси ВС; следовательно, через эту точку пройдёт и луч SA. Главную оптическую ось этот луч пересечёт в точке  , которая и является изображением точки S. Второй луч из S направлен вдоль главной оптической оси.
, которая и является изображением точки S. Второй луч из S направлен вдоль главной оптической оси. 
Выбранные нами лучи для построения изображения точки не обязательно должны пройти через линзу.
Так, например, на рисунке 285 лучи SA и SB не проходят через линзу, но могут быть использованы для построения изображения точки, которое, очевидно, определится пучком реальных лучей, вышедших из точки S и ограниченных размерами линзы. Этот реальный пучок, преломившись в линзе, пройдёт через точку  .
.
Изображение предметов в собирающей линзе
Рассматривая предмет как совокупность точек и пользуясь свойством центральных лучей, выходящих из точки после преломления в линзе, собираться также в точке, можно геометрически построить изображение предмета в линзе.
Построим, например, изображение предмета АВ в собирающей линзе (рис. 286). Для этого достаточно построить изображение двух его крайних точек А и В. При построении же изображения, например точки A, проще всего провести из этой точки два луча: один параллельно главной оптической оси линзы, другой через оптический центр линзы, т. е. по побочной оптической оси  .
. 
После прохождения линзы оба луча пересекутся в точке  . Таким же способом строим изображение
. Таким же способом строим изображение  точки В. Изображения остальных точек предмета расположатся между точками
точки В. Изображения остальных точек предмета расположатся между точками  . Таким образом,
. Таким образом,  является изображением предмета АВ. Изображение
является изображением предмета АВ. Изображение  — действительное, обратное и уменьшённое.
— действительное, обратное и уменьшённое. 
На рисунке 287 показано построение изображения предмета, расположенного относительно линзы на расстоянии, меньшем фокусного расстояния. В этом случае изображение получается мнимое.
Характер получаемого от линзы изображения предмета, т. е. его величина и положение, зависит от положения предмета относительно линзы. Местонахождение изображения предмета и его величина могут быть найдены с помощью формулы линзы.
На рисунке 288 показана установка для получения изображения с помощью линзы.
Формула линзы
Для вывода формулы линзы воспользуемся рисунком 289. Здесь АВ — предмет, — его изображение. Исходя из подобия прямоугольных треугольников FOC и  , можно написать:
, можно написать:


Из подобия треугольников  имеем:
имеем:

Так как АВ=ОС, то левые части равенств (1) и (2) равны между собой. Приравнивая правые части этих равенств, мы получим:


или, заменяя  — расстояние изображения от линзы, ВО=d— расстояние предмета от линзы, получим:
— расстояние изображения от линзы, ВО=d— расстояние предмета от линзы, получим:

откуда

или

Разделив обе части последнего равенства на  получим формулы линзы:
получим формулы линзы:

Отсчёт расстояний d, f и F производится от оптического центра линзы. Величины d и F, входящие в формулу выпуклой линзы, всегда положительные, величина же f в случае мнимых изображений отрицательна; она откладывается по ту же сторону от центра линзы, что и величина d. 
Отношение линейного размера изображения  к размеру предмета АВ называется линейным увеличением линзы.
к размеру предмета АВ называется линейным увеличением линзы.
Обозначая линейное увеличение буквой k, получаем:

Так как  то из этого следует, что линейное увеличение линзы
то из этого следует, что линейное увеличение линзы

Двояковогнутая линза
Построим изображение точки, даваемое двояковогнутой линзой. Лучи от светящейся точки S после прохождения линзы идут расходящимся пучком (рис.290), но нам будет казаться, что эти лучи выходят из одной точки, находящейся перед линзой, из точки  , которая и является мнимым изображением точки S.
, которая и является мнимым изображением точки S.
Проделав опыт с двояковогнутой линзой, легко убедиться, что изображения предметов в ней всегда мнимые, уменьшённые и прямые, независимо от того, на каком расстоянии от линзы находится предмет. 
Отражение и преломление света и его определение
Свет — это электромагнитные колебания определенного диапазона длин волн — видимое оптическое излучение (от фиолетового до красного), которые воспринимает человеческий глаз.
Отражение света — это изменение направления световой волны при падении на границу раздела двух сред, в результате чего волна продолжает распространяться в первой среде.
Преломление света – явление изменения направления распространения света при прохождении через границу раздела сред с разными оптическими свойствами. Закон прямолинейного распространения света: в однородной оптической среде свет распространяется прямолинейно. Закон отражения света: луч падающий, луч отражённый и нормаль к отражающей поверхности в точке падения лежат в одной плоскости, причём угол падения равен углу отражения.
Оптические явления на границе раздела двух прозрачных сред
Вспомним, что в однородной среде свет распространяется прямолинейно. Это дает возможность при описании распространения света в такой среде пользоваться световыми лучами.
Изменение направления распространения света происходит на границе раздела двух различных сред. Поэтому, если установить из опытов законы, позволяющие точно определять такие изменения, то с помощью световых лучей можно описывать ход многих оптических явлений, не учитывая физической природы светового излучения. Часть оптики, в которой используется такой метод описания явлений, называют геометрической оптикой. В этой главе рассматриваются законы, которым подчиняются оптические явления, происходящие на границе раздела двух прозрачных сред.
Когда на поверхность воды из воздуха падает тонкий пучок света (рис. 29.1), то можно заметить, что в точке падения О часть света отражается, а часть проникает в воду и при этом преломляется. Вспомним, что углы  и
и  соответственно называют углом падения и углом отражения (§ 24.19). Угол
соответственно называют углом падения и углом отражения (§ 24.19). Угол  составленный преломленным лучом и перпендикуляром к поверхности раздела двух сред в точке падения лучей, называют углом преломления.
составленный преломленным лучом и перпендикуляром к поверхности раздела двух сред в точке падения лучей, называют углом преломления.

Возникает вопрос: сколько энергии, принесенной излучением на поверхность раздела двух сред, унесут отраженные лучи и сколько — преломленные? Пусть излучение приносит в точку О за некоторое время энергию  Дальше эта энергия разделяется: одну ее часть
Дальше эта энергия разделяется: одну ее часть  уносят отраженные, а другую
уносят отраженные, а другую  — преломленные лучи. Из закона сохранения энергии следует, что
— преломленные лучи. Из закона сохранения энергии следует, что

Поскольку всякая среда (кроме вакуума) поглощает энергию излучения, это равенство справедливо только при измерении энергии вблизи точки О. Если световое излучение проходит в среде значительные расстояния, мало ослабляясь, то среду называют прозрачной (например, стекло, воду, спирт и т. п.). Напротив, металлы очень сильно поглощают проникающее в них световое излучение, т. е. непрозрачны для него. Большую часть падающего на них излучения они отражают.
Вспомним, что морская вода и другие электролиты — хорошие проводники электрического тока, но слабо поглощают видимое излучение и этим резко отличаются от металлов. Это объясняется тем, что в электролитах нет свободных электронов, а ионы из-за своей сравнительно большой массы не успевают следовать высокочастотным колебаниям в световом луче.
Итак, каждая среда в той или иной степени отражает и поглощает световое излучение. Отражение и поглощение падающего на тело излучения зависят от рода вещества, от состояния поверхности, от состава излучения, от угла падения лучей и других причин. При увеличении угла падения лучей  доля отраженного света увеличивается, а проникающего — уменьшается.
доля отраженного света увеличивается, а проникающего — уменьшается.
Заметим, что зависимость отражения и поглощения от частоты колебаний чаще всего имеет избирательный характер, т. е. колебания с одной частотой вещество отражает или поглощает сильно, а с другой — слабо. Например, атмосфера Земли сильно поглощает короткие волны видимого спектра и значительно слабее — его длинные волны. (Подумайте, почему в качестве сигнала об опасности используется красный свет, хотя наибольшая чувствительность глаза относится к зеленым лучам.)
Законы отражения света
С помощью опытов законы отражения для светового излучения были найдены еще в III в. до н. э. древнегреческим ученым Евклидом. В современных условиях проверка этих законов делается с помощью оптической шайбы (рис. 29.2). Она состоит из источника света А, который можно перемещать вокруг диска, разделенного на градусы. Направляя свет на отражающую поверхность 3, измеряют углы  и
и 

Законы отражения света совпадают с законами отражения волн от препятствий (§24.19).
1. Луч падающий и луч отраженный лежат в одной плоскости в перпендикуляром к отражающей поверхности, восставленным в точке падения луча.
2. Угол отражения луча равен углу его падения: 
С помощью оптической шайбы можно показать, что падающий и отраженный лучи обратимы, т. е. если падающий луч направить по пути отраженного луча, то отраженный луч пойдет по пути падающего луча.
Законы отражения для сферического фронта волны. Покажем теперь, что они справедливы и для плоского фронта волны, т. е. для случая падения на плоскую поверхность параллельных лучей.
Пусть на гладкую поверхность КМ (рис. 29.3) падает плоская волна, фронт которой в какой-либо момент времени занимает положение A1B1. Через некоторое время он займет положение АС. В этот момент времени (мы примем его за нуль) от точки А начнет распространяться отраженная элементарная волна. Пока фронт волны за время t из точки С переместится в точку В, волна из точки А распространится по полусфере на расстояние AD, равное СВ, так как  и
и  (
(  — скорость распространения волн). Новым положением фронта волны после отражения лучей будет касательная к полусфере, проведенная из точки В, т. е. прямая BD. Дальше этот фронт волны будет двигаться параллельно самому себе по направлению лучей АА” или ВВ”.
— скорость распространения волн). Новым положением фронта волны после отражения лучей будет касательная к полусфере, проведенная из точки В, т. е. прямая BD. Дальше этот фронт волны будет двигаться параллельно самому себе по направлению лучей АА” или ВВ”.

Поскольку прямоугольные треугольники ADB и АСВ имеют общую гипотенузу АВ и равные катеты AD и СВ, то они равны между собой. Поэтому  Так как
Так как  и
и  как углы со взаимно перпендикулярными сторонами, то
как углы со взаимно перпендикулярными сторонами, то  т. е. угол падения равен углу отражения, что и требовалось доказать.
т. е. угол падения равен углу отражения, что и требовалось доказать.
Зеркальное и диффузное отражение. Плоское зеркало
Когда отражение света происходит от неровной поверхности, то ход отраженного луча в каждой ее точке определяется следующим образом. В точке падения луча проводится плоскость, касательная к поверхности, от которой происходит отражение, а затем строятся углы падения и отражения по отношению к этой плоскости.
Таким способом определены направления отраженных лучей в различных точках поверхности на рис. 29.4, где видно, что лучи, которые до отражения шли параллельным пучком, после отражения идут в разных направлениях. Такое отражение называют диффузным или рассеянным. Диффузное отражение света происходит от всех шероховатых поверхностей. Рассеянный свет, идущий от поверхностей различных тел, позволяет нам видеть эти тела.

Идеально гладкую поверхность, хорошо отражающую свет, называют зеркальной. Плоская зеркальная поверхность является плоским зеркалом (кроме плоских зеркал бывают сферические, параболические и т. д.). Пучок параллельных лучей после отражения от плоского зеркала остается параллельным, но изменяет направление своего распространения (рис. 29.5). Такое отражение называют зеркальным или правильным. На практике зеркальное отражение получается, если размеры неровностей на поверхности не превышают длины волны светового излучения.

Когда световые лучи от сильного источника света после отражения от плоского зеркала попадают в глаз человека, то они ослепляют его. Диффузное отражение неприятных ощущений в глазу не вызывает.
Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь, попадает в глаз человека, то в зеркале видны изображения этих тел. Выясним, как они возникают. Сначала рассмотрим, как получается изображение одной светящейся точки в плоском зеркале.
Пусть над поверхностью зеркала КМ (рис. 29.6) находится точечный источник света S. Луч SA, который идет от источника S по перпендикуляру к зеркалу, после отражения меняет свое направление на противоположное, т. е. идет по пути AS. Из всего множества лучей, попадающих из S на зеркало выделим луч SB, который падает на зеркало под углом i. После отражения он идет по пути BD, причем  На рис. 29.6 видно, что лучи, падающие в точки А и В, после отражения идут так, как будто бы они вышли из одной точки S1, расположенной симметрично точке S относительно зеркала КМ. Докажем это.
На рис. 29.6 видно, что лучи, падающие в точки А и В, после отражения идут так, как будто бы они вышли из одной точки S1, расположенной симметрично точке S относительно зеркала КМ. Докажем это.

Угол  равен углу
равен углу  поэтому и
поэтому и  Поскольку
Поскольку  , то
, то  и
и  , т. е.
, т. е.  Это означает, что прямоугольные треугольники SAB и S1AB равны, так как имеют общий катет АВ и равные острые углы 1 и 2. Следовательно, SA =S1A. Это равенство справедливо для всех лучей, падающих из точки S на зеркало.
Это означает, что прямоугольные треугольники SAB и S1AB равны, так как имеют общий катет АВ и равные острые углы 1 и 2. Следовательно, SA =S1A. Это равенство справедливо для всех лучей, падающих из точки S на зеркало.
Таким образом, когда человек смотрит в зеркало, то он видит изображение источника света S в точке S1 хотя в действительности лучей, выходящих из точки S1 и попадающих в глаз, не существует. Поэтому такое изображение принято называть мнимым. Если в точку S1, где человек видит светящуюся точку, поместить экран, то на нем изображения точки S не получится. Это характерное Свойство мнимого изображения. Во всех других отношениях для наблюдателя мнимое изображение ничем не отличается от действительного.
Итак, в плоском зеркале получается мнимое изображение светящейся точки S, расположенное симметрично ей относительно зеркала в точке S1.
Представим теперь себе, что перед плоским зеркалом КМ находится предмет, который на рис. 29.7 условно изображен стрелкой BА. Положение изображения этого предмета в зеркале можно найти следующим образом. Опустив из крайних точек предмета перпендикуляры на зеркало и продолжив их за зеркало на расстояние, равное их длине до зеркала, получим точки A1 и B1 Соединив эти точки прямой линией, получим изображение стрелки ВА в зеркале. Это изображение будет мнимое и в натуральную величину. Оно имеет следующую особенность, отличающую его от других изображений: по сравнению с самим предметом левая и правая стороны у изображения в зеркале меняются местами. Такое изображение принято называть зеркальным.

Оказывается, что мнимыми бывают не только изображения, но и источники света. Пусть на пути лучей, которые должны сойтись в точке А (такие лучи можно получить с помощью линз), поместили плоское зеркало КМ (рис. 29.8). Тогда после отражения от зеркала лучи сойдутся в точке A1 и затем уже пойдут расходящимся пучком, т. е. в точке A1 получится действительное изображение источника света А, симметричное относительно зеркала КМ. Поскольку в точке А источника света в действительности нет, условились считать, что в ней находится мнимый источник света.

Итак, изображение действительного источника света в плоском зеркале получается мнимое и за зеркалом, а изображение мнимого источника света получается действительное и перед зеркалом.
Сферические зеркала
Зеркала, поверхности которых составляет часть поверхности шара, называют сферическими; они бывают вогнутые (рис. 29.9, а) и выпуклые (29.9, б). На рис. 29.9 R — радиус кривизны зеркала. Диаметр КМ окружности, ограничивающей зеркало, называют отверстием зеркала, а самую удаленную от него точку О зеркальной поверхности называют вершиной зеркала. Прямую, проходящую через сферический центр зеркала С и его вершину O, называют главной оптической осью зеркала, а любую другую прямую, проходящую через точку С и поверхность зеркала, называют побочной оптической осью зеркала.

Когда луч света идет по какой-либо оптической оси, то угол его падения на поверхность зеркала равен нулю, поэтому такой луч после отражения идет по той же оптической оси в обратную сторону.
Если на вогнутое зеркало падает пучок лучей, параллельных его главной оптической оси, то после отражения от зеркала эти лучи проходят через точку Ф, лежащую на главной оптической оси (рис. 29.10, а), которую называют главным фокусом зеркала. После отражения от выпуклого зеркала такие лучи идут расходящимся пучком (рис. 29.10, б), но так, что их продолжения тоже сходятся в одной точке Ф (за зеркалом) — главном фокусе зеркала.

Таким образом, вогнутые зеркала являются собирающими. Главный фокус у них действительный. Выпуклые зеркала — рассеивающие, главный фокус у них мнимый. Расстояние от главного фокуса до вершины зеркала ОФ называют главным фокусным расстоянием F.
Когда лучи падают на зеркало параллельно одной из его побочных оптических осей, например АС (рис. 29.11), то после отражения в фокусе зеркала. Если побочные оси составляют небольшой угол с главной оптической осью, то все фокусы зеркала располагаются в фокальной плоскости КМ, проходящей через главный фокус Ф перпендикулярно главной оптической оси.

Выясним, как связано главное фокусное расстояние F с радиусом кривизны зеркала R. Луч АА1, параллельный главной оптической оси зеркала, после отражения идет по пути А1Ф (рис. 29.10, а). Соединим точку А1 со сферическим центром зеркала С. Из законов отражения следует, что  Так как
Так как  то
то  Следовательно,
Следовательно,  и
и  равнобедренный, т. е.
равнобедренный, т. е.  Поскольку поверхность зеркала всегда составляет малую часть сферы, приближенно можно считать
Поскольку поверхность зеркала всегда составляет малую часть сферы, приближенно можно считать  Таким образом,
Таким образом,  Это означает, что точка Ф делит радиус зеркала ОС пополам, т. е.
Это означает, что точка Ф делит радиус зеркала ОС пополам, т. е.
 (29.1)
(29.1)
Из законов отражения следует, что падающий и отраженный лучи в сферических зеркалах обладают обратимостью. Поэтому, если источник света поместить в главный фокус вогнутого зеркала, то после отражения от зеркала лучи практически пойдут параллельно главной оптической оси зеркала (рис. 29.12).

Для получения параллельных пучков света на практике вместо сферического зеркала используют параболическое зеркало, отражающая поверхность которого является частью поверхности параболоида вращения *). Параболическое зеркало дает более направленный пучок света. На этом свойстве зеркал основано устройство прожекторов и рефлекторов (отражателей) различного рода.
*) Параболоид вращения — геометрическое тело, получающееся при вращении параболы вокруг ее оси симметрии.
Построение изображений, получаемых с помощью сферических зеркал. Формула сферического зеркала
Сферические зеркала могут давать различные изображения предметов. Для построения изображения одной точки А, создаваемого сферическим зеркалом, пользуются любыми двумя из трех лучей, показанных на рис. 29.13. Луч 1 из точки А проводится параллельно главной оптической оси. После отражения он проходит через главный фокус зеркала Ф. Луч 2 из точки А проводится через главный фокус Ф. После отражения от зеркала он идет параллельно главной оптической оси зеркала. Луч 3 проводится через сферический центр С зеркала. После отражения он идет обратно к точке А по той же прямой.

Примеры изображений предметов, создаваемых сферическими зеркалами, показаны на рис. 29.14. Заметим, что выпуклое зеркало всегда дает мнимое изображение предметов.

Выясним, как найти положение изображения светящейся точки А, расположенной на главной оптической оси ОС зеркала (рис. 29.15). Ясно, что изображение точки должно быть на этой же оси (объясните, почему).

Проведем из точки А произвольный луч АВ. В точку его падения В проведем радиус СВ. Он является нормалью (перпендикуляром) к поверхности зеркала, поэтому  что и определяет положение отраженного луча BA1. В точке А1 и получится изображение точки А. Положение точки А1 однозначно определяется положением самой точки А. Поэтому точки А и А1 называют сопряженными.
что и определяет положение отраженного луча BA1. В точке А1 и получится изображение точки А. Положение точки А1 однозначно определяется положением самой точки А. Поэтому точки А и А1 называют сопряженными.
Обозначим расстояние АО через d, А1O — через f и ОС— через R. Для зеркал, поверхность которых составляет малую часть поверхности сферы, приближенно можно считать, что  и
и  Так как
Так как  то линия ВС в треугольнике ABA1 является биссектрисой угла ABA1, а это означает, что отрезки АС и A1C пропорциональны сторонам треугольника ABA1:
то линия ВС в треугольнике ABA1 является биссектрисой угла ABA1, а это означает, что отрезки АС и A1C пропорциональны сторонам треугольника ABA1:
 или
или 
Преобразуем последнее соотношение:

После деления на  получим
получим  Заменяя R его значением из (29.1), получим формулу сопряженных точек зеркала:
Заменяя R его значением из (29.1), получим формулу сопряженных точек зеркала:
 (29.2)
(29.2)
Эта формула справедлива как для вогнутых, так и для выпуклых зеркал, но числовые значения действительных величин следует подставлять с плюсом, а мнимых — с минусом. Например, главное фокусное расстояние вогнутых зеркал берется со знаком плюс, а выпуклых — со знаком минус. Отрицательный ответ показывает, что соответствующая ему величина — мнимая.
Законы преломления света
Выше говорилось, что преломление света обусловлено изменением скорости распространения света при переходе излучения из одной среды в другую. Рассмотрим более подробно, как волновая теория объясняет преломление света.
Пусть на поверхность раздела двух прозрачных сред КМ (рис. 29.16) падает пучок параллельных лучей А’В’, фронт волны которых в начальный момент времени занимает положение АС. Если скорость распространения излучения в первой среде  больше, чем скорость их распространения
больше, чем скорость их распространения  во второй среде, то за время t перемещения фронта волны на расстояние
во второй среде, то за время t перемещения фронта волны на расстояние  в первой среде, во второй среде волны распространяются из точки А по полусфере с радиусом
в первой среде, во второй среде волны распространяются из точки А по полусфере с радиусом  Следовательно, фронт волны к этому моменту времени займет положение BD и дальше будет перемещаться параллельно самому себе в направлении АА” или ВВ”.
Следовательно, фронт волны к этому моменту времени займет положение BD и дальше будет перемещаться параллельно самому себе в направлении АА” или ВВ”.

Таким образом, при переходе из первой среды во вторую световые лучи преломляются так, что угол преломления  оказывается меньше угла падения i, т. е. лучи приближаются к перпендикуляру AN.
оказывается меньше угла падения i, т. е. лучи приближаются к перпендикуляру AN.
Найдем математическую связь между углами i и  . Из прямоугольного треугольника ABC имеем
. Из прямоугольного треугольника ABC имеем  а из треугольника ABD имеем
а из треугольника ABD имеем  Разделив почленно эти равенства, получим
Разделив почленно эти равенства, получим  Так как
Так как  то
то
 (29.3)
(29.3)
Поскольку отношение скоростей света для двух определенных сред есть величина постоянная, ее обозначают  и называют показателем преломления второй среды относительно первой:
и называют показателем преломления второй среды относительно первой:
 (29.4)
(29.4)
Из сопоставления формул (29.3) и (29.4) получаем
 (29.5)
(29.5)
Справедливость формулы (29.5) можно проверить на опытах с оптической шайбой (рис. 29.17). При этом можно убедиться еще и в том, что падающий и преломленный лучи находятся в одной плоскости с отраженным лучом.

Итак, преломление света подчиняется двум законам.
1. Луч падающий и луч преломленный лежат в одной плоскости о перпендикуляром, восставленным в точке падения луча к поверхности раздела двух сред.
2. Отношение синуса угла падения к синусу угла преломления для двух данных сред есть величина постоянная:

Из второго закона следует, что при увеличении угла падения увеличивается и угол преломления (но не пропорционально).
Падающий и преломленный лучи обладают обратимостью, т. е. если падающий луч в первой среде, изображенный на рис. 29.18, а, направить по пути преломленного луча во второй среде, то после преломления он пойдет по пути падающего луча (рис. 29.18, 6). (Докажите это сами.) Следовательно, когда луч света переходит из среды оптически более плотной в среду оптически менее плотную, то он удаляется от перпендикуляра. Ясно, что числовое значение показателя преломления в этом случае будет меньше единицы.

Именно удалением световых лучей от перпендикуляра при преломлении объясняется кажущееся уменьшение глубины водоема, когда человек смотрит в воду (рис. 29.19, а). Если на дне водоема лежит камень К на глубине h, то человек видит мнимое изображение камня K1 на глубине h1. (Покажите, что  где п — показатель преломления воды относительно воздуха.)
где п — показатель преломления воды относительно воздуха.)

Когда человек смотрит в воду сбоку, то камень кажется смещенным еще и в горизонтальном направлении (к наблюдателю), так как человек видит мнимое изображение камня (рис. 29.19, б), положение которого зависит от угла падения лучей, попадающих в глаз.
Если лучи света падают на поверхность раздела прозрачных сред перпендикулярно к этой поверхности, то они проникают в другую среду, не преломляясь.
Абсолютный показатель преломления и его связь с относительным показателем преломления
Показатель преломления среды относительно вакуума, т. е. для случая перехода световых лучей из вакуума в среду, называется абсолютным (§ 27.7) и определяется формулой (27.10) : 
При расчетах абсолютные показатели преломления берут из таблиц, поскольку их величина определена достаточно точно с помощью опытов. Так как с больше  то абсолютный показатель преломления всегда больше единицы.
то абсолютный показатель преломления всегда больше единицы.
Если световое излучение переходит из вакуума в среду, то формулу второго закона преломления записывают в виде
 (29.6)
(29.6)
Формулой (29.6) на практике часто пользуются и при переходе лучей из воздуха в среду, так как скорость распространения света в воздухе очень мало отличается от с. Это видно из того, что абсолютный показатель преломления воздуха равен 1,0029.
Когда луч идет из среды в вакуум (в воздух), то формула второго закона преломления принимает вид
 (29.7)
(29.7)
В этом случае лучи при выходе из среды обязательно удаляются от перпендикуляра к поверхности раздела среды и вакуума.
Выясним, как можно найти относительный показатель преломления  по абсолютным показателям преломления. Пусть свет переходит из среды с абсолютным показателем
по абсолютным показателям преломления. Пусть свет переходит из среды с абсолютным показателем  в среду с абсолютным показателем
в среду с абсолютным показателем  Тогда
Тогда  и
и  откуда
откуда
 (29.8)
(29.8)
Формулу второго закона преломления для такого случая часто записывают следующим образом:
 (29.9)
(29.9)
Вспомним, что по теории Максвелла абсолютный показатель преломления можно найти из соотношения (27.11):  Так как у веществ, прозрачных для светового излучения,
Так как у веществ, прозрачных для светового излучения,  практически равно единице, то можно считать, что
практически равно единице, то можно считать, что
 (29.10)
(29.10)
Поскольку частота колебаний в световом излучении имеет порядок 1014 Гц, ни диполи, ни ионы в диэлектрике, имеющие сравнительно большую массу, не успевают изменять своего положения с такой частотой, и диэлектрические свойства вещества в этих условиях определяются только электронной поляризацией его атомов (§ 15.10). Именно этим объясняется различие между значением  из (29.10) и
из (29.10) и  в электростатике. Так, у воды
в электростатике. Так, у воды  а
а  у ионного твердого диэлектрика NaCl
у ионного твердого диэлектрика NaCl  а
а  Когда вещество состоит из однородных атомов или неполярных молекул, т. е. в нем нет ни ионов, ни природных диполей, то его поляризация может быть только электронной. Для подобных веществ
Когда вещество состоит из однородных атомов или неполярных молекул, т. е. в нем нет ни ионов, ни природных диполей, то его поляризация может быть только электронной. Для подобных веществ  из (29.10) и
из (29.10) и  совпадают. Примером такого вещества является алмаз, состоящий только из атомов углерода.
совпадают. Примером такого вещества является алмаз, состоящий только из атомов углерода.
Заметим, что величина абсолютного показателя преломления, кроме рода вещества, зависит еще от частоты колебаний, или от длины волны излучения. С уменьшением длины волны, как правило, показатель преломления увеличивается. Для стекла зависимость показателя преломления от длины волны приведена на рис. 34.3.
Полное отражение света. Предельный угол
Поместим источник света в какую-либо прозрачную среду и будем наблюдать переход светового излучения в среду оптически менее плотную, например в воздух (рис. 29.20).

На поверхности раздела свет будет и отражаться, и преломляться; по мере увеличения угла падения i энергия отраженного света будет возрастать, а энергия преломленного света — убывать. Кроме того, можно еще заметить, что при некотором угле падения iп преломленный луч скользит по поверхности раздела сред, а при угле падения, большем iп, преломленных лучей вообще нет. Явления такого рода можно обнаружить только в тех случаях, когда свет падает на поверхность раздела со стороны среды оптически более плотной, т. е. когда лучи при преломлении удаляются от перпендикуляра к поверхности раздела сред. Явление, при котором световое излучение полностью отражается от поверхности раздела прозрачных сред, называют полным отражением света.
Граница, отделяющая частично отраженные лучи от полностью отраженных лучей, определяется величиной угла iп (рис. 29.20). Угол падения лучей iп, при котором их угол преломления  равен
равен  называют предельным углом падения. Заметим, что полное отражение происходит только у тех лучей, которые падают на поверхность раздела под углом i, большим предельного угла iп. Величину предельного угла в каждом случае можно определить по относительному показателю преломления двух сред. Действительно, поскольку для угла iп угол
называют предельным углом падения. Заметим, что полное отражение происходит только у тех лучей, которые падают на поверхность раздела под углом i, большим предельного угла iп. Величину предельного угла в каждом случае можно определить по относительному показателю преломления двух сред. Действительно, поскольку для угла iп угол  из формулы (29.9) имеем
из формулы (29.9) имеем

Учитывая, что  окончательно получим
окончательно получим
 (29.11)
(29.11)
Когда световое излучение переходит из какой-либо среды в вакуум (в воздух), отношение (29.11) принимает вид
 (29.11а)
(29.11а)
(Объясните, почему при переходе лучей из среды оптически менее плотной в среду более плотную полное отражение невозможно.)
Полая пробирка, опущенная в воду, и пузырьки газа в воде иногда блестят, как посеребренные. Это явление объясняется полным отражением лучей на границе жидкости или твердого тела с газообразной средой. Полное отражение света используется при устройстве светопроводящих волокон. Свет направляют внутрь прозрачного волокна через один торец, а выходит он через другой торец, многократно отражаясь от стенок волокна и следуя всем его изгибам.
Светопроводы используются для оптической связи. С помощью модуляции света, идущего по светопроводу, можно передавать по нему несравненно больший поток информации, чем по обычному высокочастотному кабелю.
По пучку светопроводящих волокон можно передавать изображение предмета, помещенного перед торцом пучка. Это используется в медицине для осмотра внутренних органов больного (при этом часть волокон используется для внутреннего освещения).
Прохождение света через пластинку с параллельными гранями и через трехгранную призму. Призма с полным отражением
Выясним, как изменяет ход световых лучей прозрачная пластинка с двумя плоскими и параллельными гранями. Примером такой пластинки является хорошее оконное стекло.
Пусть на пластинку, сделанную из вещества с показателем преломления n, падает из воздуха узкий пучок света AO1 под углом i1 (рис. 29.21). После преломления на верхней грани этот пучок идет внутри пластинки по пути O1O2, вторично преломляется на нижней грани и идет в воздухе по пути O2B. Сравним углы i1 и  Для верхней грани формула второго закона преломления в данном случае принимает вид
Для верхней грани формула второго закона преломления в данном случае принимает вид

а для нижней грани


Поскольку  и
и  равны, после почленного умножения этих равенств получим
равны, после почленного умножения этих равенств получим

откуда  и
и  означает, что луч AO1 параллелен лучу О2В. Следовательно, лучи света после прохождения через пластинку с плоскими и параллельными гранями смещаются параллельно самим себе. Расстояние, на которое смещается луч после прохождения пластинки, тем больше, чем толще пластинка и чем больше показатель преломления ее вещества. Кроме того, смещение d зависит от угла падения лучей i1. Поэтому, когда человек смотрит сквозь толстую прозрачную пластинку под углом, все Предметы кажутся ему смещенными (рис. 29.22).
означает, что луч AO1 параллелен лучу О2В. Следовательно, лучи света после прохождения через пластинку с плоскими и параллельными гранями смещаются параллельно самим себе. Расстояние, на которое смещается луч после прохождения пластинки, тем больше, чем толще пластинка и чем больше показатель преломления ее вещества. Кроме того, смещение d зависит от угла падения лучей i1. Поэтому, когда человек смотрит сквозь толстую прозрачную пластинку под углом, все Предметы кажутся ему смещенными (рис. 29.22).

В прикладной оптике часто используют прозрачные трехгранные призмы. Две грани призмы, сквозь которые лучи входят в призму и выходят из нее, называют преломляющими гранями, а двугранный угол  составленный этими гранями, называют преломляющим углом призмы.
составленный этими гранями, называют преломляющим углом призмы.
Допустим, что на призму с показателем преломления n из воздуха падает узкий пучок света AO1, какого-то определенного цвета (рис. 29.23, а). В призме он идет по пути O1O2. При выходе из призмы он удаляется от перпендикуляра к грани и идет по пути О2В. Итак, в результате прохождения сквозь призму пучок света отклоняется к ее широкой части. Поскольку до призмы свет шел по направлению AO1, а после призмы идет по направлению О2В, то смещение пучка произошло на угол  (рис. 29.23, а), который называют углом отклонения, Этот угол тем больше, чем больше показатель преломления вещества призмы n и ее преломляющий угол
(рис. 29.23, а), который называют углом отклонения, Этот угол тем больше, чем больше показатель преломления вещества призмы n и ее преломляющий угол 

Заметим, что поскольку показатель преломления n зависит от  то и отклонение лучей в призме зависит от их цвета. Например, красные лучи отклоняются на меньший угол
то и отклонение лучей в призме зависит от их цвета. Например, красные лучи отклоняются на меньший угол  чем фиолетовые. Подробнее этот вопрос рассмотрим дальше (§ 34.2).
чем фиолетовые. Подробнее этот вопрос рассмотрим дальше (§ 34.2).
Если трехгранную призму поместить в такую среду, относительно которой показатель преломления вещества призмы окажется меньше единицы, то, пройдя призму, луч AO1 (рис. 29.23, б) будет отклоняться в сторону преломляющего угла  а не к широкой части призмы, на угол
а не к широкой части призмы, на угол  (Объясните, почему параллельные лучи, падающие на призму, после выхода из нее остаются параллельными.)
(Объясните, почему параллельные лучи, падающие на призму, после выхода из нее остаются параллельными.)
Подсчет показывает, что предельный угол для стекла составляет около 42. Поэтому в стеклянной прямоугольной призме с углами по 45° легко получить полное отражение света. На рис. 29.24, а показан поворот лучей на 90° в такой призме, а на рис. 29.24, б показано, как поворачивается изображение в такой же призме. На рис. 29.24, в изображена призма прямого зрения и ход лучей в ней. Видно, что верхние и нижние лучи меняются местами, но продолжают распространяться в прежнем направлении.

Услуги по физике:
Лекции по физике:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
[spoiler title=”источники:”]
http://natalibrilenova.ru/otrazhenie-i-prelomlenie-sveta/
[/spoiler]
