Как найти расстояние до прямой начертательная геометрия

Определение расстояния от точки до прямой

Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую. В начертательной геометрии она определяется графическим путем по приведенному ниже алгоритму.

Алгоритм

1. Прямую переводят в положение, в котором она будет параллельна какой-либо плоскости проекции. Для этого применяют методы преобразования ортогональных проекций.
2. Из точки проводят перпендикуляр к прямой. В основе данного построения лежит теорема о проецировании прямого угла.
3. Длина перпендикуляра определяется путем преобразования его проекций или с использованием способа прямоугольного треугольника.

Пример

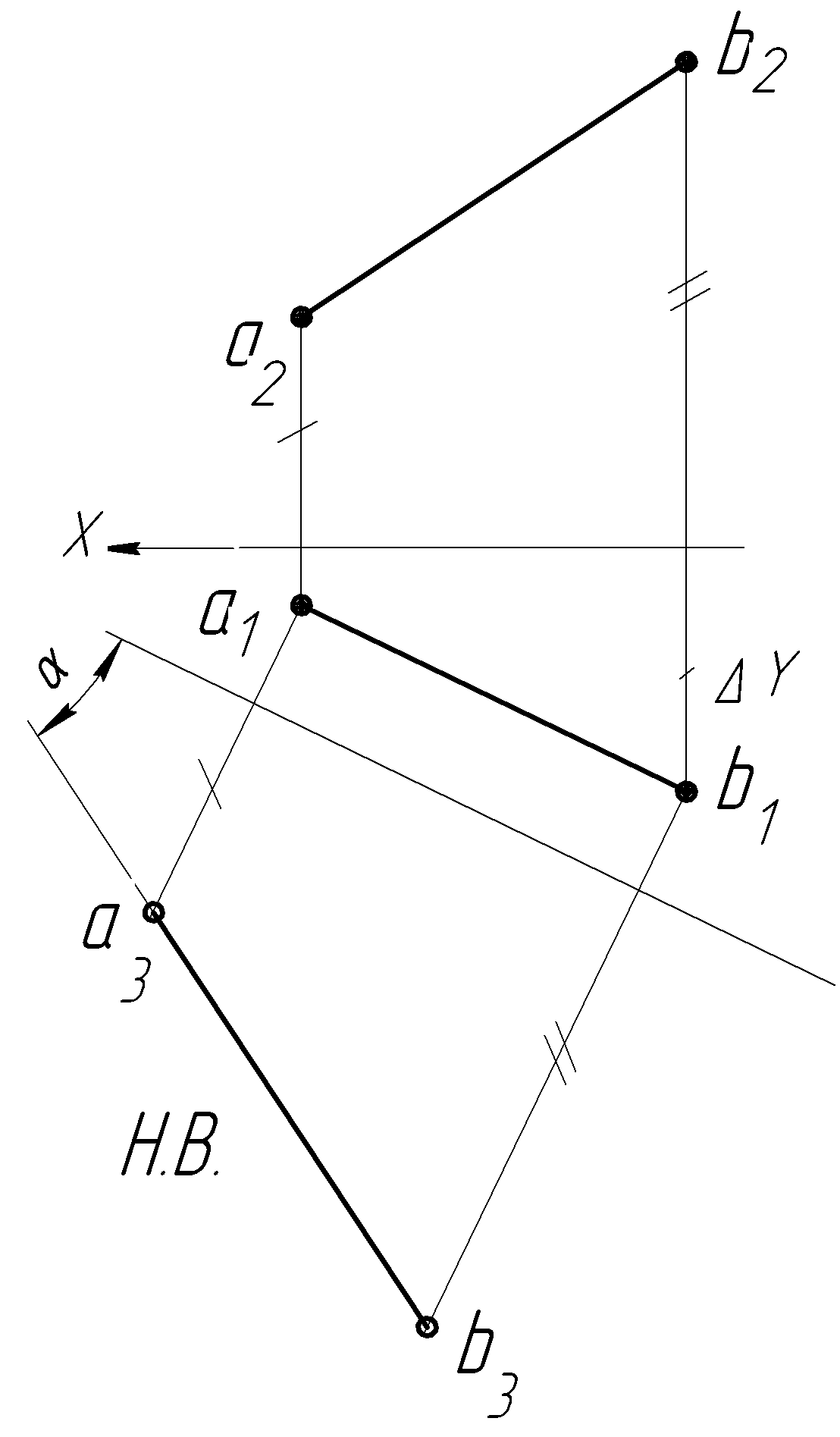
На следующем рисунке представлен комплексный чертеж точки M и прямой b, заданной отрезком CD. Требуется найти расстояние между ними.

Решение

Согласно нашему алгоритму, первое, что необходимо сделать, это перевести прямую в положение, параллельное плоскости проекции. При этом важно понимать, что после проведенных преобразований фактическое расстояние между точкой и прямой не должно измениться. Именно поэтому здесь удобно использовать метод замены плоскостей, который не предполагает перемещение фигур в пространстве.

Результаты первого этапа построений показаны ниже. На рисунке видно, как параллельно b введена дополнительная фронтальная плоскость П₄. В новой системе (П₁, П₄) точки C”₁, D”₁, M”₁ находятся на том же удалении от оси X₁, что и C”, D”, M” от оси X.

Выполняя вторую часть алгоритма, из M”₁ опускаем перпендикуляр M”₁N”₁ на прямую b”₁, поскольку прямой угол MND между b и MN проецируется на плоскость П₄ в натуральную величину. По линии связи определяем положение точки N’ и проводим проекцию M’N’ отрезка MN.

На заключительном этапе нужно определить величину отрезка MN по его проекциям M’N’ и M”₁N”₁. Для этого строим прямоугольный треугольник M”₁N”₁N₀, у которого катет N”₁N₀ равен разности (Y_M1 – Y_N1) удаления точек M’ и N’ от оси X₁. Длина гипотенузы M”₁N₀ треугольника M”₁N”₁N₀ соответствует искомому расстоянию от M до b.

Второй способ решения

• Параллельно CD вводим новую фронтальную плоскость П₄. Она пересекает П₁ по оси X₁, причем X₁∥C’D’. В соответствии с методом замены плоскостей определяем проекции точек C”₁, D”₁ и M”₁, как это изображено на рисунке.
• Перпендикулярно C”₁D”₁ строим дополнительную горизонтальную плоскость П₅, на которую прямая b проецируется в точку C’₂ = b’₂.
• Величина расстояния между точкой M и прямой b определяется длиной отрезка M’₂C’₂, обозначенного красным цветом.

Похожие задачи:

Задача 4. 2.
Определить расстояние от точки С
до прямой АВ (рисунок 24).

План решения:

а) через точку С
строим плоскость, задав ее фронталью f
и горизонталью h
(h₁  А₁В₁,
f₂  А₂В₂).
Ориентируем эту плоскость перпендикулярно
отрезку АВ, т.к. перпендикуляр
из точки С на отрезок АВ
обязательно лежит в этой плоскости;

б) задача свелась
к нахождению точки пересечения отрезка
АВ с построенной через точку С
плоскостью (f ∩
h):

‑ через фронтальную
проекцию А₂В₂
проводим вспомогательную секущую
плоскость Р_V;

‑ построим
горизонтальную проекцию линии пересечения
1₁ – 2₁;

‑ там, где
проекция прямой 1₁
– 2₁ пересекает проекцию
отрезка А₁В₁
находится проекция точки К₁,
точка К общая и для прямой АВ,
и для плоскости, заданной фронталью и
горизонталью. По линии связи отмечаем
положение точки К₂
на фронтальной проекции;

в) отрезок СК
расположен перпендикулярно отрезку АВ
(т.к. лежит в плоскости (f
∩ h)) и определяет
расстояние от точки С до прямой
АВ. Натуральную величину отрезка
находим методом прямоугольного
треугольника.

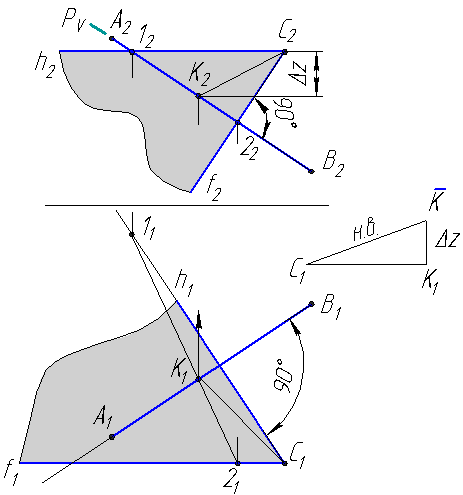
Рисунок 24 ‑
Определение расстояний от точки С
до прямой АВ

Подготовка к
контрольной работе № 1. Контрольная
работа № 1 включает задачи, объединяющие
темы 1, 2, 3, 4.

Тема 5 «Преобразование чертежа методом замены плоскостей проекций»

Задачи по теме 5
выдаются на пятой неделе, после проведения
лекции 4 [1, 2, 7].

Для решения задач
необходимо усвоить следующий теоретический
материал: способ преобразования
комплексного чертежа с помощью замены
плоскостей проекций, а именно, решение
четырех основных задач преобразования
чертежа:

– превращение
отрезка общего положения в прямую
уровня;

– превращение
отрезка общего положения в проецирующий;

– превращение
плоскости общего положения в проецирующую;

– превращение
плоскости общего положения в плоскость
уровня.

5.1 Теория к выполнению индивидуального задания

Решение задач
методами замены плоскостей
проекций сводится к выполнению
четырех основных задач:

а) преобразование
прямой общего положения в прямую уровня
(определение углов наклона прямой к
плоскостям проекций и натуральной
величины отрезка прямой);

б) преобразование
прямой общего положения в проецирующую
(определение величины двугранного
угла, расстояния между прямыми);

в) преобразование
плоскости общего положения в проецирующую
плоскость (определение углов наклона
плоскости общего положения к плоскостям
проекций, расстояния от точки до
плоскости);

г) преобразование
плоскости общего положения в плоскость
уровня (определяется натуральная
величина плоскости).

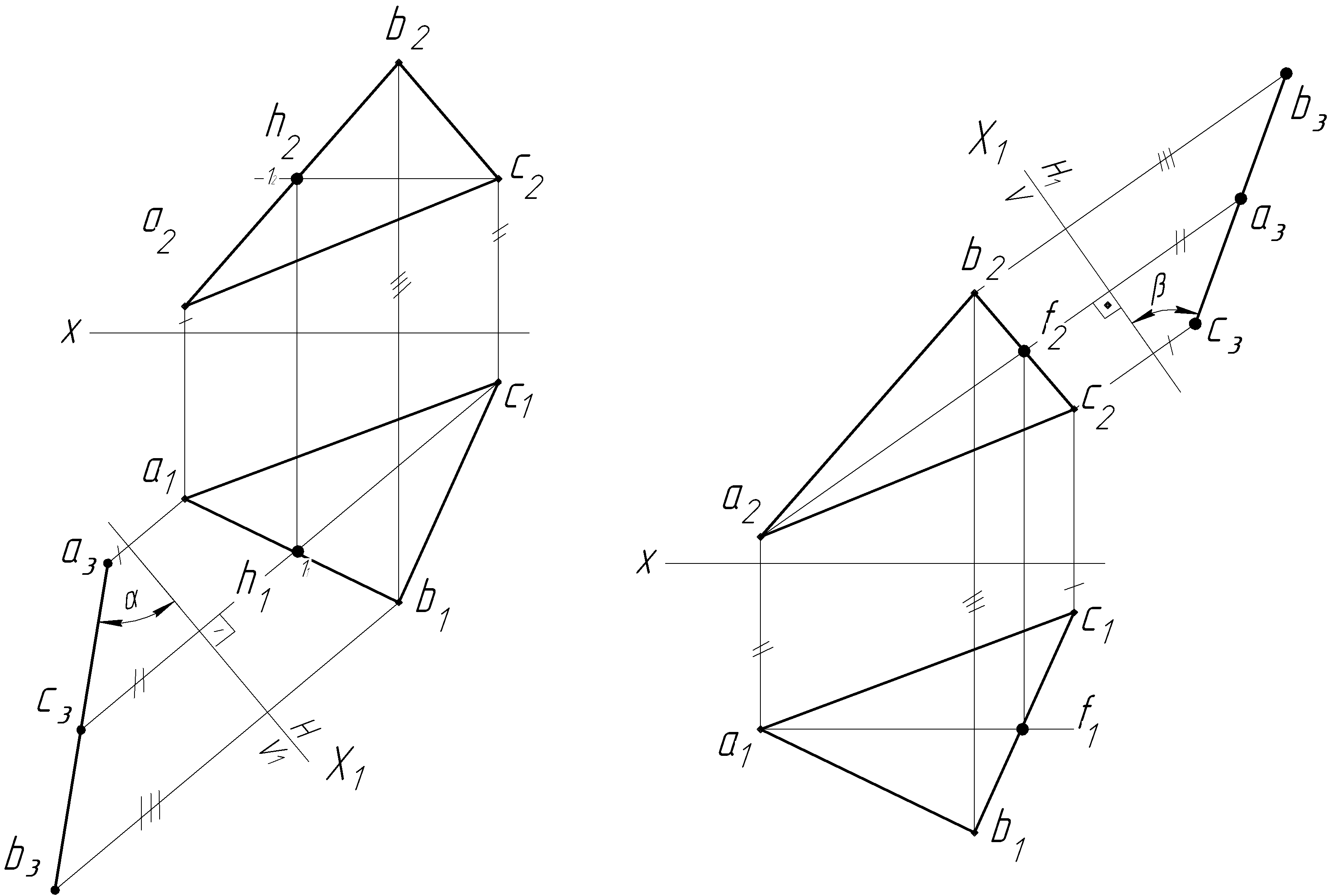
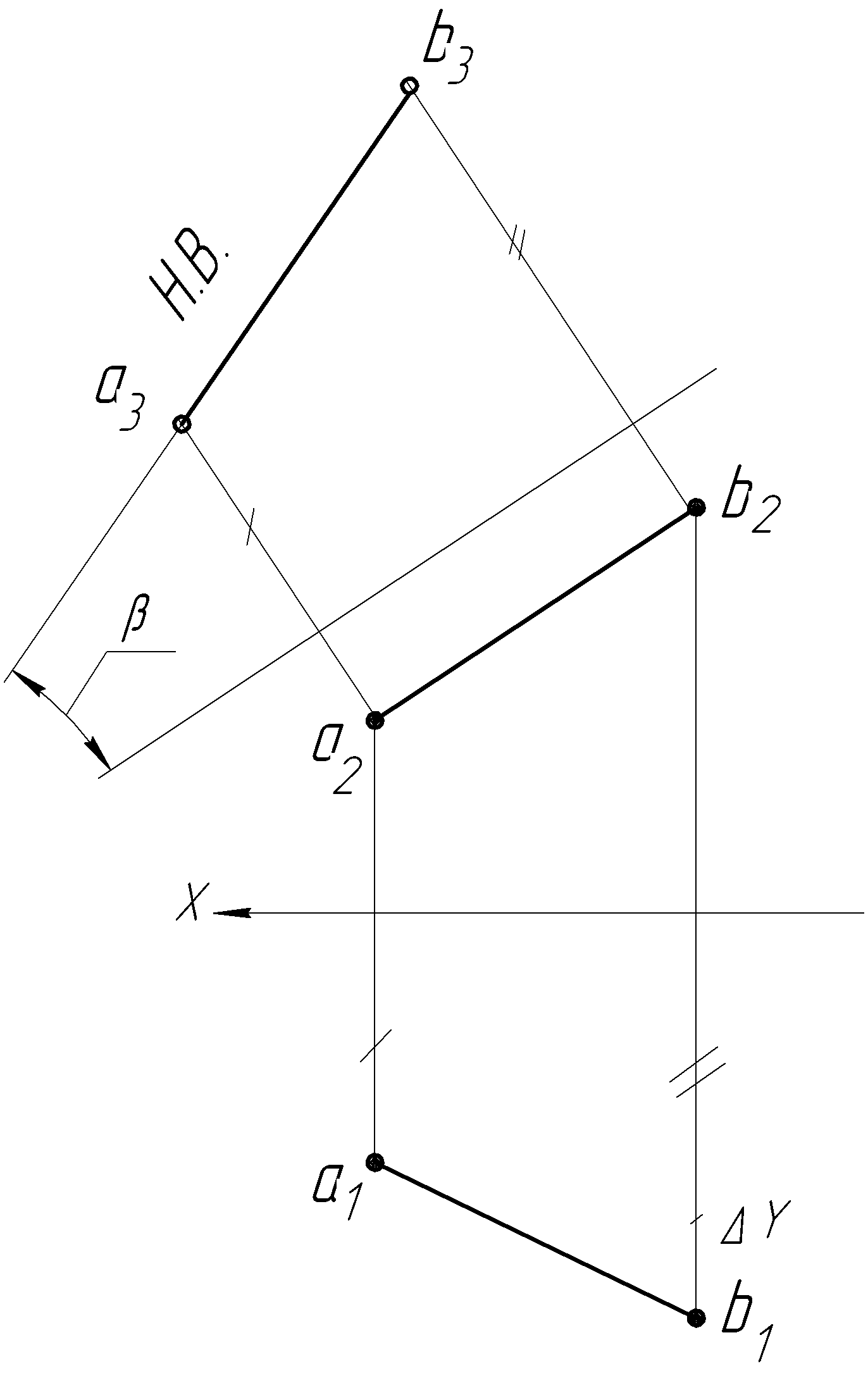
Рассмотрим вопрос
«Преобразование прямой общего
положения в прямую уровня» на
примере определения истинной
величины отрезка АВ
(рисунок 25). В
заданной системе плоскостей проекции
V/H
отрезок занимает
общее положение.

Заменим
плоскость проекций V
новой плоскостью V₁,
параллельной
заданному отрезку АВ.
Новая ось проекций
х₁
при этом, очевидно,
должна быть параллельна горизонтальной
проекции ab
отрезка. Для нахождения
новой фронтальной проекции отрезка
построены новые фронтальные проекции
его концов (точек А
и В)
в системе V₁/H.
Новая фронтальная проекция а’₁b’₁
отрезка – истинная
величина отрезка АВ.
Кроме истинной величины отрезка получаем
натуральную величину угла наклона
отрезка АВ
к плоскости проекций
Н
– это угол ,
образованный истинной величиной отрезка
АВ
и осью х₁.

На
рисунке 26 эта же задача решена путем
замены плоскости проекций H
новой плоскостью H₁.
В этом случае новая
ось должна быть расположена параллельно
а’b’.
Новая горизонтальная
проекция (а₁b₁)
отрезка – его истинная
величина. Кроме истинной величины
отрезка получаем натуральную величину
угла наклона отрезка АВ
к плоскости проекций
V
– это угол ,
образованный истинной величиной отрезка
АВ
и осью х₁.

Рисунок 25 – Определение истинной величины отрезка АВ и угла наклона его к плоскости проекций Н

Рисунок 26 – Определение истинной величины отрезка АВ и угла наклона его к плоскости проекций V

Чтобы прямую
общего положения АВ преобразовать в
проецирующую (а₄b₄),
необходимо произвести две последовательные
замены плоскостей проекций.
С помощью первой замены плоскости
V на плоскость
V₁
преобразовать прямую общего
положения АВ в прямую уровня
а₃b₃.
С помощью второй замены плоскости H
на плоскость H₁
преобразовать прямую уровня
а₃b₃
в прямую проецирующую (а₄b₄)
(рисунок 27).

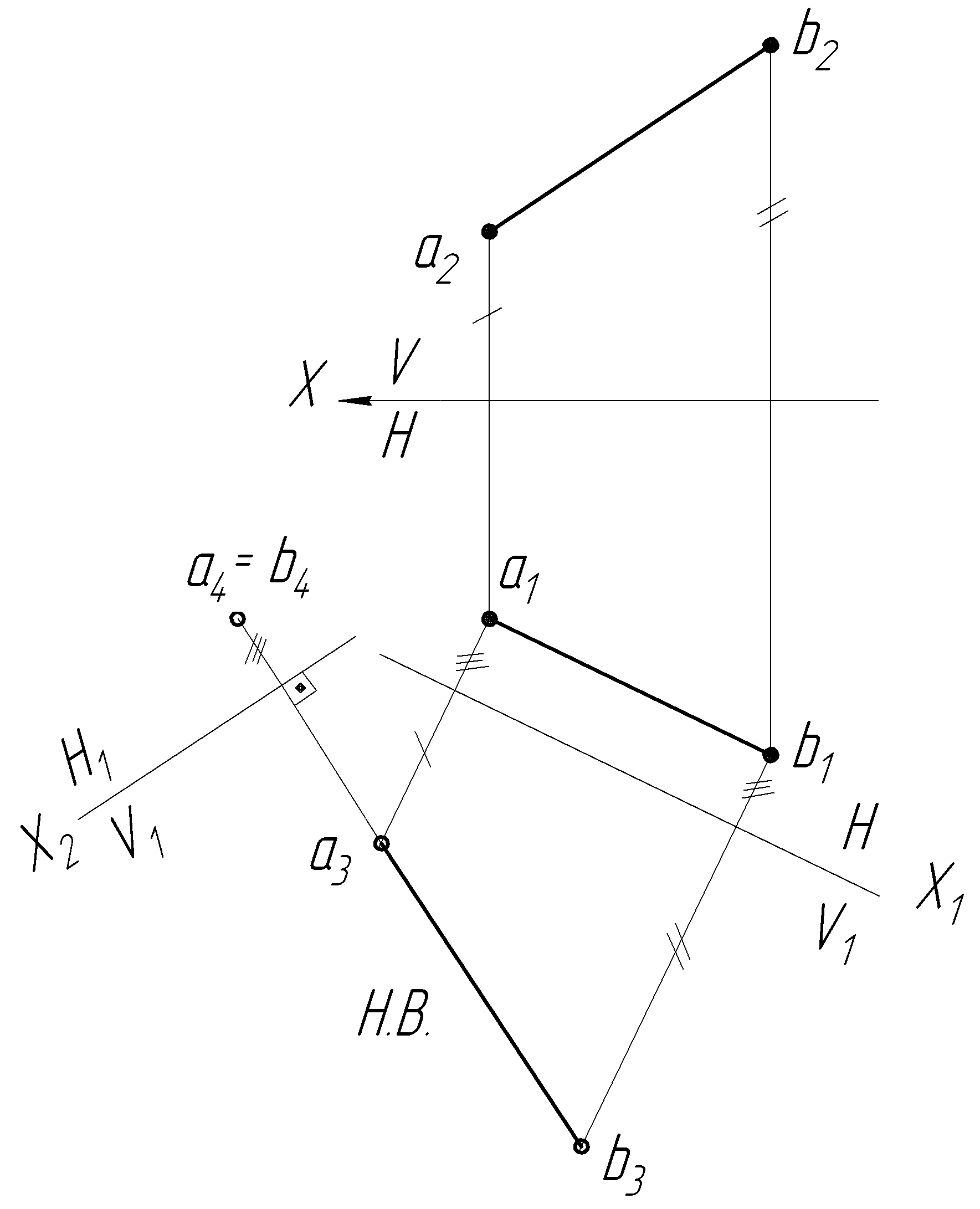
Рисунок
27 –
Преобразование
отрезка
общего положения АВ

в
проецирующую прямую

Преобразование
плоскости общего положения в проецирующую
плоскость.
Заменим
плоскость проекций V
на плоскость проекций V₁
(рисунок
28а).
Плоскость
проекций V₁
выберем
перпендикулярно плоскости треугольника
АВС
– новая ось проекций x₁
должна быть перпендикулярна
горизонтальной проекции горизонтали
плоскости h₁
треугольника АВС.
Переносим на новую фронтальную плоскость
проекций V₁
расстояния от а₂,
в₂,
с₂
до оси Х.
На новую фронтальную плоскость проекций
треугольник проецируется в виде прямой
линии c₃a₃b₃.
Угол a
– натуральная величина угла наклона
плоскости АВС
к горизонтальной плоскости проекций
H.

а б

Рисунок 28 – Преобразование плоскости общего положения в проецирующую плоскость, определение угла наклона плоскости АВС к плоскостям проекций H и V

При
определении угла наклона к фронтальной
плоскости проекций заменим плоскость
проекций H
на плоскость проекций H₁
(рисунок 28б).
Плоскость проекций
H₁
выберем
перпендикулярно плоскости треугольника
АВС
– новая ось проекций x₁
должна быть
перпендикулярна
фронтальной проекции фронтали треугольника
АВС
– f₂.
Переносим на новую горизонтальную
плоскость проекций H₁
расстояния от горизонтальных проекций
точек плоскости треугольника ‑ a₁b₁c₁
до оси Х.
На новую фронтальную плоскость проекций
треугольник проецируется в виде прямой
линии c₃a₃b₃.
Угол

– натуральная
величина угла наклона плоскости
АВС
к фронтальной плоскости проекций
V.

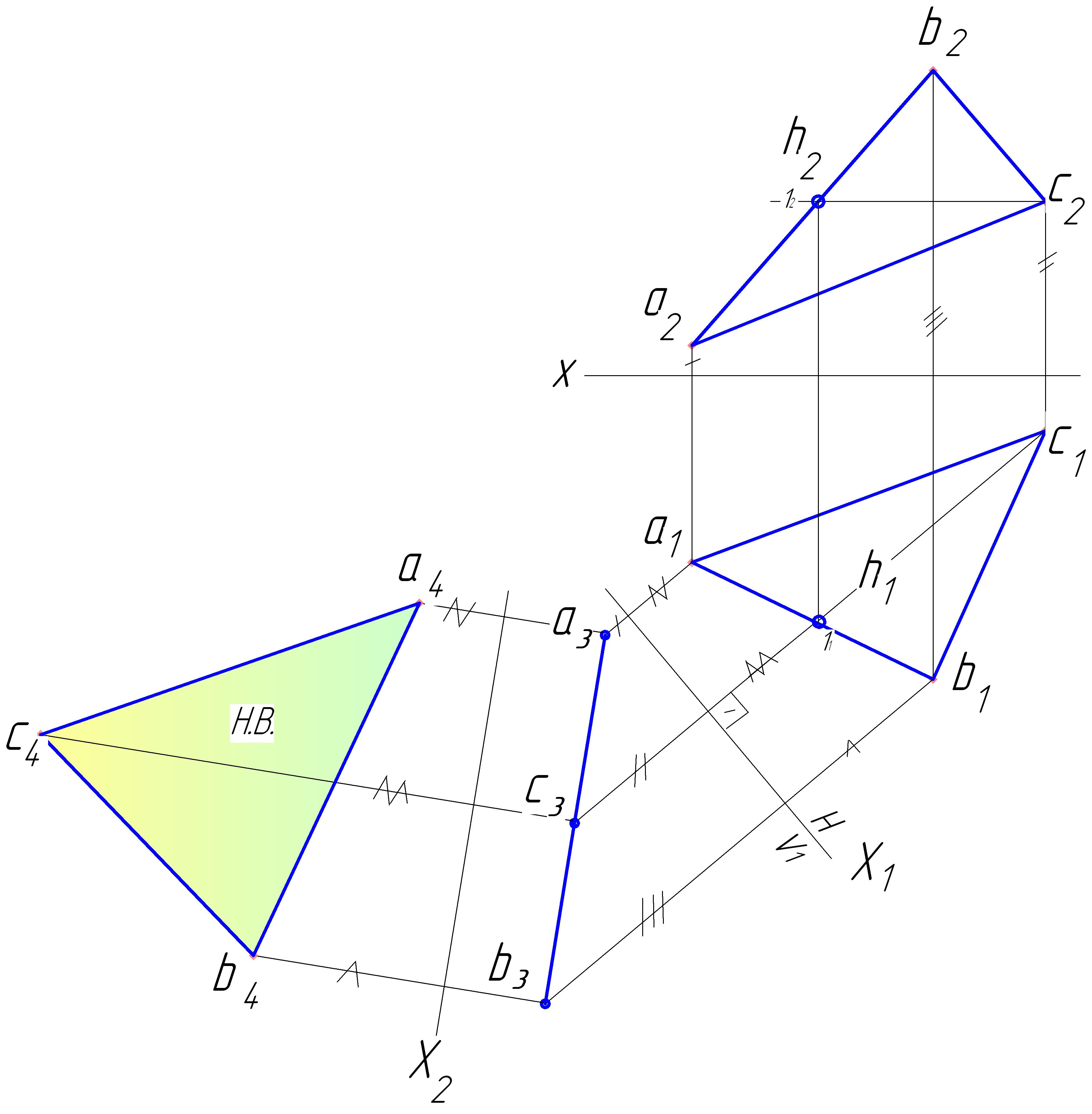
Чтобы плоскость
общего положения преобразовать в
плоскость уровня, необходимо
произвести две последовательные замены
плоскостей проекций. С
помощью первой замены плоскости V
на плоскость V₁
преобразовывают плоскость
общего положения ABC
в проецирующую плоскость a₃b₃c₃,
с помощью второй замены плоскости H
на плоскость H₁
преобразовывают проецирующую
плоскость a₃b₃c₃
в плоскость уровня а₄b₄с₄
(рисунок 29).

Рисунок 29 – Преобразование плоскости общего положения в плоскость уровня, определение истинной величины плоскости треугольника АВС

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую.

Это определение может быть положено в основу составления алгоритма графического решения задачи определения расстояния от точки до прямой.

Рис. 263 дает наглядное представление о графическом решении задачи по определению расстояния от точки А до прямой а . Через точку А можно провести множество прямых {l₁, l₂,l₃, …, l_n} , перпендикулярных к прямой а . Это множество прямых определяет плоскость γ. Чтобы выделить из {l₁, l₂,l₃, …, l_n} единственную прямую l_j, пересекающую прямую а , необходимо найти точку встречи прямой а с плоскостью γ – М = а ∩ γ; определить длину отрезка [AM].

Реализация этого алгоритма путем геометрических построений значительно упрощается, если прямая будет параллельна плоскости проекции.

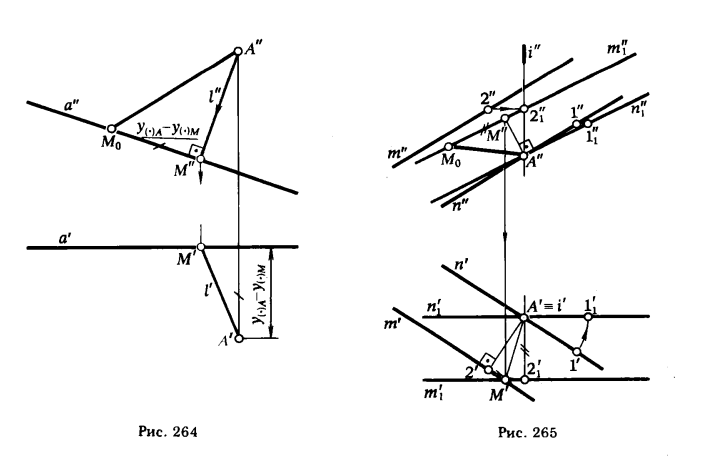
В этом случае можно без каких-либо вспомогательных построений провести проекции прямой, перпендикулярной данной и проходящей через заданную точку. На рис. 264 показано решение такой задачи. Как видно из чертежа, решение достигается минимальным числом геометрических построений. Поэтому нет смысла решать эту задачу в общем виде, а следует предварительно с помощью способов преобразования ортогональных проекций перевести прямую в положение, параллельное плоскости проекции (см. рис. 260, 261,262).

Решение задачи на определение расстояния между параллельными прямыми ничем не отличается от только что рассмотренного примера. Это утверждение базируется на том, что расстояние между параллельными прямыми определяется величиной перпендикуляра, опущенного из точки, взятой на одной прямой, на другую прямую.

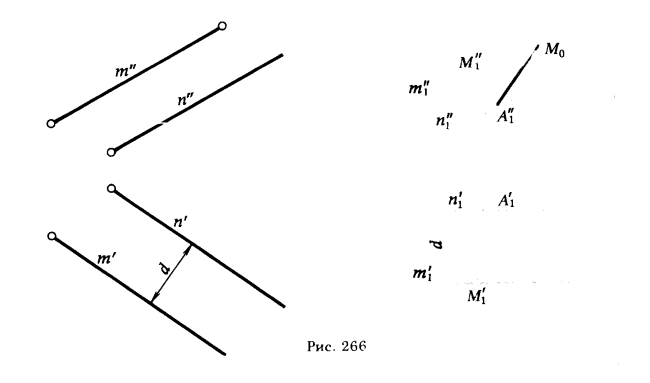
ПРИМЕР I. Определить расстояние между пераллельными прямыми m и n (рис. 26В) .

РЕШЕНИЕ. На прямой n отмечаем произвольную точку A ∈ n . Вращаем прямые m и n вокруг оси i (i ∋ A, i ⊥ π₁ ) до положения m₁|| π₂ и n₁ || π₂. Из точки A” опускаем перпендикуляр А”М” на прямую m”₁. Определяем действительную величину [AM] .

На рис. 266 показан второй вариант решения этой задачи. С помощью способа параллельного перемещения прямые тип переведены в положение, параллельное плоскости π₂. Дальнейшее решение сводится к определению расстояния от точки А, взятой на одной прямой, до другой прямой m₁.

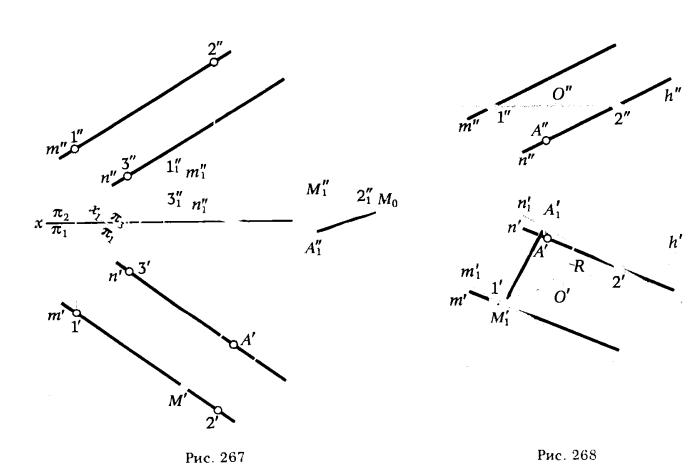
Перевод прямых m и n из общего положения в частное можно осуществить путем замены плоскости π₂ новой плоскостью π₃, параллельной прямым m и n. Решение задачи этим способом приведено на рис. 267.

На рис. 268 рассматриваемая задача решена путем вращения прямых m и n вокруг горизонтали h до положения, параллельного плоскости π₁.

Содержание:

1. Расстояние от точки до прямой и плоскости
2. Расстояние от точки до прямой особого положения
3. Расстояние от точки до прямой общего положения
4. Расстояние от точки до плоскости особого положения
5. Расстояния от точки до плоскости общего положения
6. Расстояние между параллельными плоскостями, прямой и плоскостью. Расстояние между двумя прямыми
7. Угол между прямой и плоскостью, двумя плоскостями
8. Метрические и позиционные задачи
9. Длина дуги кривой линии
10. Центр и радиус кривизны. Эволюта и эвольвента кривой
11. Эквидистанта кривой
12. Расстояние от точки до кривой линии и поверхности
13. Пересечение прямой линии с кривой поверхностью
14. Пересечение кривой линии с плоскостью

Метрическими называются задачи, решение которых связано с определением характеристик геометрических фигур, определяемых (измеряемых) линейными и угловыми величинами.

Расстояние от точки до прямой и плоскости

Расстояние от точки до плоскости – это длина перпендикуляра, который опущен из заданной точки. Чтобы найти расстояние между скрещивающимися прямыми, необходимо воспользоваться знаниями о нахождении расстояния от точки до плоскости, поскольку для определения расстояния между скрещивающимися прямыми необходимо на одной из прямой выбрать точку.

Расстояние от точки до прямой особого положения

Метрические задачи по проецированию точки, прямой и плоскости связаны с определением расстояний, площадей, углов. Все задачи на определение расстояния от точки до прямой и плоскости, между параллельными прямой и плоскостью и двумя плоскостями сводятся к задаче об определении расстояния между двумя точками. Задачи по определению площади плоской фигуры сводятся к нахождению натуральной величины этой фигуры. Определение угла между двумя прямыми, прямой и плоскостью, двумя плоскостями  невозможно без применения способов преображения комплексного чертежа (см. п. 2.1.6, 2.3.3). Методами, описанными в разделе 1, можно определить только проекции этих углов.

Для определения расстояния от точки А до прямой l необходимо провести из данной точки перпендикуляр n до прямой, определить точку N пересечения прямых n, l и найти длину отрезка AN. Последняя является искомым расстоянием  (рис. 1.51).

Расстояние от точки до прямой общего положения

Определение расстояния от точки до прямой уровня

При определении расстояния от точки до прямой l особого положения прямой угол между прямыми  l  проецируется в натуральную величину на одну из плоскостей проекций (см. п. 1.4.8), а натуральная величина отрезка АN определяется способом прямоугольного треугольника (см. п. 1.4.4) или вращением вокруг проецирующей оси (см. п. 2.2.2).

На рис. 1.52 обозначено расстояние от точки А до горизонтали h. На горизонтальной проекции построена проекция А1N1 искомого отрезка. С помощью линий проекционной связи найдена фронтальная проекция A2N2. Натуральная величина отрезка AN определена способом прямоугольного треугольника.

Расстояние от точки до прямой общего положения

Задача на определение расстояния от точки А до прямой l общего положения усложняется тем, что проекции прямого угла между прямой l и проведённым к ней перпендикуляром  не равны 90° (см. п. 1.4.8, рис. 1.25). Для решения этой задачи применяются такие способы:

а) способ вспомогательной нормальной плоскости (рис. 1.53);

б) способ замены плоскостей проекций (см. п. 2.1.3);

в) способ вращения вокруг проецирующей оси (см. п. 2.2.3).

 Способ вспомогательной нормальной плоскости

Суть способа вспомогательной нормальной плоскости

Через точку А проводится плоскость Σ общего положения, перпендикулярная прямой l (рис. 1.53 б). Эта плоскость задаётся горизонталью h и фронталью f, пересекающимися в точке А. При этом горизонтальная проекция горизонтали h1 и фронтальная проекция фронтали f2 перпендикулярны соответствующим проекциям прямой l. Основа N перпендикуляра  находится как точка пересечения прямой l с перпендикулярной её плоскостью Σ с помощью фронтально-проецирующей секущей плоскости Ф (см. п. 1.5.7). Натуральная величина отрезка AN равна искомому расстоянию от точки А до прямой l общего положения.

Расстояние от точки до плоскости особого положения

Для определения расстояния от точки А до плоскости Σ необходимо провести из данной точки перпендикуляр  до плоскости, определить точку N их пересечения и найти длину отрезка AN.

При определении расстояния от точки А до плоскости особого положения прямой угол между прямой  и одним из следов плоскости Σ проецируется в натуральную величину на соответствующую плоскость  проекций (рис. 1.54).

На рис. 1.55 определено расстояние от точки А до горизонтально-проецирующей плоскости Σ. На горизонтальной плоскости проекций через точку А1 проведена проекция  перпендикуляра до горизонтального следа  плоскости с основой N1. При этом перпендикуляр  –  горизонтальная прямая уровня. С помощью линии проекционной связи найдена фронтальная проекция A2N2. Натуральная величина отрезка AN равна длине его горизонтальной проекции А1N1.

Расстояние от точки до плоскости особого положения

– Определение расстояния от точки до горизонтально-проецирующей плоскости

Расстояния от точки до плоскости общего положения

Задача на определение расстояния от точки D до плоскости Σ общего положения определяется  таким способом. Из точки D проводится прямая , перпендикулярная плоскости Σ (см. п. 1.5.9, рис. 1.47 – 1.48), и определяется точка N их пересечения (см. п. 1.5.7, рис. 1.38). Натуральная величина отрезка DN равна расстоянию от точки D до заданной плоскости (рис. 1.56).

Расстояние от точки до плоскости общего положения

Определение расстояния от точки до плоскости

На рис. 1.57 плоскость Σ задана треугольником АВС. Для построения прямой , проходящей через точку D перпендикулярно до плоскости треугольника, в последнем  проводятся горизонталь h и фронталь f. Горизонтальная проекция h1 горизонтали перпендикулярна  горизонтальной проекции  прямой, фронтальная проекция f2 фронтали перпендикулярна  . Точка N пересечения прямой с плоскостью Σ  определяется методом вспомогательной секущей плоскости. В данном случае прямая  заключается во фронтально- проецирующую плоскость Ω, заданную фронтальным следом Ω2,и определяется линия  k пересечения плоскостей Σ, Ω. Искомая точка N является точкой пересечения прямых k, п. Длина отрезка АN определяется способом прямоугольного треугольника.

Расстояние между параллельными плоскостями, прямой и плоскостью. Расстояние между двумя прямыми

Расстояние между параллельными плоскостями Σ и Ω равно расстоянию от любой  точки D одной плоскости до другой плоскости (рис. 1.58).

Расстояние между параллельными плоскостями

Определение расстояния между параллельными плоскостями

На рис. 1.59 одна из плоскостей Σ задана прямыми a, b,  пересекающимися в точке D, другая Ω – горизонтальным и фронтальным следами . Из точки D опускается перпендикуляр  на плоскость Ω. При этом горизонтальная проекция  перпендикулярна горизонтальному следу  плоскости, фронтальная проекция  перпендикулярна фронтальному следу  Точка N пересечения прямой  с плоскостью Ω определяется методом вспомогательной секущей плоскости. в данном случае через прямую  проводится горизонтально-проецирующая плоскость Ψ, заданная горизонтальным следом Ψ1, и определяется линия k пересечения плоскостей Ω, Ψ. Искомая точка N является точкой пересечения прямых k, п. Длина отрезка DN определяется способом прямоугольного треугольника.

Расстояние между параллельными прямой l и плоскостью Σ (рис. 1.60) равно расстоянию от любой точки D прямой до плоскости.

На рис. 1.61 плоскость Σ задана горизонтальным и фронтальным следами . Из любой  точки D, принадлежащей прямой l, опускается перпендикуляр  на плоскость Σ и определяется точка N их пересечения с помощью горизонтально-проецирующей плоскости Ψ. Длина отрезка DN определяется способом прямоугольного треугольника.

Расстояние между параллельными прямой и плоскостью

Определение расстояния между параллельными прямой и плоскостью

Расстояния между параллельными прямыми равно расстоянию DN от любой точки D одной прямой до другой прямой (рис. 1.62) и может быть определено способом вспомогательной  нормальной плоскости (см. п. 1.6.1.2, рис. 1.53).

Расстояние между параллельными прямыми

Способ вспомогательной нормальной плоскости

На рис. 1.63 через точку D прямой l проводится  Σ плоскость общего положения, перпендикулярная прямой  Эта плоскость задаётся горизонталью h и фронталью f, пересекающимися в точке D. При этом горизонтальная проекция горизонтали h1 и фронтальная проекция фронтали f2 перпендикулярны соответствующим проекциям прямой . Основа N перпендикуляра  находится как точка пересечения прямой  с перпендикулярной ей плоскостью Σ с помощью фронтально-проецирующей секущей плоскости Ф. Натуральная величина отрезка DN равна искомому расстоянию между параллельными прямыми l, m.

Расстояние между скрещивающимися прямыми l, m равно наименьшему расстоянию от точек одной прямой до другой прямой (рис. 1.64) и определяется такими способами:

а) способом вспомогательной параллельной плоскости;

б) способами преобразования комплексного чертежа (см. п. 2.1.5, 2.2.5, 2.3.2).

Расстояние между скрещивающимися прямыми

Суть способа вспомогательной параллельной плоскости

Расстояние между скрещивающимися прямыми  равно расстоянию от любой точки D одной прямой до параллельной ей плоскости  Σ, проведенной через вторую прямую (рис. 1.65).

Способ вспомогательной параллельной плоскости

На рис. 1.66 через прямую  проведена плоскость Σ общего положения, заданная двумя прямыми  пересекающимися в произвольной точке А. Эта плоскость параллельна прямой l, поскольку проекции прямой  параллельны соответствующим проекциям прямой l. Для построения прямой ,  проходящей через точку D перпендикулярно плоскости Σ, в последней проводятся горизонталь h и фронталь f. Горизонтальная проекция  прямой  перпендикулярна  горизонтальной проекции h1 горизонтали, фронтальная проекция  перпендикулярна f2. Точка N пересечения прямой  с плоскостью Σ определяется методом вспомогательной секущей плоскости . В данном случае,  через прямую  проводится горизонтально-проецирующая плоскость Ω, заданная горизонтальным следом Ω2, и определяется линия k пересечения плоскостей Σ, Ω.

Искомая точка N – точка пересечения прямых k, . Длина отрезка DN определяется способом прямоугольного треугольника.

Определение расстояния между скрещивающимися прямыми

Угол между прямой и плоскостью, двумя плоскостями

Угол φ между прямой l и плоскостью Σ определяется как угол между прямой l и её проекцией  на эту плоскость (рис. 1.67 а).

Угол между прямой и плоскостью

На рис. 1.67 б плоскость Σ задана горизонтальным и фронтальным следами  Проекция прямой l на эту плоскость проходит через отрезок  , один конец которого (точка K) – точка пересечения прямой l с плоскостью  Σ, другой (точка  ) – точка пересечения прямой  с плоскостью Σ. Прямая  проходит через любую точку N прямой l перпендикулярно плоскости Σ. Горизонтальная проекция  перпендикулярна следу , фронтальная проекция  перпендикулярна до  Ортогональными проекциями на  плоскости проекций П1, П2 угла φ между прямой l и плоскостью Σ являются соответствующие  проекции угла  . Натуральная величина угла φ определяется методами преобразования комплексного чертежа (см. п. 2.1.6, 2.3.3, 2.4.2).

Угол θ между двумя плоскостями Σ, Ω называется двухгранным углом (рис. 1.68). Он определяется как угол между перпендикулярами  к линии k пересечения плоскостей (прямая принадлежит плоскости Σ, прямая  плоскости Ω).

Двухгранный угол

Вышеуказанные способы определения углов между прямой и плоскостью и двумя плоскостями относятся к прямым способам, базирующимся на использовании определения углов  φ, θ. Прямые способы имеют существенный недостаток   – громоздкость вспомогательных построений .

С целью упрощения практической реализации задачи построения углов φ, θ  и чтения комплексного чертежа применяются непрямые способы, базирующиеся на свойствах этих углов 

Свойство угла между прямой и  плоскостью

Угол φ между прямой l и плоскостью Σ дополняет вспомогательный  угол  до 90° (рис. 1.69 а):

Вспомогательный  угол  -это угол между прямой l  и перпендикуляром  проведенным из любой её точки D к плоскости Σ.

Вспомогательный угол

На рис. 1.69 б плоскость Σ задана горизонтальным и фронтальным следами . Проекции прямоq n, проведенyной через произвольную точку D прямой l перпендикулярно плоскости Σ, перпендикулярны соответствующим следам  этой плоскости. Натуральная величина угла определяется методами преобразования комплексного чертежа (см. п. 2.1.6, 2.3.3, 2.4.2).Угол φ определяется по формуле (1.1).

Свойство двухгранного угла

Угол θ между двумя плоскостями Σ, Ω равен углу  между прямыми  проходящими через произвольную точку пространства перпендикулярно этим плоскостям (рис. 1.70 а).

Непрямой способ определения двухгранного угла

На рис. 1.70 б плоскости Σ, Ω заданы горизонтальными и фронтальными следами  и  соответственно. Проекции вспомогательных прямых  перпендикулярны  соответствующим следам плоскостей Σ, Ω. Натуральная величина угла  определяется методами преобразования комплексного чертежа (см. п. 2.1.6, 2.3.3). Угол θ между плоскостями Σ, Ω равен углу  между прямыми  .

Метрические и позиционные задачи

Позиционными считаются задачи, решение которых позволяет полу-чить ответ о принадлежности точки или линии поверхности, а также зада–чи на определение общих элементов, принадлежащих различным геомет-рическим фигурам. Метрическими называются задачи, решение которых связано с нахо-ждением метрических характеристик геометрических фигур, определяе-мых линейными и угловыми величинами.

Длина дуги кривой линии

Задача на определение длины дуги s кривой линии является достаточно сложной. В начертательной геометрии она решается приближённо способом линейной интерполяции: дуга ОМ линии l разбивается на N участков  которые условно заменяются одноимёнными отрезками прямых. Длина кривой ОМ определяется как сумма длин построенных отрезков с применением способов прямоугольного треугольника (рис. 3.74 а) или вращения вокруг проецирующих осей (рис. 3.74 б).

От количества N выбранных участков зависит точность определения длины дуги

Определение длины дуги кривой линии

Задача на определение длины кривой линии намного сложнее, чем  расчёт площадей геометрических фигур и объёмов тел. В античные времена единственная удачная попытка определения длины кривой линии была предпринята для окружности.

Декарт высказывал ошибочную мысль, что «отношение между прямым и кривым неизвестно и не может быть познано человечеством»

. Первым достижением было определение длины дуги параболы Нейла в 1657 р. Позже К. Рэн и Х. Гюйгенс нашли длину дуги циклоиды. Незадолго до открытия математического анализа Дж. Грегори создал общую теорию нахождения дуги кривой линии.

 

Кристофер Рэн (Christopher Wren) – английский математик и архитектор, профессор математики в Оксфорде, член Королевского товарищества. Занимался вопросами кораблестроения, сопротивления жидкости, механикой вёсел и парусов и т.д.. Автор величественных архитектурных сооружений, в том числе Собора святого Павла.

Центр и радиус кривизны. Эволюта и эвольвента кривой

 Кривизна любой линии l в точке М характеризуется двумя основными параметрами: центром и радиусом кривизны

Центр и радиус кривизны – центр С и радиус ρ окружности , которая является точнейшим приближением  данной кривой l в окрестности её точки М (рис. 3.75 а).

Центр кривизны С находится на внутренней нормали  кривой l в данной точке М. На рис. 3.75 б показан способ определения центра кривизны С плоской кривой l в точке М. В точке М и близко к ней расположенной точке N проведены касательные  Центр кривизны С является точкой пересечения перпендикуляров  к  касательным. Радиус СМ построенной окружности  с  центром в точке С является радиусом ρ кривизны линии l в точке М..

Центр и радиус кривизны

Понятия центра и радиуса кривизны введены Лейбницем. Геометрическое место центров кривизны линии l для всех её точек называется эволютой (от латинского evolute – развитый). На рис. 3.76 показаны эволюты эллипса, дуги синусоиды и циклоиды. Для их построения на этих кривых выбирается совокупность точек   …  и проводятся касательные  … и нормали , … Точки 1, 2, … пересечения последовательных пар нормалей являются точками, принадлежащими эволюте данной кривой. Например, эволюта эллипса (рис. 3.76 а) имеет форму звезды с двумя осями симметрии; эволюта половины дуги синусоиды (рис. 3.76 б) имеет две асимптоты и одну ось симметрии; эволюта ветви циклоиды (рис. 3.76 в) имеет одну ось симметрии.

Эволюты плоских кривых

Линия  для которой заданная кривая l является эволютой, называется эвольвентой (от латинского evolvens – разворачивающий). Например, на рис. 3.76 а эллипс является эвольвентой фигуры в форме звезды.

Эволюты и эвольвенты широко используются в проектировании машин и механизмов. Например, зубчатые колёса (рис. 3.77) имеют профиль в форме кривой, эволюта которой является окружностью. Другими словами, такие зубчатые колеса имеют форму эвольвенты окружности.

 Применение эвольвенты окружности

Для построения эвольвенты окружности (рис. 3.78) последняя делится на N равных частей (как правило, N = 12) точками , … Из этих точек проводятся отрезки  …, касательные к окружности и с равномерно возрастающей длиной (от нуля до длины окружности). Эвольвента окружности проходит через точки 1, 2, …

Эвольвента окружности

Джеймс Грегори (James Gregory) – шотландский математик и астроном, член Королевского общества. Один из основателей математического анализа. Грегори является автором зеркального телескопа, метода определения расстояния от Земли до Солнца, способа числового интегрирования и разложения функций в бесконечные ряды.

Готфрид Вильгельм фон Лейбниц (Gottfried Wilhelm von Leibniz) – выдающийся немецкий философ, математик, физик, юрист, историк, дипломат, изобретатель, филолог; основатель и первый президент Берлинской академии наук,  иностранный член Французской академии наук. Автор дифференциального и интегрального исчисления, учения про анализ и синтез, проектов научных исследований магнитного поля Земли. Лейбниц впервые ввёл термин «модель» в математических исследованиях и высказал мысль о возможности машинного моделирования функций человека. Лейбниц является автором механического арифмометра, прибора использования энергии ветра, чертежа подводной лодки, идеи создания паровой машины и т.д..

Эквидистанта кривой

 Эквидистанта кривой (от латинского æquidistans – равноудалённый) – геометрическое место  концов N отрезков одинаковой длины r, отложенных на нормалях  к заданной кривой l (рис. 3.79 а).

На рис. 3.79 б построена эквидистанта  кривой l.  В точках  … кривой l проводятся касательные  … По одну сторону кривой l вдоль нормалей … откладываются отрезки, … одинаковой длины r, концы 1, 2, … которых принадлежат искомой эквидистанте.

Эквидистанта кривой

В металлообработке эквидистантой к траектории центра концевой фрезы является контур поверхности, которая получается в результате фрезерования. В системах автоматического раскроя плоских изделий (пластин, тканей и т.д.) эквидистанта является контуром, которым ограничивается припуск на обработку.

Расстояние от точки до кривой линии и поверхности

Расстояние от точки А до кривой линии  – это наименьшее из всех расстояний l от этой точки до всех точек кривой 

В начертательной геометрии расстояние l от точки А до кривой  определяется способом конической поверхности (рис. 3.80).

Суть способа конической поверхности

Строится коническая поверхность Ф с направляющей , совпадающей с данной кривой, и вершиной А, которая совпадает с данной точкой. Среди совокупности прямолинейных образующих выбирается образующая l наименьшей длины.

На рис. 3.80 построен комплексный чертёж точки А и кривой . Строятся проекции образующих  …, заданных отрезками , … Длины этих отрезков определяются способом вращения вокруг фронтально-проецирующей оси, проходящей через точку А. Натуральные величины  … вращаются вокруг горизонтально-проецирующей оси, проходящей через точку А, до общего фронтального положения уровня.

Способ конической поверхности

Среди совокупности отрезков , … выбирается наименьший, длина которого равна искомому расстоянию от точки А до кривой .

Расстояние от точки А до кривой поверхности Ω является наименьшим из всех расстояний l от этой точки до всех точек поверхности Ω.

В начертательной геометрии расстояние l от точки А до кривой поверхности Ω определяется способом конических поверхностей.

Суть способа конических поверхностей.

Строятся конические поверхности  … с вершиной А, которая совпадает с данной точкою, и направляющими , … совпадающими с направляющими поверхности Ω. Среди совокупности прямолинейных образующих каждой конической поверхности выбираются образующие  … наименьших длин. По точкам полученных образующих  …, принадлежащих поверхности Ω, строится кривая Расстояние от точки А до поверхности Ω равно расстоянию от этой точки до линии Она находится способом конической поверхности (рис. 3.80)

На рис. 3.81 построен комплексный чертёж точки А и поверхности Ω. Способом конических поверхностей (см. рис. 3.80) определяются наименьшие расстояния  … от точки А до направляющих  … По точкам 1, 2, … строятся проекции линии . Расстояние от точки А до кривой  определяется способом конической поверхности (рис. 3.80)..

Описанные выше графические способы конических поверхностей являются приближенными и требуют громоздких построений. Точное, аналитическое определение расстояния от точки до кривой линии и  поверхности является слишком сложной задачей поиска экстремума функции нескольких переменных параметров, которая может быть решена методами вариационного исчисления.

Способ конических поверхностей

Пересечение прямой линии с кривой поверхностью

Прямая линия l и кривая поверхность Ω могут иметь такие виды взаимного расположения:

а) прямая и поверхность не пересекаются (рис. 3.82 а);

б) прямая касается поверхности (см. п. 3.3, рис. 3.70 – 3.73);

в) прямая пересекает поверхность  (рис. 3.82 б), в том числе перпендикулярна  ей (см. п. 3.3, рис. 3.70 – 3.73).

Взаимное расположение прямой линии и кривой поверхности

Из п. 1.5.7 известно, что прямая пересекает поверхность первого порядка (плоскость) в одной точке. В случае поверхности второго и высших порядков прямая может пересекать поверхность в точках, количество которых не превышает порядок поверхности. Например, прямая может пересекать тор (поверхность четвертого порядка) максимум в четырёх точках (рис. 3.82 б).

Для определения точек пересечения прямой l с поверхностью Ω применяются такие способы:

а) способ вспомогательной секущей плоскости особого положения (см. п. 4.2.2.1, рис. 4.17 – 4.19);

б) способ вспомогательной секущей плоскости общего положения (см. п. 4.2.2.2, рис. 4.20 – 4.23);

в) способ замены плоскостей проекций (см. п. 4.2.2.3, рис. 4.24);

г) способ вращения вокруг проецирующей оси (см. п. 4.2.2.3, рис. 4.25 – 4.27);

д) метод последовательных приближений (см. п. 4.2.2.5);

е) способ косоугольного проецирования.

Все способы, кроме последнего, детально описаны в п. 4.1.2, 4.2.2 на примере гранных тел и поверхностей вращения.

Способ косоугольного проецирования является универсальным, то есть может быть использован для определения точек пересечения прямой l с любой кривой поверхностью.

На рис. 3.83 определена точка K пересечения прямой l с гиперболическим параболоидом Ω. Применён способ косоугольного проецирования на биссекторную плоскость  Направление проецирования і совпадает с прямой l, поэтому проекция  является точкой. Все точки и линии поверхности Ω также проецируются на биссекторную плоскость. Проекция  точки пересечения прямой l с поверхностью Ω совпадает с проекцией  Через точку  проводится образующая  принадлежащая поверхности  . С помощью линии проекционной связи определяются проекция  и проекции  искомой точки K пересечения прямой l с гиперболическим параболоидом.

Определение точки пересечения прямой линии с кривой поверхностью

Пересечение кривой линии с плоскостью

Кривая линия l и плоскость Σ могут иметь такие виды взаимного расположения:

а) линия и плоскость не пересекаются (рис. 3.84 а);

б)  плоскость касается лини (см. п. 3.3, рис. 3.70 – 3.73);

в) линия пересекает плоскость (рис. 3.84 б), в том числе перпендикулярна  ей (см. п. 3.3, рис. 3.70 – 3.73).

Взаимное расположение прямой линии и плоскости

Кривая линия может пересекать плоскость в точках, количество которых не превышает порядок кривой. Например, эллипс (кривая второго порядка) пересекает плоскость максимум в  двух точках (рис. 3.84 б).

Для определения точек пересечения линии l с плоскостью Σ применяются такие способы:

а) способ вспомогательной секущей цилиндрической поверхности (см. п. 4.2.2.4, рис. 4.29 – 4.30);

б) метод последовательных приближений (см. п. 4.2.2.5);

в) способ косоугольного проецирования.

Способ косоугольного проецирования может быть применён для определения точек пересечения плоскости Σ с любой кривой линией l.

На рис. 3.85 определены точки M, N пересечения кривой линииl с плоскостью Σ, заданной параллельными прямыми a, b, с применением способа косоугольного проецирования на биссекторную плоскость . Направление проецирования і совпадает с прямыми a, b, поэтому проекция  является прямой. Все точки линии l также проецируются на биссекторную плоскость. Проекции  точек пересечения линий l с плоскостью Σ принадлежат проекции  . С помощью линий проекционной связи определяются горизонтальная и фронтальная проекции искомых точек M, N..

Определение точек пересечения кривой линии с плоскостью

Задачи на пересечение кривой линии с поверхностью, а также на пересечение поверхности плоскостью или другой поверхностью детально рассмотрены в разделе 4.

Примеры и образцы решения задач:

• Решение задач по инженерной графике
• Решение задач по начертательной геометрии

Услуги по выполнению чертежей:

1. Заказать чертежи
2. Помощь с чертежами
3. Заказать чертеж в компасе
4. Заказать чертеж в автокаде
5. Заказать чертежи по инженерной графике
6. Заказать чертежи по начертательной геометрии
7. Заказать черчение

Учебные лекции:

1. Инженерная графика
2. Начертательная геометрия
3. Оформление чертежей
4. Чертеж общего вида и сборочный чертеж
5. Техническое рисование
6. Машиностроительные чертежи
7. Геометрические построения
8. Деление окружности на равные части
9. Сопряжение линий
10. Коробовые кривые линии
11. Построение уклона и конусности
12. Лекальные кривые
13. Параллельность и перпендикулярность
14. Методы преобразования ортогональных проекций
15. Поверхности
16. Способы проецирования
17. Способы преобразования чертежа
18. Кривые линии
19. Кривые поверхности
20. Трёхгранник Френе
21. Проецирование многогранников
22. Проецирование тел вращения
23. Развёртывание поверхностей
24. Проекционное черчение
25. Проецирование
26. Проецирование точки
27. Проецирование отрезка прямой линии
28. Проецирование плоских фигур
29. Способы преобразования проекций
30. Аксонометрическое проецирование
31. Проекции геометрических тел
32. Сечение геометрических тел плоскостями и развертки их поверхностей
33. Взаимное пересечение поверхностей тел
34. Сечение полых моделей
35. Разрезы
36. Требования к чертежам деталей
37. Допуски и посадки
38. Шероховатость поверхностей и обозначение покрытий
39. Разъемные и неразъемные соединения деталей
40. Передачи и их элементы