Солнце – звезда, которая сделала возможным появление жизни на Земле. Она создает благоприятный климат для нормального существования человека и животного мира. Поэтому вопрос каково же это расстояние до Солнца волновал людей с самого начала времен.
Оглавление
- 1 Точное расстояние на сегодняшний день
- 2 Астрономическая единица
- 3 Приливы и отливы
- 4 Афелий и перигелий
- 5 Измерения расстояния до Солнца в древней Греции
- 5.1 Предположения Аристарха Самосского
- 5.2 Измерения Гиппарха Никейского
- 6 Расчет нового времени
- 6.1 Метом прямоугольных треугольников Кристиана Гюйгенса
- 6.2 Измерения Кассини и Рише
- 7 Исследования новейшего времени
- 7.1 Метод радиолокации
- 7.2 Определение дистанции лазером
- 8 Единицы измерений космических расстояний
Точное расстояние на сегодняшний день
Земля, как и все тела в Солнечной системе, обращается вокруг Солнца по эллиптической орбите. Поэтому точной цифры для расстояния от Земли до Солнца нет.
Если смотреть относительно северного полушария, то летом, когда Земля находится в апогелии (афелии) расстояние от нее до Солнца равно 152 095 566 км, а зимой, при прохождении нашей планеты перигелия, расстояние уменьшается до 147 093 290 км.
Среднее расстояние составляет 149,6 млн км или 8,31 световой минуты. Это означает, что свет от Солнца до Земли летит 8 минут и 18 секунд. То есть мы видим Солнце в прошлом на 8 минут.
Но и эта цифра не является конечной и постоянной. Земля удаляется от Солнца, и ее орбита изменяется на 15 метров каждые 100 лет.

Астрономическая единица
Для определения расстояний внутри Солнечной системой в 2012 годы ввели новую единицу измерения – астрономическая единица. Она равна среднему расстоянию от Земли до Солнца – 149 597 870,7 километров.
Обозначается астрономическая единица – а.е. или АЕ для русскоязычных источников. Для иностранных принято обозначение «UA» — astronomical unit. Возможно написание как строчных букв, так и через точки.

Приливы и отливы
Одним из основных «дел» нашего естественного спутника Луны являются приливы и отливы. Но и здесь влияние Солнца избежать не удалось.
Хоть наша звезда и находится на таком невероятном расстоянии, она тоже влияет на уровень воды в океане.
Когда Луна и Солнце оказываются относительно Земли с одной стороны – то происходит сизигийный прилив – самый сильный подъем воды, ведь на нее оказывает влияние гравитационная сила и Луны и Солнца.
Когда же Солнце и Луна находятся относительно Земли под прямым углом, тогда происходит Квадратурный прилив – подъем воды самый незначительный, так как гравитационные силы Луны и Солнца «растягивают» океан в свою сторону.
Афелий и перигелий
Афелий или апогелий – наибольшее расстояние между Землей и Солнцем. Эту точку наша планета проходит летом с 3 по 7 июля. Перигелий – наименьшее расстояние между Землей и Солнцем, планета проходит зимой со 2 по 5 января.
Именно из-за этого зима в северном полушарии не такая холодная как могла бы быть, а лето не такое палящее, как в южном полушарии.

Измерения расстояния до Солнца в древней Греции
Именно древние греки считаются основоположниками современной астрономии. И их вычисления расстояния от Земли до Солнца постоянно совершенствовались.
В древней Греции утвердилась геометрия – как наука о внешнем мире и о формах и фигурах.
Предположения Аристарха Самосского
Одним из первых кто задался вопросом космических расстояний был Аристарх Самосский, живший в III веке до н.э. Он изучал Луну и Солнце, а также вычислял размер нашей планеты.
Ученый проводил наблюдения за фазами Луны, особенно за Лунными и Солнечными затмениями.
Взяв прямоугольный треугольник, в вершины которого он поместил Солнце, Луну и Землю, с помощью теоремы Пифагора Аристарху Самосскому удалось вычислить, что Солнце должно находится на расстоянии в 20 раз превышающим расстояние от Земли до Луны.

Древнегреческий астроном ошибся на несколько порядков. Но эта его работа внесла огромный вклад в дальнейшее изучение космоса и небесных тел.
Измерения Гиппарха Никейского
Во II веке до н.э. Гиппарх Никейский внес огромный вклад в астрономию того времени. Он первый ввел тригонометрические методы при наблюдениях за звездами. Начал использовать секстант и квадрант – специальные приборы для более точных измерений углов. Собрал все звезды в первый каталог звезд и разделил все звезды по звездным величинам. Первый рассчитал и предсказала прецессию равноденствий. Ввел теорию о затмениях.
Благодаря этому, у Гиппарха Никейского получилось рассчитать расстояние от Луны до Земли, оно получилось 71 радиуса Земли. Использую те же принципы, он вычислил расстояние до Солнца и получил результат в 490-2550 радиуса Земли. Такое большое расхождения получилось из-за малой точности приборов измерения.

Расчет нового времени
В средние века, когда появились телескопы, возможности для измерения значительно увеличились.
Так, Иоганн Кеплер первый засомневался в результатах древнегреческих астрономов, считая что они сильно занижены.
Кристиан Гюйгенс, голландский астроном, первый получил максимально точный результат, который расходится с современным только на 7%.
Метом прямоугольных треугольников Кристиана Гюйгенса
Этот метод подразумевает знания тригонометрии, когда из трех элементов прямоугольного треугольника можно найти остальные. Такими элементами в вычислениях Гюйгенса стали катит и два острых угла.
Но для этого нужно было знать значение катета — расстояние между Землей и другим небесным телом. В качестве другого объекта была взята Венера. Венера находилась в прямом углу прямоугольного треугольника, тогда как Солнце и Земля занимали два острых угла. Для нахождения расстояния между Землей и Венерой необходимо было знать размер Венеры. Но таких данных на тот момент не было, поэтому Гюйгенс сделал очень смелое предположение, что Венера равна по размеру Земле. И оказался прав. Значение острого угла, в котором находится Земля, а именно угол Солнце – Земля – Венера, был легко найден. Зная катет и острый угол легко можно найти гипотенузу – расстояние от Солнца до Земли. Гюйгенс получил значение в 160 млн км.

Измерения Кассини и Рише
Джованни Кассини и Жан Рише вплотную занимались измерением расстояний в космосе. Наблюдая за Марсом, с помощью уточного параллакса, ученым удалось найти расстояние между двумя планетами. Затем, используя метрическую системы, они смогли вычислить расстояние между Землей и Солнцем – 140 млн км.

Исследования новейшего времени
Современные технологии позволяют не только измерять расстояние с необычайной точностью, но и слетать к объекту измерений. НАСА запустила специальный зонд для изучения солнечных явлений. Он приблизится к светилу максимально близко – 6 млн км.
Метод радиолокации
С изобретением радио, его стали применять и в освоении космоса. Этот метод основан на получении сигнала отраженной волны от объекта.
Так как Солнце является очень мощным источником электромагнитных волн, то этот метод требовал определенной энергозатраты – необходимо было сгенерировать мощную волну, чтобы она не потерялась на фоне Солнца.
Так в 1961 году был получен результат в 149 599 300 км, но погрешность метода составила 2 тыс км. Тогда эксперимент повторил через год, и результат уже был 149 598 100 км, погрешность «всего лишь» 750 км.
Определение дистанции лазером
В настоящее время лазерные дальномеры – одни из самых точных приборов для измерения расстояний.
С помощью уголковых отражателей на Луне, астрономам удалось получить максимально точный результат с погрешностью в несколько сантиметров, который и считается верным на настоящее время.
Единицы измерений космических расстояний
- Астрономическая единица – среднее расстояние от Земли до Солнца. Равна 150 млн км. Удобна для измерения расстояний в Солнечной системе.
- Световой год – расстояние, которое проходит свет за один год – 9,46 трлн км. Удобно для измерения расстояния для звезд, помимо Солнца.
- Парсек – 3,26 световых года – расстояние от объекта до Солнца, где параллакс равен одной угловой секунде.
Еще больше космоса и интересных фактов в телеграмм-канале.
Солнце – звезда, которая сделала возможным появление жизни на Земле. Она создает благоприятный климат для нормального существования человека и животного мира. Поэтому вопрос каково же это расстояние до Солнца волновал людей с самого начала времен.
- Еще больше космоса и интересных фактов в телеграмм-канале.
- Поддержать канал
Точное расстояние на сегодняшний день
Земля, как и все тела в Солнечной системе, обращается вокруг Солнца по эллиптической орбите. Поэтому точной цифры для расстояния от Земли до Солнца нет.
Если смотреть относительно северного полушария, то летом, когда Земля находится в апогелии (афелии) расстояние от нее до Солнца равно 152 095 566 км, а зимой, при прохождении нашей планеты перигелия, расстояние уменьшается до 147 093 290 км.
Среднее расстояние составляет 149,6 млн км или 8,31 световой минуты. Это означает, что свет от Солнца до Земли летит 8 минут и 18 секунд. То есть мы видим Солнце в прошлом на 8 минут.
Но и эта цифра не является конечной и постоянной. Земля удаляется от Солнца, и ее орбита изменяется на 15 метров каждые 100 лет.
Астрономическая единица
Для определения расстояний внутри Солнечной системой в 2012 годы ввели новую единицу измерения – астрономическая единица. Она равна среднему расстоянию от Земли до Солнца – 149 597 870,7 километров.
Обозначается астрономическая единица – а.е. или АЕ для русскоязычных источников. Для иностранных принято обозначение «UA» — astronomical unit. Возможно написание как строчных букв, так и через точки.
Приливы и отливы
Одним из основных «дел» нашего естественного спутника Луны являются приливы и отливы. Но и здесь влияние Солнца избежать не удалось.
Хоть наша звезда и находится на таком невероятном расстоянии, она тоже влияет на уровень воды в океане.
Когда Луна и Солнце оказываются относительно Земли с одной стороны – то происходит сизигийный прилив – самый сильный подъем воды, ведь на нее оказывает влияние гравитационная сила и Луны и Солнца.
Когда же Солнце и Луна находятся относительно Земли под прямым углом, тогда происходит Квадратурный прилив – подъем воды самый незначительный, так как гравитационные силы Луны и Солнца «растягивают» океан в свою сторону.
Афелий и перигелий
Афелий или апогелий – наибольшее расстояние между Землей и Солнцем. Эту точку наша планета проходит летом с 3 по 7 июля. Перигелий – наименьшее расстояние между Землей и Солнцем, планета проходит зимой со 2 по 5 января.
Именно из-за этого зима в северном полушарии не такая холодная как могла бы быть, а лето не такое палящее, как в южном полушарии.
Измерения расстояния до Солнца в древней Греции
Именно древние греки считаются основоположниками современной астрономии. И их вычисления расстояния от Земли до Солнца постоянно совершенствовались.
В древней Греции утвердилась геометрия – как наука о внешнем мире и о формах и фигурах.
Предположения Аристарха Самосского
Одним из первых кто задался вопросом космических расстояний был Аристарх Самосский, живший в III веке до н.э. Он изучал Луну и Солнце, а также вычислял размер нашей планеты.
Ученый проводил наблюдения за фазами Луны, особенно за Лунными и Солнечными затмениями.
Взяв прямоугольный треугольник, в вершины которого он поместил Солнце, Луну и Землю, с помощью теоремы Пифагора Аристарху Самосскому удалось вычислить, что Солнце должно находится на расстоянии в 20 раз превышающим расстояние от Земли до Луны.
Древнегреческий астроном ошибся на несколько порядков. Но эта его работа внесла огромный вклад в дальнейшее изучение космоса и небесных тел.
Измерения Гиппарха Никейского
Во II веке до н.э. Гиппарх Никейский внес огромный вклад в астрономию того времени. Он первый ввел тригонометрические методы при наблюдениях за звездами. Начал использовать секстант и квадрант – специальные приборы для более точных измерений углов. Собрал все звезды в первый каталог звезд и разделил все звезды по звездным величинам. Первый рассчитал и предсказала прецессию равноденствий. Ввел теорию о затмениях.
Благодаря этому, у Гиппарха Никейского получилось рассчитать расстояние от Луны до Земли, оно получилось 71 радиуса Земли. Использую те же принципы, он вычислил расстояние до Солнца и получил результат в 490-2550 радиуса Земли. Такое большое расхождения получилось из-за малой точности приборов измерения.
Расчет нового времени
В средние века, когда появились телескопы, возможности для измерения значительно увеличились.
Так, Иоганн Кеплер первый засомневался в результатах древнегреческих астрономов, считая что они сильно занижены.
Кристиан Гюйгенс, голландский астроном, первый получил максимально точный результат, который расходится с современным только на 7%.
Метом прямоугольных треугольников Кристиана Гюйгенса
Этот метод подразумевает знания тригонометрии, когда из трех элементов прямоугольного треугольника можно найти остальные. Такими элементами в вычислениях Гюйгенса стали катит и два острых угла.
Но для этого нужно было знать значение катета — расстояние между Землей и другим небесным телом. В качестве другого объекта была взята Венера. Венера находилась в прямом углу прямоугольного треугольника, тогда как Солнце и Земля занимали два острых угла. Для нахождения расстояния между Землей и Венерой необходимо было знать размер Венеры. Но таких данных на тот момент не было, поэтому Гюйгенс сделал очень смелое предположение, что Венера равна по размеру Земле. И оказался прав. Значение острого угла, в котором находится Земля, а именно угол Солнце – Земля – Венера, был легко найден. Зная катет и острый угол легко можно найти гипотенузу – расстояние от Солнца до Земли. Гюйгенс получил значение в 160 млн км.
Измерения Кассини и Рише
Джованни Кассини и Жан Рише вплотную занимались измерением расстояний в космосе. Наблюдая за Марсом, с помощью уточного параллакса, ученым удалось найти расстояние между двумя планетами. Затем, используя метрическую системы, они смогли вычислить расстояние между Землей и Солнцем – 140 млн км.
Исследования новейшего времени
Современные технологии позволяют не только измерять расстояние с необычайной точностью, но и слетать к объекту измерений. НАСА запустила специальный зонд для изучения солнечных явлений. Он приблизится к светилу максимально близко – 6 млн км.
Метод радиолокации
С изобретением радио, его стали применять и в освоении космоса. Этот метод основан на получении сигнала отраженной волны от объекта.
Так как Солнце является очень мощным источником электромагнитных волн, то этот метод требовал определенной энергозатраты – необходимо было сгенерировать мощную волну, чтобы она не потерялась на фоне Солнца.
Так в 1961 году был получен результат в 149 599 300 км, но погрешность метода составила 2 тыс км. Тогда эксперимент повторил через год, и результат уже был 149 598 100 км, погрешность «всего лишь» 750 км.
Определение дистанции лазером
В настоящее время лазерные дальномеры – одни из самых точных приборов для измерения расстояний.
С помощью уголковых отражателей на Луне, астрономам удалось получить максимально точный результат с погрешностью в несколько сантиметров, который и считается верным на настоящее время.
Единицы измерений космических расстояний
- Астрономическая единица – среднее расстояние от Земли до Солнца. Равна 150 млн км. Удобна для измерения расстояний в Солнечной системе.
- Световой год – расстояние, которое проходит свет за один год – 9,46 трлн км. Удобно для измерения расстояния для звезд, помимо Солнца.
- Парсек – 3,26 световых года – расстояние от объекта до Солнца, где параллакс равен одной угловой секунде.
Еще больше космоса и интересных фактов в телеграмм-канале.
Представление о Земле как о шаре, который свободно, без всякой опоры находится в космическом пространстве, является одним из величайших достижений науки древнего мира.
Считается, что первое достаточно точное определение размеров Земли провёл греческий учёный Эратосфен (276—194 до н. э.), живший в Египте. Идея, положенная в основу измерений Эратосфена, весьма проста: измерить длину дуги земного меридиана в линейных единицах и определить, какую часть полной окружности эта дуга составляет. Получив эти данные, можно вычислить длину дуги в 1°, а затем длину окружности и величину её радиуса, т. е. радиуса земного шара. Очевидно, что длина дуги меридиана в градусной мере равна разности географических широт двух пунктов: ϕB – ϕA.

Рис. 3.8. Способ Эратосфена
Для того чтобы определить эту разность, Эратосфен сравнил полуденную высоту Солнца в один и тот же день в двух городах, находящихся на одном меридиане. Измерив высоту Солнца hB (рис. 3.8) в полдень 22 июня в Александрии, где он жил, Эратосфен установил, что Солнце отстоит от зенита на 7,2°. В этот день в полдень в городе Сиена (ныне Асуан) Солнце освещает дно самых глубоких колодцев, т. е. находится в зените (hA = 90°). Следовательно, длина дуги составляет 7,2°. Расстояние между Сиеной (A) и Александрией (B) около 5000 греческих стадий — l.
Стадией в Древней Греции считалось расстояние, которое проходит легко вооружённый греческий воин за тот промежуток времени, в течение которого Солнце, коснувшееся горизонта своим нижним краем, целиком скроется за горизонт.
Несмотря на кажущееся неудобство такой единицы и достаточную громоздкость словесного определения, её введение выглядело вполне оправданным, учитывая, что строгая периодичность небесных явлений позволяла использовать их движение для счёта времени.
Обозначив длину окружности земного шара через L, получим такое выражение:
 =
=  ,
,
откуда следует, что длина окружности земного шара равняется 250 тыс. стадий.
Точная величина стадии в современных единицах неизвестна, но, зная, что расстояние между Александрией и Асуаном составляет 800 км, можно полагать, что 1 стадия = 160 м. Результат, полученный Эратосфеном, практически не отличается от современных данных, согласно которым длина окружности Земли составляет 40 тыс. км.
Эратосфен ввёл в практику использование терминов «широта» и «долгота». Видимо, появление этих терминов связано с особенностями формы карт того времени: они повторяли по очертаниям побережье Средиземного моря, которое длиннее по направлению запад—восток (по долготе), чем с севера на юг (по широте).

Рис. 3.9. Параллактическое смещение
Определить географическую широту двух пунктов оказывается гораздо проще, чем измерить расстояние между ними. Зачастую непосредственное измерение кратчайшего расстояния между этими пунктами оказывается невозможным из-за различных естественных препятствий (гор, рек и т. п.). Поэтому применяется способ, основанный на явлении параллактического смещения и предусматривающий вычисление расстояния на основе измерений длины одной из сторон (базиса — BC) и двух углов B и C в треугольнике ABC (рис. 3.9).
Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя.
Чем дальше расположен предмет, тем меньше его параллактическое смещение, и чем больше перемещение наблюдателя (базис измерения), тем больше параллактическое смещение.

Рис. 3.10. Схема триангуляции
Для определения длины дуги используется система треугольников — способ триангуляции, который впервые был применён ещё в 1615 г. Пункты в вершинах этих треугольников выбираются по обе стороны дуги на расстоянии 30—40 км друг от друга так, чтобы из каждого пункта были видны по крайней мере два других. Основой для вычисления длин сторон во всех этих треугольниках является размер базиса AC (рис. 3.10). Точность измерения базиса длиной в 10 км составляет около 1 мм. Во всех пунктах устанавливают геодезические сигналы — вышки высотой в несколько десятков метров. С вершины сигнала с помощью угломерного инструмента (теодолита) измеряют углы между направлениями на два-три соседних пункта. Измерив углы в треугольнике, одной из сторон которого является базис, геодезисты получают возможность вычислить длину двух других его сторон. Проводя затем измерение углов из пунктов, расстояние между которыми вычислено, можно узнать длину двух очередных сторон в треугольнике. Зная длину сторон этих треугольников, можно определить длину дуги AB.
В какой степени форма Земли отличается от шара, выяснилось в конце XVIII в. Для уточнения формы Земли Французская академия наук снарядила сразу две экспедиции. Одна из них работала в экваториальных широтах Южной Америки в Перу, другая — вблизи Северного полярного круга на территории Финляндии и Швеции. Измерения показали, что длина одного градуса дуги меридиана на севере больше, чем вблизи экватора. Последующие исследования подтвердили, что длина дуги одного градуса меридиана увеличивается с возрастанием географической широты. Это означало, что форма Земли — не идеальный шар: она сплюснута у полюсов. Её полярный радиус на 21 км короче экваториального.
Для школьного глобуса масштаба 1 : 50 000 000 отличие этих радиусов будет всего 0,4 мм, т. е. совершенно незаметно.
Отношение разности величин экваториального и полярного радиусов Земли к величине экваториального называется сжатием. По современным данным, оно составляет  , или 0,0034. Это означает, что сечение Земли по меридиану будет не окружностью, а эллипсом, у которого большая ось проходит в плоскости экватора, а малая совпадает с осью вращения.
, или 0,0034. Это означает, что сечение Земли по меридиану будет не окружностью, а эллипсом, у которого большая ось проходит в плоскости экватора, а малая совпадает с осью вращения.
В XX в. благодаря измерениям, точность которых составила 15 м, выяснилось, что земной экватор также нельзя считать окружностью. Сплюснутость экватора составляет всего  (в 100 раз меньше сплюснутости меридиана). Более точно форму нашей планеты передаёт фигура, называемая эллипсоидом, у которого любое сечение плоскостью, проходящей через центр Земли, не является окружностью.
(в 100 раз меньше сплюснутости меридиана). Более точно форму нашей планеты передаёт фигура, называемая эллипсоидом, у которого любое сечение плоскостью, проходящей через центр Земли, не является окружностью.
В настоящее время форму Земли принято характеризовать следующими величинами:
|
сжатие эллипсоида — 1 : 298,25; |
|
средний радиус — 6371,032 км; |
|
длина окружности экватора — 40075,696 км. |
Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус.
Горизонтальным параллаксом ( p) называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения (рис. 3.11).

Рис. 3.11. Горизонтальный параллакс светила
Из треугольника OAS можно выразить величину — расстояние OS = D:
D =  ,
,
где R — радиус Земли. По этой формуле можно вычислить расстояние в радиусах Земли, а зная его величину, — выразить расстояние в километрах.
Очевидно, что чем дальше расположен объект, тем меньше его параллакс. Наибольшее значение имеет параллакс Луны, который меняется в связи с тем, что Луна обращается по эллиптической орбите, и в среднем составляет 57ʹ. Параллаксы планет и Солнца значительно меньше. Так, параллакс Солнца равен 8,8ʺ. Такому значению параллакса соответствует расстояние до Солнца, примерно равное 150 млн км. Это расстояние принимается за одну астрономическую единицу (1 а. е.) и используется при измерении расстояний между телами Солнечной системы.
Известно, что для малых углов sin p ≈ p, если угол p выражен в радианах. В одном радиане содержится 206 265ʺ. Тогда, заменяя sin p на p и выражая этот угол в радианной мере, получаем формулу в виде, удобном для вычислений:
D =  R,
R,
или (с достаточной точностью)
D =  R.
R.
Во второй половине XX в. развитие радиотехники позволило определять расстояния до тел Солнечной системы посредством радиолокации. Первым объектом среди них стала Луна. Затем радиолокационными методами были уточнены расстояния до Венеры, Меркурия, Марса и Юпитера. На основе радиолокации Венеры величина астрономической единицы определена с точностью порядка километра. Столь высокая точность определения расстояний — необходимое условие для расчётов траекторий полёта космических аппаратов, изучающих планеты и другие тела Солнечной системы. В настоящее время благодаря использованию лазеров стало возможным провести оптическую локацию Луны. При этом расстояния до лунной поверхности измеряются с точностью до сантиметров.
На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0,9ʺ?
|
Дано: p1 = 0,9ʺ D☉ = 1 а. е. p☉ = 8,8ʺ |
Решение: Известно, что параллакс Солнца на расстоянии в 1 а. е. равен 8,8ʺ. Тогда, написав формулы для расстояния до Солнца и до Сатурна и поделив их одна на другую, получим: |
|
D1 — ? |
 =
=  .
.
Откуда
D1 =  =
=  = 9,8 а. е.
= 9,8 а. е.
Ответ: D1 = 9,8 а. е.

Рис. 3.12. Угловые размеры светила
Зная расстояние до светила, можно определить его линейные размеры, если измерить его угловой радиус ρ (рис. 3.12). Формула, связывающая эти величины, аналогична формуле для определения параллакса:
D =  .
.
Учитывая, что угловые диаметры даже Солнца и Луны составляют примерно 30ʹ, а все планеты видны невооружённым глазом как точки, можно воспользоваться соотношением: sin ρ ≈ ρ. Тогда:
D =  и D =
и D =  .
.
Следовательно,
r =  R.
R.
Если расстояние D известно, то
r = Dρ,
где величина ρ выражена в радианах.
Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 30ʹ?
|
Дано: D = 400 000 км ρ = 30ʹ |
Решение: Если ρ выразить в радианах, то d = Dρ. Следовательно, |
|
d — ? |
d =  = 3490 км.
= 3490 км.
Ответ: d = 3490 км.

Вопросы 1. Какие измерения, выполненные на Земле, свидетельствуют о её сжатии? 2. Меняется ли и по какой причине горизонтальный параллакс Солнца в течение года? 3. Каким методом определяется расстояние до ближайших планет в настоящее время?

Упражнение 11 1. Чему равен горизонтальный параллакс Юпитера, наблюдаемого с Земли в противостоянии, если Юпитер в 5 раз дальше от Солнца, чем Земля? 2. Расстояние Луны от Земли в ближайшей к Земле точке орбиты (перигее) 363 000 км, а в наиболее удалённой (апогее) — 405 000 км. Определите горизонтальный параллакс Луны в этих положениях. 3. Во сколько раз Солнце больше, чем Луна, если их угловые диаметры одинаковы, а горизонтальные параллаксы равны 8,8ʺ и 57ʹ соответственно? 4. Чему равен угловой диаметр Солнца, видимого с Нептуна?
Как измерили расстояние до Солнца
Время на прочтение
5 мин
Количество просмотров 38K

Сегодня, когда астрономию вернули в школьную программу, любой старшеклассник (ну, в теории, любой) должен знать: расстояние от нашей планеты до Солнца составляет примерно 149,5 млн километров. Это расстояние еще принято называть астрономической единицей.
Но, понятно, что этот ответ как-то надо было получить и астрономам потребовалось на это несколько шагов, растянувшихся не одно тысячелетие. Ниже — о каждом шаге подробнее.
Шаг первый – безбожник Аристарх и Луна
Аристарх Самосский жил в III веке до нашей эры и был по-настоящему выдающимся астрономом. Задолго до Коперника он построил гелиоцентрическую модель устройства мира. Довольно точно определил продолжительность года в 365 + (1/4) + (1/1623) дней. Усовершенствовал солнечные часы. А еще он предпринял попытку измерить расстояние от Земли до Солнца и Луны. Этому Аристарх посвятил целый трактат (кстати, единственная письменная работа этого автора, дошедшая до нас).
С Луной у него получилось довольно близко к правильному ответу: 486400 км (по расчетам Аристарха), 380000 км (среднее расстояние по современным данным). Спустя сто лет другой античный астроном Гиппарх, кстати, уточнил эти цифры. А вот с Солнцем у Аристарха получилась нехилая промашка.
Но сначала о том, как вообще древнегреческий астроном измерял это расстояние. Известно, что иногда Солнце и Луну можно наблюдать одновременно. Причем, бывают моменты, когда Солнце освещает ровно половину Луны. Тогда угол «Земля-Луна-Солнце» — прямой, и измеряя угол «Луна-Земля-Солнце» можно с помощью тригонометрических соотношений, зная расстояние Земля-Луна, найти расстояние Земля-Солнце.
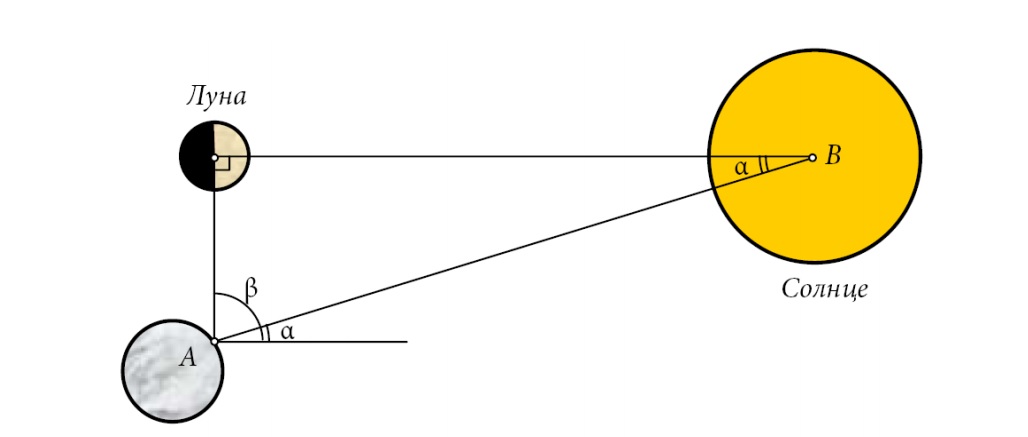
Но «гладко было на бумаге». Во-первых, Аристарху надо было поймать момент, когда освещена ровно половина Луны, а сделать это без телескопа было практически невозможно. А во-вторых, опять же без серьезной измерительной аппаратуры, точно измерить все параметры. Не удивительно, что грек ошибся, причем, очень сильно: угол α у него получился целых три градуса (в реальности он равен 10 минутам), а расстояние до Солнца всего 7,5 млн километров. Опираясь на это расстояние, Аристарх пришел к выводу, что Солнце намного больше Земли. Это и стало главным аргументом его гелиоцентризма (в центре мироздания должен быть самый большой объект).
Впрочем, ошибка в определении расстояния большой роли в науке не сыграла, вычисления Аристарха вообще не получили широкой известности (даже среди образованной части населения античных городов). Причина была скорее политической, все дело в его гелиоцентрической модели мироздания. Она противоречила геоцентрической модели, которой придерживался тогдашний научный консенсус. И есть упоминания, что его даже пытались привлечь к суду как безбожника. Спустя некоторое время сначала Гиппарх подверг критике его взгляды, а позже Птолемей (чья геоцентрическая модель успешно дожила до Коперника) и вовсе проигнорировал результаты Аристарха, способствуя их забвению на долгое время.
Шаг второй — смотрим на Венеру (Кеплер и Хоррокс)
Человечеству потребовалось почти две тысячи лет, чтобы сделать этот следующий шаг к ответу, но будем справедливы, это было нелегкое время и хватало других проблем.
И для начала, надо было выбрать другой объект, на который опираться в своих вычислениях. В 1626 году известный немецкий астроном и математик Иоганн Кеплер предложил в качестве кандидата Венеру. К тому времени астрономы уже знали про одно довольно редкое астрономическое явление – прохождение Венеры по диску Солнца, причем, оно случается дважды с разницей в несколько лет, а потом следует значительный перерыв. Предложенный Кеплером метод заключался в следующем: надо измерить время прохождения Венеры по диску Солнца из разных точек Земли. И сравнивая эти времена можно найти расстояние от Земли до Венеры и до Солнца.

Впрочем, это только звучит просто. Как минимум, надо было дождаться этого явления. Это удалось британскому астроному Джереми Хороксу, который переписывался с Кеплером и знал про его метод. Сначала британец уточнил частоту этого явления: «дубль» случается с разницей в восемь лет каждые полтора столетия. И ближайшее должно было состояться в 1639 году. Хоррокс подготовился к этому событию, он наблюдал за небом из своего дома в Мач Хул, близ Престона, а его друг делал то же самое из Солфорда, близ Манчестера. Сначала, казалось, что удача от них отвернулась, поскольку в этот день была сильная облачность, но за полчаса до захода Солнца облака разошлись и пара астрономов сумела-таки осуществить свой план. На основании наблюдений, Хоррокс рассчитал, что нашу планету от Солнца отделяет 95,6 млн км. Это было уже гораздо ближе к истине, но все равно неверно.
Шаг третий – смотрим на Марс (Кассини)
До следующего венерианского «дубля» надо было ждать полтора века и пока шло время астрономы тратили его на поиск других способов вычислить искомое расстояние. И это удалось французскому астроному итальянского происхождения Джованни Доменико Кассини. Он вообще отметился в астрономии как талантливый наблюдатель (например, это он первым увидел Большое Красное пятно на Юпитере). К тому времени астрономы уже оценили возможности, которые дает одновременное наблюдение за одним и тем же объектом из отдаленных друг от друга мест. В 1672 году Кассини на пару с другим французским астрономом Жаном Рише осуществили такой проект: первый остался в Париже, а второй отправился в Южную Африку, где у Франции были свои колонии. Они одновременно наблюдали Марс и, вычислив параллакс, определили его расстояние от Земли. Параллакс, если кто не знает, это смещение или разница в видимом положении объекта, рассматриваемого на двух разных линиях зрения. Ну а вычислять расстояние до объекта по параллаксу умели уже давно.
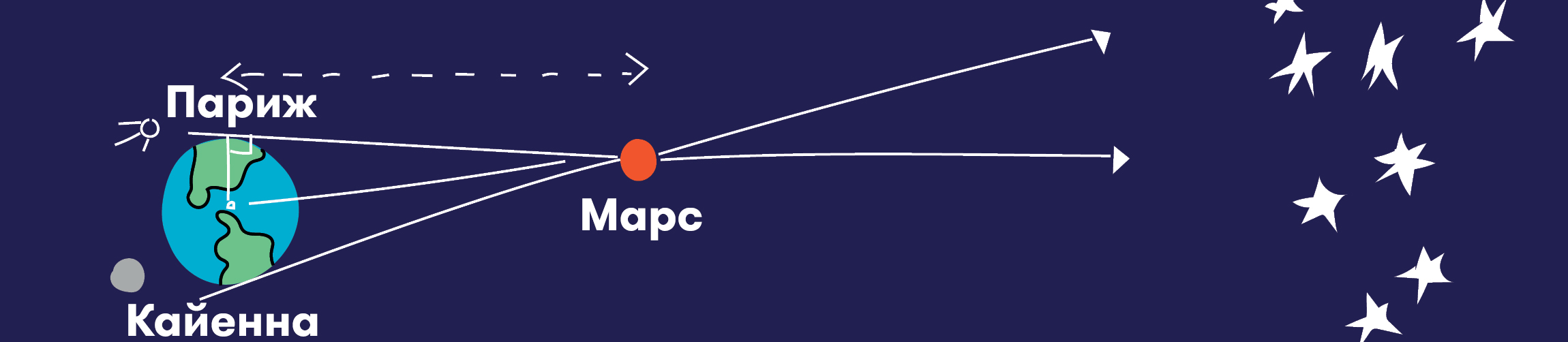
И поскольку относительные отношения различных расстояний между Солнцем и планетами уже были известны из геометрии, рассчитав по параллаксу расстояние до Марса, Кассини смог сделать то же самое и для Солнца. Его результат — 146 млн км – был уже очень близок к современным оценкам. Что интересно, в то время, когда Кассини проводил эти расчеты, он был приверженцем геоцентрической системы, то есть, расстояния он получал близкие к верным, но карту Солнечной системы строил по старинке, с Землей в центре. Позже он признал правоту Коперника, но в ограниченной степени.
Шаг четвертый – снова Венера и астрономы всего мира
Тем временем близился очередной венерианский «дубль» (в 1761 и 1769 годах) и астрономы были намерены выжать из этого события максимум. Чтобы не зависеть от погодных условий и собрать данные с разных точек на Земле, был организован большой международный проект (его считают чуть ли не первым в истории) под эгидой Французской академии наук. Заблаговременно были подготовлены и отправлены научные экспедиции к местам наблюдений. Не все закончилось гладко – экспедиция, отправленная в Новую Гвинею, без вести пропала в джунглях.
Но в целом проект удался.
Кстати, активно в нем участвовала и Россия. В нашей стране им руководил человек необычайных талантов и энергии – Михайло Ломоносов (это он, кстати, обнаружил атмосферу на Венере).
Ломоносову удалось получить аудиенцию у императрицы Екатерины II и убедить ее в важности этой работы как для науки, так и для государственного престижа. Получив поддержку казны, Ломоносов смог развернуть на территории Российской империи 40 наблюдательных пунктов. На один из них, вблизи Петербурга, приезжала сама Екатерина и с интересом смотрела в телескоп.
Вот в итоге этой большой работы астрономов по всему миру и было получено то число, которое сегодня включено в учебники. Но нет предела совершенству, и еще через сто пятьдесят лет, 8 декабря 1874 года и 6 декабря 1882 года, очередные прохождения Венеры по диску Солнца вновь наблюдали научные экспедиции по всему миру, уточняя полученные данные. А потом еще раз в 2004 и 2012 году. Впрочем, в ходе этих наблюдений получали и другие полезные данные, но это уже другая тема.
White Rabbit
Искусственный Интеллект
(313265)
12 лет назад
Проще всего – с помощью суточного параллакса – измеряются углы треугольника, вершиной которого является Солнце – а основанием – расстояние между двумя точками на Земле (это может быть и одна точка в разное время – Земля-то вращается)
PS. Свето-радиолокация Солнца очевидно невозможна – оно само излучает во всех диапазонах слишком сильно….
Я вышел родом из народаПросветленный (30667)
12 лет назад
1) Солнце тоже не точка
2) Параллакс допустим точки на краю Солнца тоже нелегко найти, потому что рядом с Солнцем звезд не видно.
3) Определяют расстояние до Венеры, Марса или астероида (по параллаксу), а потом подключают Кеплера.
Не согласны?
Солод Владислав
Профи
(602)
12 лет назад
лучи солнца достигают земли за 8 минут . скорость света есть . s=v*t вот вам пожалуйта .. а еще …делать это умел Нюьютон .. через закон всемирного тяготения . если я не ошибаюсь это был именно он
Елена ***Гуру (3682)
12 лет назад
а каким образом подсчитали, что лучи Солнца достигают земли за 8 минут?
Я вышел родом из народа
Просветленный
(30667)
12 лет назад
Вероятно, первым удаленность Солнца попытался определить Аристарх Самосский, предложивший гелиоцентрическую систему мира за полторы тысячи лет до Коперника. У него получилось, что Солнце находится в 20 раз дальше от нас, чем Луна. Эта оценка, как мы теперь знаем, заниженная в 20 раз, продержалась вплоть до эпохи Кеплера. Тот хотя сам и не измерил астрономическую единицу, но уже отметил, что Солнце должно быть гораздо дальше, чем считал Аристарх (а за ним и все остальные астрономы) .
Чем дальше от нас галактика, тем сильнее ее излучение сдвигается в красную сторону
Первую более или менее приемлемую оценку расстояния от Земли до Солнца получили Жан Доминик Кассини и Жан Рише. В 1672 году, во время противостояния Марса, они измерили его положение на фоне звезд одновременно из Парижа (Кассини) и Кайенны (Рише) . Расстояние от Франции до Французской Гвианы послужило базой параллактического треугольника, из которого они определили расстояние до Марса, а затем по уравнениям небесной механики вычислили астрономическую единицу, получив значение 140 миллионов километров.
На протяжении следующих двух веков главным инструментом для определения масштабов Солнечной системы стали прохождения Венеры по диску Солнца. Наблюдая их одновременно из разных точек земного шара, можно вычислить расстояние от Земли до Венеры, а отсюда и все остальные расстояния в Солнечной системе. В XVIII—XIX веках это явление наблюдалось четырежды: в 1761, 1769, 1874 и 1882 годах. Эти наблюдения стали одними из первых международных научных проектов. Снаряжались масштабные экспедиции (английской экспедицией 1769 года руководил знаменитый Джеймс Кук) , создавались специальные наблюдательные станции.. . И если в конце XVIII века Россия лишь предоставила французским ученым возможность наблюдать прохождение со своей территории (из Тобольска) , то в 1874 и 1882 годах российские ученые уже принимали активное участие в исследованиях. К сожалению, исключительная сложность наблюдений привела к значительному разнобою в оценках астрономической единицы — примерно от 147 до 153 миллионов километров. Более надежное значение — 149,5 миллиона километров — было получено только на рубеже XIX—XX веков по наблюдениям астероидов. И, наконец, нужно учитывать, что результаты всех этих измерений опирались на знание длины базы, в роли которой при измерении астрономической единицы выступал радиус Земли.
Семен СеменовичУченик (146)
4 месяца назад
А зачем такие сложности, когда можно получить тень в полдень, в одном месте, затем переместиться в другое место и там тоже получить тень от светила в полдень. Получив два угла и расстояние между ними получаем вершину треугольника. Так расстояние до Солнца измерил Эратосфен, но ему приписали другое. Так вот у нас история пишется.
Карен Гуюмджян
Искусственный Интеллект
(114968)
12 лет назад
Вам дали один вариант, таких вариантов бесконечность.
Дам один из них, расстояния между землёй и солнцем не существует, ибо земля находится внутри солнца, а солнце внутри земли, и там, и там, того и того – бесконечное количество.
Человеку понять невозможно, до поры и до времени.
Скоро, ибо истина есть бесконечность!
Екатерина Сомкина
Знаток
(327)
5 лет назад
Скорость света -300000кмс, свет от солнца доходит за 8 минут. Задача-узнать сколько секунд в 8 минутах, затем эти секунды умножай на скорость света 300000 кмс. и получишь расстояние до солнца. Есть одно но, скорость света округлена просто, а так скорость света 300000 с копейками, поэтому при подсчёте не 150млн получится а 144 примерно.
enotПрофи (582)
5 лет назад
А как вы узнали, что свет от Солнца идет 8 минут? Из справочника? Так расстояние там же тоже можно было посмотреть.
Семен Семенович
Ученик
(146)
4 месяца назад
С помощью прямоугольного треугольника в период Солнцестояний и Равноденствий, так как эти расстояния нам известны. По тени шеста определяем длину стороны, а затем и угол прямоугольного теугольника.
Чертим треугольник и вписываем размеры, после чего определяем угол между размером тени и гипотенузой, собственно получим два угла, а третий известен он 90°.
Главное не забыть предварительно выверить время по Солнцу, где самая короткая тень и есть полдень.
Можно привести соотношение метров к километрам и т. д., способов в геометрии много, главное желание.
