Как найти расстояние дроби

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Цели:

• Продолжить формирование умений решать задачи на движение в соединении с темой «Дроби».
• Производить соответствующие записи и вычисления.
• Развивать логическое мышление и внимание.
• Развивать умение анализировать и обобщать.
• Учить изменять условия задачи.

Ход урока

1. Орг. момент

– Что изучаем? (Дробные числа).

– Какого типа задачи учимся решать? (На движение).

– Какие 3 величины там обязательно должны быть (S, V, t).

– Сегодня мы попробуем соединить эти две темы.

– Как и где это возможно сделать? (В задачах на движение).

– Это мы попробуем сделать позже, а сначала немного повторим.

2. Устный счет.

Учитель пишет на доске.

– Найти: 1/2 от 48, 1/2 от 96, 1/2 от 78.

– Какая разница. Находим доли от числа и числа по доле.

– Объясните, как вы находили. На сколько частей делим?

– Как можно по-другому назвать 1/2.

– Найти 1/4 от 60 мин, 1/7 от 84.

– А если взять ⅔, то сколько частей надо взять.

– Сколько раз надо взять по 1/10 круга, чтобы получить целый круг?

– Сколько раз содержится в 1 круге по 1/2 .

– А по 1/4 , а по 1/10, а по 1/8.

От города до деревни 20км. Асфальтом покрыто 4/5.

Выбери схему, которая соответствует данному решению.

3. Подготовка к решению задач.

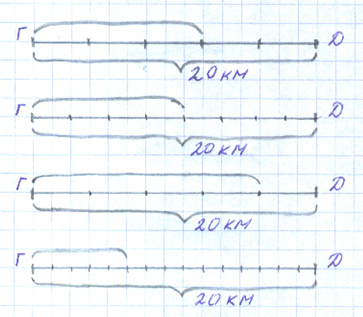
– Найдите её и докажите, что это так (у нас дробь 4/5, этот отрезок разделён на 5 частей и мы взяли 4 части).

 – Почему не подходят все остальные схемы и какие дроби на них получились? (Подписываем над отрезками).

– Какое же количество асфальта покрыто в 3 задаче? Как узнать?

20:5 • 4 = 16 км

Сколько же действий нам потребовалось, чтобы найти 4/5 (2).

– Какие? (Деление и умножение).

– Почему? (Делили на части, а потом брали их).

4. Решение задач.

Итак, мы с вами решили, что дробные числа можно применять в задачах на движение. Давайте подумаем и приведем примеры, как это возможно.

Задача. На путь из одного города в другой почтовый голубь затратил 8 часов. Из них ⅟4 он отдыхал, а остальное время летел со скоростью 10км/ч. На каком расстоянии находятся друг от друга города?

– На какую тему эта задача? (На движение).

– Какие три величины всегда есть в таких задачах? (v, t, s).

– Чертим таблицу. Читаем задачу по частям и постепенно заполняем таблицу.

Читаем 1 предложение.

– Что такое 8 часов? (Время).

– Читаем 2 предложение (в какую графу пишем?)

– Какое время он летел? (Остальное).

– (1 ученик по таблице рассказывает еще раз условие).

– Нам нужно узнать расстояние. Какие два данных нужны, чтобы ответить на вопрос (t и v).

– Какую знаем уже? (Cкорость).

– Какова же она? (10 км/ч)

– Какое данное неизвестно? (Время).

– Смотрим на 1 графу и выделяем 1 простую задачу.

1. 8 : 4 × 1 = 2ч он отдыхал.

Рассуждаем дальше:

Сколько времени он потратил непосредственно при перелёте из одного города в другой?

Формулируем вторую простую задачу.

2. 8 – 2 = 6ч он летел (время в пути).

Рассуждаем дальше.

Формулируем 3 простую задачу. (Записываем формулу) S = v × t

3. 10  = 60км расстояние между городами.

Записываем ответ.

– Как изменить условие задачи так, чтобы решение стало короче? Что для этого нужно изменить в таблице (время).

– Как? (Просто записать количество часов).

Записываем.

Сформулируем задачу.

Как узнаем (это последнее действие предыдущей задачи).

– Решаем, пишем формулу.

– Как изменить условие задачи, чтобы решение стало длиннее?

– Что нужно сделать? (оставить условие, усложнив его).

– В какую графу можно добавить новые данные (если дети затрудняются).

– А голубь всегда с одной и той же скоростью летает?

На путь из одного города в другой почтовый голубь затратил 8 часов. Из них ⅟4 часть он отдыхал. 4 часа летел со скоростью 10км/ч, а остальное время со скоростью 15км/ч. На каком расстоянии находятся друг от друга города?

1. 8 : 4 × 1 = 2ч отдыхал
2. 8 – 2 = 6ч он летел
3. 6 – 4 = 2ч остальное
4. 10 × 4 = 40км за 4 часа
5. 15 × 2 = 30км за 2 часа
6. 40 + 30 = 70км – весь путь
7. Логическая задача.

Выходные дни составляют  недели. Сколько выходных дней в году?

1. 365 : 7 = 52 (ост . 1) недели в году.
2. 7 : 7 × 2 = 2 выходных дня в неделе.
3. 2 × 52 = 104 выходных дня в году.

Сколько же от года отдыхаем в дробях (примерно ).

6. Итог.

Над чем на уроке работали? Что нового узнали? Какие темы соединяли?

вообще по правилам,чтобы найти расстояние между точками надо из координаты правого конца вычесть координату левого конца. например
А(10,5)  и В(6,3)  надо найти длину отрезка  АВ  .т.А лежит правее,чем т.В,поэтому  надо 10,5-6,3=4,2 получим расстояние между А и В.То же самое с отрицательными числами    Р(-5,8)  и М (-3,2).  т.М лежит правее,значит  -3,2-(-5,8)=-3,2+5,8=5,8-3,2=2,6  .если что не понятно,напиши.

       __0___|__|______|___|___|_|_____|____|_|____ 
         0,63 1          2    2,51   3,35     4      4,85                         
здесь большой точности не будет,все приблизительно,особенно когда есть сотые доли числа.