Как найти расстояние если движение вдогонку

Цель урока:  познакомить учащихся с
новым видом задач на движение (вдогонку).

Задачи:

• обучающие: учиться читать и
  записывать информацию, представленную в виде
  различных математических моделей, строить
  высказывания, продолжать учиться называть цели
  конкретного задания, алгоритм (план работы),
  проверять, исправлять и оценивать результаты
  работы так, как это было описано ранее.
• развивающие: способствовать развитию
  математического мышления, познавательной
  активности обучающихся,  умения пользоваться
  математической терминологией.
• воспитательные: продолжить работу по
  воспитанию взаимопомощи, культуры общения,
  способствующей созданию благоприятного
  психологического климата;
• воспитывать внимание, самостоятельность,
  самоконтроль, аккуратность, прививать интерес к
  предмету.

Тип урока:  Урок изучения и первичного
закрепления новых знаний

Методы и приемы: словесные, наглядные,
частично-поисковые.

Используемые учебники и учебные пособия: Учебник
“Математика” Алматы “Атамра” 2011

Используемое оборудование: 

• интерактивное оборудование (мультимедийный
  проектор), компьютер,
• интер.доска. 

Ход урока

1. Вводно-мотивационная часть

Загадка.

Всем она давно знакома –
Ждёт послушно возле дома,
Только выйдешь из ворот-
Куда хочешь поведёт.

(дорога)

– Какое действие совершают машины по дороге?

– Прочитайте дружно, хором наш девиз:

Смело иди вперед,
Не стой на месте,
Чего не сделает один,
Сделаем вместе!

2. Актуализация знаний. Минутка чистописания

– Запишите формулы нахождения расстояния,
скорости и времени.

S = V x t

V = S : t

t = S : V

– Чем отличаются величины: расстояние и
скорость?

– Расстояние – это путь, пройденный за
несколько единиц времени;

– Cкорость – это путь, пройденный за одну
единицу времени

3. Устный счёт (задачи на движение)

Задача №1

Шофер все сильнее давит на газ
Скорость – сто километров в час.
Тебе нетрудно будет сказать,
Сколько проедет за три часа
Автомобиль со скоростью этой?
Решай поскорее – жду ответа!

Решение:

S = U х t

100 х 3 = 300 (км)

Задача №2

За 5 часов один пешеход
Тридцать пять километров пройдет.
Должен быть ответ поскорее готов:
Сколько пройдет он за восемь часов
Если скорость свою не изменит?
Решай – и учитель ответ оценит!

Решение:

1) 35 : 5 = 7 (км/ч)

2) 7 х 8 = 56 (км)

Задача №3

Возьми-ка ручку,
Открой чистый лист,
Задачу послушай: “Прошел турист
Со скоростью пять километров в час
Сто километров.” Ответ найди:
Сколько часов он был в пути?

Решение: 100 : 5 = 20 (час.)

Задача №4

Лора задачу быстро решила:
“Пятьсот километров проедет машина
За десять часов. Какова же скорость?”
Лора решала, не беспокоясь:
Пятьсот умножает на десять скоро.
Ответ получает. Права ли Лора?

Решение:

Лора не права!

500 : 10 = 50 ( км/ч)

4. Закрепление пройденного.

– С какими видами движения вы знакомы?

– Встречное движение

– Движение в противоположных направлениях.

– Движение с отставанием.

– С какой темой мы познакомились на прошлых
уроках? (- Одновременное движение с отставанием.)

Работа по группам

(Группам раздаются карточки со схемами к
задачам)

Задание: Какое направление движения
соответствует решению?

14 км/ч+12км/ч=26км/ч

14 км/ч-12км/ч=2км/ч

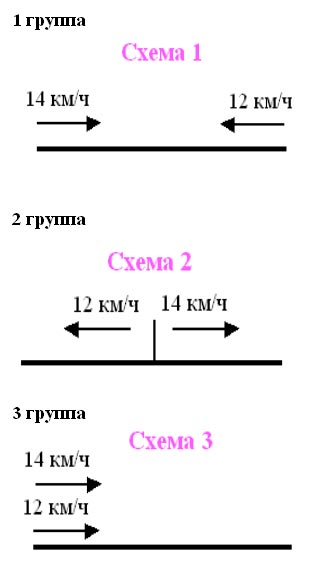
5. Проблемная ситуация. Решите задачи по
схемам.

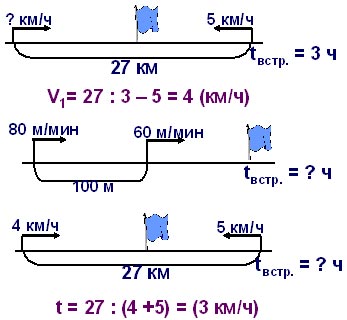
– Почему не удалось решить вторую задачу? – Это
задача на движение вдогонку.

– Не умеем находить скорость сближения при
движении вдогонку.

Постановка учебной задачи.

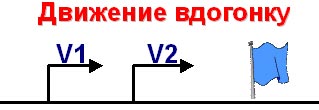
– Какова же тема нашего урока? Задачи на
движение вдогонку.

– Какие цели мы поставим?

• познакомиться со скоростью сближения при
  движении вдогонку;
• научиться решать задачи на движение вдогонку.

7. “Открытие” учащимися нового
знания.

а) Работа над задачей стр. 230 №3

– Вначале понаблюдаем, что происходит с
объектами при движении вдогонку. Заполним
таблицу, чтобы сделать верные выводы.

(Текст задачи на стр.230 №3, чертежи с числовым
лучом, таблица у каждого ученика.)

– Прочитайте условие вслух.

Из городов, длина пути между которыми 240км,
одновременно в одном направлении выехали
автомобиль и автобус. Скорость автомобиля 80 км/ч,
а скорость автобуса 56км/ч. Сколько километров
будет между ними через 2 часа?

Разбор задачи:

– В какой точке находится автомобиль? В точке 0.

– А автобус? В точке 240.

– Какое между ними расстояние до начала
движения? 240 км

– Занесите в таблицу.

– Покажите на числовом луче, где будет
находиться автомобиль через час.

В точке 80.

– И где через час будет находиться автобус. В
точке 296 .

– Как изменилось расстояние между ними?
Расстояние между объектами за каждую единицу
времени будет уменьшаться на одно и то же число.

– Как это записать? (Vб – Vм)

– Составьте выражение и внесите запись в
таблицу. 240 – (80-56) x 1 = 216 км

– Покажите на числовом луче, в каких точках
будут находиться автомобиль и автобус через два
часа. В точках 160 и 352

– Как изменилось расстояние между объектами
через два часа? Уменьшилось еще на (80-56) x 2

Узнайте, какое расстояние стало между ними
через два часа, запишите выражение в таблицу 240
– (80-56) x 2 = 192 км

– Сделайте вывод, с помощью какой формулы мы
узнали, как изменяется расстояние при движении
вдогонку? d = S – (V ₁– V ₂) x t

– Запишите формулы зависимости между
величинами: S, t, V.

Vсбл= (V ₁– V ₂) Sп = Vсбл. x t,

t встр.= S : (V ₁– V ₂), V ₁= S : t – V ₂

d = S – (V ₁– V ₂) x t

8. Для закрепления работа над задачей стр.231 №9

 

9. Рефлексия.

– Что такое скорость сближения.

(- Скорость сближения – расстояние, при котором
объекты сближаются за единицу времени.)

– Как найти скорость сближения при движении
вдогонку?

Vсбл = (Vб – Vм),

– Какие еще знания необходимы, чтобы успешно
решать задачи на движение вдогонку?

Sп = Vсбл. x t,

t встр.= S : (Vб – Vм), V1= S : t – V2

d = S – (Vб – Vм) x t

Презентация.

Рассмотрим задачи на движение вдогонку, в которых объекты движутся в одном направлении, но выезжают из разных пунктов, находящихся на некотором расстоянии друг от друга.

При движении вдогонку объекты могут как сближаться, так и удаляться.

Если скорость объекта, который идет впереди, меньше скорости идущего вслед за ним объекта, то второй догоняет первого и они сближаются.

Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:

   

   

Если скорость идущего впереди объекта больше скорости объекта, который движется следом, то второй не сможет  догнать первого и они удаляются друг от друга.

Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:

   

   

Скорость, время и расстояние связаны между собой формулой пути:

   

Задача 1.

Расстояние между двумя пунктами 20 км. Из этих пунктов в одном направлении одновременно выехали автомобиль и мотоциклист, причем автомобиль двигался впереди. Через 5 часов расстояние между ними стало 170 км. Найти скорость мотоциклиста, если скорость автомобиля 70 км/ч.

Решение:

	v, км/ч	t, ч	s, км
Автомобиль	70	5	?
Мотоциклист	?	5	?

1) 170-20=150 (км) на столько увеличилось расстояние между автомобилем и мотоциклистом за 5 часов

2) 150:5=30 (км/ч) скорость удаления автомобиля от мотоциклиста

3) 70-30=40 (км/ч) скорость мотоциклиста.

Ответ: 40 км/ч.

Задача 2.

Расстояние между двумя станциями 40 км. Из этих станций одновременно в одном направлении вышли скорый и товарный поезда, причем товарный поезд едет впереди. Через сколько часов скорый поезд догонит товарный, если его скорость равна 80 км/ч, а скорость товарного поезда — 60 км/ч?

Решение:

	v, км/ч	t, ч	s, км
Пассажирский	80	?	? на 40 км больше
Товарный	60	?	?

1) 80-60=20 (км/ч) скорость сближения поездов

2) 40:20=2 (ч) через такое время скорый поезд догонит товарный.

Ответ: через 2 ч.

Задача 3.

Расстояние между пунктами равно 50 км. Из этих пунктов одновременно в одном направлении выезжают велосипедист и мотоциклист, причем велосипедист едет впереди. Скорость велосипедиста равна 13 км/ч, скорость мотоциклиста — 38 км/ч. На каком расстоянии от пункта своего выезда мотоциклист догонит велосипедиста?

Решение:

	v, км/ч	t, ч	s, км
Мотоциклист	38	?	? на 50 км больше
Велосипедист	13	?	?

1) 38-13=25 (км/ч) скорость сближения мотоциклиста и велосипедиста

2) 50:25=2 (ч) через столько часов после своего выезда мотоциклист догонит велосипедиста

3) 38∙2=76 (км) на таком расстоянии от пункта своего выезда мотоциклист догонит велосипедиста.

Ответ: 76 км.

Задачи в которых двигаются вдогонку из разных пунктов решаются по определенному правилу. Два объекта могут сближаться или удаляться в зависимости от их скоростей.

• Если скорость объекта, который впереди больше, то они удаляются. 

• Если скорость объекта, который впереди меньше, то они сближаются