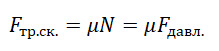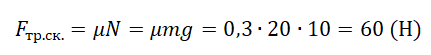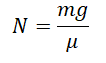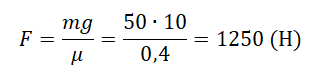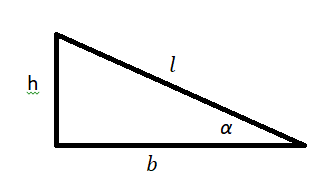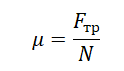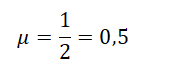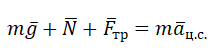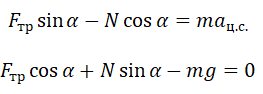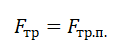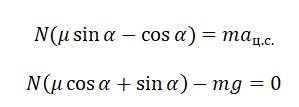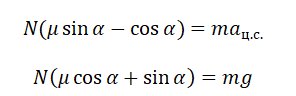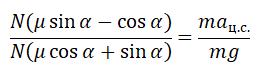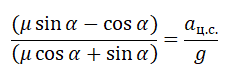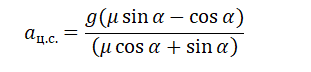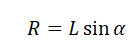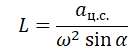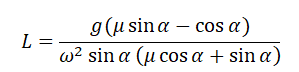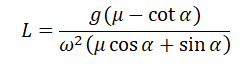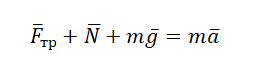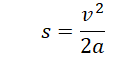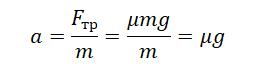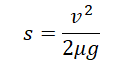Как найти расстояние, которое пройдёт тело, зная силу трения и скорость тела?
=)[_SFC_](=
Знаток
(319),
закрыт
6 месяцев назад
Если такой формулы нет, то, пожалуйста, дайте хоть какую-нибудь наводочку, которая связана с этими величинами.
Пень пнем
Мыслитель
(7285)
10 лет назад
силу трения приравниваем к массе умноженной на оскорение, отсюда считаем ускорение, оно будет отрицательным, т. е. скорость будет уменьшаться, далее по формуле считаем путь
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Ускорение тела, возникающее вследствие силы трения
Известно, что сила трения скольжения направлена в сторону, противоположную направлению относительной скорости движения трущихся тел.
Отсюда следует, что ускорение, которое такая сила сообщает движущемуся телу, тоже направлено против относительной скорости. А это значит, что действие силы трения приводит к уменьшению абсолютного значения скорости тела относительно того тела, по которому оно скользит.
Если на тело, которое скользит по неподвижной поверхности, никакие силы, кроме силы трения не действуют, то оно, в конце концов, останавливается. Рассмотри этот часто встречающийся случай.
Представим себе, что перед движущимся поездом неожиданно появилось некоторое препятствие и машинист отключил двигатель и включил тормоз. Начиная с это момента, на поезд действует только сила трения, так как сила тяжести скомпенсирована реакцией рельсов, а сила сопротивления воздуха мала. Через некоторое время $t$ поезд, пройдя расстояние $l$ – тормозной путь, остановится. Найдем время $t$, нужное для остановки, и расстояние $l$, которое поезд пройдет за это время.
Под действием сила трения $overline{F}_{mp} $поезд будет двигаться с ускорением, равным:
Выберем координатную ось $x$ так, чтобы ее положительное направление совпадало с направлением скорости движения поезда.
Рисунок 1.
Так как сила трения $overline{F}_{mp} $направлена в противоположном направлении, ее проекция на ось х отрицательна. Отрицательна и проекция вектора ускорения на ось $x$. Поэтому если абсолютное значение силы трения равно $left|overline{F}_{mp} right|$, то:
Но ускорение определяется также формулой:
где $v_{0} $- скорость поезда до начала торможения.
Время торможения при движении тела под действием силы трения
Так как нас интересует промежуток времени $t$ от начала торможения до остановки поезда, то конечная скорость $v=0$. Тогда:
«Движение тела под действием силы трения» 👇
Таким образом:
Получим выражения для времени торможения:
Нахождение пути, пройденного телом под действием силы трения
А теперь найдем тормозной путь $l$. Для этого воспользуемся формулой:
Так как $v=0$, то:
Так как $overline{a}=-frac{left|overline{F}_{mp} right|}{m} $, получим:
Из этой формулы видно, что пройденный до остановки путь пропорционален квадрату скорости. Если увеличить скорость вдвое, то потребуется вчетверо больший путь для остановки.
Пример 1
С какой скоростью двигался автомобиль, если после выключения двигателя он прошел до остановки путь равный $80$ м? Коэффициент трения принять равным $0,25$.
Дано: $l=80$м, $mu =0,25$.
Найти: $v$-?
Решение:
Воспользуемся раннее выведенными формулами для нахождения тормозного пути:
$l=frac{mv_{0}^{2} }{2overline{left|F_{mp} right|}} $. (1)
Так как $F_{mp} =mu mg$, подставим в формулу (1) и получим:
$l=frac{mv_{0}^{2} }{2mu mg} $. (2)
Выразив из формулы (2) $v_{0} $найдем величину искомой скорости:
$v_{0} =sqrt{2mu gl} =20$м/с
Ответ: Скорость автомобиля до выключения двигателя $v_{0} =20$ м/с.
Пример 2
Сноубордист массой $80$ кг, имеющий в конце спуска скорость $20$ м/с, останавливается через $40$ с после окончания спуска. Определите силу трения и коэффициент трения.
Дано: $m=80$кг, $v_{0} =20$м/с, $t=40$с.
Найти: $F_{mp} $, $mu $-?
Решение:
Уравнение движения сноубордиста будет иметь вид:
[ma=F_{mp} .]
Используя выражения для нахождения ускорения (конечная скорость $v=0$), получим:
[a=-frac{v_{0} }{t} .]
Тогда:
$F_{mp} =ma=-mfrac{v_{0} }{t} =40H$.
Так как сила трения $overline{F}_{mp} $равна $F_{mp} =mu Bg$, находим коэффициент трения $mu $:
[mu =frac{F_{mp} }{mg} =0,05.]
Ответ: $F_{mp} =40H$, $mu =0,05$.
Пример 3
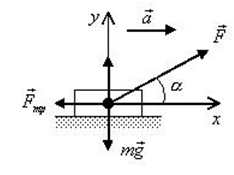
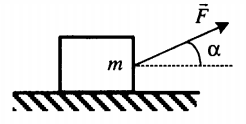
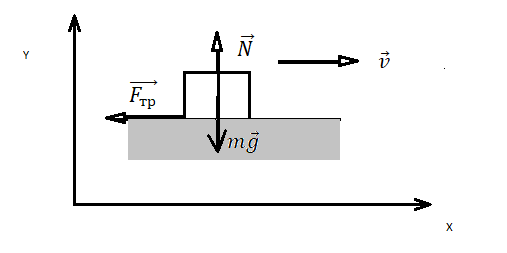
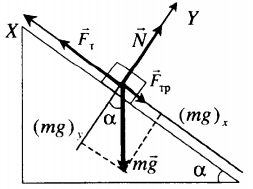
Сани массой $16$ кг перемещают по горизонтальной плоскости под действием силы $180 H$, направленной под углом $30^circ$ к горизонтали. Коэффициент терния саней о плоскость $0,5$. Определить ускорения, с которым движутся сани.
Дано: $m=16$кг, $F=180 H$, $alpha =30^circ$, $mu =0,5$.
Найти: $a$-?
Решение:
Рисунок 2.
Уравнение движения тела:
[moverline{a}=moverline{g}+overline{N}+overline{F}+overline{F}_{mp} .]
Выберем направление осей $x$ и $y$ и спроецируем на них силы и ускорение:
[begin{array}{l} {ma=Fcos alpha -F_{mp} } \ {0=-Bg+N+Fsin alpha } end{array}]
Поскольку $F_{mp} =mu N$, а из второго уравнения $N=mg-Fsin alpha $, то $F_{mp} =mu (mg-Fsin alpha )$. Тогда из первого уравнения ускорение:
$a=frac{1}{m} [Fcos alpha -mu (mg-Fsin alpha )]approx 7,6м/с^2$
Ответ: $a$=$7,6м/с^2$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Задачи на Движение
под действием силы трения
Тренировочные задания для подготовки к контрольным,
самостоятельным и диагностическим работам по теме
«ЗАДАЧИ на Движение под действием силы трения» + Решения
Модуль силы трения скольжения можно определить по формуле: Fтр = µN, где µ — коэффициент трения, N— модуль силы нормального давления (и силы реакции опоры). Максимальная сила трения покоя: (Fтр)мах = µN. При одинаковых условиях сила трения скольжения намного больше силы трения качения. Вектор силы трения скольжения всегда направлен противоположно вектору скорости тела. Коэффициент трения можно определить по формуле: µ = Fтр/N. Это величина безразмерная.
Если на тело действует только сила трения, то такое тело движется равнозамедленно до остановки. Расстояние, которое тело проходит до остановки, называют тормозным путем. Обозначают буквой l. Время торможения — время, нужное для остановки.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Автомобиль массой 5 т движется с постоянной скоростью по прямой горизонтальной дороге. Коэффициент трения шин о дорогу равен 0,03. Определите силу тяги, развиваемую двигателем.
ОТВЕТ: Fтяги = 1470 Н.
РЕШЕНИЕ:
Задача № 2.
Сани со стальными полозьями перемещают равномерно по льду, прилагая горизонтальное усилие 2 Н. Каков вес саней?
ОТВЕТ: Вес саней 100 Н.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 3.
Деревянный брусок массой 3 кг тянут по горизонтальной деревянной доске с помощью пружины. Коэффициент трения равен 0,3. Найти удлинение пружины, если ее жесткость 10 кН/м.
ОТВЕТ: Удлинение пружины 0,09 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 4.
Велосипедист, ехавший со скоростью 36 км/ч, увидел примерно в 10 м от себя препятствие и резко затормозил. Успеет ли велосипедист остановиться до препятствия?
ОТВЕТ: Велосипедист успеет остановиться до препятствия, так как S = 10 м (расстояние до препятствия), а тормозной путь велосипедиста ≈ 7 м. Если скорость движения возрастет вдвое, то тормозной путь увеличится в 4 раза.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 5.
Автомобиль движется со скоростью 10 м/с по гладкой горизонтальной дороге. Пройдя с выключенным мотором расстояние 150 м, автомобиль останавливается. Сколько времени автомобиль двигался с выключенным мотором и каков коэффициент трения при его движении?
ОТВЕТ: t = 30 с; µ = 0,033.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

ЗАДАЧИ на Движение под действием силы трения
Задача № 6.
Лыжник массой 60 кг, имеющий в конце спуска скорость 10 м/с, останавливается через 40 с после окончания спуска. Определить величину силы сопротивления.
ОТВЕТ: Fтp = 15 Н.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 7.
Тело скользит равномерно по наклонной плоскости с углом наклона 30°. Определите коэффициент трения тела о плоскость.
ОТВЕТ: µ ≈ 0,58.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 8.
С какой наибольшей скоростью может ехать мотоциклист по горизонтальной плоскости, описывая дугу радиусом 80 м, если коэффициент трения резины о почву 0,4? На какой угол от вертикального положения он при этом отклоняется?
ОТВЕТ: vмах = 17,7 м/с = 64 км/ч — наибольшая скорость движения; a ≈ 22°.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 9.
Шофер грузовика, едущего со скоростью 72 км/ч, заметил на дороге знак. Сможет ли он, не сбавляя скорости, проехать поворот, если его радиус равен 25 м? Считать коэффициент трения шин о дорогу 0,4.
ОТВЕТ: Шофер должен уменьшить скорость движения, так как радиус окружности, которую опишет грузовик при данной скорости, 100 м, а радиус поворота — 25 м. В противном случае грузовик занесет на обочину дороги.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Дополнительный материал для решения задач

Конспект урока по физике «ЗАДАЧИ на Движение под действием силы трения с решениями». Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам. Выберите дальнейшее действие:
- Вернуться к Списку конспектов по физике для 7-11 классов
- Найти конспект через Кодификатор ОГЭ по физике
- Найти конспект через Кодификатор ЕГЭ по физике
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как Fтр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Трение скольжения
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: Fтр↑↓v.
Сила трения скольжения определяется формулой:
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Полезные факты
- Если тело движется по гладкой поверхности, сила трения между ними отсутствует.
- Сила трения скольжения не зависит от площади соприкосновения тел.
- Сила трения качения обычно в несколько раз меньше силы трения скольжения. Поэтому тяжелые грузы перемещают не волоком, а с помощью тележек на колесах.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
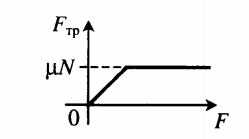
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
0 < Fтр.пок. < Fтр. ск.
Способы определения вида силы трения, возникающей между телами, и ее модуля:
- Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F < Fтр. ск., Fтр.пок. = F.
- Когда к телу прикладывается сила, модуль которой равен силе трения скольжения или превышает ее, возникает сила трения скольжения. Тело при этом начинает двигаться. Сила трения определяется формулой силы трения скольжения. Если F ≥ Fтр. ск., Fтр. = Fтр.ск.
Графически это можно изобразить так:
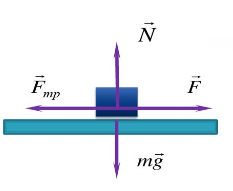
Пример №2. На горизонтальном полу стоит ящик массой 20 кг. Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Fтр.пок. = F = 36 (Н).
Описание движения тел с учетом сил трения
Тело может двигаться по горизонтальной, наклонной или вертикальной плоскости. Оно может покоиться, двигаться равномерно или с ускорением, а сила тяги, под действием которой движется тело, может быть направлена, как в сторону движения тела, так и под углом к плоскости. Поэтому применение законов Ньютона к каждому из случаев имеет свои особенности.
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости |
|
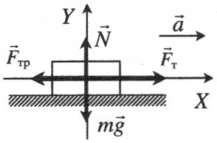 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fт – Fтр = ma Проекция на ось ОУ: N – mg = 0 |
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости |
|
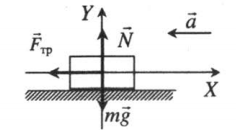 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: – Fтр = –ma Проекция на ось ОУ: N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх) |
|
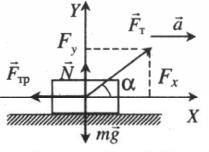 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: Fтsinα + N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз) |
|
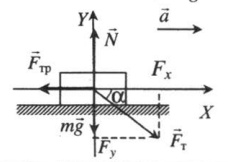 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: N – Fтsinα – mg = 0 |
Внимание! В случаях, когда сила тяги Fт направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Fтр = μN
Проекция сил на ось ОУ выглядит так:
N – Fтsinα – mg = 0
Отсюда силы реакции опоры равна:
N = Fтsinα + mg
Подставим ее в формулу для вычисления силы трения и получим:
Fтр = μN = μ (Fтsinα + mg) = 0,4(10∙0,5 + 1∙10) = 6 (Н)
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают |
|
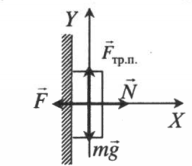 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – F = 0 Проекция на ось ОУ: Fт.п. – mg = 0 |
Тело поднимается под действием силы тяги, направленной под углом к вертикали |
|
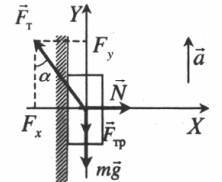 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – Fтsinα = 0 Проекция на ось ОУ: Fтcosα – Fтр – mg = 0 |
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя.
Проекция на ось ОХ:
N – F = 0
Отсюда следует, что сила должна быть равна силе реакции опоры.
Проекция на ось ОУ:
Fт.п. – mg = 0
Перепишем, выразив силу трения через силу реакции опоры:
μN – mg = 0
Отсюда выразим силу реакции опоры:
Следовательно:
Движение тела по наклонной плоскости
Движение вниз без трения |
|
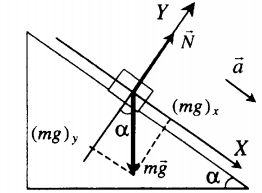 |
Второй закон Ньютона в векторной форме: |
|
mg + N = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело покоится на наклонной плоскости |
|
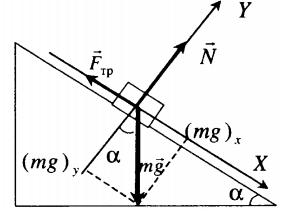 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα – Fтр.п. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело удерживают на наклонной плоскости |
|
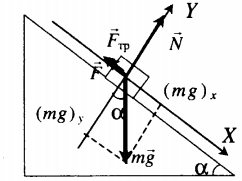 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
F + Fтр. – mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равноускоренное движение вверх с учетом силы трения |
|
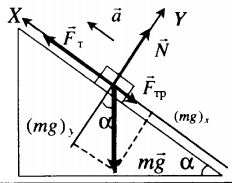 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fт + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равномерное движение вверх с учетом силы трения |
|
 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.
Переведем массу в килограммы: 200 г = 0,2 кг.
Проекция сил, действующих на тело, на ось ОХ:
mg sinα – Fтр.п. = 0
Отсюда сила трения равна:
Fтр.п. = mg sin α
Подставляем известные данные и вычисляем:
Fтр.п. = 0,2∙10∙sin30o = 2∙0,5 = 1 (Н)
Полезная информация
Задание EF18204
При исследовании зависимости силы трения скольжения Fтр от силы нормального давления Fд были получены следующие данные:
|
Fтр, Н |
1,0 |
2,0 |
3,0 |
4,0 |
|
Fд, Н |
2,0 |
4,0 |
6,0 |
8,0 |
Из результатов исследования можно сделать вывод, что коэффициент трения скольжения равен:
а) 0,2
б) 2
в) 0,5
г) 5
Алгоритм решения
1.Записать формулу, связывающую силу трения с силой нормального давления.
2.Выразить из нее коэффициент трения.
3.Взять значения силы трения и силы нормального давления из любого опыта (из любого столбца таблицы).
4.Вычислить коэффициент трения на основании табличных данных.
Решение
Силу трения и силу нормального давления связывает формула:
Fтр = μN
Отсюда коэффициент трения равен:
Сделаем расчет коэффициента трения на основании данных первого опыта (1 столбца):
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17513
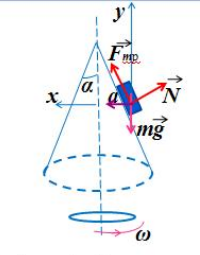
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
Алгоритм решения
1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.
2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.
3.Записать второй закон Ньютона в виде проекций на оси.
4.Через систему уравнений вывести искомую величину.
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
Второй закон Ньютона в векторном виде выглядит следующим образом:
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
Максимальное значение силы трения равно:
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
Запишем систему уравнение в следующем виде:
Поделим первое уравнение на второе и получим:
Сделаем сокращения и получим:
Отсюда центростремительное ускорение равно:
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
Отсюда центростремительное ускорение равно:
Выразим искомую величину L:
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18051
Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью υ, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, действующие на грузовик во время торможения. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Записать формулу для нахождения силы трения скольжения.
6.Записать формулу для расчета перемещения при движении с постоянным ускорением.
7.Использовать второй закон Ньютона для определения тормозного пути.
Решение
Из условий задачи нам известны следующие величины:
• Начальная скорость грузовика (до начала торможения) v0 = v.
• Коэффициент трения между колесами и дорогой μ.
Выполним чертеж. Выберем такую систему координат, в которой направление движения грузовика во время торможения совпадает с направлением оси ОХ:
Запишем второй закон Ньютона в векторной форме:
Запишем второй закон Ньютона в проекциях на оси:
Fтр = ma
N – mg = 0
Известно, что сила трения скольжения определяется формулой:
Fтр = μN = μmg
Значит, в первую ячейку таблицы мы должны поставить «1».
Перемещение при равнозамедленном движении определяется формулой (учтем, что конечная скорость равна 0, так как грузовик остановился):
Выразим ускорение через проекцию сил на ось ОХ:
Подставим найденное ускорение в формулу тормозного пути и получим:
Следовательно, во вторую ячейку таблицы мы должны поставить «4».
Полный ответ: «14».
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.4k
Влад – 15 декабря, 2007 – 21:58
Каков тормозной путь автомобиля, движущегося со скоростью 72 км/ч, если коэффициент трения равен 0,2?
Задача взята из школьной контрольной 🙂 Причём из троечного уровня. По идее она должна быть элементарной, но я ума не приложу, как её решать. Надо сказать, что в физике я не силён. Видимо что-то упустил при изучении темы… Надеюсь на вашу помощь.
- версия для печати
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Комментарии
Опубликовано 16 декабря, 2007 – 21:01 пользователем В. Грабцевич
Подсказка:
1) Ускорение сообщает телу только сила трения, воспользовавшись вторым законом Ньютона, Вы легко его найдете. Далее воспользуйтесь кинематической связью между расстоянием, скоростью и ускорением.
2) Можно воспользоваться законом сохранения энергии. Изменение кинетической энергии тела равно работе силы трения. Пробуйте. Удачи.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 16 декабря, 2007 – 22:13 пользователем Влад
Спасибо за полезные советы. Вот что у меня получилось:
В данном случае на тело по оси Х действует только сила трения, тогда по 2-му закону Ньютона: a = F/m = μmg/m = μg = 0,2 * 10 м/с2 = 2 м/с2.
(т. к. сила трения = μN, а N = mg).
V = 72 км/ч = 20 м/с.
a = V/t
t = v/a = 20 (м/с) / 2 (м/с2) = 10 с.
S = at2/2 = 2*100/2 = 100 м.
Ответ: 100 м.
Я не уверен в правильности этого решения, но всё же. Как говорится, попытка не пытка.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 17 декабря, 2007 – 19:14 пользователем В. Грабцевич
Молодец, Влад.
Несколько замечаний:
1. Старайтесь решать задачу в общем виде.
2. Чем больше промежуточных вычислений, тем большая погрешность конечного результата.
3. Рисунок в задаче обязателен, он значительно облегчает понимание задачи.
4. Для того, чтобы постичь искусство решения задач, помните принцип “от простого к сложному”. Начинайте, Влад, и у Вас все получится.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 17 мая, 2021 – 21:17 пользователем Dasas
Как у вас получилось V = 20 м/с?
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 17 мая, 2021 – 21:38 пользователем afportal
В условии задачи дана скорость 72 км/ч. Это 72 000 метров в час. Если учесть, что в 1 часе содержится 3600 секунд (60 минут по 60 секунд), то при делении 72 000 м на 3 600 секунд получаем 20 м/с.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии