
Здравствуйте, друзья и ученики 5 класса! В нашем мире располагаются множество объектов, которые находятся на различных расстояниях от нас. В науке, в частности в математике, очень важная тема – это измерение расстояний. В этой статье мы рассмотрим одну из самых важных формулы по нахождению расстояния 5 класса.
Расстояние – одна из основных величин, с которой мы сталкиваемся повседневно, и часто задаются вопросы по нему в учебных заданиях. Мы измеряем расстояние между нашими домом, школой, друзьями и много чего еще. Поэтому важно знать, как это делать наиболее эффективно и жестко.
В 5 классе вы уже знакомы с такими понятиями, как точки, прямые, стороны многоугольников, а также начинаете углубляться в изучение треугольников и их свойств. Данные сведения крайне важны для нахождения расстояния между любыми двумя точками.
Так как чем больше подпороговых элементов в тексте, тем оно всё шире привлекает внимание пользователей и максимально возрастает объёмнность контента? Но не стоит забывать о структурировании и наглядности своего текста: его нужно распределить по абзацам и сделать подход, который обеспечивал бы целевой аудитории всесторонний обзор.
Прежде чем мы перейдём к решению задач на понимание формулы, давайте изучим основные принципы определения расстояния между любыми двумя точками в пространстве.
Итак, сегодня мы научимся вычислять расстояния в геометрии с использованием формулы синусника 5 класса. Знания, которые вы получите в ходе чтения нашей статьи, станете полезными участками ваших знаний в математике, а использование формулы синуса увеличит ваши познания и поможет в достижении успеха в обучении.
Основные понятия и формулы
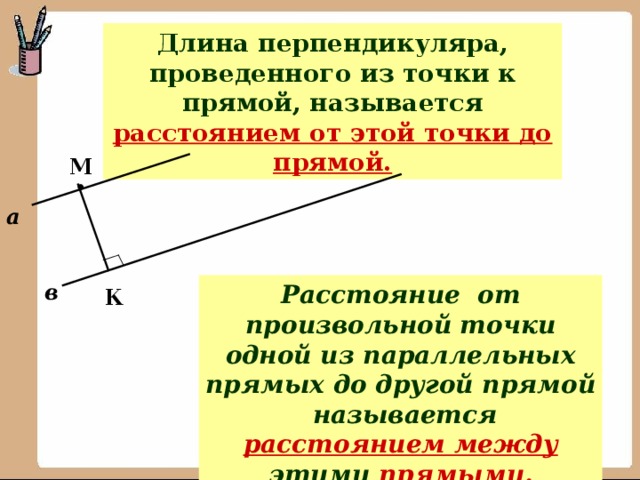
В данном разделе мы рассмотрим основные понятия и формулы, связанные с нахождение расстояния между двумя точками в пространстве.
1. Метрические пространства
Метрическое пространство – это множество точек, в котором для любых двух точек определены расстояние (метрика) () и такая она удовлетворяет следующим аксиомам:
- Невырожденность (для разных точек пространства равенство Distance (A, B) = 0 не выполняется);
- Невырожденность (для одной точки пространства Distance (A, A) = 0);
- Нераимство (для любых четырех точек пространства верно неравенство треугольника: Distance(A, B) ≤ Distance (A, C) + Distance (C, B);
- Симметричность (для любых двух точек пространства A и B верно условие Distance (A, B) = Distance (B, A).
2. Евклидово пространство

Евклидово пространство – это мультиликасное пространство (количество измерений), для которого смысл точек и сторон задается матрицей. Для нахождения расстояния между точками на плоскости используется Евклидова метрика, в которой расстояние между двумя точками определяется по следующей формуле:
Distance (A, B) = √[(x1-x2)² + (y1-y2)²]
где (x1, y1) и (x2, y2) – координаты точек на плоскости.
Для нахождения расстояния в пространстве трехмерном:
Distance (A, B) = √[(x1-x2)² + (y1-y2)² + (z1-z2)²]
где (x1, y1, z1) и (x2, y2, z2) – координаты точек в пространстве.
-
x, y, z – координатные числа измерения размерности (размерность задается своими измерениями: это целое положительное число);
-
A и B – точки;
-
дистанция – А и В являются расстоянием между точками каждый другой.
Для пространств с размерностью выше трех значений произведено аналогичное определение и используется более всего для определения расстояния и измерения пробежания пропорциональных измерениями величинах.
Подходы к определению расстояния
Метод координат: прямоугольная система

Для определения расстояния между двумя точками m и n с использованием прямоугольной системы координат, используется формула:
√((х2 – х1)² + (у2 – у1)² + (z2 – z1)²)
где х, у, z – координаты точек в трехмерном пространстве.
Метод координат: полярная система

Для измерения расстояния в полярной системе координат используется следующая формула:
r2 – r1
где r – расстояние от точки до начала системы координат (то есть получаются две меры направления от начала координат к точкам, разность которых и является расстоянием).
Нестандартные подходы
Существует также ряд других методов определения расстояния, которые могут не иметь прямой связи с геометрическим измерением пространства. Вот несколько примеров:
- Расстояние “Городской протокол”: расстояние между двумя точками с учётом маршрута, который нужно проехать по улицам и дорогам.
- Расстояние “на воде”: расстояние между двумя точками, которые рассчитываются с учётом скорости течения воды в реке, или между двумя подводными точками с учётом морского течения.
- Расстояние “через Интернет”: расстояние между двумя устройствами в информационной сети, которое рассчитывается с учётом времени прохождения сигнала между устройствами.
Как видите, определение расстояния может быть чревато различными подходами, в зависимости от задачи и условий, в которых расчитывается расстояние.
Источники
Для очевидных методов координатных определений, вашему ученику не обязательно знать источник и автора определения, так как это данные из учебника. Если ваш ученик пойдёт по пути применения нестандартных подходов как расстояний “Городской протокол” и других, вам придётся отыскать источники на интернет-ресурсах по геоинформационным системам и параметрами окружающей среды.
Анализ геометрических фигур
Основные геометрические фигуры
Ниже представлена таблица, которая определяет и объясняет основные геометрические фигуры, а также задает основные термины, связанные с ними:
| Фигура | Описание и термины |
|---|---|
| Точка | Точка – это минимальный единичный геометрический объект. В пространстве двух измерений точка определяется двумя координатами (x, y). |
| отрезок | Отрезок – это линия, ограниченная двумя точками. Отрезок характеризуется двумя концами – началом и концом. |
| Угол | Углы представляют собой соединение двух отрезков, образующих угол. Углы измеряются в градусах или радианах. Углы могут быть прямыми, острыми, тупыми и перевернутыми. |
| Дуга | Дуги – это участки кривой, таких как окружность или эллипс. Дуги, как правило, являются частью большей фигуры. |
| Прямая | Прямая представляет собой бесконечный объект в пространстве, обладающий точкой на поверхности и направлениями. |
Расстояние между двумя точками
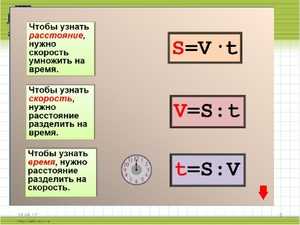
Расстояние между двумя точками в пространстве одного измерения вычисляется путём разности координат двух точек. Расстояние между двумя точками (x1, y1) и (x2, y2) в двумерном пространстве вычисляется
правилом Пифагора:
d = √((x2 – x1)^2 + (y2 – y1)^2)
Основой для анализа геометрических фигур также является масштабирование, вращение и симметрия фигур. Эти треугольники участвуют в процессе сложного анализа геометрических фигур и помогают понять перенос и изменение их формы и размера.
Обзор геометрических фигур и показание того, как на них реагируют различные операции, представляет интерес для подростков и взрослых. Оно способствует развитию зрительного восприятия и мышления, которые наглядно демонстрируются в других естественных и искусственных науках.
Программы и онлайн-калькуляторы

В наше время найти расстояние между двумя точками можно не только с помощью формулы, но и при помощи различных программ и онлайн-калькуляторов.
Одни из самых популярных программ для этих целей – это географические информационные системы, такие как Google Earth или Яндекс.Панорамы. Эти программы позволяют увидеть визуально расположение точек на карте и найти расстояние между ними, используя встроенные калькуляторы.
Онлайн-калькуляторы – очень удобный и быстрый способ найти расстояние между любыми точками, находящимися на поверхности Земли. Такие калькуляторы, как GeoDataSource или GPS Coordinates, предлагают ввести свои координаты и получать результаты нажатием одной кнопки.
Важно помнить, что многие из этих ресурсов используют формулу для расчета расстояния, основанную на геометрии плоского пространства. Это означает, что на весьма больших расстояниях (например, между разными континентами) полученные результаты будут неточными из-за приближения света к прямой линии на поверхности Земли.
Яркой альтернативой формальным электронным калькуляторам может стать математическое приложение GeoGebra. Это интерактивное программное обеспечение включает в себя широкие возможности для работы с геометрическими фигурами и заданными координатами. Здесь можно создать свою собственную наглядную модель, сделать несколько точек на плоскости и наглядно увидеть и показатим расстояние между ними.
Многие из упомянутых программ и онлайн-калькуляторов являются бесплатными и легко доступными для пользователей в Интернете. Выбирайте наиболее удобный и ваш вариант, чтобы быстро и точно найти расстояние между любыми двумя точками на нашей планете.
Практические применения знания формул расстояния
Знать формулы расстояния очень важно в повседневной жизни. Эта задача часто встречается в наших решениях разных задач. Вот несколько примеров, где расстояния и его формулы применяются:
Пример 1: Нахождение расстояния между точками на карте: если вы собираетесь проехать какую-то дистанцию с помощью автомобиля, вам нужно узнать расстояние между двумя точками на карте. Здесь формула расстояния будет полезна. Она вычислит дальность маршрута и укажет вам, сколько необходимо горючего для пути.
Пример 2: Планирование расстояний при строительстве: при проектировании домов и зданий, инженерам и строителям нужно точно знать расстояние между разными точками. Например, для установки коммуникаций, таких как канализация или водопровод. Здесь четкие расчеты на основе формул расстояния помогают получить правильные числа.
Пример 3: Научное исследование: во многих науках, таких как физика и математика, формулы расстояния активно используются для решения сложных задач. Например, при изучении астрономических объектов или при расчете тепловыделяющих аппаратов. Здесь каждый сантиметр имеет значение.
Пример 4: Атласы и карты: далее, при создании географических атласов и карт знание формул расстояния важно для правильного определения размерностей и меток. Нужно точно узнать расстояние между различными достопримечательностями.
Итак, на эти и многие другие примеры наглядно показывают, насколько важно знание и понимание формул расстояния для успешного решения различных задач.
Теоретические аспекты в каждом классе
понимать и изучать окружающий мир. В процессе обучения в 5-м классе, ученики
обучаются различным дисциплинам, таких как Математика, Русский язык, История,
География и другие.
Аспекты Математики в 5-м классе
Математика является основной наукой, которая позволяет выполнять операции с числами, такие как сложение, вычитание, умножение, деление, а также информацию о
теории множеств и системах счисления. В 5 классе ученики изучают ряды и
их свойства, а также осваивают способы решения линейных уравнений.
Аспекты Русского языка в 5-м классе
Русский язык является обязательным предметом для изучения в школах, как правило,
части учебной программы. В 5-м классе ученики учатся работать с русским языком,
уделяя внимание морфологическим, синтаксическим и семантическим аспектам
языка. Они изучают различные виды речи, грамматические категории, а также
работают со словарем и орфоэпией.
| Предмет | Теоретические аспекты | Практические навыки |
|---|---|---|
| Математика | ционным аспектам, таким как ряды, способы решения линейных уравнений, теория множеств | риторики, красноречия, публичных выступлений |
| Русский язык | морфологии, синтаксиса и семантики, различных видов речи, грамматические категории | лексического и морфологического анализа, построения предложений, работы с поэзией и прозой |
| История | аграфия, политическая история, социальные и культурные процессы | выдвигая собственные гипотезы, анализируя факты и объясняя их |
| География | различные географические объекты и процессы, климатология, ландшафтоведение | анализ карт, информирования и возможностей проекта, качественного анализа |
Таким образом, изучая теоретические аспекты в каждом классе, ученики 5-го класса
являются основой для формирования основных интеллектуальных и моральных качеств
учеников, а также предоставляет обширный социально-ориентированный и гражданский
содержаниее и основу для дальнейшего профессионального обучения.
Вопрос-ответ:
Сколько существуют формул для нахождения расстояния между двумя точками на плоскости?
Существует две основные формулы для нахождения расстояния между двумя точками на плоскости. Первая – это прямая формула расстояния, которая вычисляет расстояние между двумя точками с известными координатами (x1, y1) и (x2, y2) по закону: √[(x2-x1)² + (y2-y1)²]. Вторая формула называется формулой углового расстояния и используется для нахождения расстояния по двум углам и одной стороне треугольника, в котором данные точки являются вершинами: расстояние = обратная стороне × [sine другой стороны / sine нужного угла].
Какие известные математические задачи бывают при вычислении расстояния между двумя точками на плоскости?
При вычислении расстояния между двумя точками на плоскости может возникнуть задача нахождения квадратного корня, так как в формуле прямой формулы расстоянияSquare Root Square Root является квадратным корнем. Другая задача заключается в том, чтобы правильно считать минус и плюс во втором слагаемом формулы. И, наконец, возможно возникновение проблем с переполнением при очень больших значениях или с вычислением экспоненты и синуса в формуле углового расстояния.
Как вычислить расстояние между двумя точками на плоскости, если одна из координат является неизвестной?
Если одна из координат является未知, то нужно решить линейное уравнение для некоторых значений других уравнений. предполагая, что в формуле расстояния видно, что нужно найти значение x1 или x2, можно выполнить следующие шаги: 1) Выразить y1 или y2 от формулы в зависимости от значения x; 2) Вычислить расстояние либо по первой формуле, домножив их на √2; 3) используя обратную математику цепных связей, определить значение неизвестной координаты, пока оно равно известному расстоянию.
Можно ли находить расстояние между двумя точками на плоскости, если координаты этих точек являются комплексными числами?
Да, можно находить расстояние между двумя точками на комплексной плоскости, если их координаты являются комплексными числами. Для этого нужно использовать главную формулу расстояния, √[(x2-x1)² + (y2-y1)²]. При этом координаты точек переводим в рациональную форму, и вычисляем квадрат синуса угла между первым и вторым числами комплексной плоскости, применив формулу синусов угла между комплексными числами, а затем найти квадратный корень от суммы квадратов их модулей.