Как найти расстояние формула через высоту

Бывают случаи когда необходимо измерить расстояние до какого нибудь объекта, а под рукой нет бинокля с угломерной сеткой или она в вашей модели не предусмотрена, или вовсе у вас нет бинокля, это не беда, есть до безобразия простой способ определения расстояния до объекта любой, обычной линейкой.

Взамен шкалы бинокля мы будем использовать простую линейку, только необходимо учесть, что у бинокля и линейки разная градация делений. Одно деление шкалы у бинокля равна 5-ти тысячным, а у линейки расположенной от глаз в 50 сантиметрах 1 миллиметр необходимо считать 2-е тысячные.

Формулу для определения расстояния используем такую же как и для биноклей с угломерной сеткой.

Д=(В х 1000)/У

Д – расстояние до объекта,

В – известная нам ширина или высота объекта в метрах,

1000 – это постоянная величина,

У – угловой видимый размер объекта в тысячных.

Определим расстояние до предмета на примере

Допустим вы в поле видите одиноко стоящий дом, а так же его входную дверь. Как мы знаем стандартная высота двери равна 2-м метрам, далее внимательно смотрим на нее через шкалу линейки держа ее перед собой на расстояние примерно 50 сантиметров (полусогнутая рука будет равна этому расстоянию).

Как мы видим дверь на шкале линейки занимает 12 миллиметров, а 1 миллиметр равен 2-м тысячным, значит она занимает 12 х 2 = 24 тысячных. Далее известную нам высоту двери (2 метра) умножаем на 1000 (постоянная) и делим на 24 тысячных и в результате получаем расстояние до дома 83.3 метра. Как вы могли убедиться, все довольно просто!

Подписывайтесь на канал, ставьте лайки, пишите комментарии, ваше мнение очень важно для нас.

В данной публикации мы рассмотрим, чему равно расстояние между двумя точками, и по какой формуле оно считается (на плоскости и в пространстве). Также разберем примеры решения задач по этой теме.

Расчет расстояния между двумя точками

Расстояние между двумя точками — это длина отрезка (d), который получится, если их соединить.

Если точки A (x_a, y_a) и B (x_b, y_b) расположены на плоскости, то расстояние между ними считается по формуле:

Если точки A (x_a, y_a, z_a) и B (x_b, y_b, z_b) находятся в трехмерном пространстве, расстояние вычисляется так:

Примеры задач

Задание 1
На плоскости даны две точки: A (2, 5) и B (-3, 7). Найдем расстояние между ними.

Решение:
Воспользуемся первой формулой, представленной выше:

Задание 2
Найдем расстояние между точками A (-1, 0, 12) и B (2, 6, -4).

Решение:
Применим соответствующую формулу, подставив в нее известные нам значения:

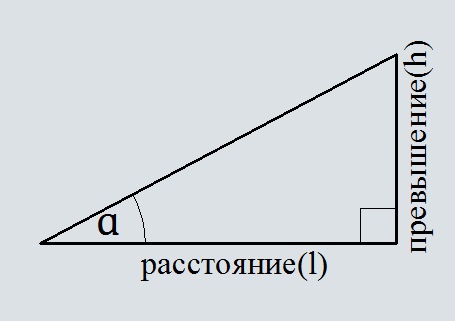
Расчёт расстояния по превышению и уклону

Похожие калькуляторы

Как найти расстояние между двумя точками?

Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.

Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.

Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
( c^2 = a^2 + b^2 ) где c — это гипотенуза, a и b — катеты.

Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.

Итак, для примера возьмем точки с координатами
первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0.
Как же нам теперь выразить точки через катеты a и b ?
Читайте дальше, все гениальное просто.

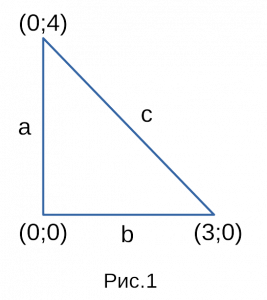
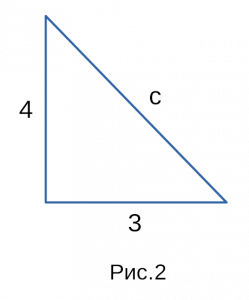
На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.

Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. ​Взгляните на формулу,
которая получилась:

Подставляем наши координаты:

В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.

Расстояние между точками

На этой странице находится все необходимое, чтобы найти расстояние между двумя точками. Просто введите координаты точек и получите ответ и подробное решение с помощью наших онлайн-калькуляторов. Кроме того на сайте можно найти координаты середины отрезка.

Расстояние между двумя точками — это длина отрезка, соединяющего эти точки.

Расстояние между двумя точками на плоскости

Формула для нахождения расстояния между двумя точками A(x_a, y_a) и B(x_b, y_b) на плоскости:

^2 + <(y_b — y_a)^2>>> , где x_a и y_a — координаты первой точки A, x_b и y_b — координаты второй точки B.

Нахождение расстояния между двумя точками на плоскости сводится к решению треугольника, а точнее — нахождению его гипотенузы. Для этого используется теорема Пифагора. Посмотрите на рисунок.

Соединив отрезком точки A и B, а также опустив перпендикуляры на оси мы получим треугольник ABC. В этом треугольнике стороны AC и BC являются катетами прямоугольного треугольника, а AB — его гипотенузой. Длины катетов AC и BC найти довольно просто:

Осталось применить теорему Пифагора и получить сторону AB, которая является гипотенузой прямоугольного треугольника и расстоянием между точками A и B:

Подставив вместо отрезков AC и BC их длины, получим итоговую формулу расстояния между двумя точками:

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника

α , β , γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b – катеты

c – гипотенуза

α , β – острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β , γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

[spoiler title=”источники:”]

http://mnogoformul.ru/rasstoyanie-mezhdu-tochkami

http://www-formula.ru/2011-10-09-11-08-41

[/spoiler]