Задания
Версия для печати и копирования в MS Word
Тип 12 № 311920
i
Центростремительное ускорение при движении по окружности (в м/c2 ) можно вычислить по формуле где
— угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.
Спрятать решение
Решение.
Выразим радиус окружности: Подставим значения переменных a и
Ответ: 5.
Аналоги к заданию № 311920: 338050 338232 350660 … Все
Раздел кодификатора ФИПИ: 1.3 Текстовые задачи.
Спрятать решение
·
Помощь
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
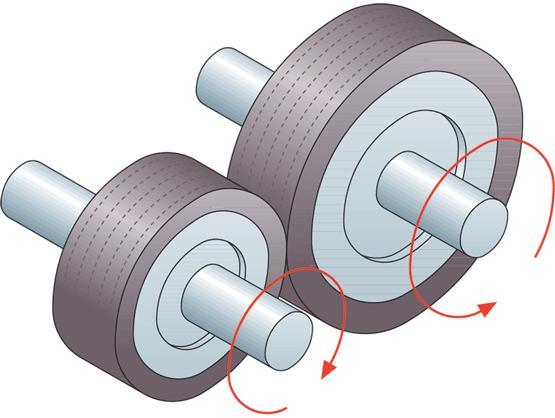
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Движение по окружности: формулы и расчеты
Перемещение тел по окружности достаточно распространено в нашей жизни и в природе. Яркими примерами этого типа перемещения являются вращения ветровых мельниц, планет вокруг своих звезд и колес транспортных средств. В данной статье рассмотрим, какими формулами движение по окружности тел описывается.
Перемещение по окружности и по прямой линии в физике
В физике вопросами движения занимается кинематика. Она устанавливает связь между величинами, описывающими этот процесс. В динамике также уделяется внимание движению, однако она ориентирована на описание причин его возникновения. Другими словами, если для кинематики главными физическими величинами являются путь и скорость, то для динамики – это действующие на тела силы.

В физике принято выделять два идеальных типа траекторий движения:
Математический аппарат для описания движения по обоим типам траекторий развит настолько хорошо, что понимание формул, например для прямолинейного движения, автоматически приводит к пониманию выражений для движения по окружности. Единственная принципиальная разница между формулами указанных типов перемещения заключается в том, что для движения по окружности удобно использовать угловые характеристики, а не линейные.

Далее в статье будем рассматривать исключительно кинематические формулы движения по окружности тел, не вдаваясь в подробности динамики.
Угловые характеристики движения: угол поворота
Прежде чем записывать формулы движения по окружности в физике, следует ввести величины, которые будут фигурировать в этих формулах.
Начнем с угла поворота. Будем обозначать его греческой буквой θ (тета). Поскольку вращение предполагает движение точки вдоль одной и той же окружности, то значение угла поворота θ за определенный промежуток времени можно использовать для определения количества оборотов, которое сделала эта точка. Напомним, что вся окружность равна 2*pi радиан, или 360o. Тогда формула для числа оборотов n через угол θ примет вид:

Здесь и далее во всех формулах угол выражается в радианах.
Пользуясь известным углом θ, также можно определить линейное расстояние, которое точка прошла вдоль окружности. Это расстояние будет равно:
Здесь r – радиус рассматриваемой окружности.
Угловая скорость и ускорение
Кинематические формулы движения по окружности точки предполагают также использование понятий угловой скорости и углового ускорения. Обозначим первую буквой ω (омега), а вторую буквой α (альфа).
Физический смысл угловой скорости ω прост: эта величина показывает, на какой угол в радианах поворачивается точка за каждую секунду времени. Данное определение имеет следующее математическое представление:
Эта формула скорости движения по окружности записана в дифференциальной форме. Полученная с ее помощью величина ω называется мгновенной скоростью. Ее удобно использовать, если движение не является равномерным, то есть происходит с переменной скоростью.
Угловое ускорение α – это величина, которая описывает быстроту изменения скорости ω, то есть:
Угловое ускорение измеряется в радианах в секунду квадратную (рад/с2). Так, 1 рад/с2 означает, что тело увеличивает за каждую секунду времени скорость на 1 рад/с.
Учитывая выражение для ω, записанное выше, равенство можно представить в такой форме:
В зависимости от особенностей движения по окружности величина α может быть постоянной, переменной или нулевой.
Равномерное движение
Когда на вращающееся тело не действует никакая внешняя сила, то угловая скорость будет оставаться постоянной сколь угодно длительное время. Такое движение получило название равномерного вращения. Оно описывается следующей формулой:
В этом выражении переменными являются всего две величины: t и θ. Скорость ω = const.
Следует отметить один важный момент: нулю равна лишь равнодействующая внешних сил на тело, внутренние же силы, действующие в системе, нулю не равны. Так, внутренняя сила заставляет вращающееся тело изменять свою прямолинейную траекторию на криволинейную (окружность). Эта сила приводит к появлению центростремительного ускорения. Последнее не изменяет ни скорость ω, ни линейную скорость v, оно лишь изменяет направление движения.
Равноускоренное движение по окружности
Формулы для этого типа перемещения можно получить непосредственно из приведенных математических выражений для величин ω и α. Равноускоренное движение предполагает, что за более-менее длительный промежуток времени модуль и направление ускорения α не изменяются. Благодаря этому можно проинтегрировать дифференциальное выражение для α и получить следующие две формулы:
Очевидно, что в первом случае движение будет равноускоренным, во втором – равнозамедленным. Величина ω0 здесь – это некоторая начальная скорость, которой вращающееся тело обладало до появления ускорения.
Для равноускоренного движения не существует конечной скорости, поскольку она может возрастать сколь угодно долго. Для равнозамедленного движения конечным состоянием будет прекращение вращения, то есть ω = 0.
Теперь запишем формулы для определения угла θ при движении с постоянным ускорением. Эти формулы получаются, если произвести двойное интегрирование по времени для выражения α через θ. Получаются следующие выражения:
То есть центральный угол θ, на который тело повернется за время t, будет равен сумме двух слагаемых. Первое слагаемое – это вклад в θ равномерного движения, второе – равноускоренного (равнозамедленного).
Связь между угловыми и линейными величинами
При рассмотрении понятия угла поворота θ уже была приведена формула, которая его связывает с линейным расстоянием L. Здесь же рассмотрим аналогичные выражения для скорости ω и ускорения α.
Линейная скорость v при равномерном движении определяется как расстояние L, пройденное за время t, то есть:
Подставляя сюда выражение для L через θ, получаем:
Мы получили связь между линейной и угловой скоростью. Важно отметить, что удобство использования угловой скорости связано с тем, что она не зависит от радиуса окружности. В свою очередь, линейная скорость v возрастает линейно с увеличением r.
Остается записать связь между линейным ускорением a и его угловым аналогом α. Чтобы это сделать, запишем выражение для скорости v при равноускоренном движении без начальной скорости v0. Получаем:
Подставляем сюда полученное выражение связи между v и ω:
Как и скорость, линейное ускорение, направленное по касательной к окружности, зависит от радиуса.
Ускорение центростремительное
Выше уже было сказано несколько слов об этой величине. Здесь приведем формулы, которые можно использовать для ее вычисления. Через скорость v выражение для центростремительного ускорения ac имеет вид:
Через угловую скорость его можно записать так:
Величина ac не имеет никакого отношения к тангенциальному ускорению a. Центростремительное ускорение обеспечивает поддержание вращающегося тела на одной окружности.
Задача на определение угловой скорости вращения планеты
Известно, что ближе всего к солнцу находится Меркурий. Полагая, что он вращается по окружности вокруг светила, мы можем определить его угловую скорость ω.
Для решения задачи следует обратиться к справочным данным. Из них известно, что планета делает полный оборот вокруг светила за 87 дней 23,23 часа земных. Это время называется периодом обращения. Учитывая, что движение происходит с постоянной угловой скоростью, запишем рабочую формулу:
Остается перевести время в секунды, подставить значение угла θ, соответствующее полному обороту (2*pi), и записать ответ: ω = 8,26*10-7 рад/c.
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
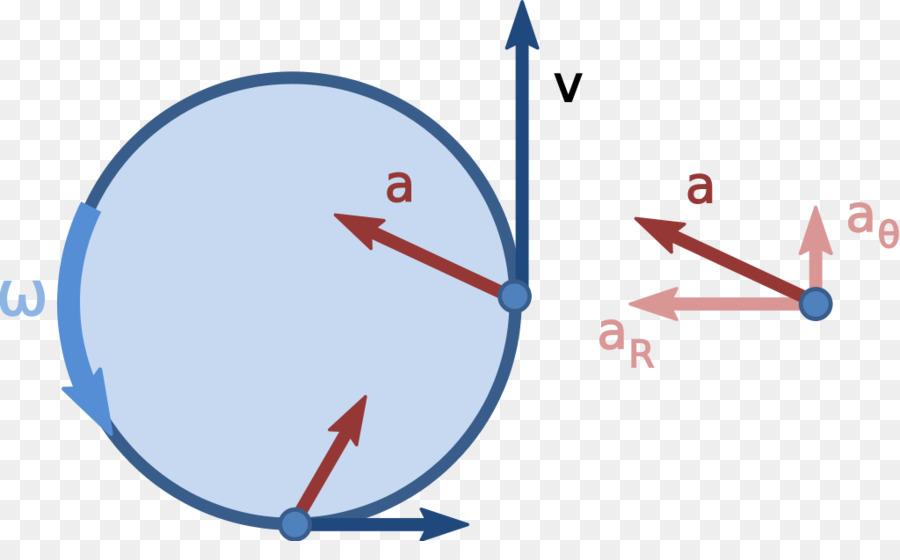
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
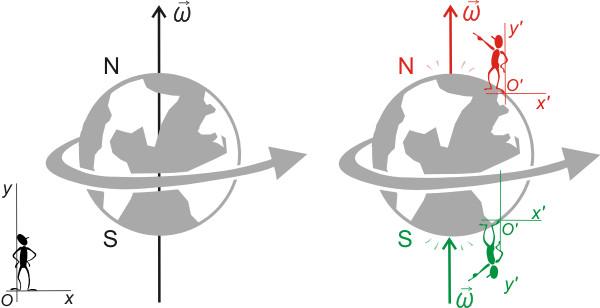
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
[spoiler title=”источники:”]
http://1ku.ru/obrazovanie/45948-dvizhenie-po-okruzhnosti-formuly-i-raschety/
http://fizmat.by/kursy/kinematika/okruzhnost
[/spoiler]
Содержание материала
- Кинематика
- Видео
- Как выглядит формула пути без времени, когда скорость тела уменьшается
- Импульс
- График скорости равномерного движения
- Виды движения и формулы длины пути
- Основные формулы электричества
- Примеры решения задач
Кинематика
К оглавлению…
Путь при равномерном движении:
Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):
Средняя скорость пути:
Средняя скорость перемещения:
Определение ускорения при равноускоренном движении:
Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:
Средняя скорость при равноускоренном движении:
Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Формула для тормозного пути тела:
Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:
Дальность полета тела при горизонтальном броске с высоты H:
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Определение периода вращения при равномерном движении по окружности:
Определение частоты вращения при равномерном движении по окружности:
Связь периода и частоты:
Линейная скорость при равномерном движении по окружности может быть найдена по формулам:
Угловая скорость вращения при равномерном движении по окружности:
Связь линейной и скорости и угловой скорости выражается формулой:
Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):
Центростремительное ускорение находится по одной из формул:
Видео
Как выглядит формула пути без времени, когда скорость тела уменьшается
Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:
[large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]
Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:
[ large begin{cases} S = v_{0} cdot t — displaystyle frac{a}{2} cdot t^{2} \ v = v_{0} — a cdot t end{cases} ]
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
График скорости равномерного движения
Т.к. скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.
Если динозавр начнет двигаться к дому, то его скорость будет положительной, т.к. направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, т.к. направление движения противоположно направлению оси $x$.
Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.
Из графика видно, что скорость с течением времени не изменяется – она постоянна в любой выбранный момент времени. Из графика положительной скорости мы видим, что $upsilon = 6 frac{м}{с}$; из графика отрицательной — $upsilon = -4 frac{м}{с}$.
Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени. Рассчитаем какой путь пройдет тело с положительной скоростью за $4 с$.
$$S = upsilon t = 6 frac{м}{с} cdot 4 c = 24 м$.$
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути $Delta s$ на отрезке времени от $t$ до $t + Delta t$ находят как:
где $langle vrangle$ – средняя путевая скорость. При равномерном движении $langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
где a – постоянное ускорение, v – начальная скорость движения.
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Далее добавляем формулы по теме: “Магнитное поле электрического тока”
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
Примеры решения задач
1. Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.
Переведем единицы измерения скорость в СИ и решим задачу.
$120 frac{км}{ч} = 120 cdot frac{1000 м}{3600 с} approx 33 frac{м}{с}$.
Дано:$upsilon=120 frac{км}{ч}$$t = 3 c$СИ:$upsilon=33 frac{м}{с}$
Найти:$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = upsilon t = 33 frac{м}{с} cdot 3 с approx 100 м$
Ответ: $100 м$
2. Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 frac{км}{ч}$. Сколько времени у них занимает такой полет?
Переведем единицы измерения скорость в СИ и решим задачу.
$40 frac{км}{ч} = 40 cdot frac{1000 м}{3600 с} approx 11 frac{м}{с}$;
$900 км = 900 000 м$.
Дано:$upsilon_{ср} = 40 frac{км}{ч}$$S = 900 км$CИ:$upsilon_{ср} = 11 frac{м}{с}$$S = 900 000 м$
Найти:$t-?$
Показать решение и ответ
Скрыть
Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = frac{s}{upsilon_{ср}} = frac{900 000 м}{11 frac{м}{с}} approx 82 000 с$.
Переведем время в часы:
$1 ч = 60 мин = 60 cdot 60 c = 3600 c$.
Тогда,
$t = frac{82 000 c}{3600 c} approx 23 ч$.
Ответ: $t = 82 000 c = 23 ч$.
Теги
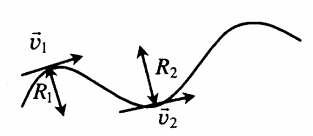
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Определение и формулы
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Определение и формулы
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные факты
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формула
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17763
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Или:
Отсюда:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 21.9k
Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:
Приняв вектор k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.
Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.
Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела