Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 апреля 2022 года; проверки требует 1 правка.
|
3-битовый двоичный куб; все вершины, соединённые ребром имеют расстояние 1 |
пример расстояний: расстояние 3 100 → 011, расстояние 2 010 → 111 |
|
4-битовый двоичный тессеракт (четырёхмерный куб) |
|
|
примеры расстояний в двоичном тессеракте: расстояние 1 0110 → 1110, расстояние 3 0100 → 1001 |
Расстоя́ние Хэ́мминга (кодовое расстояние) — число позиций, в которых соответствующие символы двух слов одинаковой длины различны[1]. В более общем случае расстояние Хэмминга применяется для строк одинаковой длины любых q-ичных алфавитов и служит метрикой различия (функцией, определяющей расстояние в метрическом пространстве) объектов одинаковой размерности.
Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей: в этом случае расстоянием Хэмминга 




Два слова, расстояние Хэмминга между которыми равно 1, называют соседними.
В некоторых системах счисления, например, в коде Грея, целые кодированные числа, различающиеся на 1, имеют расстояние Хэмминга равное 1. Говорят, что такие числа являются «соседними».
Соседнее кодирование важно при проектировании логических устройств, где необходимо исключить логические гонки.
Примеры[править | править код]
Алгоритм[править | править код]
def hamming_distance(string1, string2): if (len(string1) != len(string2)): raise Exception('Strings must be of equal length.') dist_counter = 0 for n in range(len(string1)): if string1[n] != string2[n]: dist_counter += 1 return dist_counter
Свойства[править | править код]
Множество слов равной длины образуют метрическое пространство, где для каждой пары элементов пространства определено число — расстояние Хэмминга 
(аксиома тождества).
(аксиома симметрии).
(аксиома треугольника или неравенство треугольника).
- тогда из аксиомы тождества и неравенства треугольника следует аксиома симметрии.
Расстояние Хэмминга всегда:
- где
— длина слов в символах.
Применения[править | править код]
Расстояние Хэмминга в биоинформатике и геномике[править | править код]
Для нуклеиновых кислот (ДНК и РНК) возможность гибридизации двух полинуклеотидных цепей с образованием вторичной структуры — двойной спирали — зависит от степени комплементарности нуклеотидных последовательностей обеих цепей. При увеличении расстояния Хэмминга количество водородных связей, образованных комплементарными парами оснований уменьшается и, соответственно, уменьшается стабильность двойной цепи. Начиная с некоторого граничного расстояния Хэмминга гибридизация становится невозможной.
При эволюционном расхождении гомологичных ДНК-последовательностей расстояние Хэмминга является мерой, по которой можно судить о времени, прошедшем с момента расхождения гомологов, например, о длительности эволюционного отрезка, разделяющего гены-гомологи и ген-предшественник.
Телекоммуникации[править | править код]
Алгоритм используется в телекоммуникациях для подсчета количества неправильных бит в слове фиксированной длины для оценки ошибки и поэтому иногда называется расстоянием сигналов (англ. signal distance).
См. также[править | править код]
- Расстояние Левенштейна
- Обнаружение и исправление ошибок
- Матрица расстояний
Примечания[править | править код]
- ↑ Hamming distance: The number of digit positions in which the corresponding digits of two binary words of the same length are different (Federal Standard 1037C Архивная копия от 2 марта 2009 на Wayback Machine).
Литература[править | править код]
- Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир, 1986. — 576 с.
Время на прочтение
6 мин
Количество просмотров 60K

Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.
Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.
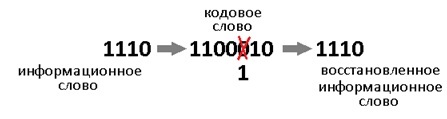
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.
Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.
К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:

Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).

Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):

Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.
Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:

В программной реализации опять же ничего сверх сложного. Делитель (1011) сдвигаем влево до самого конца на 3 разряда. И начинаем удалять (не без помощи XOR) самые левые единицы в делимом (100110), на его младшие разряды даже не смотрим. Делимое поэтапно уменьшается 100110 -> 0011110 -> 0001000 -> 0000011, когда в 4м и левее разрядах не остаётся единиц, мы останавливаемся.
Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.

В результате собираем список синдромов, и то на какую болезнь он указывает:

Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.
Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.
А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):
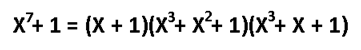
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:
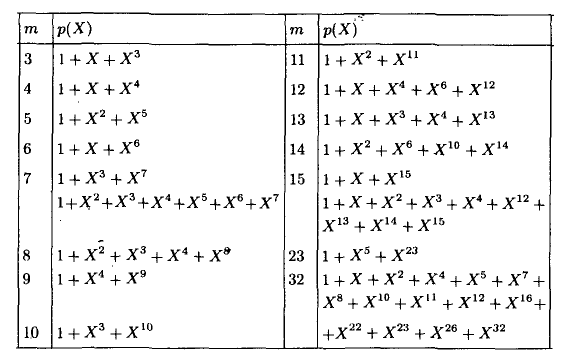
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:
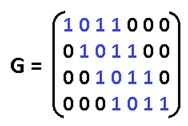
Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:

Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.

Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.
Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:

Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.
Список используемой литературы:
1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986
From Wikipedia, the free encyclopedia
|
||
| Class | String similarity | |
|---|---|---|
| Data structure | string | |
| Worst-case performance |  |
|
| Best-case performance |  |
|
| Average performance |  |
|
| Worst-case space complexity |  |

3-bit binary cube for finding Hamming distance
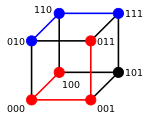
Two example distances: 100→011 has distance 3; 010→111 has distance 2
The minimum distance between any two vertices is the Hamming distance between the two binary strings.
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number of substitutions required to change one string into the other, or the minimum number of errors that could have transformed one string into the other. In a more general context, the Hamming distance is one of several string metrics for measuring the edit distance between two sequences. It is named after the American mathematician Richard Hamming.
A major application is in coding theory, more specifically to block codes, in which the equal-length strings are vectors over a finite field.
Definition[edit]
The Hamming distance between two equal-length strings of symbols is the number of positions at which the corresponding symbols are different.[1]
Examples[edit]
The symbols may be letters, bits, or decimal digits, among other possibilities. For example, the Hamming distance between:
- “karolin” and “kathrin” is 3.
- “karolin” and “kerstin” is 3.
- “kathrin” and “kerstin” is 4.
- 0000 and 1111 is 4.
- 2173896 and 2233796 is 3.
Properties[edit]
For a fixed length n, the Hamming distance is a metric on the set of the words of length n (also known as a Hamming space), as it fulfills the conditions of non-negativity, symmetry, the Hamming distance of two words is 0 if and only if the two words are identical, and it satisfies the triangle inequality as well:[2] Indeed, if we fix three words a, b and c, then whenever there is a difference between the ith letter of a and the ith letter of c, then there must be a difference between the ith letter of a and ith letter of b, or between the ith letter of b and the ith letter of c. Hence the Hamming distance between a and c is not larger than the sum of the Hamming distances between a and b and between b and c. The Hamming distance between two words a and b can also be seen as the Hamming weight of a − b for an appropriate choice of the − operator, much as the difference between two integers can be seen as a distance from zero on the number line.[clarification needed]
For binary strings a and b the Hamming distance is equal to the number of ones (population count) in a XOR b.[3] The metric space of length-n binary strings, with the Hamming distance, is known as the Hamming cube; it is equivalent as a metric space to the set of distances between vertices in a hypercube graph. One can also view a binary string of length n as a vector in 
Error detection and error correction[edit]
The minimum Hamming distance is used to define some essential notions in coding theory, such as error detecting and error correcting codes. In particular, a code C is said to be k error detecting if, and only if, the minimum Hamming distance between any two of its codewords is at least k+1.[2]
For example, consider the code consisting of two codewords “000” and “111”. The hamming distance between these two words is 3, and therefore it is k=2 error detecting. This means that if one bit is flipped or two bits are flipped, the error can be detected. If three bits are flipped, then “000” becomes “111” and the error can not be detected.
A code C is said to be k-error correcting if, for every word w in the underlying Hamming space H, there exists at most one codeword c (from C) such that the Hamming distance between w and c is at most k. In other words, a code is k-errors correcting if, and only if, the minimum Hamming distance between any two of its codewords is at least 2k+1. This is more easily understood geometrically as any closed balls of radius k centered on distinct codewords being disjoint.[2] These balls are also called Hamming spheres in this context.[4]
For example, consider the same 3 bit code consisting of two codewords “000” and “111”. The Hamming space consists of 8 words 000, 001, 010, 011, 100, 101, 110 and 111. The codeword “000” and the single bit error words “001”,”010″,”100″ are all less than or equal to the Hamming distance of 1 to “000”. Likewise, codeword “111” and its single bit error words “110”,”101″ and “011” are all within 1 Hamming distance of the original “111”. In this code, a single bit error is always within 1 Hamming distance of the original codes, and the code can be 1-error correcting, that is k=1. The minimum Hamming distance between “000” and “111” is 3, which satisfies 2k+1 = 3.
Thus a code with minimum Hamming distance d between its codewords can detect at most d-1 errors and can correct ⌊(d-1)/2⌋ errors.[2] The latter number is also called the packing radius or the error-correcting capability of the code.[4]
History and applications[edit]
The Hamming distance is named after Richard Hamming, who introduced the concept in his fundamental paper on Hamming codes, Error detecting and error correcting codes, in 1950.[5] Hamming weight analysis of bits is used in several disciplines including information theory, coding theory, and cryptography.[6]
It is used in telecommunication to count the number of flipped bits in a fixed-length binary word as an estimate of error, and therefore is sometimes called the signal distance.[7] For q-ary strings over an alphabet of size q ≥ 2 the Hamming distance is applied in case of the q-ary symmetric channel, while the Lee distance is used for phase-shift keying or more generally channels susceptible to synchronization errors because the Lee distance accounts for errors of ±1.[8] If 




The Hamming distance is also used in systematics as a measure of genetic distance.[9]
However, for comparing strings of different lengths, or strings where not just substitutions but also insertions or deletions have to be expected, a more sophisticated metric like the Levenshtein distance is more appropriate.
Algorithm example[edit]
The following function, written in Python 3, returns the Hamming distance between two strings:
def hamming_distance(string1: str, string2: str) -> int: """Return the Hamming distance between two strings.""" if len(string1) != len(string2): raise ValueException("Strings must be of equal length.") dist_counter = 0 for n in range(len(string1)): if string1[n] != string2[n]: dist_counter += 1 return dist_counter
Or, in a shorter expression:
sum(xi != yi for xi, yi in zip(x, y))
The function hamming_distance(), implemented in Python 3, computes the Hamming distance between two strings (or other iterable objects) of equal length by creating a sequence of Boolean values indicating mismatches and matches between corresponding positions in the two inputs, then summing the sequence with True and False values, interpreted as one and zero, respectively.
def hamming_distance(s1: str, s2: str) -> int: """Return the Hamming distance between equal-length sequences.""" if len(s1) != len(s2): raise ValueError("Undefined for sequences of unequal length.") return sum(el1 != el2 for el1, el2 in zip(s1, s2))
where the zip() function merges two equal-length collections in pairs.
The following C function will compute the Hamming distance of two integers (considered as binary values, that is, as sequences of bits). The running time of this procedure is proportional to the Hamming distance rather than to the number of bits in the inputs. It computes the bitwise exclusive or of the two inputs, and then finds the Hamming weight of the result (the number of nonzero bits) using an algorithm of Wegner (1960) that repeatedly finds and clears the lowest-order nonzero bit. Some compilers support the __builtin_popcount function which can calculate this using specialized processor hardware where available.
int hamming_distance(unsigned x, unsigned y) { int dist = 0; // The ^ operators sets to 1 only the bits that are different for (unsigned val = x ^ y; val > 0; ++dist) { // We then count the bit set to 1 using the Peter Wegner way val = val & (val - 1); // Set to zero val's lowest-order 1 } // Return the number of differing bits return dist; }
A faster alternative is to use the population count (popcount) assembly instruction. Certain compilers such as GCC and Clang make it available via an intrinsic function:
// Hamming distance for 32-bit integers int hamming_distance32(unsigned int x, unsigned int y) { return __builtin_popcount(x ^ y); } // Hamming distance for 64-bit integers int hamming_distance64(unsigned long long x, unsigned long long y) { return __builtin_popcountll(x ^ y); }
See also[edit]
- Closest string
- Damerau–Levenshtein distance
- Euclidean distance
- Gap-Hamming problem
- Gray code
- Jaccard index
- Levenshtein distance
- Mahalanobis distance
- Mannheim distance
- Sørensen similarity index
- Sparse distributed memory
- Word ladder
References[edit]
- ^ Waggener, Bill (1995). Pulse Code Modulation Techniques. Springer. p. 206. ISBN 9780442014360. Retrieved 13 June 2020.
- ^ a b c d Robinson, Derek J. S. (2003). An Introduction to Abstract Algebra. Walter de Gruyter. pp. 255–257. ISBN 978-3-11-019816-4.
- ^ Warren Jr., Henry S. (2013) [2002]. Hacker’s Delight (2 ed.). Addison Wesley – Pearson Education, Inc. pp. 81–96. ISBN 978-0-321-84268-8. 0-321-84268-5.
- ^ a b Cohen, G.; Honkala, I.; Litsyn, S.; Lobstein, A. (1997), Covering Codes, North-Holland Mathematical Library, vol. 54, Elsevier, pp. 16–17, ISBN 9780080530079
- ^ Hamming, R. W. (April 1950). “Error detecting and error correcting codes” (PDF). The Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. ISSN 0005-8580. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- ^ Jarrous, Ayman; Pinkas, Benny (2009). Abdalla, Michel; Pointcheval, David; Fouque, Pierre-Alain; Vergnaud, Damien (eds.). “Secure Hamming Distance Based Computation and Its Applications”. Applied Cryptography and Network Security. Berlin, Heidelberg: Springer: 107–124. doi:10.1007/978-3-642-01957-9_7. ISBN 978-3-642-01957-9.
- ^ Ayala, Jose (2012). Integrated Circuit and System Design. Springer. p. 62. ISBN 978-3-642-36156-2.
- ^ Roth, Ron (2006). Introduction to Coding Theory. Cambridge University Press. p. 298. ISBN 978-0-521-84504-5.
- ^ Pilcher, Christopher D.; Wong, Joseph K.; Pillai, Satish K. (2008-03-18). “Inferring HIV Transmission Dynamics from Phylogenetic Sequence Relationships”. PLOS Medicine. 5 (3): e69. doi:10.1371/journal.pmed.0050069. ISSN 1549-1676. PMC 2267810. PMID 18351799.
Further reading[edit]
 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.- Wegner, Peter (1960). “A technique for counting ones in a binary computer”. Communications of the ACM. 3 (5): 322. doi:10.1145/367236.367286. S2CID 31683715.
- MacKay, David J. C. (2003). Information Theory, Inference, and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
Рассмотрим,
чем определяется способность блочного
кода обнаруживать и исправлять ошибки,
возникшие при передаче.
Пусть
U
= (U0,
U1,
U2,
…Un-1)
– двоичная последовательность длиной
n.
Число
единиц
(ненулевых компонент) в этой
последовательности называется
весом
Хемминга
вектора U
и обозначается w(U).
Например,
вес Хемминга вектора U
=
( 1001011
) равен четырем, для вектора U
=
( 1111111
)
величина w(U)
составит 7 и т.д.
Таким
образом, чем больше единиц в двоичной
последовательности, тем больше ее вес
Хемминга.
Далее, пусть U и V будут
двоичными последовательностями длиной
n.
Число разрядов, в которых эти
последовательности различаются,
называется расстоянием Хемминга между
U и V и обозначается
d( U, V).
Например,
если U
=
( 1001011
), а V
= ( 0100011
), то d(
U, V) = 3.
Задав
линейный код, то есть определив все 2k
его кодовых слов, можно вычислить
расстояние между всеми возможными
парами кодовых слов. Минимальное из них
называется минимальным
кодовым расстоянием кода
и обозначается dmin.
Можно
проверить и убедиться, что минимальное
кодовое расстояние для рассматриваемого
нами в примерах (7,4)-кода
равно трем: dmin(7,4)
=
3.
Для этого нужно записать все кодовые
слова (7,4)-кода
Хемминга (всего 16 слов), вычислить
расстояния между их всеми парами и взять
наименьшее значение. Однако можно
определить dmin
блочного кода и более простым способом.
Доказано,
что расстояние между нулевым кодовым
словом и одним из кодовых слов, входящих
в порождающую матрицу (строки порождающей
матрицы линейного блочного кода сами
являются кодовыми словами, по определению),
равно dmin.
Но расстояние от любого кодового слова
до нулевого равно весу Хемминга этого
слова. Тогда dmin
равно минимальному
весу Хемминга
для
всех строк порождающей матрицы кода .
Если
при передаче кодового слова по каналу
связи в нем произошла одиночная
ошибка,
то расстояние Хемминга между переданным
словом U
и принятым вектором r
будет равно единице. Если при этом одно
кодовое слово не перешло в другое (а при
dmin
>
1 и при одиночной ошибке это невозможно),
то ошибка будет
обнаружена
при декодировании.
В
общем случае если блочный код имеет
минимальное расстояние dmin,
то он
может обнаруживать любые сочетания
ошибок при их числе, меньшем или равном
dmin
–
1,
поскольку никакое сочетание ошибок при
их числе, меньшем, чем dmin
–
1,
не может перевести одно кодовое слово
в другое.
Но
ошибки могут иметь кратность и большую,
чем dmin–
1,
и тогда они останутся
необнаруженными.
При
этом среднюю вероятность необнаруживаемой
ошибки можно определить следующим
образом.
Пусть
вероятность ошибки в канале связи равна
Pош.
Тогда вероятность того, что при передаче
последовательности длины n
в ней произойдет одна ошибка, равна
Р1
= n
Pош
( 1- Рош)n-1,
(1.36)
соответственно,
вероятность l-кратной
ошибки –
Pl
=Cnl
Pошl
( 1- Pош)n-l,
(1.37)
где
Cnl
– число возможных комбинаций из
n
символов кодовой последо-вательности
по l
ошибок.
По
каналу связи передаются кодовые слова
с различными весами Хемминга. Положим,
что ai
— число слов с весом i
в данном коде (всего слов в коде длиной
n
–
![]()
).
А
теперь определим, что такое необнаруживаемая
ошибка.
Обнаружение ошибки производится путем
вычисления синдрома принятой
последовательности. Если принятая
последовательность не является кодовым
словом ( тогда синдром не равен нулю),
то считается, что ошибка есть. Если же
синдром равен нулю, то полагаем, что
ошибки нет (принятая последовательность
является кодовым словом). Но
тем ли, которое передавалось? Или же в
результате действия ошибок переданное
кодовое слово перешло в другое кодовое
слово данного кода:
r
= U
+ е = V,
(1.38)
то
есть сумма переданного кодового слова
U
и вектора ошибки е
даст новое
кодовое слово V
? В этом случае, естественно, ошибка
обнаружена быть не может.
Но
из определения двоичного линейного
кода следует, что если
сумма кодового слова и некоторого
вектора е
есть кодовое слово, то вектор е
также представляет собой кодовое слово.
Следовательно,
необнаруживаемые ошибки будут возникать
тогда, когда сочетания ошибок будут
образовывать кодовые слова.
Вероятность
того, что вектор е
совпадает с кодовым словом, имеющим вес
i
,
равна
Pi
=
Pошi
(1- Рош)n-i
. (1.39)
Тогда полная
вероятность возникновения необнаруживаемой
ошибки
![]()
.
(1.40)
Пример:
рассматриваемый нами (7,4)-код
содержит по семь кодовых слов с весами
w
= 3 и w
= 4 и одно
кодовое слово с весом w
= 7, тогда
![]()
(1.41)
или,
при Рош
= 10
-3,
Р(Е)
7
10
-9.
Другими
словами, если по каналу передается
информация
со скоростью V
=
1кбит/с и в канале в среднем каждую
секунду
будет происходить искажение одного
символа, то в среднем семь принятых слов
на 109
переданных будут проходить через декодер
без обнаружения ошибки (одна необнаруживаемая
ошибка за 270 часов).
Таким
образом, использование даже такого
простого кода позволяет на несколько
порядков снизить вероятность
необнаруживаемых ошибок.
Теперь
предположим, что линейный блочный код
используется для исправления ошибок.
Чем определяются его возможности по
исправлению?
Рассмотрим
пример, приведенный на рис. 1.9. Пусть U
и V
представляют
пару кодовых слов кода с
кодовым расстоянием d
,
равным минимальному — d
min
для
данного
кода.

Рис.
1.9
Предположим,
передано кодовое слово U,
в
канале произошла одиночная
ошибка
и принят вектор а
(не
принадлежащий коду).
Если
декодирование производится оптимальным
способом, то есть по
методу максимального правдоподобия,
то в
качестве оценки U*
нужно
выбрать ближайшее к а
кодовое
слово.
Таковым
в данном случае будет U,
следовательно, ошибка будет устранена.
Представим
теперь, что произошло две ошибки и принят
вектор b.
Тогда
при декодировании по максимуму
правдоподобия в
качестве оценки будет выбрано ближайшее
к b
кодовое слово, и им будет
V.
Произойдет ошибка декодирования.
Продолжив
рассуждения для dmin
=
4, dmin
=
5
и т.д., нетрудно сделать вывод, что ошибки
будут устранены, если их кратность l
не превышает величины
l<
INT (( dmin – 1 )/2) ,
(1.41)
где
INT (X)
— целая часть Х.
Так,
используемый нами в качестве примера
(7,4)-код
имеет dmin
= 3 и,
следовательно, позволяет
исправлять лишь одиночные ошибки:
l
= INT
(( dmin
– 1
)/2)=INT((3-1)/2)=1
.
(1.42)
Таким
образом, возможности
линейных блочных кодов по обнаружению
и исправлению ошибок определяются их
минимальным кодовым расстоянием.
Чем
больше dmin,
тем большее число ошибок в принятой
последовательности можно исправить.
А
теперь определим вероятность того, что
возникшая в процессе передачи ошибка
не будет все же исправлена при
декодировании.
Пусть,
как и ранее, вероятность ошибки в канале
будет равна Рош.
Ошибки, возникающие в различных позициях
кода, считаем независимыми.
Вероятность
того, что принятый вектор r
будет иметь какие-нибудь (одиночные,
двукратные, трехкратные и т.д.) ошибки,
можно определить как
Рош
= P1
+ P2
+ P3
+… + Pn
,
(1.43)
где
Р1
— вероятность того, что в r
присутствует
одиночная ошибка;
Р2
—
вероятность того, что ошибка двойная и
т.д.;
Рn
— вероятность того, что все n
символов
искажены.
Определим вероятность ошибок заданной
кратности:
Р1
=
Вер{ошибка
в 1-й позиции ИЛИ ошибка во 2-й позиции
..ИЛИ в n-й позиции}
= = Рош(1-
Рош)n-1
+ Рош(1-
Рош)n-1
+…Рош(1-
Рош)n-1
= п
Рош(1-
Рош)n-;
(1.44)
Р2
=
Вер{ошибка
в 1-й И во 2-й позиции ИЛИ ошибка во 2-й И
в 3-й позиции…}
=
=
P2ош(1-Рош)n-2
+…Р2ош(1-
Рош)
n-2 =
![]()
Р2ош(1-
Рош)
n-2.
(1.45)
Аналогичным
образом
Р3
=
![]()
Р3ош(1-
Рош)n-3
и т.д.
(1.46)
Декодер,
как мы показали, исправляет все ошибки,
кратность которых не превышает
![]()
,
(1.47)
то
есть все ошибки кратности J
l будут
исправлены.
Тогда
ошибки декодирования – это ошибки с
кратностью, большей кратности исправляемых
ошибок l,
и их вероятность
![]()
![]()
.
(1.48)
Для
(7,4)-кода
Хемминга минимальное расстояние dmin
=
3,
т.е. l
=
1.
Следовательно, ошибки кратности 2 и
более исправлены не будут и
![]()
.
(1.49)
Если
Рош<<
1,
можно считать (1-
Рош)
1
и, кроме того, Р3ош<<
Р2ош.
Тогда
![]()
.
(1.50)
Так, например,
при вероятности ошибки в канале Рош
= 10 -3 вероятность
неисправления ошибки Р(N)
2 10
-5, то есть при такой
вероятности ошибок в канале кодирование
(7.4)-кодом позволяет снизить
вероятность оставшихся неисправленными
ошибок примерно в пятьдесят раз.
Если
же вероятность ошибки в канале будет
в сто раз меньше Рош
= 10 -5, то вероятность
ее неисправления составит уже Р(N)
210
-9, или в 5000 раз
меньше!
Таким
образом, выигрыш от помехоустойчивого
кодирования (который можно определить
как отношение числа ошибок в канале к
числу оставшихся неисправленными
ошибок) существенно зависит от свойств
канала связи.
Если
вероятность ошибок в канале велика, то
есть канал не очень хороший, ожидать
большого эффекта от кодирования не
приходится, если же вероятность ошибок
в канале мала, то корректирующее
кодирование уменьшает ее в значительно
большей степени.
Другими
словами, помехоустойчивое кодирование
существенно улучшает свойства хороших
каналов, в плохих же каналах оно большого
эффекта не дает.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
10.06.2015684.82 Кб14P4.pdf
- #
- #
- #
- #
| Определение: |
| Расстояние Хэмминга (англ. Hamming distance) — число позиций, в которых различаются соответствующие символы двух строк одинаковой длины. |
В более общем случае расстояние Хэмминга применяется для строк одинаковой длины любых k-ичных алфавитов и служит метрикой различия (функцией, определяющей расстояние в метрическом пространстве) объектов одинаковой размерности.
Пример
- d(1011101, 1001001)=2
- d(1538124, 1523156)=4
- d(hill, holl)=1
Свойства
Расстояние Хэмминга обладает свойствами метрики, так как удовлетворяет ее определению.
- (Если расстояние от до равно нулю, то и совпадают ())
- (Объект удален от объекта так же, как объект удален от объекта )
- (Расстояние от до всегда меньше или равно расстоянию от до через точку . Это свойство обычно называют неравенством треугольника за его естественную геометрическую аналогию: сумма двух сторон треугольника всегда больше третьей стороны.)
Доказательство неравенства треугольника
| Утверждение: |
| Пусть слова и отличаются в некоторых позициях. Тогда какое бы слово мы ни взяли, оно будет отличаться в каждой из этих позиций по крайне мере от одного из слов и . Следовательно, суммируя в правой части и , мы обязательно учтем все позиции, в которых различались слова и . Т.е. получается, что . |
См. также
- Избыточное кодирование, код Хэмминга
Источники информации
- Расстояние Хэмминга — Википедия
- Hamming distance – Wikipedia
- Математические основы информатики








