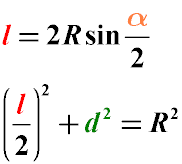Рассмотрим, как найти расстояние от центра окружности до хорды.
Расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из этой точки на данную прямую. Значит, расстояние от центра окружности до хорды равно длине перпендикуляра, проведённого из центра окружности к этой хорде.
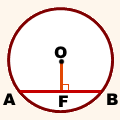
Например, расстояние от точки O — центра окружности — до хорды AB равно длине перпендикуляра OF:
![]()
Задача.
Отрезки AB и CD являются хордами окружности. Найти расстояние от центра окружности до хорды CD, если AB=24, CD=10, а расстояние от центра окружности до хорды AB равно 5.
 Дано: окружность (O; R), AB и CD — хорды,
Дано: окружность (O; R), AB и CD — хорды,
![]()
AB=24, CD=10, OF=5
Найти: OK
Решение:
 1) Соединим центр окружности с концами хорд.
1) Соединим центр окружности с концами хорд.
2) Треугольники AOB и COD — равнобедренные с основаниями AB и CD (AO=BO=CO=DO как радиусы).
Значит, их высоты OF и OK являются также медианами. Следовательно,
![]()
3) Рассмотрим треугольник AOF, где ∠AFO=90 º.
По теореме Пифагора
![]()
![]()
4) Рассмотрим треугольник COK, где ∠CKO=90 º.
По теореме Пифагора
![]()
![]()
Ответ: 12.
Содержание:
Окружность:
Определение: Кривой второго порядка называется линия, описываемая уравнением 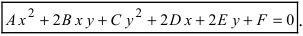
Замечание: Если коэффициенты 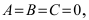
При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки 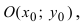 называемой центром окружности, на расстояние R, которое называется радиусом окружности.
называемой центром окружности, на расстояние R, которое называется радиусом окружности.
Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:
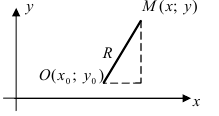
Рис. 27. Вывод уравнения окружности.
Из рисунка видно, что по теореме Пифагора 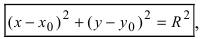 которое определяет уравнение окружности (Рис. 28):
которое определяет уравнение окружности (Рис. 28): 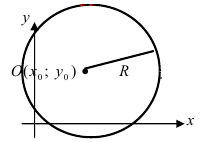
Рис. 28. Окружность. 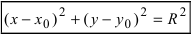
Если 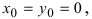 то уравнение принимает вид
то уравнение принимает вид 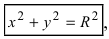 который называется каноническим уравнением окружности.
который называется каноническим уравнением окружности.
Пример:
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 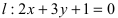 является касательной к окружности.
является касательной к окружности.
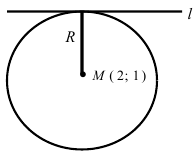
Решение:
Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.
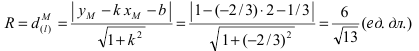
В уравнении окружности 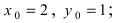 таким образом оно имеет вид:
таким образом оно имеет вид: 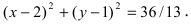
Пример:
Составить уравнение окружности, касающейся двух параллельных прямых 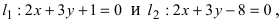 причем одной из них в т. А (1; 2).
причем одной из них в т. А (1; 2).
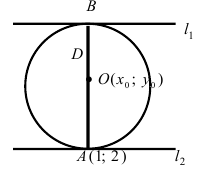
Решение:
Прежде всего определим, на какой из прямых 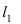 или
или 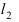 лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых
лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых 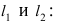
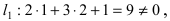 следовательно, точка A(1; 2) принадлежит линии
следовательно, точка A(1; 2) принадлежит линии 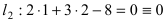 (в сокращенной форме это предложение пишут так:
(в сокращенной форме это предложение пишут так: 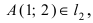 где значок
где значок 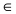 означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой
означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой 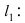
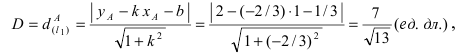
а радиус окружности 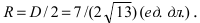 Найдём координаты центра окружности точки
Найдём координаты центра окружности точки 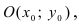 которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки
которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки 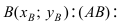 перейдем от общего уравнения прямой
перейдем от общего уравнения прямой 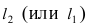 к уравнению прямой с угловым коэффициентом
к уравнению прямой с угловым коэффициентом 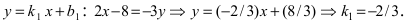 Так как прямая
Так как прямая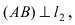 то её угловой коэффициент
то её угловой коэффициент 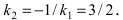 Прямая (АВ) проходит через известную точку A(1;2), следовательно,
Прямая (АВ) проходит через известную точку A(1;2), следовательно, 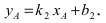 Отсюда находим
Отсюда находим 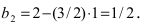 Таким образом,уравнение прямой (АВ):
Таким образом,уравнение прямой (АВ):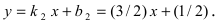
Найдем координаты точки B, которая является пересечением прямых 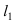 и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых
и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых 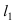 и (АВ): (В):
и (АВ): (В): 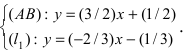 Подставим выражение для переменной у из второго у равнения в первое, получим
Подставим выражение для переменной у из второго у равнения в первое, получим 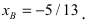 Подставив это значение во второе уравнение системы, найдем
Подставив это значение во второе уравнение системы, найдем 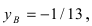 т.е.
т.е. 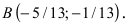
Для вычисления координат точки О применим формулы деления отрезка пополам (О): 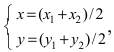 в этой формуле
в этой формуле 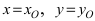 (координаты точки О),
(координаты точки О), 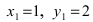 (координаты точки А),
(координаты точки А), 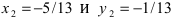 (координаты точки В), следовательно,
(координаты точки В), следовательно, 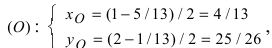 т.е. координаты точки О
т.е. координаты точки О 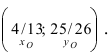
Таким образом, уравнение искомой окружности имеет вид: 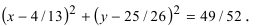
Окружность в высшей математике
Рассмотрим уравнение

которое получается из уравнения (I), если положить 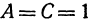 ,
, 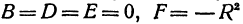 .
.
Если в формулу, выражающую расстояние между двумя точками, подставить 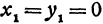 ,
, 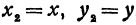 , то получим
, то получим 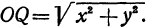 Из уравнения (1) находим, что
Из уравнения (1) находим, что 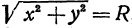 , т. е.
, т. е. 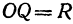 . Это значит, что все точки
. Это значит, что все точки 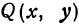 , координаты которых удовлетворяют уравнению (1), находятся на расстоянии
, координаты которых удовлетворяют уравнению (1), находятся на расстоянии 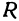 от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса
от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса  с центром в начале координат. Аналогично получаем, что уравнение
с центром в начале координат. Аналогично получаем, что уравнение 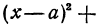
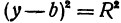 определяет окружность радиуса
определяет окружность радиуса  с центром в точке
с центром в точке 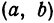 .
.
Пример:
Найдем уравнение окружности с центром в точке  и радиусом, равным 10.
и радиусом, равным 10.
Решение:
Полагая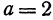 ,
, 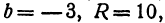 получим
получим 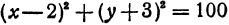 .
.
Разрешим это уравнение относительно 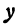 , будем иметь
, будем иметь
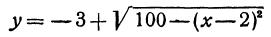
и
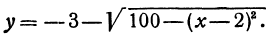
Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.
Центральный угол. Градусная мера дуги
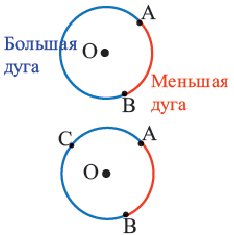
Дуга окружности. Если отметить на окружности точки  и
и  , то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка
, то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка 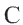 является какой-либо точкой дуги
является какой-либо точкой дуги 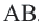 , то
, то 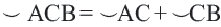 . Если точки
. Если точки  и
и  являются концами диаметра, го каждая дуга является полуокружностью.
являются концами диаметра, го каждая дуга является полуокружностью.
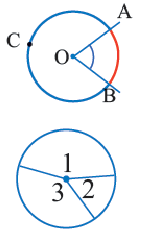
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла: 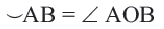
Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна 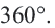
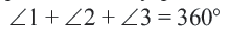
Дуги окружности и их величины

Пример: 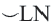 минорная дуга:
минорная дуга: 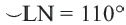
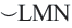 мажорная дуга:
мажорная дуга: 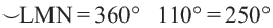
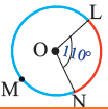
Конгруэнтные дуги
В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.
Если 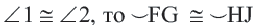
Если 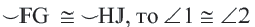
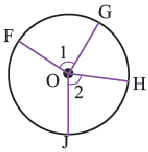
Длина дуги
Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.
Длина дуги в 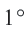 равна
равна 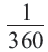 части длины окружности.
части длины окружности.
Длина дуги, соответствующей центральному углу с градусной мерой 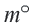 , составляет
, составляет 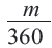 части длины окружности:
части длины окружности: 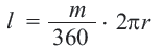
Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)
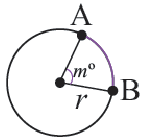
Пример №1
Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу 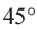 .
.
Решение:
Так как центральный угол 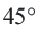 составляет
составляет 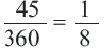 часть полного угла, то длина искомой дуги:
часть полного угла, то длина искомой дуги: 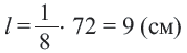
Пример №2
Найдите длину дуги, соответствующей центральному углу 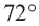 в окружности радиусом 15 см.
в окружности радиусом 15 см.
Решение: подставляя значения 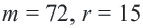 в формулу длины дуги находим:
в формулу длины дуги находим: 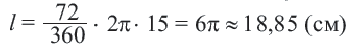
Окружность и хорда
Теорема о конгруэнтных хордах
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.
Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.
1)Если 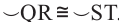 , то
, то 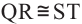
2)Если 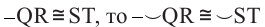
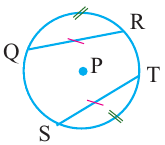
Доказательство теоремы 1:
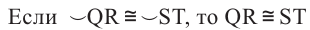

Теорема о серединном перпендикуляре хорд
Теорема 2.
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.
Если 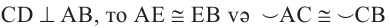
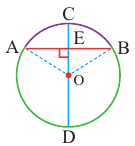
Доказательство теоремы 2.
Дано:  – центральный угол,
– центральный угол, 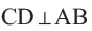
Докажите: 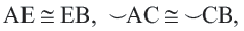
Начертите радиусы 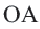 и
и 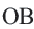 окружности.
окружности.
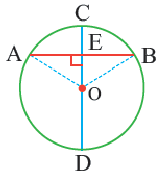
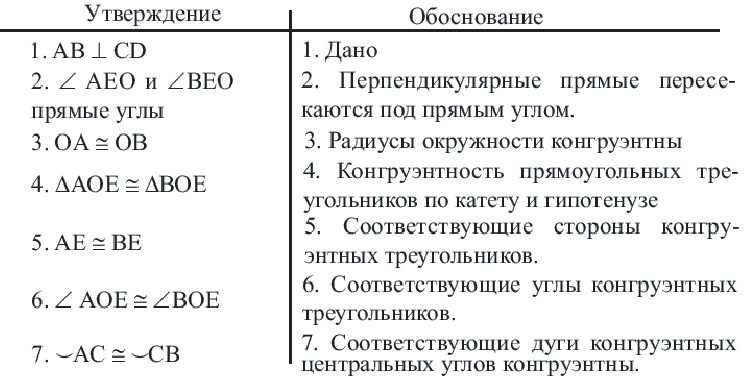
Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.
Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если 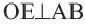 , то
, то 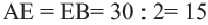 . Из
. Из 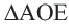 по теореме Пифагора имеем:
по теореме Пифагора имеем: 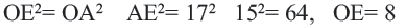
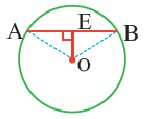
Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности
Теорема 3.
Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.
Если 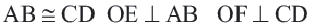 , то
, то 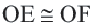
Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.
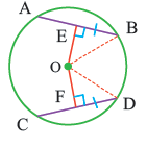
Доказательство теоремы 3
Дано: Окружность с центром 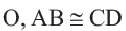
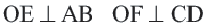
Докажите: 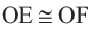
Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам.  и
и  – серединные перпендикуляры конгруэнтных хорд
– серединные перпендикуляры конгруэнтных хорд 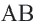 и
и 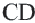 .
.  , так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности
, так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности 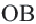 и
и 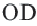 :
: 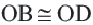 . Прямоугольные треугольники,
. Прямоугольные треугольники, 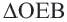 и
и 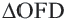 конгруэнтны (по катету и гипотенузе). Так как
конгруэнтны (по катету и гипотенузе). Так как  и
и  являются соответствующими сторонами данных треугольников, то они конгруэнтны:
являются соответствующими сторонами данных треугольников, то они конгруэнтны: 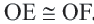 . Теорема доказана.
. Теорема доказана.
Задача. Хорды  и
и  находятся на одинаковом расстоянии от центра окружности.
находятся на одинаковом расстоянии от центра окружности. 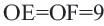 . Если радиус окружности равен 41 единице, то найдите
. Если радиус окружности равен 41 единице, то найдите 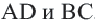 .
.
Решение: Так как хорды  и
и  находятся на одинаковом расстоянии от центра, то они конгруэнтны:
находятся на одинаковом расстоянии от центра, то они конгруэнтны: 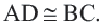
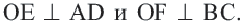 Соединим точки
Соединим точки 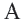 и
и 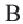 с точкой
с точкой 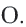 В прямоугольном треугольнике
В прямоугольном треугольнике 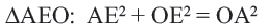
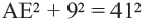 ;
; 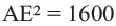 ;
; 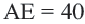 ;
; 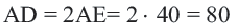
Так как 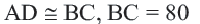
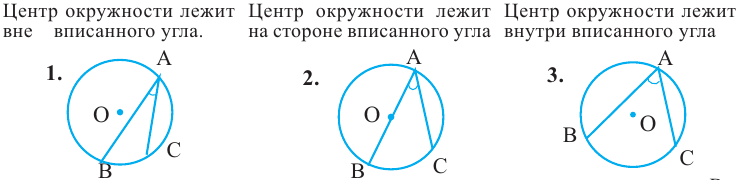
Угол, вписанный в окружность
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.
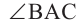 является углом вписанным в окружность с центром
является углом вписанным в окружность с центром  , а
, а  дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
Угол, вписанный в окружность:
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается. 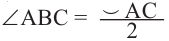
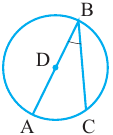
Доказательство (текстовое): 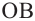 и
и 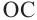 радиусы окружности и
радиусы окружности и 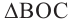 равнобедренный треугольник. Значит,
равнобедренный треугольник. Значит, 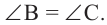 Так как
Так как 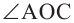 является внешним углом
является внешним углом 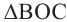 ,
, 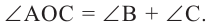 Если примем, что
Если примем, что 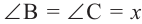 , то
, то 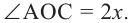 Так как градусные меры центрального угла и опирающейся на него дуги равны, то
Так как градусные меры центрального угла и опирающейся на него дуги равны, то 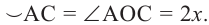 Следовательно,
Следовательно, 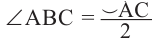 .
.
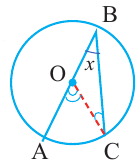
Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.
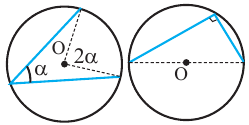
Конгруэнтные углы, вписанные в окружность
Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. 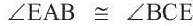 ,
, 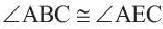 .
.
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если 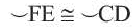 , то
, то 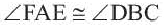 .
.
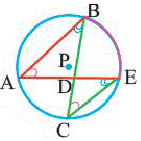

Касательная к окружности
Касательная. Признак касательной
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
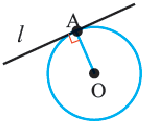
Прямая 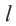 является касательной к окружности. Значит,
является касательной к окружности. Значит, 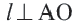 Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.

Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.
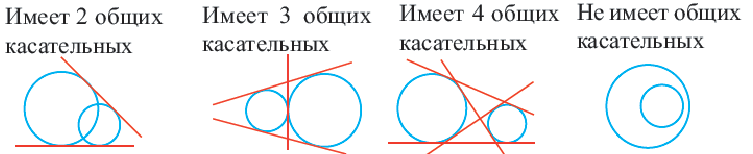
Доказательство теоремы 1. Если прямая  – касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая
– касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая  не перпендикулярна радиусу
не перпендикулярна радиусу 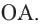 Проведем
Проведем 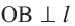 и на прямой
и на прямой  выделим отрезок
выделим отрезок 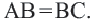 Тогда
Тогда 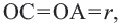 так как
так как 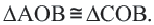 Значит, точка
Значит, точка 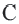 также находится на окружности. То есть прямая
также находится на окружности. То есть прямая  имеет с окружностью две общие точки, что противоречит условию. Значит,
имеет с окружностью две общие точки, что противоречит условию. Значит, 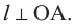
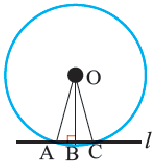
Свойства касательных, проведенных к окружности из одной точки
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.
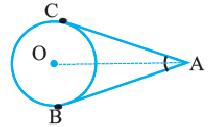
 и
и 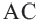 касательные, проведенные из точки
касательные, проведенные из точки 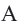 к окружности с центром
к окружности с центром 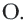
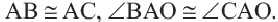
Углы, образованные секущими и касательными
Прямая, имеющая две общие точки с окружностью, называется секущей окружности.
Углы между двумя секущими
Вершина угла находится внутри окружности
Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному. 
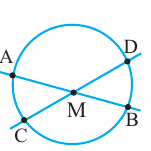
Углы между касательной и секущей
Вершина угла находится на окружности
Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.
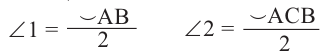
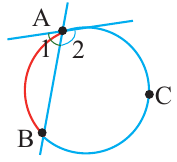
Углы, образованные касательной и секущей
Вершина угла находится вне окружности
Теорема 1.
Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.
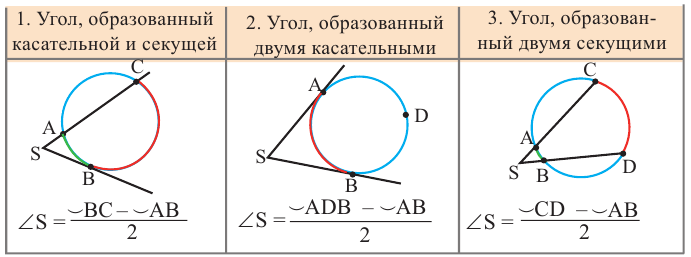
Отрезки секущих и касательных
Длина отрезков, секущих окружность
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.
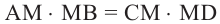
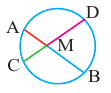
Теорема 2. Если из точки  провести две прямые, пересекающие окружность соответственно в точках
провести две прямые, пересекающие окружность соответственно в точках  и
и 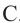 ,
, 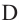 и
и 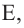 то верно равенство
то верно равенство 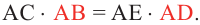
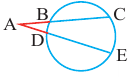
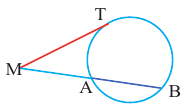
Теорема 3. Если из точки 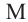 проведены прямая, которая пересекает окружность в точках
проведены прямая, которая пересекает окружность в точках  и
и  и касательная к окружности в точке
и касательная к окружности в точке 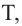 то верно равенство:
то верно равенство: 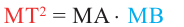
Уравнение окружности
Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом  и с центром в начале координат. Расстояние между центром окружности
и с центром в начале координат. Расстояние между центром окружности 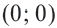 и ее любой точкой
и ее любой точкой 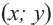 равно радиусу
равно радиусу  окружности.
окружности.
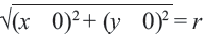 Расстояние между двумя точками
Расстояние между двумя точками
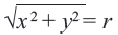 Упрощение
Упрощение
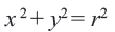 Возведение обеих частей в квадрат
Возведение обеих частей в квадрат
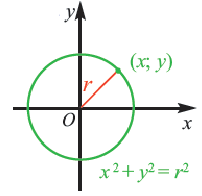
Уравнение окружности с центром в начале координат и радиусом 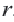 :
: 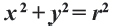
Например, уравнение окружности с центром в начале координат 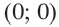 и радиусом 2 имеет вид:
и радиусом 2 имеет вид: 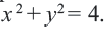
По формуле расстояния между центром окружности 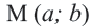 и точки
и точки 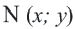 на окружности радиуса
на окружности радиуса 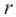 имеем
имеем 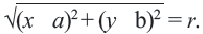 Возведя в квадрат обе части, получаем уравнение окружности с центром в точке
Возведя в квадрат обе части, получаем уравнение окружности с центром в точке 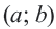 и радиусом
и радиусом 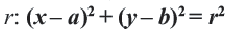
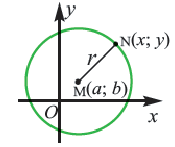
Например, уравнение окружности с центром в точке 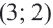 и радиусом 4 имеет вид:
и радиусом 4 имеет вид: 
Пример №3
Постройте на координатной плоскости окружность, заданную уравнением 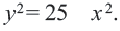
Решение: Напишем уравнение в виде 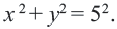 Как видно,
Как видно, 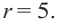
Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 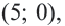
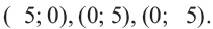 Проведем окружность через эти точки.
Проведем окружность через эти точки.
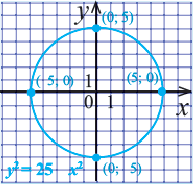
Пример №4
Точка 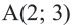 находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
Решение: Записав координаты точки 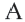 в уравнении
в уравнении 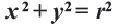 , получим:
, получим: 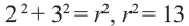 Уравнение этой окружности:
Уравнение этой окружности: 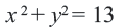
Пример №5
Найдем центр и радиус окружности, заданной уравнением 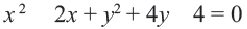
Решение: 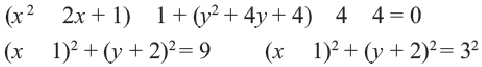
Центр окружности точка 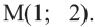 Радиус
Радиус 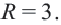
Пример №6
Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 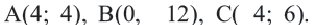 На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 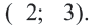 Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности,
Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности, 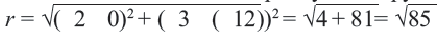
Уравнение окружности: 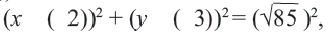
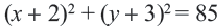
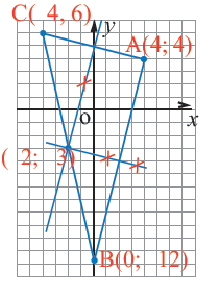
Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.
Координаты точек, находящихся на окружности, и тригонометрические отношения
Если точка 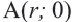 при повороте радиуса
при повороте радиуса 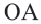 вокруг точки
вокруг точки 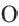 против движения часовой стрелки на угол
против движения часовой стрелки на угол 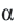 преобразуется в точку
преобразуется в точку 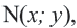 то
то 
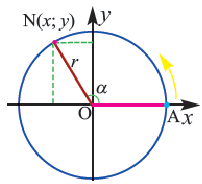
Для координат точки 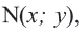 соответствующей углу поворота
соответствующей углу поворота  на окружности, верны формулы
на окружности, верны формулы 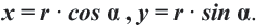 В этих формулах
В этих формулах  – угол, отсчитываемый от положительной оси
– угол, отсчитываемый от положительной оси 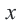 против движения часовой стрелки. Если точка
против движения часовой стрелки. Если точка 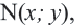 не находится на оси ординат, то
не находится на оси ординат, то 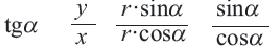 .
.
Синусы смежных углов равны, а косинусы взаимно противоположны.

Из этих формул при 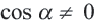 почленным делением получаем:
почленным делением получаем:
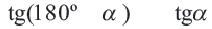
С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.
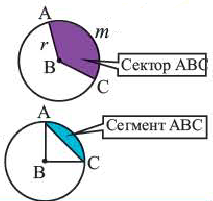
Сектор и сегмент
Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.
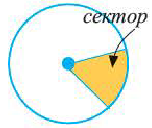
Например, часть круга, соответствующая центральному углу 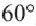 , составляет
, составляет 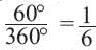 часть всего круга. Так как площадь круга
часть всего круга. Так как площадь круга 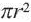 , то площадь этого сектора будет
, то площадь этого сектора будет  Сегмент часть круга, ограниченная хордой и соответствующей дугой.
Сегмент часть круга, ограниченная хордой и соответствующей дугой.
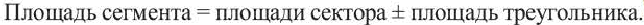
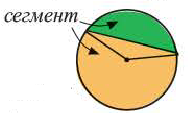
Площадь сектора
Площадь сектора: 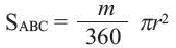
Площадь сегмента: 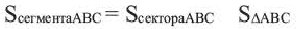
Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь 
- Эллипс
- Гипербола
- Парабола
- Многогранник
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
Окружность есть такая плоская кривая, у которой все точки находятся на равном расстоянии от одной точки, лежащей внутри ее и называемой центром.
Круг. Кругом называется часть плоскости, ограниченная окружностью.
Радиус. Радиусом называется отрезок, соединяющий центр с какой-нибудь точкой окружности. Радиус есть расстояние точки окружности от центра.
Из самого определения окружности следует, что все ее радиусы равны.
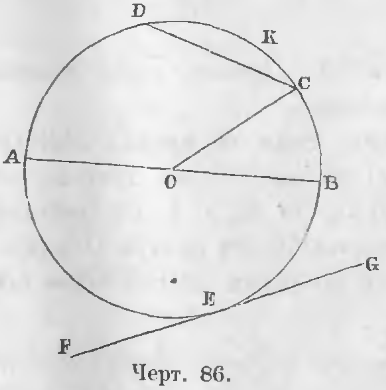
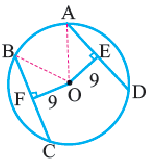
На чертеже 86 кривая линия BCDAEB есть окружность, O ее центр, отрезки OA, OB, OC — радиусы. Эти отрезки равны
OA = OB = OC.
Диаметр. Отрезок, проходящий через центр от одной точки окружности до другой, называется диаметром.
Всякий диаметр состоит из двух радиусов, а так как все радиусы равны, то следовательно и все диаметры равны.
Дуга есть часть окружности.
Слово дуга иногда обозначают знаком ◡, так что дугу BC изображают письменно: ◡BC.
Хорда. Отрезок, соединяющий две какие-нибудь точки окружности, называется хордой. Хорда есть прямая, стягивающая две точки дуги.
На чертеже 86 линия AB есть диаметр, часть окружности BC есть дуга, прямая CD есть хорда.
Сегмент есть часть плоскости, содержащийся между дугой и хордой.
Сектор есть часть плоскости, содержащийся между двумя радиусами и дугой круга.
На чертеже 86 площадь COB есть сектор, а CKD сегмент.
Касательная есть прямая, имеющая с окружностью только одну общую точку, которая называется точкой касания.
Углом при центре называется угол, имеющий вершину в центре. На чертеже 86 прямая FG есть касательная, а E точка касания.
Теорема 55. Прямая может пересечь окружность только в двух точках.
Доказательство. Если бы прямая AB кроме двух точек M и N (черт. 87) имела бы еще третью точку пересечения L, то три точки окружности M, N, L, по свойству окружности, были бы на равном расстоянии от центра O, следовательно, три отрезка MO, NO, LO были бы равны: MO = NO = LO.
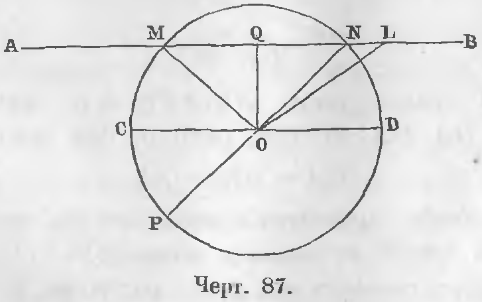
Если же NO = LO, то вышло бы, что равные наклонные находятся на неравных расстояниях от перпендикуляра OQ, что противоречит свойству косвенных, следовательно, третьей точки пересечения быть не может (ЧТД).
Теорема 56. Диаметр делит окружность и круг на две равные части.
Доказательство. Перегнем верхнюю часть круга около диаметра CD (черт. 87) до совпадения ее с нижней частью, тогда все точки верхней совпадут с точками нижней части окружности, ибо в противном случае не все точки окружности находились бы на равном расстоянии от центра.
Зависимость между углами, дугами и хордами
Теорема 57. В двух равных кругах равным углам при центре соответствуют равные дуги.
Дано. Две окружности описаны (черт. 88) одними и теми же радиусами и углы при центре равны:
∠AOB = ∠A’O’B’.
Требуется доказать, что ◡AB = ◡A’B’.
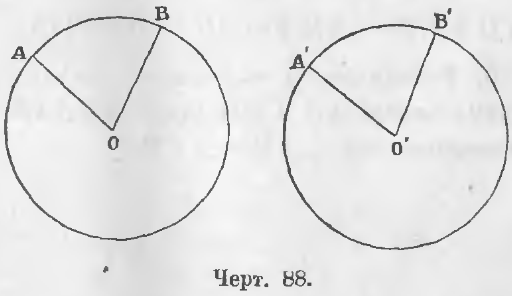
Доказательство. Наложим круг O’ на круг O так, чтобы центр O’ совпал с центром O и сторона OA со стороною O’A’. Точка A’ по равенству радиусов совпадает с точкой A. По равенству углов A’O’B’ и AOB отрезок O’B’ пойдет по отрезку OB и по равенству радиусов точка B’ упадет в точку B. Две крайние точки дуги A’B’ совпадут с двумя крайними точками дуги AB, следовательно, и все промежуточные точки дуги A’B’ совпадут с промежуточными точками дуги AB, так как окружность O’ совпадает с окружностью O, ибо они описаны равными радиусами.
Теорема 58 (обратная 57). Равным дугам соответствуют равные углы.
Дано. Дуги AB и A’B’ равны (◡AB = ◡A’B’) (черт. 88).
Требуется доказать, что ∠AOB = ∠A’O’B’.
Доказательство. Наложим сектор A’O’B’ на сектор AOB так, чтобы отрезок O’A’ совпал с отрезком OA. Дуга A’B’ упадет на дугу AB и B’ упадет в B. Отрезок B’O’ совпадет с отрезком BO и угол AOB совпадет с углом A’O’B’, следовательно,
∠AOB = ∠A’O’B’ (ЧТД).
Теорема 59. Диаметр больше всякой хорды.
Даны диаметр CD и хорда MN (черт. 87).
Требуется доказать, что CD > MN.
Доказательство. Проведем радиусы MO и NO. Ломаная линия MON больше прямой MN
MON > MN или MO + ON > MN
Так как MO = CO, NO = OD, то заменяя MO и NO равными им величинами, получим неравенства:
CO + OD > MN или CD > MN (ЧТД).
Теорема 60. Равные хорды стягивают равные дуги.
Даны равные хорды AB и CD (черт. 89) (AB = CD).
Требуется доказать, что ◡AB = ◡CD.
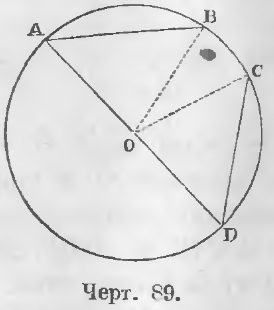
Доказательство. Соединив точки A, B, C, D с центром, имеем
∆AOB = ∆COD, ибо
OA = OC и OB = OD как радиусы, AB = CD по условию.
Следовательно, ∠AOB = ∠COD, откуда ◡AB = ◡CD (ЧТД).
Теорема 61 (обратная 60). Равные дуги стягиваются равными хордами.
Дано. Дуги AB и CD равны (черт. 89) (◡AB = ◡CD).
Требуется доказать, что AB = CD.
Доказательство. Два треугольника AOB и COD равны, ибо OA = OC и OB = OD как радиусы, ∠AOB = ∠COD ибо по условию дуги AB и CD равны, а потому и углы равны (теорема 58). Следовательно, AB = CD (ЧТД).
Теорема 62. Если дуги меньше полуокружности, то против большей дуги лежит большая хорда.
Дано. Дуга BD больше дуги AC (черт. 90) (◡BD > ◡AC).
Требуется доказать, что BD > AC.
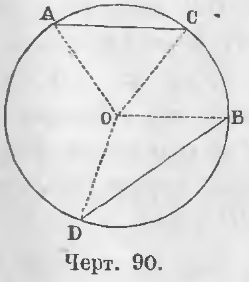
Доказательство. Соединим точки A, C, B, D с центром O. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BOD > AOC. Следовательно, BD > AC (теорема 23) (ЧТД).
Теорема 63 (обратная 62). Против большей хорды лежит большая дуга.
Дано. Хорда BD больше хорды AC (черт. 90) (BD > AC).
Требуется доказать, что ◡BD > ◡AC.
Доказательство. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BD > AC по условию. Поэтому ∠BOD > ∠AOC (теорема 24). Следовательно, ◡BD > ◡AC (ЧТД).
Взаимное отношение хорд и их расстояний от центров
Теорема 64. Радиус, перпендикулярный к хорде, делит как хорду так и дугу пополам.
Радиус OC перпендикулярен к хорде AB (черт. 91).
CO ⊥ AB.
Требуется доказать, что AD = BD и ◡AC = ◡CB.
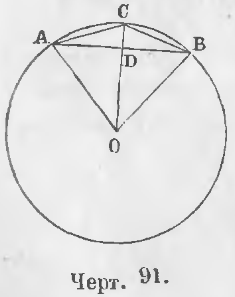
Доказательство. Соединим точки A и B с центром O. Равные наклонны OA и OB находятся на равных расстояниях от перпендикуляра OC, следовательно, AD = DB.
Если же перпендикуляр CD восставлен из середины отрезка AB, то его точка C находится на равном расстоянии от концов перпендикуляра, поэтому хорды AC и CB равны, а следовательно,
◡AC = ◡CB
т. е. дуга AB делится перпендикуляром OC пополам (ЧТД).
Следствие. Перпендикуляр, восставленный из середины хорды, проходит через центр.
Доказательство. Так как центр находится на равном расстоянии от концов хорды, то он находится на перпендикуляре, восставленном из середины хорды.
Теорема 65. Равные хорды находятся на равном расстоянии от центра.
Дано. Хорды AB и CD равны: AB = CD (черт. 92).
Требуется доказать, что их расстояния от центра равны, т. е.
OE = OF
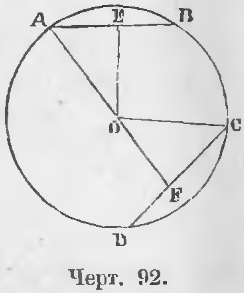
Доказательство. Соединив точки A и C с центром O, имеем два равных прямоугольных треугольника AEO и COF, ибо OA = OC как радиусы, AE = CF как половины равных хорд (теорема 64). Следовательно,
OE = OF (ЧТД).
Теорема 66 (обратная 65). На равных расстояниях от центра находятся равные хорды.
Дано. Расстояния хорд AB и CD от центра равны, т. е.
OE = OF (черт. 92).
Требуется доказать, что AB = CD.
Доказательство. Два прямоугольных треугольника AEO и COF равны, ибо имеют по равной гипотенузе и равному катету. Действительно, OE = OF по условию, OA = OC как радиусы, следовательно, AE = CF или ½AB = ½CD, откуда
AB = CD (ЧТД).
Теорема 67. Большая хорда к центру ближе меньшей.
Дано. Хорда AB больше хорды AC (черт. 93), т. е. AB > AC.
Требуется доказать, что OD < OE.
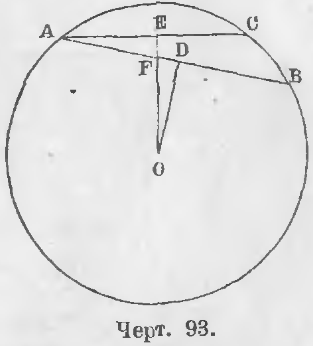
Доказательство. Линия OD перпендикулярна к AB, а линия OF наклонна, следовательно, OD < OF. Так как OF < OE, то и подавно OD < OE (ЧТД).
Свойства касательной
Прямая называется секущей, если она пересекает окружность в двух точках, и касательной, если она имеет с окружностью только одну общую точку. Эта точка называется точкой касания.
Теорема 68. Прямая, проведенная через в конец радиуса, перпендикулярно к нему, будет касательной к окружности.
Дано. Прямая AF перпендикулярно к радиусу AO в конце радиуса (черт. 94)
AF ⊥ AO.
Требуется доказать, что AF касательная к окружности.
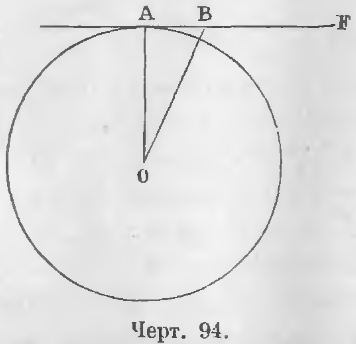
Доказательство. Всякая другая точка B перпендикуляра AB находится на расстоянии BO большем AO, ибо наклонная больше перпендикуляра, следовательно точка B находится вне окружности. Таким образом прямая AB имеет с окружностью только одну общую точку A, следовательно, она будет касательной (ЧТД).
Теорема 69 (обратная 68). Касательная к окружности, проведенная в конец радиуса, перпендикулярна к радиусу.
Дано. Прямая AF касается окружности в точке A (черт. 94).
Требуется доказать, что AF ⊥ OA.
Доказательство. Прямая AB как касательная имеет с окружностью только одну общую точку A. Всякая другая точка B лежит вне окружности, следовательно, всякий отрезок OB больше OA. Таким образом, отрезок OA есть кратчайшее расстояние точки O от AB, следовательно, OA ⊥ AB (ЧТД).
Теорема 70. Между параллельными хордами находятся равные дуги.
Дано. Хорды AB и CD параллельны: AB || CD (черт. 95).
Требуется доказать, что ◡AC = ◡BD.
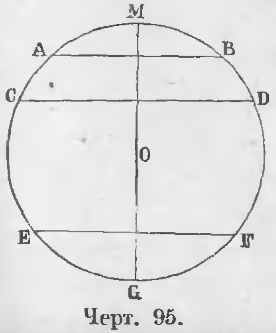
Доказательство. a) Из центра окружности O опустим перпендикуляр OM на хорду AB, тогла отрезок OM перпендикулярен и к хорде CD.
По теореме 64
◡CM = ◡MD
◡AM = ◡MB
Вычитая второе равенство из первого, получим:
◡CM – ◡AM = ◡MD – ◡MB или
◡AC = ◡BD.
b) Если параллельные хорды AB и EF (черт. 95) лежат по обе стороны центра, то, продолжив прямую OM до пересечения с окружностью в точке G, имеем:
◡MA = ◡MB, ◡GE = ◡GF.
Так как полуокружности MAG и MBG равны
MAG = MBG, то следовательно,
MAG – ◡MA – ◡GE = MBG – ◡MB – ◡GF
или ◡AE = ◡BF (ЧТД).
Относительное положение двух окружностей
Концентрические и эксцентрические круги. Два круга называются концентрическими, когда они имеют один общий центр, и эксцентрическими, когда из центры не совпадают.
На чертеже 96 представлены круги концентрические и на чертежах 97, 98, 99, 100 и 101 круги эксцентрические.
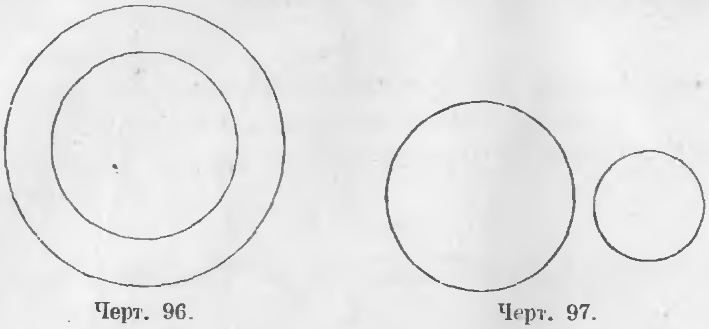
Внешние и внутренние круги. Круги называются внешними, когда все точки одного лежат вне площади другого круга, и внутренними, когда все точки одного лежат внутри площади другого круга.
На чертежах 97 и 99 изображены круги внешние, на чертежах 96, 98 и 100 круги внутренние.
Касательные окружности. Окружности называются касательными, когда они имеют одну общую точку.
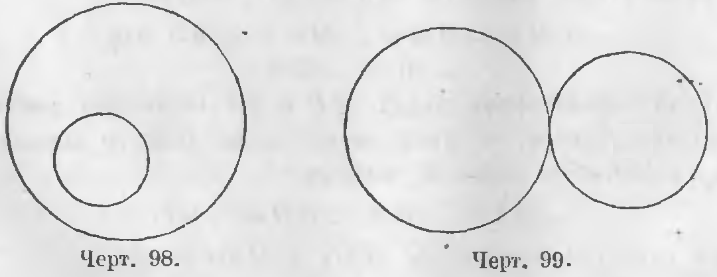
Общая точка двух касательных окружностей называется их точкой соприкосновения. Соприкосновение называется внешним, когда два круга, имея общую точку, лежат один вне другого, и внутренним, когда один круг лежит внутри другого. На черт. 99 имеем случай внешнего, а на чертеже 100 случай внутреннего соприкосновения.
Пересекающиеся окружности. Окружности называются пересекающимися, когда они имеют две общие точки (черт. 101).
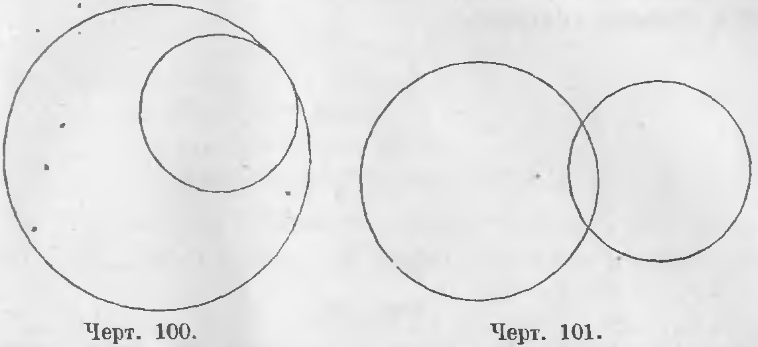
Линия центров есть отрезок, соединяющий центры двух кругов.
Теорема 71. Две окружности, имеющие общую точку на линии центров, другой общей точки иметь не могут.
Дано. Две окружности с центрами O и O’ имеют общую точку A (черт. 102).
Требуется доказать, что другой общей точки у них нет.
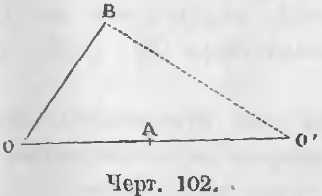
Доказательство. Положим, существует другая общая точка B, следовательно,
OB = OA и O’B = O’A.
Складывая эти равенства, мы имели бы
OB + O’B = OA + O’A или
OB + O’B = OO’
равенство несообразное, ибо ломаная не может равняться прямой.
Итак, другой общей точки быть не может (ЧТД).
Теорема 72. Две окружности, имеющие одну общую точку вне линии центров, имеют и другую общую точку по другую сторону линии центров.
Дано. Две окружности, центры которых O и O’, имеют общую точку A вне отрезка OO’ (черт. 103), соединяющей центры.
Требуется доказать, что существует и другая общая точка по другую сторону центров.
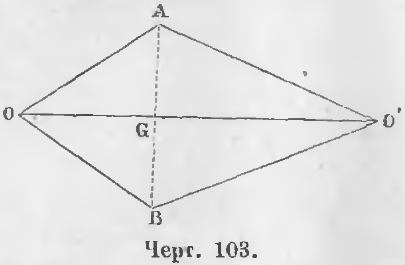
Доказательство. Из точки A опустим на линию центров перпендикуляр AG и на продолжении его отложим отрезок BG, равный AG.
Докажем, что точка B будет другая общая точка. Точка B лежит на окружности O, ибо AO = BO как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’. Точка B лежит на окружности O’, ибо AO’ = BO’ как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’, следовательно, точка B есть другая общая точка (ЧТД).
Теорема 73. Если две окружности пересекаются в двух точках, то линия центров перпендикулярна и делит пополам хорду, соединяющую точки пересечения.
Дано. Точки A и B есть точки пересечения (черт. 104) двух окружностей.
Требуется доказать, что AG = BG и AB ⊥ OO’.
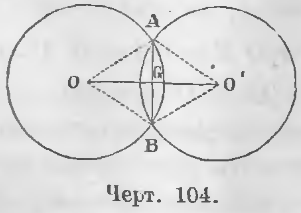
Доказательство. Треугольники OAO’ и OBO’ равны, ибо OO’ сторона общая.
OA = OB как радиусы окружности O.
O’A = O’B как радиусы окружности O’.
Следовательно,
∠AOO’ = ∠BOO’
Треугольники AOG и BOG равны, ибо OG сторона общая, AO = BO как радиусы, ∠AOG = ∠BOG по доказанному. Следовательно, AG = BG (хорда AB делится линией центров пополам), ∠AGO = ∠BGO (хорда AB перпендикулярна к линии центров).
Таким образом, хорда AB делится пополам и перпендикулярна к линии центров OO’ (ЧТД).
Расстояние между центрами окружностей
1. Если две окружности пересекаются в двух точках, расстояние центров меньше суммы и больше разности радиусов.
Действительно, с одной стороны (черт. 104)
OO’ < AO + AO’
с другой
AO + OO’ > AO’
следовательно,
OO’ > AO’ – AO
2. Если две окружности касаются, расстояние центров равно сумме радиусов, если соприкосновение внешнее, и разности радиусов, если соприкосновение внутреннее.
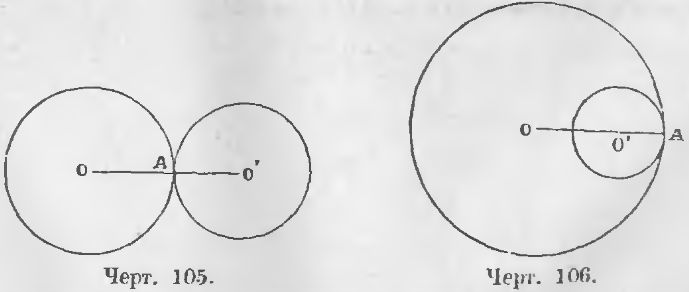
Из чертежа 105 видно, что
OO’ = AO + AO’
а из чертежа 106
OO’ = AO – AO’.
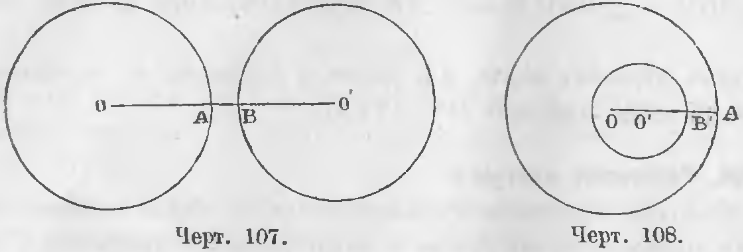
3. Если одна окружность лежит вне другой, расстояние центров больше суммы радиусов.
Из чертежа 107 видно, что
OO’ > AO + BO’
4. Если окружность лежит одна внутри другой, расстояние центров меньше разности радиусов.
Действительно, из чертежа 108 видно, что
OO’ < AO – BO’.
Измерение углов
Центральные углы. Углы, имеющие вершину при центре, называются центральными углами.
Относительно этих углов имеют место следующие теоремы.
Теорема 74. Равным центральным углам в одной и той же окружности соответствуют равные дуги.
Дано. Углы AOB и COD равны (черт. 109).
Требуется доказать, что ◡AB = ◡CD.
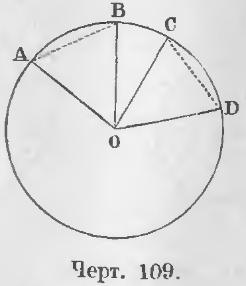
Доказательство. Проведем хорды AB и CD и соединим точки A, B, C, D с центром. Два треугольника AOB и COD равны, ибо AO = CO и BO = DO как радиусы, ∠AOB = ∠COD по условию. Следовательно, хорды AB и CD равны.
Против равных хорд лежат равные дуги, следовательно и дуги AB и CD равны: ◡AB = ◡CD (ЧТД).
Теорема 75 (обратная 74). Равным дугам в одной и той же окружности соответствуют равные углы.
Дано. Дуги AB и CD равны (черт. 109).
Требуется доказать, что ∠AOB = ∠COD.
Доказательство. Из того, что дуги AB и CD равны, следует, что и хорды AB и CD тоже равны (теорема 61).
Два треугольника AOB и COD равны, ибо AB = CD как равные хорды, AO = CO и BO = DO как радиусы. Следовательно, ∠AOB = ∠COD (ЧТД).
Теорема 76. Отношение центральных углов равно отношению соответствующих им дуг.
Даны два центральные угла AOB и COD (черт. 110).
Требуется доказать, что
AOB/COD = AB/CD.
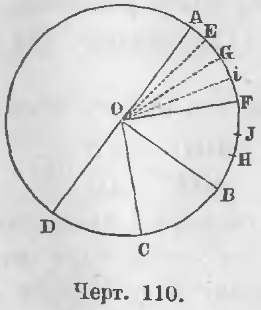
Доказательство. Здесь имеют место два случая:
1) Когда дуги AB и CD соизмеримы и 2) когда они несоизмеримы.
1-й случай. Дуги AB и CD соизмеримы.
Пусть дуга AE будет их общей мерой. Положим, что она p раз содержится в дуге AB и q раз в дуге CD. Разделив дугу AB на p, а CD на q равных частей и соединив точки деления дуг с центром O, мы разделим угол AOB на p, а угол COD на q равных углов, из которых каждый равен углу AOE.
Из равенств
AB = pAE, CD = qAE
AOB = pAOE, COD = qAOE
получаем
AOB/COD = p/q, AB/CD = p/q, откуда
AOB/COD = AB/CD (ЧТД).
2-й случай. Дуги AB и CD несоизмеримы.
Отложим дугу AF равную CD и соединим F с O. Углы AOF и COD равны.
Требуется доказать, что
AOB/AOF = AB/AF
Доказательство. A) Положим
AOB/AOF > AB/AF (1).
Для того, чтобы имело место равенство, нужно дробь во второй части неравенства (1) увеличить. Для этого следует ее знаменатель уменьшить.
Положим, мы нашли, что имеет место равенство
AOB/AOF = AB/AG (a)
Разделим дугу AB на равное число таких частей, чтобы каждая часть была менее GF; тогда одна из точек деления i упадет в промежутке между G и F. Дуги AB и Ai соизмеримы, следовательно,
AOB/AOi = AB/Ai (b).
Разделив равенства (b) на (a), находим
AOF/AOi = AG/Ai
равенство несообразное, ибо первая часть его больше, а вторая меньше 1, следовательно, допущение (1) не имеет места.
B) Допустим, что
AOB/AOF < AB/AF (2)
Тогда вторую часть этого неравенства нужно уменьшить для того, чтобы имело место равенство. Для этого нужно знаменатель дроби AB/AF увеличить. Положим, мы нашли такую точку H, чтобы удовлетворялось равенство
AOB/AOF = AB/AH (c)
Разделив дугу AB на такие равные части, чтобы каждая часть была меньше FH, мы найдем, что одна из точек деления J упадет в промежуток между F и H. Дуги AB и AJ будут соизмеримы, следовательно,
AOB/AOJ = AB/AJ (d)
Разделив равенство (d) на (c) найдем
AOF/AOJ = AH/AJ
Это равенство несообразно, ибо первое отношение меньше, а второе больше единицы, следовательно, и допущение (2) тоже не имеет места, откуда видно, что справедливо только равенство AOB/AOF = AB/AF (ЧТД).
Зная, что отношение углов равно отношению дуг, описанных равными радиусами, мы в пропорции (черт. 111)
AOB/COD = AB/CD
можем принять за единицу любую дугу. В этом случае должны принять за единицу и соответствующий ей угол.
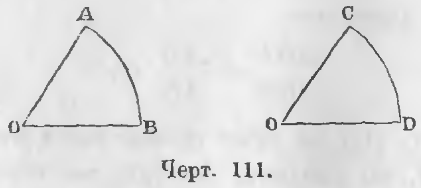
Принимая дугу CD, а следовательно, и угол COD за 1, имеем равенство
AOB/1 = AB/1
или отношение угла к своей единице равно отношению дуги к своей соответствующей единице, откуда
∠AOB = ◡AB.
Это равенство означает, что
числовая величина угла равна числовой величине дуги, или что угол измеряется дугой, описанной из его вершины, как из центра.
Мера углов и дуг
За единицу угла обыкновенно принимают прямой угол.
Углы и дуги измеряют также частями окружности.
Для этого делят окружность на 360 равных частей, называемых градусами, градус на 60 минут, минуту на 60 секунд.
Таким образом, окружность имеет 360 градусов или 360°. Градус имеет 60 минут или 60′. Минута включает 60 секунд или 360”.
Выражение 12°7’16” означает дугу круга, имеющую 12 градусов 7 минут и 16 секунд. Угол, опирающийся на эту дугу, называется также углом в 12°7’16”.
Прямой угол имеет 90°.
Теорема 77. Углы, имеющие вершину на окружности, измеряются половиной дуги, содержащейся между его сторонами.
Здесь может быть несколько случаев (черт. 112).
Первый случай. Угол BAC образуется диаметром AC и хордой AB.
Соединим центр O с точкой B; тогда
∠BOC = ∠ABO + ∠BAO
Так как ∠ABO = ∠BAO как углы равнобедренного треугольника AOB, то
BOC = 2BAO и
BAO = ½ BOC.
Угол BOC измеряется дугой BC, следовательно, угол BAO измеряется дугой ½ BC.
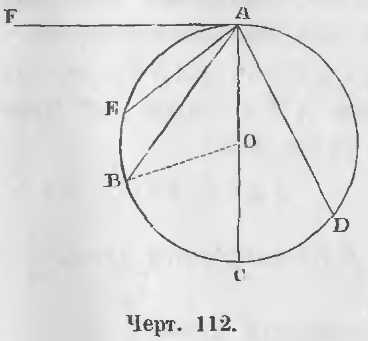
Второй случай. Угол BAD образуется двумя хордами, лежащими по обе стороны диаметра.
BAD = BAC + CAD
уг. BAD измеряется дугой ½ BC
уг. CAD измеряется дугой ½ CD.
Следовательно, угол BAD измеряется дугой
½ BC + ½ CD = ½ (BC + CD) = ½ BD.
Т. е. угол BAD измеряется половиной дуги, заключающейся между его сторонами (ЧТД).
Третий случай. Угол EAB образуется двумя хордами, лежащими по дну сторону диаметра.
EAB = EAC – BAC
EAC измеряется дугой ½ EC
BAC измеряется дугой ½ BC
следовательно, EAB измеряется дугой
½ EC – ½ BC = ½ (EC – BC) = ½ EB.
Правило остается то же.
Теорема 78. Угол, образуемый касательной и хордой, измеряется половиной дуги, стягиваемой хордой.
Доказательство. Угол FAE (черт. 112) есть угол, образуемой касательной AF и хордой AE. Проведя диаметр AC, мы получим прямой угол FAC.
FAE = FAC – EAC
Прямой угол FAC измеряется дугой ½AC.
Угол EAC измеряется дугой ½EC.
Угол FAE измеряется
½AC – ½EC = ½(AC – EC) = ½AE (ЧТД).
Теорема 79. Угол, имеющий вершину внутри окружности, измеряется полусуммой дуг, заключающихся между его основаниями.
Дан угол ACB, имеющий вершину C внутри окружности (черт. 113).
Требуется доказать, что он измеряется дугой ½(AB + DE).
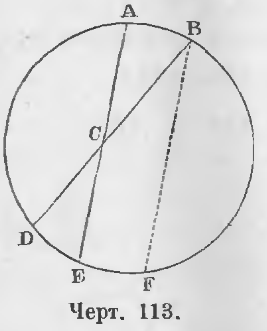
Доказательство. Из точки B проведем прямую BF параллельную AE, тогда
∠ACB = ∠DBF
Угол DBF измеряется дугой ½DF или
∠DBF = ½ DEF = ½ (DE + EF)
◡AB = ◡EF как дуги, содержащиеся между параллельными сторонами, следовательно,
ACB = ½ (DE + AB) (ЧТД).
Теорема 80. Угол, имеющий вершину вне окружности, измеряется полуразностью дуг, заключающихся между его сторонами.
Дано. Угол ACB имеет вершину вне окружности (черт. 114).
Требуется доказать, что он измеряется дугой ½ (AB – EF).
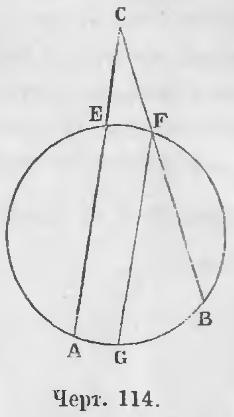
Доказательство. Проведем из точки F прямую FG параллельную AC, тогда
∠C = ∠GFB
Мера угла C равна мере угла GFB = ½ GB
GB = AB – AG
Так как AG = EF, то GB = AB – EF, следовательно, ∠C = ½ (AB – EF) (ЧТД).
Из предложенных теорем вытекают заключения:
1) Все углы, имеющие вершину на окружности и опирающиеся на диаметр, являются прямыми, ибо все они измеряются половиной полуокружности.
2) Все вписанные углы, опирающиеся на одну и туже дугу, равны.
Обратно:
3) Все прямые углы, имеющие вершину на окружности, опираются на концы диаметра.
4) Угол при центре вдвое больше угла вписанного и опирающегося на одну и ту же дугу.
Свойства углов и сторон описанного и вписанного четырехугольника
Теорема 81. Во всяком четырехугольнике, вписанном в окружность, сумма противоположных углов равна двум прямым.
Дано. Вписан четырехугольник ABCD (черт. 115).
Требуется доказать, что A + C = 2d, B + D = 2d.
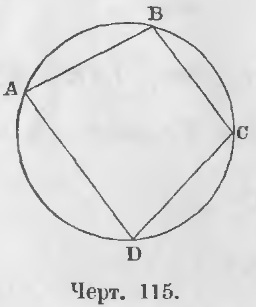
Доказательство. Угол B измеряется половиной дуги ADC, угол D измеряется половиной дуги ABC, следовательно сумма углов B + D измеряется ½ (ADC + ABC), т. е. полуокружностью.
Полуокружность есть мера двух прямых, следовательно,
B + D = 2d.
Это же заключение справедливо и для суммы углов A и C
A + C = 2d (ЧТД).
Теорема 82. Суммы противоположных сторон описанного четырехугольника равны.
Дан описанный четырехугольник ABCD (черт. 116); a, b, c, d четыре точки прикосновения его сторон с окружностью.
Требуется доказать, что AB + CD = BC + AD.
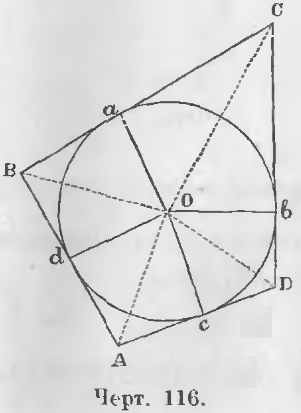
Доказательство. Соединим вершины и точки прикосновения a, b, c, d описанного четырехугольника с центром O.
Из чертежа 116 видно, что
∆OaC = ∆ObC
∆ObD = ∆OcD
∆OcA = ∆OdA
∆OdB = ∆OaB
ибо они, будучи прямоугольными, имеют по равной гипотенузе OC, OD, OA, OB и равным катетам, следовательно,
aC = bC
aB = dB
cA = dA
cD = bD
Сложив эти равенства, получаем:
aC + aB + cA + cD = bC + dB +dA + bD
или
BC + AD = CD + AB (ЧТД).
Всего: 27 1–20 | 21–27
Добавить в вариант
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 18, CD = 24, а расстояние от центра окружности до хорды AB равно 12.
Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.
Радиус окружности с центром в точке O равен 85, длина хорды AB равна 102 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 65, длина хорды AB равна 126 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 82, длина хорды AB равна 36 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Длина хорды окружности равна 96, а расстояние от центра окружности до этой хорды равно 20. Найдите диаметр окружности.
Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см.рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 90, длина хорды AB равна 144 (см.рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 10, длина хорды AB равна 16 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 26, длина хорды AB равна 48 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 87, длина хорды AB равна 126 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 61, длина хорды AB равна 22 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 50, длина хорды AB равна 28 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 75, длина хорды AB равна 90 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 50, длина хорды AB равна 80 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 65, длина хорды AB равна 66 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 75, длина хорды AB равна 42 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
Всего: 27 1–20 | 21–27
| Учебный курс | Решаем задачи по геометрии |
Определение хорды Часть кривой, заключенной между двумя точками хорды, называется дугой. Плоская фигура, заключенная между дугой и ее хордой называется сегментом. Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности – самая длинная хорда окружности. Свойства хорды к окружности
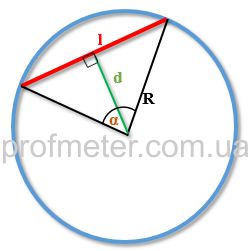
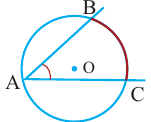
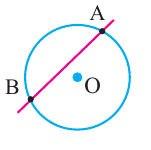
Свойства хорды и вписанного углаНа рисунке [1] вписанный угол обозначен обозначен как ACB, хорда окружности – AB
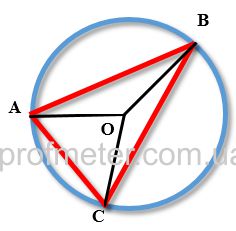
Свойства хорды и центрального углаНа рисунке [2] центральный угол обозначен как AOB, хорда как AB.
Формулы нахождения хорды Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла. Решение задач Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен. Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ. Решение. Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 Откуда Ответ: 5√10 Задача. Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.
Решение. 3,5х + 5,5х + 3х = 360 Откуда градусные величины центральных углов равны: 90 / 2 = 45 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;
Задачи про окружность | Описание курса | Треугольник (Трикутник) |
Обсудить на форуме
Записаться на курсы
Обратиться к консультанту
Пройти тест
Полный список курсов обучения
Бесплатные видеоуроки
Нужна информация!
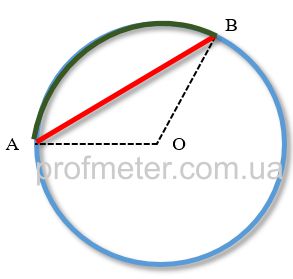
![Хорда к окружности вместе с вписанным [1] и центральными углами [2] Хорда к окружности вместе с вписанным [1] и центральными углами [2]](https://profmeter.com.ua/upload/medialibrary/b1c/horda2.jpg)