Лабораторная работа
Исследование равноускоренного движения без начальной скорости
(работа представлена в трех вариантах выполнения — в зависимости от имеющегося лабораторного оборудования)
Вариант I
Цель работы определить ускорение движения бруска по наклонной плоскости и его мгновенную скорость в конце заданного пути, пройденного за определенный промежуток времени.
прибор для изучения движения тел, штатив с муфтой и лапкой.
Теоретические обоснования
При равноускоренном движении без начальной скорости пройденное расстояние определяется по формуле:
Зная ускорение, можно определить мгновенную скорость по формуле: Описание устройства и действия прибора
Прибор для изучения движения тел {рис. 1) состоит из направляющей / длиной 60—70 см; бруска 2 с пусковым магнитом 3, закрепленным на торце алюминиевого стержня; электронного секундомера 4с двумя датчиками 5. Направляющая закрепляется в лапке штатива 6, под нее подклады вается коврик 7 из пористого пластика,
При прохождении пускового магнита мимо первого датчика отсчет времени включается, а при прохождении второго — выключается, и на экране секундомера фиксируется значение промежутка времени t, за который брусок проходит расстояние s между датчиками.
Ход работы
1. Соберите установку по рисунку 1. Направляющую закрепите в лапке штатива под углом * 30°—40° к плоскости столешницы.
2. Прочтите инструкцию на тыльной стороне секундомера по его включению и выключению. Включите секундомер.
3. Разместите брусок на направляющей так, чтобы его пусковой магнит находился на 1,5 см выше верхнего датчика.
4. Отпустите брусок. Определите расстояние s между датчиками и промежуток времени t, за который брусок прошел это расстояние. Результат измерения занесите в таблицу:
5 Не меняя расположения датчиков, проведите опыт еще 2 раза. Результаты измерений занесите в таблицу.
По результатам трех опытов рассчитайте среднее время движения бруска:
7. Вычислите ускорение движения бруска и его мгновенную скорость а конце пути s по формулам:
8. Результаты всех измерений и вычислений занесите в таблицу.
9. Сделайте вывод о характере движения бруска.
Страницы
- О сайте
- Подготовительные курсы
- Сказать “Спасибо!”
Рубрики
- Атомная физика
- Гидростатика
- Динамика
- Задачи
- Законы сохранения
- Игрушки
- Квантовая физика
- Кинематика
- Колебания и волны
- Кроссворды
- Магнетизм
- Механика
- Молекулярная физика
- Обзор сайтов
- Оптика
- Опыты
- Поделки
- Разное
- Справочный материал
- Статика
- Термодинамика
- физика
- физика
- Физики шутят
- Эксперименты
- Электрический ток
- Электродинамика
- Электростатика
- Ядерная физика
Календарь
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
| « Ноя | Янв » | |||||
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Реклама:
Какое расстояние пройдёт брусок
Рубрики: Задачи , Механика | Теги: относительное движение, сила, сила трения, скорость | 14 декабря 2011 | admin
На гладком горизонтальном полу находится длинная доска. По доске под действием постоянной горизонтальной силы тяги движется брусок массой m = 5 кг. Коэффициент трения между доской и бруском μ = 0,2. Скорость бруска v относительно пола постоянна и равна 0,8 м/с. Первоначально доска относительно пола покоится. Какое расстояние пройдёт брусок по доске к моменту, когда движение бруска относительно доски прекратиться.
5 комментариев для “Какое расстояние пройдёт брусок”
admin | 14 декабря 2011 в 21:53
Раз скорость бруска постоянна, то сумма всех сил по горизонтали равна нулю
F-Fтр =0
по вертикали то же
N-mg=0
Для доски
Fтр =Ma
mg+Mg = N1 – реакция опоры пола
Fтр = мю*m*g
a= мю*m*g/M
За время t скорость доски меняется от 0 до v. При этом доска проходит расстояние L
v=at
L=at^2/2
L=v^2/2a
L=Mv^2/(2*мю*m*g)
не хватаем массы доски в условии
Ответить
Денис | 15 декабря 2011 в 14:28
Масса доски равна 5 кг, а масса бруска равна 1 кг.
Ответить
admin | 15 декабря 2011 в 15:05
вы написали в условии “брусок массой m = 5 кг”, а массу доски вообще не указали.
Собственно это детали. Решение выше уже написал.
Ответить
Денис | 18 декабря 2011 в 14:40
Почему для доски Fтр =Ma ведь на ней стоит брусок и mg+Mg = N1 – реакция опоры пола?
Ответить
admin | 18 декабря 2011 в 17:33
вопрос не понял до конца
доска движется за счет силы трения между доской и бруском
Ответить
Оставить комментарий:
Имя (обязательно)
E-mail (не публикуется) (обязательно)
Сайт
XHTML: Вы можете использовать теги:
“Силовая” задача
О золочении, серебрении, оксидировании
Ссылки
- Редактор уравнений
Новые записи
- Из парафина сделать шарик диаметром 4 см
- Диск из алюминия диаметр 20 см
- Тщательно промытую стеклянную воронку
- «Пляска» камфоры
- Из тонкого картона (можно взять открытку) вырезать фигуры
Комментарии
- Светлана на Шпора по физике
- Светлана на Шпора по физике
- Булка на Определите удельное сопротивление провода
- Анастасия на Опорные конспекты по динамике
- Елена на Опыт со звуком
Метки
8 класс Динамика Задачи Кинематика Магнетизм Механика Оптика Опыты Поделки Термодинамика Физические викторины Экзамен Электрический ток Электростатика вечный двигатель давление задача закон Кулона закон сохранения заряд игрушка колебания и волны количество теплоты конденсатор кроссворд магнитное поле мощность напряжение напряженность ответ ответы работа решение решите задачу решить задачу свободное падение сила сила Архимеда скорость ток ускорение физика эксперимент электрон энергия
Учи физику!опыты, эксперименты, теория, практика, решения задач
- Home
- About
- RSS
Copyright © 2011 Учи физику!. All rights reserved.
Бруски, доски и кирпичи
М.А.БРАЖНИКОВ, г. Москва
Бруски, доски и кирпичи
Для учеников выпускных классов
начинается тяжёлая пора – окончание школы не за
горами, а значит, и «двойные экзамены в одном
флаконе» – выпускные и вступительные. С каждым
годом «пропасть» между уровнем базовой,
«школьной», физики и вузовской увеличивается.
Реформа образования убила «между делом» и
механику 9-го класса. А уровень вступительных
задач остался по-прежнему высоким (это
объективно, так и должно быть: законы, по которым
конструируют самолёты, не могут упроститься по
указу!). И с горечью об упущенном времени
объясняешь одиннадцатиклассникам на переменке
то, что ещё не забыл сам!
За редким исключением принципиально
новых задач абитуриентам не предлагают. Одна,
принесённая учениками после контрольного
тестирования ведущего московского вуза, была
«старой знакомой». Однако решение, указанное в
сборнике МИФИ аж 1987 г. (Справочник для
поступающих. – М.: МИФИ, 1987), показалось мне чуть
затянутым. Кроме «мифической» задачи хочу также
показать решение одной из задач письменного
выпускного экзамена по физике, который несколько
лет проводился в московской школе № 710 (сейчас
гимназия № 710 им В.К.Жудова, РАО).
• «Доска и брусок» (задача МИФИ).
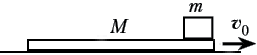
На гладкой горизонтальной?поверхности
лежит доска длиной l = 1,2 м и массой М =
1,6 кг. На край доски положили небольшое тело
массой m = 0,4 кг. Коэффициент трения между
телом и доской k = 0,3. С какой минимальной
скоростью ![]() 0
0
следует резко толкнуть доску вправо, чтобы тело
соскользнуло с неё?
• Задача «Брусок и доска».

На гладкой горизонтальной плоскости
покоится доска массой М. На доске лежит тело
массой m, которому толчком сообщают
начальную скорость ![]()
вдоль доски. Коэффициент трения между телом и
доской равен k. На какое расстояние s
сместится тело относительно доски? Считать, что
тело, смещаясь, всё время остаётся в пределах
доски.
По сути, это формулировка одной и той
же задачи.
Решение задачи 1
Рассмотрим ситуацию в лабораторной
системе отсчёта. При резком толчке брусок начнёт
проскальзывать по доске, постепенно вовлекаясь в
движение, поскольку между бруском и доской
возникают силы трения: F(M)тр
– сила, действующая на доску со стороны бруска, и F(m)тр
– сила, действующая на брусок со стороны доски.
Эти силы, согласно третьему закону Ньютона, равны
по модулю и противоположны по направлению: F(M)тр
= kmg и F(m)тр = kmg. Они
сообщают «своим» телам разные ускорения: доска
тормозит с ускорением a(M) = kgm/M,
а брусок получает ускорение a(m) = kg.
При этом относительное движение доски и бруска
прекратится, когда их скорости сравняются.
Время, за которое произойдёт
выравнивание скоростей, можно обозначить как ![]() . За время
. За время ![]() доска
доска
переместится на расстояние ![]() а брусок пройдёт в том же
а брусок пройдёт в том же
направлении, что и доска, расстояние ![]() Разность пройденных
Разность пройденных
расстояний s и составит искомое перемещение
бруска по доске, которое не должно быть меньше l:
s = s(M)– s(m)
= ![]() 0
0![]() –
– ![]() a(M)
a(M)![]() 2 –
2 – ![]()
a(m)![]() 2
2
![]() l.
l.
Время ![]()
можно найти из равенства конечных скоростей
бруска ![]() (m)
(m)
и доски ![]() (M):
(M):
![]()
Подставляя в явном виде значения
ускорений, получим следующее выражение:
![]()
(В этом месте мне хотелось бы
остановиться самому и остановить внимание тех
учеников, которые пошли бы решать задачу путём,
предложенным МИФИ. В числителе дроби стоит
количество движения (импульс, которым вначале
обладала доска!), а в знаменателе – нечто, что
имеет размерность силы. Очевидно, что, применив
второй закон Ньютона в формулировке «Импульс
силы, действующей на доску, равен изменению
импульса доски», мы пришли бы к искомому времени
на шаг быстрее:
![]()
Конечная скорость доски с бруском
получается, если использовать закон сохранения
импульса в системе «Доска и брусок».)
Подставляя время относительного
движения в выражение для s, получим
выражение для искомой скорости:
![]()
Однако есть другой способ решения – с
использованием законов сохранения.
Решение задачи 2
Рассмотрим ситуацию в лабораторной
системе отсчёта. Система «Брусок и доска» в
начале движения обладала количеством движения
(импульсом) m![]() .
.
Поскольку силы трения между доской и бруском
суть силы внутренние, трение между плоскостью и
доской отсутствует, а сила тяжести
компенсируется силой нормальной реакции
поверхности, то количество движения в системе
сохраняется и тогда, когда брусок и доска будут
двигаться вместе со скоростью u: m![]() = (M + m)u.
= (M + m)u.
Вместе с тем механическая энергия в
системе уменьшается за счёт действия силы
трения. Убыль кинетической энергии равна работе
силы трения:
![]()
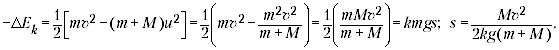
Из полученного ответа видно, что он
совпадает с предыдущим. Оба решения довольно
очевидные, хотя мне кажется, тот, кто «увидел»
второе решение, не станет решать первым способом.
Однако методически правильно показать оба
решения. Для закрепления такого подхода ещё одна
задача.
• «Кирпич и крыша».
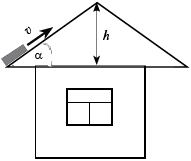
Кирпич, лежащий на краю крыши дома,
толкнули вверх вдоль ската со скоростью ![]() = 10 м/с. После упругого удара
= 10 м/с. После упругого удара
о конёк кирпич соскользнул обратно и остановился
на краю крыши. Найдите коэффициент трения k,
если конёк находится на высоте h = 2,5 м от края
крыши, а угол наклона ![]() = 30°.
= 30°.
Решение
Решаем задачу в системе отсчёта
«Земля». Вначале кирпич обладал кинетической
энергией. За уровень отсчёта потенциальной
энергии можно принять край крыши, тогда она
изначально равна нулю. В конце своего пути кирпич
уже не обладал никакой механической энергией.
Упругий удар о конёк не изменяет механической
энергии, поэтому её убыль связана с работой силы
трения вдоль ската крыши. Модуль этой силы
постоянен во время всего движения и вверх, и вниз:
Fтр = kmgcos![]() . Длина ската равна l = h/sin
. Длина ската равна l = h/sin![]() . В итоге получаем:
. В итоге получаем:
![]()
(при g = 9,81 м/с2 получается k
= 0,59, таким образом, коэффициент трения чуть
больше тангенса угла наклонной плоскости, т.е.
брусок может «физически» лежать на плоскости, не
соскальзывая, что, правда, оговорено в условии).
Конечно, данную задачу можно решить,
рассматривая движение вверх по скату крыши и
вниз. Однако применение законов сохранения
(импульса и энергии) позволяет в ряде задач
динамики, и это видно на приведённых примерах,
сэкономить усилия и время, избежав промежуточных
выкладок.
Главная » Задачи » По динамике » Задача 49. Небольшой брусок начинает скользить по наклонной плоскости, составляющей угол α с горизонтом
На чтение 3 мин Просмотров 1.6к.
Задача 49. Небольшой брусок начинает скользить по наклонной плоскости, составляющей угол α с горизонтом (рис.36). Коэффициент трения зависит от пройденного пути х по закону μ=kx, где k – постоянная. Найти путь, пройденный бруском до остановки.

Рис.36
Решение.
Применение законов динамики
В данной задаче рассматривается движение под действием переменной результирующей силы.
На брусок действует Земля с силой тяжести mg и наклонная плоскость с силой нормального давления N и силой трения Fтр, величина которой равна
Fтр=μN=kxN. (1)
По второму закону Ньютона в векторной форме имеем:
m→a=m→g+→N+→Fтр.
Спроектируем это векторное уравнение на оси координат, указанные на рисунке,
x: ma=mgsinα−Fтр, (2)
y: 0=−mgcosα+N. (3)
Разрешая полученную систему уравнений относительно ускорения, получим зависимость ускорения от координаты х:
a=g(sinα−kxcosα). (4)
Далее решается кинематическая задача, связанная с преобразованием уравнений (задача третьего класса). Воспользуемся определениями скорости и ускорения
v = dx/dt, a = dv/dt,
и исключим переменные a и dt. В результате получим дифференциальное уравнение с разделяющимися переменными v и х:
vdv=g(sinα−kxcosα)dx.
Интегрируя это уравнение от момента, соответствующего началу движения (v0=0, x0=0) до остановки (vост=0, x=xост), получим
0∫0vdv=xост∫0g(sinα−kxcosα)dx;
0=g⎛⎝sinα∙xост−kcosαx2ост2⎞⎠,
откуда искомая координата остановки равна
xост=2g∙tgαk.
(корень xост=0 соответствует началу движения).
Энергетический способ
Значительно чаще эта задача решается с помощью закона изменения энергии.

Рис.37
В состоянии I (рис.37) тело обладает потенциальной энергией
WI=Wp=mgh=mgxостsinα,
в состоянии II (рис.37) — как кинетическая, так и потенциальная энергия равна нулю
WII=0.
Энергия изменяется вследствие работы, совершаемой силой трения:
WII−WI=Aтр.
величина силы трения, как отмечалось раньше, составляет
Fтр=μN=kxmgcosα.
Как видно из формулы, сила трения зависит от пройденного расстояния (координаты х). При перемещении на расстояние dx совершается работа
dA=Fтрdxcosπ=−kxmgcosαdx.
Полная работа до остановки составит
A=−kmgcosαxост∫0xdx=−kmgcosαx2ост2.
Подставим полученные выражения в применяемый закон:
0−mgxостsinα=−kmgcosαx2ост2
и выразим искомую величину — путь, пройденный телом до остановки,
xост=2g∙tgαk.
Видно, что и в этом случае энергетический способ решения задачи оказывается более предпочтительным.
2018-04-07 ![]()
Два маленьких бруска движутся по горизонтальной поверхности стола навстречу друг другу. Масса первого бруска $m_{1} = m$, масса второго $m_{2} = 2m$. Бруски сталкиваются. На какое расстояние $L$ разъедутся бруски после удара? Непосредственно перед ударом модуль скорости первого бруска равен $v_{1} = 2v$, второго бруска — $v_{2} = v$. Удар абсолютно упругий и лобовой, движение брусков поступательное. Коэффициенты трения брусков о стол одинаковы и равны $mu$, ускорение свободного падения $g$.
Решение:
Для нахождения скоростей после удара можно воспользоваться законами сохранения энергии и импульса, однако, решение можно указать и сразу, если заметить, что суммарный импульс брусков равен нулю. Значит, после столкновения бруски поменяют направления скоростей на противоположные, а по модулю скорости останутся теми же. На первый брусок действует сила трения $mu mg$. Для нахождения расстояния $s_{1}$, на которое отъедет первый брусок от места удара, приравняем его начальную кинетическую энергию к модулю работы силы трения:
$frac{mv_{1}^{2}}{2} = mu mgs_{1}$, откуда $s_{1} = frac{v_{1}^{2} }{2 mu g} = frac{2v^{2}}{ mu g}$.
Рассуждая аналогичным образом, найдём расстояние, пройденное вторым бруском:
$s_{2} = frac{v^{2} }{2 mu g}$.
Расстояние, на которое разъедутся бруски, равно
$L = s_{1} + s_{2} = frac{5v^{2}}{ 2 mu g}$.
