Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
____ ч |
|
2. |
____ м |
12 м/с |
4 с |
|
3. |
132 м |
____ м/мин |
11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
15 часов |
|
2. |
48 м |
12 м/с |
4 с |
|
3. |
132 м |
12 м/мин |
11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе. Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
“Я люблю математику не только потому,
что
она находит применение в технике, но и потому,
что она красива”.
Петер Ропсе
Цели урока: [Приложение 1]
- Продолжать вырабатывать у учащихся умения и
навыки решения задач с использованием деления
натуральных чисел; - Развивать внимание, зрительную память,
логическое и образное мышление, активность
учащихся на уроках; - Продолжить развитие устной и письменной речи на
уроках математики; - Прививать интерес и любовь к предмету;
- Продолжить учиться видеть связь математики с
реальной действительностью; - Продолжить учиться применять свои знания в
нестандартных ситуациях.
План урока: [Приложение 1]
- Организационный момент.
- Скорость, время, расстояние – повтор формул.
- Устная работа.
- Составление задачи по рисунку.
- Викторина.
- Задача от дяди Степы-милиционера.
- Олимпиадная задача.
- Итоги урока.
Оборудование: картинки-пояснения к задачам;
ксерокопии листов с домашним заданием;
презентация к уроку; костюм для дяди
Степы-милиционера.
Перед началом урока предлагается высказаться
5-6 ученикам словами великих людей о математике.
(Высказывания ученики ищут дома и в библиотеке,
это их домашнее задание)
Ход урока
1. Повторить, как найти расстояние, время,
скорость, и решить задачи.
Дорогие ребята, в 4-м классе вы решали
много задач по математике связанных с движением,
для решения этих задач вы пользовались формулами
нахождения скорости, времени или расстояния при
равномерном движении. Эта формула выглядит так:
<Рисунок 8> [Приложение 1]
S = V·t.
В данной формуле S – это путь, V –
скорость, а t – время. Эта формула справедлива
только для случаев, когда движение было с
постоянной, т.е. не изменой скоростью.
Давайте рассмотрим пример [Приложение
1], грузовик ехал из одного города в другой 3
часа с постоянной скоростью 60 км/ч. [3] Тогда для
того, чтобы узнать расстояние между городами
нужно умножить 3 на 60 и получим 180 км.
Теперь рассчитаем, с какой скоростью
следовало ехать грузовику, чтобы проехать этот
путь за 2 часа. Для этого из формулы нужно
выразить скорость:
V=S/t = 180/2=90 км/ч.
Аналогично предыдущему примеру узнаем
время, за которое автомобиль преодолел то же
расстояние, двигаясь со скоростью 120км/ч:
t=S/V = 180/120=1,5ч.
2. Устные упражнения.
На доске оформляются краткие и
наглядные условия задач, полный текст задачи
ребята видят на слайде презентации [Приложение
1]
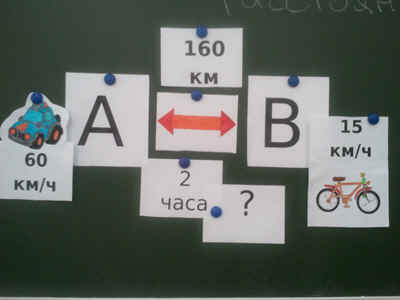
1. Из пунктов А и В навстречу друг другу
выехали автомобиль со скоростью 60 км/ч и
велосипедист со скоростью 15 км/ч. Встретятся ли
автомобиль и велосипедист через 2 часа, если
расстояние между пунктами 160 км?[2] (Решить задачу
двумя способами.)<Рисунок 1> [Приложение
1]
2. Из лагеря геологоразведчиков выехал
вездеход со скоростью 30 км/ч. Через 2 часа вслед за
ним был послан другой вездеход. С какой скоростью
он должен ехать, чтобы догнать первый через 4 часа
после своего выхода? [4] <Рисунок 2> [Приложение
1]
3. По рисунку составить задачу на
движение и решить ее. [1]
Рисунок задачи на слайде презентации [Приложение 1]
4. Викторина
(3 ряда – каждому ряду выдается по
тексту задачи (всего 3 задачи) и карточки для
наглядного составления краткой записи на доске,
а также тексты всех трех задач выводятся на
слайде [Приложение 1]). Ученикам
необходимо решить задачу, представить наглядную
краткую запись-схему у доски и предоставить ее
решение.
Первый ряд: “Автомобиль
“Москвич” за 3 часа может проехать 360 км.
Бескрылая птица страус – лучший бегун в мире –
развивает скорость до 120 км/ч. Сравните скорости
автомобиля “Москвич” и страуса. [2] <Рисунок 3>
Второй ряд: “Скорость
распространения света самая большая в природе –
300000 км/с. На Солнце произошла вспышка. Через какое
время ее увидят на Земле, если расстояние от
Земли до Солнца равно 150000000 км? [1] <Рисунок 4>
Третий ряд: “Пройденный путь
пешехода S, его скорость v и время движения t
связаны соотношением S = vt. Если пешеход за 4 часа
прошел 24 км, то его скорость равна….? [3] <Рисунок
5>
5. Входит дядя Степа-милиционер
(Один из учеников класса, желательно
посильнее который, с ним заранее разбираются
задачи, и он их дома решает) и предлагает задачу
из сборника задач по основам безопасности
дорожного движения. <Рисунок 9>
Ширина проезжей части дороги 15 м,
зеленый сигнал светофора горит 20 секунд. С какой
наименьшей скоростью может двигаться пешеход с
момента загорания светофора, чтобы благополучно
перейти дорогу? [5] <Рисунок 6>
Решение:
1) 15 м = 1500 см
2) 1500 : 20 = 75 см/с.
Ответ: пешеход может двигаться со
скоростью 75 см/с.
6. Решить олимпиадную задачу. [Приложение 1]
Из пунктов А и В, расстояние между
которыми 100 км, со скоростями 20 км/ч и 30 км/ч
выезжают навстречу друг другу два велосипедиста.
Вместе с ними со скоростью 50 км/ч вылетают две
мухи, летят до встречи, поворачивают и летят
обратно до встречи с велосипедистами, снова
поворачивают и т. д. Сколько километров пролетит
каждая муха в направлении от А до В до того
момента, когда велосипедисты встретятся? [6]
<Рисунок 7>
Решение: Велосипедисты встретятся
через 2 часа на расстоянии 40 км/ч от А. За это время
каждая муха пролетела 100 км. Муха, вылетевшая из А,
пролетела в направлении от А до В на 40 км больше,
чем в обратном направлении, и поэтому от АВ она
пролетела 70 км. Аналогично, вторая муха в
направлении от А к В пролетела на 60 км меньше, чем
в обратном, то есть 20 км.
Ответ: первая муха в направлении от А к
В пролетела 70 км, вторая – 20 км.
Запасная задача! (в зависимости от
способностей учеников, если останется 3 минутки
свободного времени на уроке) Мотоциклист едет со
скоростью 95 км/ч, а скорость велосипедиста на 76
км/ч меньше. Во сколько раз скорость мотоциклиста
больше скорости велосипедиста? Кому из них легче
остановиться? [2]
Решение:
1) 95 – 76 = 19 км/ч
2) 95 : 19 = 5 раз.
Ответ: в 5 раз легче остановиться
велосипедисту, так как при меньшей скорости
короче тормозной путь.
Итог урока: выставление оценок
наиболее отличившимся ученикам, вручение
памятных дипломов каждому ряду за умение
работать в группах.
Домашнее задание: [Приложение
1] ученикам раздаются ксерокопии
заданий.[2,3]
- Помогите французским девочкам. Однажды Жаннин и
Моника поплыли по маленькой речке, отправившись
из одного и того же места, но только Жаннин
поплыла против течения, а Моника поплыла по
течению. Оказалось, что Моника забыла снять
большие деревянные бусы. Через четверть часа
девочки повернули обратно. Кто же из них подберет
бусы Моники: сама Моника или Жаннин? (Скорость
обеих пловчих в неподвижной воде одинакова.) - Задача от дяди Степы. Скорость легкового
автомобиля 60 км/ч, а грузовика 15 км/ч. Во сколько
раз скорость легкового автомобиля больше
скорости грузовика? Какой автомобиль опаснее для
школьника, начавшего движение по пешеходному
переходу? - Задание от “Знающего человека”. Заполнить
таблицу. - Составить по одной анаграмме.
|
Объект |
Скорость
v |
Время
t |
Расстояние
S |
|
“Волга” |
100 км/ч |
5 ч |
|
|
“Ока” |
60 км/ч |
420 км |
|
|
“Москвич” |
3 ч |
240 км |
|
|
Пчела |
60 км/ч |
180 км |
|
|
Стрекоза |
2 ч |
200 км |
|
|
Стриж |
100 км/ч |
4 ч |
|
|
Меч-рыба |
100 км/ч |
300 км |
|
|
Земля (вокруг Солнца) |
30 км/ч |
24 ч |
|
|
Черепаха |
6 мин |
18 м |
|
|
Улитка |
7 ч |
35 км |
|
|
Верблюд |
8 км/ч |
5 ч |
|
|
Почтовый голубь |
50 км/ч |
150 км |
Ответы для учителя.
Задача № 1
Скорости девушек относительно
неподвижной воды одинакова. Но ведь по отношению
к воде в реке бусы остаются неподвижными – они
движутся в точности с такой же скоростью, что и
вода (со скоростью течения). Пловчихи проплывают
относительно воды одинаковое расстояние и по
истечении получаса встречаются в том месте, где в
этот момент находятся бусы. Таким образом, обе
девушки могут подобрать бусы с равным
основанием, так как встречаются в тот самый
момент, когда подплывут бусы.
Задача № 2
Опаснее легковой автомобиль, так как у него
скорость больше, кроме того, для водителя
легкового автомобиля мальчик появится
неожиданно, так как обзор будет закрыт грузовым
автомобилем.
Список литературы:
- Решение задач / Клустер Д. И. – М.: Просвещение. –
2005. - Задачи на движение/ Павлов Е. С. – красноярск. –
2002. - Решение задач на движение/ Кузнишина Т. Л. –
Новосибирск. – 1990 - Сборник задач/ Кравцова Е. Е. – М.:
Просвещение.-2008. - Справочник по безопасности дорожного движения/
Сильянов В. В. – М.: Технополиграфцентр. – 2001 - Сборник олимпиадных задач по математике/
Горбачев Н.В. – М.: МЦНМО. – 2004
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n
где v1, v2, v3, vn – значения скоростей объекта на отдельных участках пути S,
n – количество этих участков,
vср – средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
vср=(S1+S2+…+Sn)/t,
где vср – средняя скорость объекта на всем протяжении пути,
S1, S2, Sn – отдельные неравномерные участки всего пути,
t – общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
vср=S/(t1+t2+…+tn),
где S – общее пройденное расстояние,
t1, t2, tn – время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn,
где S1/t1, S2/t2, Sn/tn – формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Формулы. Вычисление по формулам. Решение текстовых задач (на движение, на проценты и т.д.)
В задачах на движение рассматриваются три взаимосвязанные величины:
S – расстояние (пройденный путь),
t – время движения и
V – скорость – расстояние, пройденное за единицу времени.
Расстояние – это произведение скорости на время движения; S = V t
Скорость – это расстояние, которое тело проходит за единицу времени;
Скорость – это частное от деления расстояния на время движения; V = S / t
Время – это частное от деления расстояния на скорость движения t = S / V
Какие могут быть ситуации?
Ситуация первая.
Два объекта движение начинают одновременно навстречу друг другу. Встречное движение.
Ситуация вторая.
Два объекта движение начинают одновременно в противоположных направлениях. Движение в противоположных направлениях из одного пункта
Ситуация третья.
Два объекта движение начинают одновременно в одном направлении.
При решении этих задач надо использовать понятия «скорость сближения» и « скорость удаления».
Задача №1.
В данный момент расстояние между двумя таксистами 345 км. На каком расстоянии будут находиться таксисты через два часа, если скорость одного 72 км /ч., а другого -68 км /ч., и они выезжают навстречу друг другу одновременно?
1-ый способ:
1) 72 + 68 =140 (км /ч.) – скорость сближения таксистов.
2)140×2 = 280 (км) – на такое расстояние таксисты приблизятся друг к другу за 2 часа.
3) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.
Ответ: 145 км.
2 – й способ решения.
1)72 × 2 =144 (км) – такое расстояние проедет один таксист за 2 часа.
2) 68 × 2 = 136 (км) – такое расстояние проедет другой таксист за 2 часа.
3)144+ 136 =280 (км) – на такое расстояние таксисты приблизятся друг к другу за 2 часа.
4) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.
Ответ: 145 км.
Задача № 2
Расстояние между городами А и В 720км. Из А в В вышел скорый поезд со скоростью 80 км /ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км /ч. Через сколько часов после выхода пассажирского поезда эти поезда встретятся?
Решение.
1)80×2=160(км) -прошёл скорый поезд за 2 часа.
2)720-160=560(км) -осталось пройти поездам.
3)80+60=140(км/ч) -скорость сближения 2 поездов.
4)560:140=4(ч) -был в пути пассажирский поезд.
Ответ:4часа.
Задача № 3.
Из двух пунктов навстречу друг другу одновременно выехали два автобуса. Скорость одного автобуса 45 км /ч, а скорость другого автобуса 72 км /ч. Первый автобус до встречи проехал 135км.
Найдите расстояние между пунктами.
Решение.
1-ый способ: .
1) 135 : 45 = 3 (часа) – ехали автобусы до встречи.
2)72×3 = 216 (км) – проехал второй автобус до встречи.
3) 135 + 216 = 351 (км) – расстояние между пунктами.
Ответ: 351 км.
2 – й способ решения.
1)135 : 45 = 3 (часа) – ехали автобусы до встречи.
2)45 +72 = 117 (км/ ч.). – скорость сближения автобусов .
3)117 × 3 = 351 (км) – расстояние между пунктами.
Ответ: 351 км.
Что такое скорость сближения?
Задача № 4.
Машина и автобус выехали из двух городов, находящихся на расстоянии 740 км навстречу друг другу со скоростями 70 км/ч и 50 км/ч. Какое расстояние будет между машинами через 5 часов?
Решение.
1 –й способ решения.
1)50 × 5 = 250 (км) – проедет машина до встречи.
2)70 × 5 = 350 (км) – проедет автобус до встречи.
3) 250 + 350 = 600 (км) – на такое расстояние они приблизятся друг к другу.
4) 740 -600 = 140 (км) – такое расстояние будет между ними через 5 часов.
Ответ: 140 км.
2 – й способ решения.
1)50 + 70 = 120 (км /ч.) – скорость сближения автобуса и машины.
2)120 × 5 = 600 (км) – на такое расстояние они приблизятся друг к другу.
3) 740 – 600 = 140 (км) – такое расстояние будет между ними через 5 часов.
Ответ: 140 км.
Задача №5.
Две гоночные машины выехали навстречу друг другу. Расстояние между ними было 660 км. Одна ехала со скоростью 100 км/ч, а другая 120 км/ч. Через какое время они встретятся?
Решение.
1)100+120=220(км/ч)- скорость сближения машин .
2)660:220=3(ч) -через такое время встретятся гоночные машины.
Ответ: через 3 часа.
Задача № 6.
Из одного логова одновременно в противоположных направлениях выбежало два тигра. Скорость одного тигра 48 км / ч., а другого – 54 км ч. Какое расстояние будет между тиграми через 2 часа?
Решение.
1-ый способ:
1)48 × 2 = 96 (км) – пробежит один тигр за 2 часа.
2)54 × 2 = 108 (км) – пробежит другой тигр за 2 часа.
3)96 + 108 = 204 (км) – будет между тиграми через 2 часа.
Ответ: 204 км.
2 – й способ
1)48 + 54 =102 (км /ч.) – скорость удаления тигров.
2)102 × 2 =204 (км) – будет между тиграми через 2 часа.
Ответ: 204 км.
Задача № 7.
Максат и Нурдаулет вышли из школы со скоростью 50 м/мин. Рома вышел вслед за ними через 6 минут со скоростью 80 м/мин. Через сколько минут Рома догонит Максата и Нурдаулета?
Решение.
1) 80 – 50 = 30 (км /ч.) –скорость сближения мальчиков.
2)50 × 6 = 300 (км) – такое расстояние было между мальчиками перед выходом из школы Ромы.
3)300 : 30 = 10 (мин.) – через такое время Рома догонит друзей.
Ответ: через 10 мин.
ИТОГИ:
1) При решении задач на движении двух объектов применяются понятия «скорость сближения» и «скорость удаления».
2)При решении задач на встречное движение и движение в противоположных направлениях скорость сближения и скорость удаления находятся сложением скоростей движущихся объектов.
3)При решении задач на движение в одном направлении скорость сближения и скорость удаления находятся вычитанием скоростей движущихся объектов.
Решение задач на проценты
Найдем 20% от 300 :
1-ый способ: 20% от 300 =300:100×20 = 60 ;
2-ой способ: 20% от 300 = 0,20 ×300 = 60 .
Задача №1
В классе 25 учеников, 40% (сорок процентов) из них девочки. Сколько девочек в классе?
Решение:
25:100 × 40 = 10 девочек ; или 25 × 0,40 = 10 девочек ;
Ответ: в классе 10 девочек.
Задача №2
В саду растет 5 кустов желтых роз. Это составляет 25% от всех роз в саду.
Сколько кустов роз в саду?
Решение:
5:25 ×100 = 20 кустов роз; или 5 : 0,25 = 20 кустов роз;
Ответ : в саду растет 20 кустов роз.
Задача №3
На стоянке стоит 40 машин, 8 из них фирмы Рено. Какой процент машин фирмы Рено от всех стоящих на стоянке?
Решение:
8 :40 ×100 = 20 % .
Ответ: на стоянке 20% машин фирмы Рено.
Вопросы к конспектам
Лыжнику необходимо было пробежать расстояние в 50 км. Начав бег на 30 мин позже назначенного срока, лыжник бежал со скоростью, больше предполагавшейся на 5 км/ч и прибежал к месту назначения вовремя. Определите скорость, с которой бежал лыжник.
На сколько процентов изменится площадь прямоугольника, если его длину уменьшить на 15% а ширину увеличить на 20%
Рабочий день уменьшился с 8 до 7 часов. На сколько процентов нужно повысить производительность труда, чтобы при тех же расценках заработная плата возросла на 5%?
Турист прошел по проселочной дороге 6 км и по шоссе 3 км, затратив на весь путь 2ч. По шоссе он прошел со скоростью на 2 км/ч больше, чем по проселочной дороге. С какой скоростью шел турист по проселочной дороге?
Автомобиль за 4 часа проезжает путь в 240 км. Если скорость автомобиля увеличится на 20 км/ч, то за сколько часов он проедет тот же путь?
В аэропорту ждут прибытия самолета 1200 пассажиров. 45% из них мужчины. 15% общего числа женщин и детей составляют дети. Найдите число мужчин и число детей?
Пассажир в метро спускается вниз по движущемуся эскалатору за 24с. Если пассажир идет с той же скоростью по неподвижному эскалатору, то он спустится за 42с. За сколько секунд он спустится стоя на ступеньках движущегося эскалатора?
Сколько воды нужно добавить к 54 кг 5%-го раствора соли в воде, чтобы получить 3%-ый раствор?
Скорость моторной лодки по течению реки равна 10,2 км/ч, а против течения реки 7,8км/ч. Найдите скорость течения реки.
Скорость течения реки 2 км/ч, собственная скорость лодки в 2,5 раза больше. Найдите расстояние, которое проплыла лодка против течения за 3 часа
Сторону квадрата увеличили на 20%. На сколько процентов увеличится периметр квадрата?
Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
____ ч |
|
2. |
____ м |
12 м/с |
4 с |
|
3. |
132 м |
____ м/мин |
11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
15 часов |
|
2. |
48 м |
12 м/с |
4 с |
|
3. |
132 м |
12 м/мин |
11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе. Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Расстояние
Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).
Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S. Можно обозначить и другой буквой, но буква S общепринята.
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 м : 25 с = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
100м : 25с = 4 (м/с)
Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 м : 50 c = 2 (м/с)
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
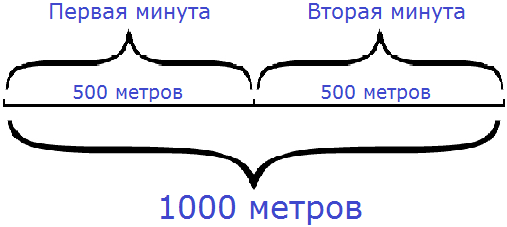
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?
Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое доедем до спортивной секции:
1000 : 500 = 2 (мин)
Время движения обозначается маленькой латинской буквой t.
Взаимосвязь скорости, времени, расстояния
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 10 минут
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s : t
Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
s = 900 метров
t = 10 минут
v = s : t = 900 : 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s : v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

“Я люблю математику не только потому,
что
она находит применение в технике, но и потому,
что она красива”.
Петер Ропсе
Цели урока: [Приложение 1]
- Продолжать вырабатывать у учащихся умения и
навыки решения задач с использованием деления
натуральных чисел; - Развивать внимание, зрительную память,
логическое и образное мышление, активность
учащихся на уроках; - Продолжить развитие устной и письменной речи на
уроках математики; - Прививать интерес и любовь к предмету;
- Продолжить учиться видеть связь математики с
реальной действительностью; - Продолжить учиться применять свои знания в
нестандартных ситуациях.
План урока: [Приложение 1]
- Организационный момент.
- Скорость, время, расстояние – повтор формул.
- Устная работа.
- Составление задачи по рисунку.
- Викторина.
- Задача от дяди Степы-милиционера.
- Олимпиадная задача.
- Итоги урока.
Оборудование: картинки-пояснения к задачам;
ксерокопии листов с домашним заданием;
презентация к уроку; костюм для дяди
Степы-милиционера.
Перед началом урока предлагается высказаться
5-6 ученикам словами великих людей о математике.
(Высказывания ученики ищут дома и в библиотеке,
это их домашнее задание)
Ход урока
1. Повторить, как найти расстояние, время,
скорость, и решить задачи.
Дорогие ребята, в 4-м классе вы решали
много задач по математике связанных с движением,
для решения этих задач вы пользовались формулами
нахождения скорости, времени или расстояния при
равномерном движении. Эта формула выглядит так:
<Рисунок 8> [Приложение 1]
S = V·t.
В данной формуле S – это путь, V –
скорость, а t – время. Эта формула справедлива
только для случаев, когда движение было с
постоянной, т.е. не изменой скоростью.
Давайте рассмотрим пример [Приложение
1], грузовик ехал из одного города в другой 3
часа с постоянной скоростью 60 км/ч. [3] Тогда для
того, чтобы узнать расстояние между городами
нужно умножить 3 на 60 и получим 180 км.
Теперь рассчитаем, с какой скоростью
следовало ехать грузовику, чтобы проехать этот
путь за 2 часа. Для этого из формулы нужно
выразить скорость:
V=S/t = 180/2=90 км/ч.
Аналогично предыдущему примеру узнаем
время, за которое автомобиль преодолел то же
расстояние, двигаясь со скоростью 120км/ч:
t=S/V = 180/120=1,5ч.
2. Устные упражнения.
На доске оформляются краткие и
наглядные условия задач, полный текст задачи
ребята видят на слайде презентации [Приложение
1]
1. Из пунктов А и В навстречу друг другу
выехали автомобиль со скоростью 60 км/ч и
велосипедист со скоростью 15 км/ч. Встретятся ли
автомобиль и велосипедист через 2 часа, если
расстояние между пунктами 160 км?[2] (Решить задачу
двумя способами.)<Рисунок 1> [Приложение
1]
2. Из лагеря геологоразведчиков выехал
вездеход со скоростью 30 км/ч. Через 2 часа вслед за
ним был послан другой вездеход. С какой скоростью
он должен ехать, чтобы догнать первый через 4 часа
после своего выхода? [4] <Рисунок 2> [Приложение
1]
3. По рисунку составить задачу на
движение и решить ее. [1]
Рисунок задачи на слайде презентации [Приложение 1]
4. Викторина
(3 ряда – каждому ряду выдается по
тексту задачи (всего 3 задачи) и карточки для
наглядного составления краткой записи на доске,
а также тексты всех трех задач выводятся на
слайде [Приложение 1]). Ученикам
необходимо решить задачу, представить наглядную
краткую запись-схему у доски и предоставить ее
решение.
Первый ряд: “Автомобиль
“Москвич” за 3 часа может проехать 360 км.
Бескрылая птица страус – лучший бегун в мире –
развивает скорость до 120 км/ч. Сравните скорости
автомобиля “Москвич” и страуса. [2] <Рисунок 3>
Второй ряд: “Скорость
распространения света самая большая в природе –
300000 км/с. На Солнце произошла вспышка. Через какое
время ее увидят на Земле, если расстояние от
Земли до Солнца равно 150000000 км? [1] <Рисунок 4>
Третий ряд: “Пройденный путь
пешехода S, его скорость v и время движения t
связаны соотношением S = vt. Если пешеход за 4 часа
прошел 24 км, то его скорость равна….? [3] <Рисунок
5>
5. Входит дядя Степа-милиционер
(Один из учеников класса, желательно
посильнее который, с ним заранее разбираются
задачи, и он их дома решает) и предлагает задачу
из сборника задач по основам безопасности
дорожного движения. <Рисунок 9>
Ширина проезжей части дороги 15 м,
зеленый сигнал светофора горит 20 секунд. С какой
наименьшей скоростью может двигаться пешеход с
момента загорания светофора, чтобы благополучно
перейти дорогу? [5] <Рисунок 6>
Решение:
1) 15 м = 1500 см
2) 1500 : 20 = 75 см/с.
Ответ: пешеход может двигаться со
скоростью 75 см/с.
6. Решить олимпиадную задачу. [Приложение 1]
Из пунктов А и В, расстояние между
которыми 100 км, со скоростями 20 км/ч и 30 км/ч
выезжают навстречу друг другу два велосипедиста.
Вместе с ними со скоростью 50 км/ч вылетают две
мухи, летят до встречи, поворачивают и летят
обратно до встречи с велосипедистами, снова
поворачивают и т. д. Сколько километров пролетит
каждая муха в направлении от А до В до того
момента, когда велосипедисты встретятся? [6]
<Рисунок 7>
Решение: Велосипедисты встретятся
через 2 часа на расстоянии 40 км/ч от А. За это время
каждая муха пролетела 100 км. Муха, вылетевшая из А,
пролетела в направлении от А до В на 40 км больше,
чем в обратном направлении, и поэтому от АВ она
пролетела 70 км. Аналогично, вторая муха в
направлении от А к В пролетела на 60 км меньше, чем
в обратном, то есть 20 км.
Ответ: первая муха в направлении от А к
В пролетела 70 км, вторая – 20 км.
Запасная задача! (в зависимости от
способностей учеников, если останется 3 минутки
свободного времени на уроке) Мотоциклист едет со
скоростью 95 км/ч, а скорость велосипедиста на 76
км/ч меньше. Во сколько раз скорость мотоциклиста
больше скорости велосипедиста? Кому из них легче
остановиться? [2]
Решение:
1) 95 – 76 = 19 км/ч
2) 95 : 19 = 5 раз.
Ответ: в 5 раз легче остановиться
велосипедисту, так как при меньшей скорости
короче тормозной путь.
Итог урока: выставление оценок
наиболее отличившимся ученикам, вручение
памятных дипломов каждому ряду за умение
работать в группах.
Домашнее задание: [Приложение
1] ученикам раздаются ксерокопии
заданий.[2,3]
- Помогите французским девочкам. Однажды Жаннин и
Моника поплыли по маленькой речке, отправившись
из одного и того же места, но только Жаннин
поплыла против течения, а Моника поплыла по
течению. Оказалось, что Моника забыла снять
большие деревянные бусы. Через четверть часа
девочки повернули обратно. Кто же из них подберет
бусы Моники: сама Моника или Жаннин? (Скорость
обеих пловчих в неподвижной воде одинакова.) - Задача от дяди Степы. Скорость легкового
автомобиля 60 км/ч, а грузовика 15 км/ч. Во сколько
раз скорость легкового автомобиля больше
скорости грузовика? Какой автомобиль опаснее для
школьника, начавшего движение по пешеходному
переходу? - Задание от “Знающего человека”. Заполнить
таблицу. - Составить по одной анаграмме.
|
Объект |
Скорость v |
Время t |
Расстояние S |
|
“Волга” |
100 км/ч |
5 ч |
|
|
“Ока” |
60 км/ч |
420 км |
|
|
“Москвич” |
3 ч |
240 км |
|
|
Пчела |
60 км/ч |
180 км |
|
|
Стрекоза |
2 ч |
200 км |
|
|
Стриж |
100 км/ч |
4 ч |
|
|
Меч-рыба |
100 км/ч |
300 км |
|
|
Земля (вокруг Солнца) |
30 км/ч |
24 ч |
|
|
Черепаха |
6 мин |
18 м |
|
|
Улитка |
7 ч |
35 км |
|
|
Верблюд |
8 км/ч |
5 ч |
|
|
Почтовый голубь |
50 км/ч |
150 км |
Ответы для учителя.
Задача № 1
Скорости девушек относительно
неподвижной воды одинакова. Но ведь по отношению
к воде в реке бусы остаются неподвижными – они
движутся в точности с такой же скоростью, что и
вода (со скоростью течения). Пловчихи проплывают
относительно воды одинаковое расстояние и по
истечении получаса встречаются в том месте, где в
этот момент находятся бусы. Таким образом, обе
девушки могут подобрать бусы с равным
основанием, так как встречаются в тот самый
момент, когда подплывут бусы.
Задача № 2
Опаснее легковой автомобиль, так как у него
скорость больше, кроме того, для водителя
легкового автомобиля мальчик появится
неожиданно, так как обзор будет закрыт грузовым
автомобилем.
Список литературы:
- Решение задач / Клустер Д. И. – М.: Просвещение. –
2005. - Задачи на движение/ Павлов Е. С. – красноярск. –
2002. - Решение задач на движение/ Кузнишина Т. Л. –
Новосибирск. – 1990 - Сборник задач/ Кравцова Е. Е. – М.:
Просвещение.-2008. - Справочник по безопасности дорожного движения/
Сильянов В. В. – М.: Технополиграфцентр. – 2001 - Сборник олимпиадных задач по математике/
Горбачев Н.В. – М.: МЦНМО. — 2004
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
- Основная формула:S=ν*t;
- Нужно сделать чертеж, который поможет определить тип задачи.
- Все цифры нужно привести в единые единицы измерения: длина и время
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.
Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.
На чтение 3 мин. Просмотров 33.3k.
Обновлено 31.08.2021
Схемы задач на движение очень просто нарисовать. Они помогают представить наглядно условие задачи и найти верное решение. В дополнение к схеме в сложных случаях или когда ученик затрудняется с решением рекомендуется рисовать таблицу, где в шапке параметры скорости, времени и расстояния. Об этом подробнее ниже.
Узнайте также, как составить схемы к задачам по математике для 2 класса
Содержание
- Простые задачи на движение
- Решение
- Обратные задачи на движение
- Как найти скорость, если известно время и расстояние
- Как найти время, когда известны скорость и расстояние
- Схемы задач на встречное движение
- Решение
- Задачи на движение в одном направлении
- Шпаргалка по решению задач на скорость, время и расстояние
Простые задачи на движение
Простые задачи про путников, лыжников, мотоциклистов и другие движущиеся объекты (встречаются даже задачки про черепах) начинают решать еще в начальных классах. Именно на этих примерах удобно разбирать составление схем.
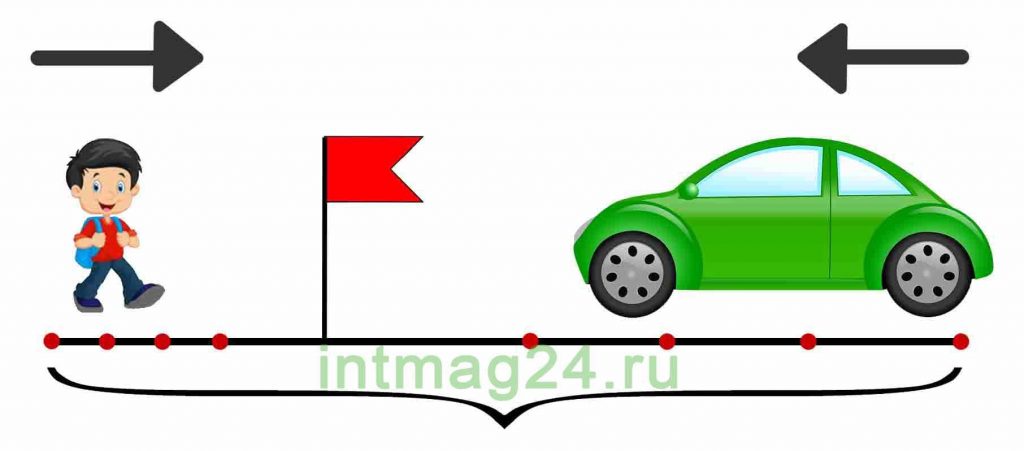
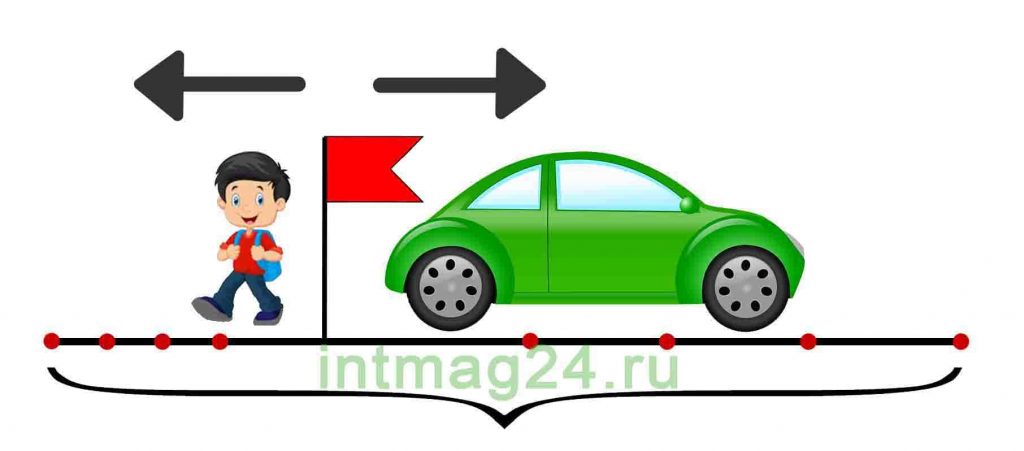
Задача 1. Пешеход вышел из пункта А в пункт Б со скоростью 5 км/ч. Через 3 часа он добрался до пункта Б. Какое расстояние между этими двумя пунктами?
Рисуем схему к задаче: прямая линия, соединяющая точки А и Б — это весь путь. Стрелкой обозначаем направление движения путника. Над стрелкой отмечаем скорость, если известна. Время или расстояние отмечаем под (или над) отрезком:
Если со схемой вы не смогли решить задачу, то предлагаю вам воспользоваться таблицей:
| скорость | время | расстояние |
| 5 км/ч | 3 ч | ? км |
Чтобы решать с помощью таблицы, запомните правила:
- Чтобы найти расстояние, нужно скорость умножить на время: S = V x t
- Чтобы найти скорость, нужно расстояние разделить на время, (это производное из первой формулы:
V = S : t ) - чтобы найти время, необходимо расстояние разделить на скорость. (также просто вывести из первой формулы:
t = S : t
Решение
5 х 3 = 15 км — расстояние между пунктами А и Б
Обратные задачи на движение
Как найти скорость, если известно время и расстояние
Чтобы не путать вас разными условиями задачи состав задачу, обратную первому примеру:
Задача 2. Расстояние между пунктами А и Б равно 15 км. Путник преодолел это расстояние за 3 часа. С какой скоростью шел пешеход?
| скорость | время | расстояние |
| ? км/ч | 3 ч | 15 км |
Решение
15 : 3 = 5 км/ч
Как найти время, когда известны скорость и расстояние
Задача 3. Расстояние между пунктами 15 км. Пешеход шел со скоростью 5 км/ч. За какое время пешеход преодолеет весь путь?
| Скорость | время | расстояние |
| 5 км/ч | ? ч | 15 км |
Решение
15 : 5 = 3 часа
Схемы задач на встречное движение
Чтобы начертить встречное движение, мы рисуем стрелочки из двух пунктов навстречу. Флажком обозначаем место встречи
Когда задачи со встречным или удаляющимся движением — это задачи на общую скорость. Скоро будет подробный урок о них на моем сайте.
Задача 4. Два пешехода вышли одновременно из пунктов А и Б навстречу друг другу. Скорость одного — 5 км/ч, другого — 3 км/ч. Через какое время они встретятся, если известно, что расстояние между пунктами 24 км?
Решение
1 способ:
5 + 3 =8 км/ч — общая скорость
24 : 8 = 3 часа
Задачи на движение в одном направлении
Задача 5. Два пешехода вышли из пунктов А и Б одновременно в одном направлении. Пешеход, который шел впереди, двигался со скоростью 3 км/ч, а второй — со скоростью 5 км/ч. Через какое время второй пешеход догонит первого, если расстояние между пунктами 2 км?
Здесь нужно выяснить скорость сближения. Так как один пешеход шел быстрее второго, то расстояние между ними сокращалось на 2 км/ч (мы посчитали так: 5 — 3 = 2 км/ч). Так как первоначальное расстояние между пунктами 2 км, то найдем время:
2км : 2 км/ч = 1 час.
Через 1 час пешеходы встретятся.
Шпаргалка по решению задач на скорость, время и расстояние
Вы можете воспользоваться данной памяткой при решении этого типа задач. Кликните для просмотра в полном размере и распечатайте, нажав на клавиатуре клавиши CTRL + P.
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
v=S/t, где
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
- vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
N=F*v*cos α , где N — механическая мощность,
F — сила,
v — скорость,
cos α — косинус угла между векторами силы и скорости.
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.