Как найти расстояние между числами на координатной - Сайт, где вы сможете решить свои вопросы

Расстояние между точками на координатной прямой

Расстояние между двумя точками на координатной прямой равно модулю разности их координат.

Формула расстояния между точками на координатной прямой:

AB = |a – b|,

где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.

Выражение |a – b| можно заменить выражением |b – a|, так как a – b и b – a являются противоположными числами и их модули равны.

Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.

Пример 1. Найти расстояние между точками L(-3) и M(5), отмеченными на координатной прямой.

Решение. Чтобы найти расстояние между точками L и M надо из координаты точки L вычесть координату точки M или наоборот, а в качестве ответа взять модуль полученного результата:

|-3 – 5| = |-8| = 8

или

|5 – (-3)| = |5 + 3| = 8.

Ответ. Расстояние между точками L и M равно 8.

Пример 2. Найдите координаты середины отрезка AB, если A(-5) и B(5).

Решение. Обозначим середину отрезка точкой C. Так как C — середина отрезка AB, то |AC| = |CB|. Значит, чтобы найти координату точки C, надо сначала вычислить длину отрезка AB и разделить её на 2, то есть, на две равные части AC и CB:

AB = |-5 – 5| = |-10| = 10;

10 : 2 = 5, значит |AC| = |CB| = 5.

Как видно из чертежа, чтобы найти координату середины отрезка, надо половину длины отрезка либо прибавить к точке с наименьшей координатой, либо отнять от точки с наибольшей координатой:

-5 + 5 = 0

или

5 – 5 = 0.

Ответ. Координата середины отрезка C(0).

Пример 3. Найдите координату точки C, которая является серединой отрезка с концами в точках A(7) и B(25).

Решение.

AB = |7 – 25| = |-18| = 18;

AC = CB = 18 : 2 = 9;

7 + 9 = 16

или

25 – 9 = 16.

Ответ. Координата точки C — 16.

Источник

Формулировка определения координатной прямой и ее отличий от обычной прямой

Из курса геометрии мы знаем, что такое прямая, но что нужно сделать с обычной прямой, чтобы она стала координатной?

Выбрать точку начала отсчета;
Выбрать направление;
Выбрать масштаб;

На рисунке 1 изображена обычная прямая, а на рисунке 2 – координатная.

Координатной прямой называется такая прямая l , на которой выбрана начальная точка О – начало отсчета, масштаб – единичный отрезок, то есть такой отрезок, длина которого считается равной единице, и положительное направление.

Описание основного свойства координатной прямой и двух основных задач, с ним связанных

Координатную прямую также называют координатной осью или осью Х.

Выясним, зачем нужна координатная прямая, для этого определим ее основное свойство. Координатная прямая устанавливает взаимооднозначное соответствие между множеством всех чисел и множеством всех точек на этой прямой. Приведем примеры:

Заданы два числа: (знак «+», модуль равен трем) и (знак «-», модуль равен трем).Изобразим эти числа на координатной прямой:

Здесь число называется координатой А, число – координатой В.

Говорят также, что образом числа есть точка С с координатой , а образом числа есть точка D с координатой :

Итак, поскольку основное свойство координатной прямой – это установление взаимооднозначного соответствия между точками и числами, то возникает две основные задачи: указать точку по заданному числу, мы это уже сделали выше, и указать число по заданной точке. Рассмотрим пример второй задачи:

Решение примеров

Пример 1:

Пусть дана точка М:

Чтобы определить по данной точке число нужно в первую очередь определить расстояние от начал отсчета до точки. В данном случае расстояние равно двум. Теперь нужно определить знак числа, то есть в каком луче прямой лежит точка М. В данном случае точка лежит справа от начала отсчета, в положительном луче, значит число будет иметь знак «+».

Пример 2:

Возьмем еще одну точку и по ней определим число:

Расстояние от начала отсчета до точки аналогично предыдущему примеру равно двум, но в данном случае точка лежит слева от начала отсчета, на отрицательном луче, значит точка N характеризует число

Формулировка основных типовых задач и решение примеров

Все типовые задачи, связанные с координатной прямой, так или иначе связаны с ее основным свойством и двумя основными задачами, которые мы сформулировали и решили.

К типовым задачам относятся:

уметь расставлять точки и их координаты;
понимать сравнение чисел:

Пример 3:

выражение означает, что точка С с координатой 4 лежит правее точки М с координатой 2:

И наоборот, если нам задано расположение точек на координатной прямой, мы должны понимать, что их координаты связаны определенным соотношением:

Пример 5:

Пусть заданы точки М(х_М) и N(x_N):

Мы видим, что точка М лежит правее точки n, значит, их координаты соотносятся как

—Определение расстояния между точками.

Пример 6:

Мы знаем, что расстояние между точками Х и А равно модулю числа . пусть даны две точки:

Тогда расстояние между ними будет равно:

-Еще одно очень важная задача – это геометрическое описание числовых множеств.

Пример 7:

Рассмотрим луч, который лежит на координатной оси, не включает свое начало, но включает все остальные точки:

Итак, у нас задано множество точек, расположенных на координатной оси. Опишем множество чисел, которое характеризуется данным множеством точек. Таких чисел и точек бесчисленное множество, поэтому данная запись выглядит так:

или

Сделаем пояснение: при втором варианте записи если ставят круглую скобку «(» значит крайнее число – в данном случае число 3, не включается в множество, если же поставить квадратную скобку «[», то крайнее число включается в множество.

Итак, мы записали аналитически числовое множество, которое характеризует заданное множество точек. аналитическая запись, как мы сказали, выполняется или в виде неравенства, или в виде промежутка.

Пример 8:

Задано множество точек:

В данном случае точка а=3 входит в множество. Опишем аналитически множество чисел:

Обратим внимание, что после или перед знаком бесконечности всегда ставят круглую скобку, так как бесконечности мы никогда не достигнем, а около числа может стоять как круглая скобка, так и квадратная, в зависимости от условий поставленной задачи.

Рассмотрим пример обратной задачи.

Пример 9:

Дана координатная прямая. Изобразить на ней множество точек, соответствующих числовому множеству и :

Координатная прямая устанавливает взаимооднозначное соответствие между любой точкой и числом, а значит и между числовыми множествами и множествами точек. Мы рассмотрели лучи, направленные как в положительном, так и в отрицательном направлении, включающие свою вершину и не включающие ее. Теперь рассмотрим отрезки.

Пример 10:

Задано множество чисел . Изобразить соответствующее множество точек

Пример 11:

Задано множество чисел . Изобразить множество точек:

Иногда чтобы показать, что концы отрезка не включаются в множество, рисуют стрелки:

Решение задач на выполнение нескольких типовых действий

Пример 12:

Дано числовое множество . Построить его геометрическую модель:

Найти наименьшее число из промежутка :

Найти наибольшее число из промежутка , если оно существует:

Мы может отнять от восьми сколь угодно малое число и сказать, что результат и будет наибольшим числом, но тут же найдем число еще меньше, и результат вычитания увеличится, так что найти наибольшее число в данном промежутке невозможно.

Обратим внимание на тот факт, что ни к одному числу на координатной прямой нельзя подобрать ближайшее число, потому что всегда найдется число еще ближе.

Сколько натуральных чисел содержится в заданном промежутке?

Из промежутка выделим следующие натуральные числа: 4, 5, 6, 7 – четыре натуральных числа.

Напомним, что натуральные числа – это числа, применяемые для счета.

Возьмем другое множество.

Пример 13:

Задано множество чисел

Построить его геометрическую модель:

Найти наименьшее число:

Очевидно, что наименьшим числом является

Найти наибольшее число:

Наибольшего числа мы найти не можем, так как единица не входит в множество.

Сколько натуральных чисел в данном множестве?

Натуральные числа – это числа используемые для счета и начинается ряд натуральных чисел с единицы, а она в множество не входит, значит натуральных чисел нет

Сколько целых чисел в данном множестве?

Напомним, что в множество целых чисел Z входят число 0 и все натуральные числа, взятые со знаками плюс и минус:

В наше множество входят такие целые числа: -3, -2, -1, 0 – четыре целых числа.

Выводы по уроку

Вывод: в данном уроке мы познакомились с понятием координатной прямой, узнали ее отличие от прямой обычной, сформулировали основное свойство и на его основании составили ряд типовых задач. Решили несколько примеров к каждой задаче и примеры, в которых решается несколько задач сразу.

Источник

В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.

Определение 1

Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.

Расстояние между точками на координатной прямой

Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.

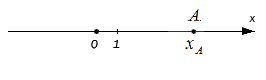
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.

Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.

К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О, необходимо будет отложить три единичных отрезка. Если точка А имеет координату -4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние ОА равно 3; во втором случае ОА = 4.

Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4111.

Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна 11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то OA=xA (число принимается за расстояние); если координата меньше нуля, то OA=-xA . В общем, эти утверждения справедливы для любого действительного числа xA.

Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:

0, если точка совпадает с началом координат;

xA , если xA>0;

-xA , если xA<0 .

При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой xA: OA=xA

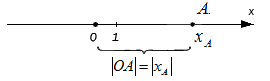
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B, лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты xA и xB : AB=xB-xA.

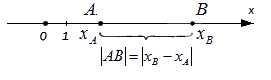
Расстояние между точками на плоскости

Исходные данные: точки A и B, лежащие на плоскости в прямоугольной системе координат Oxy с заданными координатами: A(xA, yA) и B(xB, yB) .

Проведем через точки А и B перпендикуляры к осям координат Ox и Oy и получим в результате точки проекции: Ax, Ay, Bx, By. Исходя из расположения точек А и B далее возможны следующие варианты:

– если точки А и В совпадают, то расстояние между ними равно нулю;

– если точки А и В лежат на прямой, перпендикулярной оси Ox (оси абсцисс), то точки и совпадают, а |АВ| = |АyBy|. Поскольку, расстояние между точками равно модулю разности их координат, то AyBy=yB-yA , а, следовательно AB=AyBy=yB-yA.

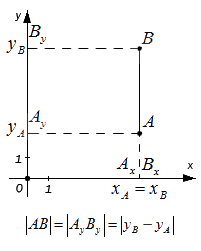
– если точки A и B лежат на прямой, перпендикулярной оси Oy (оси ординат) – по аналогии с предыдущим пунктом: AB=AxBx=xB-xA

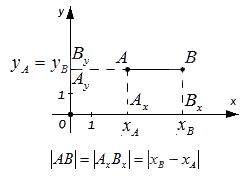
– если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:

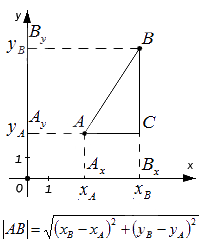
Мы видим, что треугольник АВС является прямоугольным по построению. При этом AC=AxBx и BC=AyBy. Используя теорему Пифагора, составим равенство: AB2=AC2+BC2⇔AB2=AxBx2+AyBy2 , а затем преобразуем его: AB=AxBx2+AyBy2=xB-xA2+yB-yA2=(xB-xA)2+(yB-yA)2

Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек

AB=(xB-xA)2+(yB-yA)2

Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: AB=(xB-xA)2+(yB-yA)2=02+02=0

Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:

AB=(xB-xA)2+(yB-yA)2=02+(yB-yA)2=yB-yA

Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:

AB=(xB-xA)2+(yB-yA)2=(xB-xA)2+02=xB-xA

Расстояние между точками в пространстве

Исходные данные: прямоугольная система координат Oxyz с лежащими на ней произвольными точками с заданными координатами A(xA, yA, zA) и B(xB, yB, zB) . Необходимо определить расстояние между этими точками.

Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: Ax, Ay, Az, Bx, By, Bz

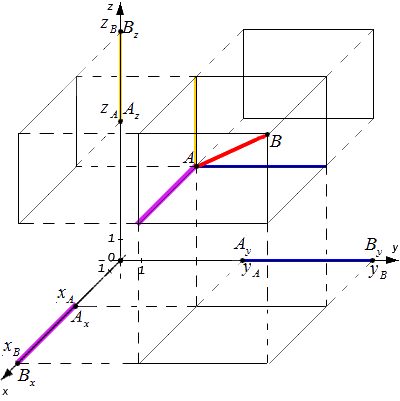
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: AxBx, AyBy и AzBz

Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: AB2=AxBx2+AyBy2+AzBz2

Используя полученные ранее выводы, запишем следующее:

AxBx=xB-xA, AyBy=yB-yA, AzBz=zB-zA

Преобразуем выражение:

AB2=AxBx2+AyBy2+AzBz2=xB-xA2+yB-yA2+zB-zA2==(xB-xA)2+(yB-yA)2+zB-zA2

Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:

AB=xB-xA2+yB-yA2+(zB-zA)2

Полученная формула действительна также для случаев, когда:

– точки совпадают;

– лежат на одной координатной оси или прямой, параллельной одной из координатных осей.

Примеры решения задач на нахождение расстояния между точками

Пример 1

Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A(1-2) и B(11+2) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B.

Решение

Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно OA=1-2=2-1
Расстояние между точками A и B определим как модуль разности координат этих точек: AB=11+2-(1-2)=10+22

Ответ: OA=2-1, AB=10+22

Пример 2

Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A(1, -1) и B (λ+1, 3) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние АВ будет равно 5.

Решение

Чтобы найти расстояние между точками A и B, необходимо использовать формулу AB=(xB-xA)2+yB-yA2

Подставив реальные значения координат, получим:AB=(λ+1-1)2+(3-(-1))2=λ2+16

А также используем имеющееся условие, что АВ=5 и тогда будет верным равенство:

λ2+16=5λ2+16=25λ=±3

Ответ: АВ = 5, если λ=±3 .

Пример 3

Исходные данные: задано трехмерное пространство в прямоугольной системе координат Oxyz и лежащие в нем точки A (1, 2, 3) и B-7, -2, 4 .

Решение

Для решения задачи используем формулу AB=xB-xA2+yB-yA2+(zB-zA)2

Подставив реальные значения, получим: AB=(-7-1)2+(-2-2)2+(4-3)2=81=9

Ответ: |АВ| = 9

Источник

Математика,

вопрос задал marselarusta,

4 года назад

как определить расстояние между двумя точками (отрицательными и положительными) на координатной оси

Ответы на вопрос

Чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.

Ответ:

Пошаговое объяснение:

От большего числа вычесть меньшее (точнее, от координаты точки, соответствующей бОльшему числу, вычесть координату точки, соответствующей меньшему числу).

Например.

Расстояние между А(-7) и B(-2)=-2 – (-7) = 5

Между C(-5) и D(3) = 3 – (-5) = 8

irinaborz:
Если не умеете или трудно понять, какое больше, то из того, что правее, вычесть то, что левее.

Новые вопросы

Источник

Урок
по алгебре в 7 классе

Тема:
Расстояние между точками на координатной прямой.

Цель:
создать условия для овладения навыками находить расстояние между точками на
координатной прямой, вычисляя модуль разности, координаты середины отрезка.

Планируемые результаты

Личностные:
проявление познавательного интереса к предмету.

Предметные:
овладение навыками находить расстояние между точками на координатной прямой,
вычисляя модуль разности, координаты середины отрезка.

Метапредметные:

–
познавательные: ориентируются на
разнообразные способы решения задач, умение обобщать и систематизировать
информацию;

–
регулятивные: учитывают правило в
планировании и контроле способа решения;

–
коммуникативные: считаются с разными
мнениями и стремятся к координации различных позиций в сотрудничестве.

Этап	Содержание
Организационный	Приветствие. Определение готовности учащихся к уроку
Мотивация	Вопросы: – Какая прямая называется координатной? – Что называется модулем числа? – Какие числовые промежутки мы знаем? – Как складывать и отнимать числа с одинаковыми и разными знаками? Считаем устно (записать на доске): а) -19 – 33 б) -42 – (-90)
Актуализация знаний	Чему равен модуль чисел: 5; -7; -13,5; 0 (устно). Сравнить: \|5-9\| и \|9-5\|, \|11,3 – 7,2\| и \|7,2 – 11,3\| (записать на доске). Предыдущие уроки были посвящены теме “Координатная прямая”. Что мы о ней знаем? Рене Декарт (включить портрет на доске) – французский ученый математик, первым предложивший геометрическое истолкование чисел и изобразивший координатную прямую в 1637 году.
Тема. Постановка учебной задачи	Пусть даны точки A(0), B(13), C(4) и D(34) (записать на доске). На каком расстоянии друг от друга находятся точки A и B, C и D? Как найти это расстояние? (посчитать длины отрезков) Что нужно найти? Всегда ли удобно изображать отрезки на координатной прямой и считать их длины? (нет, числа могут быть очень большими). В чем затруднение? (не можем найти расстояние между точками). Сформулируем цель урока (научиться находить расстояние между точками с помощью вычислений). Записываем тему урока: Расстояние между точками на координатной прямой. Формулируем правило нахождения расстояния между точками: чтобы найти расстояние между точками на координатной прямой, нужно из большей координаты вычесть меньшую. Может ли в результате вычислений получиться отрицательное число? (нет, расстояние не может быть отрицательным) Вывод: если A(a), B(b), то AB = \|a – b\| = \|b – a\|.
Работа по листу	Листы с заданиями и листы самооценки раздаются обучающимся. Объяснить, как работать с листом самооценки, как работать с заданиями, если обучающийся работает быстрее класса. Работа с учителем 1) Найдите расстояние между точками, отмеченными на координатной прямой 2) Найдите длины отрезков AB, AC, AO, AD, BD. 3) Найдите координату точки C, которая является серединой отрезка с концами в точках A(-6,8) и B(12,4). 2. Работа в парах (для ОВЗ индивидуальные задания). 1) Найти расстояние между точками координатной прямой: а) A(2) и B(2,7) б) P(9,2) и M(5,3) в) A(-15) и S(-3,24) г) C(4,6) и N(-7,8) 2) Найти координаты точки О – середины отрезка CD, если: а) C(-4) и D(4) б) C(2) и D(4) в) C(-2) и D(-6,6) 3. Самостоятельная работа (для ОВЗ индивидуальные задания). 1) Найдите длину отрезка MN, если а) M(-7), N(35) б) M(), N ( в) M(-2,76), N(-2,83) 2) Найдите координаты вершины D прямоугольника ABCD, а также его периметр
Рефлексия	Какая цель стояла на уроке? Достигли ли мы ее? Что нового узнали на уроке? Осталось ли что-то непонятным?
Домашнее задание	Карточка с заданиями в электронном виде / на листах

ЛИСТ
САМООЦЕНКИ

	Полностью самостоятельно справился с заданием – 2 балла	Справился с заданием с помощью друга – 1 балл	Не смог сделать – 0 баллов
Работа с учителем
Работа в парах
Самостоятельная работа

ЛИСТ
САМООЦЕНКИ

	Полностью самостоятельно справился с заданием – 2 балла	Справился с заданием с помощью друга – 1 балл	Не смог сделать – 0 баллов
Работа с учителем
Работа в парах
Самостоятельная работа

ЛИСТ
САМООЦЕНКИ

	Полностью самостоятельно справился с заданием – 2 балла	Справился с заданием с помощью друга – 1 балл	Не смог сделать – 0 баллов
Работа с учителем
Работа в парах
Самостоятельная работа

РАССТОЯНИЕ
МЕЖДУ ТОЧКАМИ НА КООРДИНАТНОЙ ПРЯМОЙ

Работа с
учителем

1) Найдите
расстояние между точками, отмеченными на координатной прямой (рисунок)

2) Найдите
длины отрезков AB, AC, AO, AD, BD.

3) Найдите
координату точки C, которая является серединой отрезка с концами в точках
A(-6,8) и B(12,4).

Работа в
парах

1) Найти
расстояние между точками координатной прямой:

а)
A(2) и B(2,7) в) A(-15) и S(-3,24)

б)
P(9,2) и M(5,3) г) C(4,6) и N(-7,8)

2) Найти
координаты точки О – середины отрезка CD, если:

а) C(-4) и D(4) б)
C(2) и D(4) в) C(-2) и D(-6,6)

Самостоятельная
работа

1) Найдите
длину отрезка MN, если

а) M(-7), N(35) б)
M(), N ( в) M(-2,76), N(-2,83)

2) Найдите
координаты вершины D прямоугольника ABCD, а также его периметр

РАССТОЯНИЕ
МЕЖДУ ТОЧКАМИ КООРДИНАТНОЙ ПРЯМОЙ (О)

Работа с
учителем

1) Найдите
расстояние между точками, отмеченными на координатной прямой (рисунок)

2) Найдите
длины отрезков AB, AC, AO, AD, BD.

3) Найдите
координату точки C, которая является серединой отрезка с концами в точках
A(-6,8) и B(12,4).

Работа в
парах

1) Найти
расстояние между точками координатной прямой:

а)
L(-3) и M(5)

Считать
так: LM = |5 – (-3)| = |5+3| = |8| = 8

б)
A(3) и B(-6)

Посчитай
расстояние между точками A и B самостоятельно (сколько клеток между A и B)

в)
P(9) и M(5)

г)
C(5) и N(-8)

2) Нарисуй
координатную прямую, отметь точки C и D и найди координаты точки О – середины
отрезка CD, если:

а) C(-4) и D(4) б)
C(2) и D(4)

Самостоятельная
работа

Нарисуй координатную прямую, отметь
точки M и N и найди длину отрезка MN, если

а) M(-7), N(4) б)
M(), N ( в) M(-3), N(-4)