Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Формула. Объём шара:
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
S = 4 π R 2 = π D 2
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x – x 0) 2 + ( y – y 0) 2 + ( z – z 0) 2 = R 2
Основные свойства сферы и шара
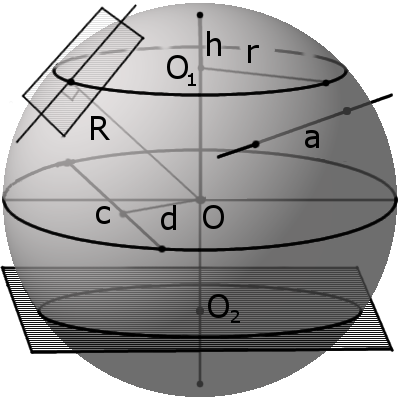
Секущая, хорда, секущая плоскость сферы и их свойства
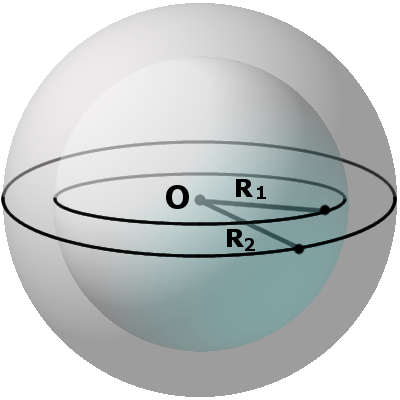
d m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m r такого круга можно найти по формуле:
где R – радиус сферы (шара), m – расстояние от центра шара до секущей плоскости.
Касательная, касательная плоскость к сфере и их свойства
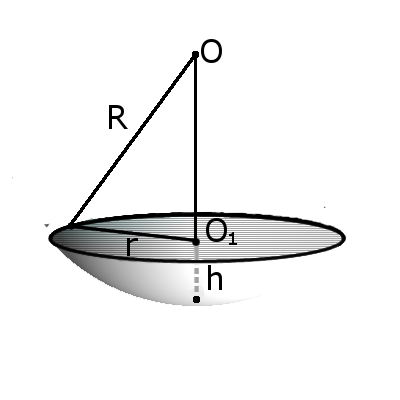
Формула. Объём сегмента сферы с высотой h через радиус сферы R:

S = π R(2 h + √ 2 h R – h 2 )
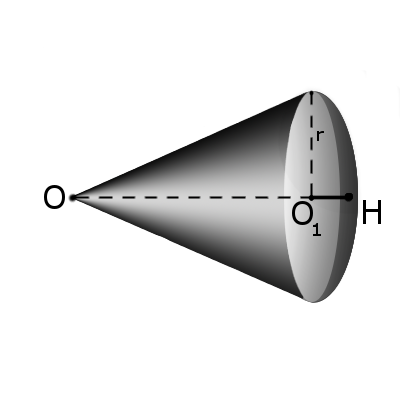
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Урок «Сфера. Уравнение сферы»
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Продолжаем изучение сферы.
На прошлых занятиях вы познакомились с определением сферы и шара.
Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.
Данная точка — центр сферы.
Заданное расстояние — радиус сферы.
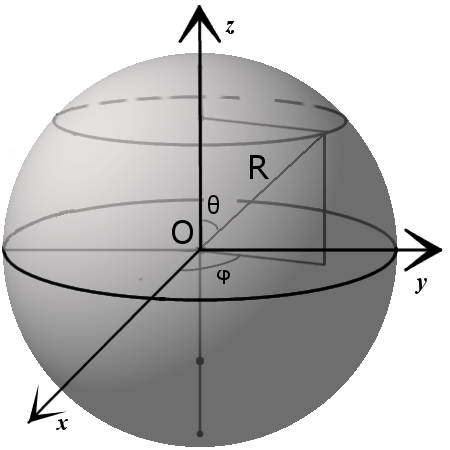
Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.
Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.
Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.
1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).
2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.
3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть
4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.
5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром
С (x0 ; y0 ; z0) и радиусом R имеет вид:
Применим полученные знания при решении задач.
Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).
1.Запишем уравнение сферы с центром
А (x0 ; y0 ; z0) и радиусом R:
2.Подставим соответствующие координаты центра сферы А в данное уравнение:
Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:
3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:
Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:
Сфера задана уравнением:
1) Найти координаты центра и радиус сферы;
2) Найти значение m, при котором точки
А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.
1. Уравнение данной сферы имеет вид:
x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4
Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:
x2+ y2+2y+1-1 + z2-4z+4-4=4
Уравнение примет вид:
x2+( y+1)2+( z-2)2-5=4 или
Таким образом, центр сферы имеет координаты:
О (0;-1;2), радиус равен R=√9=3
2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:
Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:
Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:
Таким образом, мы получили 4 значения m:
Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.
Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением
x2+ y2+ z2+2y-4z=4 с центром в точке
О (0;-1;2) и радиусом R=3.
–> –>
АвторДата добавленияРазделПодразделПросмотровНомер материала
| Инфоурок |
| 07.11.2014 |
| Геометрия |
| Видеоурок |
| 53406 |
| 1003 |
© 2022 Проект «Уроки математики»
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.
Геометрия. 11 класс
Конспект урока
Геометрия, 11 класс
Урок №8. Сфера и шар
Перечень вопросов, рассматриваемых в теме:
- что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
- что такое шар и его элементы;
- уравнение сферы;
- формула для нахождения площади поверхности сферы;
- взаимное расположение сферы и плоскости;
- теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.
Глоссарий по теме:
Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.
Круг – это часть плоскости, ограниченная окружностью.
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.
– уравнение сферы радиуса R и центром С(x0; y0; z0).
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Сегмент шара – это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.
Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Основные теоретические факты
По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.
Рисунок 1 – Сфера с центром в точке О и радиусом R
Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.
Сферу можно получить ещё одним способом – вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.
2. Уравнение сферы
Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.
Пусть сфера имеет центром точку С (x0; y0; z0) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:
МС=
Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС 2 =R 2 , то есть координаты точки М удовлетворяют уравнению:
.
Это выражение называют уравнением сферы радиуса R и центром С(x0; y0; z0).
3. Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.
1. Пусть dR. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.
2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.
3. Пусть dR. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.
Рассмотрим случай касания более подробно.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Теорема (свойство касательной плоскости).
Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема (признак касательной плоскости):
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.
4. Основные формулы
Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:
Формула для вычисления площади поверхности сферы и ее элементов:
S=4πR 2 – площадь сферы.
S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.
– площадь поверхности сектора с высотой h.
Примеры и разбор решения заданий тренировочного модуля
1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.
Площадь круга вычисляется по формуле: Sкр=πR 2 .
Площадь поверхности шара вычисляется по формуле: Sсф=4πR 2 . Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.
2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.
Площадь сферы равна Sсф=4πR 2 . То есть Sсф=100π.
По условию площадь круга некоторого радиуса r также равна 100π. Значит, r 2 =100, то есть r=10.
3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15
Окружность, вписанная в треугольник, является сечением сферы.
Найдем ее радиус.
Площадь треугольника с известными сторонами можно вычислить по формуле Герона:
С другой стороны, S=p·r.
Теперь найдем расстояние от центра шара до секущей плоскости.
4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.
Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.
Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.
[spoiler title=”источники:”]
http://urokimatematiki.ru/urok-sfera-uravnenie-sferi-1003.html
http://resh.edu.ru/subject/lesson/4034/conspect/
[/spoiler]
Не могу решить задачу по геометрии. Знаю ход решения, но с ответом из учебника не сходится
Профи
(793),
закрыт
7 лет назад
Дополнен 7 лет назад
С вычислениями все ясно, но ответов должно быть два: корень из 33 плюс 3 и корень из 33 минус 3. Чем это объясняется?
Анастасия Громова
Мыслитель
(5211)
7 лет назад
радиус сечения 4
расстояние от центра меньшей сферы до сечения 3 ( Егип етский треугольник)
расстояние от центра большей сферы= корень из (49-16)= корень 33
расстояние между центрами= 3+ корень из 33
§ 19.Расстояние между фигурами
Рассмотрим две фигуры F1 и F2. Если они имеют хотя бы одну общую точку, то расстояние между ними равно нулю (рис. 128). Если же фигуры не имеют общих точек, то рассматриваются всевозможные расстояния между каждой точкой A первой фигуры и каждой точкой B второй фигуры. Наименьшее из этих расстояний (чисел) и принимается за расстояние между фигурами F1 и F2. Как и расстояние между фигурой и точкой, расстояние между двумя фигурами F1 и F2 мы будем обозначать: ρ(F1; F2).
Из вышесказанного следует, что если ρ(F1; F2) = d и фигуры не имеют общих точек (рис. 129), то существуют такая точка A1 фигуры F1 и такая точка A2 фигуры F2, что | A1A2| = d, а для любых других точек M первой фигуры и точек N второй фигуры | MN | ⩾ d.
Рассмотрим расстояние между двумя фигурами на примере двух сфер радиусов R1 и R2 с центрами соответственно O1 и O2.
Если | O1O2 | > R1 + R2, то сферы не имеют общих точек. Пусть A — точка пересечения первой сферы с отрезком O1O2, B — точка пересечения второй сферы с этим же отрезком (рис. 130). Тогда для любых точек M первой сферы и точек N второй сферы справедливо | MN | ⩾ | A B | и, таким образом, расстояние между сферами равно длине отрезка A B и равно | O1O2 | – (R1 + R2).
|
|
|
|
|

Рис. 131

Рис. 132

Рис. 133
Если расстояние O1O2 между центрами сфер равно сумме радиусов, то сферы касаются друг друга внешним образом (рис. 131).
Если расстояние O1O2 равно модулю разности радиусов, но не равно нулю, то сферы касаются друг друга внутренним образом (рис. 132).
Если же расстояние между центрами больше модуля разности радиусов, но меньше их суммы, то сферы пересекаются по окружности (рис. 133). Во всех этих случаях расстояние между сферами равно нулю.
Если расстояние между центрами сфер меньше модуля разности радиусов, но не равно нулю, то сфера меньшего радиуса находится целиком внутри шара сферы большего радиуса, и расстоянием между этими сферами является длина отрезка AB прямой центров сфер (рис. 134). Это расстояние равно | R1 – R2 | – | O1O2|.
Если же центры сфер совпадают, а их радиусы не равны, то расстояние между этими сферами равно | R1 – R2|, причём таких точек A и B, что | AB | = | R1 – R2 | бесконечно много (рис. 135).

Рис. 134

Рис. 135
Наконец, если центры сфер совпадают, а их радиусы равны, то совпадают и сферы, следовательно, расстояние между данными сферами равно нулю.
Как видите, мы провели небольшое исследование на тему «Расстояния между двумя сферами в пространстве». Попробуйте провести аналогичное исследование о расстояниях между:
плоскостью и сферой (что сравнительно легко);
кубом и сферой с центром на прямой, содержащей диагональ куба, и радиусом, равным ребру куба (что значительно сложнее).
Поговорим теперь о расстоянии между прямой и плоскостью.
Если прямая лежит в плоскости или её пересекает, то расстояние между прямой и плоскостью равно нулю (рис. 136).
Если прямая параллельна плоскости, то, как мы отмечали в предыдущем параграфе, расстояния от любой точки прямой до плоскости равны между собой и равны длине отрезка перпендикуляра, опущенного из любой точки прямой на эту плоскость (см. рис. 120). Следовательно, расстояние между плоскостью и параллельной ей прямой равно расстоянию от любой точки этой прямой до данной плоскости.
Аналогично, расстояние между двумя параллельными плоскостями также равно длине отрезка их общего перпендикуляра (см. рис. 121).
Интересным является следующее свойство расстояний между двумя фигурами: если расстояние между фигурами F1 и F2 равно d (ρ(F1; F2) = d), а расстояние между фигурами Q1 и Q2, принадлежащими соответственно фигурам F1 и F2 (рис. 137), равно d1 (ρ(Q1; Q2) = d1), то d ⩽ d1. Это утверждение легко доказывается методом от противного.

Рис. 136

Рис. 137

Рис. 138
Теперь рассмотрим две параллельные плоскости α и β, расстояние между которыми равно h и в которых лежат соответственно прямые a и b.

Рис. 139
Если прямые a и b параллельны, то расстояние между ними либо равно h (если перпендикуляр, опущенный из точки A прямой a на плоскость β, пересечёт прямую b (рис. 138)), либо равно  (если этот перпендикуляр пересечёт плоскость β в некоторой точке K, не принадлежащей прямой b, а удалённой от неё на расстояние m (рис. 139)).
(если этот перпендикуляр пересечёт плоскость β в некоторой точке K, не принадлежащей прямой b, а удалённой от неё на расстояние m (рис. 139)).

Рис. 140
Если прямые a и b скрещиваются, то опустим из точки A прямой a перпендикуляр AK на плоскость β и через пересекающиеся прямые a и AK проведём плоскость γ, которая будет перпендикулярна каждой из двух данных параллельных плоскостей (по признаку перпендикулярности двух плоскостей). Плоскость γ пересечёт плоскость β по некоторой прямой KM (рис. 140), параллельной прямой a и пересекающей (почему?) прямую b в некоторой точке P (которая может совпасть с K). Расстояние от точки P, принадлежащей прямой b, до прямой a равно h и равно расстоянию между скрещивающимися прямыми a и b, которое, в свою очередь, равно длине их общего перпендикуляра PT, проведённого из точки P на прямую a (T ∈ a).
Пусть a и b — две скрещивающиеся прямые. Проведём через прямую a и прямую b соответственно параллельные друг другу плоскости α и β. Мы получим уже знакомую нам ситуацию, а расстояние между прямыми a и b будет равно, как было показано, расстоянию между параллельными плоскостями α и β. Если же мы хотим найти на прямых a и b такие точки P и T, чтобы длина отрезка PT была равна расстоянию между этими прямыми, то нам необходимо построить «общий перпендикуляр» двух скрещивающихся прямых. Это всегда можно сделать способом, указанным выше.
В некоторых случах для нахождения расстояния между скрещивающимися прямыми удобно использовать метод ортогонального проектирования, состоящий в следующем. Пусть a и b — скрещивающиеся прямые (рис. 141). Построим плоскость α, перпендикулярную прямой a, и спроектируем на плоскость α прямую b. Пусть эта проекция есть прямая b1. Очевидно, что плоскость β, проходящая через прямые b и b1, параллельна прямой a. Следовательно, если A — точка пересечения прямой a с плоскостью α, то расстояние ρ(a; b) = ρ(A; b1).
ЗадаЧа 1. Дана треугольная пирамида ABCD (рис. 142), все рёбра которой равны a. Найти расстояние между прямыми BC и DM, где M — середина ребра AB.
Решение. Пусть L — середина отрезка BC. Тогда плоскость ALD ⊥ BС.
Спроектируем прямую DM на плоскость ALD. Для этого из точки M опустим перпендикуляр MH на AL. Тогда MH ‖ BC и, значит, MH ⊥ (ALD), а BC ‖ (MHD). Следовательно, искомое расстояние ρ(BC; DM) есть высота ⧌ DHL, опущенная из его вершины L.

Рис. 141

Рис. 142
Рассмотрим треугольник ADL. Он равнобедренный, поскольку AL = DL =  , а его основание AD = a. Заметим, что DH — медиана ⧌ ADL, поскольку M — середина AB, а MH ‖ BC.
, а его основание AD = a. Заметим, что DH — медиана ⧌ ADL, поскольку M — середина AB, а MH ‖ BC.
Пусть LP — искомая высота ⧌ DHL, а DT — высота ⧌ DHL, опущенная из вершины D. Тогда справедливо равенство  =
=  ⇒ LP =
⇒ LP =  .
.
Медиану DH найдём из соотношения между сторонами и медианой ⧌ ADL:
AL2 + 4DH2 = 2(DL2 + AD2),
откуда DH =  .
.
Отрезок DT найдём из соотношения между сторонами и высотами треугольника ADL: AL•DT = AD•LK, где LK — высота ⧌ ADL. Отсюда получаем:
DT =  =
=  = a
= a .
.
Теперь окончательно находим
LP =  =
=  =
=  .
.
Ответ: ρ(BC; DM) =  .
.
ЗадаЧа 2. Рассмотреть рисунок 143 и убедиться, что расстояние ρ(DB1; D1C) = OH =  .
.

Рис. 143
Заметим: чтобы найти расстояние между двумя скрещивающимися прямыми, совершенно не обязательно строить их общий перпендикуляр. Удобно пользоваться следующими вытекающими из вышесказанного утверждениями: расстояние между двумя скрещивающимися прямыми равно расстоянию от любой точки одной из них до плоскости, проходящей через другую прямую параллельно первой прямой, а также равно расстоянию между параллельными плоскостями, проведёнными через две данные скрещивающиеся прямые.
Шаром
называется тело, состоящее из всех точек пространства, которые находятся на расстоянии,
не больше данного от данной точки. Эта точка называется центром
шара, а данное расстояние радиусом шара.

Граница шара называется шаровою поверхностью, или сферою. Таким образом,
точками сферы будут все точки шара, которые удалены от центра на расстоянии, которое
равно радиусу. Любой отрезок, который соединяет центр шара с точкою шаровой
поверхностью, также называется радиусом.
Шаровой поверхностью или сферой называется геометрическое
место точек пространства, равноудалённых от одной точки, которая называется
центром сферы.

Радиусом сферы называется отрезок прямой, который соединяет центр сферы
с любой её точкой, например
АО
= ОВ = R.
Хордой сферы называется отрезок прямой, который соединяет две её любых
точки.
Диаметром сферы называется хорда, которая проходит через её центр, например АС или ВD. Концы любого диаметра называют диаметрально противоположными
точками сферы.
Шаром
называется тело, ограниченное сферой.
Сферу можно получить вращением полукруга вокруг диаметра.
Сечение сферы и шара плоскостью.
Сечением сферы любой плоскостью будет окружность.
Сечением шара любой плоскостью будет круг.
Круг, полученный пересечением шара плоскостью, которая проходит через
центр, называется большим кругом шара, а круг,
полученный сечением шара плоскостью, которая не проходит через центр, называется
малым кругом шара.
Сечения равноудалённые от центра шара, равны между собой.

Из двух сечений, не одинаково удалённых от центра шара, больший радиус имеет
то, которое лежит ближе к центру.
Любая плоскость, которая проходит через центр шара, делит
его поверхность на две симметричные и равные части.
Через две точки сферы, которые не лежат на концах одного
диаметра, можно провести окружность большого круга, и до того ж только одну.
Окружности двух больших кругов при пересечении делятся
пополам.
Плоскость, касательная к шару.
Касательной плоскостью к шаровой поверхности называется
плоскость, имеющая с этой поверхностью только одну общую точку.

Плоскость, проходящая через точку А шаровой поверхности
и перпендикулярная радиусу, проведенному в точку А, называется касательной
плоскостью. Точка А называется точкой касания.
Касательная плоскость имеет с шаром только одну общую точку – точку касания.
Прямая в касательной плоскости шара, которая проходит через точку касания, называется
касательной шара в этой точке. Так как касательная
плоскость имеет с шаром только одну общую точку, то касательная прямая тоже имеет
с шаром только одну общую точку – точку касания.
Плоскость, перпендикулярная радиусу шаровой поверхности в
его конце, лежащем на этой поверхности, есть касательная плоскость.
Обратно:
Касательная плоскость перпендикулярна радиусу, проведённому
в точку касания.
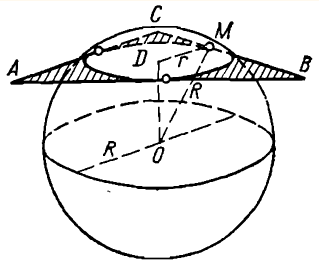
ЗАДАЧА:
Через середину радиуса шара
проведена перпендикулярная радиусу плоскость. Как относится площадь полученного
сечения к площади большого круга ?
РЕШЕНИЕ:
Начертим чертёж.
Если радиус шара
R, то
радиус круга в сечении будет:

Отношение площади этого круга к площади большего
круга равно:

Поверхность шара и его частей.
Часть шаровой поверхности, которая отделяется от шара какой-нибудь плоскостью,
называется сегментною поверхностью.

Окружность пересечения СD плоскости с шаровой
поверхностью называется основанием,
а отрезок АВ = Н радиуса, перпендикулярного к плоскости
сечения, – высотой сегментной поверхности.
Часть шаровой поверхности, заключённая между двумя параллельными секущими
плоскостями, называется шаровым поясом.

Окружности сечения С1D1 и С2D2
называются основаниями шарового пояса,
а расстояние АВ
= Н между параллельными плоскостями – высотой пояса.
Поверхность шарового сегмента, пояса и шара.
В качестве величины поверхности шарового сегмента, пояса и шара, образуемого
вращением какой-нибудь части полуокружности или всей полуокружности вокруг диаметра,
принимают предел, к которому стремится поверхность, образуемая вращением вокруг
того же диаметра правильной вписанной ломаной линии в соответствующую часть
дуги окружности при неограниченном увеличении числа её звеньев.

Сегментная поверхность равна произведению её высоты на длину
окружности большого круга:

где R – радиус большого круга шара, а Н –
высота сегментной поверхности.
ЗАДАЧА:
Определите вес котла, поверхность которого
состоит из цилиндрической поверхности и сферической поверхности двух шаровых сегментов.
Известно, что радиус
цилиндрической поверхности r = 60 см,
длина образующей этой поверхности h = 2 м,
высота сегмента h1 = 20 см.
Котёл сделан из листового железа, вес 1 м2 которого равен 12
кг.
РЕШЕНИЕ:
Для нахождения площади поверхности
котла нужно найти площади поверхностей двух сферических сегментов и площадь
поверхности цилиндрической части котла.
Определим радиус сферы, частями
которой служат поверхности сегментов, для чего построим центр сферы –
точку О.
Из прямоугольного
треугольника MON имеем:
R2 = r2 + (R – h1)2,
или
R2 = r2 + R2 – 2Rh1 + (h1)2, откуда

Подставим в это
равенство вместо r и h1 данные значения, получим:

Площадь поверхности S всего котла будет:
S
= 2πrh + 4πRh1 = 2π(rh
+ 2Rh1).
Заменив в этом равенстве R, r, h и h1 их данными значениями, получим:
S = 6,28(0,6 ∙ 2
+ 2 ∙ 1 ∙ 0,2) ≈
10,05 м2.
Умножив вес
1 м2 листового железа
на число квадратных метров прверхности котла, получаем его вес:
Р = 12 ∙
10,05 = 120,6 ≈ 121 (кг).
ОТВЕТ: 121 кг
Поверхность шарового пояса равна произведению высоты
пояса на длину окружности большого круга:

где R – радиус окружности большого круга, а Н –
высота пояса.
Площадь поверхности шара.
Пусть дана полуокружность АF с центром в
точке О.
При вращении этой полуокружности вокруг диаметра АF мы получим поверхность шара (сферу с центром
в точке О и диаметром АF).
Дадим следующее определение площади поверхности шара:
За площадь поверхности шара, полученного вращением
полукруга вокруг диаметра, принимается предел, к которому стремится
поверхность, получаемая вращением около того же диаметра правильной вписанной в
полуокружность ломаной линии при неограниченном увеличении числа её звеньев.
Формула поверхности шара такова:

где R – радиус шара.
Поверхности шаров относятся, как квадраты их радиусов или
диаметров.
Шаровой сегмент, слой и сектор.
Шаровым сегментом называется тело, отсекаемое от шара плоскостью.
Шаровым слоем называется тело, отсекаемое от шара двумя секущими параллельными
плоскостями.
Шаровым сектором называется тело, полученное вращением кругового сектора вокруг
оси, лежащей в его плоскости, проходящей через его центр и не пересекающей
сектора.
Если ось вращения совпадает с радиусом, ограничивающим круговой сектор АОС,
то полученный в результате вращения шаровой сектор называют простым, а если ось
вращения не совпадает с радиусом, ограничивающим круговой сектор СОD,
то шаровой сектор называют полым.

Линией пересечения двух сфер будет окружность.

Любая диаметральная плоскость шара
будет его плоскостью симметрии. Центр шара будет его центром симметрии.
ЗАДАЧА:
Стороны треугольника равны
15, 14 и 13
см.
Найти расстояние от плоскости треугольника до центра шара, касающегося сторон
треугольника, если радиус шара равен 5
см.
РЕШЕНИЕ:
Дан шар О радиуса
R = 5 см и ∆ АВС,
стороны которого касаются поверхность шара и равны
АВ = 15 см,
ВС = 14 см
АС
= 13 см.
Найти расстояние от центра шара до плоскости ∆ АВС.
Плоскость
∆ АВС пересекает шар О по кругу, вписанному в данный треугольник.
Основание перпендикуляра ОD,
опущенного из центра шара О на плоскость ∆ АВС, попадает в центр
круга D.
Пусть DM =
r – радиус круга D, проведений в точку касания стороны СВ поверхности шара. Тогда из прямоугольного ∆ ODM находим

Радиус шара
R = ОМ = 5
см.
Радиус круга D,
вписанного в данный треугольник, найдём по формуле

где S –
площадь, а р –
полупериметр треугольника:

Подставляя найденные значения в
формулу для ОD,
находим необходимое расстояние

ОТВЕТ: 3 см.
ЗАДАЧА:
Радиусы двух сфер равны 10
см и
17 см, а длина линии их пересечении – 16π
см. Найдите расстояние между центрами сфер.
РЕШЕНИЕ:
Дано:
ОА = 10 см,
О1А = 17 см,
Спер = 16π см.
Найти: ОО1.

16π = 2πr;
r = 8 см;
О2А = 8 см.
∆ОАО2 – прямоугольный,

∆О1АО2 – прямоугольной,

ОО1 = ОО2 + О1О2 =
6 + 15 = 21 (см).
ОТВЕТ: 21 см.
Применение тригонометрических функций для решения
стереометрических задач.
ЗАДАЧА:
Высота шарового сегмента
h. Дуга в осевом сечении равна α. Найти
площадь сферической поверхности сегмента.
РЕШЕНИЕ:
По условию задачи CD = h, ∠ AOB = α. Найти
площадь сферической поверхности сегмента (на рисунку дано его
сечение).

Площадь сферической поверхности
сегмента
S = 2πRh,
где R –
радиус сферической поверхности,
а h –
высота сегмента.
Рассмотрим ∆ ODB, в котором
OD
= R – h, OB = R.
Из этого треугольника определим

или

откуда

Подставив эти значения в
формулу для S, после очевидных преобразований получим окончательный ответ:

ОТВЕТ:

Задания к уроку 16
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Прямые и плоскости в пространстве
- Урок 2. Прямая призма
- Урок 3. Наклонная призма
- Урок 4. Правильная призма
- Урок 5. Параллелепипед
- Урок 6. Прямругольный параллелепипед
- Урок 7. Куб
- Урок 8. Пирамида
- Урок 9. Правильная пирамида
- Урок 10. Усечённая пирамида
- Урок 11. Цилиндр
- Урок 12. Вписанная и описанная призмы
- Урок 13. Конус
- Урок 14. Усечённый конус
- Урок 15. Вписанная и описанная пирамиды
- Урок 17. Комбинация тел
Если две сферы имеют только одну общую точку, то они касаются друг друга.
Центры двух сфер и точка касания лежат на одной прямой.
Сферы могут касаться внутренним и внешним образом.
Две сферы с центрами (A) и (B) касаются друг друга внешним образом.
Центры сфер (A) и (B), а также точка касания сфер (C) лежат на одной прямой.
Две сферы с центрами (E) и (F) касаются друг друга внутренним образом.
Центры (E) и (F), а также точка касания сфер (S) лежат на одной прямой.
Две сферы с центрами (W) и (T) радиусами (3ед) и (2ед) касаются внешним образом.
Определите расстояние между центрами сфер.
Обозначим точку (A) касания сфер. Тогда точки (W,A) и (T) лежат на одной прямой.
Искомое расстояние найдём так: (WT=WA+AT=3+2=5(ед)).
Две сферы с центрами (A) и (B) радиусами (3ед) и (1ед) касаются внутренним образом.
Определите расстояние между центрами сфер.
Обозначим точку (S) касания сфер. Тогда точки (A,B) и (S) лежат на одной прямой.
Искомое расстояние найдём так: (AB=AS-BS=3-1=2(ед)).






