Как найти расстояние между центрами вписанной окружности

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac<1><2>(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Центр окружности вписанной в треугольник равноудален от всех сторон.

Точка касания — это точка, в которой соприкасается
окружность и любая из сторон треугольника.

От центра вписанной окружности можно провести
перпендикуляры к любой точке касания.

Вписанная в треугольник окружность делит стороны
треугольника на 3 пары равных отрезков.

Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.

В четырехугольник

1. Не во всякий четырехугольник можно вписать окружность.
2. Если у четырехугольника суммы длин его противолежащих
   сторон равны, то окружность, может быть, вписана (Теорема Пито).
3. Центр вписанной окружности и середины двух
   диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
4. Точка пересечения биссектрис — это центр вписанной окружности.
5. Точка касания — это точка, в которой соприкасается
   окружность и любая из сторон четырехугольника.
6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac<1><2>(a+b+c+d)cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Точка касания вписанной окружности, которая лежит на любой из сторон,
равноудалены от этой конца и начала этой стороны, то есть от его вершин.

Примеры вписанной окружности

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Вневписанные окружности

Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.

Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).

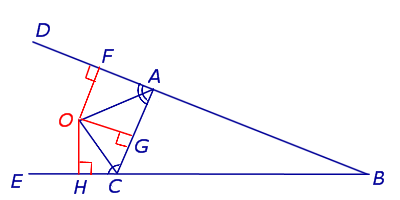
Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:

Следовательно, справедливо равенство

Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства

откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .

Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).

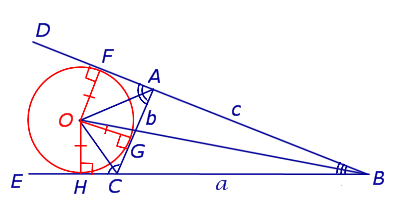
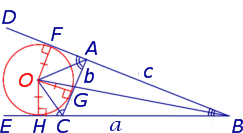
Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.

Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом r_b .

Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.

Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство

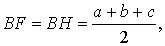
где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:

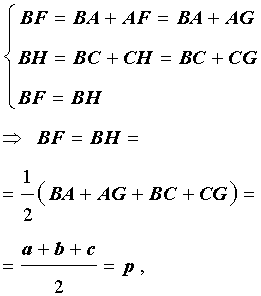
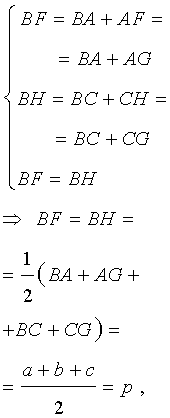
где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.

Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле

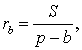
где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .

Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства

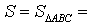
Следовательно, справедливо равенство

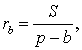
что и требовалось доказать.

Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:

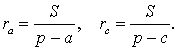
Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:

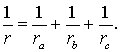
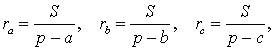
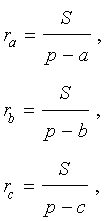
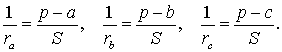
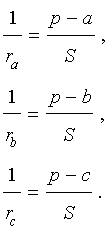
Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности

,

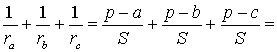
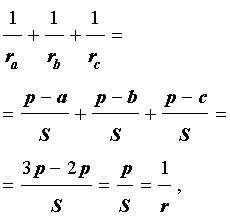
что и требовалось доказать.

Теорема 5 . Площадь треугольника можно вычислить по формуле

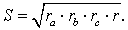
Доказательство . Перемножим формулы

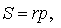
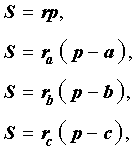
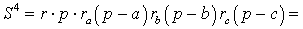
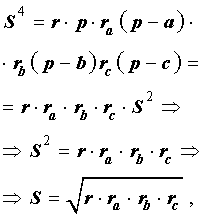
что и требовалось доказать.

Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:

Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим

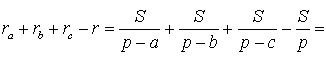
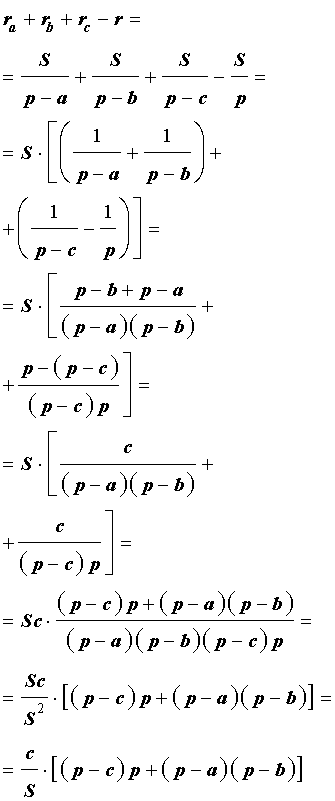
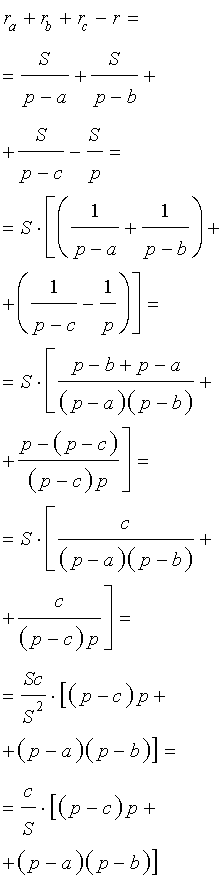
Преобразуем выражение, стоящее в квадратной скобке:

МАТЕМАТИКА

Формула Эйлера

Мы знаем, что в каждый треугольник можно вписать окружность и можно описать около него окружность. Ясно, что вписанная окружность лежит внутри описанной, поскольку вписанная окружность лежит внутри треугольника, а сам треугольник лежит внутри описанной окружности.

Радиусы вписанной и описанной окружностей и расстояние между их центрами всегда связаны между собой определенным соотношением. Справедлива следующая теорема.

Теорема. В треугольнике радиус R описанной окружности и радиус r вписанной окружности связаны с расстоянием d между их центрами соотношением

В частности, если d=0 (центры окружностей совпадают), то .

Эта формула называется формулой Эйлера.

Доказательство.

Рассмотрим треугольник АВС, у которого точка О – центр описанной окружности, а точка – центр вписанной окружности. Будем считать пока, что (рисунок 1). Проведем биссектрисы и углов А и В. Они пересекаются с описанной окружностью в некоторых точках и . Пусть P и Q – точки пересечения прямой с описанной окружностью. По теореме о произведении отрезков пересекающихся хорд , или

Заметим теперь, что поскольку и – биссектрисы углов А и В, то , а . Следовательно,

Поэтому треугольник равнобедренный: . Таким образом, соотношение можно переписать так:

Проведем теперь диаметр описанной окружности и обозначим буквой К точку касания вписанной окружности и стороны АВ. Треугольники и подобны (они прямоугольные и имеют равные углы А и ), поэтому

Откуда . Подставив это выражение, получим

В случае d=0 (рисунок 2) каждая из сторон треугольника АВС равна , а значит, этот треугольник равносторонний.

Поэтому , , и, следовательно, . Теорема доказана.

Замечание. В ходе доказательства теоремы мы установили весьма полезный факт:

Точка пересечения продолжения биссектрисы, проведенной из одной из вершин треугольника, с описанной окружностью равноудалена от двух других вершин и центра вписанной окружности.

Теорема Птолемея

В любой треугольник можно вписать окружность и около него можно описать окружность. Однако для других многоугольников это не так. Мы знаем, например, что в четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны. Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна . Эти утверждения очень похожи друг на друга. Используя скобки, их можно объединить в одно:

Описанная (вписанная) окружность для данного четырехугольника существует тогда и только тогда, когда суммы его противоположных углов (сторон) равны.

Существуют и другие характеристические свойства вписанных и описанных четырехугольников. Наиболее известное основано на теореме Птолемея.

Теорема (Птолемея). Произведение диагоналей вписанного в окружность четырехугольника равно сумме произведений противоположных сторон.

Доказательство.

Рассмотрим вписанный четырехугольник АВСD. Для удобства введем обозначение: АВ = а, ВС = b, CD = c, DA = d, AC = m, BD = n (рисунок 3) и докажем, что .

На диагонали АС возьмем такую точку М, что . Треугольники АВМ и DBC подобны по двум углам ( по построению, а углы ВАМ и BDC равны как вписанные и опирающиеся на одну и ту же дугу). Следовательно, , откуда , или (1).

Далее, треугольники МВС и ADB также подобны, так как , а углы ВСМ и BDA равны как вписанные и опирающиеся на одну и ту же дугу. Поэтому , , откуда , или (2).

Сложив равенства (1) и (2), получим , или , что и требовалось доказать.

Оказывается, что рассмотренное свойство вписанного четырехугольника является характеристическим, то есть верно и обратное утверждение.

Если в выпуклом четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон, то около него можно описать окружность.

Рекомендую далее изучить тему «Вневписанные окружности».

Спасибо, что поделились статьей в социальных сетях

Источник: Атанасян Л.С. Геометрия. Дополнительные главы к учебнику 8 кл.: Учебное пособие для учащихся школ и классов с углубленным изучением математики.

[spoiler title=”источники:”]

http://www.resolventa.ru/uslugi/uslugischoolsev.htm

Формула Эйлера. Теорема Птолемея

[/spoiler]

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 августа 2022 года; проверки требуют 2 правки.

Формула Эйлера — теорема планиметрии, связывает расстояние между центрами вписанной и описанной окружностей и их радиусами.

Теорема названа в честь Леонарда Эйлера, который опубликовал её в 1765 году.^[1]
Однако тот же результат был получен ранее Уильямом Чапплом^[en] в 1746 году.^[2]

Формулировка[править | править код]

Расстояние между центрами вписанной и описанной окружностей треугольника может быть определено по формуле

где  — радиус описанной,  — радиус вписанной окружности.

В 1969 году Георгий Александров дал развернутую формулу:

где  — стороны треугольника.

Замечания[править | править код]

• Приведённую формулу можно переписать следующим образом

  .

или

где  — стороны треугольника.

• Для сферического треугольника отношение радиуса описанной окружности к радиусу вписанной может быть меньше 2. Более того, для любого числа между 1 и 2 существует правильный сферический треугольник с отношением радиуса описанной к радиусу вписанной окружности, равным этому числу.

Доказательство[править | править код]

Пусть  — центр описанной окружности треугольника , а  — центр вписанной окружности.
Если луч пересекает описанную окружность в точке , то является средней точкой дуги .
Проведём луч и обозначим его точку пересечения с описанной окружностью как .
Тогда будет диаметром описанной окружности. Из точки опустим перпендикуляр на Тогда Запишем формулу Эйлера немного в другом виде

Можно заметить, что слева стоит степень точки относительно описанной окружности (если быть точным, то минус степень точки).
То есть, достаточно доказать равенство .
По лемме о трезубце значит, достаточно доказать, что .
Теперь заметим, что и то есть, требуемое равенство можно переписать в виде Перепишем его ещё немного: .
Это равенство следует из подобия треугольников и .
В самом деле, углы и у этих треугольников прямые, а углы и равны, потому что оба опираются на дугу (более того, отношение равно синусу угла ).

Вариации и обобщения[править | править код]

Для центра вневписанной окружности[править | править код]

Для вневписанных окружностей уравнение выглядит похоже:

где  — радиус одной из вневписанных окружностей, а  — расстояние от центра описанной окружности до центра этой вневписанной окружности^[4][5][6].

Для многоугольников[править | править код]

или эквивалентно,

• Это соотношение называют Теоремой Фусса^[en]. Оно получено Николаем Ивановичем Фуссом^[7] в 1792 году.

• Теорема Кэли о цепи Понселе обобщает теорему Эйлера на вписанно-описанные -угольники^[1].

См. также[править | править код]

• Поризм Понселе

Примечания[править | править код]

Ссылки[править | править код]

• Weisstein, Eric W. Euler Triangle Formula (англ.) на сайте Wolfram MathWorld.

Формулы для центров вневписанных окружностей треугольников

Речь пойдет о формулах для определения расстояний между
центрами вписанной и вневписанной окружностей произвольного треугольника.

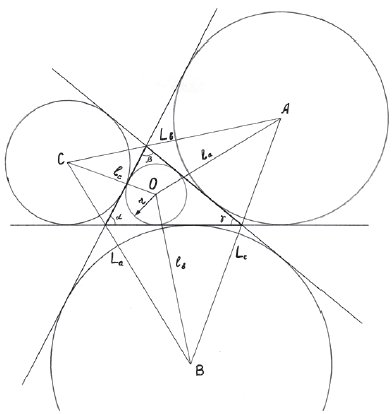
Пусть α,
β,
γ — внутренние углы
треугольника, а r — радиус вписанной в него окружности. Обозначим
расстояния между центром O вписанной окружности и центрами A, B,
C вневписанных окружностей соответственно:

OA – l_a, OB – l_b,
OC – l_c;

аналогично — расстояния между центрами вневписанных
окружностей:

BC – L_a, CA – L_b,
AB – L_c.

Тогда имеют место шесть следующих легко запоминающихся
соотношений:

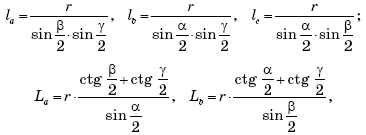
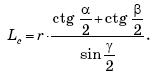
В случае равностороннего треугольника формулы предельно
упрощаются:

l_a = l_b = l_c
= l = 4r;

L_a = L_b = L_c = L =

Формулам можно придать другой вид, если учесть, что:

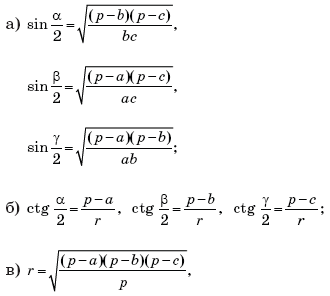
где a, b, c — стороны треугольника,

 — его полупериметр.

После соответствующих подстановок и следующих за ними
сокращений окончательно получим:

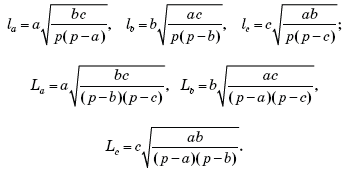
Для равностороннего треугольника

Сарбаш Р.

АДМИНИСТРАЦИЯ
ГОРОДА НИЖНЕГО НОВГОРОДА

Департамент
образования

Муниципальное бюджетное
общеобразовательное учреждение

“Школа
№ 129”

Ул.
Лескова д. 66 а, г. Нижний Новгород, 603142. Тел. 256-00-56, 256-01-11 Е-mail:
schooln129@inbox.ru

Научное общество
учащихся

Формула Эйлера. Расстояние между центрами
вписанной и описанной окружности любого треугольника.

                                                          
Подготовил ученик 10 ‘a’
класса:

Горький
Данила Максимович

Научный
руководитель:

Сударева
Евгения Аркадьевна

Нижний
Новгород 2018

Содержание
                                  стр

Введение.                                                                                                                   
3

Глава 1. Формула Эйлера. Расстояние между центрами
вписанной                      

 и описанной окружности любого треугольника .                                                   

1.1.
Основоположник  теории                                                                                 
 1.2. Формулировка и
определения                                                                                  4

1.3 .Пример
механизма решения задачи                                                                  9

Глава 2. Решение
задач                                                                                         
10

Заключение.                                                                                                             16

Список
литературы                                                                                               
17

Введение

Цель работы:
познакомиться с творческой биографией Леонарда Эйлера
и научиться решать геометрические  задачи повышенного уровня сложности, используя
теорему Эйлера.

Задачи работы:

1)    Сделать
литературный обзор теоремы Эйлера;

2)    Рассмотреть
окружность и прямую Эйлера;

3)    Решить
задачи на теорему Эйлера.

Актуальность темы исследования. Есть несколько имён в истории математических наук, которые часто
встречаются в настольных руководствах математиков, механиков и физиков и
которые, хотя бы понаслышке, известны каждому образованному человеку. К числу
их принадлежит имя петербургского академика Леонарда Эйлера, крупнейшего
учёного восемнадцатого века, который в области математики справедливо может
быть назван «веком Эйлера». Эйлер принадлежит к числу гениев, чьё  творчество
стало достоянием всего  человечества. До сих пор школьники всех  стран изучают
тригонометрию и логарифмы  в том виде, какой придал им Эйлер.  Гений Эйлера
охватывает все области математики. Великий Гаусс указывал, что изучение трудов
Эйлера всегда будет лучшим средством для познания математики. «Он общий
учитель», – говорил о нем другой великий ученый Лаплас.

    Отзывы этих ученых об
Эйлере побудили меня провести исследование жизни и творчества этого
замечательного ученого и рассмотреть избранные задачи Эйлера, имеющие отношение
к геометрии.

Я выдвинул гипотезу, что существует общий механизм решения
геометрических задач, используя теорему Эйлера и окружность Эйлера ,
позволяющий значительно упрощать решение геометрических задач.

     В первой главе рассмотрена биография великого Эйлера, его
заслуги не только в геометрии, но и в ряде точных прикладных наук.  Так
же я рассмотрел прямую и окружность Эйлера, свойства многоугольников связанные
с окружности, свойства прямой Эйлера  и свойства окружности 9 точек.

     Во второй главе мною решены       
задач , используя прямую Эйлера и теорему Эйлера.

     
В заключении я сделал вывод, что существует общий
механизм решения геометрических задач, используя теорему Эйлера и окружность Эйлера
, позволяющий значительно упрощать решение геометрических задач.

Глава
1

Формула Эйлера. Расстояние между центрами
вписанной

и описанной окружности любого треугольника
(Литературный обзор)

               1.1. Основоположник
 теории

Изучив литературные источники, я узнал много любопытных фактов о
жизни и творчестве Леонарда Эйлера. Интересный очерк об Эйлере содержит книга
В.К. Смышляева «О математике и математиках. В нем не содержится сложных формул,
математических выкладок. Очерк содержит много фактов не только о жизни ученого,
но и о его творческой деятельности. Из статьи Википедии «Эйлер, Леонард» я
узнал не только подробности биографии этого замечательного, но и о огромном
количестве задач, решённых Эйлером, причем не только математических. Меня
заинтересовало, что в элементарной геометрии Эйлер
обнаружил несколько фактов, не замеченных даже Евклидом.
Информацию о геометрических задачах Эйлера я нашел в
учебниках геометрии, авторами которых являются Смирнова И.М. и Смирнов В.А.

Ле Леонард Эйлер (нем. Leonhard Euler; 15 апреля 1707, Базель, Швейцария — 7 (18) сентября 1783, Санкт-Петербург, Российская империя) — швейцарский, немецкий и
российский математик и механик, внёсший фундаментальный вклад в
развитие этих наук (а также физики, астрономии и ряда прикладных наук). Эйлер — автор более чем 850
работ (включая два десятка фундаментальных монографий) по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и другим областям. Он глубоко изучал медицину, химию, ботанику, воздухоплавание, теорию музыки, множество европейских и древних языков.
Академик Петербургской, Берлинской, Туринской, Лиссабонской и Базельской академий наук,
иностранный член Парижской академии наук.

Почти полжизни
провёл в России, где внёс существенный вклад в становление российской науки.
В 1726 году он был приглашён работать
в Санкт-Петербург, куда переехал годом позже. С 1726 по 1741, а также с 1766 года был академиком Петербургской академии наук (будучи сначала адъюнктом, а с 1731 года — профессором); в 1741—1766 годах работал в Берлине (оставаясь одновременно
почётным членом Петербургской академии). Уже через год пребывания в России он
хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на
русском. Первые русские академики-математики (С. К. Котельников) и астрономы (С. Я. Румовский) были учениками Эйлера. Некоторые из его
потомков до сих пор живут в России.

Он
впервые сформировал теорию о расстояние между
центрами вписанной и описанной окружности любого треугольника.

Формула Эйлера — теорема планиметрии, связывает расстояние
между центрами вписанной и описанной окружностей
и их радиусами.

Эта теорема названа в
честь Леонарда Эйлера.

     
Леонард Эйлер родился в швейцарском городе Базеле в семье пастора Пауля Эйлера.
Первоначальное образование он получил у отца, образованного человека, который
интересовался многими вопросами, в частности и математикой, её он изучал под
руководством известного математика и друга Якоба Бернулли. Пауль Эйлер,
проникнутый методом и духом своего учителя, преподавал математику своему сыну.
Однако он хотел воспитать из него священника и никак не предполагал, что
математика станет всепоглощающей страстью его сына; на свои уроки он смотрел
как на умственное развлечение для обучаемого. Следуя своему плану, он отправил
Леонарда в университет. Так тринадцатилетний Эйлер стал студентом младшего
философского факультета Базельского университета.

Занятия
Эйлера шли так успешно, что через два года после поступления в университет ему
присваивают по философии степень «первые лавры», соответствующую степени
бакалавра, а в семнадцать лет за речь о сравнении философских воззрений Ньютона
и Декарта он получает учёную степень магистра искусств. Несмотря на упорные
занятия Леонарда математикой, отец долго не мог отказаться от мысли направить
сына по собственным стопам. Благочестивый и кроткий юноша, подчиняясь воле
отца, старательно изучал не только философию и богословие, но и восточные
языки, не порывая, однако, и с математикой. В 1726 году юноша окончил
университет. Отцу пришлось согласиться с желанием сына избрать специальностью
математику. Эйлер занялся поисками работы. В университете на кафедре её не
нашлось, так как жребий (не конкурс, а жребий в полном смысле) был для него не
счастливым.

В это
время в России подбирали сотрудников для только что открывшейся Петербургской
Академии наук. Друзья Эйлера – Николай и Даниил Бернулли охотно приняли в 1724
году приглашение переехать в русскую столицу.

По
вызову братьев Бернулли весной 1727 года Эйлер навсегда покидает Швейцарию. Северная
столица неласково встретила молодого швейцарца, не знающего ни одного русского
слова: в день приезда умерла царица Екатерина I, покровительница петровской Академии наук. С горечью пришлось
узнать и о смерти Николая Бернулли, не выдержавшего северного климата.

Руководство
академии, правильно оценив способности  молодого учёного, предоставило ему
возможность заняться только математическими науками.

С
самого начала пребывания в Петербурге Эйлер сумел сочетать теоретические
исследования с практической деятельностью, связанной с актуальными задачами,
стоящими перед русской наукой. Никогда при этом он не смотрел на свой переезд в
Россию как на временную гастроль. Он жил одной жизнью с академией, разделял её
интересы, откликался на задачи, которые ставила перед ним страна, ставшая ему
теперь второй родиной.

Эйлер
отличался феноменальной трудоспособностью, это был человек, одержимый
стремлением к труду, к творчеству. В 1735 году имел место поразительный факт,
подтверждающий такую характеристику, печальный по своим последствиям для
здоровья Эйлера. Академия однажды получила задание выполнить срочно
астрономическое вычисление, нужное для картографических целей. Для выполнения
его академики потребовали несколько месяцев, Эйлер же взялся выполнить задание
в кратчайший срок и, к всеобщему изумлению, справился, как говорят, за трое
суток. Но это Эйлеру не прошло даром, он заболел нервной горячкой, в результате
которой у него вытек правый глаз. Необычна была реакция Эйлера на потерю глаза.
Это несчастье вызвало у него лишь шутку: «Теперь я вдвое меньше буду
отвлекаться от занятий математикой».

Не всё
гладко было в Петербурге. Бирон-фаворит царицы Анны Иоановны – создал в
академии атмосферу невыносимую. Интриги, взаимное подсиживание, доносы
считались обычными средствами ведения дела. Как ни далёк был Эйлер от дворцовых
интриг и светских пересудов, но даже он не мог вытерпеть самоуправства и
грубостей курляндского герцога. Он был вынужден уехать в Берлин.

Но
русская академия продолжала считать его своим членом, высылая ему пособия, а он
– свои статьи в академические «Комментарии». Эйлер выполнял различные поручения
академии, закупал для неё приборы, книги. Сам он очень тосковал по Петербургу.
Там – молодость, там – лучшее, что он сделал. И он возвращается в родной Петербург,
чтобы уже никогда не выезжать из него.

До
самой смерти Эйлер трудился так же интенсивно, как и прежде. Этому не помешала
даже последовавшая на 67-м году жизни слепота второго глаза. Эйлер продолжал
работать слепым, диктуя свои труды ученикам или детям.

Вечером
18 сентября 1783 года, после вполне благополучного рабочего дня, во время игры
с внуком, Эйлер почувствовал себя плохо и с возгласом «Я умираю» потерял
сознание, а через несколько минут скончался, или, по красноречивому выражению
историка науки Кондорсэ, « Эйлер перестал жить и вычислять». Его похоронили на
Смоленском кладбище в Петербурге. Надпись на памятнике гласила: «Леонарду
Эйлеру — Петербургская Академия».

Перу
Эйлера принадлежит около девятисот работ. «Нет учёного, имя которого упоминалось
бы в учебной математической литературе столь же часто, как имя Эйлера.
Достаточно открыть 48-й том второго издания БСЭ на страницах 338-340, чтобы
найти сведения о двадцати формулах, уравнениях, интегралов и т. д., носящих имя
Эйлера. В учебниках для высшей школы их ещё больше, а многие введённые им в
обиход теоремы и методы давно перестали связывать с чьим-либо именем. Даже в
средней школе логарифмы и тригонометрию изучают до сих пор в значительной
степени «по Эйлеру», – писал академик Б. Н. Делонэ.

1.2. Формулировка и
определения

Замечательные точки и линии треугольника

К числу
замечательных точек в треугольнике относятся:

·       
точки пересечения биссектрис;

·       
точка пересечения серединных
перпендикуляров сторон;

·       
точка пересечения высот или их
продолжений;

·       
точка пересечения медиан.

Три биссектрисы
треугольника пересекаются в одной точке, являющейся центром вписанной
окружности (инцентром).

Серединные
перпендикуляры (медиатриссы) к сторонам треугольника пересекаются в одной
точке, являющейся центром описанной окружности.

Медианы
треугольника пересекаются в одной точке (центроиде треугольника) и делятся в
этой точке в отношении 2:1, считая от вершины.

Высоты
треугольника или их продолжения пересекаются в одной точке (ортоцентре
треугольника).

   Перечень
замечательных точек можно продолжить. Например, замечательной точкой является центр окружности девяти точек, так
называемой окружности Эйлера. Открытие окружности девяти точек
произошло в 1765году, тогда же Эйлер доказал теорему о свойствах замечательных
точек.

1)Определение: Окружностью называется множество
точек плоскости, равноудалённых на положительное расстояние от данной точки
(центра окружности), лежащей в этой же плоскости. Радиусом окружности
называется отрезок, соединяющий центр окружности с любой точкой окружности.
Хордой окружности называется отрезок, соединяющий две точки окружности.
Диаметром окружности называется хорда, проходящая через центр окружности.
Прямая, имеющая одну общую точку с окружностью, называется касательной к
окружности.

К числу
замечательных точек в треугольнике относятся:

·       
точки пересечения биссектрис;

·       
точка пересечения серединных
перпендикуляров сторон;

·       
точка пересечения высот или их
продолжений;

·       
точка пересечения медиан.

Три биссектрисы
треугольника пересекаются в одной точке, являющейся центром вписанной
окружности (инцентром).

Серединные
перпендикуляры (медиатриссы) к сторонам треугольника пересекаются в одной
точке, являющейся центром описанной окружности.

Медианы
треугольника пересекаются в одной точке (центроиде треугольника) и делятся в
этой точке в отношении 2:1, считая от вершины.

Высоты
треугольника или их продолжения пересекаются в одной точке (ортоцентре
треугольника).

   Перечень
замечательных точек можно продолжить. Например, замечательной точкой является центр окружности девяти точек, так
называемой окружности Эйлера. Открытие окружности девяти точек
произошло в 1765году, тогда же Эйлер доказал теорему о свойствах замечательных
точек.

Пусть в
треугольнике АВС:  Н – точка пересечения высот треугольника; точки А₁,
В₁, С₁ обозначают основания высот; А₂, В₂,
С₂ – середины соответствующих сторон; А₃, В₃,
С₃ – середины отрезков АН, ВН и СН. Докажем, что точки А₁,
В₁, С₁, А₂, В₂, С₂, А₃,
В₃, С₃ лежат на одной окружности.

Действительно, А₃В₂
– средняя линия треугольника АНС и, следовательно, А₃В₂
параллельно СС₁. В₂А₂ – средняя линия
треугольника АВС и, следовательно, В₂А₂ параллельно АВ.
Так как, отрезок СС₁ перпендикулярен  АВ, то угол А₃В₂А₂=90⁰.
Аналогично .  Поэтому точки А₂,
В₂, С₂, А₃ лежат на одной окружности с
диаметром А₂А₃. Так как отрезок АА₁
перпендикулярен ВС, то точка А₁ также принадлежит этой окружности.
Таким образом, точки А₁ и А₃ лежат на окружности,
описанной около треугольника А₂В₂С₂. 
Аналогичным образом показывается, что точки В₁ и В₃, С₁
и С₃ лежат на этой окружности. Значит, все девять точек лежат на
одной окружности.

Основные
свойства окружности:

·
Серединный перпендикуляр, проведённый к хорде окружности – её диаметр.

· Равные
хорды удалены на равные расстояния от центра окружности. Длины хорд, удалённых
на равное расстояние от центра, равны между собой.

· Касательная
к окружности перпендикулярна радиусу, проведённому в точку касания.

 · Отрезки касательных к окружности,
проведённых из одной точки, равны между собой.

·
Квадрат длины касательной равен произведению длины секущей на длину её внешней
части, т.е.  AB^2=AD×AC 
(теорема о касательной и секущей).

· Если
две пересекающиеся хорды делятся точкой пересечения на отрезки с длинами a b ,
и с d , , то a×b=c×d.

· Длина
окружности радиуса R равна 2pR.

·
Площадь круга радиуса R равна 2 p R .

Свойства,
связанные с углами:

 · Градусная мера дуги равна
величине центрального угла, опирающегося на эту же дугу.

·
Вписанный угол, опирающийся на диаметр окружности, равен 90⁰.

·
Вписанные углы, опирающиеся на одну и ту же дугу, равны.

·
Величина вписанного угла равна половине величины центрального угла,
опирающегося на ту же дугу.

· Угол
между пересекающимися хордами равен полусумме градусных мер противоположных
дуг, высекаемых хордами.

· Угол
между двумя секущими равен полуразности дуг, высекаемых секущими на окружности.

 · Угол между касательной и хордой
равен половине градусной меры дуги, заключённой между ними.

Свойства
многоугольников, связанные с окружностью:

· В
любой треугольник можно вписать окружность, центром которой является точка
пересечения биссектрис углов этого треугольника.

· Около
любого треугольника можно описать окружность, центром которой является точка
пересечения серединных перпендикуляров, проведённых к сторонам этого
треугольника.

· Если
r, R –
радиусы вписанной и описанной окружностей треугольника, то расстояние между
центрами этих окружностей d=(√R²-R×r)

(формула
Эйлера).

 · В четырёхугольник можно вписать
окружность тогда и только тогда, когда суммы длин противоположных сторон
четырёхугольника равны.

· Около
четырёхугольника можно описать окружность тогда и только тогда, когда суммы
противоположных углов четырёхугольника равны  180⁰.

2) Прямая Эйлера-может быть определена
как прямая, проходящая через центр описанной окружности и ортоцентр треугольника

Свойства:

·       
Центроид треугольника

·       
Ортоцентр треугольника

·       
Точку пересечения серединных перпендикуляров к
сторонам треугольника (центр описанной окружности)

·       
Центр окружности девяти точек

• Теорема Эйлера. Точка
  пересечения медиан M делит отрезок между центром
  описанной окружности O и ортоцентром H в
  отношении 1:2 (ОМ:MН)
• Уравнение прямой Эйлера в трилинейных
  координатах есть

x sin 2A sin
( B − C ) + y sin 2B sin
( C − A ) + z sin 2C sin
( C − A ) = 0.

Прямая Эйлера
(красная) проходит через центр описанной окружности треугольника, его
ортоцентр, центр тяжести и центр окружности девяти точек

             Окружность
девяти точек — это окружность, проходящая через середины всех трёх
сторон треугольника. Она также называется 

окружностью Эйлера.

Окружность
девяти точек получила такое название из-за следующей теоремы:

·        
Основания трёх высот произвольного
треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих
его вершины с ортоцентром,
лежат все на одной окружности.

Иначе
говоря, окружность девяти точек является описанной окружностью
для следующих трёх треугольников:

·        
ортотреугольник,

·        
дополнительный
треугольник,

·        
треугольник Эйлера

Расстояние d между центрами вписанной и описанной
окружностей треугольника может быть
определено по формуле

D²=R²-2Rr

1.3
.Пример механизма решения задачи  

Пусть О — центр описанной
окружности треугольника  ABC, а I – центр вписанной окружности. Если
луч AI пересекает описанную
окружность в точке L, то L является средней
точкой дуги BC . Проведём луч LO и обозначим его точку
пересечения с описанной окружностью как M . Тогда LM будет диаметром описанной
окружности. Из точки I опустим перпендикуляр ID  на AB.Тогда ID=r Запишем формулу Эйлера
немного в другом виде

                                D²=R²-2Rr

Можно
заметить, что слева стоит степень
точки I относительно
описанной окружности (если быть точным, то минус степень точки). То есть,
достаточно доказать равенство LI*IA=2Rr.
По лемме о трезубце LI=LB, значит , достаточно
доказать, что LI*IA=2Rr . Теперь заметим, что
2R=LM  и r=ID то есть, требуемое
равенство можно переписать в виде LI*IA=LM*ID .Перепишем его
ещё немного:LB/LM=ID/IA . Это равенство следует
из подобия треугольников  AID и MLB. В
самом деле, углы B и D у этих треугольников
прямые, а углы  и  равны, потому что оба опираются на
дугу BI (более
того, отношениюLB:LM=ID:IA  равно синусу угла BAC).

  
2
Глава

Решение
задач.

5.

                                 
х₂=-15-постороний корень

6.

7.

Ответ: d=0,35

8.

9.

10.

Катеты прямоугольного треугольника равны 7
и 24 найдите расстояние между центрами вписанной и описанной окружностей

D²=R²-2Rr

Ответ:81.25

Заключение

Изучив материалы по теме исследования, я
убедился в том, что Леонард Эйлер действительно принадлежит к числу
гениальнейших математиков всех времен. В истории точных наук его имя вполне
заслуженно ставят рядом с именами Ньютона, Декарта, Галилея. Имя Эйлера дорого
всему прогрессивному человечеству, которое чтит в нём одного из величайших
геометров мира. Огромная продуктивность Эйлера была и остаётся поводом для
изумления и восхищения каждого, кто пытался изучать его труды.
В
качестве члена Петербургской и Берлинской Академий наук Эйлер содействовал
развитию математических наук в обеих странах и распространению в них
физико-математических знаний. Леонард Эйлер был избран академиком (и почётным
академиком) в восьми странах мира. Он оставил важнейшие труды по самым
различным отраслям математики, механики, физики, астрономии и по ряду
прикладных наук. Трудно даже перечислить все отрасли, в которых трудился
великий учёный. Но в первую очередь он был математиком.                                        
В исследовательской работе я изучил задачи Эйлера из области планиметрии:
окружность Эйлера, прямая Эйлера, формула Эйлера, связывающая радиусы вписанной
и описанной окружностей. Удивительно, что даже Евклид не заметил, например, что
девять замечательных точек треугольника лежат на одной окружности. Гениальный
Эйлер это не только увидел, но и доказал. В ходе выполнения работы я
рассмотрел  современные доказательства этих задач.  Я
провел литературный обзор и рассмотрел несколько видов задач на теорему Эйлера.
Так же я рассмотрел прямую и окружность Эйлера, свойства многоугольников
связанные с окружности, свойства прямой Эйлера  и свойства окружности 9 точек.

Выдвинутая
мною гипотеза подтвердилась.  Существует общий
механизм решения геометрических задач, используя теорему Эйлера и окружность
Эйлера , позволяющий значительно упрощать решение геометрических задач.

 Следует отметить, что
свойства замечательных точек и линий треугольника, широко используются при
решении различных задач.

Так же стоит отметить, что применение
свойств замечательных точек и линий треугольника в изучении математики может
оказаться весьма эффективным. Знание их свойств значительно ускоряет решение
многих геометрических задач. 

Литература

1) Малышев, И. Г.
ЕГЭ как важнейший элемент мотивации выпускников в повышении уровня
геометрических знаний / И. Г. Малышев // Нижегородское образование. — 2008. — №
1. — С. 39 — 42.

2) Малышев, И. Г.
Тригонометрия как наиболее проблемный раздел школьной математики / И. Г.
Малышев // Нижегородское образование. — 2013. — № 3. — С. 63 — 67.

3) Малышев, И. Г.
О важности тригонометрии как раздела геометрии / И. Г. Малышев // Математика в
школе. — 2010. — № 8. — С. 52 — 54.

 4) Малышев, И. Г.
Тригонометрические неравенства в треугольнике / И. Г. Малышев // Математика в
школе. — 2012. — № 2. — С. 52 — 55.

5) Макарычев, Ю.
Н. Тригонометрия. 10 класс: учеб. пособие для общеобразоват. учреждений / Ю. Н.
Макарычев [и др.]. — М. : Просвещение, 2012. — 61 с.

 6) Малышев, И. Г.
Между Сциллой и Харибдой / И. Г. Малышев // Математика в школе. — 2014. O№ 5.
OС. 3 — 6.

                7)Сборник задач по
геометрии под редакцией М.И.Сканави  книга № 2 с. 87-            

90