Содержание
- Определение расстояния между точками по координатам
- Координаты GPS
- Вычисление расстояния между двумя точками через формулу
- Формула для нахождения расстояния между точками
- Способы решения и нахождения расстояния между точками по координатам
- Онлайн-калькулятор для расчета расстояния между точками по координатам
- Картографическая программа для нахождения расстояния между точками
- Откуда берется погрешность при расчете расстояния между точками
- 4. Определение кратчайшего расстояния между пунктами по их географическим координатам
- 4.1. Понятие об ортодромии и локсодромии. Формулы для вычисления кратчайшего расстояния между пунктами
- 4.2. Определение географических координат пунктов
- GIS-LAB
- Вычисление расстояния и начального азимута между двумя точками на сфере
- Содержание
- [править] Введение
- [править] Формулы
- [править] Сферическая теорема косинусов
- [править] Формула гаверсинусов
- [править] Модификация для антиподов
- [править] Реализация на Avenue
- [править] Реализация на языке Python
- [править] Реализация в Excel
- [править] Проверочный набор данных
- [править] Ссылки по теме
Определение расстояния между точками по координатам
Спутниковые координаты не только помогают найти маршрут до нужного места, но и позволяют рассчитать отрезок между двумя любыми точками в пространстве или на данной плоскости. Зная необходимые данные и координаты интересующих объектов, можно найти расстояние в километрах или метрах между этими длинами или отрезками нужной длины. Для этого применяется либо сложная формула для самостоятельного решения, либо онлайн-калькуляторы на сайте или картографические программы, выполняющие работу автоматически.
Координаты GPS
Координаты GPS (Global Positioning System) – это цифровые обозначения местоположения устройства в пространстве или на плоскости, указанные в формате соотнесения географических широты и долготы. Данные точки на отрезке определенной длины вычисляются при помощи связи со спутником. Запускается сложная система навигации, которая, помимо указания координат, может определить расстояние между двумя точками в пространстве или на плоскости, проложить маршрут между отрезками длины и рассчитать время перемещения как пешком, так и на разных видах транспорта. В основе работы лежит всемирная система координат WGS 84.
 Координаты GPS
Координаты GPS
Чтобы найти местоположение и расстояние между двумя данными точками или отрезками длины в пространстве и на плоскости по координатам GPS, можно пользоваться как специальным навигатором или профессиональным навигационным прибором, так и обычным смартфоном или планшетом.
Вычисление расстояния между двумя точками через формулу
Найти расстояние между двумя точками в пространстве или на плоскости можно как по прямой, так и по маршруту (с учетом расположения дорог, их поворотов, объездов и пр.). В первом случае применима специальная формула, воспользоваться которой можно как в автоматическом режиме, введя известные данные отрезков в калькулятор на сайте, так и самостоятельно, проведя итоговое решение с нужными материалами на бумаге.
Кратчайшим (прямым) расстоянием считается дуга, проходящая по поверхности Земли от точки А в точку Б. Чтобы найти ее длину, применяют так называемую модифицированную формулу гаверсинусов, учитывающую радиус планеты.
Известно, что Земля – не идеальный шар, а несколько приплюснутый, потому и радиус у нее в разных точках различен. Ввиду этого для подсчета кратчайшего расстояния между точками используется усредненное значение радиуса относительно оси (6372.795 км для Земли), что допускает погрешность итогового значения около 0,5 %.
Формула для нахождения расстояния между точками
В формуле, при помощи которой можно найти расстояния между двумя данными точками планеты с использованием координат, присутствуют следующие величины (известные из математики):
- d – центральный угол (перпендикуляр) между двумя данными точками, лежащими на большом круге (т. е. на окружности, получаемой при сечении центральной части шара плоскостью);
- r – радиус сферы (т. е. усредненное значение радиуса Земли: 6372.795 км);
- y₁ и y₂ – широта двух точек в радианах;
- x₁ и x₂ – долгота двух точек в радианах.
Получим следующую тригонометрическую формулу, плавно вытекающую из теоремы пифагора (евклидова геометрия), которая равна:
cos(d) = sin(y₁)·sin(y₂) + cos(y₁)·cos(y₂)·cos(x₁ − x₂)
Данное соотношение можно получить из прямоугольного треугольника.
Подставив в формулу заданные значения точек, и получим вычисление.
Для того чтобы найти ответ про расстояние между двумя точками координат в километрах, поможет формула:
Способы решения и нахождения расстояния между точками по координатам
Чтобы провести решение и получить ответ о расстоянии точек в пространстве или плоскости по координатам GPS, необязательно использовать формулу вручную. Ответ о расстоянии между точками по координатам получим при помощи специальных утилит.
Онлайн-калькулятор для расчета расстояния между точками по координатам
В интернете есть множество сайтов с однотипными формулами в онлайн-калькуляторах для решения и нахождения прямого расстояния между двумя точками по координатам. Для этого нужно узнать широту и долготу двух искомых точек в пространстве или на плоскости и вбить эти данные в соответствующие окошки формулы (чем больше знаков после запятой у каждой точки известно, тем точнее получим значение).
Картографическая программа для нахождения расстояния между точками
Вычислять расстояние между двумя точками на плоскости по координатам и давать точный ответ умеет любое приложение-навигатор и без вычисления по формуле, например:
- «Карты»;
- «Google.Maps»;
- «Google Планета Земля»;
- «SAS.Планета».
 Определение координат объекта в Google Maps на компьютере не по формуле
Определение координат объекта в Google Maps на компьютере не по формуле
Для определения расстояния между точками не по дорогам и маршрутам, а напрямую по двум точкам, применяется инструмент «Линейка».
Многие из популярных навигаторов способны определять расстояние по координатам двух точек онлайн без формул: это можно сделать на сайте в разделе «Азимут» или «Другие вычисления».
На заметку. Наиболее точные данные между точками предоставляют материалы и таблицы кадастровых справочников, но также в них много информации, лишней для обычного пользователя.
Откуда берется погрешность при расчете расстояния между точками
При вычислении прямого расстояния между координатами двух точек применяется подсчет длины дуги этих точек, для чего берется радиус точек (его приблизительное среднее значение ввиду особенностей формы Земли). Из-за этого возникает погрешность, т. е. мы получим не точную информацию о расстоянии между точками.
Чем больше искомое расстояние, тем больше получим погрешность в расстоянии между точками.
Также неточность между точками получим тогда, когда при вычислениях расстояния между точками берут недостаточно цифр после запятой в координатах: результат будет приблизительным.
Так, между любыми двумя известными точками на чертеже Земли можно проложить как обычное расстояние по дорогам, так и прямую линию, которая соединяет каждую точку. Вычисления точек проводят вручную или автоматически, причем во втором случае даже будет известна возможная погрешность, которую получим при нахождении расстояние между точками, неизбежная при измерении сферы Земли.
Источник
4. Определение кратчайшего расстояния между пунктами по их географическим координатам
4.1. Понятие об ортодромии и локсодромии. Формулы для вычисления кратчайшего расстояния между пунктами
Известно, что на мелкомасштабных географических картах из-за перехода от поверхности земного эллипсоида к плоскости неизбежны искажения длин линий, исключая отдельные направления, совпадающие с линией сечения поверхности эллипсоида и поверхности вспомогательных фигур (плоскости, конуса, цилиндра), используемых для проектирования. Непосредственное измерение расстояний по прямой на мелкомасштабных картах может привести к большим ошибкам, т. к. кратчайшее расстояние будет иметь вид кривой линии.
Кратчайшая линия на поверхности земного эллипсоида, представляющая собой дугу большого круга, называется ортодромией. Представить ее можно следующим образом. Если взять на глобусе две точки, удаленные друг от друга, а затем между ними натянуть нитку, то она ляжет по ортодромии. Нетрудно при этом заметить, что ортодромия будет пересекать меридианы под разными углами. Следовательно, азимуты ортодромии в разных ее точках будут различны. Сама же ортодромия на всех картах будет изображаться кривой, исключая отдельные направления (прямолинейные меридианы и экватор).
Линия на поверхности земного эллипсоида, пересекающая все меридианы под одним и тем же углом, называется локсодромией, и в общем случае она изображается спиралевидной кривой. Эта линия имеет большое значение для мореплавания, т. к. движение судна на каждом участке своего пути в открытом море обычно контролируется при помощи компаса. Имеется замечательная проекция — нормальная цилиндрическая равноугольная проекция Меркатора, которая до сих пор используется для навигационных карт. Локсодромия на этих картах изображается прямой линией.
Кратчайшее расстояние, т. е. расстояние по ортодромии, можно вычислять по географическим координатам пунктов, используя следующие формулы:
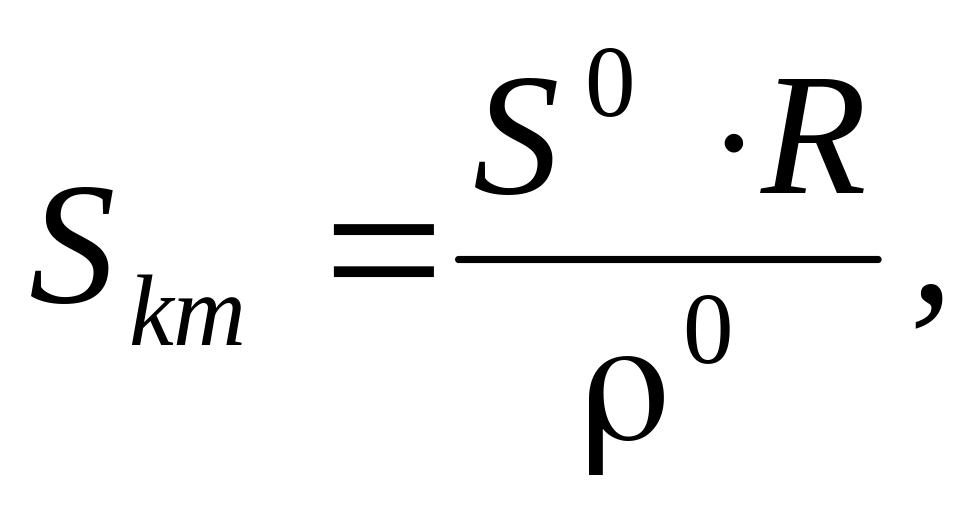 (2)
(2)
где B1 и B2— географическая широта начального и конечного пунктов;
L1 и L2 — географическая долгота начального и конечного пунктов;
R — средний радиус кривизны земного эллипсоида.
Из приведенных формул видно, что для вычисления кратчайшего расстояния необходимо определить географические координаты начального и конечного пунктов.
4.2. Определение географических координат пунктов
Для определения географических координат пунктов лучше использовать географические атласы, в которых помещены карты отдельных государств, составленные, как правило, в нормальных конических и цилиндрических проекциях, равнопромежуточных по меридиану. Использование неравнопромежуточных по меридиану проекций может привести к значительным ошибкам в определении широты, например, по нормальной цилиндрической равноугольной проекции Меркатора. В других же проекциях меридианы и параллели, а часто и те и другие вместе, изображаются кривыми линиями, что усложняет графические работы.
Для определения географических координат пункта следует провести через него меридиан и параллель.
П 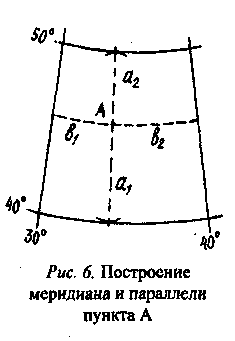 оложение меридиана пункта А можно найти следующим образом (рис. 6).
оложение меридиана пункта А можно найти следующим образом (рис. 6).
Для этого, установив ножку кругового циркуля, или измерителя, в пункт А, находят точки касания к северной и южной параллели трапеции, в которой находится этот пункт. Отрезки а1 и а2, соединяющие точки касания и данный пункт А, при правильном геометрическом построении должны находиться на одной прямой, которая и будет меридианом этого пункта.
Для построения параллели пункта А на ближайших от него меридианах измерителем откладывают отрезки, равные а1 или а2,, и плавной кривой через эти три точки проводят параллель. Положение ее в трапеции можно уточнить проверкой расстояния в других точках до северной или южной параллели, которое должно быть равно отрезку а1 или а2.
Отрезки дуг параллели b1 и b2 при измерении на практике часто заменяют хордами ввиду небольшой кривизны параллелей в пределах трапеции. При измерении хорд с помощью поперечного масштаба на картах 1 :3 000 000 — 1:10 000 000 относительная ошибка от замены дуги хордой не превысит 1%.
Для вычисления географических координат пункта А определяют частоту градусной сетки ΔВ и ΔL и с помощью измерителя и поперечного масштаба измеряют отрезки а1, а2, b1 и b (рис. 6). Вычисления координат выполняют по следующим формулам:
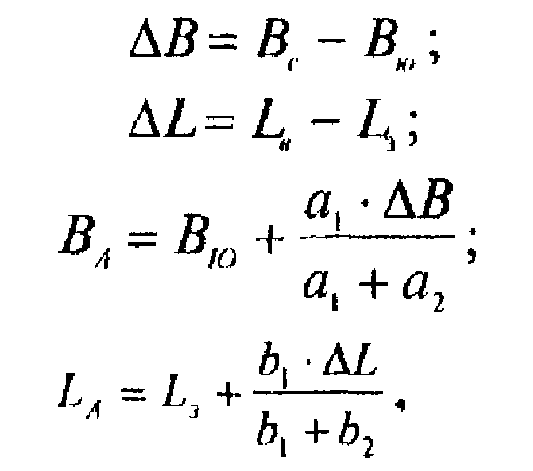
где Вс и Вю — широта северной и южной параллели трапеции; LЗ и lB — долгота западного и восточного меридиана трапеции.
Результаты вычисления координат пункта А можно проконтролировать по формулам:
Источник
GIS-LAB
Географические информационные системы и дистанционное зондирование
Вычисление расстояния и начального азимута между двумя точками на сфере
Измерение расстояния и начального азимута между точками без проекционных преобразований
Содержание
[править] Введение
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут [angles-rhumb.html отличен от постоянного], следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.
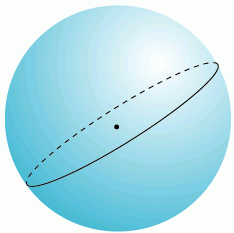

Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.
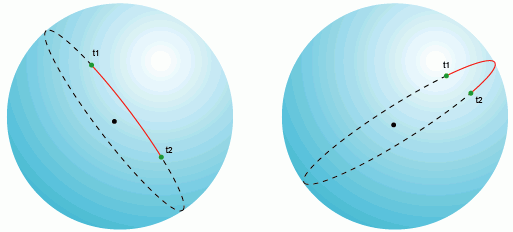

На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.
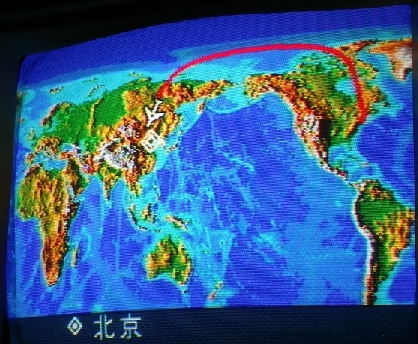

Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.
Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.
Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.
[править] Формулы
Существует три способа расчета сферического расстояния большого круга (подробнее).
[править] Сферическая теорема косинусов
В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением. Графическое изображение формул здесь и далее — из Википедии.
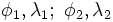 — широта и долгота двух точек в радианах
— широта и долгота двух точек в радианах
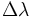 — разница координат по долготе
— разница координат по долготе
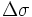 — угловая разница
— угловая разница
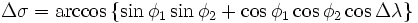
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).
[править] Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.
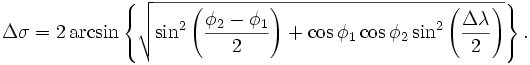
[править] Модификация для антиподов
Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.
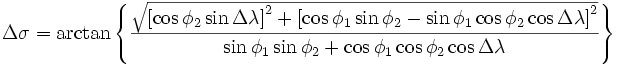
[править] Реализация на Avenue
На языке Avenue, используя последнюю формулу для вычисления расстояния большого круга между двумя точками, можно использовать следующий код. Точки для вычисления передаются другим скриптом, либо добавляются в начало данного в виде pnt = point.make(long, lat) (скачать скрипт):
Для вызова процедуры расчета длин приведенной выше, можно также воспользоваться следующим скриптом, результатом его работы будет расчет длин между точкой testpont до всех точек активной темы вида и запись результата в поле Newdist атрибутивной таблицы этой темы:
[править] Реализация на языке Python
Реализует полный вариант расчета через atan2(), более универсальнее, чем вариант для Avenue. (скачать скрипт)
[править] Реализация в Excel
Скачать пример расчета расстояния большого круга и начального азимута в Excel. Демонстрирует расчеты через закон косинусов, гаверсинус, полное уравнение и полное уравнение через atan2().
Можно также воспользоваться следующей функцией:
[править] Проверочный набор данных
Если все считается правильно, должны быть получены следующие результаты (координаты точек даны как широта/долгота, расстояние в метрах, начальный угол в десятичных градусах):
| # | Точка 1 | Точка 2 | Расстояние | Угол |
| 1 | 77.1539/-139.398 | -77.1804/-139.55 | 17166029 | 180.077867811 |
| 2 | 77.1539/120.398 | 77.1804/129.55 | 225883 | 84.7925159033 |
| 3 | 77.1539/-120.398 | 77.1804/129.55 | 2332669 | 324.384112704 |
[править] Ссылки по теме
Последнее обновление: 2014-05-14 23:41
Дата создания: 06.06.2006
Автор(ы): Максим Дубинин
Источник
На этой странице находится все необходимое, чтобы найти расстояние между двумя точками. Просто введите координаты точек и получите ответ и подробное решение с помощью наших онлайн-калькуляторов. Кроме того на сайте можно найти координаты середины отрезка.
Расстояние между двумя точками – это длина отрезка, соединяющего эти точки.
Формула расстояния между двумя точками на плоскости:
d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}}
xa и ya – координаты первой точки A,
xb и yb – координаты второй точки B
Нахождение расстояния между двумя точками на плоскости сводится к решению треугольника, а точнее – нахождению его гипотенузы. Для этого используется теорема Пифагора. Посмотрите на рисунок.
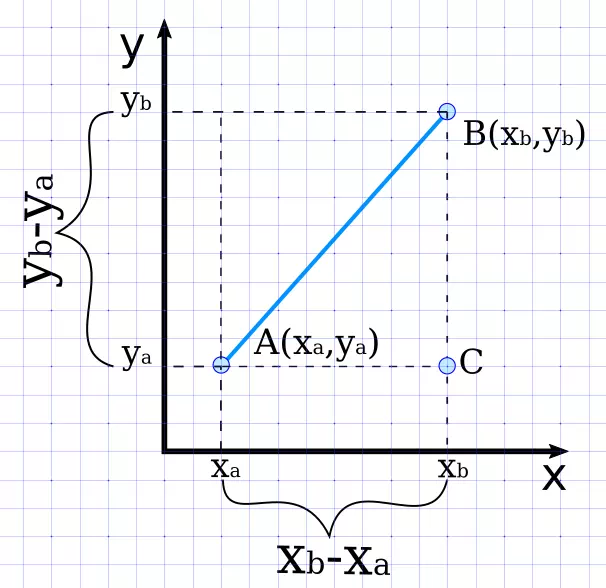
Соединив отрезком точки A и B, а также опустив перпендикуляры на оси мы получим треугольник ABC. В этом треугольнике стороны AC и BC являются катетами прямоугольного треугольника, а AB – его гипотенузой. Длины катетов AC и BC найти довольно просто:
AC = xb – xa
BC = yb – ya
Осталось применить теорему Пифагора и получить сторону AB, которая является гипотенузой прямоугольного треугольника и расстоянием между точками A и B:
AB=sqrt{{AC}^2 + {BC^2}}
Подставив вместо отрезков AC и BC их длины, получим итоговую формулу расстояния между двумя точками:
AB=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}} или d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}}
Формула расстояния между двумя точками в пространстве:
{d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2} + {(z_b – z_a)^2}}}
xa, ya и za – координаты первой точки A,
xb, yb и zb – координаты второй точки B
Примеры задач на вычисление середины отрезка
Задача 1
Найдите расстояние между точками А и В, если А(2; 7), В(-2; 7).
Решение
Подставим координаты точек в формулу расстояния между двумя точками на плоскости и вычислим результат:
d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}} = sqrt{{(-2 – 2)}^2 + {(7 – 7)^2}} = sqrt{{-4}^2 + {0^2}} = sqrt{16 + 0} = sqrt{16} = 4
Мы получили расстояние между точками и оно равно 4.
Ответ: 4.
Проверим результат с помощью калькулятора .
The length of the line segment connecting two points is defined as the distance between them. The length of the line segment connecting the specified coordinates can be used to compute the distance between two points in coordinate geometry. Let’s look at the formula for calculating the distance between two points in a two-dimensional or three-dimensional plane.
What is the Distance Between Two Points?
The distance of the line segment connecting any two points is the distance between them. There is only one line that connects two points. As a result, the distance between two points may be computed by determining the length of the line segment that connects the two spots. For example, if A and B are two points and A B = 20 cm, it implies the distance between A and B is 20 cm.

The length of the line segment connecting two points is the distance between them (but this CANNOT be the length of the curve joining them). It is important to note that the distance between two places is always positive.
Distance Between Two Points Formula
The distance formula is used to determine the distance between two points using the provided coordinates. We use the 2D distance formula or the Euclidean distance formula to calculate the distance between any two points in the 2-D plane.
Formula for Distance Between Two Points
The formula for the distance, d, between two points whose coordinates are (x1, y1) and (x2, y2) is
This is called the Distance Formula.
To find the distance between two points given in 3-D plane, we can apply the 3D distance formula, given as,
Derivation of Formula for Distance Between Two Points
To obtain the formula for calculating the distance between two points on a two-dimensional plane, assume there are two points with the coordinates, A (x1,y1) and B (x2,y2). Following that, we will suppose that the line segment connecting A and B is AB = d. We will now plot the specified points on the coordinate plane and connect them with a line.

Next, we will construct a right-angled triangle using AB as the hypotenuse.
Using Pythagoras Theorem,
AB2 = AC2 + BC2
d2 = (x2−x1)2 + (y2−y1)2
Here, the vertical distance between the given points is | y2 – y1|
The horizontal distance between the given points is | x2 – x1 |
![]() (Taking square root on both sides)
(Taking square root on both sides)
Thus, the distance formula to find the distance between two points is proved.
Using similar steps and concept, we can also derive the formula to find the distance between two points given in the 3D plane.
Steps to find the distance between two points
The following steps may be used to determine the distance between two places using the provided coordinates:
- Make a note of the coordinates of the two given points on the coordinate plane as follows: A(x1,y1) and B(x2,y2).
- We may use the distance formula to calculate the distance between two places,
![Rendered by QuickLaTeX.com d = sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2]}.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-66d2cf4b660d0aea364034dcad27d1fb_l3.png)
- Express the given answer in units.
Note: We can apply the 3D distance formula in case the two points are given in 3D plane,
Sample Problems
Problem 1: Find the distance between the two points with the coordinates given as, A(1,5) and B (2,7).
Solution:
Let (x1, y1) be (2,7) and (x2, y2) be (1,5).
The distance d between the points :
The distance between the two points is √5 units.
Problem 2: Find the distance between the two points with the coordinates given as, P (2,-6,2) and Q(7, 3, 1).
Solution:
Let (x1, y1, z1) be P (2,-6,2) and (x2, y2, z2) be Q (7,3,1).
The distance d between the points P and Q :
Problem 3: Prove that the vertices of a right-angled triangle are the points (3, 4), (7, 4), and (3, 8).
Solution:
Let us say the given points be:
P = (3, 4)
Q = (7, 4)
R = (3, 8)
Now, we will find each vertices of the right-angle triangle by distance formula.
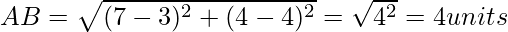
As we know the length of the sided of the right-angled triangle, by Pythagoras Theorem;
AB2 + AC2 = BC2
42+42=(4√2)2
16+16 = 32⟹32 = 32
This proves that ABC is a right-angle triangle.
Distance Between Two Points in Complex Plane
The distance between two points in a complex plane or two complex numbers z1=a+ib and z2=c+id in the complex ⟹1−2k=9+4k plane is the distance between points (a, b) and (c, d), given as,
![]()
Problem 4: Find the distance between the two complex numbers z1 = 2−5i and z2 = 7+7i
Solution:
Here, we have two complex numbers z1 = 2-5i and z2 = 7+7i.
The distance between these complex numbers is equidistance to the two points in the plane, with coordinates, (2,-5) and (7,7).
Thus, distance between the two points is
Hence, the distance between two complex numbers z_1=2-5i and z_2=7+7i is 13 units.
Problem 5: A complex number ω is 6 units apart from z1 = -3 – i and 6 units apart from z2 = 3 + 5i. Check whether the triangle formed by ω, z1, z2 is right – angled or not.
Solution:
There are 3 complex numbers ω, z1, z2.
As we know the distance between ω and z1 is 6 units and distance between ω and z2 is 6 units.
Given, ω, z1 = 6 units
ω, z2 = 6 units
Now, we will find the distance between z1 and z2 by using distance formula.
By Pythagoras Theorem, we have;
(z1z2)2=(ωz1)2+(ωz2)2
Hence, we conclude that the given triangle is right-angle triangle.
Problem 6: Find a point on the x-axis that is equidistant from the points (1, -2) and (-2, -3).
Solution:
We know that any point on the x-axis has an y-coordinate of 0. As a result, we consider the point equidistant from the provided points to be (k,0). i.e., Distance between ( k,0) and (1, -2) = Distance between (k, 0) and (-2, -3).
implies -4k-2k= 9-1
Therefore, the required point is (k, 0) =
Расстояние между двумя точками, формула
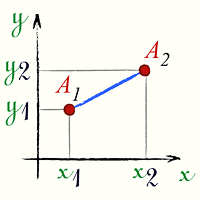
Расстояние между двумя точками
Расстояние между двумя точками A1(x1;y1) и
A2(x2;y2)
в прямоугольной системе координат выражается формулой:
[ d = sqrt{(x_2-x_1)^{2} + (y_2-y_1)^{2}} ]
Порядок точек не играет роли. Расстояние считается положительным. поэтому корень берется с одним знаком (плюс).
Вычислить, найти расстояние между двумя точками по формуле (1)
| x1 | y1 |
| x2 | y2 |
Вычислить
нажмите кнопку для расчета
Расстояние между двумя точками |
стр. 138 |
|---|
Загрузить PDF
Загрузить PDF
Представьте расстояние между двумя точками в виде отрезка прямой линии, соединяющего эти точки. Длину этого отрезка можно найти по формуле: √
Шаги
-

1
Определите координаты двух точек, расстояние между которыми вы хотите вычислить. Обозначим их Точка 1 (x1,y1) и Точка 2 (x2,y2). Неважно, как именно вы обозначите точки, главное, не перепутать их координаты при расчетах.[1]
- x1 − это горизонтальная координата (вдоль оси x) Точки 1, а x2 − горизонтальная координата Точки 2. Соответственно, y1 − вертикальная координата (вдоль оси y) Точки 1, и y2 − вертикальная координата Точки 2.
- Возьмем, например, точки (3,2) и (7,8). Если мы примем, что (3,2) − это (x1,y1), тогда (7,8) − это (x2,y2).
-

2
Ознакомьтесь с формулой для вычисления расстояния. Эта формула позволяет найти длину прямого отрезка, соединяющего две точки, Точку 1 и Точку 2. Длина этого отрезка равна квадратному корню от суммы квадратов расстояний между точками по горизонтали и вертикали. Проще говоря, это квадратный корень из
.[2]
-

3
Найдите, чему равны расстояния между точками по горизонтали и вертикали. Расстояние по вертикали найдем в виде разности y2 – y1. Соответственно, расстояние по горизонтали составит x2 – x1. Не волнуйтесь, если в результате вычитания вы получите отрицательное значение. Следующим шагом будет возведение найденных расстояний в квадрат, что в любом случае даст положительное целое число.[3]
- Найдите расстояние вдоль оси y. Для нашего примера с точками (3,2) и (7,8), где координаты (3,2) соответствуют Точке 1, а координаты (7,8) − Точке 2, находим: (y2 – y1) = 8 – 2 = 6. Это значит, что расстояние между нашими точками по оси y равно шести единицам длины.
- Найдите расстояние вдоль оси x. Для нашего примера с точками (3,2) и (7,8) получаем: (x2 – x1) = 7 – 3 = 4. Это значит, что по оси x наши точки разделяет расстояние, равное четырем единицам длины.
-

4
Возведите оба значения в квадрат. Необходимо по отдельности возвести в квадрат расстояние вдоль оси x, равное (x2 – x1), и расстояние вдоль оси y, составляющее (y2 – y1):
-

5
Сложите полученные значения. В результате вы найдете квадрат диагонали, то есть расстояния между двумя точками. В нашем примере для точек с координатами (3,2) и (7,8) находим: (7 – 3) в квадрате равно 36, и (8 – 2) в квадрате равно 16. Складывая, получаем 36 + 16 = 52.
-

6
Извлеките квадратный корень из найденной величины. Это последний шаг. Расстояние между двумя точками равно квадратному корню от суммы квадратов расстояний вдоль оси x и вдоль оси y.[4]
- Для нашего примера находим: расстояние между точками (3,2) и (7,8) равно корню квадратному из 52, то есть примерно 7,21 единицы длины.
Реклама
Советы
- Не страшно, если в результате вычитания y2 – y1 или x2 – x1 у вас получилось отрицательное значение. Поскольку затем разность возводится в квадрат, расстояние все равно будет равно положительному числу.
Реклама
Об этой статье
Эту страницу просматривали 89 362 раза.



