Как найти расстояние между двумя объектами

Приходилось ли вам сталкиваться с задачей расчёта расстояния между деформируемыми объектами в COMSOL Multiphysics®? В этой статье блога мы расскажем, как найти расстояние между объектами с помощью методов расчёта поля кратчайших расстояний. Кроме того, мы выясним, как включить поле кратчайших расстояний в состав мультифизической модели.

Расчёт расстояний с помощью оператора General Extrusion

Обозначим два объекта буквами A и B, как показано на рисунке. Допустим, нужно рассчитать три расстояния:

1. Расстояние до объекта А в виде полевой переменной. В данном случае рассчитываются расстояния и направления от всех точек вокруг и внутри объекта A до ближайшей точки на его границе (d_A).
2. Расстояние от каждой точки на границе объекта B до ближайшей точки объекта A (d_AB).
3. Координаты отрезка, определяющего кратчайшее расстояние между объектами A и B (d_AB,min).

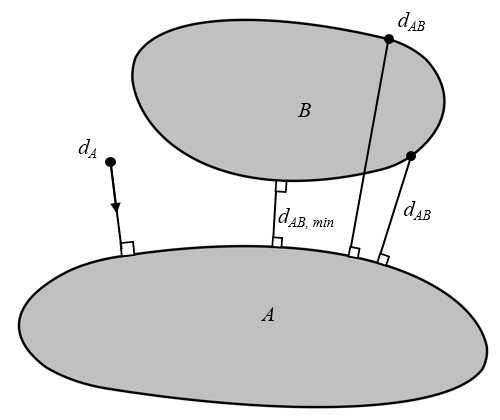
Объекты A и B, а также расстояния, которые нужно рассчитать.

Все три расстояния можно рассчитать с помощью комбинации операторов General Extrusion и Minimum в COMSOL Multiphysics. Сначала рассмотрим, как воспользоваться оператором General Extrusion. Присвоим оператору имя A_b, а в окне Source Selection выберем границы объекта А. В разделе Advanced для параметра Mesh search method выберем опцию Closest point. Описанные настройки показаны на рисунке ниже. Все остальные настройки оператора можно оставить без изменений.

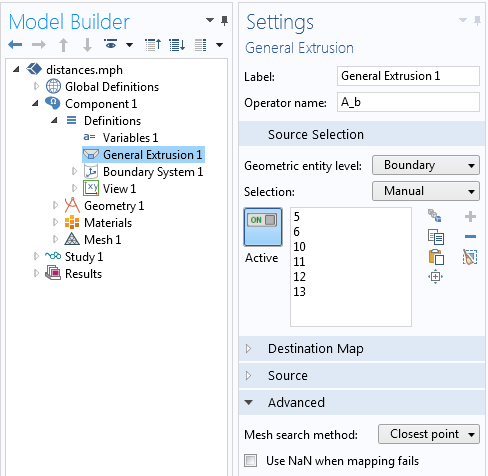
Окно настройки оператора General Extrusion, используемого для расчёта расстояния до ближайшей точки. Обратите внимание, что для параметра Method search method выбрана опция Closest Point.

Этот оператор используется в выражении для переменной d_A, имеющем вид:

sqrt((x-A_b(x))^2+(y-A_b(y))^2)

Областью определения переменной являются домены, в которых нужно рассчитать поле кратчайшего расстояния; в нашем случае это один домен. Можно также рассчитать градиент поля кратчайшего расстояния. Взяв эту величину с обратным знаком, получим -nabla d_A(mathbf{x}). Градиент задаёт компоненты векторного поля, каждый вектор которого направлен в сторону ближайшей к нему точки на границе A. С помощью оператора дифференцирования можно рассчитать производные по пространственным координатам d(d_A,x) и d(d_A,y), как показано на рисунке.

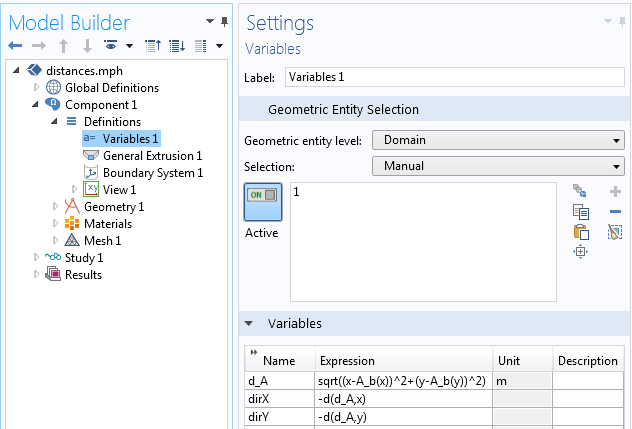
Окно настройки переменных.

Заданные переменные можно использовать в любом месте модели. Например, можно построить график поля кратчайшего расстояния или ввести зависимость свойств материала от расстояния до точки. На графике ниже показаны изолинии кратчайшего расстояния и векторы, указывающие кратчайшее направление. Обратите внимание, что расстояние рассчитывается даже для точек, лежащих за объектом B. Рассмотренный метод позволяет получить довольно много информации, но для этого потребуются значительные вычислительные ресурсы, поскольку кратчайшее расстояние рассчитывается для каждой точки домена. Однако в некоторых задачах такой объём данных избыточен, а найти нужно просто кратчайшее расстояние между объектами.

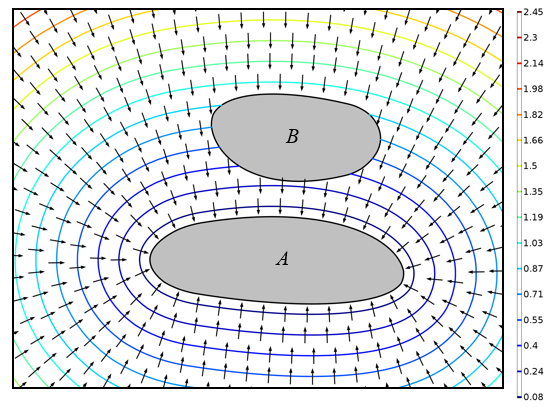
Изолинии кратчайшего расстояния и векторы, указывающие кратчайшее направление к границе объекта A (стрелки) из любой точки окружающей области.

Расчёт зазора между объектами

Теперь немного упростим задачу и найдём только длину кратчайшего пути между двумя объектами, не задумываясь о направлении. Воспользуемся тем же оператором General Extrusion, но дополнительно зададим вспомогательную переменную на границе объекта B, с помощью которой и рассчитаем расстояние.

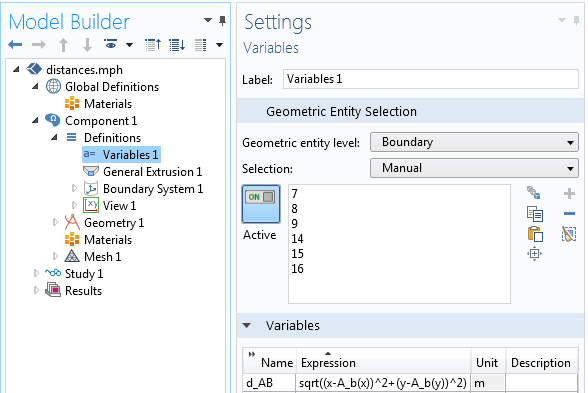
Переменная, введённая для расчёта расстояния между объектами.

Мы используем ту же самую функцию расстояния, что и в предыдущем примере, но теперь нам не потребуется строить сетку в промежуточном домене. Сетка не нужна даже внутри доменов A и B, достаточно разбить на элементы только границы объектов. Этот метод требует гораздо меньше расчётного времени, но при этом позволяет рассчитать только кратчайшее расстояние от объекта A до каждой точки на границе объекта B. Вектор направления остаётся не определён. Можно обратить все использованные определения, чтобы рассчитать кратчайшее расстояние от объекта B до каждой точки на границе объекта A. Эти данные будут распределены вдоль границ объектов, как показано на графике ниже.

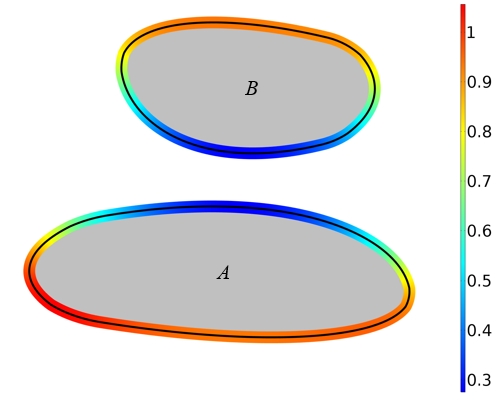
Расстояние от каждой точки на границе объекта B до ближайшей точки объекта A и наоборот.

Расчёт кратчайшего отрезка между объектами с помощью оператора Minimum

Теперь построим кратчайший отрезок, соединяющий два эти объекта. Выше было показано, как рассчитать переменные d_AB и d_BA, равные кратчайшему расстоянию между объектами A и B, а также B и A. Теперь найдём минимальное расстояние между границами объектов. Для этого добавим два оператора Minimum: один на границе объекта A, другой для объекта B. Присвоим операторам имена minA и minB, как показано на рисунке ниже.

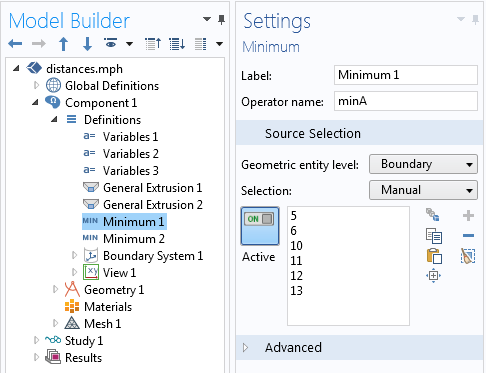
Настройка оператора Minimum на границе объекта A.

Затем с помощью введённых операторов рассчитаем минимальное расстояние. Чтобы найти координаты кратчайшего отрезка, вызовем оператор Minimum с двумя аргументами. Например, если определить переменную A_x как minA(d_BA,x), то она примет значение координаты x, при которой d_BA достигает минимального значения на границе A.

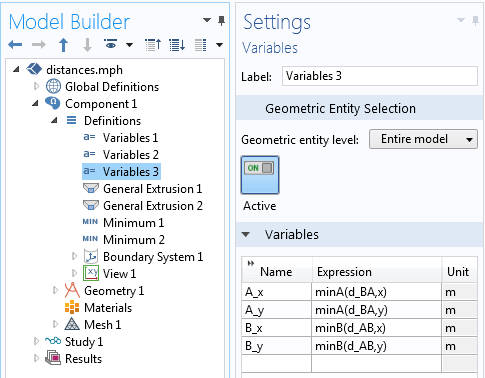
Определение координат кратчайшего отрезка между двумя доменами.

Переменные с найденными координатами можно использовать в любом месте модели. Например, с помощью функции Cut Line можно отобразить кратчайший отрезок, соединяющий два объекта, как показано на следующем рисунке. Если в области между двумя объектами сгенерирована расчётная сетка и получено решение, то можно построить распределение полевых переменных вдоль кратчайшего отрезка между объектами.

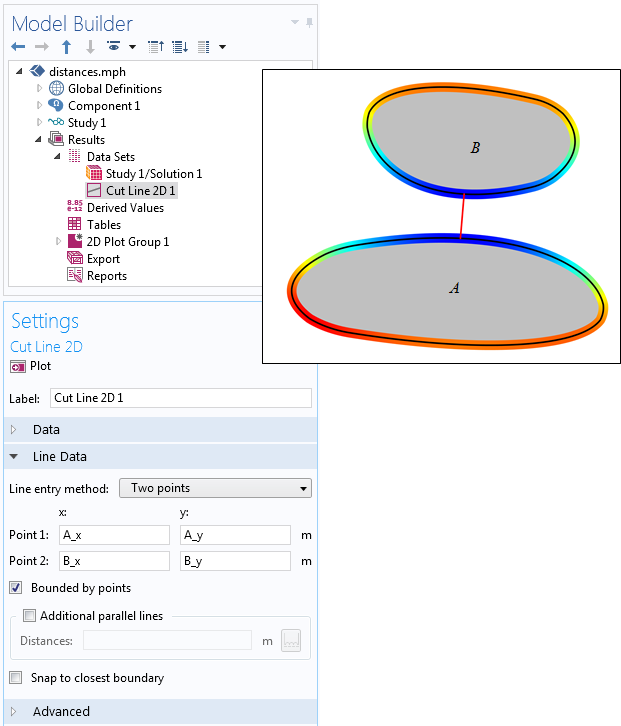
Для отображения кратчайшего отрезка между объектами использована функция Cut Line.

Использование рассчитанных расстояний и имеющиеся ограничения в COMSOL Multiphysics®

Описанные методы расчёта расстояний можно использовать в любой модели. Несмотря на то, что мы показали примеры расчёта только для двумерных областей, использованные методы можно обобщить и на трёхмерные задачи. Просто расчёт поля расстояний в 3D относительно долог, тогда как определение расстояний или зазоров между границами объектов требует меньше ресурсов.

Расчёт расстояний между негладкими фигурами немного сложнее. Ниже показано, что поле расстояний в окрестности входящих углов является негладким, поэтому вектор направления будет не определён вдоль линий, равноудалённых от двух разных частей границы. Чтобы избавиться от негладкости поля расстояний, нужно использовать более мелкую расчётную сетку.

Поле кратчайших расстояний снаружи и внутри объекта с входящими углами на грубой (слева) и более подробной сетке (справа). В данном случае гладкость поля расстояний зависит от размеров элементов сетки.

Если поле расстояний на соответствующей мелкой сетке найдено, то далее его можно использовать как любую другую переменную в нашей модели. Например, можно сделать свойства материала функцией расстояния от поверхности. Ниже показан пример такого распределения материалов.

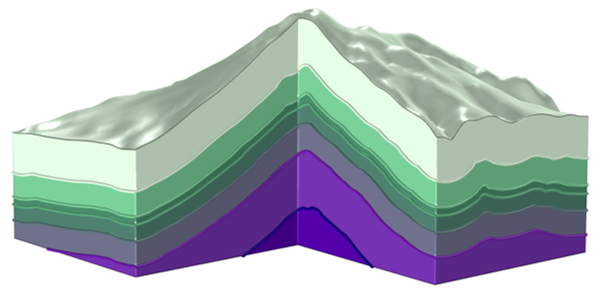
Пример распределение материала как функции от расстояния до поверхности.

Кроме того, функцию расстояния можно использовать для визуализации полученных результатов. Предположим, нужно построить график решения на определенном расстоянии от поверхности. В этом случае достаточно воспользоваться объёмным графиком с фильтром Filter. Логическое выражение в настройках фильтра позволяет отобразить результаты только в той области, которая находится на указанном расстоянии от поверхности объекта, как показано на рисунке ниже.

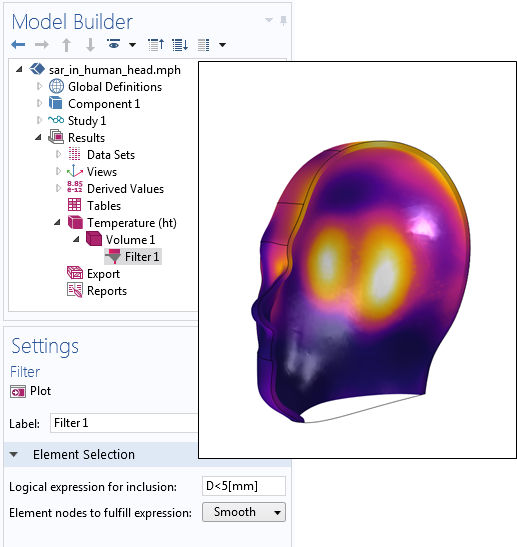
Использование функции расстояния для отображения данных в пределах пятимиллиметрового слоя от внешней поверхности модели.

Заключительные соображения о том, как рассчитать расстояние между геометрическими объектами в COMSOL Multiphysics®

Мы показали, как рассчитать поле кратчайшего расстояния до границы объекта, кратчайшее расстояние между границами объектов и кратчайший отрезок между двумя границами. Описанные подходы применимы также и для расчёта расстояний между рёбрами и точками в трёхмерных моделях. Переменные, содержащие рассчитанные расстояния, можно использовать в любом месте модели: в настройках, определениях, при обработке и визуализации результатов моделирования. В этой публикации мы показали пару примеров. Теперь ваша очередь. Расскажите, что получится у вас!

Дополнительные ссылки

• Справочные ресурсы о численном моделировании в COMSOL Multiphysics:
  • Инструменты группы Help в COMSOL Multiphysics® и их использование в моделировании
  • Using the COMSOL Website Resources for Modeling and Software Help

В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.

Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.

Расстояние между точками на координатной прямой

Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.

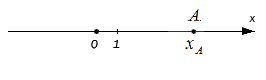
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.

Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.

К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О, необходимо будет отложить три единичных отрезка. Если точка А имеет координату -4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние ОА равно 3; во втором случае ОА = 4.

Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4111.

Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна  11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то OA=xA (число принимается за расстояние); если координата меньше нуля, то OA=-xA . В общем, эти утверждения справедливы для любого действительного числа xA.

Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:

• 0, если точка совпадает с началом координат;

• xA , если xA>0;

• -xA , если xA<0 .

При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой xA: OA=xA

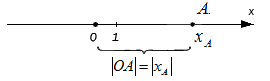
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B, лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты xA и xB : AB=xB-xA.

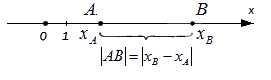
Расстояние между точками на плоскости

Исходные данные: точки A и B, лежащие на плоскости в прямоугольной системе координат Oxy с заданными координатами: A(xA, yA) и B(xB, yB) .

Проведем через точки А и B перпендикуляры к осям координат Ox и Oy и получим в результате точки проекции: Ax, Ay, Bx, By. Исходя из расположения точек А и B далее возможны следующие варианты:

– если точки А и В совпадают, то расстояние между ними равно нулю;

– если точки А и В лежат на прямой, перпендикулярной оси Ox (оси абсцисс), то точки и совпадают, а |АВ| = |АyBy|. Поскольку, расстояние между точками равно модулю разности их координат, то AyBy=yB-yA , а, следовательно AB=AyBy=yB-yA.

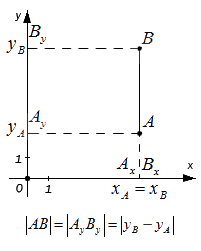
– если точки A и B лежат на прямой, перпендикулярной оси Oy (оси ординат) – по аналогии с предыдущим пунктом: AB=AxBx=xB-xA

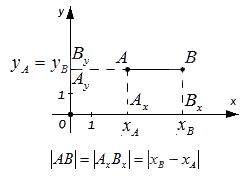
– если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:

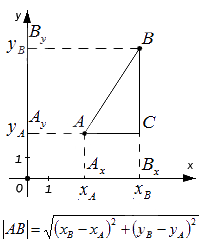
Мы видим, что треугольник АВС  является прямоугольным по построению. При этом AC=AxBx и BC=AyBy. Используя теорему Пифагора, составим равенство: AB2=AC2+BC2⇔AB2=AxBx2+AyBy2 , а затем преобразуем его: AB=AxBx2+AyBy2=xB-xA2+yB-yA2=(xB-xA)2+(yB-yA)2

Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек

AB=(xB-xA)2+(yB-yA)2

Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: AB=(xB-xA)2+(yB-yA)2=02+02=0

Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:

AB=(xB-xA)2+(yB-yA)2=02+(yB-yA)2=yB-yA

Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:

AB=(xB-xA)2+(yB-yA)2=(xB-xA)2+02=xB-xA

Расстояние между точками в пространстве

Исходные данные: прямоугольная система координат Oxyz с лежащими на ней произвольными точками с заданными координатами A(xA, yA, zA) и B(xB, yB, zB) . Необходимо определить расстояние между этими точками.

Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: Ax, Ay,  Az, Bx, By, Bz

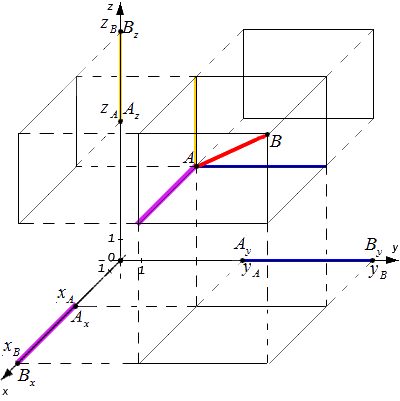
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: AxBx, AyBy и AzBz

Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: AB2=AxBx2+AyBy2+AzBz2

Используя полученные ранее выводы, запишем следующее:

AxBx=xB-xA, AyBy=yB-yA, AzBz=zB-zA

Преобразуем выражение:

AB2=AxBx2+AyBy2+AzBz2=xB-xA2+yB-yA2+zB-zA2==(xB-xA)2+(yB-yA)2+zB-zA2

Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:

AB=xB-xA2+yB-yA2+(zB-zA)2

Полученная формула действительна также для случаев, когда:

– точки совпадают;

– лежат на одной координатной оси или прямой, параллельной одной из координатных осей.

Примеры решения задач на нахождение расстояния между точками

Did this article help you?

Задача простая. Нужно вычислить расстояние между двумя точками на карте, при этом известны только их географические координаты, то есть широта и долгота. Для примера вычислим расстояние между Москвой и Питером, но данная методика, конечно же, будет применима и к другим двум точкам местности. В наше время у многих людей есть такие компасы, например при смартфонах, которые показывают не только направление, но и географические координаты.

Итак, задача: вычислить расстояние между двумя городами. Известно только одно – географические координаты, то есть широта и долгота. Посмотрим эти данные в справочнике, ну или в Википедии.

Итак, что нам известно: координаты Москвы:

55,7522 град. с.ш., 37.6156 град. в.д.

Координаты Петербурга:

59,89444 град. с.ш., 30,26417 град. в.д.

Построим с помощью Excel трапецию:

Итак, у нас есть трапеция ABCD. На ней точка D – это Москва, точка B – это Петербург. Отрезок AB проходит по меридиану Петербурга, BC – по параллели Петербурга, CD – по меридиану Москвы и AD – по параллели Москвы.

Что нам известно? Во-первых известны все географические координаты каждой из точек:

A: 55,7522, 30,26417;

B: 59,89444, 30,26417;

C: 59,89444, 37,6156;

D: 55,7522, 37,6156.

Вычислить AB и CD достаточно просто. На меридианах в градусе примерно одинаковое число километров. Это расстояние можно взять из справочных данных, и оно составляет примерно 111,1 км в каждом градусе.

Нужная нам разница в градусах – это 59,89444-55,7522, или 4,14224. А это значит, что разница в километрах – это 4,14224*111,1=460,2029 км.

Что же касается оснований трапеции, там тоже все достаточно просто. Экватор – это ноль градусов северной широты, и длина каждого градуса на экваторе около 111,3 км. Поскольку косинус ноля – это единица, то для любой параллели верна следующая формула: длина каждого градуса равна произведению 111,3 на косинус того угла, который числится в градусах северной широты (ну или южной, если это происходит южнее экватора).

Итак, с помощью Excel вычислим нужные нам косинусы:

• cos(55.7522) = 0,562773
• cos(59.89444) = 0,501595

Это значит, что 1 градус в верхнем основании нашей трапеции =111,3*0,501595=55,82749 км, а один градус в нижнем основании трапеции =111,3*0,562773=62,6366 км. Поскольку число градусов одинаково как в верхнем, так и в нижнем основаниях трапеции и составляет 37,6156-30,26417, то есть 7,35143 градуса. Но число километров в верхнем и нижнем основаниях трапеции не одинаковое.

Рассчитаем эти расстояния в километрах. BC=7,35143*55,82749=410,4119 км.

AD=7,35143*62,6366=460,469 км.

Теперь проведем высоту BH в нашей трапеции:

В прямоугольном треугольнике ABH нам известно, что гипотенуза равна 460,2029 км, малый катет тоже известен (это половина разницы между длинами оснований трапеции, то есть 0,5*[460,469-410,4119], то есть 0,5*50,05711, или 25,02856 км).

Итак, найдем высоту трапеции ABCD, ее можно вычислить с помощью теоремы Пифагора. Напомню, что мы знаем и длину гипотенузы, и длину наименьшего из катетов.

• Квадрат гипотенузы: 211786,7
• Квадрат известного катета: 626,4
• Разность между этими числами: 211160,2

Корень из этой разности – 459,5218 км. Это и есть наша высота трапеции, то есть BH.

Задача почти решена. Для нахождения расстояния между Москвой и Питером нам нужно вычислить диагональ трапеции, то есть BD. Нарисуем эту линию:

Итак, у нас есть треугольник BHD. BH мы только что вычислили (459,5218 км), HD тоже известно (нужно от большего основания трапеции отнять AH. 460,469-25,02856=435,4404).

Два катета известны, нужно найти гипотенузу. По той же теореме Пифагора, и мы увидим, что гипотенуза будет равна 633,0629 км. Это и есть расстояние от Питера до Москвы.

Проверим наши вычисления, спросив у Яндекса, сколько составляет расстояние от Питера до Москвы.

Мы увидим ответ – 634 км. При вычислениях по нашей методике получилось чуть больше, чем 633 км. Это значит, что погрешность при данном виде вычислений достаточна мала. Но если учесть, что крупные города – это не маленькие точки, а большие расстояния с севера на юг и с запада на восток, то можно сказать, что мы вычислили все правильно.

А на этом пока всё, подписывайтесь на мой канал и до новых встреч!

Здесь будет калькулятор

Расстояние между двумя точками на прямой

Рассмотрим координатную прямую, на которой отмечены 2 точки: AA и BB. Чтобы найти расстояние между этими точками, нужно найти длину отрезка ABAB. Это делается при помощи следующей формулы:

Ввиду того, что в формуле присутствует модуль, при решении не принципиально, из какой координаты какую вычитать (так как берется абсолютная величина этой разности).

То есть:

Разберем пример, чтобы лучше понять решение подобных задач.

Расстояние между двумя точками на плоскости

Рассмотрим две точки, заданные на плоскости. Из каждой отмеченной на плоскости точки нужно опустить по два перпендикуляра: На ось OXOX и на ось OYOY. Затем рассматривается треугольник ABCABC. Так как он является прямоугольным (BCBC перпендикулярно ACAC), то найти отрезок ABAB, он же является и расстоянием между точками, можно с помощью теоремы Пифагора. Имеем:

AB2=AC2+BC2AB^2=AC^2+BC^2

Но, исходя из того, что длина ACAC равна xB−xAx_B-x_A, а длина BCBC равна yB−yAy_B-y_A, эту формулу можно переписать в следующем виде:

Расстояние между двумя точками в пространстве

Нахождение расстояния между двумя точками в этом случае происходит аналогично предыдущему за исключением того, что координаты точки в пространстве задаются тремя числами, соответственно, в формулу нужно добавить еще и координату оси аппликат. Формула примет такой вид: