тупое решение в лоб – идем в поисковик, и просто тупо пишем: расстояние между отрезками
вторая же ссылка (ну лично у меня) – Ю2.30. Расстояние между отрезками
там и описание и решение и код, правда на Си
берем его и переписываем на Python, получаем:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import math
def ras (x1, y1, x2, y2, x3, y3):
## Если отрезок вертикальный - меняем местами координаты каждой точки.
if x1==x2:
x1, y1 = y1, x1
x2, y2 = y2, x2
x3, y3 = y3, x3
k=(y1-y2)/(x1-x2) ## Ищем коэффициенты уравнения прямой, которому принадлежит данный отрезок.
d=y1-k*x1
xz=(x3*x2-x3*x1+y2*y3-y1*y3+y1*d-y2*d)/(k*y2-k*y1+x2-x1)
dl=-1
if ( xz<=x2 and xz>=x1 ) or ( xz<=x1 and xz>=x2 ):
dl=math.sqrt((x3-xz)*(x3-xz)+(y3-xz*k-d)*(y3-xz*k-d)) ## Проверим лежит ли основание высоты на отрезке.
return dl
## Вводим параметры отрезков
# xa, ya, xb, yb = [1, 1, 2, 2]
# xc, yc, xd, yd = [2, 1, 3, 0]
xa, ya, xb, yb = [int(s) for s in input().split()]
xc, yc, xd, yd = [int(s) for s in input().split()]
min=-1
t=-2
s=-2
o=(xb-xa)*(-yd+yc)-(yb-ya)*(-xd+xc)
o1=(xb-xa)*(yc-ya)-(yb-ya)*(xc-xa)
o2=(-yd+yc)*(xc-xa)-(-xd+xc)*(yc-ya)
if o!=0:
t=o1/o
s=o2/o
if (t>=0 and s>=0) and (t<=1 and s<=1):
min=0 ## Проверим пересекаются ли отрезки.
else:
## Найдём наименьшую высоту опущенную из конца одного отрезка на другой.
dl1=ras(xa,ya,xb,yb,xc,yc)
min=dl1
dl2=ras(xa,ya,xb,yb,xd,yd)
if ( dl2<min and dl2!=-1 ) or min==-1 :
min=dl2
dl3=ras(xc,yc,xd,yd,xa,ya)
if ( dl3<min and dl3!=-1 ) or min==-1 :
min=dl3
dl4=ras(xc,yc,xd,yd,xb,yb)
if ( dl4<min and dl4!=-1) or min==-1 :
min=dl4
if min==-1 :
## В случае, если невозможно опустить высоту найдём минимальное расстояние между точками.
dl1=math.sqrt((xa-xc)*(xa-xc)+(ya-yc)*(ya-yc))
min=dl1
dl2=math.sqrt((xb-xd)*(xb-xd)+(yb-yd)*(yb-yd))
if dl2<min :
min=dl2
dl3=math.sqrt((xb-xc)*(xb-xc)+(yb-yc)*(yb-yc))
if dl3<min :
min=dl3
dl4=math.sqrt((xa-xd)*(xa-xd)+(ya-yd)*(ya-yd))
if dl4<min :
min=dl4
print (min)PS: ну, …. пробовали?? или нужно на подносе?
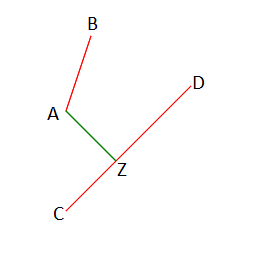
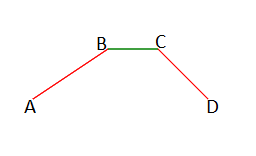
Координаты концов первого отрезка: A(xa, ya), B(xb, yb).
Координаты концов второго отрезка: C(xc, yc), D(xd, yd).
Для начала проверим не пересекаются ли отрезки.
Пусть для отрезка AB: x = t(xb – xa) + xa, y = t(yb – ya) + ya, тогда для CD: x = s(xd – xc) + xc, y = s(yd – yc) + yc, где 0 ≤ t,s ≤ 1.
Если отрезки пересекаются, то выполняются равенства:
t(xb – xa) – s(xd – xc) = xc – xa и t(yb – ya) – s(yd – yc) = yc – ya.
Полученную систему уравнений решим методом Крамера:
Δ = (xb – xa)(yс – yd) – (yb – ya)(xс – xd).
Δ1 = (xb – xa)(yс – ya) – (yb – ya)(xс – xa).
Δ2 = (xc – xa)(yс – yd) – (yc – ya)(xс – xd).
Тогда t = Δ1/Δ, s = Δ2/Δ. Если 0 ≤ t,s ≤ 1 и Δ ≠ 0, то отрезки пересекаются и расстояние между ними min равно 0, иначе с каждого конца отрезка попытаемся опустить высоту на противоположный. Если отрезок, на который опускаем высоту вертикальный, то поменяем местами координаты каждого конца отрезка и точки, с которой опускаем высоту (таким образом сохраним расстояние между точкой и отрезком, а отрезок станет горизонтальным).
Пусть k и d — коэффициенты уравнения прямой, на которую опущена эта высота. Основание высоты будет находится на прямой в точке Z, координаты Z(xz, yz) можно найти по формуле yz = kxz + d. Поскольку высота перпендикулярна отрезку — скалярное произведение их векторов равно 0. Тогда (x2 – x1)(x3 – xz)+(y2 – y1)(y3 – yz) = 0, соответственно xz = (x3x2 – x3x1 + y2y3 – y1y3 + y1d – y2d)/(ky2 – ky1 + x2 – x1), где (x3, y3) — координаты точки, с которой была опущена высота, (x1, y1) и (x2, y2) — координаты концов отрезка, принадлежащего прямой на которую опущена высота.
Вычислим длину dl каждой высоты, основание которой принадлежит одному из данных отрезков: dl = √((x3 – xz)2 + (y3 – kxz – d)2).
Минимальная длина высоты и будет наименьшим расстоянием между отрезками. В случае, если невозможно опустить высоты из одного отрезка на другой: расстояние между ними будет равно минимальному расстоянию между концами двух отрезков: min = √((x1 – x3)2 + (y1 – y3)2), где (x1, y1) — координаты одного из концов первого отрезка, а (x3, y3) — координаты одного из концов второго отрезка.
|
1123 / 292 / 73 Регистрация: 16.03.2020 Сообщений: 922 |
|
|
15.02.2023, 14:40 [ТС] |
7 |
|
Немного поспорив и поизменяв формулировки я добился следующего: Кликните здесь для просмотра всего текста Да, формула, которую я привел в прошлом ответе, не учитывает случай перпендикулярных отрезков. Для таких отрезков можно использовать следующий алгоритм: Найти проекции начальной и конечной точек каждого отрезка на другой отрезок. Вычислить вектора отрезков AB и CD и их длины. Код AB = sqrt((xB-xA)^2 + (yB-yA)^2) # Длина отрезка AB
CD = sqrt((xD-xC)^2 + (yD-yC)^2) # Длина отрезка CD
AC = (xC-xA)*(xB-xA) + (yC-yA)*(yB-yA) # Скалярное произведение векторов AC и AB
BD = (xD-xB)*(xB-xA) + (yD-yB)*(yB-yA) # Скалярное произведение векторов BD и AB
if AB == 0 and CD == 0:
distance = sqrt((xA-xC)^2 + (yA-yC)^2) # Отрезки совпадают
elif AB == 0:
distance = point_to_segment_distance(xA, yA, xC, yC, xD, yD) # Отрезок AB вырожден
elif CD == 0:
distance = point_to_segment_distance(xC, yC, xA, yA, xB, yB) # Отрезок CD вырожден
elif AC <= 0 and BD <= 0:
distance = point_to_segment_distance(xA, yA, xC, yC, xD, yD) # Проекции лежат на отрезке CD
elif AC <= 0:
distance = point_to_segment_distance(xA, yA, xC, yC, xD, yD) # Проекция точки A лежит на отрезке CD
elif BD <= 0:
distance = point_to_segment_distance(xB, yB, xC, yC, xD, yD) # Проекция точки B лежит на отрезке CD
else:
distance = min(point_to_point_distance(xA, yA, xC, yC),
point_to_point_distance(xA, yA, xD, yD),
point_to_point_distance(xB, yB, xC, yC),
point_to_point_distance(xB, yB, xD, yD)) # Проекции лежат за пределами отрезка CD
То есть вроде бы и ответ есть, но используются якобы имеющиеся функции point_to_point_distance и point_to_segment_distance. Не по теме: Интересно, что псевдокод он выдал практически полностью питоном. Вот она, пропаганда! Уже до нейросетей добралась. И язык ответа на вопрос по программированию по умолчанию в нем тоже питон…
0 |
По какой формуле найти расстояние между отрезками (прямыми) в пространстве, зная координаты их концов
Профи
(678),
закрыт
11 лет назад
Игорь Елкин
Просветленный
(49544)
11 лет назад
Как ты вообще себе представляешь это расстояние? Тебе надо найти минимальный отрезок, который соединяет две точки отрезков. Эти две точки-то сразу не определить, не то, что формулу конечную.
Составь два уравнения этих прямых (на которых отрезки) посмотри, где отрезки, может есть лёгкий вариант решения. Может у одного отрезка есть один конец, который наиболее приближен. Задай функцию от этого конца до другого отрезка, и ищи минимум.
Во-первых, для нахождения расстояния от точки (x, y) до отрезка (ax, ay)-(bx, by) не нужна никакая “бинарка”. Использовать поисковый алгоритм для нахождения этого расстояния – безобразие. Это элементарная задача вычислительной геометрии. Например, в целых числах (не выжимая процессорные такты и не беспокоясь о переполнениях)
int point_to_segment_distance_sq(int x, int y, int ax, int ay, int bx, int by)
{
// Обеспечим, чтобы наш отрезок был более горизонтальным, чем вертикальным
int dx = bx - ax, dy = by - ay;
if (std::abs(dx) < std::abs(dy))
{
std::swap(x, y);
std::swap(ax, ay);
std::swap(bx, by);
std::swap(dx, dy);
}
// Обеспечим, чтобы наш отрезок шел слева направо
if (dx < 0)
{
std::swap(ax, bx);
std::swap(ay, by);
dx = -dx;
dy = -dy;
}
// Действия, выполненные выше, нужны только для того, чтобы впоследствии
// мы могли проверить, попадает ли точка (px, py) (см. ниже) внутрь нашего
// отрезка (ax, ay)-(bx, by). Теперь это можно сделать простым сравнением
// `px < ax` и `px > bx`
// Строим уравнение прямой
int A = dy, B = -dx, C = -(A * ax + B * bx);
// Вычисляем ненормированное ориентированное расстояние от точки до прямой
int d = A * x + B * y + C;
// Находим проекцию нашей точки на прямую
int absq = A * A + B * B;
int px = x - A * d / absq, py = y - B * d / absq;
// Проверяем, не попали ли мы за пределы отрезка
if (px < ax)
{
px = ax;
py = ay;
}
else if (px > bx)
{
px = bx;
py = by;
}
// Возвращаем квадрат расстояния
x -= px;
y -= py;
return x * x + y * y;
}
Во-вторых, достаточно применить эту функцию четыре раза – для поиска расстояния от каждого из четырех концов, чтобы найти минимальное расстояние для непересекающихся отрезков. А вот именно этот особый случай – пересекающиеся отрезки – и надо еще уметь отлавливать и обрабатывать. (На самом деле вышеприведенная функция вычисляет всю необходимую информацию для такой проверки.)
