Материал данной статьи позволяет получить навык определения расстояния между двумя параллельными плоскостями при помощи метода координат. Дадим определение расстояния между параллельными плоскостями, получим формулу для его расчета и рассмотрим теорию на практических примерах.
Расстояние между двумя параллельными плоскостями: определение
Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из рассматриваемых параллельных плоскостей до другой плоскости.
Пусть заданы две параллельные плоскости ϒ1 и ϒ2. Из произвольной точки М1 плоскости ϒ1 опустим перпендикуляр М1Н1 на другую плоскость ϒ2. Длина перпендикуляра М1Н1 и будет являться расстоянием между заданными плоскостями.
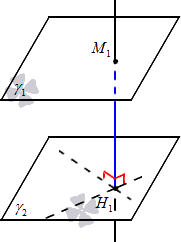
Указанное определение расстояния между параллельными плоскостями имеет взаимосвязь со следующей теоремой.
Если две плоскости параллельны, то все точки одной из параллельных плоскостей находятся на одном и том же расстоянии от другой плоскости.
Допустим, заданы две параллельные плоскости ϒ1 и ϒ2. Для получения доказательства теоремы необходимо доказать, что перпендикуляры, опущенные из различных произвольных точек одной плоскости к другой плоскости, равны. Пусть будут заданы некоторые произвольные точки М1 и М2 на плоскости ϒ1, и из них опущены перпендикуляры М1Н1 и М2Н2 на плоскость ϒ2. Таким образом, нам предстоит доказать, что М1Н1 = М2Н2.
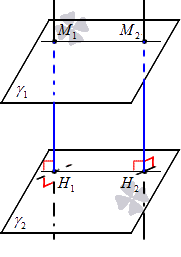
Прямые М1Н1 и М2Н2 параллельны, поскольку перпендикулярны одной плоскости. Опираясь на аксиому о единственной плоскости, проходящей через три различные точки, не лежащие на одной прямой, можем утверждать, что через две параллельные прямые проходит единственная плоскость. Будем считать, что существует некоторая плоскость ϒ3, проходящая через две параллельные прямые М1Н1 и М2Н2. Очевидным фактом является то, что плоскость ϒ3 пересекает плоскости ϒ1 и ϒ2 по прямым М1M2 и Н1Н2, которые не пересекаются, а значит – параллельны (в ином случае, заданные плоскости имели бы общую точку, что невозможно в силу их параллельности по условию задачи). Таким образом, мы наблюдаем четырехугольник М1М2Н1Н2, у которого противоположные стороны являются попарно параллельными, т.е. М1М2Н1Н2 – параллелограмм (в рассматриваемом случае – прямоугольник). Следовательно, противоположные стороны у этого параллелограмма равны, а значит |М1Н1| = |М2Н2|. Что и требовалось доказать.
Заметим также, что расстояние между параллельными плоскостями – наименьшее из расстояний между произвольными точками этих плоскостей.
Нахождение расстояния между параллельными плоскостями
По программе 10-11 классов расстояние между параллельными плоскостями определяется построением перпендикуляра из любой точки одной плоскости, опущенного к другой плоскости; после чего находится длина этого перпендикуляра (при помощи теоремы Пифагора, признаков равенства, или подобия треугольников, или определения синуса, косинуса, тангенса угла).
В случае, когда уже задана или есть возможность задать прямоугольную систему координат, то мы имеем возможность определить расстояние между параллельными плоскостями при помощи метода координат.
Пусть задано трехмерное пространство, а в нем – прямоугольная система координат и две параллельные плоскости ϒ1 и ϒ2. Найдем расстояние между этими плоскостями, опираясь, в том числе, на определение расстояния между плоскостями, данное выше.
В исходных данных – плоскости ϒ1 и ϒ2, и мы можем определить координаты (x1, y1, z1) некой точки M1, принадлежащей одной из заданных плоскостей: пусть это будет плоскость ϒ1. Также получим нормальное уравнение плоскости ϒ2: cos α·x+cos β·y+cos λ·z-p=0. В таком случае, искомое расстояние |М1Н1| будет равно расстоянию от точки М1(x1, y1, z1) до плоскости ϒ2 (ей соответствует нормальное уравнение cos α·x+cos β·y+cosγ·z-p=0). Тогда нужное расстояние вычислим по формуле: M1H1=cos α·x1+cos β·y1+cosγ·z1-p. Вывод данной формулы можно изучить в теме вычисления расстояния от точки до плоскости.
Резюмируем. Для того,чтобы определить расстояние между двумя параллельными плоскостями, необходимо:
– найти координаты (x1, y1, z1) некой точки М1, принадлежащей одной из исходных плоскостей;
– определить нормальное уравнение другой плоскости в виде cosα·x+cos β·y+cosγ·z-p=0;
– произвести расчет требуемого расстояние, используя формулу: M1H1=cos α·x1+cos β·y1+cosγ·z1-p.
Если в прямоугольной системе координат плоскость ϒ1 задается общим уравнением плоскости A·x+B·y+C·z+D1=0, а плоскость ϒ2 – общим уравнением A·x+B·y+C·z+D2=0, тогда расстояние между параллельными плоскостями необходимо вычислять по формуле:
M1H1=D2-D1A2+B2+C2
Покажем, как данная формула получена.
Пусть точка М1(x1, y1, z1) принадлежит плоскости ϒ1. В таком случае координаты этой точки будут отвечать уравнению плоскости A·x+B·y+C·z+D1=0, или верным будет равенство: A·x1+B·y1+C·z1+D1=0. Отсюда получим: A·x1+B·y1+C·z1+D1=0. Полученное равенство нам еще пригодится.
Плоскость ϒ2 будет описываться нормальным уравнением плоскости A·x+B·y+C·z+D2A2+B2+C2=0 или -A·x+B·y+C·z+D2A2+B2+C2=0 (в зависимости от знака числа D2). Однако при любом значение D2 расстояние |М1Н1| возможно рассчитать, используя формулу:
M1H1=A·x1+B·y1+C·z1+D2A2+B2+C2=A·x1+B·y1+C·z1+D2A2+B2+C2
Теперь задействуем полученное ранее равенство A·x1+B·y1+C·z1=-D1 и преобразуем формулу:
M1H1=-D1+D2A2+B2+C2=D2-D1A2+B2+C2
Даны две параллельные плоскости ϒ1 и ϒ2, описываемые уравнениями x16+y-14+z143=1 и 3x-2y+23z-20=0 соответственно. Необходимо определить расстояние между заданными плоскостями.
Решение
Решим задачу двумя способами.
- Уравнение плоскости в отрезках, которое задано в условии задачи, дает возможность определить координаты точки М1, принадлежащей плоскости, описываемой этим уравнением. Как точку М1 используем точку пересечения плоскости ϒ1 и оси Ox. Таким образом, имеем: M116, 0, 0.
Преобразуем общее уравнение плоскости ϒ2 в нормальный вид:
3x-2y+23z-20=0⇔3x-2y+23z-2032+(-2)2+232=0⇔⇔35x-25y+235z-4=0
Вычислим расстояние |М1Н1| от точки M116, 0, 0 до плоскости 35x-25y+235z-4=0:
M1H1=35·16-25·0+235·0-4=110-4=3910
Так мы получили искомое расстояние между исходными параллельными плоскостями.
- Преобразуем уравнение плоскости в отрезках в общее уравнение плоскости:
x16+y-14+z143=1⇔6x-4y+43z-1=0
Приравняем коэффициенты при переменных x, y, z в общих уравнениях плоскостей; с этой целью умножим обе части крайнего равенства на 2:
3x-2y+23z-20=0⇔6x-4y+43z-40=0
Воспользуемся формулой для нахождения расстояния между параллельными плоскостями:
M1H1=D2-D1A2+B2+C2=-40-(-1)62+(-4)2+(43)2=39100=3910.
Ответ: 3910.
Даны две параллельные плоскости, описываемые уравнениями: 6x+4y-12z+3=0 и 3x+2y-6z-2=0. Необходимо найти расстояние между этими плоскостями.
Решение
Удобнее будет использовать второй способ решения подобных задач. Умножим обе части второго уравнения на 2, и коэффициенты в уравнениях плоскостей станут равны: 6x+4y-12z+3=0 и 6x+4y-12z-4=0. Теперь можно использовать формулу:
M1H1=-4-362+42+(-12)2=7196=12
Однако попробуем найти ответ и первым способом: допустим, точка M1(x1, y1, z1) принадлежит плоскости 6x+4y-12z+3=0. Соответственно, координаты этой точки отвечают уравнению плоскости, и верным будет равенство:
6×1+4y1-12z1+3=0
Пусть y1= 0, z1 = 0, тогда x1: 6×1+4·0-12·0+3=0⇔x1=-12
Таким образом, точка получает точные координаты: M1-12, 0, 0.
Преобразуем общее уравнение плоскости 3x+2y-6z-2=0 в нормальный вид:
3x+2y-6z-2=0⇔3x+2y-6z-2=032+22+-6=0⇔37x+27y-67z-27=0
В таком случае, требуемое расстояние между плоскостями равно: 37·-12+27·0-67·0-67·0-27=-12=12
Ответ: 12.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Расстояние между плоскостями.
Определение. Расстояние между плоскостями — равно длине перпендикуляра, опущенного с одной плоскости на другую.
Формула для вычисления расстояния между плоскостями
Если заданы уравнения параллельных плоскостей Ax + By + Cz + D1 = 0 и Ax + By + Cz + D2 = 0, то расстояние между плоскостями можно найти, используя следующую формулу
| d = | |D2 – D1| |
| √A2 + B2 + C2 |
Примеры задач на вычисление расстояния между плоскостями
Пример 1.
Найти расстояние между плоскостями 2x + 4y – 4z – 6 = 0 и x + 2y – 2z + 9 = 0.
Решение. Проверим, параллельны ли плоскости, для этого умножим уравнение второй плоскости на 2
2x + 4y – 4z + 18 = 0
Так как коэффициенты при неизвестных величинах у полученного уравнения и первого уравнения равны, то для вычисления расстояния между плоскостями можно использовати приведенную выше формулу:
| d = | |18 – (-6)| | = | |24| | = | 24 | = 4 |
| √22 + 42 + (-4)2 | √36 | 6 |
Ответ: расстояние между плоскостями равно 4.
Данный калькулятор поможет найти расстояния между двумя параллельными плоскостями.
Если две плоскости не параллельны, то они пересекаются, а значит расстояние между ними равно нулю.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния между плоскостями и закрепить пройденный материал.
- Калькулятор
- Немного теории
Введите данные:
Уравнение 1-ой плоскости:
x
+
y
+
z
+ = 0
Уравнение 2-ой плоскости:
x
+
y
+
z
+ = 0
Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.
| Нравится |
На этой странице вы узнаете
- Как найти расстояние между мухой и столбом?
- Как любопытный кот, скидывая вкусняшки со стола, нашел расстояния от точки до плоскости и от прямой до плоскости?
- Внимание! Сложные расчеты! Как любопытному коту найти расстояние между плоскостью стола и полом?
Отправляясь в любое путешествие, мы проверяем, как далеко нам придется ехать. На пробежке мы смотрим, какое расстояние преодолели. А пробег на машине? Если мы с такой легкостью считаем расстояния в нашей жизни, неужели в математике должно быть что-то сложнее?
Расстояния между фигурами
Когда нам нужно дойти от дома до магазина, мы можем точно сказать, какое расстояние нам нужно пройти. Например, магазин находится в 200 метрах от дома, следовательно, мы и должны пройти 200 метров, чтобы купить что-то вкусненькое.
Таким образом, мы получаем расстояние между двумя точками.
Расстояние между точками — это длина отрезка, заключенного между ними.

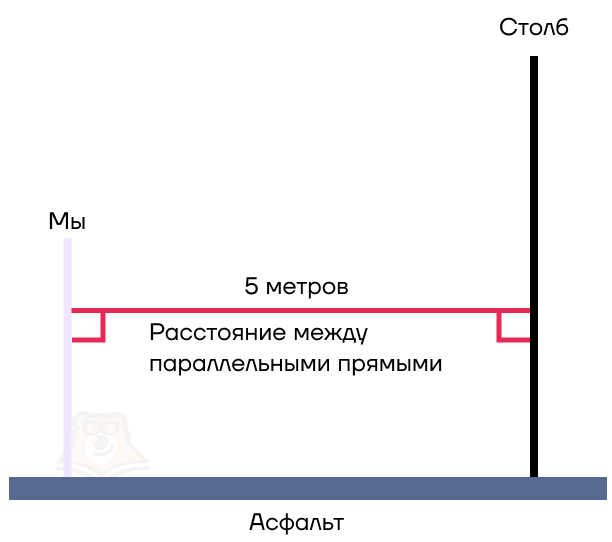
Пока мы шли в магазин, мы заметили на столбе интересное объявление о продаже цветов. Как найти расстояние от нас до этого объявления? Разумеется, пройти определенное расстояние до столба. Допустим, это будет 5 метров.
Заметим, что мы прошли по асфальту, то есть по горизонтальной поверхности. А мы и столб стоим вертикально, то есть перпендикулярны поверхности асфальта. Обратим внимание, что при этом мы со столбом будем параллельными прямыми.
Следовательно, мы пришли к выводу, что:
Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними.
Иными словами, это отрезок, который мы прошли по асфальту.
Но как только мы собрались дойти до столба и сорвать объявление, прямо мимо наших глаз пролетела муха. Она летела строго на одной высоте, долетела до столба и села на объявление.
Как найти в этом случае расстояние между мухой и столбом? На самом деле, муха пролетела ровно такое же расстояние, которое нам необходимо было пройти до столба.
Поскольку муха совсем маленькая, возьмем ее за точку. И таким образом, мы получаем расстояние между точкой и прямой.
Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую.
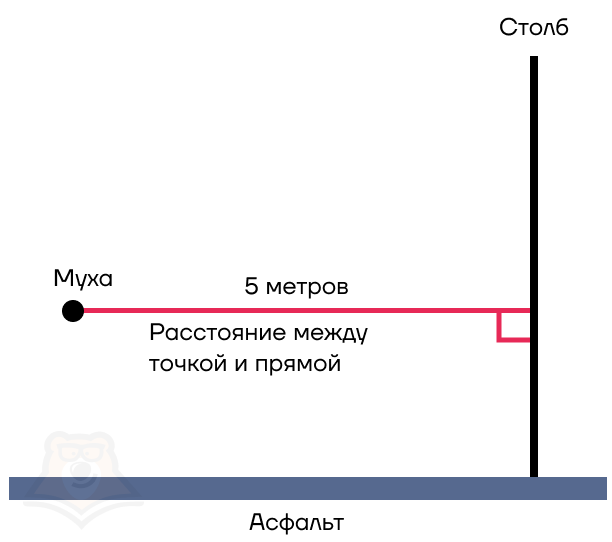
Для этого достаточно найти расстояние между точкой и прямой — длину перпендикуляра, опущенного из этой точки на прямую.
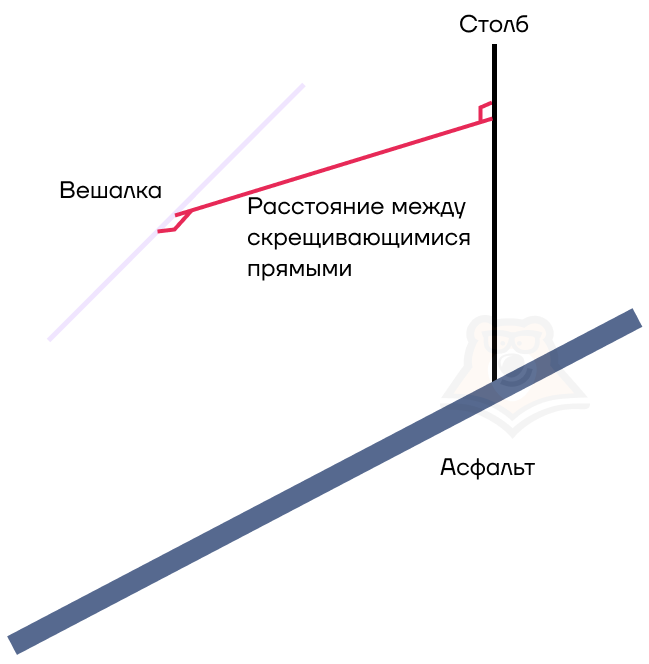
Пока мы злились на муху за то, что она опередила нас и добралась до объявления первой, мимо нас прошли грузчики, которые несли вешалку под углом к асфальту и столбу. Чему тогда будет равно расстояние между вешалкой и столбом?
Мы не можем точно сказать, что 5 метров, поскольку вешалка не параллельна столбу. Чтобы его найти, достаточно провести перпендикуляр и к столбу, и к вешалке.
Так мы нашли расстояние между скрещивающимися прямыми. Подробнее о скрещивающихся прямых можно прочесть в статье «Аксиомы стереометрии. Прямые и плоскости в пространстве».
Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра.
Удивившись тому, как много всего может произойти только со столбом, мы все-таки дошли до магазина, купили тортик и рулетик и вернулись домой. Поставили покупки на стол и пошли готовить чай.
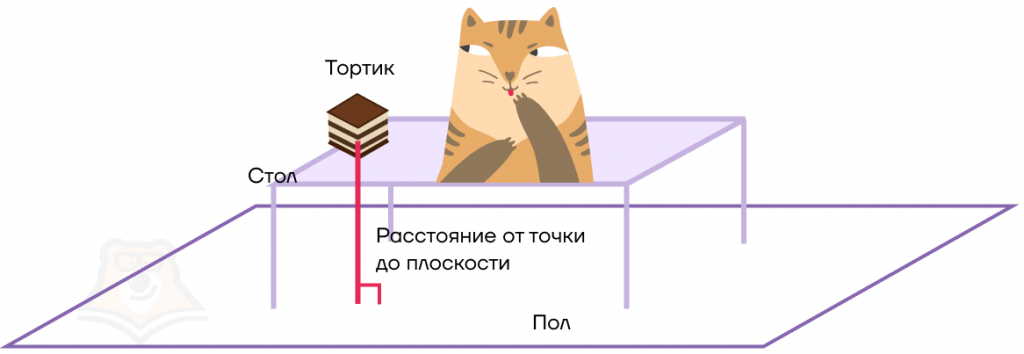
В этот момент на стол запрыгнул наш кот и решил проверить, какое расстояние от тортика до пола. И для этого он скинул наш тортик со стола.
Существует ли возможность измерить расстояние от тортика до пола, при этом не жертвовать этим самым тортиком? Представим, что пол — это плоскость, а тортик — точка. Тогда нам всего лишь нужно найти расстояние от точки до плоскости.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
Так и есть: когда кот скинул тортик, он пролетел строго вертикально до пола.
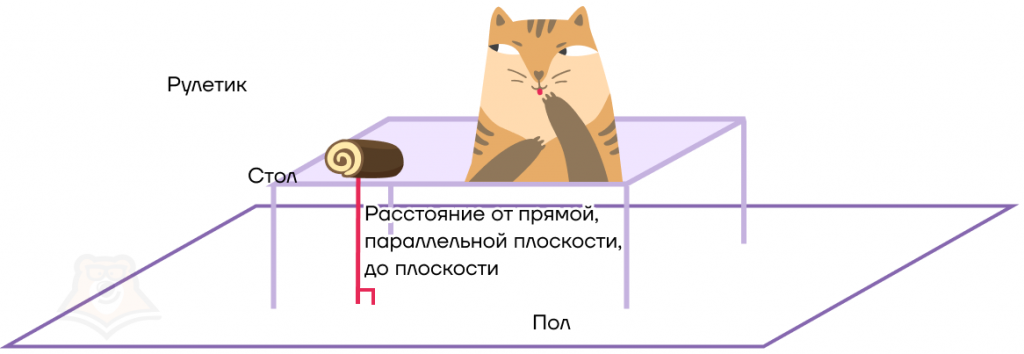
Наш кот посмотрел на упавший торт и тут резко заметил, что мы принесли еще и очень длинный рулетик! Теперь ему стало интересно, какое расстояние от рулетика до пола, поэтому он решил скинуть и его.
Расстояние от рулетика до пола можно было найти и другим способом, а именно найти расстояние от прямой до плоскости. Поскольку рулетик лежит на столе, то он параллелен полу.
Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
Заметим, что если прямая не параллельна плоскости, то рано или поздно она ее пересечет, а значит, точного расстояния между ними не будет.
Оказывается, наши вкусняшки пролетели строго вертикально вниз, то есть преодолели длину перпендикуляра, проведенного от них до пола!
Таким образом, расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между прямой, параллельной плоскости, и плоскостью — длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
Увидев, что он скинул все продукты питания, кот решил сбежать с места преступления. Но перед этим он задался вопросом, какое расстояние от плоскости столешницы до плоскости пола, чтобы рассчитать свой прыжок.
Но и в этом ему на помощь могла прийти стереометрия. Как жаль, что кот ее не знает, поэтому все проверяет на практике.
Теперь нам нужно найти расстояние между параллельными плоскостями.
Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
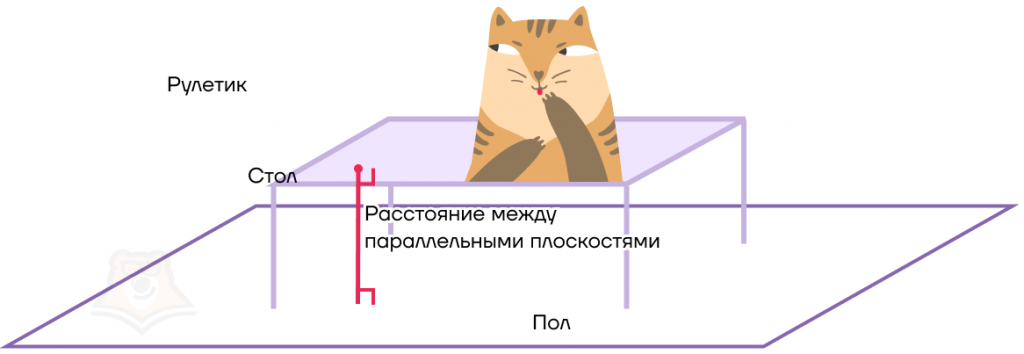
Для этого ему также нужно найти, сколько он пролетит строго вниз. Или, иначе говоря, расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки этой плоскости на вторую плоскость.
Вот так, благодаря одной прогулке до магазина и любопытству кота, мы рассмотрели, как находятся расстояния между двумя фигурами. Ничего сложного, верно?
При решении задач, конечно, в условии не встретишь любопытного кота или муху на объявлении, но кто мешает включать нам фантазию и представить условие задачи как жизненные ситуации.
Фактчек
- Расстояние между точками — это длина отрезка между ними. Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую.
- Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними. Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра.
- Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
- Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
- Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
Проверь себя
Задание 1.
Как найти расстояние между точкой и прямой?
- Найти длину любой линии от этой точки до прямой.
- Найти длину перпендикуляра, опущенного из этой точки на прямую.
- Невозможно найти расстояние между точкой и прямой.
- Ни один из вышеперечисленных вариантов.
Задание 2.
Как найти расстояние между скрещивающимися прямыми?
- Найти длину произвольной прямой между ними.
- Найти длину прямой, перпендикулярной одной из прямых и не перпендикулярной второй прямой.
- Найти длину их общего перпендикуляра.
- Невозможно найти расстояние между скрещивающимися прямыми.
Задание 3.
Как найти расстояние от точки до плоскости?
- Найти длину перпендикуляра, опущенного из этой точки на плоскость.
- Найти длину произвольной линии, проведенной из точки к плоскости.
- Найти расстояние от точки до любой прямой, лежащей в плоскости.
- Невозможно найти расстояние между точкой и плоскостью.
Задание 4.
Как найти расстояние от прямой до плоскости?
- Найти длину произвольной линии, проведенной из любой точки этой прямой до плоскости.
- Найти длину отрезка, соединяющего любую точку на прямой и любую прямую в плоскости.
- Найти длину перпендикуляра, опущенного из любой точки этой прямой на плоскость.
- Невозможно найти расстояние между прямой и плоскостью.
Задание 5.
Как найти расстояние между параллельными плоскостями?
- Невозможно найти расстояние между параллельными плоскостями.
- Найти длину перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
- Найти длину отрезка, соединяющего точку одной плоскости с произвольной точкой на второй плоскости.
- Найти длину отрезка, соединяющего две произвольные прямые в плоскостях.
Ответы: 1. — 2 2. — 3 3. — 1 4. — 3 5. — 2
Расстояние между плоскостями. Онлайн калькулятор
Страница обновляется. Могут возникнуть ошибки. Спасибо за понимание!
С помощю этого онлайн калькулятора можно найти расстояние между плоскостями. Дается подробное решение с пояснениями. Для нахождения расстояния между плоскостями, введите элементы уравнения плоскости в ячейки и нажимайте на кнопку “Решить”.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между плоскостями − теория
Заметим, сначала, что расстояние между плоскостями определена, если плоскости параллельны или, что то же самое, нормальные векторы этих плоскостей коллинеарны. Вычисление расстояния между двумя плоскостями можно свести к вычислению расстояния от точки первой плоскости до второй плоскости. Вычисление расстояния от точки до плоскости (онлайн калькулятор, теория, примеры) посмотрите на странице Расстояние от точки до плоскости онлайн.
Алгоритм вычисления расстояния между плоскостями содержит следующие шаги:
- Проверка коллинеарности нормальных векторов плоскостей.
- Нахождение некоторой точки M0 на первой плоскости.
- Вычисление расстояния между точкой M0 и второй плоскостью.
Выведем формулу вычисления расстояния между плоскостями.
Запишем уравнения двух плоскостей:
1. Проверяем коллинеарность нормальных векторов n1=(A1, B1, C1) и n2=(A2, B2, C2).
Очевидно, что нормальные векторы n1 и n2 не могут быть нулевыми векторами.Если из пары коэффициентов (A1,A2),(B1,B2), (C1,C2) один нулевой а другой − нет, то нормальные векторы n1 и n2 неколлинеарны. Т.е. задача неразрешима.
Пусть A1≠0, A2≠0. Уравнение плоскости (2) не изменится, если умножим на A1/A2:
Нормальный вектор уравнения (2′) имеет следующий вид:
Для коллинеарности векторов n1 и n’2(или n1 и n2) необходимо и достаточно выполнение следующих равенств:
или
Если удовлетворяется условие (3) (или (3′)), то векторы n1 и n’2(или n1 и n2) коллинеарны, т.е. плоскости (1) и (2′) (или (1) и (2) ) параллельны. Тогда уравнение плоскости (2′) можно представить так:
где
2. Найдем некоторую точку на плоскости (1).
Легко убедится, что точка
принадлежит плоскости (1):
3. Расстояние от точки M0(x0, y0, z0) до плоскости (2”) вычисляется с помощью выражения (подробнее смотрите на странице расстояние от точки до плоскости):
Подставляя координаты точки M0 из (4) в (5), получим формулу вычисления расстояния между плоскостями (1) и (2”) (или (1) и (2)):
где
Расстояние между плоскостями − примеры и решения
Пример 1. Найти расстояние между плоскостями
и
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 1/3.
Общее уравнение плоскости имеет вид:
где n=(A,B,C)− называется нормальным вектором плоскости.
Нормальный вектор плоскости (7) равен n1=(1, 2, −4), нормальный вектор плоскости (8′) равен n2=(1, 2, −4). n1=n2. Следовательно эти плоскости параллельны.
Найдем расстояние между плоскостями (7) и (8′), используя следующую формулу:
Подставим значения A, B, C, D1, D2 в (9):
Упростим и решим:
Ответ. Расстояние между плоскостями равен:
Пример 2. Найти расстояние между плоскостями
и
Решение.
Эти плоскости не параллельны, так как коэффициент переменного z уравнения (10) нулевой а коэффициент переменного z уравнения (11)−нет. Невозможно найти расстояние между непараллельными плоскостями.
Пример 3. Найти расстояние между плоскостями
и
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 4/3.
Нормальный вектор плоскости (12) равен n1=(4, 2, 8), нормальный вектор плоскости (13′) равен n2=(4, 16/3, 64/3). n1≠n2. Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.
