Найти расстояние между центрами вписанных окружностей
2021-11-23
Дан треугольник со сторонами 25, 25 и 48.
а) Докажите, что он тупоугольный.
б) Найдите расстояние между центрами его вписанной и описанной окружностей.
а) Пусть $AB=AC=25$, $BC=48$ – стороны треугольника $ABC$ (рис.1). По теореме косинусов
Следовательно, $angle BACgt180^<circ>$.
б) Пусть $AH$ – высота равнобедренного треугольника $ABC$ (рис.2). Тогда $H$ – середина $BC$, а т.к. $AH$ – биссектриса треугольника, то центр $O_<1>$ вписанной окружности лежит на отрезке $OH$. Поскольку треугольник $ABC$ тупоугольный с тупым углом при вершине $A$, центр $O$ его описанной окружности и вершина $A$ лежат по разные стороны от прямой $BC$, причём точка $O$ лежит на серединном перпендикуляре к стороне $BC$, т.е. на прямой $AH$. Значит, $OO_<1>=OA-O_<1>A$.
Из прямоугольного треугольника $AHB$ находим, что
Пусть $OA=R$ – радиус описанной окружности треугольника $ABC$. По теореме синусов
Пусть $S$ – площадь треугольника $ABC$, $p$ – полупериметр, $r=O_<1>H$ – радиус вписанной окружности. Тогда
Как найти расстояние между центрами окружностей
У Вас недостаточно прав для добавления комментариев.
Вам необходимо зарегистрироваться на сайте
Все права защищены 2019
Перепечатка информации возможна только при наличии
согласия администратора и активной ссылки на источник!
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
Расстояние между центрами окружностей равно разности их радиусов
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
Расстояние между центрами окружностей равно разности их радиусов
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
Расстояние между центрами окружностей равно разности их радиусов
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Внутренняя касательная к двум окружностям
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Внутреннее касание двух окружностей
Существует единственная общая внешняя касательная. Других общих касательных нет.
Окружности пересекаются в двух точках
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.
Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Внешняя касательная к двум окружностям |
 |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Внутренняя касательная к двум окружностям
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Внутреннее касание двух окружностей
Существует единственная общая внешняя касательная. Других общих касательных нет.
Окружности пересекаются в двух точках
Существуют две общих внешних касательных. Других общих касательных нет.
Внешнее касание двух окружностей
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.
Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
Формулы для длин общих касательных и общей хорды двух окружностей
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Внутреннее касание двух окружностей |
| Окружности пересекаются в двух точках |
| Внешнее касание двух окружностей |
| Каждая из окружностей лежит вне другой |
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
Длина общей хорды двух окружностей вычисляется по формуле
| Фигура | Рисунок | Формула |
| Внешняя касательная к двум окружностям |  |
|
| Внутренняя касательная к двум окружностям |  |
|
| Общая хорда двух пересекающихся окружностей |  |
| Внешняя касательная к двум окружностям |
 |
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Внутренняя касательная к двум окружностям
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
Общая хорда двух пересекающихся окружностей
Длина общей хорды двух окружностей вычисляется по формуле
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |

Длина общей хорды двух окружностей вычисляется по формуле Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, ОтветПроверено экспертомУравнение окружности с центром (a;b) и радиусом R центр окружности (-2;6) радиус 6 центр окружности (4;-5)радиус 5 по формуле расстояние между двумя точками : находим расстояние между центрами заданных окружностей Вписанная окружность
Окружность, точно можно вписать в такие геометрические фигуры, как:
В четырехугольник, можно вписать окружность, Во все вышеперечисленные фигуры Окружность невозможно вписать в прямоугольник Геометрические фигуры, в которые вписана окружность,
Описанный четырехугольник — это четырехугольник, который описан Свойства вписанной окружностиВ треугольник
[ S = frac<1><2>(a+b+c) cdot r = pr ] p — полупериметр четырехугольника. окружность и любая из сторон треугольника. перпендикуляры к любой точке касания. треугольника на 3 пары равных отрезков. Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера: с — расстояние между центрами вписанной и описанной окружностей треугольника. В четырехугольник
[ S = frac<1><2>(a+b+c+d)cdot r = pr ] p — полупериметр четырехугольника. равноудалены от этой конца и начала этой стороны, то есть от его вершин. Примеры вписанной окружностиПримеры описанного четырехугольника: Примеры описанного треугольника: Верные и неверные утверждения
Окружность вписанная в угол
Центр окружности, которая вписана в угол, К центру окружности вписанной в угол, можно провести, Длина диаметра, радиуса, хорды, дуги вписанной окружности [spoiler title=”источники:”] http://games-on-pc.ru/info/kak-najti-rasstojanie-mezhdu-centrami-okruzhnostej/ http://colibrus.ru/vpisannaya-okruzhnost/ [/spoiler] |
Нахождение расстояния между центрами окружностей
Расстояние между параллельными прямыми равно 12. На одной из них лежит вершина С, на другой — основания AB равнобедренного треугольника ABC. Известно, что AB=10. Найдите расстояние между центрами окружностей, одна из которых вписана в треугольник ABC, а вторая касается данных параллельных прямых и боковой стороны треугольника ABC.
Решение задачи
В данном уроке демонстрируется решение геометрической задачи, которое можно использовать в качестве примера при решении задач типа С4 при подготовке к ЕГЭ.
Условие задачи и ход решения для наглядности изображается схематически на рисунке. Касательно прямоугольного треугольника применяется теорема Пифагора: сумма гипотенузы равна сумма квадратов катетов. Далее площадь треугольника вычисляется с одной стороны как полупроизведение основания на высоту, а с другой — как произведение полупериметра на радиус вписанной окружности. Учитывая это, определяется радиус вписанной окружности. Затем, из подобия треугольников и следует соотношение его соответствующих сторон и, как следствие, вычисляется значение стороны . По теореме Пифагора определяется значения сторон , и . Во втором случае, когда обе окружности касаются сторон угла , их центры лежат на биссектрисе данного угла. Учитывая подобие треугольников и по первому признаку подобия, а также рассматривая трапецию , искомое расстояние между центрами окружностей определяется по формуле .
Как найти расстояние между центрами окружностей
Все права защищены 2019
Перепечатка информации возможна только при наличии
согласия администратора и активной ссылки на источник!
| Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2определяется расстоянием d между центрами этих окружностей
Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
Расстояние между центрами окружностей равно разности их радиусов
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2определяется расстоянием d между центрами этих окружностей
Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.
Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Внешняя касательная к двум окружностям |
 |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Внутренняя касательная к двум окружностям
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Внутреннее касание двух окружностей
Существует единственная общая внешняя касательная. Других общих касательных нет.
Окружности пересекаются в двух точках
Существуют две общих внешних касательных. Других общих касательных нет.
Внешнее касание двух окружностей
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Внутренняя касательная к двум окружностям
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Внутреннее касание двух окружностей
Существует единственная общая внешняя касательная. Других общих касательных нет.
Окружности пересекаются в двух точках
Существуют две общих внешних касательных. Других общих касательных нет.
Внешнее касание двух окружностей
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.
Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
Формулы для длин общих касательных и общей хорды двух окружностей
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям |
 |
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Внутренняя касательная к двум окружностям
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
Общая хорда двух пересекающихся окружностей
Длина общей хорды двух окружностей вычисляется по формуле
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Внутренняя касательная к двум окружностям
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
Общая хорда двух пересекающихся окружностей
Длина общей хорды двух окружностей вычисляется по формуле
Доказательства формул для длин общих касательных и общей хорды двух окружностей
Утверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать.
Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать.
Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,
Как найти расстояние между центрами окружностей?
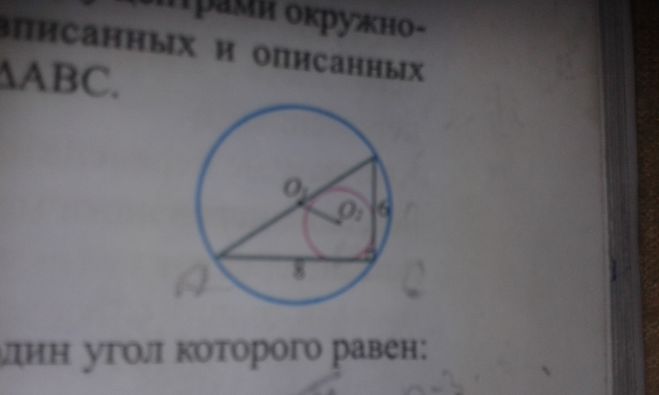
Найдите расстояние О1О2 между центрами окружносей, вписанных и описанных около АВС.?
Для начала нужно найти гипотенузу,по теореме Пифагора «Квадрат гипотенузы равен сумме квадратов катетов», это будет 36+64=100,соответственно Гипотенуза равна 10,после чего есть несколько формул,но я возьму 1,R=a*b*c/4S ,есть еще 1 формула для вписанной окружности это r=2*S/P
Скорее всего загвоздка в определении слова «периметр». Вагончик имеет три измерения: длину, ширину и высоту. Что такое периметр в обыденном понимании? Сумма сторон плоской фигуры, в данном случае прямоугольника, который получится, если начертить его в плане. Для этого нужно сложить длину и ширину вагончика, и умножить на два. Но ширина вагончика не указана, то ли забыли, то ли специально. Если бы ширина вагончика была 4 метра, то периметр и был бы 16. Но с другой стороны, трудно представить, чтобы вагончик был квадратной формы, и ширина вагончика равнялась его длине.
А показанная на рисунке формула (4+2)*2 позволяет определить периметр боковой стенки вагончика. Но ведь периметр боковой стенки нельзя назвать периметром вагончика.
P.S. И вообще, даже картинка нарисована «тяп-ляп». Все ошибки описывать не буду, но вот та, что сразу бросается в глаза: двери трамвая нарисованы с левой стороны (при правостороннем движении)Ю или с правой стороны (при левостороннем движении, такое тоже возможно), т.е. вход и выход пассажиров должны осуществляться с междупутья.
Минимизация по всем законам геометрической оптики должна сводиться к том, что отрезки от пунктов до реки параллельны
имеем два прямоугольных треугольника с общим катетом длиной а и
вторыми катетами, разность между которыми равна ширине реки х (b и b-x) и гипотенузами 3,8 для одного и 4 — х для другого (с меньшим вторым катетом)
Помогите пожалуйста вывести формулу расстояния между двумя окружностями
Никуська
Профи
(538),
на голосовании
14 лет назад
Голосование за лучший ответ
Аццкий скорпиончег
Просветленный
(23519)
14 лет назад
А как они заданы? Если две окружности заданы координатами центра и радиусами, то:
1) расстояние между центрами равно:
d^2 = (x1-x2)^2 + (y1-y2)^2
2) расстояние между самими окружностями:
s = d – r1 – r2
Похожие вопросы
Формулы для центров вневписанных окружностей треугольников
Речь пойдет о формулах для определения расстояний между
центрами вписанной и вневписанной окружностей произвольного треугольника.
Пусть α,
β,
γ — внутренние углы
треугольника, а r — радиус вписанной в него окружности. Обозначим
расстояния между центром O вписанной окружности и центрами A, B,
C вневписанных окружностей соответственно:
OA – la, OB – lb,
OC – lc;
аналогично — расстояния между центрами вневписанных
окружностей:
BC – La, CA – Lb,
AB – Lc.
Тогда имеют место шесть следующих легко запоминающихся
соотношений:
В случае равностороннего треугольника формулы предельно
упрощаются:
la = lb = lc
= l = 4r;
La = Lb = Lc = L =
Формулам можно придать другой вид, если учесть, что:
где a, b, c — стороны треугольника,
— его полупериметр.
После соответствующих подстановок и следующих за ними
сокращений окончательно получим:
Для равностороннего треугольника
Сарбаш Р.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 августа 2022 года; проверки требуют 2 правки.
Формула Эйлера — теорема планиметрии, связывает расстояние между центрами вписанной и описанной окружностей и их радиусами.
Теорема названа в честь Леонарда Эйлера, который опубликовал её в 1765 году.[1]
Однако тот же результат был получен ранее Уильямом Чапплом[en] в 1746 году.[2]
Формулировка[править | править код]
Расстояние 
где 

В 1969 году Георгий Александров дал развернутую формулу:
- где
— стороны треугольника.
- где
Замечания[править | править код]
- Приведённую формулу можно переписать следующим образом
.
- или
-
- где
— стороны треугольника.
- Для сферического треугольника отношение радиуса описанной окружности к радиусу вписанной может быть меньше 2. Более того, для любого числа между 1 и 2 существует правильный сферический треугольник с отношением радиуса описанной к радиусу вписанной окружности, равным этому числу.
- где
Доказательство[править | править код]
Пусть 


Если луч 



Проведём луч 

Тогда 




Можно заметить, что слева стоит степень точки 
То есть, достаточно доказать равенство 
По лемме о трезубце 

Теперь заметим, что 



Это равенство следует из подобия треугольников 

В самом деле, углы 






Вариации и обобщения[править | править код]
Для центра вневписанной окружности[править | править код]
Для вневписанных окружностей уравнение выглядит похоже:
где 

Для многоугольников[править | править код]
Во вписанно-описанном четырёхугольнике ABCD с центрами вписанной и вписанной окружностей соответственно I и О.
- или эквивалентно,
- Это соотношение называют Теоремой Фусса[en]. Оно получено Николаем Ивановичем Фуссом[7] в 1792 году.
- Теорема Кэли о цепи Понселе обобщает теорему Эйлера на вписанно-описанные
-угольники[1].
См. также[править | править код]
- Поризм Понселе
Примечания[править | править код]
- ↑ 1 2 Авксентьев, Е. А. Инвариантные меры и теоремы о замыкании типа Понселе Архивная копия от 14 августа 2016 на Wayback Machine
- ↑ Chapple, William (1746), An essay on the properties of triangles inscribed in and circumscribed about two given circles, Miscellanea Curiosa Mathematica Т. 4: 117–124, <https://archive.org/details/miscellaneacuri01unkngoog/page/n142>. The formula for the distance is near the bottom of p.123.
- ↑ Svrtan, Dragutin & Veljan, Darko (2012), Non-Euclidean versions of some classical triangle inequalities, Forum Geometricorum Т. 12: 197–209, <http://forumgeom.fau.edu/FG2012volume12/FG201217index.html> Архивная копия от 28 октября 2019 на Wayback Machine.
- ↑ Roger Nelson. Euler’s triangle inequality via proof without words // Mathematics Magazine. — February 2008. — Вып. 81(1). — С. 58—61.
- ↑ R. A. Johnson. Modern Geometry. — Boston: Houghton Mifflin, 1929. — С. 187.
- ↑ Lev Emelyanov, Tatiana Emelyanova. Euler’s formula and Poncelet’s porism // Forum Geometricorum. — 2001. — Вып. 1. — С. 137–140..
- ↑ Nicolas Fuss// https://en.wikipedia.org/wiki/Nicolas_Fuss Архивная копия от 17 февраля 2020 на Wayback Machine
Ссылки[править | править код]
- Weisstein, Eric W. Euler Triangle Formula (англ.) на сайте Wolfram MathWorld.




































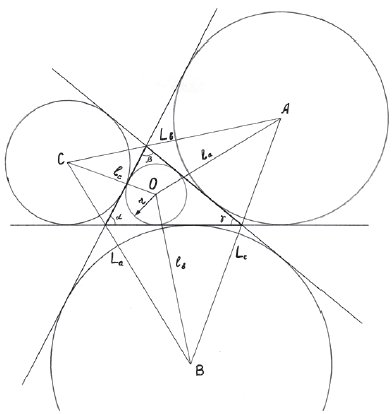
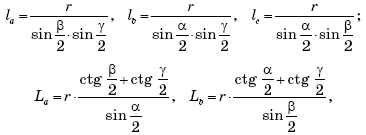
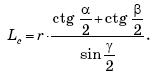
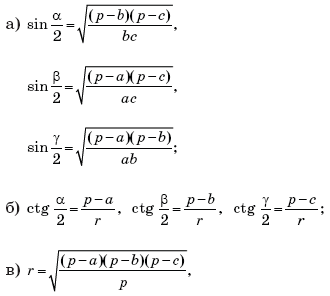
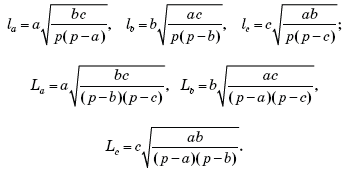


![{displaystyle d^{2}={frac {a,b,c,}{a+b+c}}left[{frac {a,b,c,}{(a+b-c),(a-b+c),(-a+b+c)}}-1right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39c506d1d116d011ec395ee10aa8c0515ebe51a8)









