Как найти расстояние между комплексными числами

Что такое комплексное число

Комплексное число — это выражение типа (z;=;a;+;ib). Здесь a и b будут являться любыми действительными числами, а i — специальным числом, называемым мнимой единицей. Действительная часть комплексного числа обозначается как (a;=;RE;z ), а мнимая часть — (b;=;Im;z).

Во множестве комплексных чисел содержится множество вещественных чисел. Если множество комплексных чисел — это всевозможные пары (x, y), то содержащееся в нем множество вещественных чисел — это пары (x, 0). Те же комплексные числа, которые задают пары (0, y) являются мнимыми.

Что такое модуль комплексного числа

Модуль комплексного числа — это длина вектора, который изображает комплексное число.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Любое комплексное число кроме 0 может быть выражено в тригонометрической форме.

(z;=;left|zright|;cdot;(cosleft(varphiright);+;isinleft(varphiright)))

В этом виде (left|zright|) — модуль комплексного числа z. Может обозначаться как p и r. 

Если (left|zright|;=;r,) то r будет обозначать длину радиус-вектора точки M (x, y).

Вычисление модуля комплексного числа, если в алгебраической форме оно выглядит как z = x + iy, возможно по следующей формуле:

(left|zright|;=;sqrt{x^2;+;y^2})

То есть модуль комплексного числа можно вычислить как квадратный корень из суммы квадратов действительной и мнимой его частей.

Модуль комплексного числа имеет следующие свойства:

1. Модуль не отрицателен — (left|xright|;geq;0). (left|xright|;=;0) только в том случае, если z = 0.
2. Модуль суммы двух комплексных чисел будет меньше или равен сумме модулей: (left|z_1;+;z_2right|;leq;left|z_1right|;+;left|z_2right|.)
3. Модуль результата умножения двух комплексных числе будет равен произведению модулей: (left|z_1;cdot;z_2right|;=;left|z_1right|;cdot;left|z_2right|.)
4. Модуль результата деления двух комплексных чисел будет равняться частному модулей: (left|z_1;div;z_2right|;=;left|z_1right|;div;left|z_2right|.)
5. Модуль неравенства комплексных чисел будет равен расстоянию между этими числами на комплексной плоскости: (left|z_1;-;z_2right|;=;sqrt{left(x_1;-;x_2right)^2;+;left(y_1;-;y_2right)^2}).

Что такое аргумент комплексного числа

Аргумент комплексного числа — это угол (varphi) радиус-вектора точки, соответствующей комплексному числу (z;:;varphi;=;arg;z) на комплексной плоскости. Этот угол измеряется в радианах.

Каждое комплексное число, которое не равно нулю, имеет бесконечное множество аргументов. Эти аргументы отличаются друг от друга на целое число полный оборотов — (360^circ;cdot;k) при k — любое число.

Связь аргумента комплексного числа с его координатами отражена в следующих формулах:

(tanleft(varphiright);=;frac ba)

(cosleft(varphiright);=;frac a{sqrt{a^2;+;b^2}})

(sinleft(varphiright);=;frac b{sqrt{a^2;+;b^2}})

Важно помнить, что ни одна из этих формул отдельно недостаточна для того, чтобы найти аргументы. Формулы используются в совокупности, а также учитывается номер четвертый на координатной плоскости, в которой находится комплексное число.

Аргумент может быть записан в тригонометрической форме. Для комплексного числа (z = x + iy), это будет выглядеть следующим образом:

(z;=;r;(cosleft(varphiright);+;i;sinleft(varphiright)))

Здесь (r) будет модулем комплексного числа (z), а (varphi) — arg z.

Важно отметить, arg z имеет смысл лишь при (z neq 0), комплексное число ноль не имеет аргумента.

Как вывести формулу модуля

В соответствии с теоремой Пифагора длина вектора с координатами a и b равна (sqrt{a^2;+;b^2}).

Так как именно эта величина называется модулем комплексного числа (z = a + bi), тогда (left|xright|;=;sqrt{a^2;+;b^2}).

Примеры решения задач

Задача 

Найти модуль числа (z;=;-5;+;15i)

Решение

(x;=;Re;z;=;-15) — действительная часть, а (y;=;Im;z;=;15) — мнимая часть комплексного числа (z;=;-5;+;15i.)

Таким образом, модуль числа равен следующему выражению:

(r;=;sqrt{x^2;+;y^2};=sqrt{{(-5)}^2;+;15^2};=;sqrt{25;+;225};=;sqrt{250} )

Ответ: (r;=;sqrt{250})

Задача

Найти расстояние между числами (z_1;=;1;-;3i,;z_2;=;-2;+;2i) на комплексной плоскости.

Решение

Расстояние между двумя комплексными числами находятся как модуль разности комплексных чисел. Используем необходимую формулу:

(left|z_1;-;z_2right|;=;sqrt{{(x_1;-;x_2)}^2;+;left(y_1;-;y_2right)^2};=;sqrt{(1;-;{(-2))}^2;+;{(-2;-;2)}^2};=;sqrt{34})

Ответ: (sqrt{34})

Задача

Найти значение аргумента комплексного числа (sqrt{34}) и выразить его в тригонометрической форме.

Решение

Если действительно частью комплексного числа (z;=;1;+;sqrt{3i}) является число (x = Re z = 1), а мнимой частью является (y = Im z;=sqrt3), то аргумент можно вычислить по формуле:

(varphi;=;arg;z;=;arctg;frac yx;=;arctg;frac{sqrt3}1;=;arctg;sqrt3;=;frac{mathrmpi}3)

Теперь для нахождения тригонометрической формы записи комплексного числа необходимо найти модуль. 

(r;=;sqrt{x^2;+;y^2};=;sqrt{1^2;+;{(sqrt3)}^2};=;sqrt{1+3};=;sqrt4;=;2)

Исходя из этого, тригонометрическая форма комплексного числа выглядит следующим образом:

(z;=;2;(cosleft(frac{mathrmpi}3right);+;i;sinleft(frac{mathrmpi}3right)))

Ответ: аргумент равен (frac{mathrmpi}3). Тригонометрическая форма записана выше.

Задача

Найти модуль и аргумент числа (z = 2 – i)

Решение

Найдем (left|zright|;=;sqrt{2^2;+;{(-;1)}^2};=;sqrt5.)

Так как (Re z = 2 > 0), (Im z = -1 < 0), точка расположена в 4 четверти. Тогда из равенства (tanleft(varphiright);=;-frac12) следует:

(varphi;=;arctanleft(-frac12right))

Ответ: (varphi;=;arctanleft(-frac12right))

1

Контрольная
работа №1

Задание
7

Даны
три комплексных числа

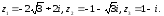
1)
выполните действия

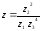
в алгебраической, тригонометрической
и показательной формах;

2)
найдите расстояние между точками

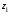
и

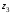
на комплексной плоскости.

Решение

1)
а) Найдем число
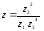в
в алгебраической
форме.

Найдем
поэтапно:

z₂²
=

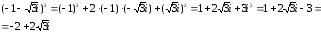
z₃⁴
= [(1-i)²]²
= (1 – 2i
+ i²)²
= (1 – 2i
– 1)²
= (- 2i)²
= 4i²
= – 4

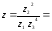
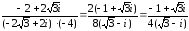
Найдем
частное двух комплексных чисел по
формуле:

=

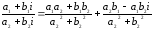
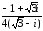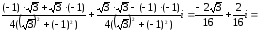
Итак,

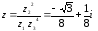
б)
Тригонометрическая форма комплексного
числа: w
= r(cos
+ isin),
где

–
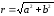
модуль комплексного числа,

 =

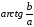
аргумент комплексного числа

Представим
числа z₁,
z₂,
z₃
в тригонометрической форме:

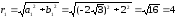
₁
=

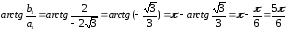
(угол находится во 2-ой четверти).

z₁
= r₁(cos₁
+ isin₁)
= 4(cos

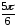
+ isin
)

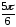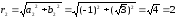
₂
=

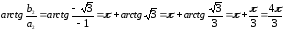
(угол находится в 3-ей четверти).

z₂
= r₂(cos₂
+ isin₂)
= 2(cos

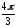
+ isin
)

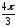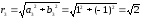
₃
=

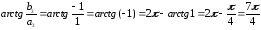
(угол находится в 4-ой четверти).

z₃
= r₃(cos₃
+ isin₃)
=
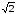(cos

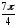
+ isin
)

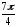Для
нахождения z₂²
воспользуемся формулой Муавра:

(r
(cos
+ i sin))
ⁿ
= rⁿ
(cos n
+ i sin n)

z₂²
= r₂²(cos2₂
+ isin2₂)
= 2²
(cos

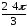
+ isin
)
=

=

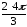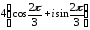
Аналогично
находим
z₃⁴
= r₃⁴(cos4₂
+ isin4₂)
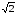= ()⁴
(cos

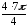
+ isin
)
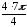= 4(cos 7
+ isin 7)
= 4(cos (6
+ )
+ isin (6
+ ))
= 4(cos 
+ i sin )

Находим

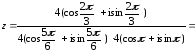
Произведение
двух комплексных чисел в тригонометрической
форме находят по формуле

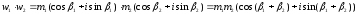
Тогда

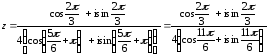
Частное
двух комплексных чисел в тригонометрической
форме находят по формуле

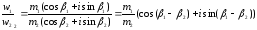
Тогда

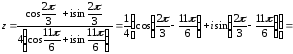
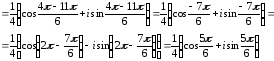
в)
z
= r
e
^i
φ
– показательная форма комплексного
числа.

z₁
= r₁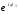
= 4e

z₂
= r₂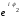
= 2e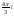

z₃
= r₃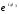
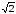=e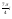

Далее
воспользуемся формулой Муавра:

(r
)
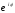ⁿ
= r
ⁿ

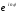
z₂²
= 2² e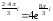

Аналогично
находим z₃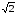⁴
= ()⁴
=
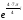4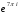

Находим

2)
Найдем расстояние d
между точками

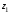
и

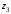
на комплексной плоскости, которое равно
модулю их разности.

Разность
двух комплексных чисел вычисляем по
формуле:

(а₁
+ b₁
i) – (а₂
+ b₂
i) = (a₁
– a₂)
+ (b₁
– b₂)
i

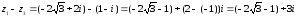
Тогда
расстояние d
между точками

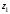
и

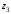
будет

d
=

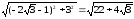
Ответ:
1)
–
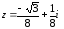алгебраическая форма;
–
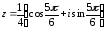тригонометрическая форма; z
=
;
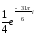2)

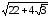
Задание
17

Решить
уравнение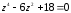
на множестве комплексных чисел.

Решение

Решим
заданное биквадратное уравнение

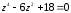
относительно z²:

z²
=

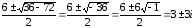
Это
уравнение относительно z²
не имеет решений на множестве действительных
чисел и имеет два решения (z₁²
= 3 + 3i
и z₂²
= 3 – 3i)
на множестве комплексных чисел.

Тогда
z₁
=

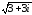
и z₂
=

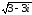
Квадратным
корнем из комплексного числа будет
комплексное число, квадрат которого
равен данному комплексному числу.

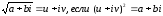.Числа
u
и vопределим
из равенств

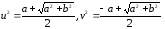
Обозначим
z₁
=
=
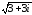u
+ iv.
Тогда

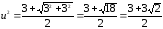
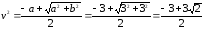
Соответственно

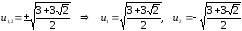
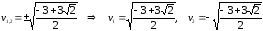
Получили
два значения корней:

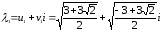
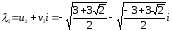
Аналогично
обозначим z₂
=
=
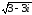w
– it.
Тогда

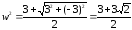
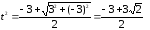
Соответственно

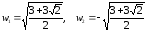
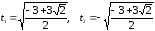
Получили
два значения корней:

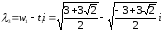
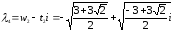
Как
видим, корни λ₁
и λ₃,
λ₂
и λ₄
являются соответственно сопряженными,
т.к. чила z₁
и z₂
– сопряженные.

Ответ:
,

,

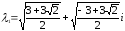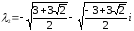
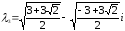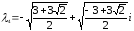
Задание
27

Решите
систему уравнений
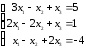тремя
способами:

1)
методом Крамера;

2)
методом обратной матрицы;

3)
методом Гаусса.

Решение

а)
Составим матрицу А системы из коэффициентов
этой системы и найдем определитель
матрицы:

А
=

∆ =

=

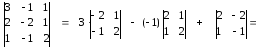
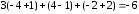
Т.к.
∆ ≠ 0, значит ранг r(A)
матрицы системы и ранг расширенной
матрицы

 

r
(A) равны:
r (A) = r (A) = 3. Значит,
система уравнений совместна и имеет

единственное
решение.

Решим
заданную систему по формулам Крамера.

Решение
системы найдем с помощью вспомогательных
определителей ∆х₁,
∆х₂,
∆х₃:

х₁
= ∆х₁
, х₂
= ∆х₂,
х₃
= ∆х₃

∆
∆ ∆

∆х₁
=

=

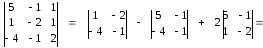
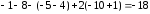
∆х₂
=

=

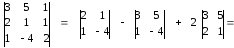
∆х₃
=

=

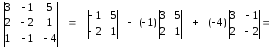
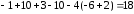
Найдем
корни уравнения:

х₁
= ∆х₁
= -18
= 3

∆
–
6

х₂
= ∆х₂
= – 6
= -1

∆
–
6

х₃
= ∆х₃
= 18
= -3

∆
–
6

б)
Решим данную систему методом Гаусса,
для чего проведем последовательных
элементарных преобразований строк
расширенной матрицы, стремясь к тому,
к тому, чтобы каждая строка, кроме первой,
начиналась с нулей, и число нулей до
первого ненулевого элемента в каждой
следующей строке было больше, чем в
предыдущей.

Представим
систему в виде расширенной матрицы:

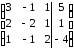
Поменяем
1-ую и 3-ю строки местами:

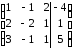
Из
2-ой строки вычтем 1-ую, умноженную на 2.
Из 3-ей строки вычтем 1-ую, умноженную на
3:

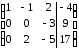
2-ую
строку разделим на (-3) и поменяем ееместами
с 3-ей:

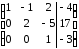
Получили
эквивалентную исходной систему:

 х₁
– х₂
+ 2х₃
= – 4

 2х₂
– 5х₃
= 17

 х₃
= – 3

Последовательно
снизу вверх находим:

х₃
= – 3,

2х₂
– 5 
(-3) = 17 
2х₂
= 2 
х₂ =
1

х₁
– 1 + 2 
(-3) = – 4 
х₁ =
3

в)
Решим исходную систему матричным
методом.

Рассмотрим
три матрицы системы:

матрицу
системы А =

матрицу-
столбец неизвестных В =

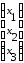
матрицу-
столбец правых частей (свободных членов)
С =

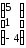
Тогда
систему можно записать в матричном
виде: АВ = С, а т.к. определитель матрицы
А ∆ = detA
= – 6 ≠ 0, то ее решение можно записать в
матричном виде: В = А^-1С,
где А^-1
– матрица, обратная к матрице А.

Составим
матрицу из алгебраических дополнений
к элементам матрицы. А затем транспонируем
ее, т.е. поменяем ее строки на столбцы,
а столбцы на строки и найдем обратную
матрицу А^-1
по формуле:

А^-1
=

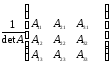
, где А_ij
– алгебраические дополнения соответствующих
элементов.

А₁₁
= (-1)¹⁺¹

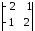
= – 2 · 2 – (-1) · 1 = – 3

А₁₂
= (-1)¹⁺²
=
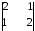– (2 · 2 – 1 · 1) = – 3

А₁₃
= (-1)¹⁺³

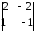
= 2 · (-1) – (-2)· 1 = 0

А₂₁
= (-1)²⁺¹

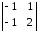
= – ((-1) · 2 – 1· (-1) = 1

А₂₂
= (-1)²⁺²

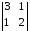
= 3 · 2 – 1 · 1 = 5

А₂₃
= (-1)²⁺³

= – (3 · (-1) – 1 · (-1)) = 2

А₃₁
= (-1)³⁺¹

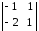
= (-1) · 1 – (- 2) · 1 = 1

А₃₂
= (-1)³⁺²

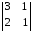
= – (3 · 1 – 2 · 1) = – 1

А₃₃
= (-1)³⁺³

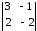
= 3 · (- 2) – 2 · (-1) = – 4

А^-1
=

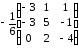
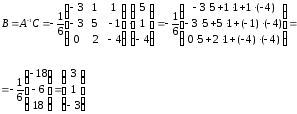
Таким
образом, х₁
= 3; х₂
= 1; х₃
= – 3

Ответ:
х₁
= 3; х₂
= 1; х₃
= – 3

Задание
37

Даны
три вектора


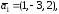
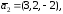
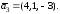
Докажите, что векторы

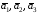
образуют базис, и определите, какая это
тройка векторов: правая или левая.

Решение

3)
Найдем смешанное произведение векторов

:

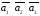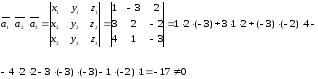
Т.к.
≠
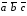0, значит данные векторы не компланарны.
Таким образом, они линейно независимы
и образуют базис. При этом, они образуют
левую тройку векторов, т.к. их смешанное
произведение – число отрицательное:

=
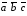
– 17 
0.

Ответ:
Векторы

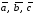
образуют
базис, тройка векторов

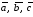
– левая.

Задание
47

Даны
координаты вершин треугольной пирамиды
А₁А₂А₃А₄:

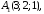
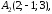
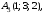
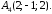Найдите:

1)
угол между ребрами

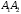
и

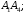
2)
площадь грани

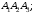
3)
высоту, опущенную из вершины

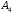
на грань

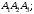
4)
уравнение прямой, проходящей через
ребро

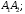
5)
уравнение плоскости, которой принадлежит
грань

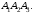
6)
массу материальной треугольной пирамиды

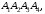
изготовленной из меди плотности

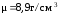
(считая, что 1 масштабная единица в
системе координат равна 1 см).

Решение

1)
Найдем направляющий вектор прямой
А₁А₂:

-.

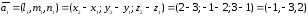Аналогично
найдем направляющий вектор прямой А₁А₄:

–
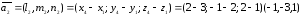направляющий вектор прямой А₁А₄
.

Угол
между ребрами А₁А₂
и А₁А₄
найдем как угол 
между векторами
:

_ ^
_

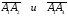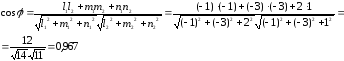
Следовательно,
(А₁А₂,
А₁А₄)
= 
= arccos
0,967 
0,258(рад) 
14,76 ^о

2)
Найдем площадь грани А₁ А₂
А_3.

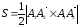
Имеем

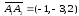
_Найдем

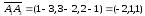
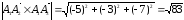
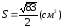
3) Найдем уравнение
высоты, опущенной из вершины

на грань
;
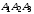по формуле:

,

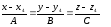
где N(A,
B,C) –
нормальный вектор к плоскости А₁А₂
А₃, являющийся направляющим
вектором искомой высоты.

Имеем:

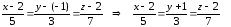
4)
Запишем уравнение прямой, проходящей
через ребро А₁А₂
в виде уравнения прямой, проходящей
через две точки А₁
и А₂:

–
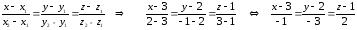
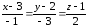уравнение прямой
А₁А₂.

5)
Найдем уравнение плоскости, которой
принадлежит грань А₁А₂
А₃
по трем точкам:

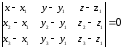
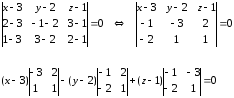
(x-3)(
– 3 – 2) – (y
– 2)( -1 + 4) + ( z
– 1)(-1 – 6) = 0

–
5(x-3)
– 3(y
– 2) – 7( z
– 1) = 0

–
5x
– 3y
– 7z
+ 28 = 0 

5x
+ 3y
+ 7z
– 28 = 0 – общее уравнение плоскости А₁А₂
А₃.

=
(A,
B,
C)
= (5, 3, 7) – нормальный вектор плоскости
А₁А₂
А₃.

6)
Массу пирамиды

изготовленной из меди плотности
,
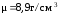найдем по формуле:

m =
 V,
где V – объем пирамиды.

Найдем объём
пирамиды по формуле:

V =
,

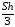где S-
площадь грани А₁ А₂ А_3, h
– высота, опущенная из вершины А₄.

Найдем длину
высоты h как расстояние
от точки А₄ (2; -1; 2) до

плоскости А₁
А₂ А₃:

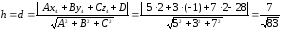
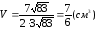
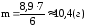
Ответ:
1) 14,76
^о;
2)
;
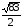3)
;

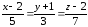4);

;
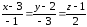5) 5x
+ 3y
+ 7z
– 28 = 0; 6) 10,4 грамма.

Задание
57

Изобразите
геометрическое место точек, заданных
уравнением

:

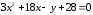1)
на плоскости,

2)
в пространстве.

Решение

1. Преобразуем
   уравнение, выделив полный квадрат:

3(х²
+ 6х + 9) – у – 27 + 28 = 0

3(х
+ 3)²
= у – 1

(х
+ 3)²
=
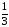(у
– 1)

Введем
новые координаты:

х
+ 3 = х,
у – 1 = у

Тогда
уравнение примет вид

х
′ ²
=
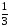
у′

Получили
каноническое уравнение параболы
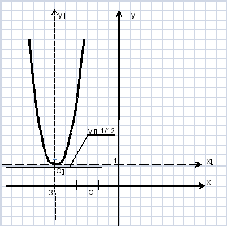
симметричной относительно оси ординат.
Ветви ее обращены в положительную
сторону оси ординат. Вершина находится
в точке О′ (- 3; 1) в системе координат
хОу.

2р
=
,
р =

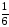
Изобразим
полученную параболу на плоскости хОу:

В
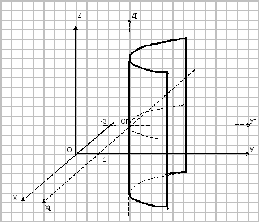
пространстве данное уравнение описывает
параболический цилиндр, который
пересекает плоскость хОу по параболе
с вершиной в точке (-3, 1, 0).