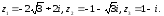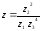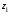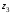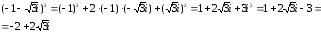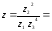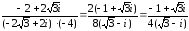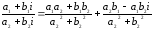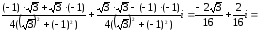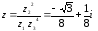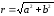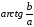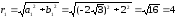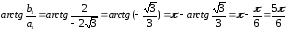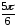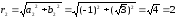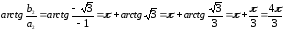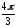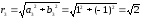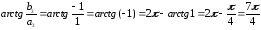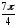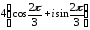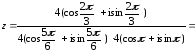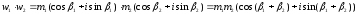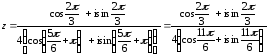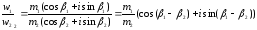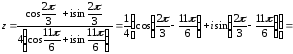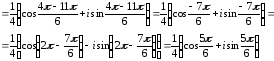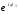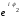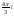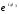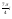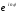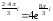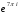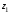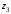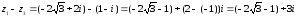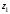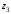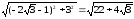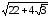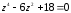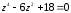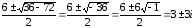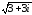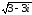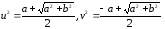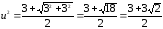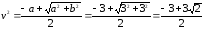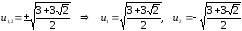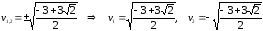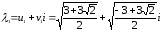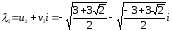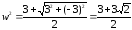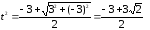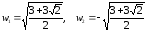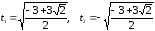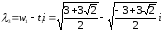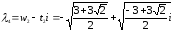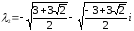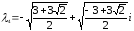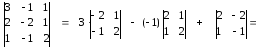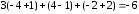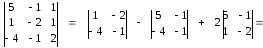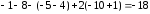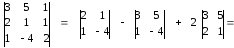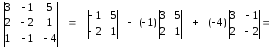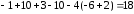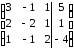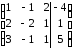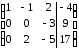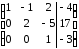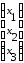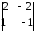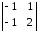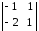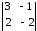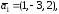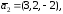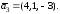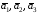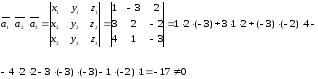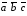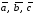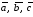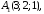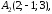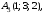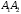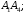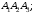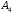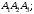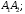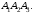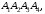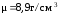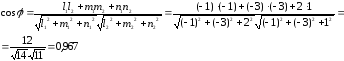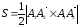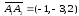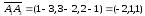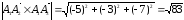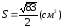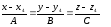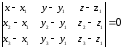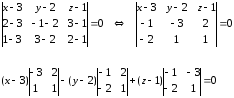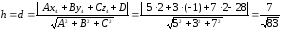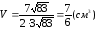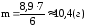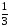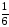Как найти расстояние между комплексными точками - Сайт, где вы сможете решить свои вопросы

Комплексные числа

Краткая теория

Комплексным числом

называется
выражение вида

, где

– действительные
числа, а символ

удовлетворяет
условию

Число

называется
действительной частью комплексного
числа и обозначается

–
мнимой частью и обозначается

–
мнимой единицей.

Комплексные числа

называется
комплексно-сопряженными. Так, если

, то

Сложение, вычитание и умножение
комплексным чисел, заданных в алгебраической форме, выполняются по правилам
сложения, вычитания и умножения двучленов вида

с заменой
каждый раз

на

. Деление выполняется по формуле:

Геометрически комплексное число

изображается
точкой

на координатной
плоскости или радиус-вектором

этой точки.

Тригонометрическая форма комплексного числа

имеет вид:

где

– модуль числа

;

– его аргумент

– величина угла
между положительным направлением оси

и
радиусом-вектором

(см. рисунок),
причем величина угла считается положительной, если отсчет ведется против
часовой стрелки, и отрицательной – если по часовой стрелке.

Величина угла

определяется из
системы уравнений:

Значение

(или

) обозначается

и называется
главным.

Действия над комплексными числами в тригонометрической форме

Если

то

то есть при умножении комплексных
чисел, заданных в тригонометрической форме, их модули перемножаются, аргументы
складываются, а при делении модули делятся, а аргументы вычитаются.
Геометрический умножение данного комплексного числа на другое комплексное
число, отличное от нуля, означает поворот радиус-вектора, изображающего данное
число, против часовой стрелки на угол, равный аргументу другого числа.
Аналогично деление означает поворот радиуса-вектора данного числа по часовой
стрелке на угол, равный аргументу другого числа, и деление этого вектора на
модуль другого числа.

При возведении в степень
используется формула Муавра

Все значения корня степени

из комплексного
числа

находятся по
формуле

Показательная форма комплексного числа

имеет вид

, где

– формула
Эйлера.

Действия над комплексными числами в показательной форме

Если

то

Если

то

Примеры решения задач

Задача 1

Даны комплексные числа

.
Вычислить

Решение

Последовательно вычисляем:

Окончательно получаем:

Ответ:

Задача 2

1) Записать число

в
алгебраической форме;

2) изобразить его на
координатной плоскости;

3) записать число

в
тригонометрической и показательной формах;

4) вычислить

;

5) найти все корни
уравнения

Решение

1) Запишем число

в
алгебраической форме:

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

2) Изобразим число

на
координатной плоскости:

3) Запишем
число

в
тригонометрической и показательной формах

Модуль комплексного числа:

Вектор

лежит в 4-й четверти. Аргумент комплексного
числа:

Комплексное число в тригонометрической форме:

Комплексное число в показательной форме:

4) Возведем
комплексное число в заданную степень:

5) Найдем корни
уравнения

Получаем:

Тогда корни уравнения:

Задача 3

Даны три комплексных числа

1) выполните действия в
алгебраической, тригонометрической и показательной формах;

2) найдите расстояние
между точками

на
комплексной плоскости.

Решение

1) Запишем числа в тригонометрической форме:

Вектор

лежит в
2-й четверти

Число в показательной форме:

Число в тригонометрической форме:

Вектор

лежит в
4-й четверти

Число в показательной форме:

Число в тригонометрической форме:

Вектор

лежит в
3-й четверти

Число в показательной форме:

Число в тригонометрической форме:

Выполним действия в алгебраической форме:

Выполним действия в тригонометрической форме:

Выполним действия в
показательной форме:

2) Найдем расстояние между
точками

на
комплексной плоскости:

Источник

Расстояние между комплексными числами

Знаток

(264),
на голосовании

7 месяцев назад

Голосование за лучший ответ

иван иванов

Искусственный Интеллект

(131335)

8 месяцев назад

Модуль комплексного числа $z=x+iy$ равен длине вектора, соответствующего данному числу на комплексной плоскости, $$|z|= sqrt{x^2+y^2}.$$ Несложно проверить, что расстояние между двумя точками комплексной плоскости $z_1$ и $z_2$ равно $|z_1-z_2|$. То есть, модуль разности двух комплексных чисел есть расстояние между точками на комплексной плоскости, которым соответствуют этим числам.

Источник

The length of the line segment connecting two points is defined as the distance between them. The length of the line segment connecting the specified coordinates can be used to compute the distance between two points in coordinate geometry. Let’s look at the formula for calculating the distance between two points in a two-dimensional or three-dimensional plane.

What is the Distance Between Two Points?

The distance of the line segment connecting any two points is the distance between them. There is only one line that connects two points. As a result, the distance between two points may be computed by determining the length of the line segment that connects the two spots. For example, if A and B are two points and A B = 20 cm, it implies the distance between A and B is 20 cm.

The length of the line segment connecting two points is the distance between them (but this CANNOT be the length of the curve joining them). It is important to note that the distance between two places is always positive.

Distance Between Two Points Formula

The distance formula is used to determine the distance between two points using the provided coordinates. We use the 2D distance formula or the Euclidean distance formula to calculate the distance between any two points in the 2-D plane.

Formula for Distance Between Two Points

The formula for the distance, d, between two points whose coordinates are (x₁, y₁) and (x_2,y₂) is

$d = sqrt{[(x_2 - x_1 )^2 +(y_2 - y_1)^2]}$

This is called the Distance Formula.

To find the distance between two points given in 3-D plane, we can apply the 3D distance formula, given as,

$d = sqrt{[(x_2 - x_1 )^2 +(y_2 - y_1)^2 + (z_2 - z_1 )^2]}$

Derivation of Formula for Distance Between Two Points

To obtain the formula for calculating the distance between two points on a two-dimensional plane, assume there are two points with the coordinates, A (x₁,y₁) and B (x₂,y₂). Following that, we will suppose that the line segment connecting A and B is AB = d. We will now plot the specified points on the coordinate plane and connect them with a line.

Next, we will construct a right-angled triangle using AB as the hypotenuse.

Using Pythagoras Theorem,

AB²= AC²+ BC²

d² = (x₂−x₁)² + (y₂−y₁)²

Here, the vertical distance between the given points is | y₂ – y₁|

The horizontal distance between the given points is | x₂ – x₁ |

$d = sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2] }$ (Taking square root on both sides)

Thus, the distance formula to find the distance between two points is proved.

Using similar steps and concept, we can also derive the formula to find the distance between two points given in the 3D plane.

Steps to find the distance between two points

The following steps may be used to determine the distance between two places using the provided coordinates:

Make a note of the coordinates of the two given points on the coordinate plane as follows: A(x₁,y₁) and B(x₂,y₂).
We may use the distance formula to calculate the distance between two places, $d = sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2]}.$
Express the given answer in units.

Note: We can apply the 3D distance formula in case the two points are given in 3D plane,

Sample Problems

Problem 1: Find the distance between the two points with the coordinates given as, A(1,5) and B (2,7).

Solution:

Let (x₁, y₁) be (2,7) and (x₂, y₂) be (1,5).

The distance d between the points : $d = sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2]}$

$implies sqrt{[(2-1)^2 + (7-5)^2]}$

$implies sqrt{[1^2 + 2^2]}$

The distance between the two points is √5 units.

Problem 2: Find the distance between the two points with the coordinates given as, P (2,-6,2) and Q(7, 3, 1).

Solution:

Let (x₁, y₁, z₁) be P (2,-6,2) and (x₂, y₂, z₂) be Q (7,3,1).

The distance d between the points P and Q : $d = sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2+(z_2-z_1)^2]}$

$implies sqrt{(7-2)^2+(3-(-6))^2+(1-2)^2)}$

$implies sqrt{ 5^2+9^2+(-1)^2}$

Problem 3: Prove that the vertices of a right-angled triangle are the points (3, 4), (7, 4), and (3, 8).

Solution:

Let us say the given points be:

P = (3, 4)

Q = (7, 4)

R = (3, 8)

Now, we will find each vertices of the right-angle triangle by distance formula.

$AB=sqrt{(7-3)^2+(4-4)^2}=sqrt{4^2}=4units$

$BC=sqrt{(3-7)^2+(8-4)^2}=sqrt{(-4)^2+4^2}=4sqrt{2}units$

$AC=sqrt{(3-3)^2+(8-4)^2}=sqrt{4^2}=4units$

As we know the length of the sided of the right-angled triangle, by Pythagoras Theorem;

AB²+ AC²= BC²

4²+4²=(4√2)²

16+16 = 32⟹32 = 32

This proves that ABC is a right-angle triangle.

Distance Between Two Points in Complex Plane

The distance between two points in a complex plane or two complex numbers z₁=a+ib and z₂=c+id in the complex ⟹1−2k=9+4k plane is the distance between points (a, b) and (c, d), given as,

$| z_2 - z_1 |= sqrt{[(a − c)^2 + (b − d)^2]}$

Problem 4: Find the distance between the two complex numbers z₁= 2−5i and z₂= 7+7i

Solution:

Here, we have two complex numbers z₁= 2-5i and z₂= 7+7i.

The distance between these complex numbers is equidistance to the two points in the plane, with coordinates, (2,-5) and (7,7).

Thus, distance between the two points is

$implies sqrt{(7-2)^2+(7-(-5))^2}$

$implies sqrt{5^2+12^2}implies sqrt{25+144}$

Hence, the distance between two complex numbers z_1=2-5i and z_2=7+7i is 13 units.

Problem 5: A complex number ω is 6 units apart from z₁= -3 – i and 6 units apart from z₂= 3 + 5i. Check whether the triangle formed by ω, z₁, z₂ is right – angled or not.

Solution:

There are 3 complex numbers ω, z₁, z₂.

As we know the distance between ω and z₁ is 6 units and distance between ω and z₂ is 6 units.

Given, ω, z₁= 6 units

ω, z₂= 6 units

Now, we will find the distance between z₁and z₂ by using distance formula.

$z_1z_2=sqrt{(3-(-3)+(5-(-1))}$

$implies sqrt{6^2+6^2}$

By Pythagoras Theorem, we have;

(z₁z₂)²=(ωz₁)²+(ωz₂)²

$implies (6sqrt{2})^2=6^2+6^2$

Hence, we conclude that the given triangle is right-angle triangle.

Problem 6: Find a point on the x-axis that is equidistant from the points (1, -2) and (-2, -3).

Solution:

We know that any point on the x-axis has an y-coordinate of 0. As a result, we consider the point equidistant from the provided points to be (k,0). i.e., Distance between ( k,0) and (1, -2) = Distance between (k, 0) and (-2, -3).

$implies sqrt{[(1-k)^2 + (-2-0)^2]} = sqrt{[(-2-k)^2 + (-3-0)^2]}$

implies -4k-2k= 9-1

$implies k=frac{-4}{3}$

Therefore, the required point is (k, 0) = $(frac{-4}{3}, 0).$

Источник

Контрольная
работа №1

Задание
7

Даны
три комплексных числа

1)
выполните действия

в алгебраической, тригонометрической
и показательной формах;

2)
найдите расстояние между точками

и

на комплексной плоскости.

Решение

1)
а) Найдем число
в
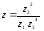
в алгебраической
форме.

Найдем
поэтапно:

z₂²
=

z₃⁴
= [(1-i)²]²
= (1 – 2i
+ i²)²
= (1 – 2i
– 1)²
= (- 2i)²
= 4i²
= – 4

Найдем
частное двух комплексных чисел по
формуле:

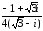
Итак,

б)
Тригонометрическая форма комплексного
числа: w
= r(cos
+ isin),
где

–
модуль комплексного числа,

 =

аргумент комплексного числа

Представим
числа z₁,
z₂,
z₃
в тригонометрической форме:

₁
=

(угол находится во 2-ой четверти).

z₁
= r₁(cos₁
+ isin₁)
= 4(cos

+ isin
)

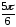
₂
=

(угол находится в 3-ей четверти).

z₂
= r₂(cos₂
+ isin₂)
= 2(cos

+ isin
)

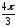
₃
=

(угол находится в 4-ой четверти).

z₃
= r₃(cos₃
+ isin₃)
=
(cos

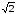
+ isin
)

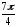
Для
нахождения z₂²
воспользуемся формулой Муавра:

(r
(cos
+ i sin))ⁿ
= rⁿ
(cos n
+ i sin n)

z₂²
= r₂²(cos2₂
+ isin2₂)
= 2²(cos

+ isin
)
=

=

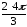
Аналогично
находим
z₃⁴
= r₃⁴(cos4₂
+ isin4₂)
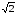
= ()⁴(cos

+ isin
)
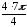
= 4(cos 7
+ isin 7)
= 4(cos (6
+ )
+ isin (6
+ ))
= 4(cos 
+ i sin )

Находим

Произведение
двух комплексных чисел в тригонометрической
форме находят по формуле

Тогда

Частное
двух комплексных чисел в тригонометрической
форме находят по формуле

Тогда

в)
z
= r
eⁱ^φ
– показательная форма комплексного
числа.

z₁
= r₁
= 4e

z₂
= r₂
= 2e

z₃
= r₃
=e

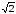
Далее
воспользуемся формулой Муавра:

(r
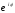
)ⁿ
= r
ⁿ

z₂²
= 2²e

Аналогично
находим z₃⁴
= ()⁴
=
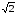
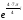
4

Находим

2)
Найдем расстояние d
между точками

и

на комплексной плоскости, которое равно
модулю их разности.

Разность
двух комплексных чисел вычисляем по
формуле:

(а₁
+ b₁
i) – (а₂
+ b₂
i) = (a₁
– a₂)
+ (b₁
– b₂)
i

Тогда
расстояние d
между точками

и

будет

d
=

Ответ:
1)
–
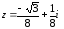
алгебраическая форма;
–
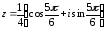
тригонометрическая форма; z
=
;
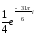
2)

Задание
17

Решить
уравнение
на множестве комплексных чисел.

Решение

Решим
заданное биквадратное уравнение

относительно z²:

z²
=

Это
уравнение относительно z²
не имеет решений на множестве действительных
чисел и имеет два решения (z₁²
= 3 + 3i
и z₂²
= 3 – 3i)
на множестве комплексных чисел.

Тогда
z₁
=

и z₂
=

Квадратным
корнем из комплексного числа будет
комплексное число, квадрат которого
равен данному комплексному числу.

.Числа
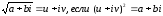
u
и vопределим
из равенств

Обозначим
z₁
=
=
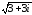
u
+ iv.
Тогда

Соответственно

Получили
два значения корней:

Аналогично
обозначим z₂
=
=
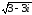
w
– it.
Тогда

Соответственно

Получили
два значения корней:

Как
видим, корни λ₁
и λ₃,
λ₂
и λ₄
являются соответственно сопряженными,
т.к. чила z₁
и z₂
– сопряженные.

Ответ:
,

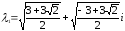
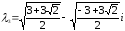
Задание
27

Решите
систему уравнений
тремя
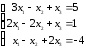
способами:

1)
методом Крамера;

2)
методом обратной матрицы;

3)
методом Гаусса.

Решение

а)
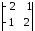
Составим матрицу А системы из коэффициентов
этой системы и найдем определитель
матрицы:

А
=

∆ =

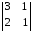
Т.к.
∆ ≠ 0, значит ранг r(A)
матрицы системы и ранг расширенной
матрицы

 

r
(A) равны:
r (A) = r (A) = 3. Значит,
система уравнений совместна и имеет

единственное
решение.

Решим
заданную систему по формулам Крамера.

Решение
системы найдем с помощью вспомогательных
определителей ∆х₁,
∆х₂,
∆х₃:

х₁
= ∆х₁
, х₂
= ∆х₂,
х₃
= ∆х₃

∆
∆ ∆

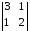
∆х₁
=

∆х₂
=

∆х₃
=

Найдем
корни уравнения:

х₁
= ∆х₁
= -18
= 3

∆
–
6

х₂
= ∆х₂
= – 6
= -1

∆
–
6

х₃
= ∆х₃
= 18
= -3

∆
–
6

б)
Решим данную систему методом Гаусса,
для чего проведем последовательных
элементарных преобразований строк
расширенной матрицы, стремясь к тому,
к тому, чтобы каждая строка, кроме первой,
начиналась с нулей, и число нулей до
первого ненулевого элемента в каждой
следующей строке было больше, чем в
предыдущей.

Представим
систему в виде расширенной матрицы:

Поменяем
1-ую и 3-ю строки местами:

Из
2-ой строки вычтем 1-ую, умноженную на 2.
Из 3-ей строки вычтем 1-ую, умноженную на
3:

2-ую
строку разделим на (-3) и поменяем ееместами
с 3-ей:

Получили
эквивалентную исходной систему:

 х₁
– х₂
+ 2х₃
= – 4

 2х₂
– 5х₃
= 17

 х₃ = – 3

Последовательно
снизу вверх находим:

х₃ = – 3,

2х₂ – 5 
(-3) = 17 
2х₂
= 2 
х₂=
1

х₁
– 1 + 2 
(-3) = – 4 
х₁=
3

в)
Решим исходную систему матричным
методом.

Рассмотрим
три матрицы системы:

матрицу
системы А =

матрицу-
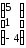
столбец неизвестных В =

матрицу-
столбец правых частей (свободных членов)
С =

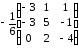
Тогда
систему можно записать в матричном
виде: АВ = С, а т.к. определитель матрицы
А ∆ = detA
= – 6 ≠ 0, то ее решение можно записать в
матричном виде: В = А^-1С,
где А^-1
– матрица, обратная к матрице А.

Составим
матрицу из алгебраических дополнений
к элементам матрицы. А затем транспонируем
ее, т.е. поменяем ее строки на столбцы,
а столбцы на строки и найдем обратную
матрицу А^-1
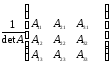
по формуле:

А^-1
=

, где А_ij
– алгебраические дополнения соответствующихэлементов.

А₁₁
= (-1)¹⁺¹

= – 2 · 2 – (-1) · 1 = – 3

А₁₂
= (-1)¹⁺²=
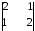
– (2 · 2 – 1 · 1) = – 3

А₁₃
= (-1)¹⁺³

= 2 · (-1) – (-2)· 1 = 0

А₂₁
= (-1)²⁺¹
= – ((-1) · 2 – 1· (-1) = 1

А₂₂
= (-1)²⁺²
= 3 · 2 – 1 · 1 = 5

А₂₃
= (-1)²⁺³
= – (3 · (-1) – 1 · (-1)) = 2

А₃₁
= (-1)³⁺¹
= (-1) · 1 – (- 2) · 1 = 1

А₃₂
= (-1)³⁺²
= – (3 · 1 – 2 · 1) = – 1

А₃₃
= (-1)³⁺³
= 3 · (- 2) – 2 · (-1) = – 4

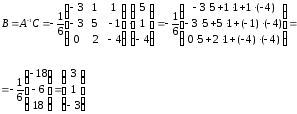
А^-1
=

Таким
образом, х₁
= 3; х₂
= 1; х₃
= – 3

Ответ:
х₁
= 3; х₂
= 1; х₃
= – 3

Задание
37

Даны
три вектора

Докажите, что векторы

образуют базис, и определите, какая это
тройка векторов: правая или левая.

Решение

3)
Найдем смешанное произведение векторов

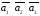
Т.к.
≠
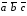
0, значит данные векторы не компланарны.
Таким образом, они линейно независимы
и образуют базис. При этом, они образуют
левую тройку векторов, т.к. их смешанное
произведение – число отрицательное:

=
– 17 
0.

Ответ:
Векторы
образуют
базис, тройка векторов
– левая.

Задание
47

Даны
координаты вершин треугольной пирамиды
А₁А₂А₃А₄:

Найдите:

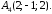
1)
угол между ребрами

и

2)
площадь грани

3)
высоту, опущенную из вершины

на грань

4)
уравнение прямой, проходящей через
ребро

5)
уравнение плоскости, которой принадлежит
грань

6)
массу материальной треугольной пирамиды

изготовленной из меди плотности

(считая, что 1 масштабная единица в
системе координат равна 1 см).

Решение

1)
Найдем направляющий вектор прямой
А₁А₂:

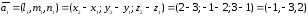
Аналогично
найдем направляющий вектор прямой А₁А₄:

–
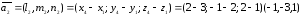
направляющий вектор прямой А₁А₄
.

Угол
между ребрами А₁А₂и А₁А₄
найдем как угол 
между векторами
:

_ ^
_

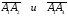
Следовательно,
(А₁А₂,
А₁А₄)
= 
= arccos
0,967 
0,258(рад) 
14,76 ^о

2)
Найдем площадь грани А₁ А₂
А_3.

Имеем

_Найдем

3) Найдем уравнение
высоты, опущенной из вершины

на грань
;
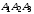
по формуле:

где N(A,
B,C) –
нормальный вектор к плоскости А₁А₂
А₃, являющийся направляющим
вектором искомой высоты.

Имеем:

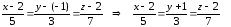
4)
Запишем уравнение прямой, проходящей
через ребро А₁А₂
в виде уравнения прямой, проходящей
через две точки А₁
и А₂:

–
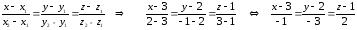
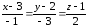
уравнение прямой
А₁А₂.

5)
Найдем уравнение плоскости, которой
принадлежит грань А₁А₂
А₃
по трем точкам:

(x-3)(
– 3 – 2) – (y
– 2)( -1 + 4) + ( z
– 1)(-1 – 6) = 0

–
5(x-3)
– 3(y
– 2) – 7( z
– 1) = 0

–
5x
– 3y
– 7z
+ 28 = 0 

5x
+ 3y
+ 7z
– 28 = 0 – общее уравнение плоскости А₁А₂
А₃.

=
(A,
B,
C)
= (5, 3, 7) – нормальный вектор плоскости
А₁А₂
А₃.

6)
Массу пирамиды

изготовленной из меди плотности
,
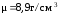
найдем по формуле:

m =
 V,
где V – объем пирамиды.

Найдем объём
пирамиды по формуле:

V =
,

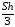
где S-
площадь грани А₁ А₂ А_3,h
– высота, опущенная из вершины А₄.

Найдем длину
высоты h как расстояние
от точки А₄(2; -1; 2) до

плоскости А₁
А₂ А₃:

Ответ:
1) 14,76
^о;
2)
;
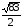
3)
;

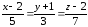
4);

;
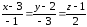
5) 5x
+ 3y
+ 7z
– 28 = 0; 6) 10,4 грамма.

Задание
57

Изобразите
геометрическое место точек, заданных
уравнением

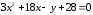
1)
на плоскости,

2)
в пространстве.

Решение

Преобразуем
уравнение, выделив полный квадрат:

3(х²
+ 6х + 9) – у – 27 + 28 = 0

3(х
+ 3)²
= у – 1

(х
+ 3)²
=
(у
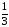
– 1)

Введем
новые координаты:

х
+ 3 = х,
у – 1 = у

Тогда
уравнение примет вид

х
′²
=
у′

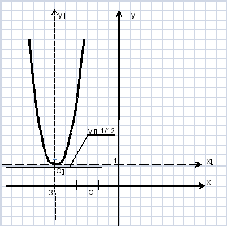
Получили
каноническое уравнение параболы
симметричной относительно оси ординат.
Ветви ее обращены в положительную
сторону оси ординат. Вершина находится
в точке О′ (- 3; 1) в системе координат
хОу.

2р
=
,
р =

Изобразим
полученную параболу на плоскости хОу:

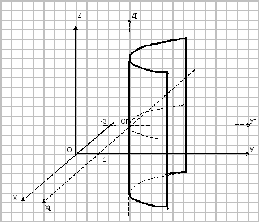
В
пространстве данное уравнение описывает
параболический цилиндр, который
пересекает плоскость хОу по параболе
с вершиной в точке (-3, 1, 0).

Источник

Ко́мпле́ксная^[1] плоскость — геометрическое представление множества комплексных чисел .

Геометрическое представление комплексного числа

Точка двумерной вещественной плоскости $mathbb {R} ^{2}$ , имеющая координаты (x,y) , изображает комплексное число z=x+iy , где:

— действительная (вещественная) часть комплексного числа,

— его мнимая часть.

Другими словами, комплексному числу z=x+iy соответствует радиус-вектор с координатами (x,y). Алгебраическим операциям над комплексными числами соответствуют операции над соответствующими им точками или векторами. Тем самым различные соотношения между комплексными числами получают наглядное изображение на комплексной плоскости:

Комплекснозначные функции комплексного переменного интерпретируются как отображения комплексной плоскости в себя. Особую роль в комплексном анализе играют конформные отображения.

Множества на комплексной плоскости[править | править код]

Открытые множества[править | править код]

Фундаментальное понятие окрестности вводится на комплексной плоскости очень просто — окрестностью ${{mathcal U}}_{{z_{0}}}$ точки $z_{0}in {mathbb C}$ называется множество вида ${{mathcal U}}_{{z_{0}}}={zcolon |z-z_{0}|<r},,r>0$ . Геометрически на комплексной плоскости окрестности имеют очень простой вид — это просто окружности с центром в определенных точках комплексной плоскости. Иногда для удобства требуется рассматривать проколотые окрестности ${dot {{mathcal U}}}_{{z_{0}}}={{mathcal U}}_{{z_{0}}}setminus {z_{0}}$ .

Теперь определим открытое множество — согласно одному из вариантов классического определения из общей топологии, открытым множество будет, если оно для любой своей точки содержит некоторую её окрестность. Определение окрестности у нас уже есть, соответственно, открытое множество на полностью определено.

Предельная точка и замкнутое множество[править | править код]

Определить предельную точку тоже будет нетрудно — точка $z_{0}in {mathbb C}$ будет предельной для множества , если для произвольной окрестности ${{mathcal U}}_{{z_{0}}}$ пересечение ${{mathcal U}}_{{z_{0}}}cap G$ будет не пусто. Другими словами, точка является предельной, если в произвольной «близости» к ней всегда можно будет найти точки множества. Множество предельных точек иногда называется производным и обозначается .

Множество будет называться замкнутым, если для него справедливо включение . Ясно видно, что для произвольного множества множество будет замкнуто; оно называется замыканием множества .

Граница[править | править код]

Точка $z_{0}in {mathbb C}$ будет называться граничной для множества , если для произвольной окрестности ${{mathcal U}}_{{z_{0}}}$ пересечения ${{mathcal U}}_{{z_{0}}}cap G$ и ${{mathcal U}}_{{z_{0}}}cap ({{mathbb C}}setminus G)$ будут не пусты. Множество всех граничных точек называется граничным множеством
или просто границей.

Всюду плотные множества[править | править код]

Множество будет называться всюду плотным в ином множестве , если для произвольной точки $z_{0}in G$ и любой окрестности ${{mathcal U}}_{{z_{0}}}$ пересечение ${{mathcal U}}_{{z_{0}}}cap E$ не пусто.

Связность[править | править код]

Расстояние между множествами[править | править код]

Как известно из элементарной математики, на комплексной плоскости расстояние между двумя точками равно модулю их разности. Теперь определим расстояние между точкой $z_{0}$ и некоторым множеством как величину ${mathrm {dist}},(z_{0},G)=inf _{{zin G}}|z-z_{0}|$ .

На базе этого понятия уже можно определить расстояние между двумя произвольными множествами в : ${mathrm {dist}},(G_{1},G_{2})=inf _{{zin G_{1}}}{mathrm {dist}},(z,G_{2})=inf _{{zin G_{2}}}{mathrm {dist}},(z,G_{1})$ .

Связность[править | править код]

Множество называется связным, если для него выполнено соотношение $inf _{{z_{1},z_{2}in G}}|z_{1}-z_{2}|=0$ . Если данная величина не равна нулю, то множество называется несвязным. Можно показать, что несвязное множество можно представить в виде объединения (конечного или счетного) $sum G_{n}$ , где $G_{n}$ — непересекающиеся связные множества, называемые связными компонентами множества . Мощность множества связных компонент называется порядком связности.

Выпуклые, звёздные и линейно связные множества[править | править код]

Множество называется звёздным относительно точки $z_{0}in G$ , если для произвольной точки zin G выполняется включение $overline {z_{0}z}subset G$ .

Множество называется выпуклым, если оно звёздно относительно любой своей точки. Множество $G^{*}$ называется выпуклой оболочкой множества , если оно выпукло, $Gsubset G^{*}$ и для любого выпуклого множества $G^{{**}}$ , содержащего множество выполняется включение $G^{*}subset G^{{**}}$ .

Ломаной Gamma называется множество точек комплексной плоскости, представимое в виде объединения отрезков. Множество называется линейно связным, если для двух произвольных точек $z_{1},z_{2}in G$ существует ломаная такая, что выполняется $z_{1},z_{2}in Gamma$ .

Можно доказать, что любое линейно связное множество будет связным. Отсюда немедленно следует, что связны все выпуклые и звёздные множества.

Кривые на [править | править код]

Кривые и пути[править | править код]

Кривой или путём на комплексной плоскости называется отображение вида . Особо стоит отметить, что при таком определении можно конкретизировать не только вид кривой, который будет зависеть от аналитических свойств функции , но и её направление. Для примера, функции и будут определять одинаковую по виду кривую, но проходимую в противоположных направлениях.

Гомотопия кривых[править | править код]

Кривые $varphi _{0}(t)colon [0;1]to {mathbb C}$ и $varphi _{1}(t)colon [0;1]to {mathbb C}$ называются гомотопными, если существует кривая , зависящая от параметра таким образом, что $xi (t,0)equiv varphi _{0}$ и $xi (t,1)equiv varphi _{1}$ .

Аналитическая геометрия на комплексной плоскости[править | править код]

Исследование плоских фигур нередко облегчается, если перенести их на комплексную плоскость. Многие теоремы планиметрии допускают наглядную и компактную запись с помощью комплексных чисел, например^[2]:

Три (различные) точки ${displaystyle z_{1},z_{2},z_{3}}$ лежат на одной прямой тогда и только тогда, когда выполняется условие:

${displaystyle {frac {z_{1}-z_{3}}{z_{2}-z_{3}}}}$

является вещественным числом.

Четыре (различные) точки ${displaystyle z_{1},z_{2},z_{3},z_{4}}$ лежат на одной окружности (или на одной прямой) тогда и только тогда, когда выполняется условие:

отношение ${displaystyle {frac {z_{1}-z_{3}}{z_{2}-z_{3}}}:{frac {z_{1}-z_{4}}{z_{2}-z_{4}}}}$

является вещественным числом.

Параметрическое уравнение прямой на комплексной плоскости имеет вид^[4]:

где

— комплексные числа,

— произвольный вещественный параметр.

Угол между двумя прямыми и равен В частности, прямые перпендикулярны, когда — чисто мнимое число. Две прямые параллельны тогда и только тогда, когда есть вещественное число; если при этом также вещественно, то обе прямые совпадают. Каждая прямая рассекает комплексную плоскость на две полуплоскости: на одной из них выражение ${displaystyle t=operatorname {Im} {frac {z-v}{u}}}$ положительно, на другой — отрицательно^[4].

Уравнение окружности с центром и радиусом имеет чрезвычайно простой вид: Неравенство описывает внутренность окружности^[4]. Часто удобна параметрическая форма уравнения окружности^[5]: ${displaystyle z=c+e^{ivarphi }.}$

Расширенная комплексная плоскость и бесконечно удалённая точка[править | править код]

В комплексном анализе часто полезно рассматривать расширенную комплексную плоскость^[6], дополненную по сравнению с обычной бесконечно удалённой точкой :

{widehat {mathbb {C} }}=mathbb {C} cup {infty }

Геометрически точка infty изображается точкой сферы Римана (её «северный полюс»).

При таком подходе неограниченно возрастающая (по модулю) последовательность считается сходящейся к бесконечно удалённой точке. Алгебраические операции с бесконечностью не производятся, хотя несколько алгебраических соотношений имеют место^[6]:

${frac {z}{infty }}=0; z+infty =infty (zneq infty )$
$zcdot infty =infty ; {frac {z}{0}}=infty (zneq 0)$

-окрестностью бесконечно удалённой точки считается множество точек , модуль которых больше, чем , то есть внешняя часть -окрестностей начала координат.

Расширенная комплексная плоскость называется также сферой Римана, так как она изоморфна обычной сфере $S^{2}$ (изоморфизм можно установить, например, при помощи стереографической проекции). Комплекснозначные функции в некоторых случаях могут быть продолжены на сферу Римана. Поскольку прямые на плоскости (при стереографической проекции) переходят в окружности на сфере, содержащие бесконечно удалённую точку, комплексные функции удобнее рассматривать на сфере.^{[уточнить]}

Примечания[править | править код]

↑
Двойное ударение указано согласно следующим источникам.
- Большая советская энциклопедия, 3-е изд. (1973), том 12, стр. 588, статья Ко́мпле́ксные числа.
- Советский энциклопедический словарь (1982), стр. 613, статья Ко́мпле́ксное число.
- Последнее издание «Словаря трудностей русского языка» (Розенталь Д. Э., Теленкова М. А., Айрис-пресс, 2005, стр. 273) указывает оба варианта: «ко́мплексные (компле́ксные) числа».
- В Большой российской энциклопедии (том 14, 2010 год) по необъяснённым причинам предлагаются одновременно ударения Компле́ксное число (стр. 691), но Ко́мплексный анализ (стр. 695).
↑ Привалов И. И., 1984, с. 43.
↑ Соломенцев Е. Д., 1988, с. 10.
↑ ¹ ² ³ Ahlfors Lars V., 1979, с. 17—18.
↑ Соломенцев Е. Д., 1988, с. 12.
↑ ¹ ² Свешников А. Г., Тихонов А. Н., 1967, с. 20—21.

Литература[править | править код]

Арнольд В. И. Геометрия комплексных чисел, кватернионов и спинов, МЦНМО, 2002.
Понтрягин Л. Комплексные числа, Квант, № 3, 1982.
Привалов И. И. Введение в теорию функций комплексного переменного. — 13-е изд.. — М.: Физматлит, 1984. — 432 с.
Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной.. — М.: Наука, 1967. — 304 с.
Соломенцев Е. Д. Функции комплексного переменногои их применения. — М.: Высшая школа, 1988. — 167 с. — ISBN 5-06-003145-6.
Шабат Б. В. Введение в комплексный анализ: учебник для студентов механико-математических специальностей университетов, СПб.: 2004.
Ahlfors Lars V. Complex analysis. An introduction to the theory of analytic functions of one complex variable. — Third edition. — Harvard University: McGraw-Hill Book Company, 1979. — 317 с. — ISBN 0-07-000657-1.

Источник

Комплексные числа

Действия над комплексными числами в тригонометрической форме

Действия над комплексными числами в показательной форме

Примеры решения задач

Задача 1

Задача 2

Задача 3

Расстояние между комплексными числами

What is the Distance Between Two Points?

Distance Between Two Points Formula

Sample Problems

Distance Between Two Points in Complex Plane

Множества на комплексной плоскости[править | править код]

Открытые множества[править | править код]

Предельная точка и замкнутое множество[править | править код]

Граница[править | править код]

Всюду плотные множества[править | править код]

Связность[править | править код]

Расстояние между множествами[править | править код]

Связность[править | править код]

Выпуклые, звёздные и линейно связные множества[править | править код]

Кривые и пути[править | править код]

Гомотопия кривых[править | править код]

Аналитическая геометрия на комплексной плоскости[править | править код]

Расширенная комплексная плоскость и бесконечно удалённая точка[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как найти доп множители для дробей

Как найти работу в познани

Как найти выборочную дисперсию в статистике

Добавить комментарий Отменить ответ