Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
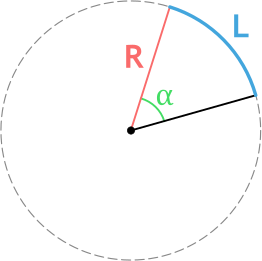
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:
Сегмент
Угол в градусах, образуемый радиусами сектора
Точность вычисления
Знаков после запятой: 2
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Точность вычисления
Знаков после запятой: 2
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Площадь сегмента круга по радиусу и высоте
Точность вычисления
Знаков после запятой: 2
Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
далее используется формула [1] для получения площади.
15 вычислений по сегменту круга в одной программе
Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:
- длина дуги
- угол
- хорда
- высота
- радиус
- площадь
Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.
Круговой сегмент – все варианты расчета
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Математика
Окружность есть такая плоская кривая, у которой все точки находятся на равном расстоянии от одной точки, лежащей внутри ее и называемой центром.
Круг. Кругом называется часть плоскости, ограниченная окружностью.
Радиус. Радиусом называется отрезок, соединяющий центр с какой-нибудь точкой окружности. Радиус есть расстояние точки окружности от центра.
Из самого определения окружности следует, что все ее радиусы равны.
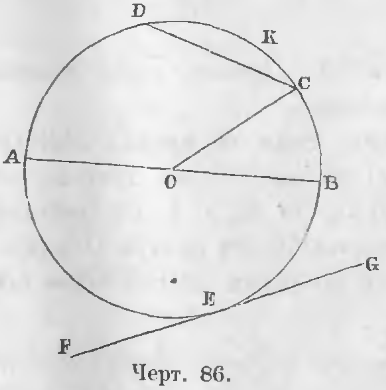
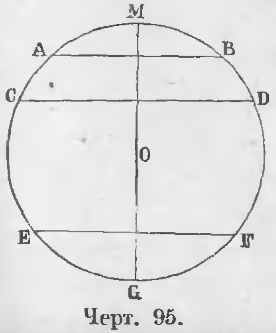
На чертеже 86 кривая линия BCDAEB есть окружность, O ее центр, отрезки OA, OB, OC — радиусы. Эти отрезки равны
Диаметр. Отрезок, проходящий через центр от одной точки окружности до другой, называется диаметром.
Всякий диаметр состоит из двух радиусов, а так как все радиусы равны, то следовательно и все диаметры равны.
Дуга есть часть окружности.
Слово дуга иногда обозначают знаком ◡, так что дугу BC изображают письменно: ◡BC.
Хорда. Отрезок, соединяющий две какие-нибудь точки окружности, называется хордой. Хорда есть прямая, стягивающая две точки дуги.
На чертеже 86 линия AB есть диаметр, часть окружности BC есть дуга, прямая CD есть хорда.
Сегмент есть часть плоскости, содержащийся между дугой и хордой.
Сектор есть часть плоскости, содержащийся между двумя радиусами и дугой круга.
На чертеже 86 площадь COB есть сектор, а CKD сегмент.
Касательная есть прямая, имеющая с окружностью только одну общую точку, которая называется точкой касания.
Углом при центре называется угол, имеющий вершину в центре. На чертеже 86 прямая FG есть касательная, а E точка касания.
Теорема 55. Прямая может пересечь окружность только в двух точках.
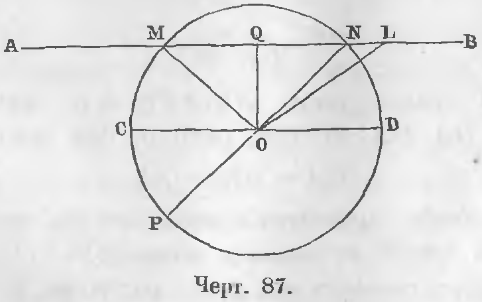
Доказательство. Если бы прямая AB кроме двух точек M и N (черт. 87) имела бы еще третью точку пересечения L, то три точки окружности M, N, L, по свойству окружности, были бы на равном расстоянии от центра O, следовательно, три отрезка MO, NO, LO были бы равны: MO = NO = LO.
Если же NO = LO, то вышло бы, что равные наклонные находятся на неравных расстояниях от перпендикуляра OQ, что противоречит свойству косвенных, следовательно, третьей точки пересечения быть не может (ЧТД).
Теорема 56. Диаметр делит окружность и круг на две равные части.
Доказательство. Перегнем верхнюю часть круга около диаметра CD (черт. 87) до совпадения ее с нижней частью, тогда все точки верхней совпадут с точками нижней части окружности, ибо в противном случае не все точки окружности находились бы на равном расстоянии от центра.
Зависимость между углами, дугами и хордами
Теорема 57. В двух равных кругах равным углам при центре соответствуют равные дуги.
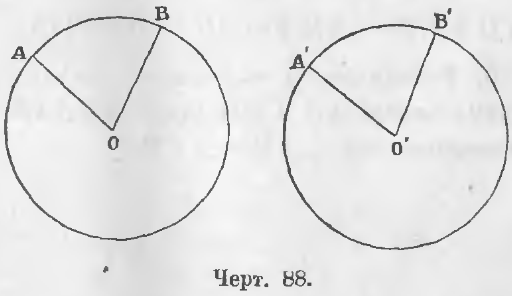
Дано. Две окружности описаны (черт. 88) одними и теми же радиусами и углы при центре равны:
Требуется доказать, что ◡AB = ◡A’B’.
Доказательство. Наложим круг O’ на круг O так, чтобы центр O’ совпал с центром O и сторона OA со стороною O’A’. Точка A’ по равенству радиусов совпадает с точкой A. По равенству углов A’O’B’ и AOB отрезок O’B’ пойдет по отрезку OB и по равенству радиусов точка B’ упадет в точку B. Две крайние точки дуги A’B’ совпадут с двумя крайними точками дуги AB, следовательно, и все промежуточные точки дуги A’B’ совпадут с промежуточными точками дуги AB, так как окружность O’ совпадает с окружностью O, ибо они описаны равными радиусами.
Теорема 58 (обратная 57). Равным дугам соответствуют равные углы.
Дано. Дуги AB и A’B’ равны (◡AB = ◡A’B’) (черт. 88).
Требуется доказать, что ∠AOB = ∠A’O’B’.
Доказательство. Наложим сектор A’O’B’ на сектор AOB так, чтобы отрезок O’A’ совпал с отрезком OA. Дуга A’B’ упадет на дугу AB и B’ упадет в B. Отрезок B’O’ совпадет с отрезком BO и угол AOB совпадет с углом A’O’B’, следовательно,
Теорема 59. Диаметр больше всякой хорды.
Даны диаметр CD и хорда MN (черт. 87).
Требуется доказать, что CD > MN.
Доказательство. Проведем радиусы MO и NO. Ломаная линия MON больше прямой MN
MON > MN или MO + ON > MN
Так как MO = CO, NO = OD, то заменяя MO и NO равными им величинами, получим неравенства:
CO + OD > MN или CD > MN (ЧТД).
Теорема 60. Равные хорды стягивают равные дуги.
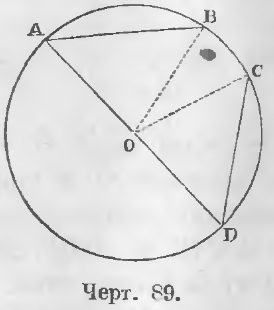
Даны равные хорды AB и CD (черт. 89) (AB = CD).
Требуется доказать, что ◡AB = ◡CD.
Доказательство. Соединив точки A, B, C, D с центром, имеем
OA = OC и OB = OD как радиусы, AB = CD по условию.
Следовательно, ∠AOB = ∠COD, откуда ◡AB = ◡CD (ЧТД).
Теорема 61 (обратная 60). Равные дуги стягиваются равными хордами.
Дано. Дуги AB и CD равны (черт. 89) (◡AB = ◡CD).
Требуется доказать, что AB = CD.
Доказательство. Два треугольника AOB и COD равны, ибо OA = OC и OB = OD как радиусы, ∠AOB = ∠COD ибо по условию дуги AB и CD равны, а потому и углы равны (теорема 58). Следовательно, AB = CD (ЧТД).
Теорема 62. Если дуги меньше полуокружности, то против большей дуги лежит большая хорда.
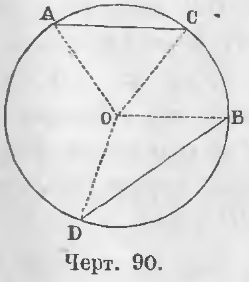
Дано. Дуга BD больше дуги AC (черт. 90) (◡BD > ◡AC).
Требуется доказать, что BD > AC.
Доказательство. Соединим точки A, C, B, D с центром O. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BOD > AOC. Следовательно, BD > AC (теорема 23) (ЧТД).
Теорема 63 (обратная 62). Против большей хорды лежит большая дуга.
Дано. Хорда BD больше хорды AC (черт. 90) (BD > AC).
Требуется доказать, что ◡BD > ◡AC.
Доказательство. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BD > AC по условию. Поэтому ∠BOD > ∠AOC (теорема 24). Следовательно, ◡BD > ◡AC (ЧТД).
Взаимное отношение хорд и их расстояний от центров
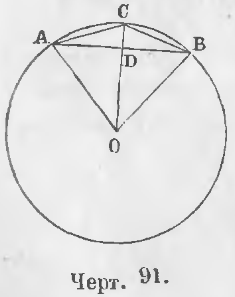
Теорема 64. Радиус, перпендикулярный к хорде, делит как хорду так и дугу пополам.
Радиус OC перпендикулярен к хорде AB (черт. 91).
Требуется доказать, что AD = BD и ◡AC = ◡CB.
Доказательство. Соединим точки A и B с центром O. Равные наклонны OA и OB находятся на равных расстояниях от перпендикуляра OC, следовательно, AD = DB.
Если же перпендикуляр CD восставлен из середины отрезка AB, то его точка C находится на равном расстоянии от концов перпендикуляра, поэтому хорды AC и CB равны, а следовательно,
т. е. дуга AB делится перпендикуляром OC пополам (ЧТД).
Следствие. Перпендикуляр, восставленный из середины хорды, проходит через центр.
Доказательство. Так как центр находится на равном расстоянии от концов хорды, то он находится на перпендикуляре, восставленном из середины хорды.
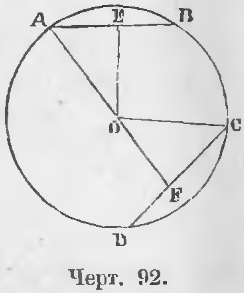
Теорема 65. Равные хорды находятся на равном расстоянии от центра.
Дано. Хорды AB и CD равны: AB = CD (черт. 92).
Требуется доказать, что их расстояния от центра равны, т. е.
Доказательство. Соединив точки A и C с центром O, имеем два равных прямоугольных треугольника AEO и COF, ибо OA = OC как радиусы, AE = CF как половины равных хорд (теорема 64). Следовательно,
Теорема 66 (обратная 65). На равных расстояниях от центра находятся равные хорды.
Дано. Расстояния хорд AB и CD от центра равны, т. е.
Требуется доказать, что AB = CD.
Доказательство. Два прямоугольных треугольника AEO и COF равны, ибо имеют по равной гипотенузе и равному катету. Действительно, OE = OF по условию, OA = OC как радиусы, следовательно, AE = CF или ½AB = ½CD, откуда
Теорема 67. Большая хорда к центру ближе меньшей.
Дано. Хорда AB больше хорды AC (черт. 93), т. е. AB > AC.
Требуется доказать, что OD ⊥ AO.
Требуется доказать, что AF касательная к окружности.
Доказательство. Всякая другая точка B перпендикуляра AB находится на расстоянии BO большем AO, ибо наклонная больше перпендикуляра, следовательно точка B находится вне окружности. Таким образом прямая AB имеет с окружностью только одну общую точку A, следовательно, она будет касательной (ЧТД).
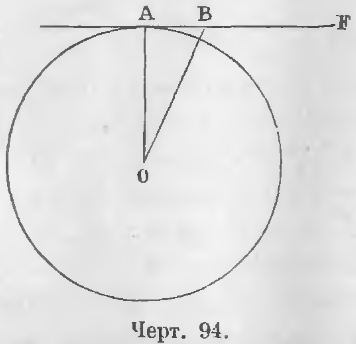
Теорема 69 (обратная 68). Касательная к окружности, проведенная в конец радиуса, перпендикулярна к радиусу.
Дано. Прямая AF касается окружности в точке A (черт. 94).
Требуется доказать, что AF ⊥ OA.
Доказательство. Прямая AB как касательная имеет с окружностью только одну общую точку A. Всякая другая точка B лежит вне окружности, следовательно, всякий отрезок OB больше OA. Таким образом, отрезок OA есть кратчайшее расстояние точки O от AB, следовательно, OA ⊥ AB (ЧТД).
Теорема 70. Между параллельными хордами находятся равные дуги.
Дано. Хорды AB и CD параллельны: AB || CD (черт. 95).
Требуется доказать, что ◡AC = ◡BD.
Доказательство. a) Из центра окружности O опустим перпендикуляр OM на хорду AB, тогла отрезок OM перпендикулярен и к хорде CD.
Вычитая второе равенство из первого, получим:
◡CM – ◡AM = ◡MD – ◡MB или
◡AC = ◡BD.
b) Если параллельные хорды AB и EF (черт. 95) лежат по обе стороны центра, то, продолжив прямую OM до пересечения с окружностью в точке G, имеем:
Так как полуокружности MAG и MBG равны
MAG = MBG, то следовательно,
MAG – ◡MA – ◡GE = MBG – ◡MB – ◡GF
или ◡AE = ◡BF (ЧТД).
Относительное положение двух окружностей
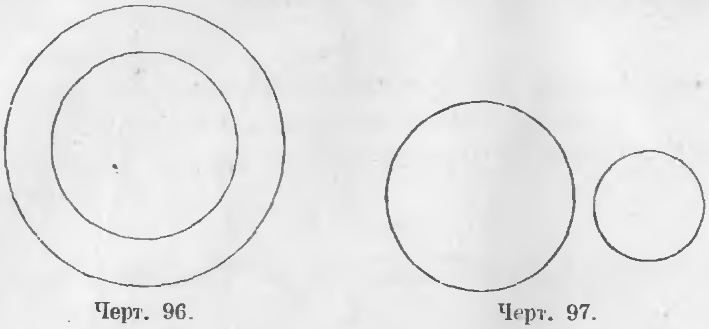
Концентрические и эксцентрические круги. Два круга называются концентрическими, когда они имеют один общий центр, и эксцентрическими, когда из центры не совпадают.
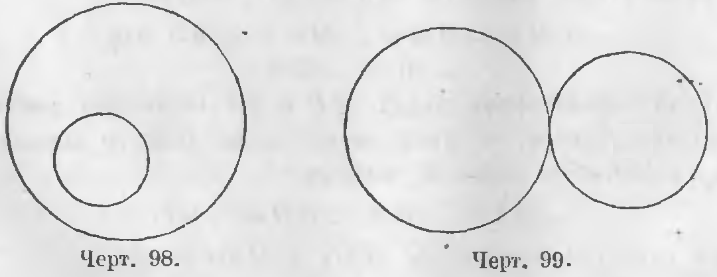
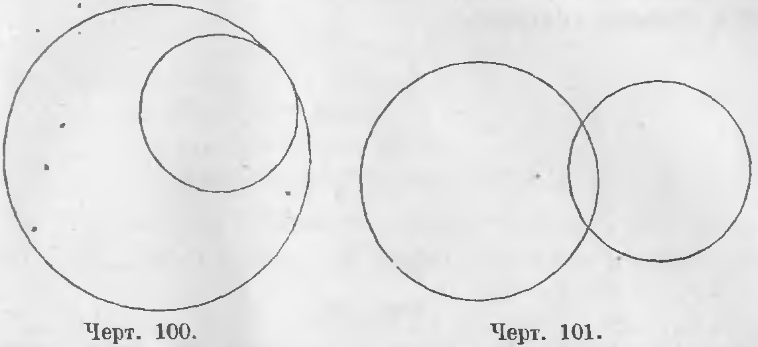
На чертеже 96 представлены круги концентрические и на чертежах 97, 98, 99, 100 и 101 круги эксцентрические.
Внешние и внутренние круги. Круги называются внешними, когда все точки одного лежат вне площади другого круга, и внутренними, когда все точки одного лежат внутри площади другого круга.
На чертежах 97 и 99 изображены круги внешние, на чертежах 96, 98 и 100 круги внутренние.
Касательные окружности. Окружности называются касательными, когда они имеют одну общую точку.
Общая точка двух касательных окружностей называется их точкой соприкосновения. Соприкосновение называется внешним, когда два круга, имея общую точку, лежат один вне другого, и внутренним, когда один круг лежит внутри другого. На черт. 99 имеем случай внешнего, а на чертеже 100 случай внутреннего соприкосновения.
Пересекающиеся окружности. Окружности называются пересекающимися, когда они имеют две общие точки (черт. 101).
Линия центров есть отрезок, соединяющий центры двух кругов.
Теорема 71. Две окружности, имеющие общую точку на линии центров, другой общей точки иметь не могут.
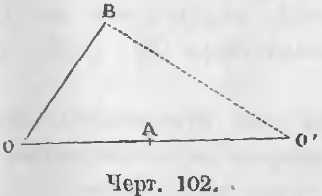
Дано. Две окружности с центрами O и O’ имеют общую точку A (черт. 102).
Требуется доказать, что другой общей точки у них нет.
Доказательство. Положим, существует другая общая точка B, следовательно,
OB = OA и O’B = O’A.
Складывая эти равенства, мы имели бы
OB + O’B = OA + O’A или
OB + O’B = OO’
равенство несообразное, ибо ломаная не может равняться прямой.
Итак, другой общей точки быть не может (ЧТД).
Теорема 72. Две окружности, имеющие одну общую точку вне линии центров, имеют и другую общую точку по другую сторону линии центров.
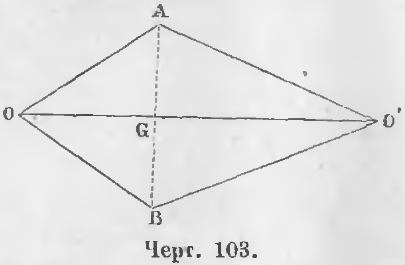
Дано. Две окружности, центры которых O и O’, имеют общую точку A вне отрезка OO’ (черт. 103), соединяющей центры.
Требуется доказать, что существует и другая общая точка по другую сторону центров.
Доказательство. Из точки A опустим на линию центров перпендикуляр AG и на продолжении его отложим отрезок BG, равный AG.
Докажем, что точка B будет другая общая точка. Точка B лежит на окружности O, ибо AO = BO как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’. Точка B лежит на окружности O’, ибо AO’ = BO’ как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’, следовательно, точка B есть другая общая точка (ЧТД).
Теорема 73. Если две окружности пересекаются в двух точках, то линия центров перпендикулярна и делит пополам хорду, соединяющую точки пересечения.
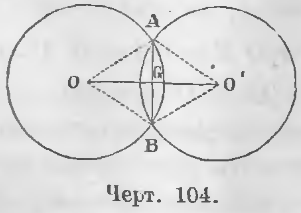
Дано. Точки A и B есть точки пересечения (черт. 104) двух окружностей.
Требуется доказать, что AG = BG и AB ⊥ OO’.
Доказательство. Треугольники OAO’ и OBO’ равны, ибо OO’ сторона общая.
OA = OB как радиусы окружности O.
O’A = O’B как радиусы окружности O’.
Треугольники AOG и BOG равны, ибо OG сторона общая, AO = BO как радиусы, ∠AOG = ∠BOG по доказанному. Следовательно, AG = BG (хорда AB делится линией центров пополам), ∠AGO = ∠BGO (хорда AB перпендикулярна к линии центров).
Таким образом, хорда AB делится пополам и перпендикулярна к линии центров OO’ (ЧТД).
Расстояние между центрами окружностей
1. Если две окружности пересекаются в двух точках, расстояние центров меньше суммы и больше разности радиусов.
Действительно, с одной стороны (черт. 104)
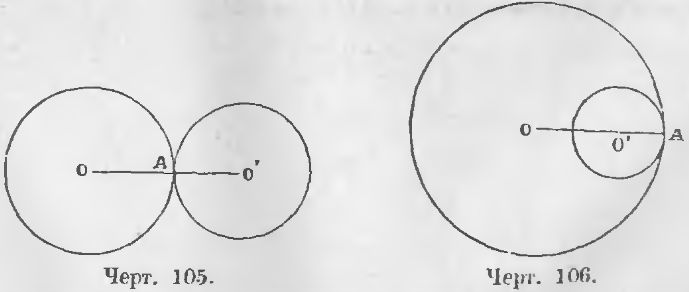
2. Если две окружности касаются, расстояние центров равно сумме радиусов, если соприкосновение внешнее, и разности радиусов, если соприкосновение внутреннее.
Из чертежа 105 видно, что
а из чертежа 106
3. Если одна окружность лежит вне другой, расстояние центров больше суммы радиусов.
Из чертежа 107 видно, что
4. Если окружность лежит одна внутри другой, расстояние центров меньше разности радиусов.
Действительно, из чертежа 108 видно, что
Для того, чтобы имело место равенство, нужно дробь во второй части неравенства (1) увеличить. Для этого следует ее знаменатель уменьшить.
Положим, мы нашли, что имеет место равенство
Разделим дугу AB на равное число таких частей, чтобы каждая часть была менее GF; тогда одна из точек деления i упадет в промежутке между G и F. Дуги AB и Ai соизмеримы, следовательно,
Разделив равенства (b) на (a), находим
равенство несообразное, ибо первая часть его больше, а вторая меньше 1, следовательно, допущение (1) не имеет места.
AOB/AOF ∆ ObC
∆ ObD = ∆ OcD
∆ OcA = ∆ OdA
∆ OdB = ∆ OaB
ибо они, будучи прямоугольными, имеют по равной гипотенузе OC, OD, OA, OB и равным катетам, следовательно,
aC = bC
aB = dB
cA = dA
cD = bD
Всё про окружность и круг
Окружность – это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол – это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Лекция по теме “Сопряжения”
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
При касании двух окружностей между собой точка касания А является их общей точкой. Она находится на пересечении окружностей с прямой, проходящей через центры касающихся окружностей.
Касание называется внешним, если расстояние между центрами касающихся окружностей равно сумме их радиусов (R1+R2). Рис. 1 .
Касание называется внутренним, если расстояние между центрами касающихся окружностей равно разности их радиусов (R1-R2). Рис. 2 .
Рис. 1 Сопряжения окружностей дугами
окружностей. Плавный переход от одной дуги к другой достигается при том условии, когда точка их касания расположена на прямой, соединяющей центры этих окружностей.
В этом случае мы также сталкиваемся с различными вариантами.
Сопряжение двух дуг окружностей третьей дугой окружности может быть внешнее и внутреннее.
Внешним называется сопряжение, когда сопрягаемые окружности остаются вне сопрягающей дуги.
Рис. 2 Внешнее сопряжение. (Рис. 3).
Даны две дуги радиусов R 1 и R 2 соответственно с центрами О 1 и О 2 , а также радиус сопрягающей дуги R.
Центр сопрягающей дуги должен быть равно удален от заданных дуг окружностей на расстояние R. Поэтому проводим вспомогательные дуги из центра О 1 радиусом R 1 +R, а из центра О 2 радиусом R 2 +R до взаимного их пересечения в искомом центре сопрягающей дуги. Для
Рис. 3 определения точек касания (сопряжения)
1 и 2 проводим прямые, соединяющие
центры окружностей О 1 и О 2 с найденным центром сопрягающей дуги. В заключение радиусом R проводим сопрягающую дугу между точками 1 и 2.
Внутреннее сопряжение. (Рис. 4).
Даны две дуги окружностей с радиусами R 1 и R 2 и центрами О 1 и О 2 . Задан радиус R сопрягающей окружности.
Сопрягаемые окружности находятся внутри сопрягающей дуги.
Расстояние между искомым центром сопрягающей дуги и центрами заданных окружностей равно разнице радиусов. Поэтому из центра О 1 делаем засечку R-R 1 , а из центра О 2 засечку RR 2 до их взаимного пересечения, являющегося центром сопрягающей дуги.
Из полученного центра проводим пря-
Рис. 4 мые через центры О 1 и О2 для определения точек сопряжения 1 и 2, между
которыми очерчиваем сопрягающую дугу радиусом R .
Сложное сопряжение. (Рис. 5).
Даны две дуги окружностей с радиусами R 1 и R 2 и центрами О 1 и О 2 . Задан радиус R сопрягающей окружности. С окружностью радиусом R 1 и дугой радиуса R мы имеем внутреннее сопряжение, а с окружностью радиуса R 2 и дугой радиуса R – внешнее сопряжение.
Приводим построение к известному:
Рис. 5 из центра О 1 радиусом R-R 1 делаем засечку, из центра О2 радиусом R+R 2
до их взаимного пересечения, который является центром сопрягающей дуги.
Из полученного центра проводим прямые через центры О 1 и О2 для определения точек сопряжения 1 и 2, между которыми очерчиваем сопрягающую дугу радиусом R.
Сопряжение двух параллельных прямых двумя дугами окружностей.
Дано: две параллельные прямые МН и PF с точками сопряжения на них А и В. На прямой АВ задается точка касания С сопрягающих дуг окружностей. Их центры и размеры радиусов определяем, строя перпендикуляры из точек касания А и В. Затем восставляем перпендикуляры в серединах отрезков АС и СВ, на которых в точках пересечения находим центры сопрягающих
дуг. Линия, соединяющая центры двух
Рис. 6 дуг, должна пройти через точку С (как
контроль графического построения).
Если точка сопряжения С задается в середине АВ, то радиусом R 1 = R 2 (например , гусек).
Сопряжение дуги окружности с прямой линией дугой заданного радиуса.
Дано: прямая АВ, дуга окружности радиуса R 1 и радиус R. Проведем вспомогательную линию, параллельную АВ, на расстоянии R.
Зная, что центр сопрягающей дуги должен отстоять от заданной прямой и дуги окружности радиуса R 1 на равное расстояние, проведем вспомогательную линию, параллельную АВ, на расстоянии R, а из центра О 1 вспомогательную дугу
Рис. 7 радиусом R1+R. В их пересечении нахо-
дится искомый центр О 1 .
Для нахождения точек сопряжения проведем прямую, соединяющую центры О 1 и О 2 (найдем точку 1), и опустим перпендикуляр из О 2 на прямую АВ (найдем точку 2).
Из точки О 2 опишем сопрягающую дугу радиусом R от точки 1 до точки 2.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
[spoiler title=”источники:”]
http://www.stranamam.ru/post/8974384/
http://infourok.ru/lekciya-po-teme-sopryazheniya-5101037.html
[/spoiler]

{L = dfrac{pi R alpha}{180degree}}
Длина дуги окружности – важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности – через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Содержание:
- калькулятор длины дуги окружности
- формула длины дуги окружности через радиус и угол
- формула длины дуги окружности по формуле Гюйгенса
- примеры задач
Если обобщить, то дуга окружности – это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:
-
Полная окружность – это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r – радиус окружности.
-
Полуокружность – это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
-
Сектор окружности – это область, ограниченная дугой окружности и двумя ее радиусами.
Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.
Формула длины дуги окружности через радиус и угол
{L = dfrac{pi R alpha}{180degree}}
R – радиус окружности
α – центральный угол (угол между радиусами) в градусах
{L = R alpha}
R – радиус окружности
α – центральный угол (угол между радиусами) в радианах
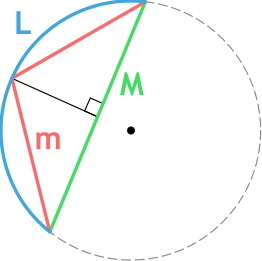
Формула длины дуги окружности по формуле Гюйгенса
{L approxeq 2m + dfrac{2m-M}{3}}
m – длина хорды m
M – длина хорды M
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак “равно или почти равно”, который записывается так – «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.
Примеры задач на нахождение длины дуги
Задача 1
Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.
Решение
Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.
Ответ: {pi : см approx 3.14 : см.}
Введем известные значения в калькулятор для проверки полученного ответа.
Задача 2
Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.
Решение
Задача аналогична предыдущей. Также воспользуемся первой формулой.
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.
Ответ: {2.5 pi : см approx 7.85398 : см.}
В проверке ответа нам снова поможет калькулятор .
Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.
Геометрия круга
Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..
Давайте сначала рассмотрим, какие у круга бывают части и как они называются.
- Окружность — линия, ограничивающая круг.
- Дуга — часть окружности.
- Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
- Хорда — отрезок, соединяющий две точки окружности.
- Сегмент — часть круга, ограниченная хордой и дугой.
- Сектор — часть круга, ограниченная двумя радиусами и дугой.
Интересующие нас величины и их обозначения:
Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.
- Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
- Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
- Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.
Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.
Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).
И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.
И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.
1. Даны диаметр D и длина дуги L


высота сегмента 

2. Даны диаметр D и длина хорды X


высота сегмента 

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол 
3. Даны диаметр D и центральный угол φ


длина хорды 

4. Даны диаметр D и высота сегмента H


длина хорды 

6. Даны длина дуги L и центральный угол φ


длина хорды 

8. Даны длина хорды X и центральный угол φ


диаметр 

9. Даны длина хорды X и высота сегмента H


диаметр 

10. Даны центральный угол φ и высота сегмента H


длина дуги 

Внимательный читатель не мог не заметить, что я пропустил два варианта:
5. Даны длина дуги L и длина хорды X
7. Даны длина дуги L и высота сегмента H
Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?
Задача эта сводится к решению уравнений:


и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.
Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:
длина окружности 
площадь круга 
площадь сектора 
площадь сегмента 
И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.
Программа Segment
-
Длина дуги
Длина дуги окружности представляет собой часть длины самой окружности, поэтому она также будет зависеть от радиуса окружности. Поскольку дуга окружности образована определенным центральным углом, то ее длина, как и площадь сектора круга, – это определенная часть исходной длины окружности, относящаяся к ней как центральный угол сектора к полному углу круга в 360°. Поэтому формула длины дуги будет выглядеть следующим образом:
Формула длины дуги окружности через диаметр образуется подстановкой вместо радиуса половины диаметра:
Также можно подставить вместо радиуса корень из произведения площади круга на число π, выведенный из формулы площади круга:
Существует также формула Гюйгенса для расчета длины дуги окружности через хорду. Для того чтобы ей воспользоваться нужно провести перпендикуляр из середины хорды, соединяющий ее с самой дугой, а из точки соединения перпендикуляра с дугой провести еще два отрезка к концам хорды. Таким образом, мы получаем два конгруэнтных перпендикулярных треугольника, гипотенузы которых мы будем использовать в формуле под обозначением l, а саму хорду назовем L. Следует учитывать, что для углов более 60 градусов формула Гюйгенса дает ощутимую погрешность в расчетах.