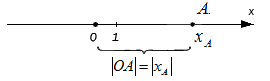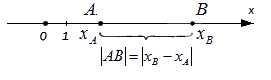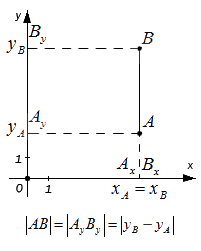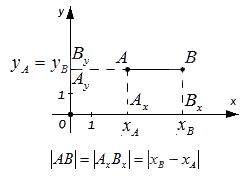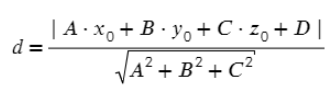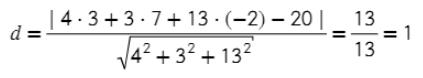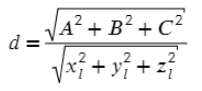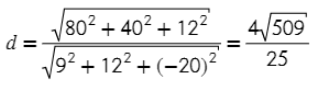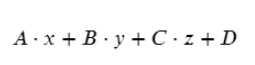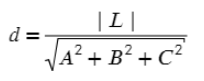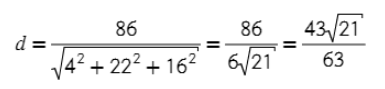В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
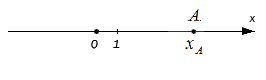
Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.
К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О, необходимо будет отложить три единичных отрезка. Если точка А имеет координату -4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние ОА равно 3; во втором случае ОА = 4.
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4111.
Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна 11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то OA=xA (число принимается за расстояние); если координата меньше нуля, то OA=-xA . В общем, эти утверждения справедливы для любого действительного числа xA.
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
- 0, если точка совпадает с началом координат;
- xA , если xA>0;
- -xA , если xA<0 .
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой xA: OA=xA
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B, лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты xA и xB : AB=xB-xA.
Расстояние между точками на плоскости
Исходные данные: точки A и B, лежащие на плоскости в прямоугольной системе координат Oxy с заданными координатами: A(xA, yA) и B(xB, yB) .
Проведем через точки А и B перпендикуляры к осям координат Ox и Oy и получим в результате точки проекции: Ax, Ay, Bx, By. Исходя из расположения точек А и B далее возможны следующие варианты:
– если точки А и В совпадают, то расстояние между ними равно нулю;
– если точки А и В лежат на прямой, перпендикулярной оси Ox (оси абсцисс), то точки и совпадают, а |АВ| = |АyBy|. Поскольку, расстояние между точками равно модулю разности их координат, то AyBy=yB-yA , а, следовательно AB=AyBy=yB-yA.
– если точки A и B лежат на прямой, перпендикулярной оси Oy (оси ординат) – по аналогии с предыдущим пунктом: AB=AxBx=xB-xA
– если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
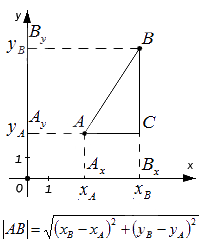
Мы видим, что треугольник АВС является прямоугольным по построению. При этом AC=AxBx и BC=AyBy. Используя теорему Пифагора, составим равенство: AB2=AC2+BC2⇔AB2=AxBx2+AyBy2 , а затем преобразуем его: AB=AxBx2+AyBy2=xB-xA2+yB-yA2=(xB-xA)2+(yB-yA)2
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
AB=(xB-xA)2+(yB-yA)2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: AB=(xB-xA)2+(yB-yA)2=02+02=0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
AB=(xB-xA)2+(yB-yA)2=02+(yB-yA)2=yB-yA
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
AB=(xB-xA)2+(yB-yA)2=(xB-xA)2+02=xB-xA
Расстояние между точками в пространстве
Исходные данные: прямоугольная система координат Oxyz с лежащими на ней произвольными точками с заданными координатами A(xA, yA, zA) и B(xB, yB, zB) . Необходимо определить расстояние между этими точками.
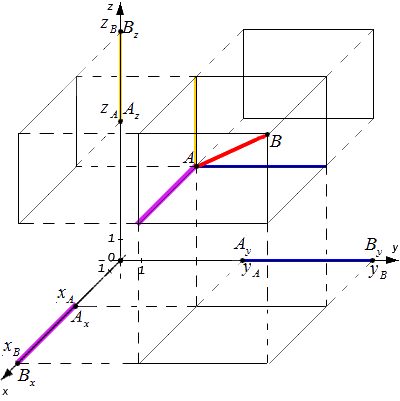
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: Ax, Ay, Az, Bx, By, Bz
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: AxBx, AyBy и AzBz
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: AB2=AxBx2+AyBy2+AzBz2
Используя полученные ранее выводы, запишем следующее:
AxBx=xB-xA, AyBy=yB-yA, AzBz=zB-zA
Преобразуем выражение:
AB2=AxBx2+AyBy2+AzBz2=xB-xA2+yB-yA2+zB-zA2==(xB-xA)2+(yB-yA)2+zB-zA2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
AB=xB-xA2+yB-yA2+(zB-zA)2
Полученная формула действительна также для случаев, когда:
– точки совпадают;
– лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A(1-2) и B(11+2) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B.
Решение
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно OA=1-2=2-1
- Расстояние между точками A и B определим как модуль разности координат этих точек: AB=11+2-(1-2)=10+22
Ответ: OA=2-1, AB=10+22
Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A(1, -1) и B (λ+1, 3) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние АВ будет равно 5.
Решение
Чтобы найти расстояние между точками A и B, необходимо использовать формулу AB=(xB-xA)2+yB-yA2
Подставив реальные значения координат, получим:AB=(λ+1-1)2+(3-(-1))2=λ2+16
А также используем имеющееся условие, что АВ=5 и тогда будет верным равенство:
λ2+16=5λ2+16=25λ=±3
Ответ: АВ = 5, если λ=±3 .
Исходные данные: задано трехмерное пространство в прямоугольной системе координат Oxyz и лежащие в нем точки A (1, 2, 3) и B-7, -2, 4 .
Решение
Для решения задачи используем формулу AB=xB-xA2+yB-yA2+(zB-zA)2
Подставив реальные значения, получим: AB=(-7-1)2+(-2-2)2+(4-3)2=81=9
Ответ: |АВ| = 9
На этой странице находится все необходимое, чтобы найти расстояние между двумя точками. Просто введите координаты точек и получите ответ и подробное решение с помощью наших онлайн-калькуляторов. Кроме того на сайте можно найти координаты середины отрезка.
Расстояние между двумя точками – это длина отрезка, соединяющего эти точки.
Формула расстояния между двумя точками на плоскости:
d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}}
xa и ya – координаты первой точки A,
xb и yb – координаты второй точки B
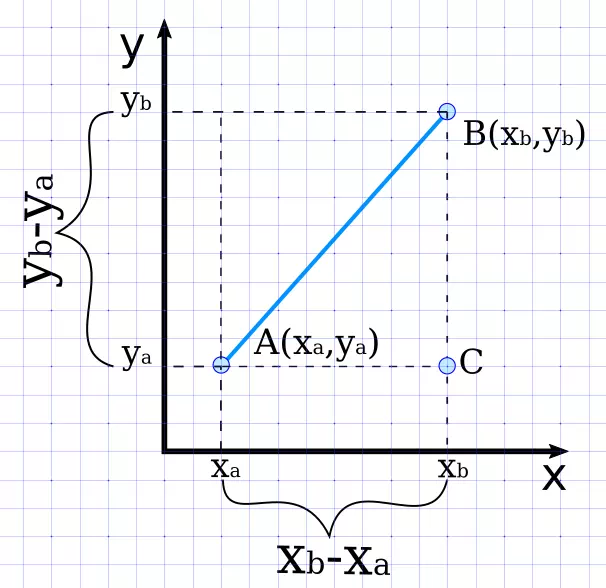
Нахождение расстояния между двумя точками на плоскости сводится к решению треугольника, а точнее – нахождению его гипотенузы. Для этого используется теорема Пифагора. Посмотрите на рисунок.
Соединив отрезком точки A и B, а также опустив перпендикуляры на оси мы получим треугольник ABC. В этом треугольнике стороны AC и BC являются катетами прямоугольного треугольника, а AB – его гипотенузой. Длины катетов AC и BC найти довольно просто:
AC = xb – xa
BC = yb – ya
Осталось применить теорему Пифагора и получить сторону AB, которая является гипотенузой прямоугольного треугольника и расстоянием между точками A и B:
AB=sqrt{{AC}^2 + {BC^2}}
Подставив вместо отрезков AC и BC их длины, получим итоговую формулу расстояния между двумя точками:
AB=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}} или d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}}
Формула расстояния между двумя точками в пространстве:
{d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2} + {(z_b – z_a)^2}}}
xa, ya и za – координаты первой точки A,
xb, yb и zb – координаты второй точки B
Примеры задач на вычисление середины отрезка
Задача 1
Найдите расстояние между точками А и В, если А(2; 7), В(-2; 7).
Решение
Подставим координаты точек в формулу расстояния между двумя точками на плоскости и вычислим результат:
d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}} = sqrt{{(-2 – 2)}^2 + {(7 – 7)^2}} = sqrt{{-4}^2 + {0^2}} = sqrt{16 + 0} = sqrt{16} = 4
Мы получили расстояние между точками и оно равно 4.
Ответ: 4.
Проверим результат с помощью калькулятора .
Метод координат (расстояние между точкой и плоскостью, между прямыми)
Расстояние между точкой и плоскостью.
Расстояние между точкой и прямой.
Расстояние между двумя прямыми.
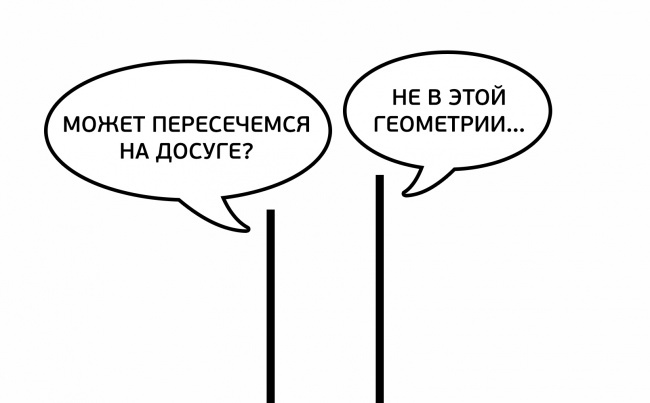
Первое, что полезно знать, это как найти расстояние от точки до плоскости:
Значения A, B, C, D – коэффициенты плоскости
x, y, z – координаты точки
Задача. Найти расстояние между точкой А = (3; 7; −2) и плоскостью 4x + 3y + 13z – 20 = 0.
Все дано, можно сразу подставить значения в уравнение:
Задача. Найдите расстояние от точки К = (1; −2; 7) до прямой, проходящей через точки V = (8; 6; −13) и T = (−1; −6; 7).
- Находим вектор прямой.
- Вычисляем вектор, проходящий через искомую точку и любую точку на прямой.
- Задаем матрицу и находим определитель по двум полученным векторам в 1-ом и 2-ом пункте.
- Расстояние получим, когда квадратный корень из суммы квадратов коэффициентов матрицы поделим на длину вектора, который задает прямую (Думаю непонятно, поэтому перейдем к конкретному примеру).
1) TV = (8−(−1); 6−(−6); -13-7) = (9; 12; −20)
2) Вектор найдем через точки K и T, хотя так же можно было бы через K и V или любую другую точку на данной прямой.
TK = (1−(−1); −2−(−6); 7-7) = (2; 4; 0)
3) Получится матрица без коэффициента D (здесь он не нужен для решения):
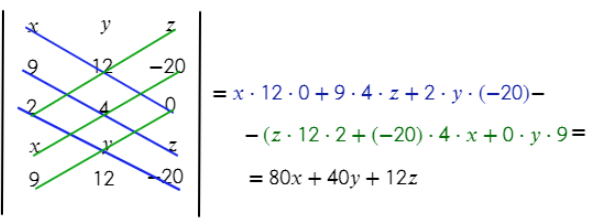
4) Плоскость получилась с коэффициентами А = 80, В = 40, С = 12,
x, y, z – координаты вектора прямой, в данном случае – вектор TV имеет координаты (9; 12; −20)
Задача. Найти расстояние между прямой, проходящей через точки Е = (1; 0; −2), G = (2; 2; −1), и прямой, проходящей через точки M = (4; −1; 4), L = (−2; 3; 0).
- Задаем векторы обеих прямых.
- Находим вектор, взяв по одной точке с каждой прямой.
- Записываем матрицу из 3-х векторов (две строчки из 1-го пункта, одна строчка из 2-го) и находим ее численный определитель.
- Задаем матрицу из двух первых векторов (в пункте 1). Первую строчку задаем как x, y, z.
- Расстояние получим, когда разделим получившееся значение из пункта 3 по модулю на квадратный корень из суммы квадратов пункта 4.
Перейдем к цифрам:
1) EG = (2−1; 2−0; −1−2) = (1; 2; −3)
ML = (−2−4; 3−(−1); 0−4) = (−6; 4; −4)
2) Найдем вектор EM (можно было так же найти EL или GM, или GL).
EM = (1−4; 0−(−1); −2−4) = (−3; 1; −6)
3) Составляем матрицу из трех выше найденных векторов и находим определитель.
4) Составляем матрицу из первых двух выше найденных векторов и находим определитель
без коэффициента D (здесь он не нужен для решения).
Вспомним, что уравнение плоскости задается так:
В нашем случае А = 4, В = 22, С = 16, D = 0.
5) Итоговая формула выглядит так, где L= −86 (из 3 пункта)
Будь в курсе новых статеек, видео и легкого математического юмора.
На первый взгляд может показаться, что математика сложна и коварна, но это далеко не так. Если приложить усилия к её изучению, то можно удивиться тому, насколько быстро вы измените своё мнение о ней. Давайте же разберём одну из тем, которая поможет находить расстояние от точки до точки при различных условиях. После того как вы изучите данную статью, вы можете решить предоставленные задания, чтобы лучше закрепить пройденный материал.
Математические термины
Для начала введём некоторые определения.
Определения
Расстояние между точками – это измерение отрезка, находящегося между этими точками, составляющего длину расстояния.
Эти отрезки располагаются в определенном масштабе, потому как необходимо знать единицу длины для их измерения, без этого нельзя.
Функция – это связь величин, выражаемая в зависимости одной переменной Y, от второй переменной X.
Произвольная функция (точка) – это такая точка, которую можно расположить в любом месте.
Координатная прямая – это прямая, на которой изображают точку отсчёта 0 и единичные отрезки. Прямой также задают направление.
Действительные числа – это совокупность рациональных и иррациональных чисел.
Рациональное число – это такое число, которое может находиться в виде обыкновенной дроби, в отличие от иррационального числа.
Иррациональное число – это бесконечная непериодическая десятичная дробь. Такое число нельзя представить в виде обыкновенной дроби.
Модуль или же абсолютная величина – это обязательно неотрицательное число, которое является расстоянием определённых точек.
Как определить расстояние между точками, находящимися на координатной прямой
Важно
Чтобы найти расстояние от одной точки до другой, т.е. длину этого отрезка, нужно сравнить его с другим таким отрезком в заданном масштабе.
Действительные числа
Рассмотрим этот способ на примере:
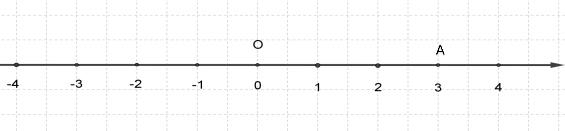
Здесь мы имеем координатную прямую OX, на которой отмечена точка A. Она произвольная, поэтому мы можем задать ей любое действительное число, пусть это будет 3.
Отрезок – это единица длины, поэтому все отрезки, что мы отложили от точки O нужно сложить, вследствие чего полученное количество единичных отрезков будет равняться длине отрезка OA. В данном случае здесь три отрезка, поэтому и ответ таков.
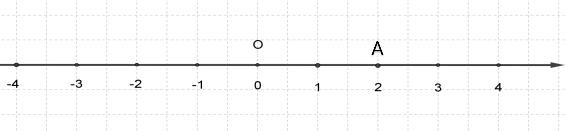
Ещё один пример, где точку отсчёта O и произвольную точку A соединяют 2 отрезка. Это значит, что расстояние длин всех единичных отрезков OA равно 2. Если же точка A будет иметь другое число, например: 6, то мы откладываем от точки O именно 6 единичных отрезков и получаем искомое расстояние.
Рациональные числа
С действительным числами всё понятно, а что делать с рациональными? Представим, что координаты точки A равны 5,5. Из этого следует, что нам нужно отложить из точки O сначала 5 единичных отрезков, то есть, целое число, а после прибавить 0,5. Иногда это кажется невозможным, ведь некоторые числа трудно представить в виде отрезка, из-за чего приходится искать самое приближенное значение числа.
Иррациональные числа
Иррациональным числам данный метод не подходит, потому как такие числа нельзя поставить на координатной прямой OX. Для примера приведём числа √5, √8, √17. Здесь можно перейти к отвлечённому представлению и посмотреть на эти числа таким образом:
- 0>A – если 0 больше A, то A имеет отрицательное значение координат: |OA| = (–A).
- 0<A – если 0 меньше A, то A имеет положительное значение координат: |OA| = (A).
Также можно сказать, что это подходит и к действительным числами. Если точка A будет находиться на начальной точке O, то и расстояние между ними будет равно 0. Здесь нужно уметь хорошо работать с рисунком, тогда всё будет понятно.
- Модуль
Важно помнить, что расстояние между точками не может быть отрицательным.
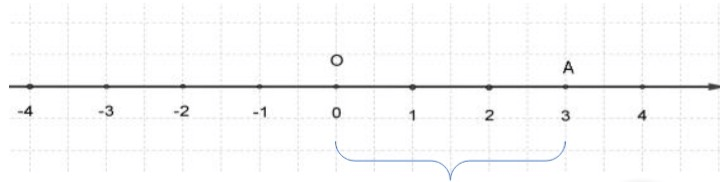
В данном случае у нас есть модуль числа A, что является расстоянием OA и это число 3.
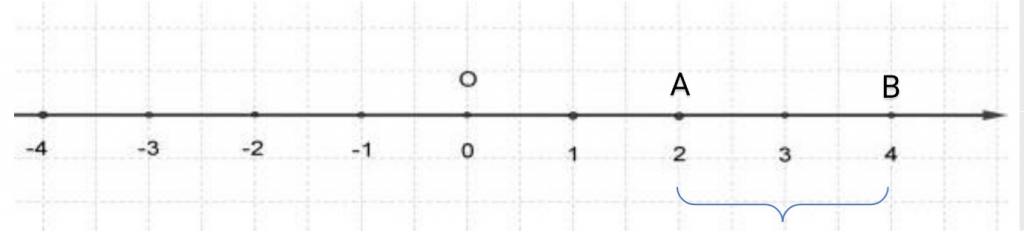
Если на координатной прямой будут точки A и B, то их расстояние нужно определить по модулю разности этих координат. Получается, чтобы найти длину отрезка AB, необходимо из числа точки B отнять число точки A:
4-2=2.
Как определить расстояние между двумя точками на плоскости
Представим прямоугольную систему координат и плоскость на ней, с находящимися там точками A и B. Далее проведём прямые от этих точек к осям Ox и Oy, как на изображении. В следствие этого образовались точки Ax и Ay, а также Bx и By.
Из этого можно вывести несколько вариантов:
- Ось Ox
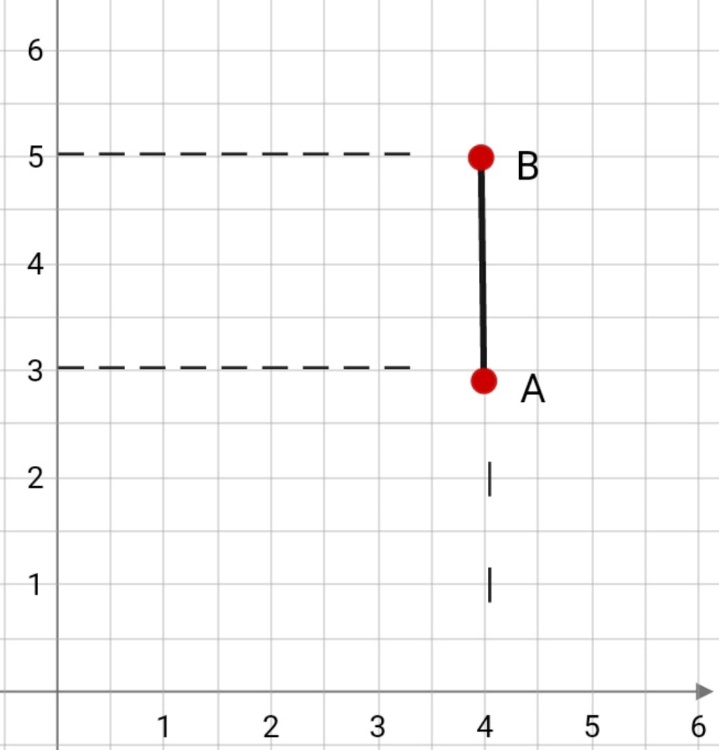
В случае расположения точек A и B на прямой, которая в свою очередь перпендикулярна оси Ox – точки A и B совпадают, а модуль AB равен модулю AyBy. Как говорилось ранее, для нахождения длины промежутка (расстояния) между двумя точками, нужно найти разность модуля заданных координат, поэтому можно сказать, что:
|AB| = |AyBy| = |yB – yA|.
При этом совпадении их расстояние равняется 0.
Формула
Формула для нахождения расстояния между двумя точками на плоскости:
[|A B|=sqrt{(} x B-x A)^{2}+(y B-y A)^{2}=sqrt{0}^{2}+(y B-y A)^{2}]
- Ось Oy
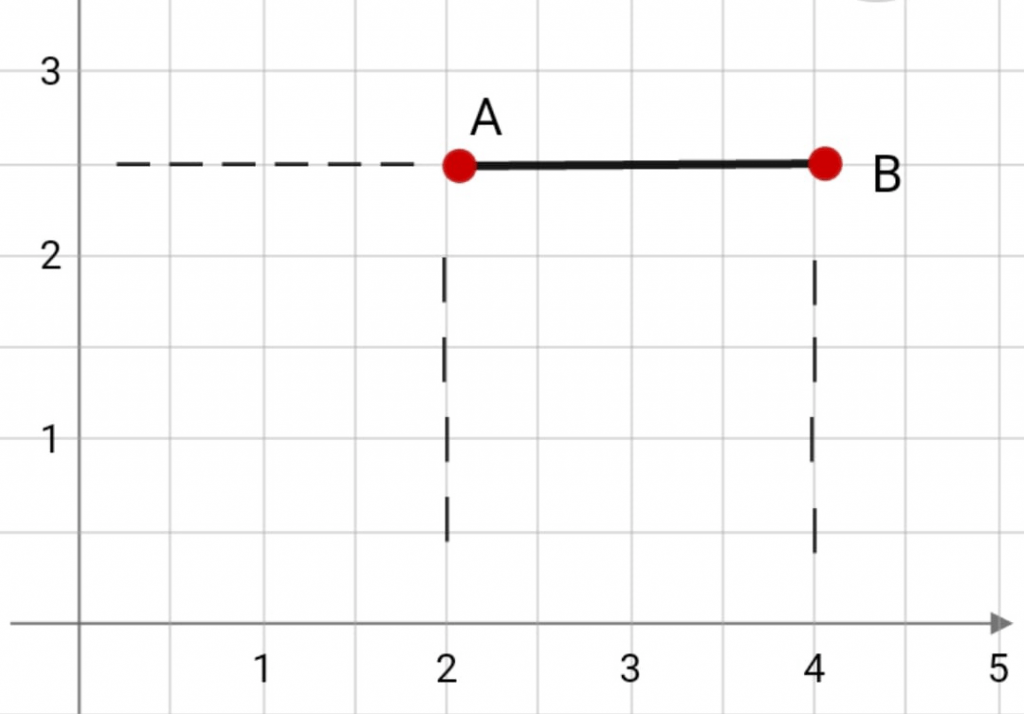
Теперь рассмотрим тот случай, когда прямая перпендикулярна оси Oy. Находится расстояние таким же образом, но уже с участием xB и xA: |AB| = |AxBx| = |xB – xA|.
Формула
Формула для нахождения расстояния между двумя точками на плоскости:
[left.|A B|=sqrt{(} x B-x A)^{2}+(y B-y A)^{2}=sqrt{(} x B-x Aright)^{2}+0^{2}]
- Точки не лежат на прямой, которая перпендикулярна оси Ox и Oy
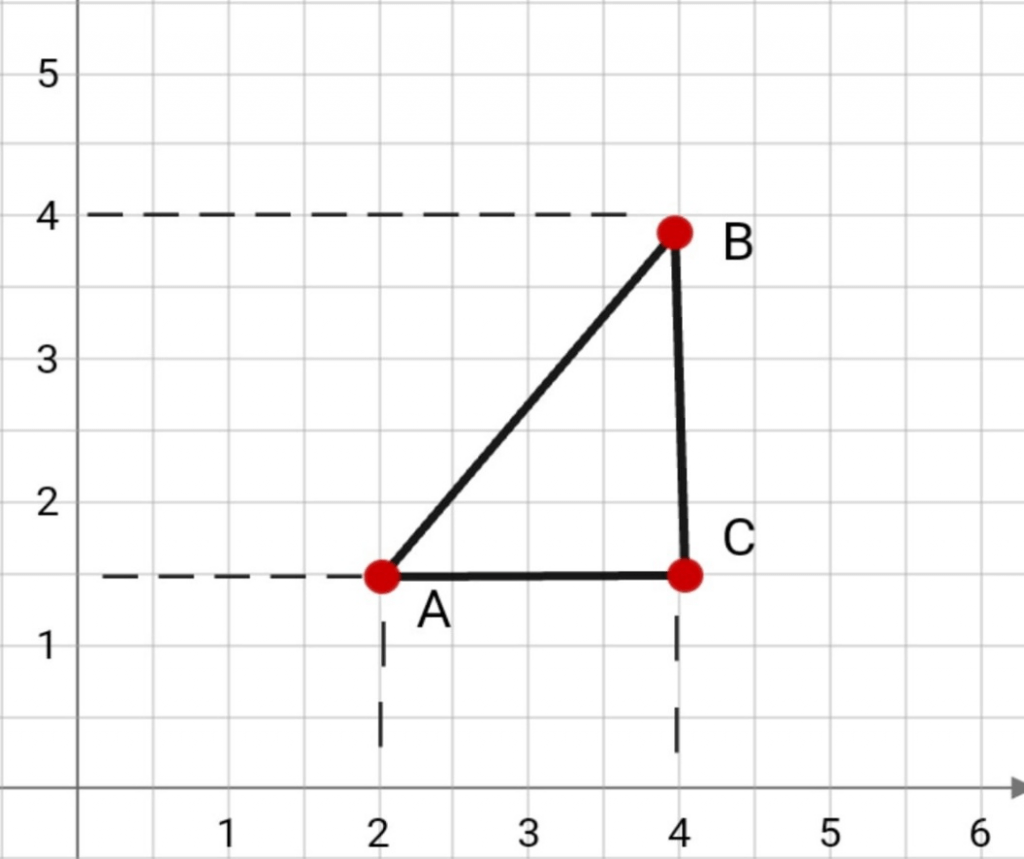
Теперь поговорим о прямоугольном треугольнике ABC. Чтобы найти расстояние на плоскости между точкой A и точкой B, необходимо воспользоваться формулой:
|AB| = √(xB – xA)² + (yB – yA)².
Эта формула доказывает правильность ранее написанных утверждений к тем заданиям, на графиках которых точки лежат на прямой, перпендикулярной Ox и Oy.
Если точки совпадают, к ним справедливо равенство:
|AB| = √(xB – xA)² + (yB – yA)² = √0² + 0² = 0.
По рисунку видно, что:
|AC| = |AxBx|, а также |BC|=|AyBy|. Далее вспомним теорему Пифагора и с её помощью запишем равенство:
|AB|² = |AC|² + |BC|²
|AB|² = |AxBx|² + |AyBy|²
√|AxBx|² + |AyBy|²
√|xB – xA|² + |yB – yA|²
√(xB – xA)² + (yB – yA)²
Пример
Найдите расстояние между двумя точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (3, –1), а также B (X + 3, 7). Также надо найти значение действительного числа X, зная, что при них расстояние между точками будет равно 10.
Чтобы решить эту задачу, необходимо использовать формулу:
|AB| = √(xB – xA)² + (yB – yA)².
После этого действия подставляем вышеприведённые числа:
√(X + 3 – 3)² + (7 – ( – 1))² = √X² + 64.
Далее обратим внимание на то, что |AB| = 10 и составим равенство:
√X² + 64 = 10
X² + 64 = 100
X = ± 6
Ответ: |AB| = 10, при X = ±6.
Нет времени решать самому?
Наши эксперты помогут!
Как определить расстояние между точками в пространстве
Более сложным заданием на нахождение расстояния является то, где точки расположены в пространстве, а не на плоскости.
Возьмём точки, имеющие свои координаты: A (xA, yA, zA), B (xB, yB, zB). Они размещены на прямоугольной системе координат Oxyz. Имея эти данные, мы можем приступить к поиску расстояния между этими точками.
Итак, проведём плоскости через наши точки A и B, которые должны быть перпендикулярными осям с заданными координатами. Таким образом мы получаем точки точки проекции: Ax, Ay, Az, Bx, By, Bz. Так и получился параллелепипед, диагональ которого равна расстоянию точек.
Правило
Для нахождения диагонали нужно вспомнить, что она находится путем сложения квадратных измерений точек проекции:
[|A B|^{2}=|A x B x|^{2}+|A y B y|^{2}+left.|A| z B zright|^{2}]
После чего выполним такие действия:
|AxBx| = |xB – xA|
|AyBy| = |yB – yA|
|AzBz| = |zB – zA|
Теперь выполним преобразование получившегося выражения:
|AB|² = |AxBx|² + |AyBy|² + |AzBz|² = |xB – xA|² + |yB – yA|² + |zB – zA|² = (xB – xA)² + (yB – yA)² + (zB – zA)².
После всех этих действий мы можем выделить основную формулу, которая применяется для нахождения расстояния точек в пространстве:
=√(xB – xA)² + (yB – yA)² + (zB – zA)².
Её можно применять в тех случаях, когда точки располагаются на прямой, которая параллельна координатной оси или же они находятся на этой координатной оси. При совпадении точек эта формула также действительна.
Пример
Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (2, 3, 4), а также B (-6, -1, 5).
Перейдём к решению, воспользовавшись формулой:
√(xB – xA)² + (yB – yA)² + (zB – zA)².
Подставляем имеющиеся значения:
√(–6 – 2)² + (–1 – 3)² + (5 – 4)² = √64 + 16 + 1 = √81 = 9.
Ответ: расстояние |AB| равно 9.
Задачи для самостоятельного решения
- Задача
Найдите расстояние между точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (2, 5), а также B (6, 4). - Задача
Найдите расстояние между точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (1, 6), а также B (1, 25). - Задача
Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (1, -3, 4), а также B (4, 1, 4). - Задача
Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (2, -2, 7), а также B (6, 2, 5).
Ответы с решением:
- Решение первой задачи
Для решения понадобится формула:
|AB| = √(xB – xA)² + (yB – yA)².
Далее подставляем числа:
|AB| = √(6 – 2)² + (4 – 5)² = √4² + (–1)² = √16 + 1 = √17.
Ответ: |AB| равен √17. - Решение второй задачи
Формула для нахождения:
|AB| = √(xB – xA)² + (yB – yA)².
Подставляем:
|AB| = √(1 – 1)² + (25 – 6)² = √(0)² + (19)² = √0 + 361 = √361 = 19
Ответ: |AB| равен 19. - Решение третьей задачи
Запишем формулу:
√(xB – xA)² + (yB – yA)² + (zB – zA)².
Подставим числа:
√(4 – 1)² + (1 – (–3))² + (4 – 4)² = √(3)² + (4)² + (0)² = √9 + 16 + 0 = √25 = 5.
Ответ: |AB| равняется 5. - Решение четвертой задачи
Записываем формулу для решения:
√(xB – xA)² + (yB – yA)² + (zB – zA)²
Заменим на координаты точек:
√(6 – 2)² + (2 – (–2))² + (5 – 7)² = √(4)² + (4)² + (–2)² = √16 + 16 + 4= √36 = 6.
Ответ: |AB| равняется 6.
Здесь будет калькулятор
Расстояние между двумя точками на прямой
Рассмотрим координатную прямую, на которой отмечены 2 точки: AA и BB. Чтобы найти расстояние между этими точками, нужно найти длину отрезка ABAB. Это делается при помощи следующей формулы:
AB=∣a−b∣AB=|a-b|,
где a,ba, b — координаты этих точек на прямой (координатной прямой).
Ввиду того, что в формуле присутствует модуль, при решении не принципиально, из какой координаты какую вычитать (так как берется абсолютная величина этой разности).
То есть:
∣a−b∣=∣b−a∣|a-b|=|b-a|
Разберем пример, чтобы лучше понять решение подобных задач.
На координатной прямой отмечены точка AA, координата которой равна 99 и точка BB с координатой −1-1. Нужно найти расстояние между этими двумя точками.
Решение
Здесь a=9,b=−1a=9, b=-1
Пользуемся формулой и подставляем значения:
AB=∣a−b∣=∣9−(−1)∣=∣10∣=10AB=|a-b|=|9-(-1)|=|10|=10
Ответ
10
Расстояние между двумя точками на плоскости
Рассмотрим две точки, заданные на плоскости. Из каждой отмеченной на плоскости точки нужно опустить по два перпендикуляра: На ось OXOX и на ось OYOY. Затем рассматривается треугольник ABCABC. Так как он является прямоугольным (BCBC перпендикулярно ACAC), то найти отрезок ABAB, он же является и расстоянием между точками, можно с помощью теоремы Пифагора. Имеем:
AB2=AC2+BC2AB^2=AC^2+BC^2
Но, исходя из того, что длина ACAC равна xB−xAx_B-x_A, а длина BCBC равна yB−yAy_B-y_A, эту формулу можно переписать в следующем виде:
AB=(xB−xA)2+(yB−yA)2AB=sqrt{(x_B-x_A)^2+(y_B-y_A)^2},
где xA,yAx_A, y_A и xB,yBx_B, y_B — координаты точек AA и BB соответственно.
Необходимо найти расстояние между точками CC и FF, если координаты первой (8;−1)(8;-1), а второй — (4;2)(4;2).
Решение
xC=8x_C=8
yC=−1y_C=-1
xF=4x_F=4
yF=2y_F=2
CF=(xF−xC)2+(yF−yC)2=(4−8)2+(2−(−1))2=16+9=25=5CF=sqrt{(x_F-x_C)^2+(y_F-y_C)^2}=sqrt{(4-8)^2+(2-(-1))^2}=sqrt{16+9}=sqrt{25}=5
Ответ
5
Расстояние между двумя точками в пространстве
Нахождение расстояния между двумя точками в этом случае происходит аналогично предыдущему за исключением того, что координаты точки в пространстве задаются тремя числами, соответственно, в формулу нужно добавить еще и координату оси аппликат. Формула примет такой вид:
AB=(xB−xA)2+(yB−yA)2+(zB−zA)2AB=sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}
Найти длину отрезка FKFK в пространстве, если координаты точек его концов таковы: (−1;−1;8)(-1;-1;8) и (−3;6;0)(-3;6;0). Ответ округлить до целого числа.
Решение
F=(−1;−1;8)F=(-1;-1;8)
K=(−3;6;0)K=(-3;6;0)
FK=(xK−xF)2+(yK−yF)2+(zK−zF)2=(−3−(−1))2+(6−(−1))2+(0−8)2=117≈10.8FK=sqrt{(x_K-x_F)^2+(y_K-y_F)^2+(z_K-z_F)^2}=sqrt{(-3-(-1))^2+(6-(-1))^2+(0-8)^2}=sqrt{117}approx10.8
По условию задачи нам нужно округлить ответ до целого числа.
Ответ
10