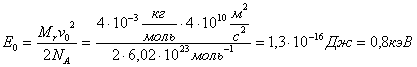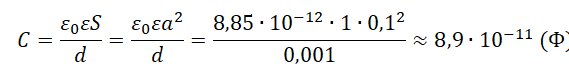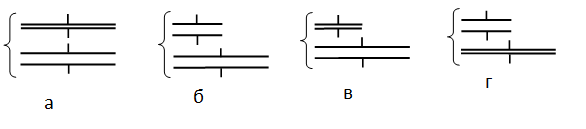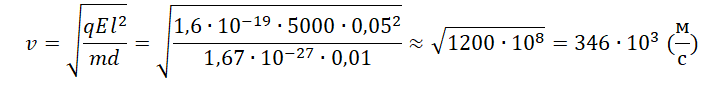где M – молярная масса, M=Mr∙10-3=4∙10-3кг/моль,
Mr – относительная атомарная масса (из таблицы
Менделеева), Mr=4,
NA – число Авогадро, NA=6,02∙1023моль-1.
Следовательно, начальная
энергия частицы равна:
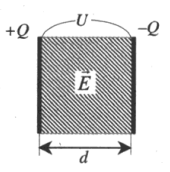
2. Расстояние
между обкладками конденсатора.
Емкость плоского конденсатора определяется по формуле:
,
где ε –
относительная диэлектрическая проницаемость вещества, заполняющего пространство
между обкладками конденсатора (для воздуха ε=1),
ε0 –
электрическая постоянная, ε0=8,85∙10-12,
d – расстояние между обкладками конденсатора,
S – площадь пластины, ,
где l – длина квадратной пластины.
Следовательно, расстояние
между обкладками конденсатора определяется по формуле:
3. Энергия заряженного конденсатора
Энергии
заряженного конденсатора вычисляется
по формуле:
,
где С –
электроемкость конденсатора; U – разность потенциадов.
4. Заряд на
обкладках конденсатора.
Энергии
заряженного конденсатора вычисляется
также по формуле:
,
где q – заряд конденсатора.
Следовательно, заряд на обкладках конденсатора:
Алгоритм решения.
Расчет для заданных условий.
1.
2.
3.
4.
Графические зависимости.
Вывод.
Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.
Плоский конденсатор — система двух разноименно заряженных пластин.
Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:
U=Ed
Электроемкость конденсатора
Определение
Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.
Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).
Электроемкость конденсатора определяется формулой:
C=ε0εSd
- ε0 — диэлектрическая постоянная, равная 8,85∙10–12 Кл2/(Н∙м2);
- ε — диэлектрическая проницаемость среды;
- S (м2) — площадь каждой пластины.
Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.
Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:
C=QU=qU
Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.
Энергия конденсатора
Формула энергии конденсатора
Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:
Wэ=q22C=CU22
Подсказки к задачам
| Конденсатор отключен от источника | q = q′ |
| Конденсатор подключен к источнику | U = U′ |
| Количество теплоты и энергия конденсатора | Q = ∆Wэ |
Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.
10 см = 0,1 м
1 мм = 0,001 м
Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.
Площадь квадратной пластины равна квадрату ее стороны:
S = a2
Соединения конденсаторов
| Последовательное соединение | Параллельное соединение | |
| Схема | 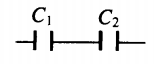 |
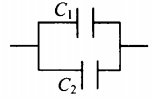 |
| Напряжение |
U=U1+U2 |
U=U1=U2 |
| Заряд |
q=q1=q2 |
q=q1+q2 |
| Электроемкость |
1C=1C1+1C2 |
C=C1+C2 |
Подсказки к задачам
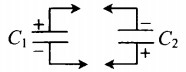
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами. | Схема соединения конденсаторов одноименными полюсами:
Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами. |
Схема соединения конденсаторов разноименными полюсами: Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
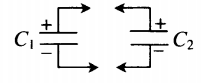
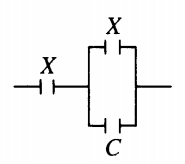
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.
Электрическая емкость параллельного соединения равна:
Cпарал=X+C
Электроемкость последовательного соединения:
1Cпослед=1Cпарал+1X=1X+C+1X
Учтем, что суммарная электроемкость равна C:
1C=1X+C+1X
Преобразуем, умножим выражение на CX(X+C):
X(X+C)=CX+C(X+C)
Раскроем скобки:
X2+XC=CX+CX+C2
X2−CX−C2=0
Решив уравнение, получим: X = 25,9 пФ.
Разбор задач на тему «Заряженная частица в поле конденсатора»
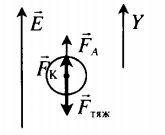
| Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U? | Условие равновесия исходит из второго закона Ньютона:
−Fтяж+−FK+−FA=0 ρш > ρ, поэтому −Fтяж> −FA. В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так: Проекция второго закона Ньютона на ось ОУ: FK+FA=Fтяж Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения: Fтяж=ρш43πr3g Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения: FА=ρ43πr3g Сила Кулона: FK=qUd qUd+ρ43πr3g=ρш43πr3g q=(ρш43πr3g−ρ43πr3g)dU=4πr3gd(ρш−ρ)3U |
| Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l? | 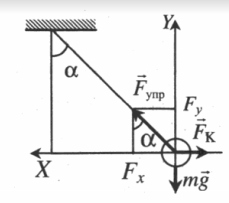
Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−Fупр=0 Проекции на оси ОХ и ОУ соответственно: Fупрsinα−FK=0 Fупрcosα−mg=0 Отсюда: kΔlsinα=qUd kΔlcosα=mg Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их: (kΔl)2sin2α+(kΔl)2cos2α=(qUd)2+(mg)2 (kΔl)2(sin2α+cos2α)=(qUd)2+(mg)2 sin2α+cos2α=1 (kΔl)2=(qUd)2+(mg)2 U=dq√(kΔl)2−(mg)2 |
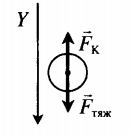
| Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=0 Проекция на вертикальную ось: Fтяж−FK=0 Fтяж=mg FK=qUd mg=qUd d=qUmg |
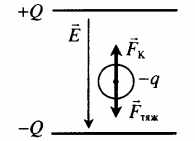
| Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью −E, направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли? | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок: Если Fтяж > FK, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны: a=mg−qEm s=b Если Fтяж < FK, то шарик движется с ускорением верх. Ускорение и перемещение в этом случае равны: a=qE−mgm s=d Начальная скорость шарика равна нулю. Поэтому перемещение также равно: s=at22 Сделаем вычисления для случая Fтяж > FK: at22=b mg−qEmt22=b t=√2bmmg−qE Выполняя вычисления для случая Сделаем вычисления для случая Fтяж < FK, получим: t=√2bmqE−mg |
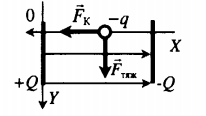
| Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого −E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a Если сила Кулона направлена вправо, то sx = d. Если сила Кулона направлена вправо, то sx = b. Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево. Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно: ax=qEm ay=g Проекции перемещений на эти же оси: sx=axt22 sx=Δh=gt22 axt22=b Или: qEmt22=b Так как время движения шарика по вертикали и горизонтали одинаково: t2=2Δhg=2mbqE Δh=mbgqE |
Задание EF17979
Введите ответ в поле ввода
Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?
Для каждой величины определите соответствующий характер изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Определить, от чего зависит емкость конденсатора, и как она изменится при уменьшении зазора между его обкладками.
2.Определить, от чего зависит величина заряда конденсатора, и как она изменится после уменьшения зазора между его обкладками.
3.Определить, от чего зависит разность потенциалов между обкладками конденсатора, и как она изменится при уменьшении зазора.
Решение
Емкость конденсатора определяется формулой:
C=ε0εSd
Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.
Вот как взаимосвязана электроемкость и заряд конденсатора:
C=qU
Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.
С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.
Ответ: 113
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18574
Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.
Алгоритм решения
1.Проанализировать каждый этап эксперимента.
2.Установить, от чего зависит угол отклонения стрелки электрометра.
3.Выяснить, что поменяется при смещении одной пластины конденсатора относительно другой, и что при этом произойдет со стрелкой электрометра.
Решение
На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.
На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:
C=ε0εSd
S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.
Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.
На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:
C=qU
Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.
Ответ: Увеличатся
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18695
Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?
Алгоритм решения
- Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
- Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.
Решение
Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18703
Ответ записать в км/с, округлив до десятков.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
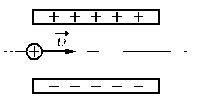
2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.
3.Выяснить, при каком условии протон успеет вылететь из конденсатора.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса протона: m = 1,67∙10–27 кг.
• Заряд протона: q = 1,6∙10–19 Кл.
• Расстояние между обкладками конденсатора: d = 1 см.
• Длина пластин конденсатора: l = 5 см.
• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.
1 см = 0,01 м
5 см = 0,05 м
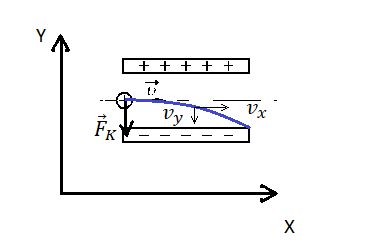
Сделаем рисунок:
Изначально протон обладает только горизонтальной скоростью v, равной vx. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.
Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью vx:
t=lvx=lv
Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):
0,5d=at22
Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:
t=√da
Приравняем правые части уравнений времени и получим:
lv=√da
Отсюда скорость равна:
v=√al2d
Ускорение выразим из второго закона Ньютона:
FK=ma=qUd
a=qUmd
Но известно, что:
U=Ed
Поэтому:
a=qEdmd=qEm
Отсюда:
Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙103 м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.
Ответ: 350
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6k
Основные параметры конденсатора
Номинальная
емкость
Сном
относится к главному параметру и
измеряется в фарадах [Ф], названная в
честь выдающегося английского физика
Майкла Фарадея.

Емкостью
в одну фараду обладает конденсатор,
который накапливает заряд, величиной
в один кулон, если приложить к пластинкам
напряжение один вольт. Сном
зависит от материала диэлектрика и
конструкции конденсатора (взаимного
расположения обкладок)
Сном
=εεоS/d
[Ф], где
εо
–
диэлектрическая постоянная εо
= 8,85 х 10-12
Ф/м,
ε
– относительная диэлектрическая
проницаемость, которая характеризует
способность диэлектрика к поляризации.
Диэлектрическая
проницаемость ε
показывает, во сколько раз заряд
конденсатора с данным диэлектриком
превосходит заряд аналогичного
накопителя, если между его пластинками
той же площади и находящихся на таком
же расстоянии вакуум. Для воздуха ε
равна единице, то есть практически ничем
не отличается от вакуума. Сухая бумага
обладает диэлектрической проницаемостью
в два раза больше воздуха; фарфор – в
четыре с половиной раза ε
= 4,5. Конденсаторная керамика имеет ε
= 10..200 единиц.
Отсюда вытекает
важный вывод: чтобы получить максимальную
емкость при сохранении прежних
геометрических размеров, следует
применять диэлектрик с максимальной
диэлектрической проницаемостью. Поэтому
в широко распространённых плоских
конденсаторах используют керамику.
S
– площадь обкладок конденсатора,
d
– расстояние
между обкладками (толщина диэлектрика).
Физический
смысл данной формулы следующий: чем
больше площадь обкладок, тем больше
зарядов на ней может расположиться
(накопиться); чем больше расстояние
между пластинами и соответственно между
зарядами, тем меньшая сила их взаимного
притяжения – тем слабее они удерживаются
на обкладках, поэтому зарядам легче
покинуть обкладки, что приводит к
снижению их числа, следовательно и
уменьшению емкости конденсатора.
Ранее часто можно
было услышать такое утверждение, что
емкость в 1 Ф – это очень много – почти
емкость нашей планеты. Однако сейчас,
с появлением суперконденсаторов так
больше не говорят, поскольку емкость
последних достигает сотни фарад. Тем
не менее в большинстве электронных схем
используют накопители меньшей C –
пикофарады, нанофарады и микрофарады.
Фактическое
значение емкости может отличаться от
номинального на величину допускаемого
отклонения в процентах.
Для
емкостей, также как для резисторов,
установлены семь рядов номинальных
значений: ЕЗ, Е6, Е12, Е24, Е48, Е95, Е192 . Каждый
ряд имеет свой класс точности

В
зависимости от класса точности
(допустимого отклонения) производятся
стандартные значения емкости, то есть
стандартные номиналы конденсаторов.
Емкость в приведенной ниже таблице
исчисляется пикофарадами. Любое значение
из таблицы может быть умножено на 0,1 или
1 или 10 и т.д.

Температурный
коэффициент емкости
Протекание
электрического тока через любой
радиоэлектронный элемент вызывает его
нагрев, ввиду неизбежного наличия
сопротивления. Чем больше ток и выше
сопротивление, тем интенсивнее нагревается
прибор. Такое явление в большинстве
случаев является вредным и может привести
к изменению параметров схемы, а
соответственно и нарушить режим работы
всего устройства. Поэтому нагрев
радиоэлектронных элементов всегда
учитывается при проектировании изделия.
Характеристики конденсаторов также
склонны изменятся с изменением температуры
и с этим обязательно нужно считаться.
Для этого введен температурный
коэффициент емкости,
сокращенно
ТКЕ.
ТКЕ
показывает, насколько отклоняется
емкость конденсатора от номинального
значения с ростом температуры. Значение
емкости С0
конденсатора
приводится для температуры окружающей
среды +20 С.
ТКЕ
= (1/С0
)
(dС
dT
) [1C]
Рост температуры
может вызвать как рост емкости, так и
ее уменьшение. В зависимости от этого
различают конденсаторы с положительным
и отрицательным температурным
коэффициентом емкости.
Следует
знать, чем меньше значение ТКЕ, тем более
стабильными характеристиками обладает
конденсатор. Особое внимание уделяют
ТКЕ при разработке измерительного
оборудования высокого класса точности,
где критичны значительные отклонения
параметров любого радиоэлектронного
элемента.
Тангенс угла
потерь
Потери,
неизбежно возникающие при работе
конденсатора, главным образом определяются
свойствами диэлектрика, расположенного
между обкладками конденсатора, и
характеризуются тангенсом
угла потерь tg δ.
Производители стремятся снизить значение
угла tg δ
и за счет этого улучшить характеристики
конденсаторов. Поэтому наибольшее
применение получила специальная
керамика, обладающая минимальным
тангенсом угла потерь. Значения тангенса
угла потерь у керамических высокочастотных,
слюдяных, полистирольных и фторопластовых
конденсаторов находятся в пределах
(10…15)х10-4,
поликарбонатных (15…25)х10-4,
керамических низкочастотных 0,035, оксидных
5…35%.
Обратной
величиной тангенса угла потерь
конденсатора является добротность,
равная
QC=1/tgδ.
Конденсаторы
высокого качества обладают добротностью
свыше тысячи единиц.
Номинальное
напряжение
— напряжение, обозначенное на конденсаторе
(или указанное в документации), при
котором он может работать в заданных
условиях в течение срока службы с
сохранением параметров в допустимых
пределах. Все конденсаторы имеют какое-то
предельное напряжение, которое можно
на них подавать. Дело все в том, что может
произойти пробой диэлектрика, и
конденсатор выйдет из строя. Чаще всего
это напряжение пишут на самом корпусе
конденсатора. Например, на электролитическом
конденсаторе.
Кроме
номинального рабочего напряжения в
технических условиях обычно указывается
испытательное напряжение. При выборочном
выходном контроле оценивают способность
конденсатора выдерживать кратковременные
перегрузки Uисп
= (1,5 – 2)U
ном
Ток
утечки конденсатора
Дело все в том, что
какой бы ни был диэлектрик, конденсатор
все равно рано или поздно разрядится,
так как через диэлектрик, как ни странно,
все равно течет ток. Величина этого тока
у разных конденсаторов тоже разная.
Электролитические конденсаторы обладают
самым большим током утечки.
Также
ток утечки зависит от напряжения между
обкладками конденсатора. Здесь уже
работает закон Ома: I=U/Rдиэлектрика.
Поэтому, никогда не стоит подавать
напряжение больше, чем максимально
рабочее напряжение, прописанное на
конденсаторе.
Удельная
емкость конденсатора
Суд
= Сном/V
(Sподложки),
где
Сном
–номинальная
емкость конденсатора,
V
– объем
конденсатора,
Sподложки
– площадь,
которую занимает конденсатор на подложке.
Величина
удельной емкости должна быть максимально
возможной, т. к. желательно получить
конденсатор с необходимой величиной
емкости при минимальных размерах.
Хотите
сделать конденсатор с огромной удельной
емкостью, делайте площадь пластин как
можно больше, расстояние между пластинами
как можно меньше и выбирайте диэлектрик
с максимальным значением диэлектрической
проницаемости. К сожалению, все эти
способы получения максимальной Суд
имеют серьезные ограничения.
Уменьшение толщины
диэлектрика ограничено электрической
прочностью материала.
Выбор
материала с большой диэлектрической
проницаемостью приводит к ограничению
частотного диапазона применения
конденсатора, т.к. как правило, такие
материалы обладают большим значением
тангенса угла
диэлектрических потерь tg δ.
Поэтому часто, для
увеличения удельной емкости используют
разные конструктивные решения.
Расстояние между пластинами в плоском конденсаторе. Калькулятор онлайн.
Онлайн калькулятор вычисления расстояния между пластинами в плоском конденсаторе, позволит найти расстояние между пластинами через электроемкость и площадь пластины, а
также через площадь пластины, напряжение и заряд на пластине. Калькулятор произведет вычисление и даст подробное решение. Единицы измерения, могут включать любые приставки Си.
Калькулятор автоматически переведет одни единицы в другие.
Калькулятор вычислит:
Расстояние между пластинами в плоском конденсаторе через электроемкость и площадь пластины.
Расстояние между пластинами в плоском конденсаторе через площадь пластины, напряжение и заряд на пластине.
Расстояние между пластинами в плоском конденсаторе через электроемкость и площадь пластины
Плоский конденсатор представляет собой две параллельные проводящие пластины, разделенные диэлектриком, расположенные на малом расстоянии друг от друга.
Расстояние между пластинами в плоском конденсаторе определяется формулой, где
ε0 – электрическая постоянная, ε0 = 8.85418781762039 × 10-12
ε – диэлектрическая проницаемость диэлектрика
S – площадь пластины
C – емкость плоского конденсатора
Единицей измерения расстояния является – Метр (м, m).
Диэлектрическая проницаемость ε =
Площадь пластины S =
Электроемкость C
Единица измерения расстояния d
Расстояние между пластинами в плоском конденсаторе через площадь пластины, напряжение и заряд на пластине
Плоский конденсатор представляет собой две параллельные проводящие пластины, разделенные диэлектриком, расположенные на малом расстоянии друг от друга.
Расстояние между пластинами в плоском конденсаторе определяется формулой, где
ε0 – электрическая постоянная, ε0 = 8.85418781762039 × 10-12
ε – диэлектрическая проницаемость диэлектрика
S – площадь пластины
U – напряжение
Q – заряд на пластине
Единицей измерения расстояния является – Метр (м, m).
Диэлектрическая проницаемость ε =
Площадь пластины S =
Напряжение U =
Заряд Q =
Единица измерения расстояния d
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
1
. Два одинаковых положительных заряда 0,1 мкКл находятся в воздухе на расстоянии 8 см друг от друга. Определить напряженность поля в точке О, находящейся на середине отрезка, соединяющего заряды, и в точке А, расположенной на расстоянии 5 см от зарядов (рис. 4).
Дано Q 1 =Q 2 =10 -7 Кл, ε=1, r 0 =0,08м, r 1 =0,05м
Найти: Ео, Е А.
Решение. Напряженность поля, создаваемого зарядами, находится по принципу суперпозиции. Результирующая напряженность Е равна векторной сумме напряженностей, создаваемых каждым зарядом в данной точке поля: Е=Е 1 +Е 2 (1). Напряженность электрического поля, создаваемая отдельным зарядом, определяется по формуле.
Кроме того, мы можем считать, что электрический заряд будет распределяться почти равномерно в каждом одной из внутренних поверхностей проводящих пластин, а эффектами накопления электрического заряда по краям можно пренебречь. То есть исследуемая система очень близка к идеальной модели параллельного плоского конденсатора, электрическая мощность которого равна.
После зарядки конденсатора аккумулятор отключается. Когда пластины будут изолированы, они будут поддерживать количество загрузки. И поскольку электрическая мощность является фактором, который зависит от геометрии системы, и он не изменился, разность потенциалов между проводниками будет по-прежнему составлять 9 В, даже если они больше не подключены к клеммам аккумулятора.

, надо сначала построить векторы напряженностей. Так как заряды Q 1
и Q 2
положительные, векторы E 1
и Е 2
направлены от точки О в сторону от зарядов, создающих это поле (см. рис. 4). Кроме того, по условию задачи заряды равны и расположены на одинаковом расстоянии от точки О Поэтому с учетом направления векторов из формулы (1) получаем E 0 =E 1,0 -E 2,0
но так E 1,0 =E 2,0 ,
то Е 0 =0
.
Если конденсатор заполнен линейной диэлектрической средой, емкость увеличивается в κ, называемом диэлектрической проницаемостью материала. В результате соотношение между зарядом, хранящимся в проводниках, и разностью потенциалов между ними изменяется. И если нагрузка не может измениться, поскольку проводники изолированы, она должна сделать разность потенциалов между пластинами, хотя будет продолжаться, что они должны быть эквипотенциальными поверхностями.
Поскольку расстояние между пластинами остается небольшим по сравнению с их размерами, мы можем гарантировать, что электрическое поле сохраняет свое направление перпендикулярно проводящим плоскостям во всей области между ними.
В точке А
напряженность поля вычисляется по формуле (1); построение векторов проводится аналогично. Результирующий вектор напряженности Е А
является диагональю параллелограмма (см. рис. 4), следовательно, Е А =E 1 +Е 2
или Е А =2Е 1 сosα
, так как Е 1 =Е 2 .
Из рис. 4 имеем . Напряженность поля в точке А
определяем по формуле
Следовательно, эквипотенциальные поверхности будут плоскостями, параллельными проводникам. Давайте посмотрим на эквипотенциальную поверхность, которая соответствует диэлектрическому интерфейсу. Поскольку они оба являются диэлектриками, мы будем считать идеальными, там не может быть никакого свободного электрического заряда. Обратите внимание, что упомянутая поверхность имеет те же электрические характеристики, что и виртуальная разгруженная и изолированная проводящая поверхность и, следовательно, эквивалентна ей.
То есть электрические свойства диэлектрической системы не будут изменены, если тонкий изолированный и незаряженный проводящий лист будет помещен на поверхность диэлектрика вдали от области пустот. Один из них полностью заполнен диэлектрической проницаемостью κ = 2 и толщиной и еще одним вакуумом с разделением между проводниками.
Емкости конденсаторов ассоциации.
Подставив в (3) числовые значения, получим
Ответ: E 0 =0, E A =432 кВ/м
2.
Электроемкость плоского воздушного конденсатора С=1 нФ,
расстояние между обкладками 4 мм
. На помещенный между обкладками конденсатора Q=4,9 нКл
действует сила F=98 мкН
. Площадь обкладки 100 см 2 .
Определить: напряженность поля и разность потенциалов между обкладками, энергию поля конденсаторов и объемную плотность энергии.
И разница в потенциале в этом должна быть суммой разностей потенциалов в отношениях ассоциации. Где значение потенциала виртуального плавающего драйвера в эквивалентной системе будет. То есть, это будет значение эквипотенциала, которое соответствует интерфейсу воздух-диэлектрик.
Короче говоря, вводя диэлектрический лист между проводящими плоскостями, когда они были изолированы и заряжены величинами, разность потенциалов между ними уменьшается до значения.
В эквивалентной последовательной ассоциации смещение одной из проводящих плоскостей приводит к изменению емкости пустого конденсатора, тогда как диэлектрическое заполнение остается неизменным, чтобы не изменять форму или положение листа.
F=9,8 . 10 -5 H, Q=4,9 . 10 -9 Кл, C=10 -9 Ф, S=10 -2 м 2 , d=4 . 10 -3 м, ε=1, ε 0 =8,85 . 10 -12 Ф/м
Найти: E, U, WЭ,ω.
Решение. Поле между обкладками конденсатора считаем однородным. Напряженность поля конденсатора определяется из выражения”. E=F/Q
, где F
– сила, с которой поле действует на заряд Q
, помещенный между обкладками конденсатора.
Подставив числовые значения, найдём
Эквивалентная емкость будет.
Поэтому в конденсаторе, где проводники полностью влияют, а величины заряда в двух проводниках противоположны, мы будем иметь. Следовательно, энергии, хранящиеся в системе в трех проанализированных конфигурациях, будут.
То есть, помещая диэлектрик при постоянной нагрузке, электростатическая энергия, запасенная в системе, уменьшается. Следовательно, электрическое поле между пластинами выполняет работу по вводу диэлектрического листа. И наоборот, для того, чтобы восстановить значение емкости и разность потенциалов путем смещения одной из проводящих плоскостей, необходимо выполнить внешнюю работу, которая преобразуется в увеличение электрической энергии, хранящейся в системе.
Е=9,8 . 10 -5 Н/4,9 . 10 -9 Кл=2 . 10 4 В/м=20кВ/м
Разность потенциалов между обкладками U=Ed
. Подставив числовые значения, получим
U=2 . 10 -4 В/м. 4 . 10 -3 м=80В
Энергии поля конденсатора
Подставив в числовые значения, получим
Плотность энергии – объем поля конденсатора; находи
В принципе, конденсатор в своем простейшем выражении образован двумя облицовочными металлическими пластинами, отделенными друг от друга минимальным расстоянием, и диэлектриком, который определяется как непроводящий материал электричества, который находится между указанными пластинами. Величина емкости конденсатора прямо пропорциональна площади его пластин и обратно пропорциональна расстоянию, которое их разделяет.
Технология электролитических конденсаторов
В широком спектре технологий изготовления конденсаторов электролиты являются наиболее мощными из-за уменьшения разделения между пластинами, увеличения площади, обращенной к ним, и использования диэлектрика высокого давления диэлектрик. Электролитические конденсаторы названы в честь того, что диэлектрический материал, который они содержат, представляет собой кислоту, называемую электролитом, и применяется в жидком состоянии. Изготовление электролитического конденсатора начинается путем обертывания двух листов алюминия, разделенных поглощающей бумагой, смоченной электролитической кислотой.
Ответ: , U=80В, Е=20кВ/м,
3
. Найти, как изменятся электроемкость и энергия плоского воздушного конденсатора, если параллельно его обкладкам ввести металлическую пластину толщиной 1 мм
. Площадь обкладки конденсатора и пластины 150 см 2
, расстояние между обкладками 6 мм.
Конденсатор заряжен до 400 В
и отключен от батареи.
Затем электрический ток циркулирует между пластинами, чтобы вызвать химическую реакцию, которая приведет к образованию оксидного слоя на алюминии, причем этот оксид электролита является истинным диэлектриком конденсатора. Для того, чтобы он подключался к электронной схеме, конденсатор будет иметь свои соединительные клеммы, заклепленные или свариваемые с точечной сваркой. Наконец, весь сборник будет вставлен в металлический корпус, который придаст ему механическую жесткость и будет герметично закрыт, в общем, резиновой пробкой, что предотвратит испарение кислоты на ранней стадии.
Дано: ε=1, d 0 =10 -3 м, S=150см 2 =15 . 10 -3 м 2 , d=6 . 10 -3 м
Решение. Емкость и энергия конденсатора при внесении в него металлической пластины изменятся. Это вызвано тем, что при внесении металлической пластины уменьшается расстояние между пластинами от d
до (d-do)
(рис. 5). Используем формулу электроёмкости плоского конденсатора
Очень распространенным термином на жаргоне производителей электролитических конденсаторов является то, что протоконденсатор, который называется изготовленными и собранными конденсаторами, которые еще не были циркулированы, для образования слоя оксида электролита. Этот термин будет использован позже для лучшего понимания в этой же статье.
Различные электролитические отказы
Следует пояснить, что, несмотря на наличие конденсаторов с бумажным диэлектриком, в случае электролитов бумага между пластинами служит для равномерного распределения кислоты по всей ее поверхности. Неудача в однородности оксидного слоя, образовавшегося в какой-то момент пластины, вызывает короткое замыкание или уменьшение рабочего напряжения конденсатора. Это условие увеличивает ток утечки, который вызывает внутренний перегрев и последующее расширение и испарение кислоты, которое, преодолевая герметичность резиновой заглушки взрывом, может разрушить конденсатор.
(1), где S
-площадь обкладки; d
– расстояние между обкладками. В данном случае получим, что изменение электроемкости конденсатора равно
Подставив числовые значения, получим
Так как электрическое поле в плоском конденсаторе однородно, плотность энергии во всех его точках одинакова и равна , (2) где Е
– напряженность поля между обкладками конденсатора. При внесении металлической пластины параллельно обкладкам напряженность поля осталась неизменной, а объем электрического поля уменьшился на Следовательно, изменение энергии (конечное значение ее меньше начального) произошло вследствие уменьшения объема поля конденсатора:
Если герметичное уплотнение конденсатора плохое, кислота высушивается и перестает действовать как диэлектрик. В этом случае значение емкости постепенно уменьшается. Конденсатор, который в течение примерно 4 лет не получает напряжения, начинает деформироваться внутри. Вот почему следует соблюдать особую осторожность, зная дату изготовления этих почти скоропортящихся компонентов или спрашивать время простоя электронного устройства, если оно готово его отремонтировать.
Поскольку клеммы конденсатора прикреплены заклепками или точками пайки к пластинам, в обоих случаях есть определенное контактное сопротивление. Если конденсатор работает в условиях высокой пульсации, такой как, например, фильтрация переключаемого источника, эти электрические связи нагреваются и окисляются. При нагревании и охлаждении они расширяются и сжимаются соответственно; эти последовательные сокращения и растяжения вызовут ослабление контактов контактов, даже оставляя конденсатор в открытом или прерывистом состоянии, обычно называемом ложными контактами.
(3)
Напряженность поля Е определяется через градиент потенциала: E=-U/d
, (4) где U
– разность потенциалов; d
– расстояние между обкладками. Формула (3) с учетом (4) принимает вид:
(5)
С другой стороны, эти ложные контакты приводят к перегреву, что ускоряет процесс, в виде порочного круга. Это особое условие – это тот, который часто путает самых опытных техников, потому что прибор может работать правильно в начальный момент зажигания и не достигает почти нескольких градусов температуры и наоборот.
Измерение и испытание электролитических конденсаторов
Хотя есть несколько тестов и измерений, которые могут быть выполнены на конденсаторе, мы упомянем те, которые особенно доступны техническому специалисту или специалисту по ремонту и которые полезны для обнаружения и устранения неисправностей электронного оборудования.
Подставляя числовые значения в формулу (5), получаем
Ответ: ,
4.
Сила тока в резисторе линейно нарастает за 4 с
от 0
до 8 А
. Сопротивление резистора 10 Ом.
Определить количество теплоты, выделившееся в резисторе за первые 3c
.
Конденсатор в очень плохом состоянии должен отражать такое состояние в своей емкости, однако на практике 10% -ное изменение емкости может скрыть больший ущерб, до 120%, если кто-то захочет оценить конденсатор, измеряя его эквивалентное сопротивление серии. Чем больше разность потенциалов на сопротивлении, тем лучше условие конденсатора. Эта проверка позволит измерить сопротивление терминала его клемм, его соединение с пластинами, состояние сушки внутреннего электролита и слоя оксида, то есть, насколько далеко это конденсатор от его исходного состояния протоконденсатора, и будет очень полезным для быстрого определения динамического состояния конденсаторов, все еще подключенных к их рабочим цепям. Эквивалентный измеритель сопротивления серии также может использоваться.
. Большинство конденсаторов имеют между своими листами непроводящее или диэлектрическое вещество.
Дано: t 0 =0, t 1 =4с, I=0, I 1 =8A, t 2 =3с.
Найти Q
.
Решение. По закону Джоуля-Ленца dQ=I 2 Rdt
(1) Так как сила тока является функцией времени, то I=kt
, (2) где k
– коэффициент пропорциональности, численно равный приращению тока в единицу времени:
Следовательно, . За первые три секунды выделиться количество теплоты
Плоский воздушный конденсатор имеет емкость C
. Как изменится его емкость, если расстояние между его пластинами уменьшить в 3 раза?
1) увеличится в 3 раза
2) уменьшится в 3 раза
3) увеличится в 9 раз
4) уменьшится в 9 раз
Решение.
d
между пластинами: Уменьшения расстояния между пластинами в 3 раза приведет к увеличению емкости в 3 раза.
Правильный ответ: 1.
Ответ: 1
Как изменится емкость плоского воздушного конденсатора, если площадь обкладок уменьшить в 2 раза, а расстояние между ними увеличить в 2 раза?
1) увеличится в 2 раза
2) уменьшится в 2 раза
3) не изменится
4) уменьшится в 4 раза
Решение.
Емкость плоского воздушного конденсатора прямо пропорциональна площади обкладок и обратно пропорциональна расстоянию d
между пластинами: Уменьшение площади обкладок в 2 раза и увеличение расстояния между пластинами в 2 раза приведет к уменьшению емкости в 4 раза.
Правильный ответ: 4.
Ответ: 4
Как изменится емкость плоского воздушного конденсатора, если расстояние между его обкладками увеличить в 2 раза?
1) увеличится в 2 раза
2) уменьшится в 2 раза
3) увеличится в 4 раза
4) уменьшится в 4 раза
Решение.
Емкость плоского воздушного конденсатора обратно пропорциональна расстоянию d
между пластинами: Увеличение расстояния между пластинами в 2 раза приведет к уменьшению емкости в 2 раза.
Правильный ответ: 2.
Ответ: 2
Гость
23.05.2014 16:27
как так расстояние уменьшилось в 2 раза значит ёмкость должна была увеличится ведь d/2 2 переходит в числитель и умножается с ES?!
Сергей Тигольских
Если яблоко поделить на двоих, Вам достанется меньше.
Расстояние между двумя точечными электрическими зарядами увеличили в 2 раза, и оба заряда увеличили в 2 раза. Сила взаимодействия между зарядами
1) уменьшилась в 4 раза
2) уменьшилась в 8 раз
3) уменьшилась в 16 раз
4) не изменилась
Решение.
Согласно закону Кулона, сила взаимодействия электрических зарядов прямо пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними: Таким образом, увеличение расстояния между зарядами в 2 раза и увеличение обоих зарядов в 2 раза не приведет к изменению силы взаимодействия.
Правильный ответ: 4.
Ответ: 4
Капля, имеющая положительный заряд при освещении потеряла один электрон. Каким стал заряд капли?
Решение.
Электрон несет отрицательный заряд Таким образом, согласно закону сохранения электрического заряда, после потери одного электрона заряд капли стал равен
Правильный ответ: 3.
Ответ: 3
Как изменится емкость плоского воздушного конденсатора, если расстояние между его пластинами уменьшить в 2 раза?
1) увеличится в 4 раза
2) увеличится в 2 раза
3) уменьшится в 2 раза
4) уменьшится в 4 раза
Решение.
Емкость плоского воздушного конденсатора обратно пропорциональна расстоянию d
между пластинами: Уменьшение расстояния между пластинами в 2 раза приведет к увеличению емкости в 2 раза.
Правильный ответ: 2.
Ответ: 2
Как надо изменить заряд на обкладках плоского конденсатора, чтобы после увеличения зазора между обкладками в 3 раза, напряженность электрического поля в зазоре уменьшилась в итоге вдвое?
1) увеличить в 4 раза
2) оставить прежним
3) уменьшить в 2 раза
4) увеличить в 2 раза
Решение.
Напряженность электрического поля внутри плоского конденсатора не зависит от расстояния между обкладками, а определяется только поверхностной плотностью электрического заряда на них: Следовательно, для того, чтобы напряженность электрического поля в зазоре уменьшилась в 2 раза, необходимо уменьшить заряд обкладок в 2 раза.
Правильный ответ: 3.
Ответ: 3
Гость
22.04.2012 22:33
почему не принимается во внимание условие, что зазор между обкладками увеличивается в 3 раза?
Гость
Добрый день!
Как сказано в решении, величина поля не зависит от расстояния между пластинами, изменение этого параметра никак не сказывается на величине напряженности электрического поля.
Гость
19.01.2013 16:07
E=KQ/R В КВАДРАТЕ НАПРЯЖЕННОСТЬ ЗАВИСИТ ОТ РАССТОЯНИЯ МЕЖДУ ПЛАСТИНАМИ!
Гость
Добрый день!
То, что вы написали, это напряженность электрического поля, создаваемого точечным зарядом. Конденсатор состоит из двух параллельных пластин. Эту, естественно, использовать нельзя.
Плоский конденсатор зарядили и отключили от источника тока. Как изменится энергия электрического поля внутри конденсатора, если увеличить в 2 раза расстояние между обкладками конденсатора?
1) увеличится в 2 раза
2) увеличится в 4 раза
3) уменьшится в 2 раза
4) уменьшится в 4 раза
Решение.
Энергия электрического поля внутри плоского конденсатора пропорциональна квадрату заряда его обкладок и обратно пропорциональна емкости конденсатора: При увеличении расстояния между обкладками конденсатора в 2 раза, заряды на них не изменятся, а емкость станет в два раза меньше: Следовательно, энергия электрического поля увеличится в 2 раза.
Правильный ответ: 1.
Ответ: 1
Гость
26.05.2013 13:21
Энергия же обозначается буквой W, а не Е.
Гость
03.02.2014 22:14
Не понимаю,почему мы не использовали формулу CU*2/2
Алексей
Добрый день!
Используйте, если нравится, только не забывайте, что при разведении пластин изменится не только емкость конденсатора, но и напряжение между пластинами
В подключенном к источнику постоянного тока плоском конденсаторе при увеличении в 2 раза расстояния между обкладками энергия электрического поля
1) увеличится в 2 раза
2) увеличится в 4 раза
3) уменьшится в 2 раза
4) уменьшится в 4 раза
Решение.
Энергия электрического поля внутри плоского конденсатора пропорциональна произведению емкости конденсатора и квадрата приложенного к нему напряжения: При увеличении расстояния между обкладками конденсатора в 2 раза, напряжение на конденсаторе не изменится, а емкость станет в два раза меньше: Следовательно, энергия электрического поля уменьшится в 2 раза.
Правильный ответ: 3.
Ответ: 3
Гость
01.05.2012 05:44
Добрый день!
Скажите пожалуйста, почему в этой и предыдущей задаче были использованы разные формулы, в чём разница?
Гость
Добрый день!
Различие в том, что в предыдущей задаче конденсатор отключен от источника, а в
этой — подключен.
В задачах требуется определить, как меняется энергия конденсатора при увеличении расстояния между обкладками. Всегда надо стараться использовать такие формулы, в которых “меняется” минимальное количество величин. В данной задаче напряжение остается все время постоянным (оно равно напряжению на источнике), а вот заряд на пластины конденсатора при их раздвижении изменяется (он набегает с источника). Поэтому логично использовать формулу для энергии конденсатора . Тогда сразу понятно, как меняется эта величина при изменении емкости. Можно было бы использовать и вторую формулу , но тут надо еще понять, как меняется заряд при изменении емкости, то есть привлечь формулу , то есть по сути снова прийти к . В предыдущей задаче все наоборот, заряд пластин там измениться не может, так как ему неоткуда взяться, а вот напряжение изменяется, поэтому сразу приходит мысль о том, что луче взять формулу .
Резюмирую все выше сказанное:
В принципе достаточно помнить одну формулу для энергии (любую) и формулу, определяющую емкость конденсатора (). Все остальное можно получить. Однако, если Вы помните несколько вариантов, используя их можно избежать некоторой лишней мороки.
Гость
21.04.2013 13:10
Добрый день.
Но если мы высчитываем энергию по формуле CU^2/2, то почему учитываем только зависимость C от d, но не учитываем зависимость U от d: U=Ed?
Алексей
Добрый день!
Встречный вопрос: “А почему Вы не учитываете зависимость от ?”
Если конденсатор подключен к источнику, то напряжение между его обкладками остается постоянным, в этом и суть. А вот напряженность поля уменьшается при увеличении расстояния между обкладками.
Как изменится электроемкость конденсатора, если заряд на его обкладках увеличить в 2 раза?
1) увеличится в 2 раза
2) уменьшится в 2 раза
3) не изменится
4) увеличится в 4 раза
Решение.
Электроемкость конденсатора не зависит от заряда на его обкладках, она определяется его геометрическими размерами. При увеличении заряда на обкладках в 2 раза электроемкость конденсатора не изменится.
Правильный ответ: 3.
Ответ: 3
Гость
20.04.2012 18:25
Формула для конденсатора ведь С=q/U.
Гость
При изменении заряда на конденсаторе изменится величина электрического поля в нем, а значит, и напряжение. Эти величины изменяются пропорционально, поэтому емкость не изменяется. Аналогично для формулы : величина сопротивления не зависит от напряжения или силы тока, а определяется свойствами проводника.
Гость
08.06.2012 18:35
НУ на вопрос то вы так и не ответили!
Формула то С=q/U.
Гость
Я ответил, просто Вы никак не хотите понять. Давайте еще пример. Пусть у нас есть вода, ее плотность определяется следующим соотношением: . Если взять воду массой в 2 раза больше, разве ее плотность поменяется? Конечно нет, потому что она будет занимать вдвое больший объем. И вообще, если у Вас нет ни капли воды, плотность ее все равно известная величина, приведенная во всех таблицах.
Точно также и для конденсатора, даже если он у вас совсем без заряда, у него все равно есть емкость (для плоского конденсатора она определяется формулой: ). Емкость – это неотъемлемая характеристика конденсатора, она зависит только от его устройства.
Если заряд на обкладках конденсатора уменьшить в 2 раза, то его емкость
1) увеличится в 2 раза
2) не изменится
3) уменьшится в 2 раза
4) уменьшится в 4 раза
Решение.
Электроемкость конденсатора не зависит от заряда на его обкладках, она определяется его геометрическими размерами. При уменьшении заряда на обкладках в 2 раза электроемкость конденсатора не изменится.
Правильный ответ: 2.
Ответ: 2
Гость
03.02.2013 14:03
Добрый день. А как же пресловутая формула c=q/U? Почему её нельзя применить в данном случае?
Гость
День добрый!
Эту формула остается справедливой, просто нельзя ее использовать буквально. Эта формула определяет такой параметр системы, как емкость, и утверждает, что для фиксированного конденсатора заряд на конденсаторе и напряжение между обкладками пропорциональны. То есть при уменьшении заряда в 2 раза, в 2 раза уменьшится и напряжение.
Аналогичная ситуация, например, с формулами и . Вы же не будете утверждать, что если подключить резистор к вдвое меньшему напряжению, то его сопротивление уменьшится. Или что плотность пропорциональна массе тела? Эти формулы как раз и утверждают, что некоторые величины нельзя поменять независимо. Например, нельзя запихнуть 2 кг воды в тот же объем, что занимает 1 кг.