Из точки А к плоскости проведены две наклонные АВ и АС, образующие между собой прямой угол. Найти расстояние между основаниями наклонных, если наклонные образуют с плоскостью углы 30°и 60°, а расстояние от точки А до плоскости 10 см.
Доброго времени суток, уважаемые читатели!
Даю онлайн-консультации по математике при подготовке к ЕГЭ, ОГЭ, ВПР и домашних работ из учебников. Самые интересные задания и их решения выкладываю на своём канале.
Самое сложное здесь – построить чертёж.
Если соединить в один треугольник две наклонные, расстояние между основаниями наклонных и расстояние от точки А до плоскости, то конструкция выглядит так.
Давайте разберемся в решении данной задачи.
Первый способ.
Теперь треугольник АВС расположим не перпендикулярно к данной плоскости, а под наклоном. В этом случае точки В, Н и С не будут лежать на одной прямой. Тогда все данные задачи сливаются не в треугольник, а в тетраэдр. Это выглядит так.
Решение будет отличаться от представленного ранее первого способа.
Как заметит внимательный читатель, ответы в первом и во втором решениях совпадают.
Если на тетраэдр посмотреть под другим углом, то можно увидеть треугольник.
Я представила вам два способа решения задачи и не знаю, оба верны или только одно.
Как вы считаете?
Дорогие десятиклассники!
Успехов в решении математических задач и в подготовке к ЕГЭ.
С вами автор канала Любовь.
Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?
Определение.
Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.

рисунок 1
Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).
Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.
На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.
Точка B — основание перпендикуляра, точка C — основание наклонной AC.
Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.
Из точки к прямой можно провести бесконечно много наклонных.
Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.
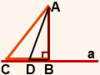
рисунок 2
На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
AC и AD.
CD=BC-BD.
Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.

рисунок 3
На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
AC и AD:
CD=BC-BD.
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
В следующий раз рассмотрим свойства наклонных.
Людии добрые!!! Это очееень сроооочно!!! Помогииите с задачей по геометрии!!
Ученик
(138),
закрыт
7 лет назад
Алёнка
Мудрец
(15254)
7 лет назад
Получаетс равнобедренный прямоугольный треугольник
Растояние от точки до плоскости- высота ( она же медиана и биссектриса), которая делит угол 90 пополам. Образуются два равнобедренных прямоугольных треугольника с углами при основании 45
Растояние от точки до плоскости= половине расстояния между основаниями наклонных, т. е расстояние между основаниями равно 4V2
Вот так вот работает этот сайт. Ты написал в вопросе “Как решить задачу по геометрии”. Кто-то раньше по поводу решения совершенно другой задачи так сформулировал вопрос, и теперь ВСЕ вопросы с ЛЮБЫМИ задачами которые озаглавлены так, будут закрываться. Точно так же будут впредь закрываться и все вопросы, названные “Помогите решить задачу по геометрии!”, даже если в них будут совсем другие задачи. Поэтому впредь, в заголовок вопроса пиши само условие, а не просьбу помочь. Ну а теперь, по существу.
Пусть общая точка наклонных А. Одна наклонная АВ, другая АС. Нужно найти расстояние ВС. Опустим из точки А перпендикуляр АО на плоскость. Соединим точку О отрезками с точками В и С.
ОВ и ОС – проекции, угол ВОС равен 120 градусам.
Треугольники АОВ и АОС – прямоугольные с остроыми углами АВО и АСО по 30 градусов.
Значит АО равно 4*(1/2)=2 см, а АВ=АС=4*(√(3)/2)=2*√(3) см. В получившемся из проекций равнобедренном треугольнике треугольнике ВОС проведем высоту ОК (она же и медиана и биссектриса). Треугольники ВОК и СОК – прямоугольные с острым углом в 30 градусов. Значит ВК=СК=2*√(3)*√(3)/2=3 см, отсюда ВС=3+3=6 см.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,651 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,896 -
разное
16,900
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
