Светило науки – 3713 ответов – 0 раз оказано помощи
Ответ:
2 ед.
Объяснение:
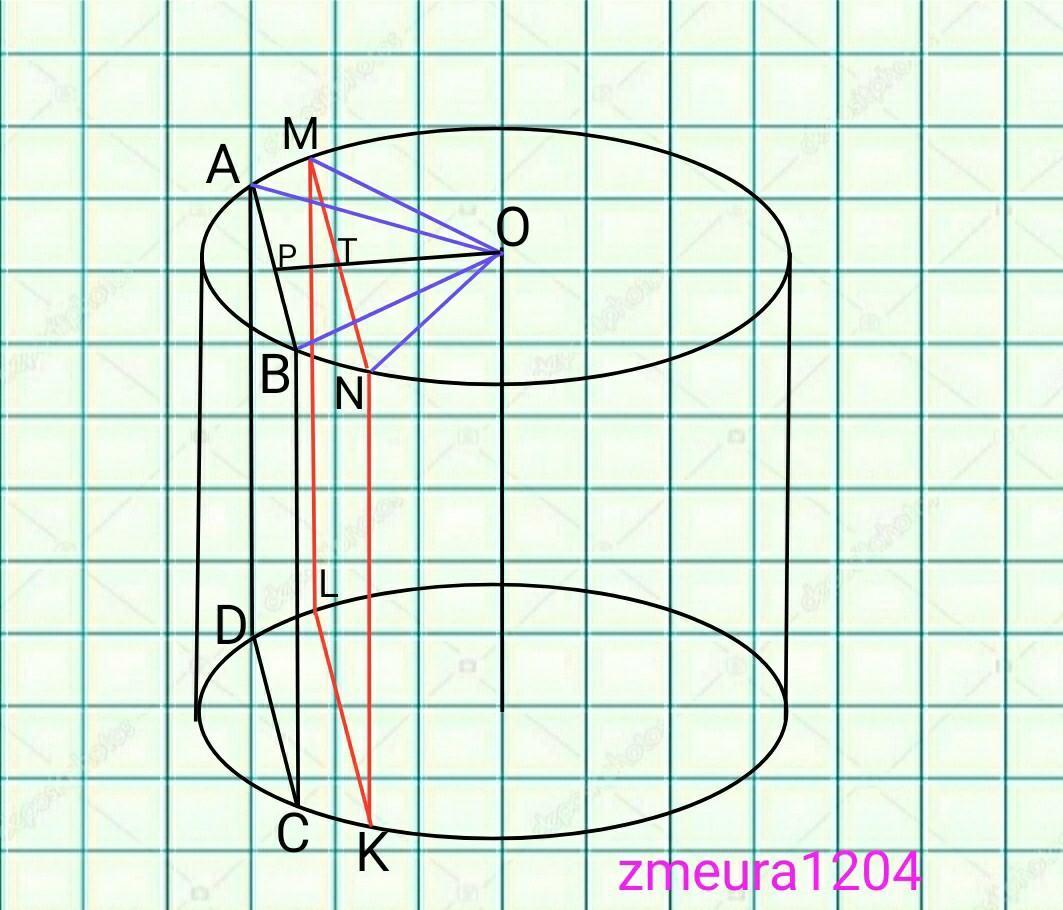
S(MNKL)=160 ед²
S(ABCD)=120 ед²
NK=ML=BC=AD=10см высота.
PT=?
Решение:
S(MNKL)=МN*NK; →
MN=S(MNKL)/NK=160/10=16 ед
∆МNO- равнобедренный треугольник.
МО=ОN=10 ед радиусы.
ТО- высота, медиана и биссектриса ∆MNO.
МТ=ТN
MT=MN/2=16/2=8 ед
∆MTO- прямоугольный треугольник.
По теореме Пифагора
ТО=√(МО²-МТ²)=√(10²-8²)=6 ед.
S(ABCD)=AB*BC; →
AB=S(ABCD)/BC=120/10=12 ед
∆АОВ- равнобедренный треугольник.
АО=ОВ=10 ед радиусы.
РО- высота, медиана и биссектриса ∆АОВ.
АР=РВ
АР=АВ/2=12/2=6 ед.
∆АРО- прямоугольный треугольник.
По теореме Пифагора:
РО=√(АО²-АР²)=√(10²-6²)=8 ед.
РТ=РО-ТО=8-6=2 ед.
Ответ:
2 ед.
Объяснение:
S(MNKL)=160 ед²
S(ABCD)=120 ед²
NK=ML=BC=AD=10см высота.
PT=?
Решение:
S(MNKL)=МN*NK; →
MN=S(MNKL)/NK=160/10=16 ед
∆МNO- равнобедренный треугольник.
МО=ОN=10 ед радиусы.
ТО- высота, медиана и биссектриса ∆MNO.
МТ=ТN
MT=MN/2=16/2=8 ед
∆MTO- прямоугольный треугольник.
По теореме Пифагора
ТО=√(МО²-МТ²)=√(10²-8²)=6 ед.
S(ABCD)=AB*BC; →
AB=S(ABCD)/BC=120/10=12 ед
∆АОВ- равнобедренный треугольник.
АО=ОВ=10 ед радиусы.
РО- высота, медиана и биссектриса ∆АОВ.
АР=РВ
АР=АВ/2=12/2=6 ед.
∆АРО- прямоугольный треугольник.
По теореме Пифагора:
РО=√(АО²-АР²)=√(10²-6²)=8 ед.
РТ=РО-ТО=8-6=2 ед.
Приложения:
Геометрия 10-11 класс. Цилиндр
Скачать файл в формате pdf.
Геометрия 10-11 класс. Цилиндр
Прямым круговым цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону. Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований.
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник. Две его стороны – образующие цилиндра, а две другие – параллельные хорды оснований. В частности, прямоугольником является осевое сечение. Это – сечение цилиндра плоскостью, проходящей через его ось.
Площадь боковой поверхности цилиндра находится по формуле: ({S_{{text{б}}{text{.п}}{text{.}}}} = 2,pi ,R,H); площадь полной поверхности цилиндра находится по формуле: (S = 2,pi ,R,H + 2pi ,{R^2}); объем цилиндра находится по формуле: (V = pi ,{R^2},H), где R – радиус основания; H – длина высоты цилиндра.
Задачи для самостоятельного решения
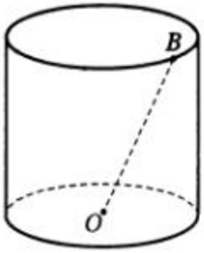
| Задача 1. Образующая цилиндра равна 20, расстояние от точки B до центра нижнего основания равно 29. Найдите диаметр цилиндра.
Ответ
ОТВЕТ: 42. |
 |
| Задача 2. Прямоугольник с диагональю 24 вращают вокруг одной из сторон, другая сторона составляет с этой диагональю угол 60°. Найдите площадь основания полученного тела вращения, деленную на π.
Ответ
ОТВЕТ: 144. |
|
| Задача 3. Высота и диаметр основания цилиндра равны 5. Найдите площадь боковой поверхности цилиндра, деленную на π.
Ответ
ОТВЕТ: 25. |
|
| Задача 4. Площадь боковой поверхности цилиндра равна 81π, а диаметр основания – 9. Найдите высоту цилиндра.
Ответ
ОТВЕТ: 9. |
|
| Задача 5. Длина развертки боковой поверхности цилиндра равна 24π, высота – 5. Найдите расстояние от центра верхнего основания до точки лежащей на окружности нижнего основания.
Ответ
ОТВЕТ: 13. |
|
| Задача 6. Площадь боковой поверхности цилиндра равна площади его основания. Во сколько раз диаметр основания больше высоты цилиндра?
Ответ
ОТВЕТ: 4. |
|
| Задача 7. Высота цилиндра равна 12, площадь боковой поверхности – 240π. Вычислите площадь сечения, параллельного оси цилиндра и отстоящего от него на расстояние 6.
Ответ
ОТВЕТ: 192. |
|
| Задача 8. Площадь боковой поверхности цилиндра равна 100π. Осевым сечением цилиндра является квадрат. Найдите площадь полной поверхности цилиндра, деленную на π.
Ответ
ОТВЕТ: 150. |
|
| Задача 9. Площади сечений параллельных оси цилиндра, находящихся по разные стороны от оси, равны 48 и 36, расстояние между сечениями равно 7. Высота цилиндра равна 6. Найдите радиус основания цилиндра.
Ответ
ОТВЕТ: 5. |
|
| Задача 10. Площади сечений параллельных оси цилиндра, находящихся по одну стороны от оси, равны 120 и 160. Радиус и высота цилиндра равна 10. Найдите расстояние между плоскостями сечений.
Ответ
ОТВЕТ: 2. |
|
| Задача 11. Правильная треугольная призма вписана в цилиндр, радиус основания которого равен (2sqrt 3 ,) а высота цилиндра равна 2. Найдите площадь боковой поверхности призмы.
Ответ
ОТВЕТ: 36. |
|
| Задача 12. Прямоугольник со сторонами (sqrt {frac{5}{pi }} ) и (sqrt {frac{{125}}{pi }} ) вращается вокруг меньшей стороны. Найдите площадь полной поверхности тела вращения.
Ответ
ОТВЕТ: 300. |
|
| Задача 13. Прямоугольник со сторонами (2sqrt {frac{7}{pi }} ) и (2sqrt {frac{1}{{7pi }}} ) вращается вокруг прямой, проходящей через середины больших сторон. Найдите площадь полной поверхности тела вращения.
Ответ
ОТВЕТ: 18. |
|
| Задача 14. Высота цилиндра равна 3. Равнобедренный треугольник ABC с боковой стороной 10 и ∠А = 120° расположен так, что его вершина A лежит на окружности нижнего основания цилиндра, а вершины B и C — на окружности верхнего основания. Найдите синус угла между плоскостью ABC и плоскостью основания цилиндра.
Ответ
ОТВЕТ: 0,6. |
Задача. Высота цилиндра равна 3, а радиус основания равен 13.
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
Решение.
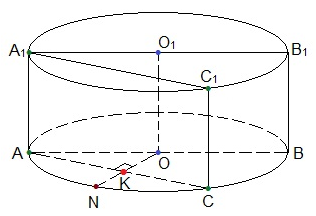Плоскость сечения, параллельная основанию цилиндра представляет собой прямоугольник AA1C1C, площадь которого S = AC ∙ AA1.
Так как по условию Sсеч. = 72
и АА1 = 3, то АС = 72 : 3 = 24.
Заметим, что хорда AC немногим меньше диаметра основания цилиндра (АВ = 2R = 2 ∙ 13 = 26).
Так как плоскость АА1С параллельна оси цилиндра ОО1, то расстояние до нее от точки О — длина перпендикуляра, проведенного из точки О к АС.
Проведем радиус ON перпендикулярно хорде AC.
Радиус, перпендикулярный хорде, делит ее и стягиваемую ею дугу пополам.
Точка K — середина AC, поэтому АК = АС : 2 = 24 : 2 = 12.
OK – искомый отрезок.
Рассмотрим прямоугольный треугольник АКО. По теореме Пифагора:
ОК2 = АО2 – АК2 = 132 – 122 =169 – 144 = 25, отсюда ОК = 5.
Это и есть расстояние от плоского сечения до центра основания цилиндра.
Ответ: 5.
Навигация
Задание 14. Математика ЕГЭ. Высота цилиндра равна 3, а радиус основания равен 13. Найдите расстояние от плоскости сечения до центра основания цилиндра.
Задание. Высота цилиндра равна 3, а радиус основания равен 13.
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
Решение:
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра. Так, чтобы площадь этого сечения равнялась 72.
Построим плоскость, проходящую параллельно оси цилиндра. Для этого из точек ВА и СD проведем прямые параллельные оси цилиндра ОО1, проведем хорды BC и AD. Прямоугольник ABCD – искомое сечение.
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
Найдем расстояние от плоскости сечения до центра основания цилиндра такое, чтобы площадь сечения была равна 72.
Рассмотрим треугольник ∆ВОС – равнобедренный, так как ОВ = ОС = Rосн.
Проведем медиану ОК, в равнобедренном треугольнике медиана является высотой, следовательно, ОК перпендикулярна ВС. Значит, ОК – расстояние от плоскости сечения до центра основания цилиндра.
SABCD = AB·BC
BC = SABCD/AB
BC = 72/3 = 24
ВК = КС = 12
Из прямоугольного треугольника ∆ОВК по теореме Пифагора найдем ОК:
ОК2 = ОВ2 – ВК2
ОК2 = 132 – 122 = 25
ОК = 5
Ответ: 5
Оставить комментарий
Рубрики
- Демоверсия ЕГЭ по информатике
- Демоверсия ЕГЭ по математике
- Демоверсия ОГЭ по информатике
- Демоверсия ОГЭ по математике
- Материалы по аттестации
- Решаем ЕГЭ по математике
- Задание 1
- Задание 10
- Задание 11
- Задание 12
- Задание 13
- Задание 14
- Задание 15
- Задание 16
- Задание 2
- Задание 3
- Задание 4
- Задание 5
- Задание 6
- Задание 7
- Задание 8
- Задание 9
- Решаем ОГЭ по математике
- Задание 21
- Задание 22
- Задание 24
- Скачать экзаменационные варианты по информатике
- ЕГЭ по информатике
- ОГЭ по информатике
- Скачать экзаменационные варианты по математике
- ЕГЭ по математике
- ОГЭ по математике
- Тематическое планирование
