Материал данной статьи позволяет получить навык определения расстояния между двумя параллельными плоскостями при помощи метода координат. Дадим определение расстояния между параллельными плоскостями, получим формулу для его расчета и рассмотрим теорию на практических примерах.
Расстояние между двумя параллельными плоскостями: определение
Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из рассматриваемых параллельных плоскостей до другой плоскости.
Пусть заданы две параллельные плоскости ϒ1 и ϒ2. Из произвольной точки М1 плоскости ϒ1 опустим перпендикуляр М1Н1 на другую плоскость ϒ2. Длина перпендикуляра М1Н1 и будет являться расстоянием между заданными плоскостями.
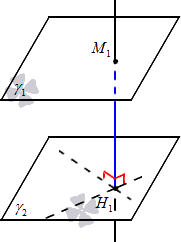
Указанное определение расстояния между параллельными плоскостями имеет взаимосвязь со следующей теоремой.
Если две плоскости параллельны, то все точки одной из параллельных плоскостей находятся на одном и том же расстоянии от другой плоскости.
Допустим, заданы две параллельные плоскости ϒ1 и ϒ2. Для получения доказательства теоремы необходимо доказать, что перпендикуляры, опущенные из различных произвольных точек одной плоскости к другой плоскости, равны. Пусть будут заданы некоторые произвольные точки М1 и М2 на плоскости ϒ1, и из них опущены перпендикуляры М1Н1 и М2Н2 на плоскость ϒ2. Таким образом, нам предстоит доказать, что М1Н1 = М2Н2.
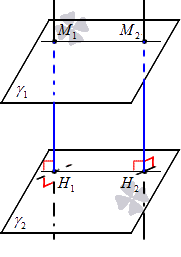
Прямые М1Н1 и М2Н2 параллельны, поскольку перпендикулярны одной плоскости. Опираясь на аксиому о единственной плоскости, проходящей через три различные точки, не лежащие на одной прямой, можем утверждать, что через две параллельные прямые проходит единственная плоскость. Будем считать, что существует некоторая плоскость ϒ3, проходящая через две параллельные прямые М1Н1 и М2Н2. Очевидным фактом является то, что плоскость ϒ3 пересекает плоскости ϒ1 и ϒ2 по прямым М1M2 и Н1Н2, которые не пересекаются, а значит – параллельны (в ином случае, заданные плоскости имели бы общую точку, что невозможно в силу их параллельности по условию задачи). Таким образом, мы наблюдаем четырехугольник М1М2Н1Н2, у которого противоположные стороны являются попарно параллельными, т.е. М1М2Н1Н2 – параллелограмм (в рассматриваемом случае – прямоугольник). Следовательно, противоположные стороны у этого параллелограмма равны, а значит |М1Н1| = |М2Н2|. Что и требовалось доказать.
Заметим также, что расстояние между параллельными плоскостями – наименьшее из расстояний между произвольными точками этих плоскостей.
Нахождение расстояния между параллельными плоскостями
По программе 10-11 классов расстояние между параллельными плоскостями определяется построением перпендикуляра из любой точки одной плоскости, опущенного к другой плоскости; после чего находится длина этого перпендикуляра (при помощи теоремы Пифагора, признаков равенства, или подобия треугольников, или определения синуса, косинуса, тангенса угла).
В случае, когда уже задана или есть возможность задать прямоугольную систему координат, то мы имеем возможность определить расстояние между параллельными плоскостями при помощи метода координат.
Пусть задано трехмерное пространство, а в нем – прямоугольная система координат и две параллельные плоскости ϒ1 и ϒ2. Найдем расстояние между этими плоскостями, опираясь, в том числе, на определение расстояния между плоскостями, данное выше.
В исходных данных – плоскости ϒ1 и ϒ2, и мы можем определить координаты (x1, y1, z1) некой точки M1, принадлежащей одной из заданных плоскостей: пусть это будет плоскость ϒ1. Также получим нормальное уравнение плоскости ϒ2: cos α·x+cos β·y+cos λ·z-p=0. В таком случае, искомое расстояние |М1Н1| будет равно расстоянию от точки М1(x1, y1, z1) до плоскости ϒ2 (ей соответствует нормальное уравнение cos α·x+cos β·y+cosγ·z-p=0). Тогда нужное расстояние вычислим по формуле: M1H1=cos α·x1+cos β·y1+cosγ·z1-p. Вывод данной формулы можно изучить в теме вычисления расстояния от точки до плоскости.
Резюмируем. Для того,чтобы определить расстояние между двумя параллельными плоскостями, необходимо:
– найти координаты (x1, y1, z1) некой точки М1, принадлежащей одной из исходных плоскостей;
– определить нормальное уравнение другой плоскости в виде cosα·x+cos β·y+cosγ·z-p=0;
– произвести расчет требуемого расстояние, используя формулу: M1H1=cos α·x1+cos β·y1+cosγ·z1-p.
Если в прямоугольной системе координат плоскость ϒ1 задается общим уравнением плоскости A·x+B·y+C·z+D1=0, а плоскость ϒ2 – общим уравнением A·x+B·y+C·z+D2=0, тогда расстояние между параллельными плоскостями необходимо вычислять по формуле:
M1H1=D2-D1A2+B2+C2
Покажем, как данная формула получена.
Пусть точка М1(x1, y1, z1) принадлежит плоскости ϒ1. В таком случае координаты этой точки будут отвечать уравнению плоскости A·x+B·y+C·z+D1=0, или верным будет равенство: A·x1+B·y1+C·z1+D1=0. Отсюда получим: A·x1+B·y1+C·z1+D1=0. Полученное равенство нам еще пригодится.
Плоскость ϒ2 будет описываться нормальным уравнением плоскости A·x+B·y+C·z+D2A2+B2+C2=0 или -A·x+B·y+C·z+D2A2+B2+C2=0 (в зависимости от знака числа D2). Однако при любом значение D2 расстояние |М1Н1| возможно рассчитать, используя формулу:
M1H1=A·x1+B·y1+C·z1+D2A2+B2+C2=A·x1+B·y1+C·z1+D2A2+B2+C2
Теперь задействуем полученное ранее равенство A·x1+B·y1+C·z1=-D1 и преобразуем формулу:
M1H1=-D1+D2A2+B2+C2=D2-D1A2+B2+C2
Даны две параллельные плоскости ϒ1 и ϒ2, описываемые уравнениями x16+y-14+z143=1 и 3x-2y+23z-20=0 соответственно. Необходимо определить расстояние между заданными плоскостями.
Решение
Решим задачу двумя способами.
- Уравнение плоскости в отрезках, которое задано в условии задачи, дает возможность определить координаты точки М1, принадлежащей плоскости, описываемой этим уравнением. Как точку М1 используем точку пересечения плоскости ϒ1 и оси Ox. Таким образом, имеем: M116, 0, 0.
Преобразуем общее уравнение плоскости ϒ2 в нормальный вид:
3x-2y+23z-20=0⇔3x-2y+23z-2032+(-2)2+232=0⇔⇔35x-25y+235z-4=0
Вычислим расстояние |М1Н1| от точки M116, 0, 0 до плоскости 35x-25y+235z-4=0:
M1H1=35·16-25·0+235·0-4=110-4=3910
Так мы получили искомое расстояние между исходными параллельными плоскостями.
- Преобразуем уравнение плоскости в отрезках в общее уравнение плоскости:
x16+y-14+z143=1⇔6x-4y+43z-1=0
Приравняем коэффициенты при переменных x, y, z в общих уравнениях плоскостей; с этой целью умножим обе части крайнего равенства на 2:
3x-2y+23z-20=0⇔6x-4y+43z-40=0
Воспользуемся формулой для нахождения расстояния между параллельными плоскостями:
M1H1=D2-D1A2+B2+C2=-40-(-1)62+(-4)2+(43)2=39100=3910.
Ответ: 3910.
Даны две параллельные плоскости, описываемые уравнениями: 6x+4y-12z+3=0 и 3x+2y-6z-2=0. Необходимо найти расстояние между этими плоскостями.
Решение
Удобнее будет использовать второй способ решения подобных задач. Умножим обе части второго уравнения на 2, и коэффициенты в уравнениях плоскостей станут равны: 6x+4y-12z+3=0 и 6x+4y-12z-4=0. Теперь можно использовать формулу:
M1H1=-4-362+42+(-12)2=7196=12
Однако попробуем найти ответ и первым способом: допустим, точка M1(x1, y1, z1) принадлежит плоскости 6x+4y-12z+3=0. Соответственно, координаты этой точки отвечают уравнению плоскости, и верным будет равенство:
6×1+4y1-12z1+3=0
Пусть y1= 0, z1 = 0, тогда x1: 6×1+4·0-12·0+3=0⇔x1=-12
Таким образом, точка получает точные координаты: M1-12, 0, 0.
Преобразуем общее уравнение плоскости 3x+2y-6z-2=0 в нормальный вид:
3x+2y-6z-2=0⇔3x+2y-6z-2=032+22+-6=0⇔37x+27y-67z-27=0
В таком случае, требуемое расстояние между плоскостями равно: 37·-12+27·0-67·0-67·0-27=-12=12
Ответ: 12.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Расстояние между плоскостями.
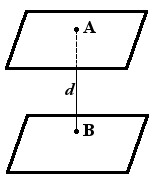
Определение. Расстояние между плоскостями — равно длине перпендикуляра, опущенного с одной плоскости на другую.
Формула для вычисления расстояния между плоскостями
Если заданы уравнения параллельных плоскостей Ax + By + Cz + D1 = 0 и Ax + By + Cz + D2 = 0, то расстояние между плоскостями можно найти, используя следующую формулу
| d = | |D2 – D1| |
| √A2 + B2 + C2 |
Примеры задач на вычисление расстояния между плоскостями
Пример 1.
Найти расстояние между плоскостями 2x + 4y – 4z – 6 = 0 и x + 2y – 2z + 9 = 0.
Решение. Проверим, параллельны ли плоскости, для этого умножим уравнение второй плоскости на 2
2x + 4y – 4z + 18 = 0
Так как коэффициенты при неизвестных величинах у полученного уравнения и первого уравнения равны, то для вычисления расстояния между плоскостями можно использовати приведенную выше формулу:
| d = | |18 – (-6)| | = | |24| | = | 24 | = 4 |
| √22 + 42 + (-4)2 | √36 | 6 |
Ответ: расстояние между плоскостями равно 4.
Расстояние между плоскостями.

Формула для вычисления расстояния между плоскостями
Если заданы уравнения параллельных плоскостей A x + B y + C z + D1 = 0 и A x + B y + C z + D2 = 0, то расстояние между плоскостями можно найти, используя следующую формулу
| d = | |D2 – D1| |
| √ A 2 + B 2 + C 2 |
Примеры задач на вычисление расстояния между плоскостями
Решение. Проверим, параллельны ли плоскости, для этого умножим уравнение второй плоскости на 2
2 x + 4 y – 4 z + 18 = 0
Так как коэффициенты при неизвестных величинах у полученного уравнения и первого уравнения равны, то для вычисления расстояния между плоскостями можно использовати приведенную выше формулу:
| d = | |18 – (-6)| | = | |24| | = | 24 | = 4 |
| √ 2 2 + 4 2 + (-4) 2 | √ 36 | 6 |
Ответ: расстояние между плоскостями равно 4.
Расстояние между плоскостями. Онлайн калькулятор
Страница обновляется. Могут возникнуть ошибки. Спасибо за понимание!
С помощю этого онлайн калькулятора можно найти расстояние между плоскостями. Дается подробное решение с пояснениями. Для нахождения расстояния между плоскостями, введите элементы уравнения плоскости в ячейки и нажимайте на кнопку “Решить”.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между плоскостями − теория
Заметим, сначала, что расстояние между плоскостями определена, если плоскости параллельны или, что то же самое, нормальные векторы этих плоскостей коллинеарны. Вычисление расстояния между двумя плоскостями можно свести к вычислению расстояния от точки первой плоскости до второй плоскости. Вычисление расстояния от точки до плоскости (онлайн калькулятор, теория, примеры) посмотрите на странице Расстояние от точки до плоскости онлайн.
Алгоритм вычисления расстояния между плоскостями содержит следующие шаги:
- Проверка коллинеарности нормальных векторов плоскостей.
- Нахождение некоторой точки M0 на первой плоскости.
- Вычисление расстояния между точкой M0 и второй плоскостью.
Выведем формулу вычисления расстояния между плоскостями.
Запишем уравнения двух плоскостей:
Очевидно, что нормальные векторы n1 и n2 не могут быть нулевыми векторами.Если из пары коэффициентов (A1,A2),(B1,B2), (C1,C2) один нулевой а другой − нет, то нормальные векторы n1 и n2 неколлинеарны. Т.е. задача неразрешима.
Нормальный вектор уравнения (2′) имеет следующий вид:
Для коллинеарности векторов n1 и n’2(или n1 и n2) необходимо и достаточно выполнение следующих равенств:
Если удовлетворяется условие (3) (или (3′)), то векторы n1 и n’2(или n1 и n2) коллинеарны, т.е. плоскости (1) и (2′) (или (1) и (2) ) параллельны. Тогда уравнение плоскости (2′) можно представить так:
2. Найдем некоторую точку на плоскости (1).
Легко убедится, что точка
принадлежит плоскости (1):
3. Расстояние от точки M0(x0, y0, z0) до плоскости (2”) вычисляется с помощью выражения (подробнее смотрите на странице расстояние от точки до плоскости):
Подставляя координаты точки M0 из (4) в (5), получим формулу вычисления расстояния между плоскостями (1) и (2”) (или (1) и (2)):
Расстояние между плоскостями − примеры и решения
Пример 1. Найти расстояние между плоскостями
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 1/3.
Общее уравнение плоскости имеет вид:
где n=(A,B,C)− называется нормальным вектором плоскости.
Нормальный вектор плоскости (7) равен n1=(1, 2, −4), нормальный вектор плоскости (8′) равен n2=(1, 2, −4). n1=n2. Следовательно эти плоскости параллельны.
Найдем расстояние между плоскостями (7) и (8′), используя следующую формулу:
Упростим и решим:
Ответ. Расстояние между плоскостями равен:
Пример 2. Найти расстояние между плоскостями
Эти плоскости не параллельны, так как коэффициент переменного z уравнения (10) нулевой а коэффициент переменного z уравнения (11)−нет. Невозможно найти расстояние между непараллельными плоскостями.
Пример 3. Найти расстояние между плоскостями
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 4/3.
Нормальный вектор плоскости (12) равен n1=(4, 2, 8), нормальный вектор плоскости (13′) равен n2=(4, 16/3, 64/3). n1≠n2. Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.
Расстояние между двумя параллельными плоскостями: определение и примеры нахождения
Материал данной статьи позволяет получить навык определения расстояния между двумя параллельными плоскостями при помощи метода координат. Дадим определение расстояния между параллельными плоскостями, получим формулу для его расчета и рассмотрим теорию на практических примерах.
Расстояние между двумя параллельными плоскостями: определение
Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из рассматриваемых параллельных плоскостей до другой плоскости.
Пусть заданы две параллельные плоскости ϒ 1 и ϒ 2 . Из произвольной точки М 1 плоскости ϒ 1 опустим перпендикуляр М 1 Н 1 на другую плоскость ϒ 2 . Длина перпендикуляра М 1 Н 1 и будет являться расстоянием между заданными плоскостями.
Указанное определение расстояния между параллельными плоскостями имеет взаимосвязь со следующей теоремой.
Если две плоскости параллельны, то все точки одной из параллельных плоскостей находятся на одном и том же расстоянии от другой плоскости.
Допустим, заданы две параллельные плоскости ϒ 1 и ϒ 2 . Для получения доказательства теоремы необходимо доказать, что перпендикуляры, опущенные из различных произвольных точек одной плоскости к другой плоскости, равны. Пусть будут заданы некоторые произвольные точки М 1 и М 2 на плоскости ϒ 1 , и из них опущены перпендикуляры М 1 Н 1 и М 2 Н 2 на плоскость ϒ 2 . Таким образом, нам предстоит доказать, что М 1 Н 1 = М 2 Н 2 .
Прямые М 1 Н 1 и М 2 Н 2 параллельны, поскольку перпендикулярны одной плоскости. Опираясь на аксиому о единственной плоскости, проходящей через три различные точки, не лежащие на одной прямой, можем утверждать, что через две параллельные прямые проходит единственная плоскость. Будем считать, что существует некоторая плоскость ϒ 3 , проходящая через две параллельные прямые М 1 Н 1 и М 2 Н 2 . Очевидным фактом является то, что плоскость ϒ 3 пересекает плоскости ϒ 1 и ϒ 2 по прямым М 1 M 2 и Н 1 Н 2 , которые не пересекаются, а значит – параллельны (в ином случае, заданные плоскости имели бы общую точку, что невозможно в силу их параллельности по условию задачи). Таким образом, мы наблюдаем четырехугольник М 1 М 2 Н 1 Н 2 , у которого противоположные стороны являются попарно параллельными, т.е. М 1 М 2 Н 1 Н 2 – параллелограмм (в рассматриваемом случае – прямоугольник). Следовательно, противоположные стороны у этого параллелограмма равны, а значит | М 1 Н 1 | = | М 2 Н 2 | . Что и требовалось доказать.
Заметим также, что расстояние между параллельными плоскостями – наименьшее из расстояний между произвольными точками этих плоскостей.
Нахождение расстояния между параллельными плоскостями
По программе 10 – 11 классов расстояние между параллельными плоскостями определяется построением перпендикуляра из любой точки одной плоскости, опущенного к другой плоскости; после чего находится длина этого перпендикуляра (при помощи теоремы Пифагора, признаков равенства, или подобия треугольников, или определения синуса, косинуса, тангенса угла).
В случае, когда уже задана или есть возможность задать прямоугольную систему координат, то мы имеем возможность определить расстояние между параллельными плоскостями при помощи метода координат.
Пусть задано трехмерное пространство, а в нем – прямоугольная система координат и две параллельные плоскости ϒ 1 и ϒ 2 . Найдем расстояние между этими плоскостями, опираясь, в том числе, на определение расстояния между плоскостями, данное выше.
В исходных данных – плоскости ϒ 1 и ϒ 2 , и мы можем определить координаты ( x 1 , y 1 , z 1 ) некой точки M 1 , принадлежащей одной из заданных плоскостей: пусть это будет плоскость ϒ 1 . Также получим нормальное уравнение плоскости ϒ 2 : cos α · x + cos β · y + cos λ · z – p = 0 . В таком случае, искомое расстояние | М 1 Н 1 | будет равно расстоянию от точки М 1 ( x 1 , y 1 , z 1 ) до плоскости ϒ 2 (ей соответствует нормальное уравнение cos α · x + cos β · y + cos γ · z – p = 0 ). Тогда нужное расстояние вычислим по формуле: M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 – p . Вывод данной формулы можно изучить в теме вычисления расстояния от точки до плоскости.
Резюмируем. Для того,чтобы определить расстояние между двумя параллельными плоскостями, необходимо:
– найти координаты ( x 1 , y 1 , z 1 ) некой точки М 1 , принадлежащей одной из исходных плоскостей;
– определить нормальное уравнение другой плоскости в виде cos α · x + cos β · y + cos γ · z – p = 0 ;
– произвести расчет требуемого расстояние, используя формулу: M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 – p .
Если в прямоугольной системе координат плоскость ϒ 1 задается общим уравнением плоскости A · x + B · y + C · z + D 1 = 0 , а плоскость ϒ 2 – общим уравнением A · x + B · y + C · z + D 2 = 0 , тогда расстояние между параллельными плоскостями необходимо вычислять по формуле:
M 1 H 1 = D 2 – D 1 A 2 + B 2 + C 2
Покажем, как данная формула получена.
Пусть точка М 1 ( x 1 , y 1 , z 1 ) принадлежит плоскости ϒ 1 . В таком случае координаты этой точки будут отвечать уравнению плоскости A · x + B · y + C · z + D 1 = 0 , или верным будет равенство: A · x 1 + B · y 1 + C · z 1 + D 1 = 0 . Отсюда получим: A · x 1 + B · y 1 + C · z 1 + D 1 = 0 . Полученное равенство нам еще пригодится.
Плоскость ϒ 2 будет описываться нормальным уравнением плоскости A · x + B · y + C · z + D 2 A 2 + B 2 + C 2 = 0 или – A · x + B · y + C · z + D 2 A 2 + B 2 + C 2 = 0 (в зависимости от знака числа D 2 ). Однако при любом значение D 2 расстояние | М 1 Н 1 | возможно рассчитать, используя формулу:
M 1 H 1 = A · x 1 + B · y 1 + C · z 1 + D 2 A 2 + B 2 + C 2 = A · x 1 + B · y 1 + C · z 1 + D 2 A 2 + B 2 + C 2
Теперь задействуем полученное ранее равенство A · x 1 + B · y 1 + C · z 1 = – D 1 и преобразуем формулу:
M 1 H 1 = – D 1 + D 2 A 2 + B 2 + C 2 = D 2 – D 1 A 2 + B 2 + C 2
Даны две параллельные плоскости ϒ 1 и ϒ 2 , описываемые уравнениями x 1 6 + y – 1 4 + z 1 4 3 = 1 и 3 x – 2 y + 2 3 z – 20 = 0 соответственно. Необходимо определить расстояние между заданными плоскостями.
Решение
Решим задачу двумя способами.
- Уравнение плоскости в отрезках, которое задано в условии задачи, дает возможность определить координаты точки М 1 , принадлежащей плоскости, описываемой этим уравнением. Как точку М 1 используем точку пересечения плоскости ϒ 1 и оси O x . Таким образом, имеем: M 1 1 6 , 0 , 0 .
Преобразуем общее уравнение плоскости ϒ 2 в нормальный вид:
3 x – 2 y + 2 3 z – 20 = 0 ⇔ 3 x – 2 y + 2 3 z – 20 3 2 + ( – 2 ) 2 + 2 3 2 = 0 ⇔ ⇔ 3 5 x – 2 5 y + 2 3 5 z – 4 = 0
Вычислим расстояние | М 1 Н 1 | от точки M 1 1 6 , 0 , 0 до плоскости 3 5 x – 2 5 y + 2 3 5 z – 4 = 0 :
M 1 H 1 = 3 5 · 1 6 – 2 5 · 0 + 2 3 5 · 0 – 4 = 1 10 – 4 = 3 9 10
Так мы получили искомое расстояние между исходными параллельными плоскостями.
- Преобразуем уравнение плоскости в отрезках в общее уравнение плоскости:
x 1 6 + y – 1 4 + z 1 4 3 = 1 ⇔ 6 x – 4 y + 4 3 z – 1 = 0
Приравняем коэффициенты при переменных x , y , z в общих уравнениях плоскостей; с этой целью умножим обе части крайнего равенства на 2 :
3 x – 2 y + 2 3 z – 20 = 0 ⇔ 6 x – 4 y + 4 3 z – 40 = 0
Воспользуемся формулой для нахождения расстояния между параллельными плоскостями:
M 1 H 1 = D 2 – D 1 A 2 + B 2 + C 2 = – 40 – ( – 1 ) 6 2 + ( – 4 ) 2 + ( 4 3 ) 2 = 39 100 = 3 9 10 .
Ответ: 3 9 10 .
Даны две параллельные плоскости, описываемые уравнениями: 6 x + 4 y – 12 z + 3 = 0 и 3 x + 2 y – 6 z – 2 = 0 . Необходимо найти расстояние между этими плоскостями.
Решение
Удобнее будет использовать второй способ решения подобных задач. Умножим обе части второго уравнения на 2 , и коэффициенты в уравнениях плоскостей станут равны: 6 x + 4 y – 12 z + 3 = 0 и 6 x + 4 y – 12 z – 4 = 0 . Теперь можно использовать формулу:
M 1 H 1 = – 4 – 3 6 2 + 4 2 + ( – 12 ) 2 = 7 196 = 1 2
Однако попробуем найти ответ и первым способом: допустим, точка M 1 ( x 1 , y 1 , z 1 ) принадлежит плоскости 6 x + 4 y – 12 z + 3 = 0 . Соответственно, координаты этой точки отвечают уравнению плоскости, и верным будет равенство:
6 x 1 + 4 y 1 – 12 z 1 + 3 = 0
Пусть y 1 = 0 , z 1 = 0 , тогда x 1 : 6 x 1 + 4 · 0 – 12 · 0 + 3 = 0 ⇔ x 1 = – 1 2
Таким образом, точка получает точные координаты: M 1 – 1 2 , 0 , 0 .
Преобразуем общее уравнение плоскости 3 x + 2 y – 6 z – 2 = 0 в нормальный вид:
3 x + 2 y – 6 z – 2 = 0 ⇔ 3 x + 2 y – 6 z – 2 = 0 3 2 + 2 2 + – 6 = 0 ⇔ 3 7 x + 2 7 y – 6 7 z – 2 7 = 0
В таком случае, требуемое расстояние между плоскостями равно: 3 7 · – 1 2 + 2 7 · 0 – 6 7 · 0 – 6 7 · 0 – 2 7 = – 1 2 = 1 2
[spoiler title=”источники:”]
http://matworld.ru/analytic-geometry/rasstojanie-mezhdu-ploskostjami.php
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/rasstojanie-mezhdu-dvumja-parallelnymi-ploskostjam/
[/spoiler]
Расстояние между плоскостями. Онлайн калькулятор
Страница обновляется. Могут возникнуть ошибки. Спасибо за понимание!
С помощю этого онлайн калькулятора можно найти расстояние между плоскостями. Дается подробное решение с пояснениями. Для нахождения расстояния между плоскостями, введите элементы уравнения плоскости в ячейки и нажимайте на кнопку “Решить”.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между плоскостями − теория
Заметим, сначала, что расстояние между плоскостями определена, если плоскости параллельны или, что то же самое, нормальные векторы этих плоскостей коллинеарны. Вычисление расстояния между двумя плоскостями можно свести к вычислению расстояния от точки первой плоскости до второй плоскости. Вычисление расстояния от точки до плоскости (онлайн калькулятор, теория, примеры) посмотрите на странице Расстояние от точки до плоскости онлайн.
Алгоритм вычисления расстояния между плоскостями содержит следующие шаги:
- Проверка коллинеарности нормальных векторов плоскостей.
- Нахождение некоторой точки M0 на первой плоскости.
- Вычисление расстояния между точкой M0 и второй плоскостью.
Выведем формулу вычисления расстояния между плоскостями.
Запишем уравнения двух плоскостей:
1. Проверяем коллинеарность нормальных векторов n1=(A1, B1, C1) и n2=(A2, B2, C2).
Очевидно, что нормальные векторы n1 и n2 не могут быть нулевыми векторами.Если из пары коэффициентов (A1,A2),(B1,B2), (C1,C2) один нулевой а другой − нет, то нормальные векторы n1 и n2 неколлинеарны. Т.е. задача неразрешима.
Пусть A1≠0, A2≠0. Уравнение плоскости (2) не изменится, если умножим на A1/A2:
Нормальный вектор уравнения (2′) имеет следующий вид:
Для коллинеарности векторов n1 и n’2(или n1 и n2) необходимо и достаточно выполнение следующих равенств:
или
Если удовлетворяется условие (3) (или (3′)), то векторы n1 и n’2(или n1 и n2) коллинеарны, т.е. плоскости (1) и (2′) (или (1) и (2) ) параллельны. Тогда уравнение плоскости (2′) можно представить так:
где
2. Найдем некоторую точку на плоскости (1).
Легко убедится, что точка
принадлежит плоскости (1):
3. Расстояние от точки M0(x0, y0, z0) до плоскости (2”) вычисляется с помощью выражения (подробнее смотрите на странице расстояние от точки до плоскости):
Подставляя координаты точки M0 из (4) в (5), получим формулу вычисления расстояния между плоскостями (1) и (2”) (или (1) и (2)):
где
Расстояние между плоскостями − примеры и решения
Пример 1. Найти расстояние между плоскостями
и
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 1/3.
Общее уравнение плоскости имеет вид:
где n=(A,B,C)− называется нормальным вектором плоскости.
Нормальный вектор плоскости (7) равен n1=(1, 2, −4), нормальный вектор плоскости (8′) равен n2=(1, 2, −4). n1=n2. Следовательно эти плоскости параллельны.
Найдем расстояние между плоскостями (7) и (8′), используя следующую формулу:
Подставим значения A, B, C, D1, D2 в (9):
Упростим и решим:
Ответ. Расстояние между плоскостями равен:
Пример 2. Найти расстояние между плоскостями
и
Решение.
Эти плоскости не параллельны, так как коэффициент переменного z уравнения (10) нулевой а коэффициент переменного z уравнения (11)−нет. Невозможно найти расстояние между непараллельными плоскостями.
Пример 3. Найти расстояние между плоскостями
и
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 4/3.
Нормальный вектор плоскости (12) равен n1=(4, 2, 8), нормальный вектор плоскости (13′) равен n2=(4, 16/3, 64/3). n1≠n2. Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.
Лекция
№5
Взаимное
расположение двух и трех плоскостей.
Расстояние от точки до плоскости.
Расстояние между двумя параллельными
плоскостями. Угол между плоскостями.
Лемма 5.1.
(Условие
параллельности вектора и плоскости).
Пусть в
аффинной системе координат задана
плоскость
![]()
общим уравнением![]()
и вектор
![]() .
.
Вектор
![]()
параллелен плоскости
![]() тогда
тогда
и только тогда, когда
выполняется условие:
![]() .
.
Доказательство.
Пусть
![]() .
.
Докажем, что выполняется условие
![]() .
.
1.
Рассмотрим
![]() .
.
Отложим
от неё вектор
![]() .
.
2. Пусть
![]() ,
,
тогда вектор
![]() .
.
Запишем условие равенства векторов
![]()
и
![]() :
:
![]()
3. Так как
![]() ,
,
то
ее координаты удовлетворяют уравнению
плоскости, т.е.
![]()
![]() ,
,
где
![]()
(точка
![]()
принадлежит плоскости ).
(<=)
повторить
все рассуждения в обратном направлении.
Ч.т.д.
Лемма 5.2.
Пусть в
прямоугольной системе координат
плоскость
задана общим уравнением:
![]() .
.
Тогда
вектор
![]() перпендикулярен
перпендикулярен
плоскости
![]() .
.
Доказательство.
Пусть
вектор
![]()
параллелен плоскости .
Применяя
условие параллельности вектора и
плоскости, получим:
![]()
вектор
![]() перпендикулярен
перпендикулярен
плоскости
![]() .
.
Ч.т.д.
Взаимное
расположение двух плоскостей.
В аффинной системе
координат поверхность, заданная
уравнением первой степени, является
плоскостью. Выясним, при каких условиях
два уравнения
![]()
и
![]() :
:
I.
Определяют одну и ту же плоскость;
II.
Определяют две параллельные плоскости;
III.
Определяют две пересекающиеся плоскости.
I.
Условия, при которых уравнения
![]()
и
![]()
определяют
одну и ту же плоскость.
Теорема 5.3.
Для
того чтобы два
уравнения
![]()
и
![]()
в аффинной системе координат определяли
одну и ту же плоскость, необходимо и
достаточно, чтобы все коэффициенты в
уравнениях были пропорциональны.
Необходимость:
Дано: уравнения
плоскостей
![]() :
:
![]()
(1)
![]()
![]()
(2)
Докажем:
![]() .
.
Доказательство:
1.
Данные уравнения определяют одну и ту
же плоскость
![]() .
.
Значит, векторы нормалей
![]()
и ![]()
будут коллинеарны, т.е.
![]()
или
![]() .
.
2.
Подставим выражения в уравнение (1) и
выразим
![]() :
:
![]()
3.
Найдем отношение
![]() :
:
![]() .
.
4.
Значит,
![]()
Достаточность:
Дано:
уравнения:
![]() :
:
![]()
(1)
![]()
![]()
(2)
![]() .
.
Докажем,
что уравнения (1) и (2) задают одну и ту же
плоскость
![]() .
.
Доказательство:
1.
Выразим из условия теоремы
![]()
коэффициенты
![]() :
:
![]()
-
Подставим
данные выражения в уравнение (1):
![]()
или
![]()
3.
Значит, уравнениями (1) и (2) задаётся одна
плоскость в аффинной системе координат.
II.
Условие параллельности двух прямых.
Теорема
5.4.
Два
уравнения
![]()
и
![]()
в аффинной системе координат определяют
две параллельные плоскости, если
коэффициенты при переменных
![]()
в уравнениях пропорциональны.
III.
Условие пересечения двух прямых.
Теорема
5.5.
Два
уравнения
![]()
и
![]()
в аффинной системе координат определяют
две пересекающие плоскости, если
коэффициенты при переменных
![]()
в уравнениях не пропорциональны.
Взаимное расположение
плоскостей
![]()
и
![]()
определяется и рангами расширенной и
основной матриц, соответствующих системе
уравнений данных плоскостей:

Пусть:
-

– расширенная
матрица ранга

-

-основная
матрица ранга
 .
.
-
Если
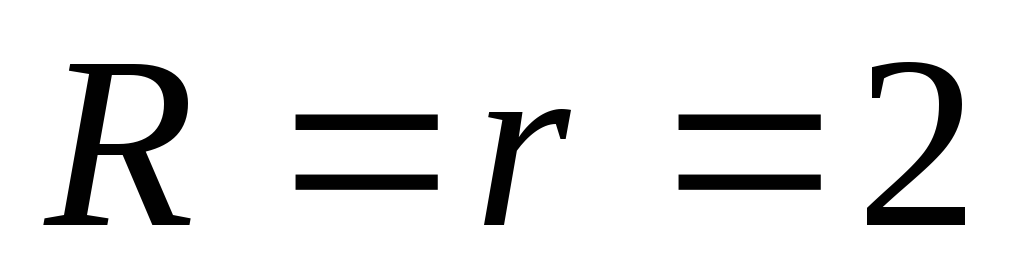 ,
,
то плоскости

и

пересекаются; -
Если
 ,
,
то плоскости

и

совпадают; -
Если
 ,
,
то плоскости

и

параллельны.
Пучок плоскостей.
Определение
5.6. Пучком
плоскостей называется совокупность
плоскостей пространства, проходящих
через одну прямую.
Пусть плоскости
![]()
и
![]()
пересекаются, причем
![]() :
:
![]() ;
;
![]() :
:
![]()
Помножим уравнения
плоскостей
![]()
и
![]()
соответственно на числа
![]()
и q,одновременно
не равные 0, и сложим полученные равенства:
![]() (*)
(*)
![]() ,
,
где
Коэффициенты при
х,у,z
не равны
нулю одновременно,
т.к. одновременное равенство нулю
позволяет говорить, что
![]() .
.
По условию параллельности плоскостей
имеем, что
![]()
=> противоречит
условию.
Уравнение (*)
есть
уравнение плоскости, проходящей через
общую прямую двух данных плоскостей.
![]() —
—
уравнение пучка
плоскостей.
Пример.
Задача:
Составить
уравнение плоскости, проходящей через
точку А(2,3,1) и прямую, определяемую
плоскостями:х+у-2z+1=0
и 2x–y+z-4=0.
Определение
5.7.
Совокупность
всех плоскостей, проходящих через точку
пересечения трех основных плоскостей,
называются связкой
плоскостей.
![]() —уравнение
—уравнение
связки.
Расстояние от
точки до плоскости.
З адача:
адача:
Найти расстояние от точки
![]() до
до
плоскости :
![]() .
.
Решение:
1.
![]() ,
,
![]()
2.
![]()
3. Вектор
![]()
![]()
=>![]()
![]()
4. Так как точка
![]() принадлежит
принадлежит
плоскости, то имеем:
![]()
![]()
5.
![]()
или
![]()
– расстояние
от точки Мо до плоскости.
Расстояние
между двумя параллельными плоскостями.
Задача:
Найти расстояние между параллельными
плоскостями
![]()
и
![]() ,
,
заданными своими уравнениями:
![]()
и
![]() .
.

Угол между
плоскостями.
Определение
5.8.
Углом между плоскостями называется
любой из двух двугранных углов,
образованный
этими плоскостями.
 —формула
—формула
угла между
![]()
и
![]() .
.
Соседние файлы в папке вопрос 6
- #
- #
