By visualizing the shape of the surfaces you should realize that the shortest distance will be between some point on the surface when $x=y$ (a parabola) and the plane when $x=y$ (a line).
There are at least two methods for solving this. First, there is a general fact that if $L$ is a line with vector equation $r(t)=(a,b,c)+t(alpha,beta,gamma)$ where $(alpha,beta,gamma)$ is a unit vector and $P=(x_0,y_0,z_0)$ a point in $mathbb{R}^3$
and if $d$ is the distance from $P$ to $L$, then
$$d^2=(x_0-a)^2+(y_0-b)^2+(z_0-c)^2-[alpha(x_0-a)+beta(y_0-b)+gamma(z_0-c)]^2$$
Under this fact we can simply solve the problem by fixing the line $x+x-2z=8$ and varying $x$ along the curve $z=x^2+x^2$.
To this end, let $(a,b,c)=(0,0,-4)$ and the unit direction vector is $frac{1}{sqrt{3}}(1,1,1)$. Then our problem becomes minimizing the function $f(x)=d^2(P(x),L)$ where $P(x)$ is any point along the parabola.
$$f(x)= 2x^2+(2x^2+4)^2-frac{1}{3}(2x+2x^2+4)$$
$$f'(x)=frac{1}{3}(32x^3 -24x^2 + 68x-16)=0$$
now use whatever method you want to solve this (the cubic formula, rational root test, or bisection method starting at $0$ and $1$).
You’ll find that $f'(frac{1}{4})=0$ and consequently $d=frac{31}{4sqrt{6}}$.
Alternatively, you could do the more obvious but less elegant method of simply using the normal distance function between the surfaces and minimizing it.
To this end, let $(x,y,z)$ describe the surface of the parabola and $(u,v,w)$ describe the plane.
As before, $x=y$ and $u=v$ and $w=frac{1}{2}(u+u-8)$ and $z=x^2+x^2$.
Then the function we want to minimize is
$$f((x,y,z),(u,v,w))=f(x,u)=2(x-u)^2 + (u-4-2x^2)^2$$
The minimum occurs at
$$nabla f(x,u)=(-8ux-4u+16x^3+36x,6u-4x^2-4x-8)=(0,0)$$
solve for $u$ in terms8 of $x$ from the second equation. That is $u=frac{1}{6}(4x^2+4x+8)$ then plug this into the other equation and you’ll end up with a multiple of the cubic equation we found in the first method.
The solution for this is as before.
Приходилось ли вам сталкиваться с задачей расчёта расстояния между деформируемыми объектами в COMSOL Multiphysics®? В этой статье блога мы расскажем, как найти расстояние между объектами с помощью методов расчёта поля кратчайших расстояний. Кроме того, мы выясним, как включить поле кратчайших расстояний в состав мультифизической модели.
Расчёт расстояний с помощью оператора General Extrusion
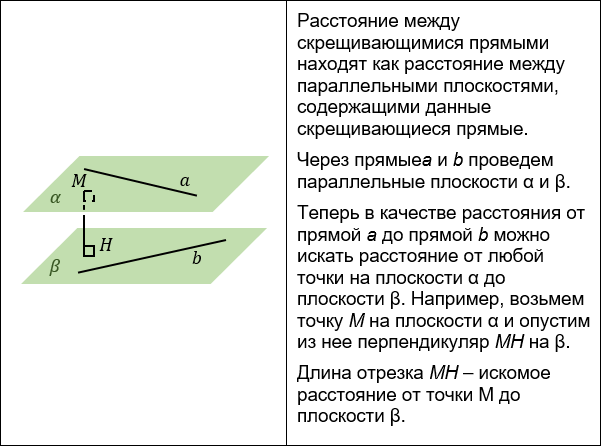
Обозначим два объекта буквами A и B, как показано на рисунке. Допустим, нужно рассчитать три расстояния:
- Расстояние до объекта А в виде полевой переменной. В данном случае рассчитываются расстояния и направления от всех точек вокруг и внутри объекта A до ближайшей точки на его границе (dA).
- Расстояние от каждой точки на границе объекта B до ближайшей точки объекта A (dAB).
- Координаты отрезка, определяющего кратчайшее расстояние между объектами A и B (dAB,min).
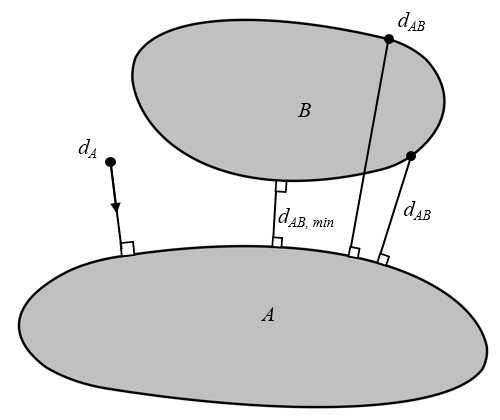
Объекты A и B, а также расстояния, которые нужно рассчитать.
Все три расстояния можно рассчитать с помощью комбинации операторов General Extrusion и Minimum в COMSOL Multiphysics. Сначала рассмотрим, как воспользоваться оператором General Extrusion. Присвоим оператору имя A_b, а в окне Source Selection выберем границы объекта А. В разделе Advanced для параметра Mesh search method выберем опцию Closest point. Описанные настройки показаны на рисунке ниже. Все остальные настройки оператора можно оставить без изменений.
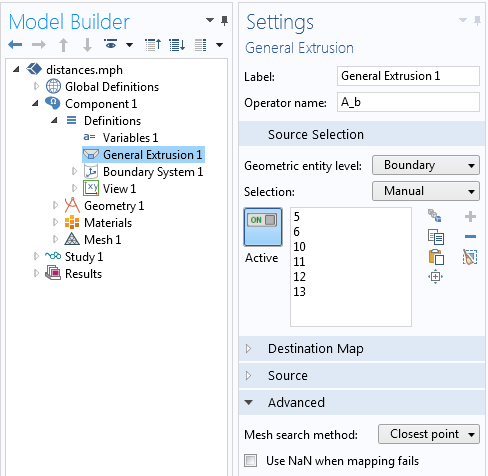
Окно настройки оператора General Extrusion, используемого для расчёта расстояния до ближайшей точки. Обратите внимание, что для параметра Method search method выбрана опция Closest Point.
Этот оператор используется в выражении для переменной d_A, имеющем вид:
sqrt((x-A_b(x))^2+(y-A_b(y))^2)
Областью определения переменной являются домены, в которых нужно рассчитать поле кратчайшего расстояния; в нашем случае это один домен. Можно также рассчитать градиент поля кратчайшего расстояния. Взяв эту величину с обратным знаком, получим -nabla d_A(mathbf{x}). Градиент задаёт компоненты векторного поля, каждый вектор которого направлен в сторону ближайшей к нему точки на границе A. С помощью оператора дифференцирования можно рассчитать производные по пространственным координатам d(d_A,x) и d(d_A,y), как показано на рисунке.
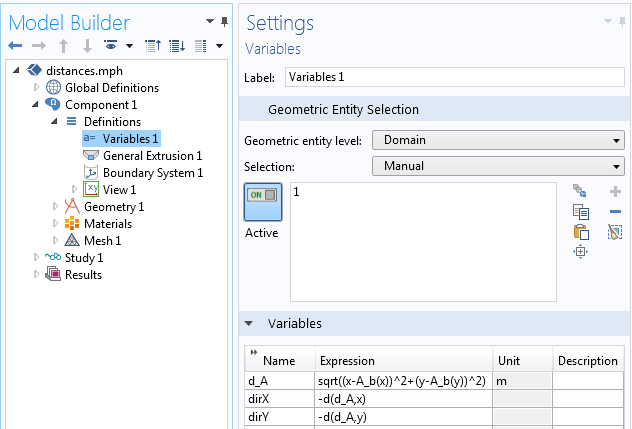
Окно настройки переменных.
Заданные переменные можно использовать в любом месте модели. Например, можно построить график поля кратчайшего расстояния или ввести зависимость свойств материала от расстояния до точки. На графике ниже показаны изолинии кратчайшего расстояния и векторы, указывающие кратчайшее направление. Обратите внимание, что расстояние рассчитывается даже для точек, лежащих за объектом B. Рассмотренный метод позволяет получить довольно много информации, но для этого потребуются значительные вычислительные ресурсы, поскольку кратчайшее расстояние рассчитывается для каждой точки домена. Однако в некоторых задачах такой объём данных избыточен, а найти нужно просто кратчайшее расстояние между объектами.
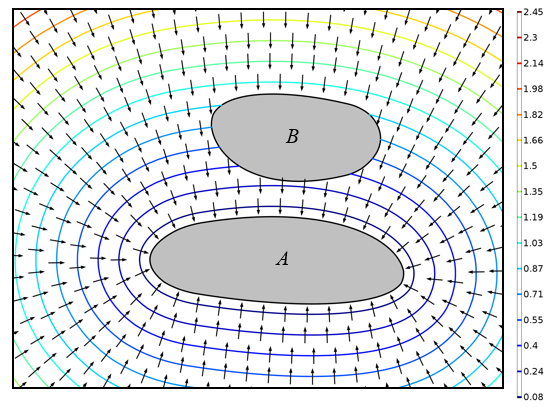
Изолинии кратчайшего расстояния и векторы, указывающие кратчайшее направление к границе объекта A (стрелки) из любой точки окружающей области.
Расчёт зазора между объектами
Теперь немного упростим задачу и найдём только длину кратчайшего пути между двумя объектами, не задумываясь о направлении. Воспользуемся тем же оператором General Extrusion, но дополнительно зададим вспомогательную переменную на границе объекта B, с помощью которой и рассчитаем расстояние.
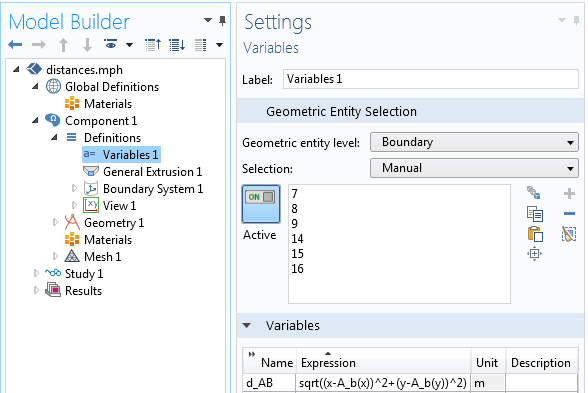
Переменная, введённая для расчёта расстояния между объектами.
Мы используем ту же самую функцию расстояния, что и в предыдущем примере, но теперь нам не потребуется строить сетку в промежуточном домене. Сетка не нужна даже внутри доменов A и B, достаточно разбить на элементы только границы объектов. Этот метод требует гораздо меньше расчётного времени, но при этом позволяет рассчитать только кратчайшее расстояние от объекта A до каждой точки на границе объекта B. Вектор направления остаётся не определён. Можно обратить все использованные определения, чтобы рассчитать кратчайшее расстояние от объекта B до каждой точки на границе объекта A. Эти данные будут распределены вдоль границ объектов, как показано на графике ниже.
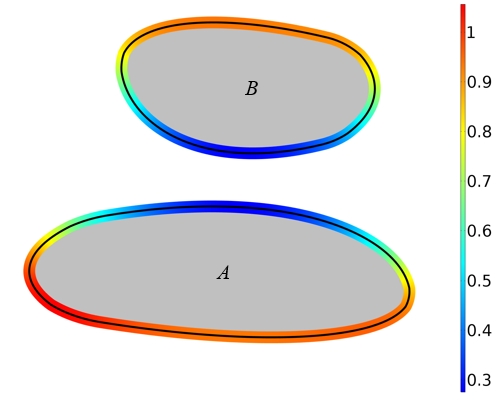
Расстояние от каждой точки на границе объекта B до ближайшей точки объекта A и наоборот.
Расчёт кратчайшего отрезка между объектами с помощью оператора Minimum
Теперь построим кратчайший отрезок, соединяющий два эти объекта. Выше было показано, как рассчитать переменные d_AB и d_BA, равные кратчайшему расстоянию между объектами A и B, а также B и A. Теперь найдём минимальное расстояние между границами объектов. Для этого добавим два оператора Minimum: один на границе объекта A, другой для объекта B. Присвоим операторам имена minA и minB, как показано на рисунке ниже.
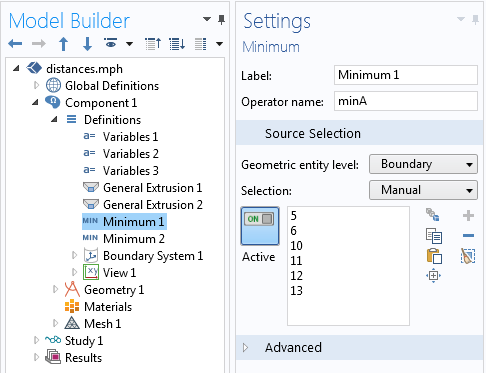
Настройка оператора Minimum на границе объекта A.
Затем с помощью введённых операторов рассчитаем минимальное расстояние. Чтобы найти координаты кратчайшего отрезка, вызовем оператор Minimum с двумя аргументами. Например, если определить переменную A_x как minA(d_BA,x), то она примет значение координаты x, при которой d_BA достигает минимального значения на границе A.
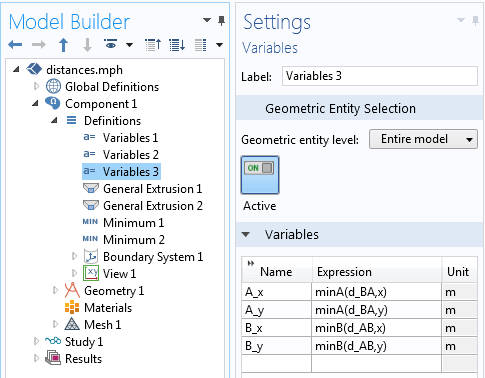
Определение координат кратчайшего отрезка между двумя доменами.
Переменные с найденными координатами можно использовать в любом месте модели. Например, с помощью функции Cut Line можно отобразить кратчайший отрезок, соединяющий два объекта, как показано на следующем рисунке. Если в области между двумя объектами сгенерирована расчётная сетка и получено решение, то можно построить распределение полевых переменных вдоль кратчайшего отрезка между объектами.
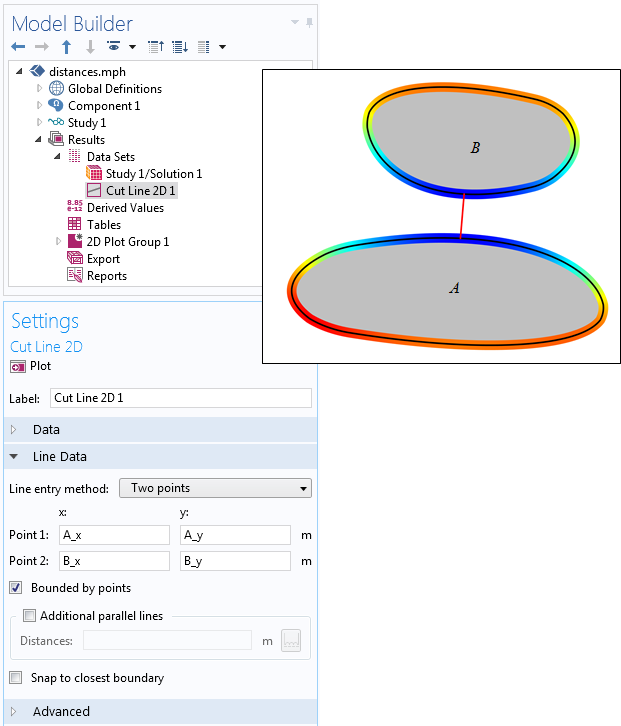
Для отображения кратчайшего отрезка между объектами использована функция Cut Line.
Использование рассчитанных расстояний и имеющиеся ограничения в COMSOL Multiphysics®
Описанные методы расчёта расстояний можно использовать в любой модели. Несмотря на то, что мы показали примеры расчёта только для двумерных областей, использованные методы можно обобщить и на трёхмерные задачи. Просто расчёт поля расстояний в 3D относительно долог, тогда как определение расстояний или зазоров между границами объектов требует меньше ресурсов.
Расчёт расстояний между негладкими фигурами немного сложнее. Ниже показано, что поле расстояний в окрестности входящих углов является негладким, поэтому вектор направления будет не определён вдоль линий, равноудалённых от двух разных частей границы. Чтобы избавиться от негладкости поля расстояний, нужно использовать более мелкую расчётную сетку.

Поле кратчайших расстояний снаружи и внутри объекта с входящими углами на грубой (слева) и более подробной сетке (справа). В данном случае гладкость поля расстояний зависит от размеров элементов сетки.
Если поле расстояний на соответствующей мелкой сетке найдено, то далее его можно использовать как любую другую переменную в нашей модели. Например, можно сделать свойства материала функцией расстояния от поверхности. Ниже показан пример такого распределения материалов.
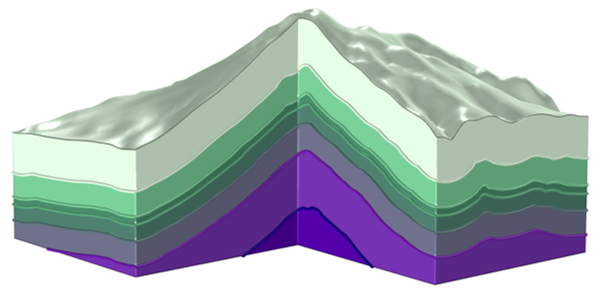
Пример распределение материала как функции от расстояния до поверхности.
Кроме того, функцию расстояния можно использовать для визуализации полученных результатов. Предположим, нужно построить график решения на определенном расстоянии от поверхности. В этом случае достаточно воспользоваться объёмным графиком с фильтром Filter. Логическое выражение в настройках фильтра позволяет отобразить результаты только в той области, которая находится на указанном расстоянии от поверхности объекта, как показано на рисунке ниже.
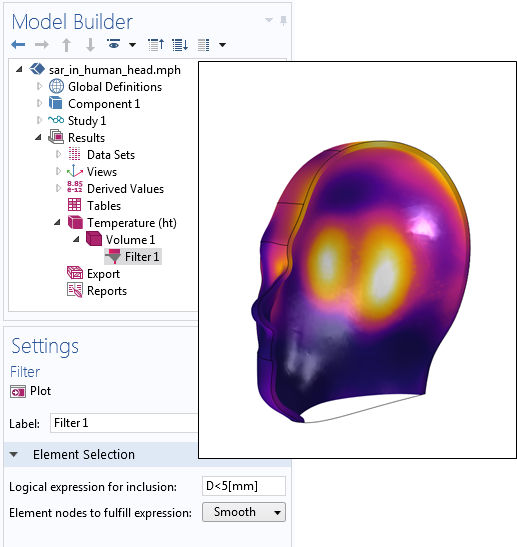
Использование функции расстояния для отображения данных в пределах пятимиллиметрового слоя от внешней поверхности модели.
Заключительные соображения о том, как рассчитать расстояние между геометрическими объектами в COMSOL Multiphysics®
Мы показали, как рассчитать поле кратчайшего расстояния до границы объекта, кратчайшее расстояние между границами объектов и кратчайший отрезок между двумя границами. Описанные подходы применимы также и для расчёта расстояний между рёбрами и точками в трёхмерных моделях. Переменные, содержащие рассчитанные расстояния, можно использовать в любом месте модели: в настройках, определениях, при обработке и визуализации результатов моделирования. В этой публикации мы показали пару примеров. Теперь ваша очередь. Расскажите, что получится у вас!
Дополнительные ссылки
- Справочные ресурсы о численном моделировании в COMSOL Multiphysics:
- Инструменты группы Help в COMSOL Multiphysics® и их использование в моделировании
- Using the COMSOL Website Resources for Modeling and Software Help
Содержание
English version
Вычисление расстояний между геометрическими объектами
Расстояние между точками $ X=(x_{1},dots,x_n) $ и $ Y=(y_{1},dots,y_n) $ из пространства $ mathbb R^{n}_{} $ понимается в стандартной евклидовой метрике:
$$ sqrt{(x_1-y_1)^2+dots+(x_n-y_n)^2} . $$
Для согласования дальнейших обозначений будем всегда считать точки пространства $ mathbb R^{n}_{} $ векторами-столбцами.
Линейные многообразия
Расстояние от точки до линейного многообразия (плоскости)
Задача. Найти расстояние от точки $ X_{0} in {mathbb R}^{n} $ до линейного многообразия (плоскости) $ mathbb M $ в $ {mathbb R}^{n} $, заданного системой уравнений
$$
left{
begin{array}{ccc}
c_{11}x_1+c_{12}x_2+dots+c_{1n}x_n &=& h_1 \
dots & & dots \
c_{m1}x_1+c_{m2}x_2+dots+c_{mn}x_n &=& h_m
end{array}
right.
$$
или, в матричном виде
$$
CX={mathcal H} quad npu quad
C=left(
begin{array}{cccc}
c_{11}& c_{12} & dots & c_{1n} \
dots & & & dots \
c_{m1}& c_{m2} & dots & c_{mn}
end{array}
right)_{mtimes n} ,
{mathcal H} =left(
begin{array}{c}
h_1 \ vdots \ h_m
end{array}
right),
X=left(
begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
$$
При этом предполагается, что $ mle n_{} $ и что ранг матрицы $ C_{} $ равен $ m_{} $, то есть система уравнений совместна и определяемое ею многообразие в $ {mathbb R}^{n} $ является $ (n-m)_{} $-мерным.
Т
Теорема 1. [1]. Составим квадратную матрицу порядка $ m+1_{} $:
$$
M=left(
begin{array}{cc}
Ccdot C^{top} & CX_0- {mathcal H} \
(CX_0- {mathcal H})^{top} & 0
end{array}
right)
$$
Расстояние от точки $ X_{0} $ до линейного многообразия $ mathbb M $ вычисляется по формуле
$$
d= sqrt{-frac{det M}{det(Ccdot C^{top})}} .
$$
Доказательство
☞
ЗДЕСЬ.
=>
Расстояние от точки $ X_{0}=(x_{10},dots,x_{n0})^{top} $ до гиперплоскости (или, в случае $ n=2 $, прямой)
$$ c_1x_1+dots+c_nx_n= h $$
равно
$$ d= frac{|c_1x_{10}+dots+c_nx_{n0}-h|}{sqrt{c_1^2+dots+c_n^2}} . $$
Ближайшая к $ X_0 $ точка гиперплоскости:
$$
X_{ast}=X_0- frac{c_1x_{10}+dots+c_nx_{n0}-h}{c_1^2+dots+c_n^2} left(begin{array}{c} c_1 \ vdots \ c_n end{array} right) , .
$$
Пусть теперь линейное многообразие (плоскость) задано параметрически
$$
mathbb M= { Y_0+lambda_1 Y_1+dots+lambda_k Y_k quad mid quad
{lambda_1,dots,lambda_k} subset {mathbb R} }
$$
при фиксированных столбцах
$$ {Y_0,Y_1,dots,Y_k }subset {mathbb R}^n . $$
Предположим, что эти столбцы линейно независимы. Составим из них матрицы
$$
L=left[ Y_1|dots|Y_k right]_{ntimes k} quad u quad tilde L = left[ Y_1|dots|Y_k| X_0-Y_0 right]_{ntimes (k+1)}
$$
(здесь $ |_{} $ означает конкатенацию).
Т
Теорема 2. Расстояние $ d_{} $ от точки $ X_{0} $ до линейного многообразия $ mathbb M $ вычисляется по формуле
$$
d=sqrt{frac{det(tilde L^{top}cdot tilde L)}{det( L^{top}cdot L)}} .
$$
Доказательство. Утверждение теоремы 2 является частным случаем общего результата о вычислении расстояния от точки до линейного многообразия в евклидовом пространстве.
♦
На основании свойств определителя Грама, матрица $ L^{top}cdot L_{} $ — при сделанном предположении о линейной независимости $ {Y_1,dots,Y_{k} } $ —
будет положительно определенной, а матрица $ tilde L^{top}cdot tilde L_{} $ при любых столбцах
$ {Y_0,Y_1,dots,Y_{k} } $ имеет неотрицательный определитель.
Т
Теорема 3. Ближайшая к точке $ X_0 $ точка многообразия $ mathbb M_{} $ (проекция точки на многообразие) определяется по формуле
$$
X_{ast}=Y_0+ L(L^{top}cdot L_{})^{-1} L^{top} (X_0-Y_0) , .
$$
Доказательство
☞
ЗДЕСЬ.
П
Пример. Найти расстояние от точки $ X_{0}=(1,1,1,1)^{top} $ до плоскости
$$
left{begin{array}{rrrrc}
3x_1&+x_2&-x_3&+x_4&=1 \
x_1 & -2x_2&+x_3&+2x_4&=2.
end{array}
right.
$$
Решение. 1-й способ: применение теоремы 1. Имеем:
$$
C=left( begin{array}{rrrr}
3 & 1 & -1 & 1 \
1 & -2 & 1 & 2
end{array}
right), {mathcal H}= left( begin{array}{r} 1 \ 2 end{array} right),
$$
$$
Ccdot C^{top} =
left( begin{array}{cc}
12 & 2 \
2 & 10
end{array}
right), CX_0=left( begin{array}{r} 4 \ 2 end{array} right),
CX_0-{mathcal H}=left( begin{array}{r} 3 \ 0 end{array} right) ,
$$
$$
frac{left| begin{array}{ccc}
12 & 2 & 3 \
2 & 10 & 0 \
3 & 0 & 0
end{array}
right|}{left| begin{array}{cc}
12 & 2 \
2 & 10
end{array}
right|}=frac{-90}{116}=-frac{45}{58} .
$$
2-й способ: применение теоремы 2. Общее решение системы уравнений, задающей плоскость:
$$ x_3=frac{5}{3}x_1+frac{4}{3}x_2, x_4=1-frac{4}{3}x_1+frac{1}{3}x_2 . $$
Таким образом, плоскость может быть представлена в параметрическом виде
$$
Y_0+lambda_1 Y_1 + lambda_2 Y_2 quad npu quad Y_0 = left( begin{array}{r} 0 \ 0 \ 0 \ 1 end{array}
right), Y_1=left( begin{array}{r} 0 \ 3 \ 4 \ 1 end{array}
right), Y_2=left( begin{array}{r} 3 \ 0 \ 5 \ -4 end{array}
right) .
$$
Имеем:
$$
L=
left( begin{array}{rr}
0 & 3 \
3 & 0 \
4 & 5 \
1 & -4
end{array}
right), tilde L =left( begin{array}{rrr}
0 & 3 & 1 \
3 & 0 & 1 \
4 & 5 & 1 \
1 & -4 & 0
end{array}
right),
frac{left| begin{array}{ccc}
26 & 16 & 7 \
16 & 50 & 8 \
7 & 8 & 3
end{array}
right|}{left| begin{array}{cc}
26 & 16 \
16 & 50
end{array}
right|}=frac{810}{1044}=frac{45}{58} .
$$
Координаты ближайшей точки к $ X_{0} $:
$$
X_{ast}= left(begin{array}{c} 1 \ 1 \ 1 \ 1 end{array}right)+left( begin{array}{rr}
0 & 3 \
3 & 0 \
4 & 5 \
1 & -4
end{array}
right)left( begin{array}{ccc}
26 & 16 \
16 & 50 \
end{array}
right)^{-1}
left(begin{array}{rrrr}
0 & 3 & 4 & 1 \
3 & 0 & 5 & -4
end{array}
right)left(begin{array}{c} 1 \ 1 \ 1 \ 0 end{array}right)=frac{1}{58}
left(begin{array}{c} 16 \ 37 \ 76 \ 49 end{array}right) , .
$$
Ответ. $ d=sqrt{45/58} approx 0.8808303295 $.
Расстояние между линейными многообразиями (плоскостями)
Пусть линейные многообразия в $ {mathbb R}^{n} $ заданы параметрически
$$
mathbb M_1={ X_0+ lambda_1 X_1+dots + lambda_k X_k mid {lambda_1,dots,lambda_k } subset mathbb R } ;
$$
$$
mathbb M_2={ Y_0+mu_1Y_1+dots+mu_{ell}Y_{ell} mid {mu_1,dots,mu_{ell} } subset mathbb R }
$$
при фиксированных столбцах
$$ {X_0,X_1,dots,X_k,Y_0,Y_1,dots,Y_{ell}}subset {mathbb R}^n . $$
Составим из этих столбцов матрицы
$$
P=left[ X_1|dots|X_k| Y_1|dots | Y_{ell} right]_{ntimes (k+ell)} quad u quad tilde P = left[ X_1|dots|X_k| Y_1|dots | Y_{ell}| X_0-Y_0 right]_{ntimes (k+ell+1)}
$$
(здесь $ |_{} $ означает конкатенацию).
Т
Теорема. Расстояние между линейными многообразиями $ mathbb M_1 $ и $ mathbb M_2 $ вычисляется по формуле
$$
d=sqrt{frac{det(tilde P^{top}cdot tilde P)}{det( P^{top}cdot P)}} .
$$
§
На основании свойств определителя Грама имеем:
$$
det (P^{top}cdot P) > 0 quad iff quad mbox{ столбцы } {X_1,dots,X_k,Y_1,dots,Y_{ell} } mbox{ линейно независимы};
$$
$$ det(tilde P^{top}cdot tilde P) ge 0 quad mbox{ при } forall {X_0,X_1,dots,X_k,Y_0,Y_1,dots,Y_{ell} } .
$$
П
Пример. [2]. Найти расстояние между плоскостями
$$
left( begin{array}{r} 89 \ 37 \ 111 \ 13 \54 end{array}
right) + lambda_1 left( begin{array}{r} 1 \ 1 \ 0 \ -1 \ -1 end{array}
right) + lambda_2 left( begin{array}{r} 1 \ -1 \ 0 \ -1 \ 1 end{array}
right) quad mbox{ и } quad
left( begin{array}{r} 42 \ -16 \ -39 \ 71 \3 end{array}
right) + mu_1 left( begin{array}{r} 1 \ 1 \ 0 \ 1 \ 1 end{array}
right) + mu_2 left( begin{array}{r} 1 \ -1 \ 0 \ 1 \ -1 end{array}
right) .
$$
Решение.
$$
P^{top}cdot P=4cdot E_{4 times 4}, quad
tilde P^{top}cdot tilde P=
left(begin{array}{ccccc}
4 & 0 & 0 & 0 & 107 \
0 & 4 & 0 & 0 & 103 \
0 & 0 & 4 & 0 & 93\
0 & 0 & 0 & 4 & -115 \
107 & 103 & 93 & -115 & 33483
end{array}
right) .
$$
Ответ. $ d=150_{} $.
Квадратичные многообразия (квадрики)
В последующих пунктах, касающихся вычисления расстояний между геометрическими объектами, хотя бы один из которых представлен квадратным уравнением, используется следующая идеология решения. Первоначальной целью ставится построение уравнения расстояний, т.е. алгебраического уравнения от одной переменной, среди корней которого находится квадрат искомого расстояния. После нахождения этого корня, координаты ближайшей точки (или пары ближайших точек) находятся в виде рациональных функций от величины квадрата расстояния. Таким образом, мы «переворачиваем» традиционную схему решения оптимизационных задач:
стационарные точки
$ rightarrow $
критические значения
Такая реверсия традиционного подхода оправдана, с одной стороны, тем, что задача сводится к одномерной — поиску корней полинома от одной переменной. Причем нас будет интересовать, как правило, единственный корень этого полинома — минимальный положительный. С другой стороны, уравнение расстояний удается построить в результате чисто алгебраической процедуры: конечного числа элементарных алгебраических операций над коэффициентами уравнений, задающих многообразия. Алгоритм основан на аппарате исключения переменных в системах нелинейных алгебраических уравнений, и ключевым объектом в нем оказывается вычисление дискриминанта полинома (от одной или двух переменных).
Расстояние от точки до квадрики
Т
Теорема 1. Пусть квадрика в $ {mathbb R}^{n} $, задана уравнением
$$
X^{top}AX+2B^{top}X-1=0 , (A=A^{top}) .
$$
Квадрат расстояния до нее от не лежащей на ней точки
$$ X_{0} in {mathbb R}^{n}, quad ( X_0^{top}AX_0+2 B^{top}X_{0}-1ne 0 ) $$
равен минимальному положительному корню уравнения расстояний
$$
{mathcal F}(z)=0 quad npu quad {mathcal F}(z)={mathcal D}_{mu} left( Phi(mu,z) right) .
$$
Здесь
$$
Phi(mu,z)=det left( left[ begin{array}{cc} A & B \ B^{top} & -1
end{array} right]
+ mu left[ begin{array}{cc} -E & X_0 \ X_0^{top} & z-X_0^{top}X_0 end{array} right] right),
$$
$ {mathcal D}_{} $ означает дискриминант полинома $ Phi(mu,z) $, рассматриваемого относительно переменной $ mu_{} $, а $ E_{} $ — единичная матрица порядка $ n_{} $. Дополнительно предполагается, что указанный корень не является кратным.
=>
[3]. Квадрат расстояния от начала координат $ {mathbb O} in {mathbb R}^{n} $ до квадрики в $ {mathbb R}^{n} $, заданной уравнением
$$
X^{top}AX+2,B^{top}X-1=0 ,
$$
равен минимальному положительному корню уравнения расстояний
$$
{mathcal F}(z)=0, quad npu quad {mathcal F}(z)={mathcal D}_{mu} left(
f(mu)(mu z-1)-B^{top}q(A,mu)B right) ,
$$
и при условии, что указанный корень не является кратным. Здесь $ f(mu_{})=det (A-mu E) $ — характеристический полином матрицы $ A_{} $, а $ q(A,mu)_{} $ — матрица взаимная матрице $ A-mu E_{} $.
=>
В частном случае $ B={mathbb O}_{} $ (квадрика центрирована к началу координат), имеем:
$$
{mathcal F}(z)=left[z^nf(1/z) right]^2{mathcal D}_{mu}(f(mu)) ,
$$
и расстояние от начала координат до квадрики оказывается равным $ 1/sqrt{lambda_{max}^{}} $,
где $ lambda_{max}^{} $ — максимальное собственное число матрицы $ A_{} $.
П
Пример. Найти расстояние от начала координат до эллипсоида
$$ 7,x_1^2+6,x_2^2+5,x_3^2-4,x_1x_2-4,x_2x_3-3,x_1-4,x_2+5,x_3-18=0 .$$
Решение. Здесь
$$A = left(
{begin{array}{rrr}
frac{7}{18} & -frac{1}{9} & 0 \
&& \
-frac{1}{9} & frac{1}{3} & -frac{1}{9} \
&& \
0 & -frac{1}{9} & frac{5}{18}
end{array}}
right),quad
B = left(
begin{array}{r}
-frac{1}{12} \
\
-frac{1}{9} \
\
frac{5}{36}
end{array}
right) ,$$
$$
f(mu)=det (A-mu E)=-mu ^{3} + mu ^{2} – frac{11}{36} mu
+ frac {1}{36}
$$
Матрица взаимная матрице $ A-mu E_{} $:
$$
q(A, mu)= left(
begin{array}{ccc}
mu ^{2} – frac{11}{18} mu + frac{13}{162} & – frac{1}{9} mu + frac{5}{162} & frac{1}{81} \
&& \
– frac{1}{9} mu + frac{5}{162} & mu^2 -frac{2}{3}mu+frac{35}{324} & – frac{1}{9} mu +frac{7}{162} \
&& \
frac{1}{81} & – frac{1}{9} mu + frac{7}{162} &
mu ^{2} – frac{13}{18}mu+frac{19}{162}
end{array}
right) .
$$
$$
Phi(mu,z)=f(mu)(mu z-1)-B^{top}q(A,mu)B=
$$
$$
=-z mu ^{4} + (z+1) mu ^{3} +
left(-frac {11}{36} z – frac{673}{648}right) mu ^{2}
+left( frac {1}{36} z + frac {241}{729} right) mu –
frac {1621}{52488} .
$$
Воспользуемся детерминантным представлением дискриминанта:
$$
{mathcal F}(z) = {mathcal D}_{mu} (Phi(mu,z)) = frac{1}{16} times
$$
$$
times
left|
begin{array}{cccccc}
4z & – 3z-3 & frac{11}{18}z +
frac{673}{324} & – frac{1}{36} z – frac{241}{729} & 0 & 0 \
&&&&& \
0 & 4z & – 3z-3 & frac{11}{18} z + frac{673}{324} & – frac{1}{36} z
– frac{241}{729} & 0 \
&&&&& \
0 & 0 & 4z & – 3z-3 & frac{11}{18}z
+ frac{673}{324} & – frac{1}{36} z – frac{241}{729} \
&&&&& \
0 & 0 & – z – 1 & frac{11}{18}z + frac{673}{324} & – frac{1}{12} z
– frac{241}{243} & frac{1621}{13122} \
&&&&& \
0 & – z – 1 & frac{11}{18}z + frac{673}{324} & – frac{1}{12}z
– frac{241}{243} & frac{1621}{13122} & 0 \
&&&&& \
– z – 1 & frac{11}{18} z + frac{673}{324} & – frac{1}{12} z
– frac{241}{243} & frac{1621}{13122} & 0 & 0
end{array}
right| =
$$
$$
=2^{-11}3^{-24} (
38263752,z^6-966487788,z^5+9376985736,z^4-43882396481,z^3+$$
$$
+102982092872,z^2-116747905827,z+50898162294)
quad .
$$
Вещественные корни уравнения расстояний:
$$ z_1approx 1.394685, z_2 approx 5.701814, z_3 approx 7.043941, z_4 approx 7.590060 . $$
Ответ. $ d= sqrt{z_1} approx 1.180968 $.
Нахождение точки на квадрике, ближайшей к заданной точке $ X_{0} $, возможно с помощью следующего результата.
T
Теорема 2. При выполнении условий теоремы 1, координаты точки $ X_{ast} $ квадрики, ближайшей к точке $ X_{0} $ находятся по формуле
$$ X_{ast}=-A^{-1} B – mu_{ast} (A -mu_{ast}E)^{-1} (A^{-1} B+X_0)=(mu_{ast}E- A)^{-1} (B+mu_{ast} X_0) . $$
Здесь $ mu_{ast} $ означает кратный корень полинома $ Phi(mu,z_{ast}) $, где полином $ Phi(mu,z) $ берется из формулировки теоремы 1, а
$ z_{ast}^{} $ означает минимальный положительный корень уравнения расстояний.
Этот результат требует пояснений. Итак, поскольку дискриминант полинома $ Phi(mu,z_{ast}) $ обращается в нуль, то у этого полинома — как полинома по $ mu_{} $ — имеется кратный корень $ mu =mu_{ast} $. Можно доказать [4], что при условии простоты корня $ z=z_{ast} $ уравнения расстояний $ mathcal F(z)=0 $ кратность корня $ mu =mu_{ast} $ для полинома $ Phi(mu,z_{ast}) $ будет равна ровно $ 2_{} $, и других кратных корней этот полином не имеет. Но тогда, выражение для $ mu_{ast}^{} $ может быть найдено в виде рациональной функции коэффициентов полинома $ Phi(mu,z_{ast}) $. Последнее утверждение может быть доказано разными способами, и в качестве самого наглядного выберем тот, что основан на свойствах дискриминанта, например, на том, что изложено
☞
ЗДЕСЬ.
=>
При выполнении условия предыдущей теоремы, координаты точки $ X_{ast}^{} $, ближайшей на квадрике к точке $ X_{0} $, являются рациональными функциями от квадрата расстояния.
=>
Точка $ X_{ast} $ квадрики $ X^{top}AX+2,B^{top}X-1=0 $, ближайшая к началу координат $ X_0= mathbb O $, находится по формуле:
$$ X_{ast} = – frac{1}{f(mu_{ast})} q(A,mu_{ast}) B . $$
Здесь $ f(mu_{})=det (A-mu E) $ — характеристический полином матрицы $ A_{} $, $ q(A,mu)_{} $ — матрица взаимная матрице $ A-mu E_{} $, а $ mu_{ast} $ означает кратный корень уравнения
$$f(mu)(mu z_{ast}-1)-B^{top}q(A,mu)B=0 , $$
где $ z_{ast}^{} $ — величина квадрата расстояния от $ mathbb O_{} $ до квадрики.
П
Пример. Найти ближайшую к началу координат точку эллипсоида из предыдущего примера.
Решение. Подставляем $ z_{}=z_{ast} approx 1.394685 $ в формулу для определения кратного корня, т.е. в отношение двух конкретных миноров детерминантного представления дискриминанта:
$$
mu=-frac{left|
begin{array}{cccc}
4z & – 3z-3 & frac{11}{18} z + frac{673}{324} & 0 \
&&& \
0 & 4z & – 3z-3 & – frac{1}{36} z – frac{241}{729} \
&&& \
0 & – z – 1 & frac{11}{18}z + frac{673}{324} & frac{1621}{13122} \
&&& \
– z – 1 & frac{11}{18}z + frac{673}{324} & – frac{1}{12}z – frac{241}{243} & 0
end{array}
right|}
{left|
begin{array}{cccc}
4z & – 3z-3 & frac{11}{18} z + frac{673}{324} & – frac{1}{36} z – frac{241}{729} \
&&& \
0 & 4z & – 3z-3 & frac{11}{18}z + frac{673}{324} \
&&& \
0 & – z – 1 & frac{11}{18}z + frac{673}{324} & – frac{1}{12}z – frac{241}{243} \
&&& \
– z – 1 & frac{11}{18}z + frac{673}{324} & – frac{1}{12}z – frac{241}{243} & frac{1621}{13122}
end{array}
right|}
$$
получаем $ mu_{ast}^{} approx 0.572670 $. Подставляем это значение в формулу для определения $ X_{ast}^{} $ из последнего следствия:
$$
X_{ast}approx left(begin{array}{r}
0.071171 \ -0.867719 \ 0.797924
end{array}
right) .
$$
Проверка. Если подставить вместо $ X_{ast} $ его приближенное значение, то получим:
$$
X_{ast}^{top} X_{ast} approx mathbf{1.39468}4, X_{ast}^{top}AX_{ast}+2,B^{top}X_{ast}-1 approx 2.9cdot 10^{-5} ,
$$
и вектор $ {mathbb O}X_{ast} $ перпендикулярен эллипсоиду в точке $ X_{}=X_{ast} $:
$$
AX_{ast}+B approx left(begin{array}{r}
0.040757\ -0.496917 \ 0.456948
end{array} right)approx mu_{ast} X_{ast} .
$$
Более подробный анализ уравнения расстояний для частных случаев плоскости $ mathbb R^{2} $ и трехмерного пространства $ mathbb R^{3} $ (в частности, почему существенно условие простоты минимального положительного корня, упомянутое в теореме 1)
☞
ЗДЕСЬ.
Расстояние от линейного многообразия (плоскости) до квадрики
Задача. Найти расстояние от эллипсоида в $ {mathbb R}^{n} $, заданного уравнением
$$
X^{top}AX+2B^{top}X-1=0 , (A=A^{top})
$$
до линейного многообразия (плоскости) в $ {mathbb R}^{n} $, заданной системой уравнений
$$
left{
begin{array}{ccc}
c_{11}x_1+c_{12}x_2+dots+c_{1n}x_n &=& 0 \
dots & & dots \
c_{m1}x_1+c_{m2}x_2+dots+c_{mn}x_n &=& 0
end{array}
right. iff
CX={mathbb O} quad npu quad
C=left(
begin{array}{cccc}
c_{11}& c_{12} & dots & c_{1n} \
dots & & & dots \
c_{m1}& c_{m2} & dots & c_{mn}
end{array}
right)_{mtimes n}
$$
При этом предполагается, что $ mle n_{} $ и что ранг матрицы $ C_{} $ равен $ m_{} $, т.е.
определяемая системой плоскость в $ {mathbb R}^{n} $ является $ (n-m)_{} $-мерной.
Т
Теорема. [3]. Необходимое и достаточное условие того, что линейное многообразие (плоскость) пересекает эллипсоид зависит от знакоопределенности матрицы $ A_{} $:
$$0 le left|
begin{array}{lrc}
A & B & C^{top}\
B^{top} & -1 & {mathbb O}\
C & {mathbb O} & mathbb{O}
end{array} right| times
left{ begin{array}{l}
(-1)^{m-1} mbox{при} A mbox{пол. определенной}, \
(-1)^n mbox{при} A mbox{отр. определенной}
end{array} right.$$
=>
Условие равенства нулю определителя из теоремы является необходимым и достаточным для существования точки касания эллипсоида и плоскости.
Т
Теорема. [3]. Если условие предыдущей теоремы не выполняется, то квадрат расстояния от эллипсоида
до плоскости совпадает с минимальным положительным корнем полинома
$$
{mathcal F}(z) ={mathcal D}_mu left( mu^m left|
begin{array}{ccc}
A & B & C^{top}\
B^{top} & -1 + mu z & mathbb{O}\
C & mathbb{O} & frac{1}{mu} C cdot C^{top}
end{array}
right| right),
$$
в предположении, что этот корень не является кратным. Здесь $ {mathcal D}_{} $ — дискриминант полинома, рассматриваемого относительно переменной $ mu_{} $.
=>
Если строки матрицы $ C_{} $ ортонормированны, то преобразованием
определителя в теореме можно понизить его порядок: выражение под знаком дискриминанта
можно преобразовать в
$$left|
begin{array}{cc}
A-mu C^{top} C & B \
B^{top} & -1+mu z
end{array}
right|.$$
П
Пример. Найти расстояние от оси $ {mathbb O}x_{1} $ до эллипсоида
$$
7, x_1^2+6, x_2^2 +5, x_3^2 -4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0 .
$$
Решение. Здесь
$$
A=
left(
begin{array}{rrr}
-frac{7}{54} & frac{1}{27} & 0 \
&&\
frac{1}{27} & -frac{1}{9} & frac{1}{27} \
&&\
0 & frac{1}{27} & -frac{5}{54}
end{array}
right), B=left(
begin{array}{r}
frac{37}{108} \
\
frac{1}{9} \
\
-frac{1}{36}
end{array}
right)
$$
и можно взять
$$
C=
left(
begin{array}{ccc}
0 & 1 & 0 \
0 & 0 & 1
end{array}
right) .
$$
Матрица $ A_{} $ отрицательно определена, условие пересечения прямой и эллипсоида не выполняется:
$$
left|
begin{array}{ccc}
A & B & C^{top}\
B^{top} & -1 & {mathbb O}\
C & {mathbb O} & mathbb{O}
end{array} right| times (-1)^3 = – frac{143}{11664} < 0 .
$$
Имеем, на основании следствия:
$$
left|
begin{array}{cc}
A-mu C^{top} C & B \
B^{top} & -1+mu z
end{array}
right|=left|
begin{array}{cccc}
-frac{7}{54} & frac{1}{27} & 0 & frac{37}{108} \
&&&\
frac{1}{27} & -frac{1}{9}-mu & frac{1}{27} & frac{1}{9} \
&&&\
0 & frac{1}{27} & -frac{5}{54}-mu & -frac{1}{36} \
&&&\
frac{37}{108} & frac{1}{9} & -frac{1}{36} & -1 + mu z
end{array}
right| =
$$
$$
=-frac{7}{54}z mu^3+left(-frac{73}{2916}z+frac{143}{11664}right)mu^2+left(-frac{1}{972}z-frac{1069}{314928}right)mu-frac{1621}{4251528}
$$
и дискриминант полученного полинома по переменной $ mu_{} $ равен
$$
{mathcal F}(z)=2^{-16}3^{-30}
left(1331935488,z^4-38807307008,z^3+245988221152,z^2-1086769525104,z+61289436065 right)
$$
Положительные корни последнего полинома: $ z_1 approx 0.057128, z_2 approx 22.545607_{} $.
Ответ. $ d_{} = sqrt{z_1} approx 0.239015 $.
Как правило, степень полинома $ {mathcal F}(z)_{} $ равна $ 2m_{} $, т.е. удвоенному количеству линейных уравнений, задающих плоскость. В частном случае $ m=1_{} $ получаем квадратное уравнение:
=>
Расстояния в $ {mathbb R}^{n} $ от плоскости
$$ c_1x_1+dots+c_nx_n = h iff CX=h $$
до ближайшей и до самой дальней точек эллипсоида
$$
X^{top}AX+2B^{top}X-1=0 , (A=A^{top})
$$
совпадают с модулями корней полинома:
$$
{mathcal F}(Z)=left|
begin{array}{ccc}
A & B & C^{top}/|C|\
B^{top} & -1 & Z-h/|C|\
C/|C| & Z-h/|C| & 0
end{array} right| .
$$
Здесь $ |C|=sqrt{c_1^2+dots+c_n^{2}} $ и предполагается, что поверхности не пересекаются.
П
Пример. Найти расстояние от прямой $ 2, x_1- x_{2}=0 $ до эллипса
$$ 7,x_1^2-4,x_1x_2 + 6, x_2^2-47, x_1 -24, x_{2} +124 = 0 .$$
Решение. Здесь
$$
{mathcal F}(Z)=left|
begin{array}{ccc}
A & B & C^{top}/|C| \
B^{top} & -1 & Z-h/|C| \
C/|C| & Z-h/|C| & 0
end{array} right| =
left|
begin{array}{cccc}
-frac{7}{124} & frac{1}{62} & frac{47}{248} & frac{2}{sqrt{5}} \
&&& \
frac{1}{62} & – frac{3}{62} & frac{3}{31} &- frac{1}{sqrt{5}} \
&&& \
frac{47}{248} & frac{3}{31} & -1 & Z \
&&& \
frac{2}{sqrt{5}} & – frac{1}{sqrt{5}} & Z & 0
end{array} right| =
$$
$$
=-frac{1}{307520}left(760,Z^2+1592sqrt{5}, Z+2383 right)
$$
и корни этого полинома:
$$ -frac{199}{190}sqrt{5}pm frac{1}{76} sqrt{13570} . $$
Ответ.
$$ d = left| -frac{199}{190}sqrt{5}+ frac{1}{76} sqrt{13570} right| approx 0.809219_{} . $$
Расстояние между квадриками
Т
Теорема. Пусть $ X^{top} A_{1} X =1 $ и $ X^{top} A_{2} X =1 $ – квадрики в $ {mathbb R}^{n} $, причем первая является эллипсоидом. Квадрики не пересекаются тогда и только тогда, когда матрица $ A_{1}-A_2 $ является знакоопределенной.
Доказательство
☞
ЗДЕСЬ.
Т
Теорема. [3,4]. Если выполняется условие предыдущей теоремы, то квадрат расстояния между
$$ mbox{эллипсоидом} X^{top} A_{1} X =1 mbox{и квадрикой} X^{top} A_{2} X =1 $$
совпадает с минимальным положительным корнем уравнения расстояний
$$
{mathcal F}(z)=0 quad npu quad {mathcal F}(z)={mathcal D}_{lambda} left( Phi(lambda,z) right) .
$$
Здесь
$$
Phi(lambda,z)=det (lambda A_1 +
(z- lambda) A_2 – lambda (z-lambda) A_1 A_2),
$$
$ {mathcal D}_{} $ — дискриминант полинома рассматриваемого относительно переменной $ lambda_{} $.
Дополнительно предполагается, что указанный корень не является кратным.
П
Пример. Найти расстояние между эллипсами
$$10,x_1^2-12,x_1x_2+8,x_2^2=1 qquad u qquad x_1^2+x_1x_2+x_2^2=1 . $$
Решение. Здесь
$$
A_1=
left(
begin{array}{rr}
10 & – 6 \
-6 & 8
end{array}
right), quad
A_2=
left(
begin{array}{rr}
1 & frac{1}{2} \
frac{1}{2} & 1
end{array}
right)
$$
и матрица $ A_{1}-A_2 $ положительно определена. Следовательно эллипсы не пересекаются.
$$
Phi(lambda,z)=det (lambda A_1 + (z- lambda) A_2 – lambda (z-lambda) A_1 A_2)=
$$
$$
=33,lambda^4+left(-66z+frac{149}{2}right)lambda^3+left(33,z^2-61,z+frac{83}{4}right)lambda^2+left(-frac{27}{2}z^2+frac{45}{2}zright)lambda+frac{3}{4},z^2
$$
и дискриминант этого полинома по переменной $ lambda_{} $ равен
$$
{mathcal F}(z)=frac{3}{16}z^2 ({scriptstyle 936086976}, z^6-{scriptstyle 10969697376},z^5+
{scriptstyle 50706209664}, z^4
-{scriptstyle 115515184664}, z^3+{scriptstyle 130176444432}, z^2
-{scriptstyle 59826725574},z+{scriptstyle 2866271785}) .
$$
Положительные корни уравнения расстояний $ {mathcal F}(z)=0 $:
$$
z_1 approx 0.053945666, z_2 approx 1.3340583883, z_3 approx 1.95921364, z_4 approx 2.8785867381 .
$$
Ответ. $ d_{}= sqrt{z_1} approx 0.23226206 $.
Как правило, степень полинома $ {mathcal F}(z)_{} $ из последней теоремы (после отбрасывания постороннего множителя $ z^{n(n-1)}_{} $) равна $ n(n+1)_{} $.
Нахождение координат ближайших точек на квадриках (обеспечивающих найденное расстояние)
возможно по алгоритму:
1.
Если $ z=z_{ast} $ — корень полинома $ {mathcal F}(z) $, то это значит, что полином
$$ Phi(lambda, z_{ast}) = det ( lambda A_1 +(z_{ast}-lambda)A_2 – lambda (z_{ast}-lambda) A_2A_1) $$
имеет кратный корень $ lambda_{} = lambda_{ast} $. При выполнении условий теоремы, этот корень будет единственным второй кратности и его можно выразить в виде рациональной функции от $ z_{ast} $ с помощью субдискриминантов.
2.
Столбец координат $ X_{ast}^{} $ точки первой квадрики, удовлетворяет тогда однородной системе уравнений
$$ ( lambda_{ast} A_1 +(z_{ast}-lambda_{ast})A_2 – lambda_{ast} (z_{ast}-lambda_{ast}) A_2A_1) X = mathbb O , $$
которая имеет бесконечное множество решений, поскольку определитель ее матрицы равен нулю. Из этого бесконечного множества мы выделяем те решения, что удовлетворяют условию $ X^{top}A_{1}X=1 $.
При выполнении условий теоремы таких решений будет два (что соответствует симметрии задачи, см. рисунок).
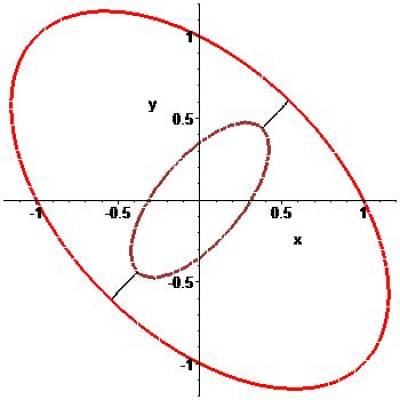
Аналогично, столбец координат $ Y_{ast}^{} $ точки на второй квадрике $ Y^{top}A_{2}Y=1_{} $ будет решением системы уравнений
$$ ( lambda_{ast} A_1 +(z_{ast}-lambda_{ast})A_2 – lambda_{ast} (z_{ast}-lambda_{ast}) A_1A_2) Y = mathbb O . $$
Заметим, что матрицы рассматриваемых линейных систем различаются лишь транспонированием.
Для нахождения решений воспользуемся одним из результатов теории систем линейных уравнений. Составим столбец из
алгебраических дополнений к элементам какой-либо строки матрицы
$$ M= lambda_{ast} A_1 +(z_{ast}-lambda_{ast})A_2 – lambda_{ast} (z_{ast}-lambda_{ast}) A_2A_1 . $$
Тогда вектор $ X_{ast}^{} $ отличается от этого столбца лишь множителем, который определится из условия $ X^{top}A_{1}X=1_{} $. Аналогично, для получения столбца координат $ Y_{ast}^{} $ возьмем столбец из алгебраических дополнений к элементам какого-либо столбца той же матрицы $ M_{} $ и домножим его на константу, чтобы обеспечить выполнение условия $ Y^{top}A_{2}Y=1_{} $.
3.
Получившиеся пары $ X_{ast},Y_{ast}^{} $ надо согласовать: они должны подчиняться условию
$$ (X_{ast}-Y_{ast})^{top}(X_{ast}-Y_{ast})=z_{ast} . $$
П
Пример. Найти ближайшие точки эллипсов из предыдущего примера.
Решение. Для найденного значения $ z_{ast}=z_1 approx 0.053945666_{} $ определитель матрицы
$$
M=left(
begin{array}{cc}
7,lambda^2+(-7z+9)lambda+z & -2lambda^2+(2,z-frac{13}{2})lambda+frac{1}{2}z \
& \
-lambda^2+(z-frac{13}{2})lambda+frac{1}{2}z & 5lambda^2+(-5z+7)lambda+z
end{array}
right)
$$
как полином по $ lambda_{} $ будет иметь кратный корень. Этот корень определяем1) с помощью субдискриминантов в виде:
$$
lambda=-frac{-725274,z^5+1455894,z^4+frac{11286981}{2}z^3-frac{26486523}{2}z^2+frac{42000075}{8}z}
{17591706,z^4-109992894,z^3+frac{450450691}{2}z^2-frac{315606253}{2}z+frac{77466805}{8}} .
$$
Подстановка сюда $ z=z_{ast}^{} $ даст $ lambda_{ast} approx -0.13576051_{} $.
Далее, при найденных значениях $ z_{} $ и $ lambda_{} $ система линейных уравнений
$$ MX=mathbb O_{2times 1} $$
должна иметь бесконечное множество решений относительно вектора $ X_{2times 1}^{} $. Одно из
этих решений может быть построено (см. упражнение
☞
ЗДЕСЬ ) с помощью алгебраических дополнений к элементам, например,
второй строки матрицы $ M_{} $:
$$
left(
begin{array}{c}
2lambda^2-(2,z-frac{13}{2})lambda-frac{1}{2}z \
\
7,lambda^2+(-7z+9)lambda+z
end{array}
right)
quad
begin{array}{c}
longrightarrow \
z=z_{ast}, lambda= lambda_{ast}
end{array} quad
X=left(
begin{array}{c}
-0.8579069 \
\
-0.9876166
end{array}
right) .
$$
Любое другое решение получается домножением полученного на произвольную константу («растяжением» вектора). Воспользуемся этим, чтобы добиться выполнения условия $ X^{top}A_{1} X =1_{} $.
$$
X_{ast}=frac{1}{sqrt{X^{top}A_1 X}} X approx
left(
begin{array}{c}
-0.3838312 \
-0.4418639
end{array}
right) .
$$
Аналогично, для нахождения точки на другом эллипсе, мы решаем систему
$$ M^{top}Y=mathbb O_{2times 1} , $$
представив ее решение опять-таки с помощью алгебраических дополнений к элементам второго столбца
матрицы $ M_{} $:
$$
left(
begin{array}{c}
lambda^2-(z-frac{13}{2})lambda-frac{1}{2}z \
\
7,lambda^2+(-7z+9)lambda+z
end{array}
right)
quad
begin{array}{c}
longrightarrow \
z=z_{ast}, lambda= lambda_{ast}
end{array} quad
left(
begin{array}{c}
-0.8836615 \
\
-0.9876166
end{array}
right) quad Rightarrow quad
Y_{ast} approx
left(
begin{array}{c}
-0.5449964 \
\
-0.6091105
end{array}
right) .
$$
Ответ. $ pm (0.3838312,, 0.4418639)_{} $ и $ pm (0.5449964,, 0.6091105)_{} $ соответственно (знаки должны быть согласованы).
Проверка. Если в ответе взять знак $ +_{} $:
$$ X_{ast}-Y_{ast} =
left(
begin{array}{c}
-0.1611652 \
-0.1672466
end{array}
right)= lambda_{ast} A_1X_{ast}=(lambda_{ast}-z_{ast})A_2Y_{ast},quad (X_{ast}-Y_{ast})^{top}(X_{ast}-Y_{ast})approx mathbf{0.0539456}4 .
$$
Т
Теорема. [3,4].Пусть
$$ X^{top} A_{1}X+2,B^{top}_1X-1=0 mbox{и} X^{top} A_{2}X+2,B^{top}_2X-1=0 $$
— квадрики в $ {mathbb R}^{n}_{} $, причем первая является эллипсоидом. Квадрики пересекаются тогда и только тогда, когда
среди вещественных корней полинома
$$
Theta (z) = {mathcal D}_lambda left( det left( left[
begin{array}{cc}
A_2 & B_2\
B_2^{top} & -1-z
end{array} right] – lambda left[
begin{array}{cc}
A_1 & B_1\
B_1^{top} & -1
end{array} right] right) right)
$$
имеются числа разных знаков или нуль. Здесь $ {mathcal D}_{} $ — дискриминант полинома рассматриваемого относительно переменной $ lambda_{} $.
Условие теоремы проверяется чисто алгебраически, т.е. без привлечения численных методов нахождения корней полинома. См. следствие к теореме Йоахимшталя
☞
ЗДЕСЬ.
=>
Для того, чтобы существовала точка касания квадрик
$$ X^{top} A_{1}X+2,B^{top}_1X-1=0 mbox{и} X^{top} A_{2}X+2,B^{top}_2X-1=0 $$
необходимо и достаточно, чтобы было выполнено условие
$$
{mathcal D}_lambda left( det left( left[
begin{array}{cc}
A_2 & B_2\
B_2^{top} & -1
end{array} right] – lambda left[
begin{array}{cc}
A_1 & B_1\
B_1^{top} & -1
end{array} right] right) right) =0 .
$$
Т
Теорема. [3,4]. Если не выполняется условие предыдущей теоремы, то квадрат расстояния между
$$ mbox{эллипсоидом} quad X^{top} A_{1}X+2,B^{top}_1X-1=0 quad mbox{ и квадрикой } quad X^{top} A_{2}X+2,B^{top}_2X-1=0 $$ совпадает с минимальным положительным корнем полинома
$$
{mathcal F}(z) =
$$
$$
={mathcal D}_{mu_1, mu_2} left( det left( mu_1 left[
begin{array}{cc}
A_1 & B_1\
B_1^{top} & -1
end{array} right] + mu_2 left[
begin{array}{cc}
A_2 & B_2\
B_2^{top} & -1
end{array} right] – left[
begin{array}{cc}
A_2 A_1 & A_2 B_1\
B_2^{top} A_1 & B_2^{top}B_1 – mu_1 mu_2 z
end{array} right] right) right),
$$
в предположении, что этот корень не является кратным. Здесь $ {mathcal D}_{} $ — дискриминант полинома рассматриваемого относительно переменных $ mu_{1}, mu_{2} $.
П
Пример. Найти расстояние между эллипсами
$$-frac{1}{2},x_1^2+frac{1}{2},x_1x_2-frac{3}{2},x_2^2+frac{5}{2},x_1+4,x_2=1 $$
и
$$-frac{1}{84},x_1^2-frac{4}{189},x_2^2-frac{1}{3}, x_1=1 . $$
Решение. Здесь
$$
A_1=
left(
begin{array}{rr}
-frac{1}{2} & frac{1}{4} \
\
frac{1}{4} & -frac{3}{2}
end{array}
right), quad
B_1=left(
begin{array}{c}
frac{5}{4} \ \ 2
end{array}
right), quad
A_2=
left(
begin{array}{cc}
-frac{1}{84} & 0 \
\
0 & -frac{4}{189}
end{array}
right),quad B_2=left(
begin{array}{r}
-frac{1}{6} \ \ 0
end{array}
right) .
$$
Проверяем сначала условия пересечения поверхностей.
$$
Theta (z) = {mathcal D}_lambda left(-begin{array}{c} frac{157}{32} end{array} lambda^3-left{ begin{array}{c} frac{4315}{3024} end{array} + begin{array}{c} frac{11}{16}z end{array} right}lambda^2+left{-begin{array}{c} frac{11}{2646} end{array} + begin{array}{c} frac{43}{1512} end{array} z right}lambda- begin{array}{c} frac{1}{3969}end{array} z + begin{array}{c} frac{4}{11907} end{array}right)=
$$
$$
=begin{array}{c}frac{1}{{scriptstyle 9219465541730304}} end{array}
({scriptstyle 505118694465},z^4-{scriptstyle 1023679248858},z^3-
{scriptstyle 7568287236783},z^2+
{scriptstyle 33720131260536},z +{scriptstyle 34005894083152}) .
$$
Полином имеет два вещественных корня, оба отрицательны. Эллипсы не пересекаются. Далее,
$$
Psi(mu_1,mu_2,z)=det left( mu_1 left[
begin{array}{cc}
A_1 & B_1\
B_1^{top} & -1
end{array} right] + mu_2 left[
begin{array}{cc}
A_2 & B_2\
B_2^{top} & -1
end{array} right] – left[
begin{array}{cc}
A_2 A_1 & A_2 B_1\
B_2^{top} A_1 & B_2^{top}B_1 – mu_1 mu_2 z
end{array} right] right) =
$$
$$
=frac{11}{16}zmu_1^3 mu_2+frac{43}{1512}zmu_1^2mu_2^2+frac{1}{3969}zmu_1mu_2^3+
frac{157}{32}mu_1^3-frac{4315}{3024}mu_1^2mu_2+
$$
$$
+frac{275}{12096}zmu_1^2mu_2+frac{11}{2646}mu_1mu_2^2+frac{2}{3969}zmu_1mu_2^2+frac{4}{11907}mu_2^3+frac{3925}{24192}mu_1^2+
$$
$$
+frac{11}{63504}zmu_1mu_2-frac{619}{31752}mu_1mu_2+frac{8}{11907}mu_2^2+frac{157}{127008}mu_1+frac{11}{47628}mu_2 .
$$
Вычисляем дискриминант этого полинома по переменным $ mu_{1} $ и $ mu_{2} $, представив соответствующий результант
$$
{mathcal R}_{mu_1,mu_2}left(frac{partial Psi}{partial mu_1}, frac{partial Psi}{partial mu_2}, Psi right)
$$
в виде определителя матрицы Безу2):
$$
mathfrak B=
left(
begin{array}{cccc}
-{scriptstyle 949850},z-{scriptstyle 38319304} & -{scriptstyle 76994841},z+
{scriptstyle 29798905836} & dots & \
{scriptstyle 179712037934},z^2-{scriptstyle 6628863332080},z-{scriptstyle 18668859390944800} & & dots & \
dots &&& dots \
& & &
end{array}
right)
$$
Выражения для элементов первой и последней строк
☞
ЗДЕСЬ.
$$
{mathcal F}(z) =det (mathfrak B) equiv 3869893(20090,z+3526681)^2 times
$$
$$
times
({scriptstyle 12866891832025},z^{12}-{scriptstyle 2445505463588880},z^{11}-{scriptstyle 10867111637549652716},z^{10}-{scriptstyle 3123865087697933253136},z^9+
$$
$$
+{scriptstyle 1561852119815441835822424},z^8+{scriptstyle 1041845279230362476059640640},z^7+{scriptstyle 302844249329911871856294474624},z^6+
$$
$$
+{scriptstyle 50781476668832773753935668661952},z^5+{scriptstyle 2215513880036430404751762329796624},z^4-
$$
$$
-{scriptstyle 646131957386364232922218724008039168},z^3-{scriptstyle 99189074464451279399168578577559865856},z^2-
$$
$$
-{scriptstyle 5789019527920299026625801973715386789888},z+{scriptstyle 60730952901233749068462660878127980941312})
$$
Первый сомножитель по $ z_{} $ является «посторонним»3) и отбрасывается. Положительные корни второго сомножителя:
$$
9.0183982802, 121.59673276, 582.35840496, 1031.42118655
$$
Ответ. $ d approx sqrt{9.0183982802} approx 3.00306481 $.
Нахождение ближайших точек на квадриках (обеспечивающих найденное расстояние) возможно по следующему алгоритму.
1.
После нахождения (с необходимой точностью) минимального положительного корня $ z_{ast}^{} $ полинома $ {mathcal F}(z) $, установим соответствующие ему значения $ mu_{1}^{} $ и $ mu_{2}^{} $. Соответствие понимается в том смысле, что при $ z=z_{ast}^{} $ дискриминант полинома
$$
Psi(mu_1,mu_2,z)=det left( mu_1 left[
begin{array}{cc}
A_1 & B_1\
B_1^{top} & -1
end{array} right] + mu_2 left[
begin{array}{cc}
A_2 & B_2\
B_2^{top} & -1
end{array} right] – left[
begin{array}{cc}
A_2 A_1 & A_2 B_1\
B_2^{top} A_1 & B_2^{top}B_1 – mu_1 mu_2 z
end{array} right] right)
$$
— как полинома по переменным $ mu_{1},mu_{2} $ — обращается в нуль, то есть этот полином обладает кратным корнем, который мы обозначим $ (mu_{1ast},mu_{2ast}) $. Этот корень может быть найден в виде рациональной функции от $ z_{ast}^{} $ с помощью миноров матрицы Безу.
Если матрица Безу $ mathfrak B_{} $ порядка $ N_{} $ построена для мономиального базиса, в котором первые три монома имеют вид $ 1,mu_1, mu_{2} $, то, обозначив $ {mathfrak B}_{N1}, {mathfrak B}_{N2}, {mathfrak B}_{N3}^{} $ алгебраические дополнения элементов ее последней строки, будем иметь
$$
mu_{1ast} = frac{mathfrak B_{N2}}{mathfrak B_{N1}}; mu_{2ast} = frac{mathfrak B_{N3}}{mathfrak B_{N1}} .
$$
2.
Составим матрицу
$$ M= mu_{1ast} A_1+mu_{2ast}A_2-A_2A_1 . $$
Тогда координатные столбцы ближайших точек на квадриках вычисляются по формулам:
$$
X_{ast}=M^{-1} (A_2B_1-mu_{1ast} B_1-mu_{2ast}B_2),
Y_{ast}=(M^{-1})^{^{top}} (A_1B_2 – mu_{1ast} B_1-mu_{2ast}B_2).
$$
П
Пример. Найти ближайшие точки эллипсов из предыдущего примера.
Решение. Подставляем найденное значение квадрата расстояния $ z=z_{ast}^{} $ в формулы для определения компонент кратного корня:
$$
mu_1=frac{mathfrak B_{9,2}}{mathfrak B_{9,1}}equiv -frac{2}{21} frac{p_2(z)}{p_1(z)},
mu_2=frac{mathfrak B_{9,3}}{mathfrak B_{9,1}}equiv -frac{1099}{8} frac{p_3(z)}{p_1(z)}
$$
при
$$
p_1(z)={scriptstyle 30581063813712982235616866861258531260075854083860480}+dots
+{scriptstyle 42267948346218643456100},z^{13} ,
$$
$$
p_2(z)={scriptstyle 6423295122838229007549546733287643446036432415004672}+dots +
{scriptstyle 10295520700745795900000},z^{13}
$$
и
$$
p_3(z)={scriptstyle 11528328181753695140063436659475618124233172074496}+dots
+{scriptstyle 303317089743521700},z^{13} .
$$
(Полные представления
☞
ЗДЕСЬ.)
В результате, получаем:
$$
mu_{1ast}approx 0.0420933593 ,
mu_{2ast}approx 0.5932113733 .
$$
Матрица $ M_{} $:
$$
M=mu_{1ast} A_1+mu_{2ast}A_2-A_2A_1=
left(begin{array}{rr}
-0.0340611008 & 0.0134995303 \
0.0158143451 & -0.1074408089
end{array}
right)
$$
и по указанным выше формулам получаем
Ответ.
$$ X_{ast}approx left(begin{array}{r}
-0.4824707833 \
1.1065143947
end{array}
right),
Y_{ast}approx left(
begin{array}{r}
-3.46262940675\
0.73630788509
end{array}
right) .
$$
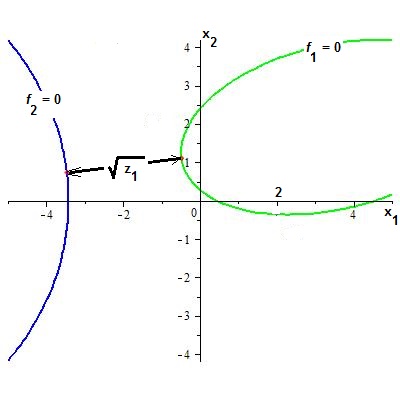
Проверка.
$$
(X_{ast}-Y_{ast})^{top}(X_{ast}-Y_{ast})approx mathbf{9.018398280}3 ,
$$
$$
X_{ast}^{top}A_1X_{ast}+2B_1^{top}X_{ast}-1 approx 1cdot 10^{-9} ,
Y_{ast}^{top}A_2Y_{ast}+2B_2^{top}Y_{ast}-1approx -3cdot 10^{-10} ,
$$
и вектор $ X_{ast}-Y_{ast}^{} $ перпендикулярен обоим эллипсам в соответствующих ближайших точках:
$$
A_1X_{ast}+B_1=
left(begin{array}{r}
1.767863990 \
0.219610712
end{array}
right)=mu_{2ast} (X_{ast}-Y_{ast}),
A_2Y_{ast}+B_2=
left(begin{array}{r}
-0.1254448880 \
-0.0155832356
end{array}
right)=-mu_{1ast} (X_{ast}-Y_{ast}) .
$$
Как правило, степень полинома $ {mathcal F}(z)_{} $ из последней теоремы (после отбрасывания постороннего множителя) равна $ 2n(n+1)_{} $. Коэффициенты этого полинома могут быть чудовищны.
П
Пример. Найти расстояние между эллипсоидами
$$
7,x_1^2+6,x_2^2+5,x_3^2-4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0$$
и
$$ 189,x_1^2+x_2^2+189,x_3^2+2,x_1x_3-x_2x_3-27=0 .$$
Решение. Здесь
$$
mathcal F (z)= underbrace{scriptstyle{891807829233048602 dots 129270962946048}}_{146} , z^{24} + dots +
underbrace{scriptstyle{11195843896426573542 dots 420939042193186989409}}_{189}
$$
Ответ. $ d approx sqrt{1.3537785005} approx 1.1635198754_{} $
Алгебраические кривые и многообразия
Расстояние от точки до плоской алгебраической кривой
Задача. Пусть алгебраическая кривая задана уравнением
$$ Phi(x,y)=0 . $$
Здесь $ Phi_{}(x,y) $ — отличный от константы полином от $ x_{} $ и $ y_{} $ с вещественными коэффициентами. Требуется найти расстояние до этой кривой от начала координат.
Здесь возникает проблема, которую для рассмотренных выше случаев удавалось либо обойти, либо же сравнительно дешево решить: это проблема существования решения. Дело в том, что уравнение может не иметь вещественных решений, то есть не определять никакой кривой на плоскости $ mathbb R^{2} $.
Будем решать задачу сначала для частного случая — пусть полином $ Phi_{}(x,y) $ является четным по переменной
$ y_{} $. Геометрически это означает, что кривая (если она существует) будет зеркально симметричной относительно оси $ mathbb Ox $. А с аналитической точки зрения такой полином можно представить в виде полинома
$$ F(x,Y) equiv Phi_{}(x,y) quad npu quad Y=y^2 . $$
Т
Теорема 1 [6]. Пусть $ Phi_{}(x,y) equiv Phi_{}(x,-y) $. Уравнение $ Phi_{}(x,y)=0 $ не имеет вещественных решений если одновременно выполняются два условия:
a) уравнение $ Phi(x,0)=0 $ не имеет вещественных решений;
б) уравнение
$$ mathcal F(z)=mathcal D_x( F(x,z-x^2))=0 $$
не имеет положительных решений.
Если хотя бы одно из этих условий не выполняется, то квадрат расстояния от начала координат до кривой $ Phi(x_{},y)=0 $ равен либо квадрату минимального по модулю вещественного корня уравнения $ Phi(x,0)=0 $, либо же минимальному положительному корню уравнения $ mathcal F(z)= 0 $, при условии, что последний не является кратным. Здесь $ {mathcal D}_{} $ — дискриминант полинома, рассматриваемого относительно переменной $ x_{} $.
П
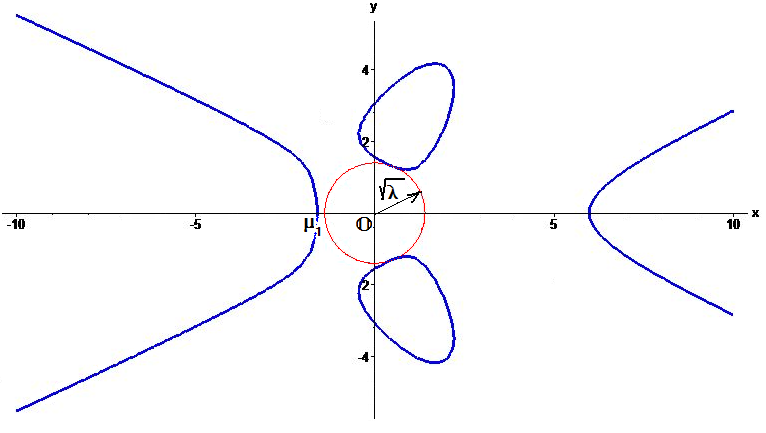
Пример. Найти расстояние от начала координат до кривой
$$ Phi(x,y)=x^6-5,x^4y^2-y^6-6,x^5+6,xy^4+10,y^4+25,x-45=0 . $$
Решение. Уравнение
$$ Phi(x,0)=x^6-6,x^5+25,x-45=0 $$
имеет вещественные корни $ mu_1approx -1.621919 $ и $ mu_2 approx 5.986387 $.
Далее,
$$ F(x,Y)=x^6-5,x^4Y-Y^3-6,x^5+6,xY^2+10,Y^2+25,x-45 $$
и полином
$$
mathcal F(z)=mathcal D_x (F(x,z-x^2))=
{scriptstyle 124422592},z^{15}-{scriptstyle 1996675968}z^{14}-{scriptstyle 26107738048},z^{13}+{scriptstyle 270691240064},z^{12}+
{scriptstyle 1462429768576}z^{11}
$$
$$
-{scriptstyle 31070151855680}z^{10}+
{scriptstyle 104850679100160},z^9+{scriptstyle 106422502370800},z^8-{scriptstyle 1956603249193600},z^7+{scriptstyle 1683409252901600},z^6+
$$
$$
+{scriptstyle 3565828983027500}z^5
-{scriptstyle 23058839076745500},z^4+{scriptstyle 30272455856370000},z^3+{scriptstyle 28139412928130000},z^2-{scriptstyle 97452805338000000}, z+
$$
$$
+{scriptstyle 171049864407603125}
$$
имеет минимальный положительный корень равный $ lambda approx 1.965293 $. Поскольку $ sqrt{lambda} < |mu_1| $, то получаем
Ответ. $ d approx 1.334155 $.
Понятно как решать задачу и в случае четности полинома $ Phi_{}(x,y) $ по переменной $ x_{} $.
Но как решить задачу в общем случае — когда свойства четности нет ни по одной из переменных? — Надо эту четность «сделать». Рассмотрим полином
$$ tilde F(x,Y) equiv Phi_{}(x,y) Phi_{}(x,-y) quad npu quad Y=y^2 . $$
Т
Теорема 2 [6]. Уравнение $ Phi_{}(x,y)=0 $ не имеет вещественных решений если одновременно выполняются два условия:
a) уравнение $ Phi(x,0)=0 $ не имеет вещественных решений;
б) уравнение
$$ widetilde{mathcal F}(z)=mathcal D_x( widetilde{F} (x,z-x^2))=0 $$
не имеет положительных решений.
Если хотя бы одно из этих условий не выполняется, то квадрат расстояния от начала координат до кривой $ Phi(x_{},y)=0 $ равен либо квадрату минимального по модулю вещественного корня уравнения $ Phi(x,0)=0 $, либо же минимальному положительному корню уравнения $ widetilde{mathcal F}(z)= 0 $, при условии, что последний не является кратным. Здесь $ {mathcal D}_{} $ — дискриминант полинома, рассматриваемого относительно переменной $ x_{} $.
П
Пример. Найти расстояние от начала координат до кривой
$$
begin{array}{lll}
Phi(x,y) & = & 32,x^4y+64,x^2y^3+32,y^5-16,x^4-96,x^2y^2-80,y^4+
\
&& +48,x^2y+80,y^3+120,x^2-576,xy+56,y^2+160,x-118,y+71=0 .
end{array}
$$
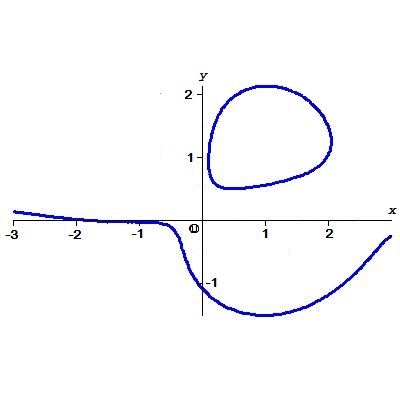
Решение. Опуская промежуточные выкладки, привожу только выражение для дискриминанта:
$$ widetilde{mathcal F}(z) equiv widetilde{mathcal F}_1(z) widetilde{mathcal F}_2^2(z) $$
при
$$
widetilde{mathcal F}_1(z) =
{scriptstyle 87241523200},z^{15}-{scriptstyle 244343373824},z^{14}+
{scriptstyle 6135125901312},z^{13}-{scriptstyle 99762334334976},z^{12}+{scriptstyle 122650759266304},z^{11}-
$$
$$
-{scriptstyle 2018722496380928},z^{10}
+{scriptstyle 36775841922285568},z^9+{scriptstyle 83476886207856640},z^8-{scriptstyle 125448251244072960},z^7-{scriptstyle 3659244138715855872},z^6-
$$
$$
-{scriptstyle 16653164114254566912},z^5-{scriptstyle 39789124482714260608},z^4+{scriptstyle 21724179049244829584},z^3-{scriptstyle 2250891598084946580},z^2+{scriptstyle 484733011031273132},z-
$$
$$
-{scriptstyle117947376101831257}
$$
и
$$
widetilde{mathcal F}_2(z) =4096,z^6+18432,z^5+18176,z^4-1501440,z^3+305136,z^2+2195912,z+709721
, .
$$
Полином $ widetilde{mathcal F}_1(z) $ имеет три вещественных корня: $ lambda_1 approx 0.208349, lambda_2 approx 0.360823, lambda_3 approx 6.480707 $. Вещественные корни $ Phi(x,0) $: $ mu_1 approx -1.835484, mu_2 approx 3.306151 $.
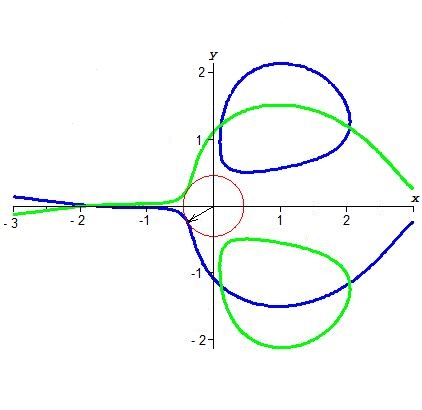
Сомножитель $ widetilde{mathcal F}_2^2(z) $ я отбросил как «посторонний», т.е. его корни — все они кратные — не сравнивал по величине с $ lambda_1 $ и $ mu_1^2 $. Откуда, собственно, этот сомножитель взялся? Будет ли он присутствовать и в общем случае, т.е. можно ли в полиноме $ widetilde{mathcal F} $ из теоремы $ 2 $ выделить сомножитель в виде квадрата некоторого другого полинома? — Для того, чтобы угадать происхождение этого множителя всё же вычислим его положительные корни: $ xi_1 approx 1.483677, xi_2 approx 5.553837 $. Теперь изобразим на последнем рисунке окружности $ x^2+y^2= xi_{1,2} $:
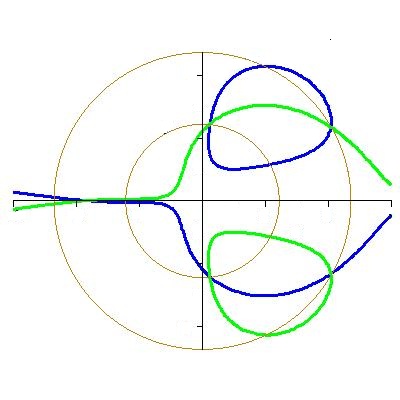
Окружности прошли через точки пересечения кривых $ Phi_{}(x,y) = 0 $ и $ Phi_{}(x,-y) =0 $.
Гипотеза. Разложим полином $ Phi_{}(x,y) $ по степеням $ y_{} $ и выделим четные и нечетные слагаемые по этой переменной:
$$ Phi_{}(x,y) equiv F_1(x,Y)+ y F_2(x,Y) qquad npu quad Y=y^2 . $$
С точностью до постоянного сомножителя, имеет место тождество
$$ widetilde{mathcal F}_2(z) equiv mathcal R_x(F_1(x,z-x^2),F_2(x,z-x^2)) . $$
Здесь $ mathcal R_{} $ — результант полиномов, рассматриваемых относительно переменной $ x_{} $.
Ответ. $ d approx 0.456453 $.
Расстояние в пространстве матриц
до некоторых критических многообразий:
-
до многообразия вырожденных матриц;
-
до многообразия матриц, имеющих собственное число на мнимой оси $ mathfrak{Re}(z)=0 $ комплексной плоскости;
-
до многообразия матриц, имеющих кратные собственные числа
☞
ЗДЕСЬ.
Разные задачи
Обобщенная задача Ферма-Торричелли
Задача. Пусть на плоскости заданы три точки $ P_1=(x_1,y_1),P_2=(x_2,y_2),P_3=(x_3,y_3) $, не лежащие на одной прямой.
Определить координаты точки $ P_{ast}=(x_{ast},y_{ast}) $, решающей задачу оптимизации:
$$
min_{(x,y)} F(x,y) quad mbox{ для } quad F(x,y)= sum_{j=1}^3m_j sqrt{(x-x_j)^2+(y-y_j)^2} .
$$
Здесь числа $ m_1,m_2,m_3 $ предполагаются положительными и в дальнейшем называются весами.
Задача известна под различными названиями: (обобщенная) задача Ферма-Торричелли-Штейнера,
задача Вебера, задача об оптимальном расположении (узловой) станции4), задача о трёх заводах.
П
Пример. В точках $ P_{1},P_2,P_3 $ расположены источники полезных ископаемых: железной руды, угля и воды соответственно. Известно, что для производства одной тонны стали необходимо иметь $ m_{1} $ тонн руды, $ m_2 $ тонн угля и $ m_3 $ тонн воды. В предположении, что стоимость перевозки одной тонны груза не зависит от его природы, где следует расположить сталелитейное производство так, чтобы минимизировать транспортные издержки?
§
Подробное обсуждение этой задачи (и к ней примыкающих)
☞
ЗДЕСЬ.
Задача о точке Лемуана-Греба
Задача. Найти точку плоскости, cумма квадратов расстояний от которой до сторон треугольника, лежащего в этой же плоскости, минимальна.
В русскоязычной литературе [5] иногда называется задачей Кэзи5), однако в других источниках атрибуция приведенной задачи Кэзи не подтверждена. См. краткое описание
истории задачи
☞
ЗДЕСЬ.
Решение. Пусть $ d_1, d_2,d_3 $ — расстояния от точки $ P_{} $ плоскости до сторон треугольника с длинами
$ D_1, D_2, D_3 $ соответственно. Воспользуемся тождеством Лагранжа:
$$ (d_1^2+ d_2^2+d_3^2)(D_1^2+ D_2^2+D_3^2)equiv $$
$$ equiv (d_1D_1+ d_2D_2+d_3D_3)^2+(d_1D_2-d_2D_1)^2+(d_2D_3-d_3D_2)^2+
(d_1D_3-d_3D_1)^2 . $$
Величина $ d_1D_1+ d_2D_2+d_3D_3 $ является постоянной, не зависящей от координат точки $ P_{} $:
$$ d_1D_1+ d_2D_2+d_3D_3 =2S , $$
где $ S_{} $ — площадь данного треугольника. Следовательно
$ min (d_1^2+d_2^2+d_3^2) $
достигается при условиях
$$ d_1D_2-d_2D_1=0, d_2D_3-d_3D_2=0, d_1D_3-d_3D_1=0 , $$
то есть когда
$$ frac{d_1}{D_1}=frac{d_2}{D_2}=frac{d_3}{D_3} . $$
Определяемая этими соотношениями точка называется точкой Лемуана6) или точкой Греба7); в ней пересекаются симедианы треугольника.
Интересна параллель этой задачи с решаемой в пункте
☞
РАССТОЯНИЕ ДО ПЛОСКОСТИ: в трехмерном пространстве найти ближайшую к началу координат точку плоскости $ D_1x+D_2y+D_3z=2 S $. Решением будет точка с координатами $ (d_1,d_2,d_3) $.
Еще некоторые задачи
§
Построение прямой на плоскости, сумма квадратов расстояний до которой от заданных точек минимальна
☞
ЗДЕСЬ
Задачи учебные
Источники
[1]. Чезаро Э. Элементарный учебник алгебраического анализа и исчисления бесконечно малых. c.360-361
[2]. Икрамов Х.Д. Задачник по линейной алгебре. М.Наука. 1975 .
[3]. Uteshev A.Yu., Yashina M.V. Distance Computation from an Ellipsoid to a Linear or a Quadric Surface in)) $ {mathbb R}^{n} $. Lect.Notes Comput. Sci. 2007. V.4770. P.392-401
[4]. Uteshev A.Yu., Yashina M.V. Metric Problems for Quadrics in Multidimensional Space. J.Symbolic Computation, 2015, Vol. 68, Part I, P. 287-315. Текст
☞
ЗДЕСЬ (pdf)
[5]. Попов Г.Н. Сборник исторических задач по элементарной математике. М.-Л.ГТТИ.1932
[6]. Uteshev A.Yu., Goncharova M.V. Metric problems for algebraic manifolds: Analytical approach. Constructive Nonsmooth Analysis and Related Topics (dedicated to the memory of V.F. Demyanov) (CNSA), 2017, IEEE, http://ieeexplore.ieee.org/document/7974027/

В этом параграфе рассматривается измерение расстояний между основными фигурами стереометрии (точкой и плоскостью, прямой и плоскостью, плоскостями).
Измерение расстояний между различными физи- 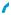
 ческими объектами является одним из самых рас-
ческими объектами является одним из самых рас-  пространённых видов математической деятельности человека. Если размерами объекта можно пренебречь, то речь
пространённых видов математической деятельности человека. Если размерами объекта можно пренебречь, то речь
идет об измерении расстояний между точками, то есть об определении длин отрезков. В других случаях моделирование данных объектовспомощьюточекприизмерениирасстояниймеждуними нецелесообразно или бессмысленно, например, когда речь идет об измерении расстояния между электролампой и столом (рис. 480), если первую можно отождествлять с точкой, то для моделирования стола более пригодна плоскость или ее часть. Аналогичная ситуация возникает при определении расстояния между фасадами зданий (рис. 481), что при математическом моделировании сводится к определению расстояния между параллельными плоскостями; при установлении вертикального рельса на определенном расстоянии от стены (рис. 482) (определение расстояния между параллельными прямой и плоскостью) и т. п.
|
Измерение расстояний в пространстве |
441 |
Рассмотрим вопрос об измерении расстояний между самыми простыми фигурами в пространстве. Содержание понятия рассто– яния остаётся таким же, как и в планиметрии. Например, рассто– яние d от точки А до прямой а — это кратчайшее расстояние меж– ду этой точкой и точками прямой (рис. 483), а расстояние между параллельными прямыми а и b — это длина d кратчайшего из отрезков, соединяющих точки этих прямых (рис. 484).
Такое же содержание имеет и общее понятие расстояния меж– ду фигурами. Например, измерение расстояния d от пункта А до озера В (рис. 485), расстояния d между озёрами A и В (рис. 486) сводится к измерению кратчайшего отрезка, соединяющего точки этих обьектов.
Обобщение понятия расстояния между фигурами в пространс– тве не вызывает затруднений.
Расстоянием между фигурами называют длину кратчайшего из отрезков, соединяющих точки дан ных фигур.
Если фигуры пересекаются, то будем считать, что расстояние между ними равно нулю. Это и понятно, так как фигуры в целом «не удалены» друг от друга. Для фигур, не имеющих общих точек, расстояние между ними является одной из мер их взаимного рас– положения.
Понятно,чтозадачанахождениярасстояниймеждупроизволь– ными геометрическими фигурами является слишком общей, а потому ограничимся детальным рассмотрением расстояний меж– ду простейшими фигурами пространства — точками, прямыми, плоскостями. Как и в планиметрии, эти расстояния реализуются через длины соответствующих перпендикуляров. Кроме того, к указанным ситуациям часто сводится задача об измерении рас– стояний между более сложными фигурами.

|
442 |
Перпендикулярность прямых и плоскостей |
Теорема 1 (о расстоянии от точки до плоскости).
Расстояние от точки до плоскости равно длине перпендикуляра, проведенного из данной точки на данную плоскость.
Этосвойстворасстоянияотточкидоплос– кости непосредственно вытекает из свойс– тва наклонных и перпендикуляров. Дейс– твительно, перпендикуляр, проведенный
из точки к плоскости, меньше наклонных, проведенных из той же точки к плоскости
(рис. 487).
Теорема 2 (о расстоянии между прямой и плоскостью).
Расстояние между прямой и параллельной ей плоскостью равно длине перпендикуляра, проведенного из произвольной точки прямой к данной плоскости.
Обоснование этого свойства о расстоянии между прямой и плос– костью опирается на свойства прямой, параллельной плоскости, и теорему 1 о расстоянии от точки к плоскости.
Действительно, расстояние от каждой точки прямой до плоскости равно длине перпен– дикуляра, проведенного из данной точки к
плоскости. Для точек прямой, параллельной плоскости, эти расстояния являются равны–
ми (рис. 488).
Теорема 3 (о расстоянии между параллельными плоскостя– ми).
Расстояние между параллельными плоскостями равно длине перпендикуляра, проведенного из произвольной точки одной плоскости ко второй плоскости.
Обоснование теоремы 3 аналогично обос– нованию теоремы 2. Отличие заключается лишь в том, что перпендикуляры проводят– ся из всех точек одной плоскости ко второй
(рис. 489).
Приведеннымисвойствамиширокопользу– ются в различных сферах деятельности чело– века, в быту. Например, с их помощью опреде– ляют расстояния от самолета до поверхности
|
Измерение расстояний в пространстве |
443 |
|
|
земли, от светильника до пола, от провода линии электропередач |
||
|
до поверхности земли, между потолком и полом и т. п. |
||
|
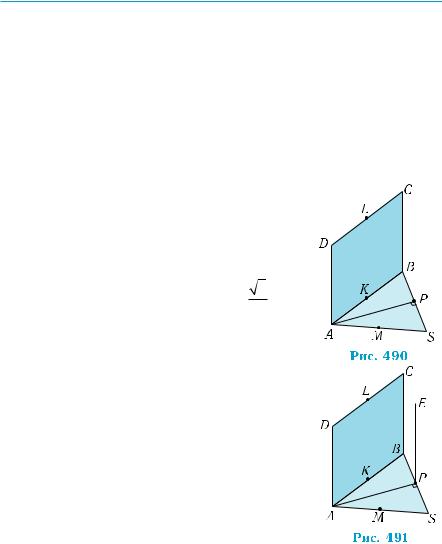
Пример 1. |
Плоскости правильного треугольника ABS и квад– |
|
|
рата ABCD со стороной а перпендикулярны, точки L, K, M явля– |
||
|
ються серединами соответственно сторон DC, AB, AS. Найти рас– |
||
|
стояние: |
||
|
1) от точки А до прямой ВS; |
||
|
2) от точки А до плоскости SBC; |
||
|
3) от прямой |
AD до плоскости SBC; |
|
|
4) между плоскостями MKL и SBC. |
||
|
1)РасстояниеотточкиАдопрямойBS рав– |
||
|
нодлинеперпендикуляра,проведенногоизточ– |
||
|
ки А к прямой BS в плоскости ABS. Поскольку |
||
|
треугольник ABS — правильный, то таким пер– |
||
|
пендикуляром будет медиана АР |
этого тре |
|
|
угольника (рис. 490). Её длина равна |
3 a. |
|
|
2 |
||
|
2) Расстояние от точки А до плоскости SBC |
||
|
равно, по свойству расстояния от точки до |
||
|
плоскости (теорема 1), длине перпендикуля– |
||
|
ра, проведенного из точки А к плоскости SBC. |
||
|
Этим перпендикуляром будет отрезок АР, где |
||
|
Р — середина стороны SB (рис. 490). Действи– |
||
|
тельно, отрезок АР перпендикулярен стороне |
||
|
SB треугольника ABS, так как он является |
||
|
медианой правильного треугольника. Прямая |
||
|
ВС перпендикулярна плоскости ABS, ибо она |
||
|
лежит в одной из перпендикулярных плоскос– |
||
|
тей и перпендикулярна линии их пересече– |
||
|
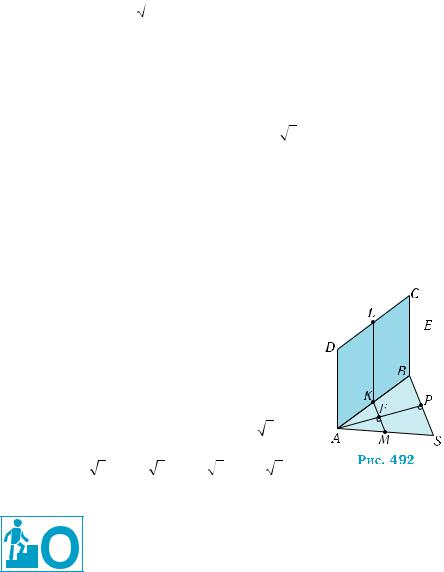
ния. Проведем через точку Р прямую РЕ, па– |
||
|
раллельную прямой ВС (рис. 491). Она лежит |
||
|
в плоскости |
SBC (почему?) и перпендикуляр– |
|
|
на плоскости ABS, по теореме о двух параллельных прямых, одна |
||
|
из которых перпендикулярна плоскости (теорема 1 § 19): ВС || РЕ, |
||
|
ВС ABS. Поэтому РЕ ABS. По определению прямой, перпен– |
||
|
дикулярной плоскости, РЕ АР. По признаку перпендикулярнос– |
||
|
ти прямой и плоскости (теорема 1 §18), АР SBС. Длина перпен– |
|
444 |
Перпендикулярность прямых и плоскостей |
||
|
дикуляра АР равна |
3 |
a. Это и является искомым расстоянием от |
|
|
2 |
|||
|
точки А до плоскости SBC. |
3) Прямая AD и плоскость SBC параллельны, по признаку па– раллельности прямой и плоскости (теорема 1 § 11): AD||ВС. Поэто–
|
му искомое расстояние, по свойству расстояния между прямой и |
||||
|
плоскостью (теорема 2), равно расстоянию от точки А |
плоскости |
|||
|
SBC и, по предыдущему заданию, равно |
3 |
a. |
||
|
2 |
||||
|
4) Плоскости MKL и SBC параллельны, по признаку парал– |
||||
|
лельности плоскостей (теорема 1 §12): KМ || BC (KМ — средняя |
||||
|
линия треугольника ABS), KL || BC (KL — отрезок, соединяющий |
||||
|
середины параллельных сторон квадрата |
ABCD), |
поэтому |
MKL || SBC. Следовательно, искомое расстояние, по свойству рас–
стояния между параллельными плоскостями (теорема 3), равно
|
длине перпендикуляра, проведенного из произвольной точки |
|||||||||||||||
|
плоскости MKL |
к плоскости SBC. Возьмем точ– |
||||||||||||||
|
ку пересечения |
F отрезков |
MK и АР (рис. 492). |
|||||||||||||
|
Поскольку АР |
является перпендикуляром к |
||||||||||||||
|
плоскости SBC (см. задание 2), то FP — перпен– |
|||||||||||||||
|
дикуляр к этой плоскости. Его длина равна |
|||||||||||||||
|
1 AP , так как средняя линия треугольника де– |
|||||||||||||||
|
2 |
|||||||||||||||
|
лит медиану, которую она пересекает, пополам |
|||||||||||||||
|
(почему?). Искомое расстояние равно |
3 |
a. ■ |
|||||||||||||
|
4 |
|||||||||||||||
|
Ответ: 1) |
3 |
a; 2) |
3 |
a; |
3) |
3 |
a; 4) |
3 |
a. |
||||||
|
2 |
2 |
2 |
4 |
||||||||||||
Рассмотримболеедетальнодоказательствосвойстврас– стояний в пространстве. Поскольку теорема 1 является прямым следствием свойств наклонных и перпендику–
ляров,рассмотримдоказательствотеоремы2.
Доказательство теоремы 2
Пусть имеем прямую l и параллельную ей плоскость α (рис. 493). Поскольку расстояние между прямой l и плоскостью α — это длина кратчайшего отрезка, соединяющего их точки, то длина наклонной, соединяющей точки прямой и плоскости, не

|
Измерение расстояний в пространстве |
445 |
может быть искомым расстоянием. Докажем, что длины всех перпендикуляров, проведен– ных из точек прямой l к плоскости α, равны
между собой. А потому расстояние между прямой и плоскостью равно длине каждого из таких перпендикуляров.
Проведем из двух точек А и В прямой l перпендикуляры АA1 и ВB1 к плоскости α.
Поскольку прямые, перпендикулярные одной плоскости, парал– лельны между собой (теорема 2 § 19), то через прямые АA1 и ВB1 можно провести плоскость, содержащую l. Пряма A1B1 является линией пересечения этой плоскости с плоскостью α (почему?). Од– нако в этом случае АВ || А1В1 , то есть четырехугольник АА1В1В является параллелограммом (даже прямоугольником). Отсюда
АА1 = ВB1. ■
Доказательство теоремы 3 аналогично доказательству преды– дущей теоремы.
Доказательство теоремы 3
Как и в теореме 2, наклонная, соединяющая две точки па– раллельных плоскостей, не может определять расстояние меж– ду ними. А все перпендикуляры, проведенные из точек одной из плоскостей ко второй, параллельны, по теореме о параллельности прямых, перпендикулярных плоскости (теорема 2 § 19). Кстати, они одновременно перпендикулярны обеим плоскостям, по теоре– ме о параллельных плоскостях, одна из которых перпендикуляр– на прямой (теорема 3 § 19).
Пусть α и β — параллельные плоскости, а АА1 и ВВ1 — два произвольных перпенди– 
куляра, соединяющие точки этих плоскостей  (рис. 494). Они параллельны, а потому рав–
(рис. 494). Они параллельны, а потому рав– 

ны, по теореме об отрезках параллельных  прямых между параллельными плоскостями
прямых между параллельными плоскостями 
 (теорема 4 § 12). Можно и непосредственно
(теорема 4 § 12). Можно и непосредственно 
 доказать равенство этих отрезков, рассмотрев
доказать равенство этих отрезков, рассмотрев 


 четырехугольник АА1В1В, как это было сдела– но при доказательстве теоремы 2. ■
четырехугольник АА1В1В, как это было сдела– но при доказательстве теоремы 2. ■
С помощью понятия расстояния можно характеризовать парал– лельность прямой и плоскости, параллельность плоскостей. При этом справедливыследующиеутверждения,обратныетеоремам2и3.
|
446 |
Перпендикулярность прямых и плоскостей |
Теорема 4 (признак параллельности прямой и плоскости).
Если все точки прямой лежат на одинаковом, отличном от нуля, расстоянии от плоскости, то прямая и плоскость параллельны.
Теорема 5 (признак параллельности плоскостей).
Если все точки одной плоскости лежат на одинаковом, отличном от нуля, расстоянии от второй плоскости, то эти плоскости параллельны.
Действительно, при выполнении условий этих утверждений соответствующие фигуры не могут иметь общих точек, иначе бы расстояние между ними равнялось нулю.
Утверждения будут правильными, если условия выполняются не для всех точек, а для нескольких. В первом утверждении до– статочно допустить, что условие выполняется для двух точек пря– мой, во втором — для трех точек, не лежащих на одной прямой (рис. 495, 496). Попробуйте доказать это самостоятельно. Приве– денные утверждения широко используются в практике как при– знаки параллельности прямой и плоскости, двух плоскостей. Так, параллельность поверхности стола полу обеспечивается одинако– вой длиной его ножек.
|
Пример 2. |
В тетраэдре SABC основание |
||
|
АВС — равносторонний треугольник со сто– |
|||
|
роной 6 см, боковые грани SAB, |
SAC, SBC — |
||
|
равнобедренные треугольники |
с боковым |
||
|
ребром 5 см. Найти расстояние от центра О |
|||
|
основания до плоскости боковой грани. |
|||
|
Расстояние от точки О до плоскости SBC |
|||
|
равно длине перпендикуляра ОK из точки О |
|||
|
к плоскости SBC (рис. 497). Точка О лежит на |
|||
|
пересечении медиан (и высот!) треугольника |
|||
|
АВС,причем OD = 1 AD = |
6 3 = |
3 .Посколь |
|
|
3 |
3 2 |
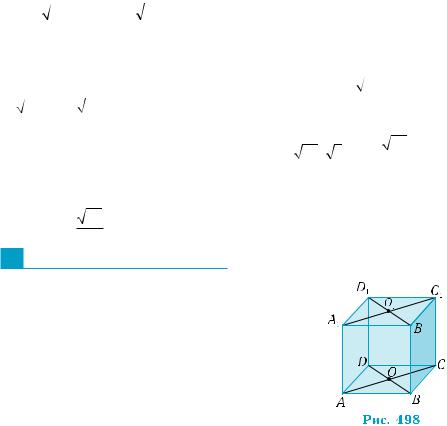
Ответ.
|
Измерение расстояний в пространстве |
447 |
|
ку в треугольнике SBC медиана SD также является высотой, то |
|
|
SD BC, поэтому BC ODC |
и SBC ODC. Следовательно, пер– |
|
пендикуляр из точки О на плоскость BSC совпадает с перпенди– |
|||
|
куляром ОK из точки О на прямую SD, являющейся линией пере– |
|||
|
сечения плоскостей |
SAD |
и |
SBC. По теореме Пифагора, |
|
SD = SB2 − BD2 = 52 |
−32 = 4 |
(см).Посколькуортогональные про |
|
|
екции боковых рёбер на основание одинаковы, то S ортогонально |
проектируется в центр описанной около треугольника АВС ок– ружности, то есть в точку О. Поэтому треугольник SOD — прямо–
угольный. По теореме Пифагора, имеем: SO = SD2 −OD2 =
= 16 −3 = 13 (см). Нетрудно увидеть (докажите это, пользуясь подобием треугольников или различными формулами площади
|
треугольника), что OK = (SO · OD) : SD = ( 13 3):4 = |
39 |
(см). |
|
|
4 |
|||
|
до дру– |
|||
|
Понятно, учитывая симметрию, что расстояния от точки О |
|||
|
гих боковых граней такие же. ■ |
439 см.
|
99 |
Контрольные вопросы |
|
1. |
На рис. 498 изображен куб ABCDA1B1C1D1; |
|
точки О, О1 — центры граней ABCD и |
|
|
A1B1C1D1. |
|
|
1) Какая из точек A1, О1, В1 лежит ближе к |
|
|
плоскости АВС? |
|
|
2) Какие из рёбер куба наиболее удалены |
|
|
от плоскости АА1В1В? |
|
|
3) Какое из расстояний больше: от прямой |
|
|
АО1 до плоскости DCC1 или от прямой AD1 |
|
|
до плоскости BDС1? |
|
|
2. |
4) Чему равно расстояние между плоскостями ADD1 и ВСС1? |
|
Пусть прямая а параллельна плоскости α. Могут ли точки |
|
|
прямой а находиться на различных расстояниях от точек |
|
|
3. |
плоскости α? |
|
Верно ли, что если расстояние от прямой до плоскости отлич– |
|
|
4. |
но от нуля, то прямая и плоскость параллельны? |
|
Известно, что отрезок AB удален от плоскости α на 3 см. Озна– |
|
|
5. |
чает ли это, что прямая AB удалена от плоскости α на 3 см? |
|
Верно ли, что две плоскости совпадают, если расстояние меж– |
|
|
ду ними равно нулю? |
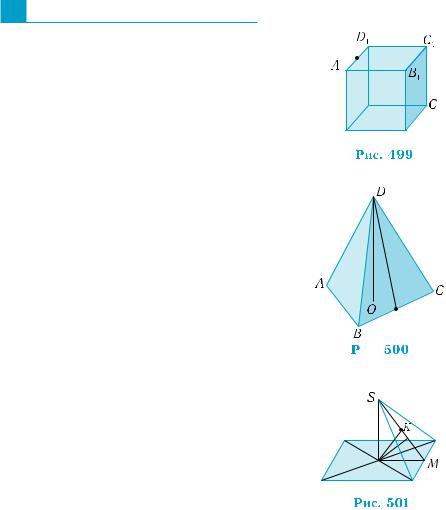
|
448 |
Перпендикулярность прямых и плоскостей |
6.Верно ли, что расстояние от отрезка до плоскости равно рас– стоянию от одного из его концов до этой плоскости?
7.Все стороны треугольника АВС находятся на расстоянии 3 от плоскости α. Параллельны ли плоскости АВС и плоскость α?
8.Какую фигуру образуют точки, равноудаленные от данной плоскости?
9.Как нужно закреплять провод на столбах, чтобы обеспечить его параллельность к поверхности земли?
10.Как измерить высоту дерева, не поднимаясь на его верхушку?
Графические упражнения
1.Нарис.499изображенкубABCDA1B1C1D1
сребром а, точки М, М1 — середины рё–  бер АD, А1D1 соответственно. Найдите
бер АD, А1D1 соответственно. Найдите  расстояние:
расстояние:
1)от точки А до прямой АВ; 
2)от точки D1 до прямой АВ; 
3)от точки А1 до плоскости ВСС1В1; 
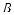
4)от точки А1 до плоскости АВ1С1В;
5)от точки М до плоскости AB1C1D;
6)от прямой A1D1 до плоскости AB1C1D;
7)от прямой AD1 до плоскости AB1C1D;
8)между плоскостями AA1D1 и BB1C1.
2.На рис. 500 изображен правильный тетраэдр ABCD, F — середина ВС, О — центр грани АВС. Длина какого отрезка
равна расстоянию: 
1)от точки D до плоскости АВС; 
2)от точки D до прямой ВС; 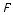
3)от точки С до плоскости АОВ?
3.Из центра О квадрата ABCD (рис. 501) 
 проведен перпендикуляр OS к плоскости квадрата. Точка М — середина ВС, Р — основание высоты треугольника OMS,
проведен перпендикуляр OS к плоскости квадрата. Точка М — середина ВС, Р — основание высоты треугольника OMS, 
его медиана. Длине какого отрез– ка равно расстояние: 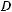

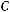
1)от точки O до плоскости BCS; 

2)от точки S до плоскости АВС; 
3)от точки С до плоскости BDS? 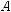
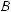 OK —
OK —

|
Измерение расстояний в пространстве |
449 |
Задачи
|
462. |
ТочкаD находитсянарасстоянии8смотвершинравносторон– |
||||
|
него треугольника ABC со стороной 4 см. Найдите расстояние: |
|||||
|
1°) от точки B |
до плоскости DOC, где O — центр треуголь– |
||||
|
ника ABC; |
до плоскости ABC; |
||||
|
2°) от точки D |
|||||
|
3) от плоскости, проходящей через середины отрезков DA, |
|||||
|
463. |
DB, DC, до плоскости треугольника ABC. |
||||
|
Пусть точка O |
является серединой катета AC прямоугольно– |
||||
|
го равнобедренного треугольника с гипотенузой AB = 4 см; |
|||||
|
OP — перпендикуляр к плоскости треугольника длиной |
|||||
|
2 см. Найдите расстояние: |
|||||
|
1°) от точки B до плоскости AOP; |
|||||
|
2°) от плоскости, проходящей через середины сторон CB и |
|||||
|
AB параллельно OP, до плоскости |
CPA; |
||||
|
3) от точки O до плоскости PAB. |
|||||
|
464°. Из точки K — середины гипотенузы АВ равнобедренно– |
|||||
|
го прямоугольного треугольника |
АВС с катетами длиной |
||||
|
8 см — проведен перпендикуляр |
KS к плоскости треуголь– |
||||
|
ника. Длина KS составляет 6 см. Найдите расстояние: |
|||||
|
1) от точки С до плоскости |
АKS; |
||||
|
2) от точки А до плоскости |
KСS; |
||||
|
3) от точки S до прямой ВС. |
|||||
|
465. Дан куб ABCDA1B1C1D1 с ребром а. Найдите расстояние: |
|||||
|
1°) от точки А1 |
до плоскости BDD1; |
||||
|
2°) от прямой |
B1D1 до плоскости АВС; |
||||
|
3°) между противоположными гранями куба; |
|||||
|
4°) от точки А1 |
до прямой BD; |
||||
|
5) между прямыми AD1 иСС1; |
|||||
|
6*) от точки А1 до плоскости AB1D1; |
|||||
|
7*) между плоскостями CD1B1 и DA1B. |
|||||
|
466. ТочкаМлежитнарасстоянииb отвсехвершинквадратаАВСD |
|||||
|
со стороной а и центром в точке О. Найдите расстояние: |
|||||
|
1°) от точки М |
до плоскости |
АВС; |
|||
|
2°) от точки А до плоскости |
ВМD; |
3)от точки О до плоскости МСD, если b = 23 a ;
4)от точки М до прямой СD;
5)между прямыми ОМ и АD.
467.Концы отрезка удалены от некоторой плоскости на 1 см и 4 см. Найдите расстояние от середины отрезка до плоскости.

|
450 |
Перпендикулярность прямых и плоскостей |
468. Катеты прямоугольного треугольника равны 16 см и 12 см. На каком расстоянии от плоскости треугольника лежит точка,
удаленная от каждой вершины треугольника на 10 2 см? 469. Сторона равностороннего треугольника равна 6 см. На ка–
ком расстоянии от плоскости треугольника расположена точка, удалённая на 9 см от:
1) сторон треугольника;
2*) каждой из прямых, содержащих стороны треугольника?
470°. Если из двух точек, находящихся на различных расстояни– ях от плоскости, провести к этой плоскости равные наклон– ные, то большей будет проекция наклонной, проведенной из более близкой к плоскости точки. Докажите это.
471. Если из точки А, находящейся вне плоскости α, опустить перпендикуляр на эту плоскость, а из его основания провес– ти перпендикуляр к прямой ВС, лежащей в плоскости α, то плоскость, проходящая через эти перпендикуляры, будет перпендикулярна прямой ВС. Докажите это.
472*.Плиту прямоугольной формы подняли краном так, что три её вершины удалены от поверхности земли, соответственно, на 2 м, 3 м и 4 м. На каком расстоянии от земли находится четвертая вершина?
473*.Точка А удалена от сторон угла, равного 60°, на 20 см и 7 см, а от его вершины — на 25 см. Найдите расстояние от точки А до плоскости угла.
474*.Точка, лежащая вне плоскости прямого угла, находится на расстоянии 4 см от каждой из его сторон. Найдите расстоя– ние от точки до вершины угла, если точка удалена от плос–
кости угла на 7 см.
475. Плоскости квадрата АВСD и равностороннего треугольника АВМ взаимно перпендикулярны, АВ = а. Постройте общий перпендикуляр к прямой АС и к медиане МО треугольника и определите длину этого перпендикуляра.
476. Пусть АВ — общий перпендикуляр к скрещивающимся пря– мым а и b. Точки A и С лежат на прямой а, точки В и D — на прямой b; АС = ВD. Докажите, что АСВ = ВDС.
Упражнения для повторения
477.В одной полуплоскости, ограниченной прямой АВ, построе–
ны углы: ВАС = 38°, САD = 68°, DАЕ = 85°, ЕАK = 99°.
Определите KАС.
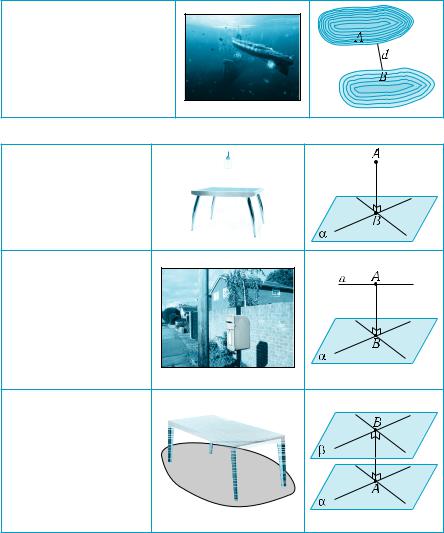
|
Измерение расстояний в пространстве |
451 |
478.Один из смежных углов втрое больше разности между ними. Определите их градусную меру.
479.Наблюдатель, находящийся на берегу озера на высоте h над уровнем воды, видит тучку под углом α, а ее отображение — под углом β к горизонту. Найдите высоту тучки над поверх–
ностью озера при α = 53°27′, β = 55°42′, h = 76,8 м.
Итог
Основное определение
Расстоянием между
произвольными фигу–
рами называют длину кратчайшего из отрез– ков, соединяющих точки данных фигур.
Свойства расстояний
Расстояние от точки до плоскости равно длине перпендику– ляра, проведенного из данной точки к данной плоскости.
Расстояние между прямой и параллель– ной ей плоскостью равно длине перпен– дикуляра, проведен– ного из произволь– ной точки прямой к данной плоскости.
Расстояние между па– раллельными плос– костями равно длине перпендикуляра,про– веденного из произ– вольной точки одной плоскости ко второй плоскости.
Расстояния
Задача на нахождения расстояния в стереометрической фигуре является главной и самой важной из всех. Прежде всего определимся с тем, что имеется ввиду под словом «расстояние», ведь их может быть бесконечно много.
Расстояние между объектами в геометрии – это кратчайшее из расстояний между ними.
Обозначение:

В стереометрии найти расстояние можно между следующими комбинациями фигур:
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ
Расстояние между точками– это длина отрезка, соединяющего эти точки.
В задачах на стереометрию мы не можем просто воспользоваться линейкой, и длину этого отрезка должны найти аналитически. Поэтому длину отрезка AB между точками A и B находят как сторону треугольника, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон.
То есть если в задаче предлагается найти расстояние между точками, нужно задать себе вопрос: «В каком треугольнике этот отрезок является стороной?», затем построить этот треугольник и найти в нем нужную сторону.
Например:

|
|
|
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.

Этот отрезок перпендикуляра можно вычислить, включив его в треугольник (или трапецию) в качестве одной из высот. То есть нужно задать себе вопрос: «В каком треугольнике этот отрезок является высотой?», затем построить этот треугольник и найти в нем высоту.
Например:
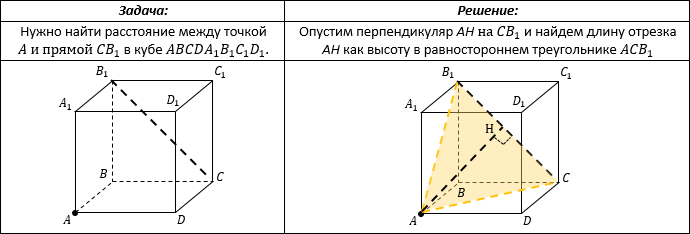
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПЛОСКОСТЬЮ
Существует несколько способов нахождения расстояния от точки до плоскости:
- Построение перпендикуляра из точки на плоскость.
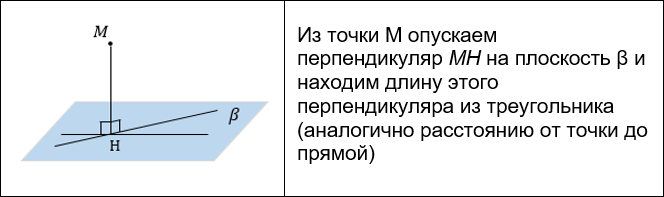
- К этому способу обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной линии с M.
- Построение перпендикуляра из точки прямой к плоскости.
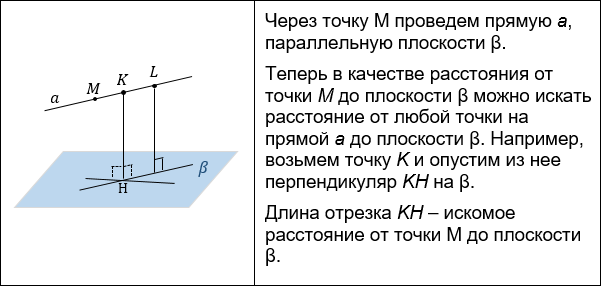
- Построение перпендикуляра из точки плоскости на плоскость.
К этому способу, аналогично, обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной плоскости с M.

- Через двойное выражение объема.
Расстояние от точки M до плоскости β – это перпендикуляр, опущенный из точки на плоскость, то есть по сути это высота в некоторой пирамиде с вершиной M и плоскостью основания, лежащей на β. Если легко вычислить объем этой пирамиды, используя другое основание и другую высоту, то через этот объем можно найти нужное расстояние.
Например:

РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Существует несколько способов нахождения расстояния между скрещивающимися прямыми:
1. Построение взаимного перпендикуляра.

2. Построение параллельной прямой.
К этому способу обращаются, если строить взаимный перпендикуляр неудобно и одна из скрещивающихся прямых уже заключена в удобную плоскость.
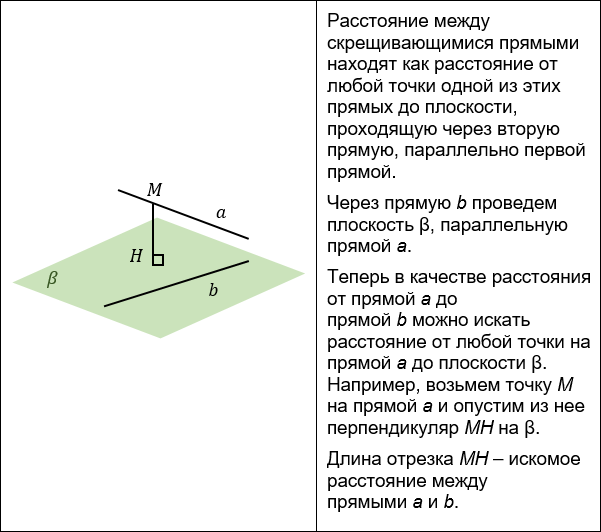 К этому способу обращаются, если строить взаимный перпендикуляр неудобно и скрещивающиеся прямые уже заключены в удобные плоскости.
К этому способу обращаются, если строить взаимный перпендикуляр неудобно и скрещивающиеся прямые уже заключены в удобные плоскости.
3. Построение параллельной плоскости.