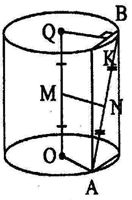
Как найти расстояние между прямыми в цилиндре

Как найти расстояние между прямыми в цилиндре

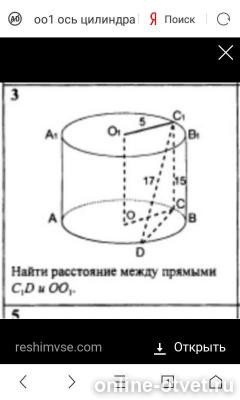
В цилиндре с радиусами ОС и ОС1 равными 5, высотой 15, на окружности радиуса ОС взята точка Д, С1Д = 17. Найти расстояние между прямыми С1Д и ОО1.

seleznev11

Светило науки – 1142 ответа – 11350 раз оказано помощи

Найдем хорду основания
С1Д1 (проекцию отрезка С1Д на основание) по теореме пифагора

С1Д1^2= С1Д^2 – h^2=17^2-15^2=
289-225=64

С1Д1=8.

Искомое расстояние
будет равно перпендикуляру проведенному из центра основания к хорде С1Д1. 
Рассмотрим треугольник С1Д1О1.
С1О1=Д1О1 так как являются радиусами. В равнобедренном треугольнике высота
является и медианой значит по теореме Пифагора найдем высоту треугольника С1Д1О1.
5^2-4^2=25-16=9
расстояние между
прямыми С1Д и ОО1 = 3 см

Источник

Цели и задачи урока:

  • Знакомство учащихся  со
    стереометрическими  задачами на применение
    свойств цилиндра и скрещивающихся прямых.
  • Способствовать формированию и развитию у
    учащихся пространственных представлений;
    повторить  определения, свойства цилиндра и
    скрещивающихся прямых  при решении
    комбинированных задач на  нахождение
    расстояния, угла между двумя скрещивающихся
    прямыми в прямом круговом цилиндре.
  • Формировать умения анализировать,
    устанавливать связь между элементами содержания
    ранее изученного материала, способность к
    самоанализу, рефлексии.
  • Содействовать развитию интереса к оперированию
    геометрическими понятиями и образами,
    личностной активности учащихся; создать условия
    для творческой самореализации личности.  

Оборудование: 16 персональных
компьютеров для учащихся, персональный
компьютер учителя, проектор, раздаточный
материал в виде готовых чертежей с задачами,
листы для отчета о проделанной работе, модели
  цилиндра и призмы. Презентации учителя к
уроку .

ХОД УРОКА

1. Организационный момент (2 мин.)

После проверки готовности класса к уроку,
учитель сообщает тему, цели и задачи практикума и
отмечает, что урок проходит  с использованием
компьютерной презентации, выполненной в Power Point.
Учитель проводит инструктирование учащихся по
технике безопасности при работе в компьютерном
классе.

2. Актуализация опорных знаний и умений
учащихся (10 мин.)

Тестирование с самопроверкой

Для диагностики и коррекции основных понятий и
формул, необходимых на уроке учитель предлагает
учащимся ответить на вопросы теста. С условиями
заданий теста учащиеся знакомятся с помощью
слайдов презентации. Оценивает ответы учащихся
компьютер. Максимальная оценка 3 балла – за три
правильных ответа. На каждом слайде необходимо
нажать кнопку с номером ответа. Неверно
выбранный ответ откроет слайд решение задачи или
напомнит теоретический материал.

1. Дан куб. Угол между прямыми A1D1 и    BC1
равен …

1) 90°; 2)  45°; 3) 60°.   

2. Дан куб . Угол между прямыми A D1 и  BD равен …

1) 90°; 2) 45°; 3) 60°.   

3.   На основании цилиндра взяты две
непараллельные друг другу хорды AN и BM, не
проходящие через центры оснований. Тогда
расстояние между хордами…

1) равно образующей цилиндра  ;  2) больше
высоты цилиндра  3)   меньше образующей
цилиндра

4. Концы отрезка AB лежат на окружностях
оснований цилиндра   AB  и OQ не
параллельные друг другу отрезки.  Тогда
расстояние между прямой AB и осью цилиндра OQ
неравно длине отрезка …

1) MN;  2) QK ;  3) OA.

5  Высота цилиндра 8 см, радиус основания 5 см.
Цилиндр пересечен плоскостью параллельно оси
так, что в сечении получился квадрат. Тогда
расстояние от этого сечения до оси цилиндра
равно…   

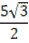  1. см ; 2) 4 см  ;
     3)  3 см  

3. Решение задачи №1 (8 мин.)

Учитель предлагает вниманию учащихся задачу:
Концы отрезка AB лежат на окружностях оснований
цилиндра. Высота цилиндра равна 16, радиус
основания равен 10, а угол между прямой AB и
плоскостью основания цилиндра равен 45°. Найдите
расстояние между осью цилиндра и параллельной ей
плоскостью, проходящей через точки A и B.

Вопросы для обсуждения:

  1. Назовите угол между прямой AB и плоскостью
    основания цилиндра. Ответ обоснуйте.
  2. Каким четырехугольником является  сечение
    цилиндра AA1BB1? 
  3. Какое взаимное расположение прямых AB и OO1  в
    пространстве?
  4. Как найти расстояние между осью цилиндра и
    параллельной ей плоскостью, проходящей через
    точки A и B?

Далее в ходе обсуждения условия задачи,
приходим к решению задачи.

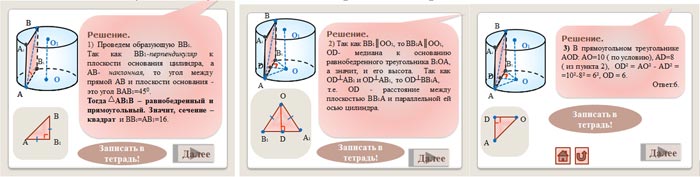
Отмечаем какой теоретический материал
использовался при решении задачи:

  1. Прямой круговой цилиндр
  2. Определение скрещивающихся прямых
  3. Расстояние между двумя скрещивающихся прямыми
  4. Угол между наклонной и плоскостью
  5. Терема Пифагора
  6. Тригонометрические функции острых углов
  7. Решение прямоугольных треугольников
  8. Свойства равнобедренного треугольника

4. Решение задачи №2 (8 мин.)

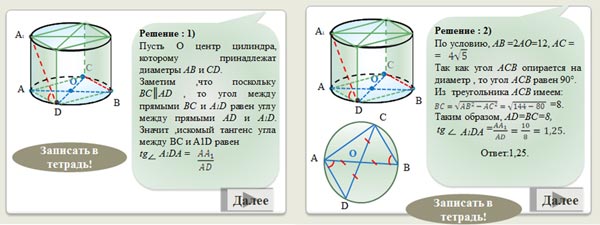
Учитель предлагает вниманию учащихся задачу:

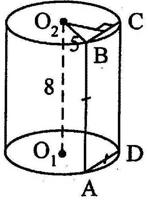
Радиус основания цилиндра равен 6, высота равна
10. Отрезки AB и CD – диаметры одного из оснований
цилиндра, AC =

Отрезок AA1 – образующая цилиндра. Найдите
тангенс угла между прямыми   BC и A1D

Вопросы для обсуждения:

  1. Какое взаимное расположение прямых   BCи
    A1D   в пространстве?
  2. Как найти угол между прямыми BC и A1D?
  3. Угол ACB опирается на диаметр окружности.
    Что   можно сказать о его величине?  

Далее в ходе обсуждения условия задачи,
приходим к решению задачи.

Отмечаем какой теоретический материал
использовался при решении задачи

  1. Прямой круговой цилиндр
  2.  Определение скрещивающихся прямых
  3.  Угол между двумя скрещивающихся прямыми
  4.  Терема Пифагора
  5.  Вписанный угол, опирающийся на диаметр
  6. Тригонометрические функции острых углов
  7. Решение прямоугольных треугольников  

5. Самостоятельная работа по решению
задач с использованием готовых чертежей и
последующей проверкой или самопроверкой (10 мин.)

Учащиеся получают тексты задач по вариантам в
печатном виде и на слайдах презентации. Учитель
контролирует работу  учащихся, определяет
степень усвоения изученного материала. Через
определенное время краткое решение задач можно
проверить, используя слайды презентации.

Вариант №1

  1. Концы отрезка AB лежат на окружностях оснований
    цилиндра. Радиус  основания цилиндра равен 15,
    длина отрезка AB равна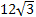 , а угол между прямой AB и плоскостью
    основания цилиндра равен 30?. Найдите расстояние
    между осью цилиндра и параллельной ей
    плоскостью, проходящей через точки A и B.
  2. Радиус основания цилиндра равен 1, высота равна 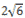  Отрезки AB и CD
    – диаметры одного из оснований цилиндра. Отрезок
    AA1 –  образующая цилиндра, AD =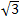 . Найдите косинус угла между
    прямыми   BD и A1C 

6. Отчёт о проделанной на уроке работе
(5 мин.)

В конце занятия учащимся  заполняют бланк
отчета о проделанной на уроке работе.
Тестирование с самопроверкой.

Приложение 1

Источник

Концы отрезка AB лежат на окружностях оснований цилиндра. Найдите расстояние между прямой AB и осью цилиндра, если радиус цилиндра равен 10, его высота  — 5, а AB=13.

Спрятать решение

Решение.

Итак, OO_1  — ось цилиндра. Прямая AB лежит в плоскости ADB. В треугольнике DOA заметим, что AO=OD=r, тогда этот треугольник равнобедренный, а OH  — медиана, биссектриса и высота. Следовательно, расстояние между осью цилиндра и прямой AB равно длине OH. Найдем её.

Так как BD  —высота, angle ADB=90 градусов, тогда найдем AD по теореме Пифагора:

AB в квадрате =BD в квадрате плюс AD в квадрате

AD=12.

Так как точка H  — середина AD, AH=HD=6.

И наконец, в triangle DHO найдем OH по теореме Пифагора:

DO в квадрате =DH в квадрате плюс OH в квадрате

OH=8.

Ответ: 8.

Источник

rdunghanomel635

rdunghanomel635

Вопрос по геометрии:

Найдите расстояние между

Изображение к вопросу

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!

Ответы и объяснения 1

knalincate

knalincate

Находим СД = √(17²-15²) = √( 289 – 225) = √64 = 8.
С1Д лежит в плоскости, параллельной ОО1, поэтому общий перпендикуляр к ним – это высота ОЕ в равнобедренном треугольнике ОСД.
Искомое расстояние  ОЕ между ОО1 и С1Д равно:
ОЕ = √(5² – (8/2)²) = √(25 – 16) = √9 = 3.

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

  • Отвечать достоверно на те вопросы, на которые знаете
    правильный ответ;
  • Писать подробно, чтобы ответ был исчерпывающий и не
    побуждал на дополнительные вопросы к нему;
  • Писать без грамматических, орфографических и
    пунктуационных ошибок.

Этого делать не стоит:

  • Копировать ответы со сторонних ресурсов. Хорошо ценятся
    уникальные и личные объяснения;
  • Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
    знаю» и так далее;
  • Использовать мат – это неуважительно по отношению к
    пользователям;
  • Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Источник

14. Задачи по стереометрии


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Нахождение расстояния между скрещивающимися прямыми

(blacktriangleright) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.

Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.

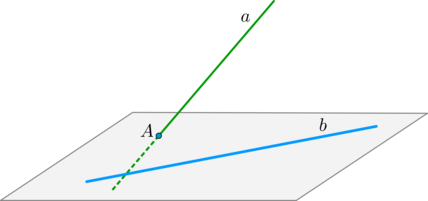
(blacktriangleright) Т.к. через одну из скрещивающихся прямых проходит ровно одна плоскость, параллельная другой прямой, то расстояние между скрещивающимися прямыми — это расстояние между одной из этих прямых и плоскостью, проходящей через вторую прямую параллельно первой.

Таким образом, если прямые (a) и (b) скрещиваются, то:

Шаг 1. Провести прямую (cparallel b) так, чтобы прямая (c) пересекалась с прямой (a). Плоскость (alpha), проходящая через прямые (a) и (c), и будет плоскостью, параллельной прямой (b).

Шаг 2. Из точки пересечения прямых (a) и (c) ((acap c=H)) опустить перпендикуляр (HB) на прямую (b) (первый способ).

Или из любой точки (B’) прямой (b) опустить перпендикуляр на прямую (c) (второй способ).

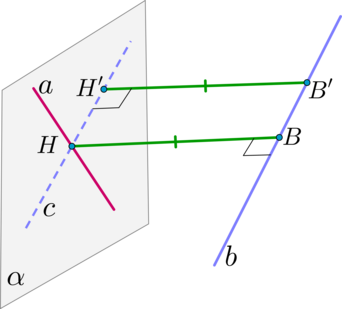
В зависимости от условия задачи какой-то из этих двух способов может быть гораздо удобнее другого.


Задание
1

#2452

Уровень задания: Легче ЕГЭ

В кубе (ABCDA_1B_1C_1D_1), ребро которого равно (sqrt{32}), найдите расстояние между прямыми (DB_1) и (CC_1).

Прямые (DB_1) и (CC_1) скрещиваются по признаку, т.к. прямая (DB_1) пересекает плоскость ((DD_1C_1)), в которой лежит (CC_1), в точке (D), не лежащей на (CC_1).

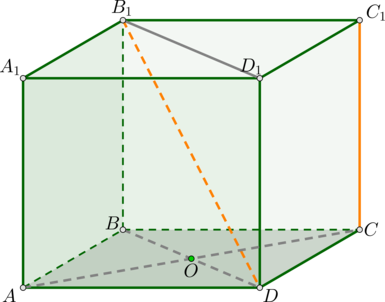
Расстояние между скрещивающимися прямыми будем искать как расстояние между прямой (CC_1) и плоскостью, проходящей через (DB_1) параллельно (CC_1). Т.к. (DD_1parallel CC_1), то плоскость ((B_1D_1D)) параллельна (CC_1).
Докажем, что (CO) – перпендикуляр на эту плоскость. Действительно, (COperp BD) (как диагонали квадрата) и (COperp DD_1) (т.к. ребро (DD_1) перпендикулярно всей плоскости ((ABC))). Таким образом, (CO) перпендикулярен двум пересекающимся прямым из плоскости, следовательно, (COperp (B_1D_1D)).

(AC), как диагональ квадрата, равна (ABsqrt2), то есть (AC=sqrt{32}cdot sqrt2=8). Тогда (CO=frac12cdot AC=4).

Ответ: 4


Задание
2

#2453

Уровень задания: Сложнее ЕГЭ

Дан куб (ABCDA_1B_1C_1D_1). Найдите расстояние между прямыми (AB_1) и (BC_1), если ребро куба равно (a).

1) Заметим, что эти прямые скрещиваются по признаку, т.к. прямая (AB_1) пересекает плоскость ((BB_1C_1)), в которой лежит (BC_1), в точке (B_1), не лежащей на (BC_1).
Расстояние между скрещивающимися прямыми будем искать как расстояние между прямой (BC_1) и плоскостью, проходящей через (AB_1) параллельно (BC_1).

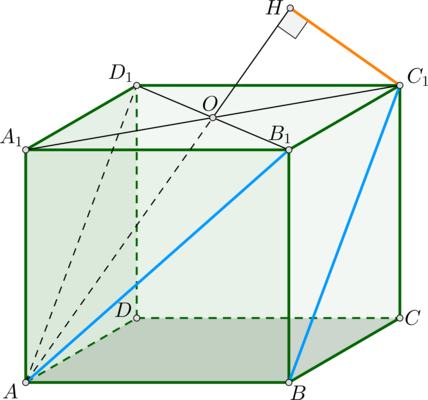
Для этого проведем (AD_1) — она параллельна (BC_1). Следовательно, по признаку плоскость ((AB_1D_1)parallel BC_1).

2) Опустим перпендикуляр (C_1H) на эту плоскость и докажем, что точка (H) упадет на продолжение отрезка (AO), где (O) – точка пересечения диагоналей квадрата (A_1B_1C_1D_1).
Действительно, т.к. по свойству квадрата (C_1Operp B_1D_1), то по теореме о трех перпендикуляр проекция (HOperp B_1D_1). Но (triangle AB_1D_1) равнобедренный, следовательно, (AO) – медиана и высота. Значит, точка (H) должна лежать на прямой (AO).

3) Рассмотрим плоскость ((AA_1C_1)).

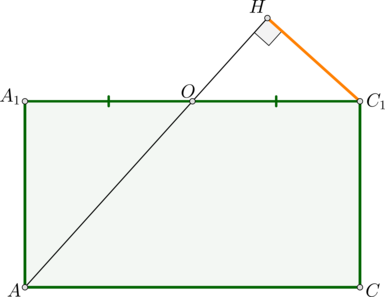
(triangle AA_1Osim triangle OHC_1) по двум углам ((angle
AA_1O=angle OHC_1=90^circ), (angle AOA_1=angle HOC_1)). Таким образом,

[dfrac{C_1H}{AA_1}=dfrac{OC_1}{AO} qquad (*)]

По теореме Пифагора из (triangle AA_1O): [AO=sqrt{a^2+dfrac{a^2}2}=dfrac{sqrt6}2a.]

Следовательно, из ((*)) теперь можно найти перпендикуляр

[C_1H=dfrac a{sqrt3}.]

Ответ:

(dfrac a{sqrt3})


Задание
3

#2439

Уровень задания: Сложнее ЕГЭ

Дан куб (ABCDA_1B_1C_1D_1). Найдите расстояние между прямыми (A_1B) и (AC_1), если ребро куба равно (sqrt6).

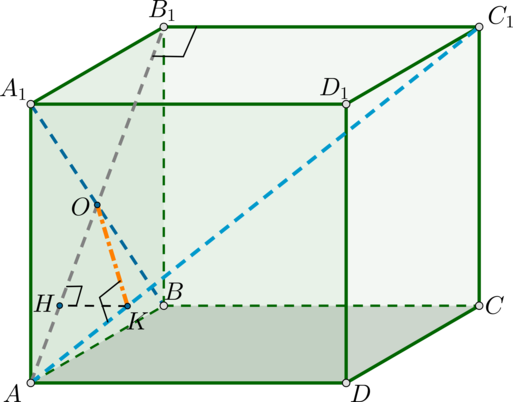
По определению угол между скрещивающимися прямыми – это угол между одной прямой и плоскостью, проходящей через вторую прямую параллельно первой. Найдем плоскость, проходящую через (A_1B) параллельно (AC_1).

Заметим, что данные прямые являются скрещивающимися. Т.к. (B_1C_1perp (AA_1B_1)), то проекция наклонной (AC_1) на эту плоскость – это прямая (AB_1).

Пусть (AB_1cap A_1B=O). Опустим из точки (O) на (AC_1) перпендикуляр (OK) и докажем, что это и есть искомое расстояние. Т.к. по определению расстояние между скрещивающимися прямыми – длина отрезка, перпендикулярного обеим прямым, то осталось доказать, что (OK) перпендикулярен прямой (A_1B).
Действительно, проведем (KHparallel B_1C_1) (следовательно, (Hin
AB_1)). Тогда т.к. (B_1C_1perp (AA_1B_1)), то и (KHperp
(AA_1B_1)). Тогда по теореме о трех перпендикулярах (т.к. проекция (HOperp A_1B)) наклонная (KOperp A_1B), чтд.
Таким образом, (KO) – искомое расстояние.

Заметим, что (triangle AOKsim triangle AC_1B_1) (по двум углам). Следовательно,

[dfrac{AO}{AC_1}=dfrac{OK}{B_1C_1} quad Rightarrow quad
OK=dfrac{sqrt6cdot sqrt2}{2sqrt3}=1.]

Ответ: 1

УСТАЛ? Просто отдохни

Источник

Добавить комментарий