Как найти расстояние между ребрами треугольной пирамиды

Каталог заданий.
2. Расстояния между противоположными рёбрами пирамиды

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Среди огромного количества стереометрических
задач в учебниках геометрии, в различных
сборниках задач, пособиях по подготовке в ВУЗы
крайне редко встречаются задачи на нахождение
расстояния между скрещивающимися прямыми.
Возможно, это обусловлено как узостью их
практического применения (относительно школьной
программы, в отличие от “выигрышных” задач на
вычисление площадей и объемов), так и сложностью
данной темы.

Практика проведения ЕГЭ показывает, что многие
учащиеся вообще не приступают к выполнению
заданий по геометрии, входящих в экзаменационную
работу. Для обеспечения успешного выполнения
геометрических заданий повышенного уровня
сложности необходимо развивать гибкость
мышления, способность анализировать
предполагаемую конфигурацию и вычленять в ней
части, рассмотрение которых позволяет найти путь
решения задачи.

Школьный курс предполагает изучение четырех
способов решения задач на нахождение расстояния
между скрещивающимися прямыми. Выбор способа
обусловлен, в первую очередь, особенностями
конкретной задачи, предоставленными ею
возможностями для выбора, и, во вторую очередь,
способностями и особенностями
“пространственного мышления” конкретного
учащегося. Каждый из этих способов позволяет
решить самую главную часть задачи – построение
отрезка, перпендикулярного обеим скрещивающимся
прямым (для вычислительной же части задач
деление на способы не требуется).

Основные способы решения задач на нахождение
расстояния между скрещивающимися прямыми

Нахождение длины общего перпендикуляра двух
скрещивающихся прямых, т.е. отрезка с концами на
этих прямых и перпендикулярного каждой из этих
прямых.

Нахождение расстояния от одной из
скрещивающихся прямых до параллельной ей
плоскости, проходящей через другую прямую.

Нахождение расстояния между двумя
параллельными плоскостями, проходящими через
заданные скрещивающиеся прямые.

Нахождение расстояния от точки, являющейся
проекцией одной из скрещивающихся прямых, на
перпендикулярную ей плоскость (так называемый
“экран”) до проекции другой прямой на ту же
самую плоскость.

Проведем демонстрацию всех четырех способов на
следующей простейшей задаче: “В кубе с
ребром а найти расстояние между любым ребром
и диагональю не пересекающей его грани”. Ответ: .

1 способ.

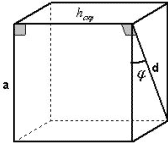
Рисунок 1

h_скр перпендикулярна плоскости боковой
грани, содержащей диагональ d и
перпендикулярна ребру, следовательно, h_скр
и является расстоянием между ребром а и
диагональю d.

2 способ.

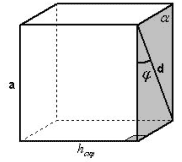
Рисунок 2

Плоскость A параллельна ребру и проходит через
данную диагональ, следовательно, данная h_скр
является не только расстоянием от ребра до
плоскости A, но и расстоянием от ребра до данной
диагонали.

3 способ.

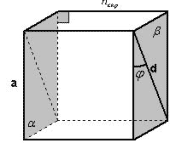
Рисунок 3

Плоскости A и B параллельны и проходят через две
данные скрещивающиеся прямые, следовательно,
расстояние между этими плоскостями равно
расстоянию между двумя скрещивающимися прямыми.

4 способ.

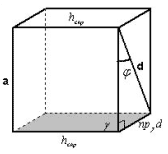
Рисунок 4

Плоскость A перпендикулярна ребру куба. При
проекции на A диагонали d данная диагональ
обращается в одну из сторон основания куба.
Данная h_скр является расстоянием между
прямой, содержащей ребро, и проекцией диагонали
на плоскость C, а значит и между прямой,
содержащей ребро, и диагональю.

Остановимся подробнее на применении каждого
способа для изучаемых в школе многогранников.

СПОСОБ I.

Применение первого способа достаточно
ограничено: он хорошо применяется лишь в
некоторых задачах, так как достаточно сложно
определить и обосновать в простейших задачах
точное, а в сложных – ориентировочное
местоположение общего перпендикуляра двух
скрещивающихся прямых. Кроме того, при
нахождении длины этого перпендикуляра в сложных
задачах можно столкнуться с непреодолимыми
трудностями.

Примеры

Задача 1. В прямоугольном параллелепипеде с
размерами a, b, h найти расстояние между
боковым ребром и не пересекающейся с ним
диагональю основания.

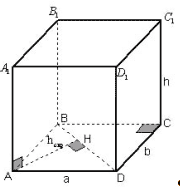
Рисунок 5

Пусть AHBD.
Так как А₁А перпендикулярна плоскости АВСD ,
то А₁А
AH.

AH перпендикулярна обеим из двух скрещивающихся
прямых, следовательно AH?- расстояние между
прямыми А₁А и BD. В прямоугольном
треугольнике ABD, зная длины катетов AB и AD, находим
высоту AH, используя формулы для вычисления
площади прямоугольного треугольника. Ответ:

Задача 2. В правильной 4-угольной пирамиде с
боковым ребром L и стороной основания a
найти расстояние между апофемой и стороной
основания, пересекающей боковую грань,
содержащую эту апофему.

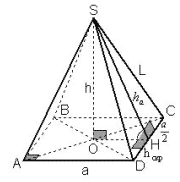
Рисунок 6

SHCD как
апофема, ADCD,
так как ABCD – квадрат. Следовательно, DH –
расстояние между прямыми SH и AD. DH равно половине
стороны CD. Ответ:

СПОСОБ II

Применение этого способа также ограничено в
связи с тем, что если можно быстро построить (или
найти уже готовую) проходящую через одну из
скрещивающихся прямых плоскость, параллельную
другой прямой, то затем построение
перпендикуляра из любой точки второй прямой к
этой плоскости (внутри многогранника) вызывает
трудности. Однако в несложных задачах, где
построение (или отыскивание) указанного
перпендикуляра трудностей не вызывает, данный
способ является самым быстрым и легким, и поэтому
доступен.

Примеры

Задача 2. Решение уже указанной выше задачи
данным способом особых трудностей не вызывает.

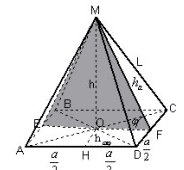
Рисунок 7

Плоскость EFM параллельна прямой AD, т. к AD || EF.
Прямая MF лежит в этой плоскости, следовательно,
расстояние между прямой AD и плоскостью EFM равно
расстоянию между прямой AD и прямой MF. Проведем OHAD. OHEF, OHMO,
следовательно, OH(EFM),
следовательно, OH – расстояние между прямой AD и
плоскостью EFM, а значит, и расстояние между прямой
AD и прямой MF. Находим OH из треугольника AOD.

Ответ:

Задача 3. В прямоугольном параллелепипеде с
размерами a,b и h найти расстояние между
боковым ребром и не пересекающейся с ним
диагональю параллелепипеда.

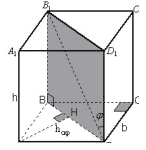
Рисунок 8

Прямая AA₁ параллельна плоскости BB₁D₁D,
B₁D принадлежит этой плоскости,
следовательно расстояние от AA₁ до
плоскости BB₁D₁D равно расстоянию между
прямыми AA₁ и B₁D. Проведем AHBD. Также, AH B₁B,
следовательно AH(BB₁D₁D), следовательно AHB₁D, т. е. AH –
искомое расстояние. Находим AH из прямоугольного
треугольника ABD.

Ответ:

Задача 4. В правильной шестиугольной призме
A:F₁ c высотой h и стороной основания a
найти расстояние между прямыми:

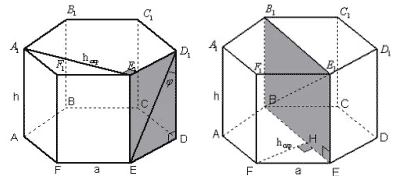
Рисунок 9 Рисунок 10

а) AA₁ и ED₁.

Рассмотрим плоскость E₁EDD₁. A₁E₁EE₁, A₁E₁E₁D₁,
следовательно

A₁E₁ (E₁EDD₁). Также A₁E₁ AA₁.
Следовательно, A₁E₁ является
расстоянием от прямой AA₁ до плоскости E₁EDD₁.
ED₁(E₁EDD₁).,
следовательно AE₁ – расстояние от прямой AA₁
до прямой ED₁. Находим A₁E₁ из
треугольника F₁A₁E₁ по теореме
косинусов. Ответ:

б) AF и диагональю BE₁.

Проведем из точки F прямую FH перпендикулярно BE.
EE₁FH, FHBE, следовательно
FH(BEE₁B₁),
следовательно FH является расстоянием между
прямой AF и (BEE₁B₁), а значит и
расстоянием между прямой AF и диагональю BE₁.
Ответ:

СПОСОБ III

Применение этого способа крайне ограничено,
так как плоскость, параллельную одной из прямых
(способ II) строить легче, чем две параллельные
плоскости, однако способ III можно использовать в
призмах, если скрещивающиеся прямые принадлежат
параллельным граням, а также в тех случаях, когда
в многограннике несложно построить параллельные
сечения, содержащие заданные прямые.

Примеры

Задача 4.

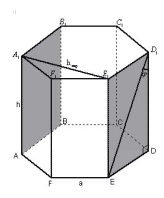
Рисунок 11

а) Плоскости BAA₁B₁ и DEE₁D₁
параллельны, так как AB || ED и AA₁ || EE₁. ED₁DEE₁D₁,
AA₁(BAA₁B₁),
следовательно, расстояние между прямыми AA₁
и ED₁ равно расстоянию между плоскостями BAA₁B₁
и DEE₁D₁. A₁E₁AA₁, A₁E₁A₁B₁, следовательно, A₁E₁BAA₁B₁.
Аналогично доказываем, что A₁E₁(DEE₁D₁). Т.о., A₁E₁
является расстоянием между плоскостями BAA₁B₁
и DEE₁D₁, а значит, и между прямыми AA₁
и ED₁. Находим A₁E₁ из треугольника
A₁F₁E₁, который является
равнобедренным с углом A₁F₁E₁,
равным .
Ответ:

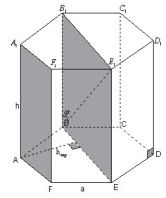
Рисунок 12

б) Расстояние между AF и диагональю BE₁
находится аналогично.

Ответ:.

Задача 5. В кубе с ребром а найти
расстояние между двумя непересекающимися
диагоналями двух смежных граней.

Данная задача рассматривается как
классическая в некоторых пособиях, но, как
правило, ее решение дается способом IV, однако
является вполне доступной для решения с помощью
способа III.

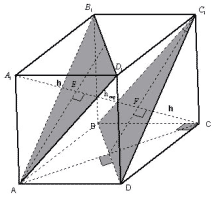
Рисунок 13

Некоторую трудность в данной задаче вызывает
доказательство перпендикулярности диагонали A₁C
обеим параллельным плоскостям (AB₁D₁ ||
BC₁D). B₁CBC₁ и BC₁A₁B₁, следовательно,
прямая BC₁ перпендикулярна плоскости A₁B₁C,
и следовательно, BC₁A₁C. Также, A₁CBD.
Следовательно, прямая A₁C перпендикулярна
плоскости BC₁D. Вычислительная же часть
задачи особых трудностей не вызывает, так как h_скр
= EF находится как разность между диагональю куба
и высотами двух одинаковых правильных пирамид A₁AB₁D₁
и CC₁BD.

Ответ:

СПОСОБ IV.

Данный способ имеет достаточно широкое
применение. Для задач средней и повышенной
трудности его можно считать основным. Нет
необходимости применять его только тогда, когда
один из трех предыдущих способов работает проще
и быстрее, так как в таких случаях способ IV может
только усложнить решение задачи, или сделать его
труднодоступным. Данный способ очень выгодно
использовать в случае перпендикулярности
скрещивающихся прямых, так как нет необходимости
построения проекции одной из прямых на “экран”

Примеры.

Задача 5. Все та же “классическая” задача
(с непересекающимися диагоналями двух смежных
граней куба) перестает казаться сложной, как
только находится “экран” – диагональное
сечение куба.

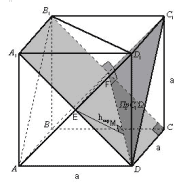
Рисунок 14

Экран:

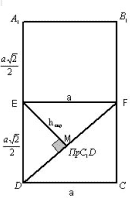
Рисунок 15

Рассмотрим плоскость A₁B₁CD. C₁F (A₁B₁CD),
т. к. C₁FB₁C
и C₁FA₁B₁.
Тогда проекцией C₁D на “экран” будет
являться отрезок DF. Проведем EMDF. Отрезок EM и будет являться расстоянием
между двумя непересекающимися диагоналями двух
смежных граней. Находим EM из прямоугольного
треугольника EDF. Ответ:.

Задача 6. В правильной треугольной пирамиде
найти расстояние и угол между скрещивающимися
прямыми: боковым ребром l и стороной
основания a.

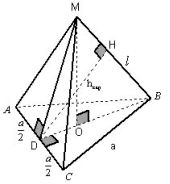
Рисунок 16

В данной и аналогичных ей задачах способ IV
быстрее других способов приводит к решению, так
как построив сечение, играющее роль “экрана”,
перпендикулярно AC (треугольник BDM), видно, что
далее нет необходимости строить проекцию другой
прямой (BM) на этот экран. DH – искомое расстояние. DH
находим из треугольника MDB, используя формулы
площади. Ответ: .

Сообщения без ответов | Активные темы

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Расстояние между вершиной треугольной призмы и тетраэдра в форуме Геометрия	Viktors	5	157	31 мар 2022, 18:14
Найти объём правильной треугольной пирамиды в форуме Геометрия	rafael999	2	567	22 сен 2013, 20:37
Объясните почему у пирамиды с 12 ребрами 7 граней в форуме Геометрия	drinke81	35	383	31 янв 2023, 21:01
Объем треугольной пирамиды в форуме Аналитическая геометрия и Векторная алгебра	Cris_21	2	303	19 фев 2017, 15:09
Сечение треугольной пирамиды в форуме Геометрия	hpbhpb	26	1234	07 окт 2015, 06:09
Объем правильной треугольной пирамиды в форуме Геометрия	Aspid	3	440	22 июн 2014, 13:40
Найти расстояние от вершины основания пирамиды в форуме Геометрия	newtagi	11	1029	12 май 2014, 21:35
Даны вершины треугольной пирамиды abcd в форуме Аналитическая геометрия и Векторная алгебра	SVTATY	3	685	28 окт 2014, 16:39
Объём треугольной пирамиды зная длину её рёбер в форуме Аналитическая геометрия и Векторная алгебра	And76	5	219	19 фев 2022, 00:38
Найти расстояние между прямыми АВ и СD. в форуме Аналитическая геометрия и Векторная алгебра	Tanya_1995	4	903	03 май 2014, 15:47

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 3

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)

Краткая теория

---

Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.

Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.

Пример решения задачи

Задача

Даны координаты
вершин пирамиды 
. Найти:

Сделать чертеж.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Длина ребра

Длину ребра

 найдем по
формуле расстояния между 2-мя точками:

Угол между ребрами

Угол между ребрами

 и

 найдем как угол
между направляющими векторами

  и

:

Косинус угла между
векторами:

Угол между ребром и гранью. Векторное произведение

Вычислим угол между
ребром

 и гранью

.

Для этого вычислим
координаты нормального вектора плоскости

 –им будет
векторное произведение векторов 

 и

.

 

Найдем векторное произведение. Для этого

вычислим определитель:

Нормальный вектор
плоскости:

  

Синус угла:

Площадь грани

Вычислим площадь
грани

. Она будет численно равна половине модуля векторного
произведения векторов

    и 

:

Искомая площадь:

Объем пирамиды. Смешанное произведение векторов

Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов

  и

:

Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:

Искомый объем
пирамиды:

Уравнение прямой в пространстве

Вычислим уравнение
прямой

.  Направляющим
вектором искомой прямой является вектор

. Кроме того, прямая проходит через точку

 

Уравнение искомой
прямой:

Уравнение плоскости

Вычислим уравнение
плоскости

. Нормальный вектор плоскости

. кроме того, плоскость проходит через точку

 -уравнение
грани

 

Уравнение высоты, опущенной на грань

Составим уравнение
высоты, опущенной на грань

 из вершины

:

Нормальный вектор

 является
направляющим вектором высоты, кроме того, высота проходит через точку

 

Искомое уравнение
высоты:

Сделаем схематический чертеж: