Светило науки – 1378 ответов – 9244 помощи
1) Осуществим дополнительное построение:
Проведём отрезок СЕ параллельно диагонали ВD => AC перпендикулярен СЕ.
Также проведём отрезок СК параллельно отрезку МN
Из этого следует, что четырёхугольник ВСЕD – параллелограмм ( СЕ || ВD , BC || DE ).
Aналогично, четырёхугольник МСКN – параллелограмм ( CK || MN, МС || KN )
Поэтому, BC = DE , MC = NK, BD = CE = 13
AE = AD + DE = AD + BC
AK = AN + NK = (1/2) × AD + (1/2) × BC = (1/2) × ( ВС + AD )
Значит, K – середина отрезка АЕ , АК = КЕ
Поэтому , МN = CK – медиана в ∆ АСЕ
2) Рассмотрим ∆ АСЕ ( угол АСЕ = 90° ):
” В прямоугольном треугольнике медиана равна половине гипотенузы ” →
По теореме Пифагора:
AE² = 13² + 5² = 169 + 25 = 194
AE = √194
Значит, искомый отрезок MN, равный отрезку СК, имеет длину:
СК = MN = (1/2) × AE = (1/2) × √194 = √194/2
ОТВЕТ: √194/2

Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Так как средняя линия трапеции равна полусумме оснований, то
(displaystyle MN=frac{AD+BC}{2}=frac{16+12}{2}=frac{28}{2}=14small.)
Воспользуемся свойством средней линии трапеции.
Правило
Свойство средней линии трапеции
Средняя линия трапеции параллельна основаниям трапеции.
(displaystyle MNparallel BCparallel AD)
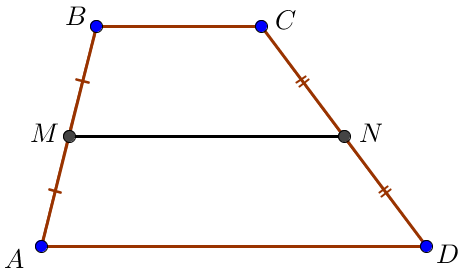
Рассмотрим четырехугольник (displaystyle AMNDsmall.) В нем стороны (displaystyle MN) и (displaystyle AD) параллельны по свойству трапеции. Прямые (displaystyle AM) и (displaystyle DN) не параллельны, так как содержат боковые стороны исходной трапеции.
Значит, четырехугольник (displaystyle AMND) является трапецией.
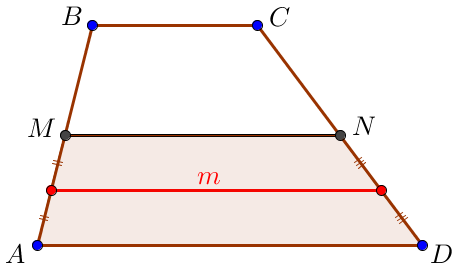
В задаче требуется найти расстояние между серединами сторон (displaystyle AM) и (displaystyle NDsmall,) то есть длину (displaystyle m) средней линии трапеции (displaystyle AMNDsmall.)
Так как средняя линия трапеции равна полусумме оснований, то
(displaystyle m=frac{AD+MN}{2}=frac{16+14}{2}=frac{30}{2}=15small.)
Ответ: (displaystyle 15{small .})
АВСD – данная трапеция, АD и ВС – основания.
Р – середина ВС, М – середина АD.
РМ – отрезок, соединяющий середины оснований (его еще называют: вторая средняя линия трапеции) . По условию он равен полусумме длин оснований. Значит, он равен средней линии КЕ.
Если в трапеции обе средние линии равны, то ее диагонали перпендикулярны (это свойство такое есть) . А значит, угол между диагоналями трапеции равен 90 градусов.
Если надо доказательство этого свойства, то это будет так:
Четырехугольник РЕМК – параллелограмм (так как РЕ параллельно ВD, КМ параллельно ВD, тогда РЕ параллельно КМ. РЕ = 1/2 ВD, КМ = 1/2 ВD, тогда РЕ = КМ. Если в четырехугольнике две противоположные стороны параллельны и равны, то этот четырехугольник параллелограмм)
А посколько его диагонали РМ и КЕ равны, то это прямоугольник.
РЕ перпендикулярно МЕ, тогда и ВD перпендикулярно АС.
Ответ: MN = 2
Объяснение:
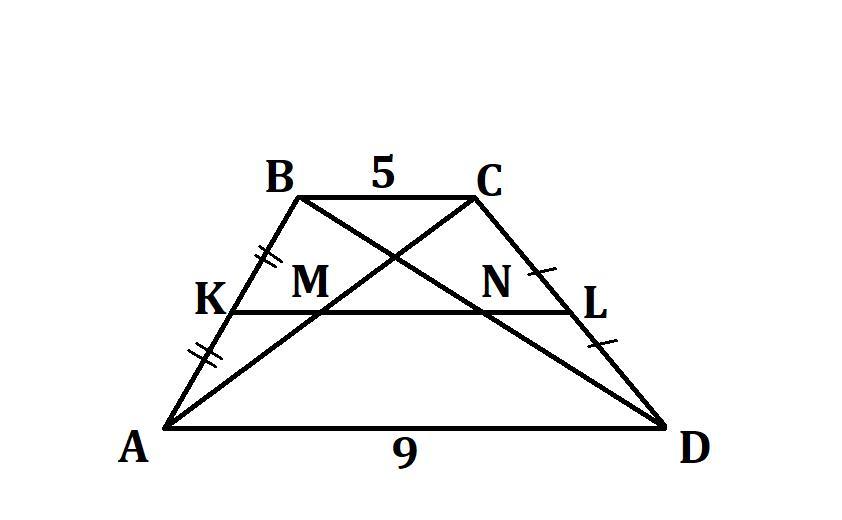
В трапеции ABCD известны основания AD = 9 и BC = 5. Найдите расстояние между серединами диагоналей трапеции (буквенное обозначение получившегося отрезка – MN).
**********
- Средняя линия трапеции проходит через середины диагоналей.
М – середина диагонали АС, N – середина диагонали ВD.
K и L – середины боковых сторон АВ и СD соответственно, то есть KL – средняя линия трапеции ABCD.
⇒ KМ – средняя линия ΔАВС, KM || BC.
⇒ М ∈ KL, поскольку через точку K можно провести на плоскости единственную прямую, параллельную прямой ВС.
KM = 1/2 · BC
Аналогично, N – середина диагонали BD, NL – средняя линия ΔDCB, NL || BC, N ∈ KL.
NL = 1/2 · BC
По свойству средней линии трапеции,
#SPJ3
Приложения: