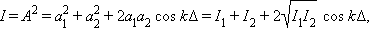
Рис.
6
Сделаем рисунок. Здесь (рис.6) приняты
обозначения: L – расстояние от источников
до экрана,
– угол наблюдения, d – расстояние между
источниками.
В
точке O наблюдается так называемый
нулевой максимум, т.к. в эту точку волны
от обоих источников приходят в одинаковой
фазе. Для того чтобы интерференционная
картина была отчетливо различима,
необходимо выполнение условия
![]()
.
Тогда из рисунка можно определить, что
![]()
![]()
.
Здесь
xm
расстояние от центра интерференционной
картины до максимума с номером «m».
Следовательно,
![]()
.
Подстановка
значения
дает, что максимум
интенсивности будет
наблюдаться при значениях:
![]()
.
Величина xm
также определяет расстояние от «0»
максимума до максимума с номером «m».
Координаты
минимума
интенсивности определяются
из условия:
![]()
,
где m=0,1,2,…
Назовем расстояние
между двумя соседними максимумами
интенсивности расстоянием
между интерференционными полосами,
а расстояние между соседними минимумами
интенсивности
шириной
интерференционной полосы.
Видно, что расстояние между полосами и
ширина полосы имеют одинаковое значение,
равное
![]()
.
Данное значение легко можно получить,
если посчитать расстояние между двумя
соседними максимума или минимумами.
Рекомендуется расчет провести студентам
самостоятельно. Из приведенного выражения
следует, что для получения отчетливой
интерференционной картины необходимо,
чтобы выполнялось условие
,
о чем и говорилось выше.
Ширина
интерференционных полос и расстояние
между ними зависят от длины волны .
Только в центре картины при x=0, совпадут
максимумы всех длин волн. Если в установке
Юнга источник испускает белый цвет, то
только нулевой (главный) максимум
окажется белым (здесь совпадут максимумы
всех длин волн), все остальные максимумы
будут окрашены. По мере удаления от
центра максимумы разных длин волн
(разных цветов) смещаются друг относительно
друга все больше и больше. Это приводит
к смазыванию интерференционной картины
при наблюдении ее в белом цвете. В
монохроматическом свете (монохроматическим
называется свет, которому соответствует
дона определенная длина волны) число
различимых полос интерференции заметно
возрастает.
Измерив
расстояние между полосами x
и зная значения L и d, можно вычислить .
Именно из опытов по интерференции света
были впервые определены длины волн для
световых лучей разного цвета.
Оранжево-красному участку спектра
соответствуют более длинные волны
(к=780-600нм),
а сине-фиолетовому – более короткие
(ф=480-420нм).
.52.4. Интерференция в тонких пленках.
Наиболее типичным
и распространенным примером интерференции
света в природе является интерференция
в тонких пленках (мыльные пузыри, радужная
пленка нефти на воде и т.д.).
Пусть на прозрачную
тонкую пластинку толщиной d падает
плоская световая волна под углом
(рис.7). Разность хода, приобретенная
лучами 1 и 2 до того, как они сойдутся в
точке С будет равна:
![]()

Рис.
7
,
где
S1=ВС;
S2=АО+ОС.
Но
АО=ОС=d/cos,
поэтому S2=2d/cos.
В
свою очередь ВС=АСsin,
а АС=2АД=2dtg,
поэтому S1=2dtgsin.
Воспользовавшись
приведенными равенствами и соотношением
![]()
,
получим, что

Для
получения окончательной разности хода
необходимо учесть, что световые волны,
как и всякие другие волны, отражаясь от
оптически более
плотной
среды (луч 1 в точке С) получают
дополнительную разность фаз равную ,
т.е. возникает добавочная разность хода
равная /2.
При отражении от среды оптически менее
плотной (точка О) скачка фазы не происходит.
Таким
образом, при падении на пластинку плоской
волны образуются две отраженные волны,
разность хода которых определяется
формулой:
![]()
В
предположении, что лучи 1 и 2 когерентны,
в результате падения на плоскопараллельную
пленку пучка лучей в отраженном и
проходящем свете на экране получаются
чередующиеся темные и светлые полосы
в случае монохроматического света и
цветные полосы в случае белого света.
ДОПОЛНЕНИЕ 1.
Строго
говоря, лучи 1 и 2 (или две плоские
отраженные волны, распространяющиеся
в одном направлении) смогут интерферировать,
если будут соблюдены условия временной
и пространственной когерентности.
Вспомним, что
когерентностью называется согласованное
протекание нескольких колебательных
или волновых процессов. Степень
согласованности может быть различной.
Соответственно можно ввести понятие
степени
когерентности
двух волн.
Различают
временную и пространственную когерентность.
Понятие когерентности является
относительным: две волны могут вести
себя как когерентные при наблюдении с
одним прибором (с малой инерционностью)
и как некогерентные при наблюдении с
другим прибором (с большой инерционностью).
Для характеристики когерентных свойств
волн вводится время
когерентности
tког.,
которое определяет такое время, за
которое случайное изменение фазы
достигает значения ~.
За время tког.
колебание как бы забывает свою
первоначальную фазу и становится
некогерентным по отношению к самому
себе.
Воспользовавшись
понятием когерентности, можно сказать,
что когда tприбора>>tког.,
то прибор не зафиксирует интерференцию.
Если же tприбора<<tког.,
то прибор (глаз, фотопластинка и пр.)
обнаружит четкую интерференционную
картину.
Соответственно,
длиной когерентности называется
расстояние
![]()
,
на которое перемещается волна за время
tког..
Длина когерентности есть то расстояние,
на котором случайное измерение фазы
достигает значения ~.
Для получения интерференционной картины
путем деления естественной волны на
две части необходимо, чтобы оптическая
разность хода была меньше, чем длина
когерентности. Это требование ограничивает
число видимых интерференционных полос.
С увеличением номера полосы “m” разность
хода растет, поэтому четкость полос
делается все хуже и хуже.
При
интерференции немонохроматических
волн время когерентности и длина
когерентности определяются выражениями:
![]()
и

.
Пространственная
когерентность.
П

Рис.
8
усть источник имеет угловые размеры
(рис.8). Если
![]()
,
то можно наблюдать интерференцию. Отсюда
следует, что наибольшее расстояние,
между щелями, при котором можно наблюдать
интерференцию от источника с угловым
размером ,
определяется из условия
![]()
;
Будем
называть длиной пространственной
когерентности или радиусом когерентности
некое расстояние ког.,
при смещении на которое вдоль некой
волновой поверхности случайное изменение
фазы достигает значения ~.

.
Для Солнца, например, ~0,01рад;
~0,5мкм
ког.=0,05мкм.
По мере удаления от источника степень
пространственной когерентности
возрастает.
Вследствие
ограничений, накладываемых временной
и пространственной когерентностями,
интерференция
при освещении тонкой пластинки наблюдается
только в том случае, если толщина
пластинки не
превышает нескольких сотых долей
миллиметра.
При освещении светом с большой степенью
когерентности интерференция наблюдается
и при отражении от более толстых пластинок
и пленок.
Рассмотрим
теперь интерференцию монохроматического5
света при падении на пленку или пластинку
расходящегося пучка лучей (например,
при падении сферической волны).
В
этом случае результаты интерференции
отраженного (и проходящего) света в
различных точках пластинки зависят от
углов падения
лучей. Лучи, падающие под одинаковым
углом 1,
создадут на экране совокупность одинаково
освещенных точек, образующих криволинейную
темную (или светлую) полосу. Каждой из
этих полос соответствует определенное
значение угла .
Поэтому они называются полосами
равного наклона.
При нарушении плоскопараллельности
пленки или пластинки форма полос равного
наклона искажается. Этим используются
при проверке качества шлифовки
плоскопараллельных стеклянных пластин,
причем обнаруживают отклонение от
плоскопараллельности, равное 0,01мкм.
Справка 3.
![]()
–
временная когерентность
Т.к. оптические разности хода для
проходящего и и отраженного света
отличаются на
![]()
,
максимум интерференции в отраженном
свете будет соответствовать минимуму
в проходящем и наоборот.
С
увеличением толщины (d) плоскопараллельной
пластины влияние угла наклона становится
все менее заметным, полосы равного
наклона становятся все ближе и ближе
друг к другу. И при больших толщинах
плоскопараллельных пластин интерференцию
света в них наблюдать не удается.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лабораторная работа № 81
ИЗУЧЕНИЕ ИНТЕРФЕРЕНЦИИ СВЕТА ОТ ДВУХ ЩЕЛЕЙ
Цель
работы:
определение расстояния между щелями с помощью интерференционных полос в опыте
Юнга.
Приборы и
принадлежности: модульный учебный комплекс МУК-0.
- Теоретическое
введение
Интерференция света –
явление, заключающееся в пространственном перераспределении энергии светового
излучения при суперпозиции электромагнитных волн. Необходимое условие
интерференции любых волн – их когерентность – согласованное протекание во
времени и пространстве нескольких колебательных или волновых процессов.
Строго когерентны лишь монохроматические волны – неограниченные в
пространстве волны с постоянными во времени
частотой, амплитудой и начальной фазой. Рассмотрим два точечных когерентных
источника S1 и S2, колебания
которых происходят с одинаковой частотой, а разность фаз колебаний равна нулю
(источники синфазны). Пусть от источника S1 распространяются бегущие волны в среде 1 с показателем преломления n1, а от источника S2 – в среде 2
с показателем преломления n2 (рис.1). На рисунке
линия ОО1 – граница между этими
прозрачными средами.

На границе ОО1 выберем точку Р и определим
условие минимума и максимума амплитуды результирующего колебания в этой точке
пространства. Обозначим ![]() и
и ![]() . Для электромагнитных волн колебания вектора
. Для электромагнитных волн колебания вектора ![]() от двух когерентных
от двух когерентных
источников 1 и 2 определяются выражениями:
![]() и
и ![]() , (1.1)
, (1.1)
![]() – амплитуда
– амплитуда
гармонических колебаний, ![]() – волновое число.
– волновое число.
В точке наблюдения Р происходит
сложение колебаний одинаковой частоты. Будем считать, что эти колебания
происходят вдоль одного направления. Разность фаз колебаний в этой точке
равна
![]() , (1.2.)
, (1.2.)
где ![]() – волновое число;
– волновое число; ![]() – скорость
– скорость
распространения
электромагнитной волны в среде с
показателем преломления ![]()
, с
– скорость этой волны в вакууме.
Так как ![]() ,
,
(1.3.)
где ![]() – волновое число для
– волновое число для
среды с ![]() (вакуум),
(вакуум),
![]()
– длина волны в
среде с ![]() .
.
Тогда разность фаз колебаний
![]() (1.4.)
(1.4.)
определяет результирующее колебание в точке Р.
Величина ![]() – оптический путь,
– оптический путь,
разность этих величин для двух волн ![]() – оптическая
– оптическая
разность хода, а
![]() .
.
(1.5.)
Из условия минимума
при сложении колебаний
![]() , (1.6.)
, (1.6.)
![]() получаем:
получаем:
![]() . (1.7.)
. (1.7.)
Условие максимума: ![]() (колебания
(колебания
происходят в одной фазе) и
![]() . (1.8)
. (1.8)
Можно утверждать, что при
сложении колебаний в любой точке пространства результирующее колебание
определяется величиной оптической разности хода волн.
- Описание рабочей
установки и метода измерений
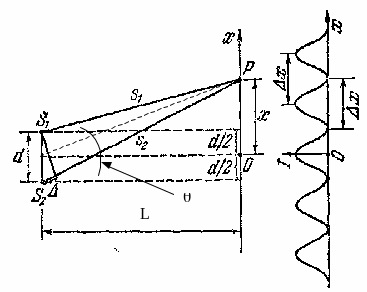
Рассмотрим
монохроматическую световую волну (длина волны в вакууме ![]() ) с плоским фронтом, падающую на непрозрачный экран с двумя
) с плоским фронтом, падающую на непрозрачный экран с двумя
узкими щелями (оптическая схема близка к схеме опыта Юнга). Пусть экран, где
расположены узкие щели, может поворачиваться относительно точки О – середины
расстояния d между источниками ![]() и
и ![]() (рис. 2) на
(рис. 2) на
некоторый угол ![]() . В условиях эксперимента
. В условиях эксперимента
![]() , где а – ширина
, где а – ширина
щели.
Можно показать, что
распространение волн от щелей одинакового размера а при
![]() в плоскопараллельных
в плоскопараллельных
пучках света происходит таким же образом, как и от двух точечных источников.
Теорию таких двух источников мы и рассмотрим ниже.
Экран наблюдения (лист
бумаги или миллиметровки) располагается на расстоянии ОА=L, отсчитываемом от точки О; х – координата точки наблюдения
Р равна АР.
Оптическая разность хода
лучей 1 и 2 от плоского фронта до щелей равна ![]() , а оптическая разность хода лучей 1 и 2 после прохождения
, а оптическая разность хода лучей 1 и 2 после прохождения
щелей ![]() и
и ![]() равна
равна ![]()
![]() . На экран Э лучи 1 и 2 приходят с
. На экран Э лучи 1 и 2 приходят с
разностью хода ![]() (2.1)
(2.1)
Рассчитаем ![]() . Из прямоугольных треугольников
. Из прямоугольных треугольников ![]() и
и ![]() :
:
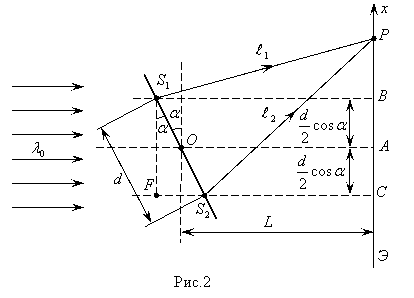
![]() ;
;
(2.2)
![]() ;
;
(2.3)
![]() ; (2.4)
; (2.4)
При условии ![]() <<L
<<L ![]() и
и ![]() . Учтем, что
. Учтем, что ![]()
![]() (2.5)
(2.5)
или ![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
Из условия максимума для
интерферирующих лучей 1 и 2 ![]() , где
, где ![]() тогда
тогда ![]() и координаты
и координаты
точек экрана с максимальной
интенсивностью света можно рассчитать по формуле
![]() , (2.8)
, (2.8)
расстояние между соседними максимумами
![]() .
.
(2.9)
Измеряя ![]() между серединами ярких полос, можно определить
между серединами ярких полос, можно определить
![]() , (2.10)
, (2.10)
где ![]() – расстояние до экрана для каждого значения
– расстояние до экрана для каждого значения ![]() .
.
Работа выполняется на
установке МУК – 0, внешний вид которой изображен на рис. 3,

где 1 – устройство с полупроводниковым лазерным
осветителем;
2 – турель, на которой смонтированы объекты
исследования для лабораторных работ по интерференции и дифракции;
3 – диафрагма;
4 – поляризатор, закрепленный на турели во
вращающейся обойме со стрелкой – указателем и транспортиром;
5 – турель с объектом исследования, используемый в работах по поляризации света;
6 – стойка;
7 – устройство, содержащее поворотную стеклянную
пластинку, использующуюся в опытах по изучению закона Брюстера;
8 – основание оптического блока.
- Порядок выполнения работы и обработка результатов измерений
- Тумблером «сеть» включите лазерный монохроматический источник
света ( мкм), что соответствует красному видимому свету.
мкм), что соответствует красному видимому свету. - Положите лист белой или миллиметровой бумаги на основание оптического блока (8).
- Поверните турель 2 и установите исследуемый объект – две щели в
положение, перпендикулярное направлению светового пучка. - С помощью ручки 3 установите стрелку, закрепленную на оси
вращения пластинки с двумя щелями, на угол 00. - На бумаге должна появиться дифракционная картина – ряд
чередующихся красных полосок (см. рис.4)

- Зарисуйте дифракционную картину.
- Для угла поворота
 по своему
по своему
рисунку измерьте расстояние между серединами интерференционных
максимумов (см. рис). Результаты запишите в таблицу.
(см. рис). Результаты запишите в таблицу. - По формуле
 определите
определите
расстояние между щелями (при d<<L и можно считать
можно считать  мм). Численное значение L указано на передней панели установки.
мм). Численное значение L указано на передней панели установки. - Опыт повторите для угла поворота
 . Пронаблюдайте изменение дифракционной картины,
. Пронаблюдайте изменение дифракционной картины,
зарисуйте ее и рассчитайте d. - Результаты измерений и вычислений занесите в таблицу.
Таблица
|
№ |
|
L, мм |
мм |
мкм |
d, мкм |
<d>, мкм |
|
1. 2. |
00 |
465 |
0,65 |
|||
|
1. 2. |
600 |
465 |
0,65 |
- Рассчитайте погрешность измерения d дифференциальным методом.
- Вопросы для допуска
к работе
- Сформулируйте цель работы.
- Объясните сущность интерференции света.
- Схема установки и порядок выполнения работы.
5.
Вопросы для защиты работы
- Какими условиями определяется когерентность волн?
- Роль когерентности волн при интерференции.
- Оптическая длина пути и оптическая разность хода.
- Выведите связь между разностью фаз интерферирующих лучей и
оптической разностью хода. - Условия максимумов и минимумов при интерференции волн.
- Вывод рабочей формулы.
Литература
- И.В. Савельев. Курс общей физики. – М.: Наука, 1988. – т.2
- Б.М. Яворский, А.А. Детлаф. Курс
физики. – М.: Высшая школа, 1982. – т.3
Главная
»
Самолетостроение
»
Физика (3 семестр)
»
Опыт Юнга. Расчет интерференционной картины от двухисточников. Расстояние между полосами.
Опыт Юнга. Расчет интерференционной картины от двухисточников. Расстояние между полосами.
Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S1 и S2 (рис. 3.7.3). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
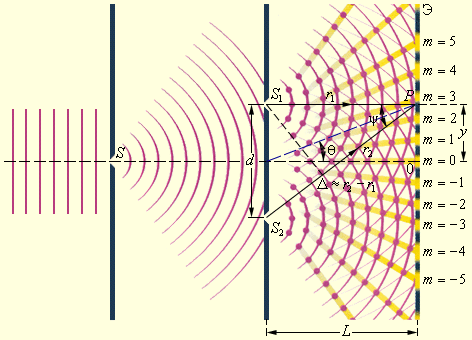 |
| Рисунок 3.7.3.
Схема интерференционного опыта Юнга |
Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S1 и S2, которые в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн, освещались светом одного источника S. При симметричном расположении щелей вторичные волны, испускаемые источниками S1 и S2, находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r1и r2. Следовательно, фазы колебаний, создаваемых волнами от источников S1 и S2 в точке P, вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S1 и S2распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции.
Монохроматическая (или синусоидальная) волна, распространяющаяся в направлении радиус-вектора 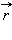 , записывается в виде
, записывается в виде
где a – амплитуда волны, k = 2π / λ – волновое число, λ – длина волны, ω = 2πν – круговая частота. В оптических задачах под E следует понимать модуль вектора напряженности электрического поля волны. При сложении двух волн в точке P результирующее колебание также происходит на частоте ω и имеет некоторую амплитуду A и фазу φ:
E = a1 · cos (ωt – kr1) + a2 · cos (ωt – kr2) = A · cos (ωt – φ).
Приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существует; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A2.
Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P:
|
|
(*) |
где Δ = r2 – r1 – так называемая разность хода.
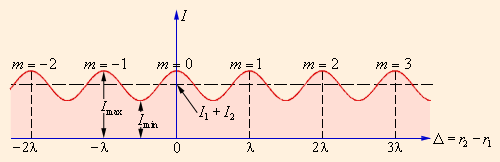
Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = mλ (m = 0, ±1, ±2, …). При этом Imax = (a1 + a2)2 > I1 + I2. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивностиImin = (a1 – a2)2 < I1 + I2. На рис. 3.7.4 показано распределение интенсивности света в интерференционной картине в зависимости от разности хода Δ.
 |
| Рисунок 3.7.4.
Распределение интенсивности в интерференционной картине. Целое число m – порядок интерференционного максимума |
В частности, если I1 = I2 = I0, т. е. интенсивности обеих интерферирующих волн одинаковы, выражение (*) приобретает вид:
В этом случае Imax = 4I0, Imin = 0.
Формулы (*) и (**) являются универсальными. Они применимы к любой интерференционной схеме, в которой происходит сложение двух монохроматических волн одной и той же частоты.
Если в схеме Юнга через y обозначить смещение точки наблюдения от плоскости симметрии, то для случая, когда d << L и y << L (в оптических экспериментах эти условия обычно выполняются), можно приближенно получить:
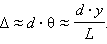
При смещении вдоль координатной оси y на расстояние, равное ширине интерференционной полосы Δl, т. е. при смещении из одного интерференционного максимума в соседний, разность хода Δ изменяется на одну длину волны λ. Следовательно,
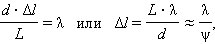
где ψ – угол схождения «лучей» в точке наблюдения P. Выполним количественную оценку. Допустим, что расстояние d между щелями S1 и S2 равно 1 мм, а расстояние от щелей до экрана Э составляет L = 1 м, тогда ψ = d / L = 0,001 рад. Для зеленого света (λ = 500 нм) получим Δl = λ / ψ = 5 · 105 нм = 0,5 мм. Для красного света (λ = 600 нм) Δl = 0,6 мм. Таким путем Юнг впервые измерил длины световых волн, хотя точность этих измерений была невелика.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
Предположим, что если установить две лампочки, то можно было бы наблюдать какую-нибудь цветную интерференционную картину. Это происходит из-за того, что фазы световых волн, создаваемых лампочками, случайны и не согласованы.
Когерентными источниками называют такие источники волн, частоты которых одинаковы и разность фаз между ними постоянна во времени. Этих двух условий хватит для того, чтобы источники могли создавать устойчивую интерференционную картину.
Если эти источники когерентны и излучают синфазно, то в точке, в которой измеряется амплитуда, их разность фаз будет:
(Delta varphi=k Delta L=k(L_2 n_2-L_1 n_1).) ((1))
Если рассматривать интерференционную картину в общем случае, то максимумы её будут в тех точках, где волны приходят синфазно, то есть разность хода равна целому числу длин волн:
(boxed{Delta L=nlambda,; n in Z}). ((2))
Минимумы будут наблюдаться в точках, в которых волны приходят в противофазе, то есть:
(boxed{Delta L=left(n+frac{1}{2}right) lambda,; n in Z}). ((3))
Когерентности разных световых волн можно достичь разными методами.
Метод Юнга
Свет от источника света (S) проходит через две узкие щели (S_1) и (S_2), расположенные на расстоянии (d), на расстоянии (L) от них находится экран. Щели (S_1) и (S_2) являются когерентными источниками, поэтому на экране наблюдается интерференционная картина (рис. (1)).

Рис. (1). Опыт Юнга
Оптическая разность хода (Delta=r_2-r_1) (рис. (1)):
(Delta=frac{xa}{L}), ((4))
где (a) — расстояние между щелями (S_1) и (S_2),
(L) — расстояние от щели ((S_1) или (S_2)) до экрана,
(x) — координата минимума (или максимума) интенсивности в конкретной точке экрана.
Условия максимумов и минимумов определяются так:
(boxed{x_{max}=frac{lambda L}{d} cdot m,; m in Z}), ((5))
(boxed{x_{min}=frac{lambda L}{d} cdot left(m+frac{1}{2}right),; m in Z}). ((6))
Ноль на оси абсцисс выбирается по главному максимуму. Вследствие зеркальной симметрии эксперимента относительно горизонтальной плоскости ((I(x)=I(-x))) в формулах ((5)) и ((6)) есть знак плюс-минус.
Два плоских зеркала расположены под углом, близким к развёрнутому. На них светит источник (S). В итоге на экран светит свет от двух мнимых источников (S_1) и (S_2) (изображения источника (S) в зеркалах), из-за чего на экране наблюдается интерференционная картина.
Бипризма Френеля
Точно также работает бипризма Френеля, только вместо зеркал два мнимых изображения источника создаются призмой.
Источники:
Рис. 1. Опыт Юнга. © ЯКласс.