Рис.
6
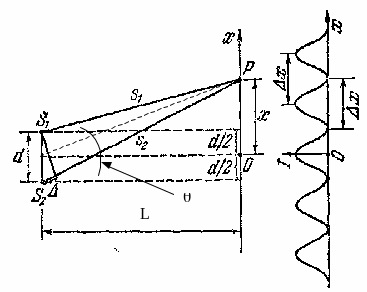
Сделаем рисунок. Здесь (рис.6) приняты
обозначения: L – расстояние от источников
до экрана,
– угол наблюдения, d – расстояние между
источниками.
В
точке O наблюдается так называемый
нулевой максимум, т.к. в эту точку волны
от обоих источников приходят в одинаковой
фазе. Для того чтобы интерференционная
картина была отчетливо различима,
необходимо выполнение условия
![]()
.
Тогда из рисунка можно определить, что
![]()
![]()
.
Здесь
xm
расстояние от центра интерференционной
картины до максимума с номером «m».
Следовательно,
![]()
.
Подстановка
значения
дает, что максимум
интенсивности будет
наблюдаться при значениях:
![]()
.
Величина xm
также определяет расстояние от «0»
максимума до максимума с номером «m».
Координаты
минимума
интенсивности определяются
из условия:
![]()
,
где m=0,1,2,…
Назовем расстояние
между двумя соседними максимумами
интенсивности расстоянием
между интерференционными полосами,
а расстояние между соседними минимумами
интенсивности
шириной
интерференционной полосы.
Видно, что расстояние между полосами и
ширина полосы имеют одинаковое значение,
равное
![]()
.
Данное значение легко можно получить,
если посчитать расстояние между двумя
соседними максимума или минимумами.
Рекомендуется расчет провести студентам
самостоятельно. Из приведенного выражения
следует, что для получения отчетливой
интерференционной картины необходимо,
чтобы выполнялось условие
,
о чем и говорилось выше.
Ширина
интерференционных полос и расстояние
между ними зависят от длины волны .
Только в центре картины при x=0, совпадут
максимумы всех длин волн. Если в установке
Юнга источник испускает белый цвет, то
только нулевой (главный) максимум
окажется белым (здесь совпадут максимумы
всех длин волн), все остальные максимумы
будут окрашены. По мере удаления от
центра максимумы разных длин волн
(разных цветов) смещаются друг относительно
друга все больше и больше. Это приводит
к смазыванию интерференционной картины
при наблюдении ее в белом цвете. В
монохроматическом свете (монохроматическим
называется свет, которому соответствует
дона определенная длина волны) число
различимых полос интерференции заметно
возрастает.
Измерив
расстояние между полосами x
и зная значения L и d, можно вычислить .
Именно из опытов по интерференции света
были впервые определены длины волн для
световых лучей разного цвета.
Оранжево-красному участку спектра
соответствуют более длинные волны
(к=780-600нм),
а сине-фиолетовому – более короткие
(ф=480-420нм).
.52.4. Интерференция в тонких пленках.
Наиболее типичным
и распространенным примером интерференции
света в природе является интерференция
в тонких пленках (мыльные пузыри, радужная
пленка нефти на воде и т.д.).
Пусть на прозрачную
тонкую пластинку толщиной d падает
плоская световая волна под углом
(рис.7). Разность хода, приобретенная
лучами 1 и 2 до того, как они сойдутся в
точке С будет равна:
![]()

Рис.
7
,
где
S1=ВС;
S2=АО+ОС.
Но
АО=ОС=d/cos,
поэтому S2=2d/cos.
В
свою очередь ВС=АСsin,
а АС=2АД=2dtg,
поэтому S1=2dtgsin.
Воспользовавшись
приведенными равенствами и соотношением
![]()
,
получим, что

Для
получения окончательной разности хода
необходимо учесть, что световые волны,
как и всякие другие волны, отражаясь от
оптически более
плотной
среды (луч 1 в точке С) получают
дополнительную разность фаз равную ,
т.е. возникает добавочная разность хода
равная /2.
При отражении от среды оптически менее
плотной (точка О) скачка фазы не происходит.
Таким
образом, при падении на пластинку плоской
волны образуются две отраженные волны,
разность хода которых определяется
формулой:
![]()
В
предположении, что лучи 1 и 2 когерентны,
в результате падения на плоскопараллельную
пленку пучка лучей в отраженном и
проходящем свете на экране получаются
чередующиеся темные и светлые полосы
в случае монохроматического света и
цветные полосы в случае белого света.
ДОПОЛНЕНИЕ 1.
Строго
говоря, лучи 1 и 2 (или две плоские
отраженные волны, распространяющиеся
в одном направлении) смогут интерферировать,
если будут соблюдены условия временной
и пространственной когерентности.
Вспомним, что
когерентностью называется согласованное
протекание нескольких колебательных
или волновых процессов. Степень
согласованности может быть различной.
Соответственно можно ввести понятие
степени
когерентности
двух волн.
Различают
временную и пространственную когерентность.
Понятие когерентности является
относительным: две волны могут вести
себя как когерентные при наблюдении с
одним прибором (с малой инерционностью)
и как некогерентные при наблюдении с
другим прибором (с большой инерционностью).
Для характеристики когерентных свойств
волн вводится время
когерентности
tког.,
которое определяет такое время, за
которое случайное изменение фазы
достигает значения ~.
За время tког.
колебание как бы забывает свою
первоначальную фазу и становится
некогерентным по отношению к самому
себе.
Воспользовавшись
понятием когерентности, можно сказать,
что когда tприбора>>tког.,
то прибор не зафиксирует интерференцию.
Если же tприбора<<tког.,
то прибор (глаз, фотопластинка и пр.)
обнаружит четкую интерференционную
картину.
Соответственно,
длиной когерентности называется
расстояние
![]()
,
на которое перемещается волна за время
tког..
Длина когерентности есть то расстояние,
на котором случайное измерение фазы
достигает значения ~.
Для получения интерференционной картины
путем деления естественной волны на
две части необходимо, чтобы оптическая
разность хода была меньше, чем длина
когерентности. Это требование ограничивает
число видимых интерференционных полос.
С увеличением номера полосы “m” разность
хода растет, поэтому четкость полос
делается все хуже и хуже.
При
интерференции немонохроматических
волн время когерентности и длина
когерентности определяются выражениями:
![]()
и

.
Пространственная
когерентность.
П

Рис.
8
усть источник имеет угловые размеры
(рис.8). Если
![]()
,
то можно наблюдать интерференцию. Отсюда
следует, что наибольшее расстояние,
между щелями, при котором можно наблюдать
интерференцию от источника с угловым
размером ,
определяется из условия
![]()
;
Будем
называть длиной пространственной
когерентности или радиусом когерентности
некое расстояние ког.,
при смещении на которое вдоль некой
волновой поверхности случайное изменение
фазы достигает значения ~.

.
Для Солнца, например, ~0,01рад;
~0,5мкм
ког.=0,05мкм.
По мере удаления от источника степень
пространственной когерентности
возрастает.
Вследствие
ограничений, накладываемых временной
и пространственной когерентностями,
интерференция
при освещении тонкой пластинки наблюдается
только в том случае, если толщина
пластинки не
превышает нескольких сотых долей
миллиметра.
При освещении светом с большой степенью
когерентности интерференция наблюдается
и при отражении от более толстых пластинок
и пленок.
Рассмотрим
теперь интерференцию монохроматического5
света при падении на пленку или пластинку
расходящегося пучка лучей (например,
при падении сферической волны).
В
этом случае результаты интерференции
отраженного (и проходящего) света в
различных точках пластинки зависят от
углов падения
лучей. Лучи, падающие под одинаковым
углом 1,
создадут на экране совокупность одинаково
освещенных точек, образующих криволинейную
темную (или светлую) полосу. Каждой из
этих полос соответствует определенное
значение угла .
Поэтому они называются полосами
равного наклона.
При нарушении плоскопараллельности
пленки или пластинки форма полос равного
наклона искажается. Этим используются
при проверке качества шлифовки
плоскопараллельных стеклянных пластин,
причем обнаруживают отклонение от
плоскопараллельности, равное 0,01мкм.
Справка 3.
![]()
–
временная когерентность
Т.к. оптические разности хода для
проходящего и и отраженного света
отличаются на
![]()
,
максимум интерференции в отраженном
свете будет соответствовать минимуму
в проходящем и наоборот.
С
увеличением толщины (d) плоскопараллельной
пластины влияние угла наклона становится
все менее заметным, полосы равного
наклона становятся все ближе и ближе
друг к другу. И при больших толщинах
плоскопараллельных пластин интерференцию
света в них наблюдать не удается.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Интерференция света:
Фаза — аргумент периодической функции, определяющий значение физической величины в любой момент времени t. Она определяет состояние колебательной системы (координаты, скорости, ускорения) в любой момент времени при заданной амплитуде. Монохроматической волной называется электромагнитное излучение постоянной частоты.
Рассмотрим процесс наложения волн длиной 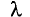
Монохроматические волны одной и той же частоты, приходящие от этих источников в некоторую точку пространства Р, возбуждают в ней гармонические колебания той же частоты.
В силу этого, разность фаз колебаний, возбуждаемых рассматриваемыми источниками в точке Р, остается постоянной с течением времени, даже если начальные фазы этих колебаний различны.
Волны называются когерентными, если разность фаз колебаний, возбуждаемых ими, не изменяется с течением времени. Соответственно, свойство, характеризующее согласованность протекания в пространстве и времени нескольких колебательных или волновых процессов, называется когерентностью (от латинского слова cohaerens — связанный, сцепленный).
Опыт показывает, что амплитуда результирующего колебания в точке Р, создаваемого двумя одинаковыми источниками, зависит от геометрической разности хода волн до рассматриваемой точки:

Если разность хода волн  равна целому числу длин волн
равна целому числу длин волн 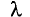 (четному числу полуволн
(четному числу полуволн 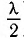 ) то волны приходят в точку Р (см. рис. 33) синфазно и усиливают друг друга. В этом случае говорят о выполнении условия максимума:
) то волны приходят в точку Р (см. рис. 33) синфазно и усиливают друг друга. В этом случае говорят о выполнении условия максимума:
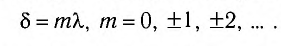
Действительно, разность фаз колебаний в рассматриваемой точке в этом случае
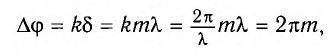
т. е. кратна 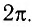 .
.
В случае, когда разность хода волн равна нечетному числу полуволн, волны приходят в точку Р в противофазе и ослабляют друг друга. Это соответствует выполнению условия минимума:
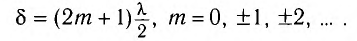
Убедитесь самостоятельно, что разность фаз колебаний в этом случае
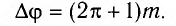
Таким образом, в результате сложения колебаний, возбуждаемых когерентными волнами на поверхности воды, образуется устойчивая картина распределения минимумов и максимумов результирующего колебания (рис. 34). Это означает, что когерентные волны интерферируют друг с другом.

Интерференция (от латинских слов inter — взаимно, между собой и fеrio — ударяю, поражаю) — явление сложения двух или более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующихся максимумов и минимумов амплитуд результирующего колебания.
Пространственная картина устойчивого во времени распределения амплитуд результирующего колебания при интерференции называется интерференционной картиной.
Вследствие того, что энергия волны пропорциональна квадрату амплитуды, энергия результирующего колебания в общем случае не равна сумме энергий складываемых колебаний, так как 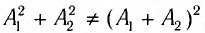 . Так, в точках максимума результирующая амплитуда колебаний возрастает в два раза, а энергия, соответственно, в четыре. Однако не будем забывать, что в точках минимума колебания отсутствуют вовсе. Таким образом, явление интерференции приводит к перераспределению энергии в пространстве, причем суммарная энергия колебаний во всех точках среды при этом остается равной сумме энергий интерферирующих волн.
. Так, в точках максимума результирующая амплитуда колебаний возрастает в два раза, а энергия, соответственно, в четыре. Однако не будем забывать, что в точках минимума колебания отсутствуют вовсе. Таким образом, явление интерференции приводит к перераспределению энергии в пространстве, причем суммарная энергия колебаний во всех точках среды при этом остается равной сумме энергий интерферирующих волн.
Отметим, что если бы в точке Р складывались две некогерентные волны с одинаковыми амплитудами, то энергия результирующего колебания была бы равна сумме энергий отдельных волн, независимо от положения точки Р относительно источника. Это означало бы просто удвоение энергии, принесенной одной из волн в данную точку.
Закономерности интерференции волн носят универсальный характер, т. е. справедливы для волн любой природы.
При рассмотрении интерференции света (электромагнитных волн) следует учесть, что длина волны света в веществе изменяется в зависимости от показателя преломления вещества. Это эквивалентно замене геометрической разности хода на оптическую разность хода
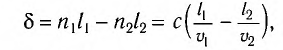
т. е. разность расстояний, пройденных волнами, с учетом различных скоростей 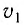 и
и 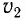 их распространения в средах с показателями преломления
их распространения в средах с показателями преломления 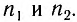
В вакууме (с = 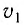 =
=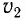 ) оптическая разность хода совпадает с геометрической. При оптической разности хода, кратной четному числу полуволн (целому числу длин волн), наблюдается максимум интерференции света, а при оптической разности хода, кратной нечетному числу полуволн, — минимум.
) оптическая разность хода совпадает с геометрической. При оптической разности хода, кратной четному числу полуволн (целому числу длин волн), наблюдается максимум интерференции света, а при оптической разности хода, кратной нечетному числу полуволн, — минимум.
Распространенные бытовые источники света (лампы накаливания, лампы дневного света, свечи и т. д.) не являются когерентными, т. е. не позволяют наблюдать явление интерференции.
Изобретение и распространение когерентных источников излучения — лазеров — сделало демонстрацию явления интерференции достаточно простой.
Для получения интерференционной картины при отсутствии лазеров пользуются классической интерференционной схемой (схемой Юнга), где пучок света разделяется на два пучка с помощью отверстий В и С в ширме (рис. 35). Поскольку эти пучки созданы одним и тем же источником, они являются когерентными. На экране в области DE наблюдается интерференционная картина.
Классический эксперимент по наблюдению интерференции Томас Юнг провел в 1801 г. Это позволило измерить длину световой волны и убедительно подтвердить волновую природу света.
Рассмотрим еще один распространенный случай интерференции — сложение волн с одинаковыми частотами, распространяющихся в противоположных направлениях (например, падающей и отраженной волны), приводящее к образованию в пространстве устойчивой картины чередования максимумов амплитуды колебаний (пучностей) и минимумов (узлов).
Волна, возникающая в результате сложения двух волн одинаковой частоты, распространяющихся в противоположных направлениях, называется стоячей волной (рис. 36).
Пример решения задачи:
Рассчитайте положения максимумов и минимумов интерференционной картины на экране MN, находящемся на расстоянии L = АО = 2,0 м от двух одинаковых когерентных источников света 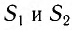 , которые расположены в вакууме на расстоянии
, которые расположены в вакууме на расстоянии 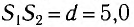 мм друг от друга (рис. 37). Длина волны излучения источников
мм друг от друга (рис. 37). Длина волны излучения источников 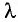 = 600 нм. Найдите расстояние
= 600 нм. Найдите расстояние 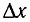 между соседними максимумами.
между соседними максимумами.
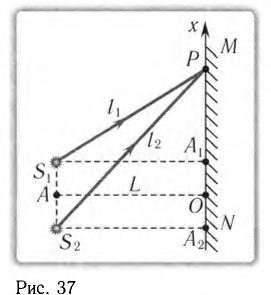
Решение
До некоторой точки Р на экране волны проходят пути 
Максимумы интенсивности будут наблюдаться при условии
а минимумы при условии – 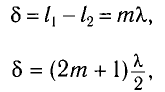
где m = 0, ±1, ±2…..
По теореме Пифагора из треугольников 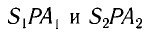 находим
находим
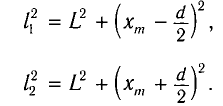
Откуда
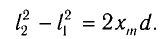
С учетом того, что 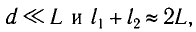 находим
находим
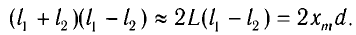
С учетом условия максимумов получаем
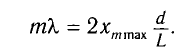
Откуда расстояние от центра экрана до т-й светлой полосы находится из соотношения
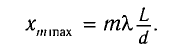
Из условия минимумов находим положение темных полос:
Откуда 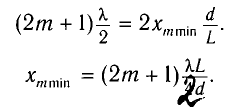
Расстояние между соседними максимумами 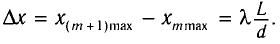
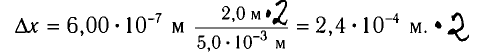
Из полученной формулы видно, что ширина интерференционных полос увеличивается при уменьшении расстояния d между когерентными источниками.
Ответ: 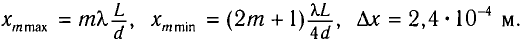
Волновая природа света и дисперсия света
Показатель преломления среды относительно вакуума называется абсолютным показателем преломления этой среды. Абсолютный показатель преломления среды показывает, во сколько раз скорость света в этой среде меньше скорости света в вакууме:
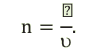
Луч света, падающий на боковую грань треугольной призмы, отклоняется к основанию призмы.
Природа света
Несколько веков имели место два разных представления о природе света: корпускулярная и волновая природа света.
Основоположником представлений о корпускулярной природе света является И. Ньютон. Он считал, что свет является потоком частиц (корпускул). Прямолинейное распространение света и его отражение легко объяснялись согласно этому представлению.
Основоположником представлений о волновой природе света является голландский ученый Христиан Гюйгенс (1629-1695). Основной причиной возникновения этих представлений является прохождение световых лучей сквозь друг друга при распространении подобно волнам. В XIX веке английский ученый Томас Юнг (1773-1829) провел эксперименты, в которых обнаружил многочисленные факты, подтверждающие волновую природу света. Основоположник теории электромагнитного поля Дж. Максвелл теоретически обосновал электромагнитную волновую природу света. Согласно современным представлениям свет и другие электромагнитные волны обладают двойной – корпускулярной и волновой природой.
- Заказать решение задач по физике
Дисперсия света
Одним из явлений, доказывающих волновую природу света, является дисперсия света.
Дисперсия света — это зависимость показателя преломления среды от частоты (длины волны) падающего света.
Впервые это явление исследовал Исаак Ньютон. Он поместил прозрачную стеклянную треугольную призму на пути тонкого пучка солнечного света, попадающего в затемненную комнату через маленькое отверстие в ставнях. Пройдя призму, солнечный луч разделился на спектр из семи составных цветных лучей. Последовательность цветов составных частей в дисперсионном спектре всегда одинакова: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.
Среди монохроматических (содержащих свет одного цвета) лучей наиболее сильно преломляются фиолетовые лучи, а меньше других – красные (см: а). Причина явления объясняется на основе волновых представлений о свете. Так, абсолютный показатель преломления среды показывает, во сколько раз скорость света в этой среде меньше, чем в вакууме:

Здесь 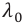 – длина световой волны в вакууме.
– длина световой волны в вакууме. 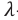 – длина световой волны в среде. Значит, подвергающийся наименьшему преломлению красный свет имеет наименьший показатель преломления. А это означает, что красный свет обладает наибольшей длиной волны (или наименьшей частотой). Фиолетовый свет, наоборот, обладает наибольшим показателем преломления и наименьшей длиной волны (или наибольшей частотой). Из проведенных в дальнейшем экспериментов было определено, что дисперсионный спектр видимого света охватывает в шкале электромагнитных волн часть с длинами волн от
– длина световой волны в среде. Значит, подвергающийся наименьшему преломлению красный свет имеет наименьший показатель преломления. А это означает, что красный свет обладает наибольшей длиной волны (или наименьшей частотой). Фиолетовый свет, наоборот, обладает наибольшим показателем преломления и наименьшей длиной волны (или наибольшей частотой). Из проведенных в дальнейшем экспериментов было определено, что дисперсионный спектр видимого света охватывает в шкале электромагнитных волн часть с длинами волн от 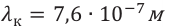 (красный) до
(красный) до 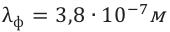 (фиолетовый).
(фиолетовый).
Результат. Таким образом, явление дисперсии показало, что белый свет обладает сложным строением – состоит из монохроматических световых лучей разного цвета. Каждый монохроматический луч света обладает собственной частотой и длиной волны. Поэтому при прохождении монохроматического луча через стеклянную призму он, только преломляясь, изменяет своё направление (не разлагается на составные, не меняет окраски). Если разложенный призмой свет, состоящий из монохроматических составляющих, направить на вторую перевернутую призму, то на выходе из второй призмы опять получится белый свет.
Согласно физике цвета, ни один из трех основных цветов – красный, зеленый и синий, не могут получиться при смешивании двух других. Однако смешиванием основных цветов можно получить все остальные цвета и их оттенки.
Многоцветное восприятие нами окружающего мира объясняется явлениями поглощения, преломления и отражения света. Например, лист бумаги воспринимается нашим зрением белым потому, что он отражает падающий на него белый свет полностью. Если тело полностью поглощает падающий на него свет, то он воспринимается как черный, например, сажа.
Интерференция волн и интерференция света
• Самые часто встречаемые колебания в природе являются колебаниями в связанных системах. В связанных колебательных системах колебания передаются от одного звена системы другой. Например, бросив в воду камень, можно наблюдать распространение концентрических водных кругов из точки падения камня. Нам кажется, что происходит распространение воды в виде выпуклостей и впадин.
Какая связанная система создает волну в воде?
Какие явления происходят в среде при распространении волны?
Обратите внимание на картину, образованную на неподвижной поверхности воды поплавками удочек рыболовов (а). При встрече волн друг с другом происходит их сложение. В результате в определенных точках пространства они усиливают друг друга (а, 1), а в других ослабляют (а, 2).

Интерференция волн
В исследовании вы наблюдали результат сложения когерентных волн, созданных на поверхности воды гармоническими колебаниями шариков генератора с одинаковой частотой.
Когерентные волны — это волны, созданные различными источниками колебания, имеющими одинаковую частоту колебаний и постоянную разность фаз, не зависящую от времени.
Результирующие колебания, образованные сложением когерентных волн, в зависимости от разности между расстояниями от источника колебаний до точки их встречи или усиливаются, или ослабляются – происходит интерференция волн.
Интерференция волн -усиление или ослабление амплитуды колебаний результирующей волны в результате сложения когерентных волн (лат. “интер” взаимно, “ферио” – ударю).
Усиление или ослабление амплитуды результирующей волны определяется условиями максимума и минимума интерференции.
Условие максимума интерференции
Максимум интерференции наблюдается в точках пространства (поверхности), в которых максимумы слагаемых волн накладываются друг на друга. Это зависит от разницы пройденных волнами путей от источника колебаний до этой точки.
Интерференционный максимум результирующей волны образуется в точках, в которых разность хода складываемых волн равна нулю или четному числу полудлин волн (разность фаз равна нулю или четному количеству  ) (d):
) (d):
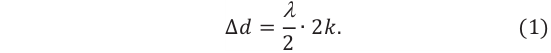
Здесь 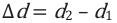 – разность путей, проходимых волнами до точки сложения (разность хода), k– порядок максимума, является целым числом: k= 0,1, 2,…. Между разностью фаз и разностью хода когерентных волн существует такая связь:
– разность путей, проходимых волнами до точки сложения (разность хода), k– порядок максимума, является целым числом: k= 0,1, 2,…. Между разностью фаз и разностью хода когерентных волн существует такая связь:
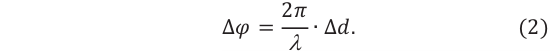
Учитывая выражение (1) в формуле (2), для разницы фаз максимума интерференции получим:
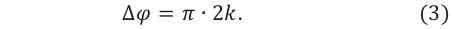
В этом случае при равенстве амплитуд складываемых волн амплитуда результирующего колебания будет равна сумме амплитуд исходных волн (е):
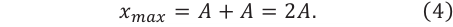
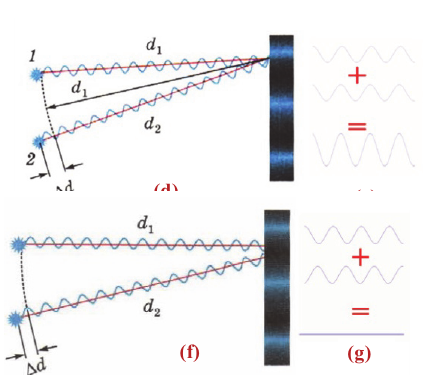
Условие минимума интерференции
Минимумы интерференции наблюдаются в тех точках пространства, в которые волны доходят в противофазе. При этом максимум одной волны совпадает с минимумом другой. В результате волны ослабляют друг друга.
Минимум интерференции наблюдается в точках, в которых разность хода слагаемых волн равна нечетному числу полудлин волн (разность фаз равна нечетному количеству 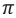 ) (f):
) (f):
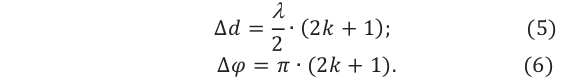
Если при этом амплитуды складываемых волн равны, то в точке минимума интерференции амплитуда результирующей волны уменьшается до нуля (g):
Интерференция света
Интерференция – характерное свойство всех видов волн, в том числе и световых. Так, две световые волны при сложении в пространстве могут усиливать или ослаблять друг друга, даже может случиться и такой вариант: свет + свет = темнота.
Интерференция света – явление увеличения или уменьшения амплитуды результирующих световых колебаний в разных точках пространства вследствие сложения двух когерентных световых волн.
Долгие годы не могли найти способ получения когерентных световых волн, поэтому невозможно было доказать способность световых волн интерферировать.
Только в начале XIX века с помощью несложного устройства Томас Юнг смог наблюдать интерференцию света (h).
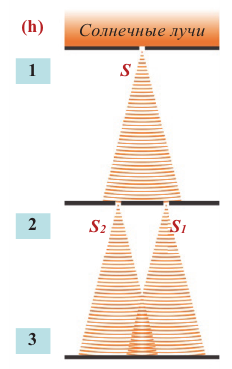

Классический опыт по наблюдению интерференции света состоит в следующем: солнечный свет освещает непрозрачный экран 1 и, пройдя через малое отверстие S в этом экране (проделанное булавкой), попадает на экран 2. Световые лучи, вышедшие из малых отверстий S1 и S2 на втором экране, являются когерентными. В результате интерференции этих волн на экране 3 появляются интерференционные полосы. В центральной части экрана наблюдаются чередующиеся цветные и темные полосы. По мере удаления от центра интерференционная картина ослабевает. Используя условие максимумов в этих опытах, Юнг смог на основе формулы (1) измерить длины световых волн для разных цветов. Как ни странно, первый опыт по интерференции света был проведен отрицающим его волновую природу Исааком Ньютоном. Поместив на стеклянной пластине плоско-выпуклую стеклянную линзу выпуклой стороной вниз, он осветил её сверху (i, 1). Посмотрев на линзу сверху, Ньютон увидел чередующиеся светлые и темные концентрические круги (i, 2), которые впоследствии стали называть кольцами Ньютона. Но ни Ньютон, ни повторявшие этот интересный опыт в течение более чем 100 лет ученые не смогли объяснить причину возникновения этих колец. И только в 1802 году Юнгу удалось объяснить происхождение колец Ньютона. Он объяснил кольца Ньютона таким образом: когда пучок света падает на плоскую поверхность линзы, то он, проходя сквозь нее, частично отражается от нижней сферической поверхности линзы (см. i-З, луч 1), а частично – от поверхности стеклянной пластинки, на которой лежит линза (см. i-З, луч 2). Вследствие такого многократного отражения образуются два когерентных луча. Эти лучи, складываясь, в соответствии с максимумами и минимумами интерференции создают интерференционную картину чередующихся темных и светлых концентрических кольца.
Определение длины световой волны
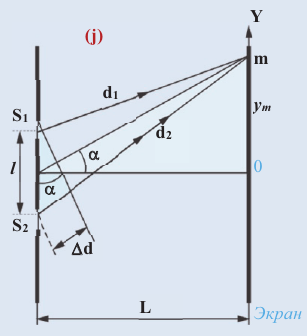
Представим, что расстояние между источниками когерентных волн S1 и S2 намного меньше расстояния от источников до экрана (j): 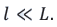 В таком случае световые волны, исходящие из этих источников и дошедшие до точки экрана m с координатой
В таком случае световые волны, исходящие из этих источников и дошедшие до точки экрана m с координатой 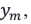 , можно считать параллельными. Разность хода между этими лучами:
, можно считать параллельными. Разность хода между этими лучами:
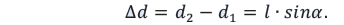
Вследствие малости угла 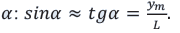
Условие интерференционного максимума в этом случае будет:

Отсюда можно найти длину волны:

- Дифракция света
- Принцип Гюйгенса — Френеля
- Прохождение света через плоскопараллельные пластинки и призмы
- Поляризация света
- Преломление света
- Полное отражение
- Дисперсия света
- Электромагнитная природа света
Интерференция волн.
-
Сложение колебаний.
-
Когерентные источники.
-
Условие максимума и минимума.
-
Интерференционная картина.
-
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: интерференция света.
В предыдущем листке, посвящённом принципу Гюйгенса, мы говорили о том, что общая картина волнового процесса создаётся наложением вторичных волн. Но что это значит – “наложением”? В чём состоит конкретный физический смысл наложения волн? Что вообще происходит, когда в пространстве одновременно распространяются несколько волн? Этим вопросам и посвящён данный листок.
к оглавлению ▴
Сложение колебаний.
Сейчас мы будем рассматривать взаимодействие двух волн. Природа волновых процессов роли не играет – это могут быть механические волны в упругой среде или электромагнитные волны (в частности, свет) в прозрачной среде или в вакууме.
Опыт показывает, что волны складываются друг с другом в следующем смысле.
Принцип суперпозиции. Если две волны накладываются друг на друга в определённой области пространства, то они порождают новый волновой процесс. При этом значение колеблющейся величины в любой точке данной области равно сумме соответствующих колеблющихся величин в каждой из волн по отдельности.
Например, при наложении двух механических волн перемещение частицы упругой среды равно сумме перемещений, создаваемых в отдельности каждой волной. При наложении двух электромагнитных волн напряжённость электрического поля в данной точке равна сумме напряжённостей в каждой волне (и то же самое для индукции магнитного поля).
Разумеется, принцип суперпозиции справедлив не только для двух, но и вообще для любого количества накладывающихся волн. Результирующее колебание в данной точке всегда равно сумме колебаний, создаваемых каждой волной по отдельности.
Мы ограничимся рассмотрением наложения двух волн одинаковой амплитуды и частоты. Этот случай наиболее часто встречается в физике и, в частности, в оптике.
Оказывается, на амплитуду результирующего колебания сильно влияет разность фаз складывающихся колебаний. В зависимости от разности фаз в данной точке пространства две волны могут как усиливать друг друга, так и полностью гасить!
Предположим, например, что в некоторой точке фазы колебаний в накладывающихся волнах совпадают (рис. 1).
 |
| Рис. 1. Волны в фазе: усиление колебаний |
Мы видим, что максимумы красной волны приходятся в точности на максимумы синей волны, минимумы красной волны – на минимумы синей (левая часть рис. 1). Складываясь в фазе, красная и синяя волны усиливают друг друга, порождая колебания удвоенной амплитуды (справа на рис. 1).
Теперь сдвинем синюю синусоиду относительно красной на половину длины волны. Тогда максимумы синей волны будут совпадать с минимумами красной и наоборот – минимумы синей волны совпадут с максимумами красной (рис. 2, слева).
 |
| Рис. 2. Волны в противофазе: гашение колебаний |
Колебания, создаваемые этими волнами, будут происходить, как говорят, в противофазе – разность фаз колебаний станет равна . Результирующее колебание окажется равным нулю, т. е. красная и синяя волны попросту уничтожат друг друга (рис. 2, справа).
к оглавлению ▴
Когерентные источники.
Пусть имеются два точечных источника, создающие волны в окружающем пространстве. Мы полагаем, что эти источники согласованы друг с другом в следующем смысле.
Когерентность. Два источника называются когерентными, если они имеют одинаковую частоту и постоянную, не зависящую от времени разность фаз. Волны, возбуждаемые такими источниками, также называются когерентными.
Итак, рассматриваем два когерентных источника и
. Для простоты считаем, что источники излучают волны одинаковой амплитуды, а разность фаз между источниками равна нулю. В общем, эти источники являются “точными копиями” друг друга (в оптике, например, источник
служит изображением источника
в какой-либо оптической системе).
Наложение волн, излучённых данными источниками, наблюдается в некоторой точке . Вообще говоря, амплитуды этих волн в точке
не будут равны друг другу – ведь, как мы помним, амплитуда сферической волны обратно пропорциональна расстоянию до источника, и при разных расстояниях
и
амплитуды пришедших волн окажутся различными. Но во многих случаях точка
расположена достаточно далеко от источников – на расстоянии гораздо большем, чем расстояние между самими источниками. В такой ситуации различие в расстояниях
и
не приводит к существенному отличию в амплитудах приходящих волн. Следовательно, мы можем считать, что амплитуды волн в точке
также совпадают.
к оглавлению ▴
Условие максимума и минимума.
Однако величина , называемая разностью хода, имеет важнейшее значение. От неё самым решительным образом зависит то, какой результат сложения приходящих волн мы увидим в точке
.
 |
| Рис. 3. Усиление колебаний в точке P |
В ситуации на рис. 3 разность хода равна длине волны . Действительно, на отрезке
укладываются три полных волны, а на отрезке
– четыре (это, конечно, лишь иллюстрация; в оптике, например, длина таких отрезков составляет порядка миллиона длин волн). Легко видеть, что волны в точке
складываются в фазе и создают колебания удвоенной амплитуды – наблюдается, как говорят, интерференционный максимум.
Ясно, что аналогичная ситуация возникнет при разности хода, равной не только длине волны, но и любому целому числу длин волн.
Условие максимума. При наложении когерентных волн колебания в данной точке будут иметь максимальную амплитуду, если разность хода равна целому числу длин волн:
(1)
Теперь посмотрим на рис. 4. На отрезке укладываются две с половиной волны, а на отрезке
-три волны. Разность хода составляет половину длины волны (d=lambda /2[/math]).
 |
| Рис. 4. Гашение колебаний в точке P |
Теперь нетрудно видеть, что волны в точке складываются в противофазе и гасят друг друга – наблюдается интерференционный минимум. То же самое будет, если разность хода окажется равна половине длины волны плюс любое целое число длин волн.
Условие минимума.
Когерентные волны, складываясь, гасят друг друга, если разность хода равна полуцелому числу длин волн:
(2)
Равенство (2) можно переписать следующим образом:
.
Поэтому условие минимума формулируют ещё так: разность хода должна быть равна нечётному числу длин полуволн.
к оглавлению ▴
Интерференционная картина.
А что, если разность хода принимает какое-то иное значение, не равное целому или полуцелому числу длин волн? Тогда волны, приходящие в данную точку, создают в ней колебания с некоторой промежуточной амплитудой, расположенной между нулём и удвоенным значением 2A амплитуды одной волны. Эта промежуточная амплитуда может принимать все значения от 0 до 2A по мере того, как разность хода меняется от полуцелого до целого числа длин волн.
Таким образом, в той области пространства, где происходит наложение волн когерентных источников и
, наблюдается устойчивая интерференционная картина – фиксированное не зависящее от времени распределение амплитуд колебаний. А именно, в каждой точке
данной области амплитуда колебаний принимает своё значение, определяемое разностью хода
приходящих сюда волн, и это значение амплитуды не меняется со временем.
Такая стационарность интерференционной картины обеспечивается когерентностью источников. Если, например, разность фаз источников будет постоянно меняться, то никакой устойчивой интерференционной картины уже не возникнет.
Теперь, наконец, мы можем сказать, что такое интерференция.
Интерференция – это взаимодействие волн, в результате которого возникает устойчивая интерференционная картина, то есть не зависящее от времени распределение амплитуд результирующих колебаний в точках области, где волны накладываются друг на друга.
Если волны, перекрываясь, образуют устойчивую интерференционную картину, то говорят попросту, что волны интерферируют. Как мы выяснили выше, интерферировать могут только когерентные волны. Когда, например, разговаривают два человека, то мы не замечаем вокруг них чередований максимумов и минимумов громкости; интерференции нет, поскольку в данном случае источники некогерентны.
На первый взгляд может показаться, явление интерференции противоречит закону сохранения энергии – например, куда девается энергия, когда волны полностью гасят друг друга? Но никакого нарушения закона сохранения энергии, конечно же, нет: энергия просто перераспределяется между различными участками интерференционной картины. Наибольшее количество энергии концентрируется в интерференционных максимумах, а в точки интерференционных минимумов энергия не поступает совсем.
На рис. 5 показана интерференционная картина, созданная наложением волн двух точечных источников и
. Картина построена в предположении, что область наблюдения интерференции находится достаточно далеко от источников. Пунктиром отмечена ось симметрии интерференционной картины.
 |
| Рис. 5. Интерференция волн двух точечных источников |
Цвета точек интерференционной картины на этом рисунке меняются от чёрного до белого через промежуточные оттенки серого. Чёрный цвет – интерференционные минимумы, белый цвет – интерференционные максимумы; серый цвет – промежуточное значение амплитуды, и чем больше амплитуда в данной точке, тем светлее сама точка.
Обратите внимание на прямую белую полосу, которая идёт вдоль оси симметрии картины. Здесь расположены так называемые центральные максимумы. Действительно, любая точка данной оси равноудалена от источников (разность хода равна нулю), так что в этой точке будет наблюдаться является интерференционный максимум.
Остальные белые полосы и все чёрные полосы слегка искривлены; можно показать, что они являются ветвями гипербол. Однако в области, расположенной на большом расстоянии от источников, кривизна белых и чёрных полос мало заметна, и выглядят эти полосы почти прямыми.
к оглавлению ▴
Интерференционный опыт, изображённый на рис. 5, вместе с соответствующим методом расчёта интерференционной картины называется схемой Юнга. Эта схема лежит в основе знаменитного
опыта Юнга (речь о котором пойдёт в теме Дифракция света). Многие эксперименты по интерференции света так или иначе сводятся к схеме Юнга.
В оптике интерференционную картину обычно наблюдают на экране. Давайте ещё раз посмотрим на рис. 5 и представим себе экран, поставленный перпендикулярно пунктирной оси.
На этом экране мы увидим чередование светлых и тёмных интерференционных полос.
На рис. 6 синусоида показывает распределение освещённости вдоль экрана. В точке O, расположенной на оси симметрии, находится центральный максимум. Первый максимум в верхней части экрана, соседний с центральным, находится в точке A. Выше идут второй, третий (и такдалее) максимумы.
 |
| Рис. 6. Интерференционная картина на экране |
Расстояние , равное расстоянию между любыми двумя соседними максимумами или минимумами, называется шириной интерференционной полосы. Сейчас мы займёмся нахождением этой величины.
Пусть источники находятся на расстоянии друг от друга, а экран расположен на расстоянии
от источников (рис. 7 ). Экран заменён осью
; начало отсчёта
, как и выше, отвечает центральному максимуму.
 |
| Рис. 7. Вычисление координат максимумов |
Точки и
служат проекциями точек
и
на ось
и расположены симметрично относительно точки
. Имеем:
.
Точка наблюдения может находиться на оси
(на экране) где угодно. Координату точки
мы обозначим
. Нас интересует, при каких значениях
в точке
будет наблюдаться интерференционный максимум.
Волна, излучённая источником , проходит расстояние:
. (3)
Теперь вспомним, что расстояние между источниками много меньше расстояния от источников до экрана: . Кроме того, в подобных интерференционных опытах координата
точки наблюдения также гораздо меньше
. Это означает, что второе слагаемое под корнем в выражении (3) много меньше единицы:
.
Раз так, можно использовать приближённую формулу:
(4)
Применяя её к выражению (4), получим:
(5)
Точно так же вычисляем расстояние, которое проходит волна от источника до точки наблюдения:
. (6)
Применяя к выражению (6) приближённую формулу (4), получаем:
. (7)
Вычитая выражения (7) и (5), находим разность хода:
. (8)
Пусть – длина волны, излучаемой источниками. Согласно условию (1), в точке
будет наблюдаться интерференционный максимум, если разность хода равна целому числу длин волн:
Отсюда получаем координаты максимумов в верхней части экрана (в нижней части максимумы идут симметрично):
При получаем, разумеется,
(центральный максимум). Первый максимум рядом с центральным соответствует значению
и имеет координату
.Такой же будет и ширина интерференционной полосы:
.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Интерференция волн.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
07.05.2023
Спрятать решение
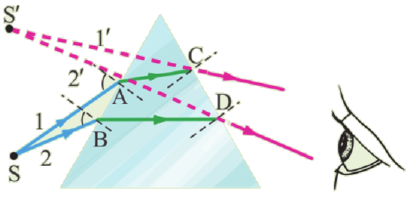
Решение.
В данном случае наблюдается интерференция от двух источников света — источником А и его изображением в зеркале А1. Условие интерференционного максимума Найдем расстояние от каждого источника до точки максимума. Из прямоугольного треугольника (см. рис.) получаем:
и
Тогда из уравнений получаем
Учитывая, что
при получаем условие максимума для каждого случая:
и
Тогда расстояние между ближайшими максимума будет равно
Ответ: 1,2 мм.
Источник: Гельфгат И. М. Сборник задач по физике для 11 класса, Х.: «Гимназия», 2004 (№ 7.38)
МИНИСТЕРСТВО СЕЛЬСКОГО
ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ДЕПАРТАМЕНТ
НАУЧНО-ТЕХНОЛОГИЧЕСКОЙ ПОЛИТИКИ И ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ
АГРАРНЫЙ УНИВЕРСИТЕТ
Оптика
Методические указания к выполнению
лабораторных работ на интерактивной доске
Часть 5

![]() п. Персиановский 2012 г.
п. Персиановский 2012 г.
Е.Г.
Баленко
Т. Ю.
Тарусова
Оптика
Методические указания к выполнению
лабораторных работ на интерактивной доске
Часть 5
п.
Персиановский 2012 г.
УДК 63(06):531/534
ББК 22.2
Б-20
Составители: кандидат
с/х наук, доцент Баленко Е. Г.
ст. преподаватель Тарусова Т. Ю.
Баленко, Е. Г.
Оптика.
Часть 5: Методические указания к выполнению лабораторных работ на
интерактивной доске для студентов сельскохозяйственного
ВУЗа. /Е. Г. Баленко, Т. Ю. Тарусова //пос. Персиановский: ДонГАУ.- 2012.- 48
с.
Методические
разработки содержат описание и методику проведения лабораторных работ на
интерактивной доске по основным разделам физики.
Таблиц – 10
Рис. (схем) – 20
Рецензенты: Заведующий кафедрой «МО и ППП», доктор технических наук, профессор
Коханенко В. Н; кандидат технических наук, доцент кафедры «Высшая математика и
физика» Мокриевич А. Г.
Утверждено
методической комиссией факультета БТЭТ (протокол № 5 от «22» мая 2012 г.)
Рекомендовано
к изданию методическим советом ДонГАУ (протокол № 8 от «14» сентября 2012
г.)
© Баленко Е. Г.,
Тарусова Т. Ю.
©Донской
государственный аграрный университет, 2012 г.
Введение
Данные методические разработки предназначены для студентов
всех специальностей, изучающих курс «Физика».
Они соответствуют требованиям типовых программ и
государственным стандартам вышеуказанного курса и отражают многолетний опыт
преподавания дисциплины для студентов первого и второго курсов в Дон ГАУ в
течение I – III семестров.
Методические разработки охватывают основные разделы курса
физики и знакомят студентов с сущностью физических явлений и методами измерения
физических величин.
Работа 5.1
ИНТЕРФЕРЕНЦИЯ СВЕТА. ОПЫТ ЮНГА
Цель работы: 1) наблюдение
интерференционной картины от двух параллельных щелей в монохроматическом свете;
2) определение длины волны лазерного
излучения.
 |
 Схема экспериментальной установки
Схема экспериментальной установки
1, 2, 3 – штативы, 4,5 – регулировочные винты,
Л –
газовый лазер, БП – блок питания лазера,
П – пластинка со щелями, Э – экран
Описание установки и методики измерений
Источником
монохроматического излучения в данной работе является газовый лазер Л,
закрепленный горизонтально в штативе 1; включение лазера осуществляется
тумблером на панели блока питания БП. В штативе 2 размещена
непрозрачная зачерненная пластинка П, на которую нанесены несколько пар
горизонтальных щелей, расположенных на малом расстоянии d
друг от друга (фронтальное изображение пластинки со щелями дано на схеме установки
справа). Ослабив регулировочный винт 4, можно перемещать пластинку П
по вертикали, направляя лазерный луч на различные пары щелей. Интерференционная
картина наблюдается на экране Э, закрепленном в штативе 3 и
удаленном на расстояние D от пластинки со щелями (на схеме плоскости
пластинки П и экрана Э перпендикулярны плоскости чертежа).
Газовый
лазер испускает узкий пучок монохроматического (красного) цвета. Как известно,
свет представляет собой электромагнитную волну; в случае узкого пучка фронт
этой волны можно считать плоским. Уравнение плоской волны имеет вид

(1)
где E(r,t) –
проекция светового вектора (напряженности электрического поля) на плоскость его
колебаний в точке, находящейся на расстоянии r от источника света
в момент времени t ; Em – амплитуда колебаний; w – циклическая частота; l – длина волны излучения.
Из
выражения (1) следует, что значение Е определяется фазой колебаний
![]()
(2)
Попадая
на пластинку П, луч лазера проходит через две узкие и близко
расположенные друг к другу щели S1 и S2 (рис. 1).
Каждую из этих щелей можно рассматривать как источ-ник света, причем благодаря
одинаковой частоте и постоянной во времени разности фаз эти источники
когерентны. Расхо-дящиеся от них световые пучки перекрываются, и на экране Э
можно наблюдать результат их наложения, т.е. картину интерференции.

В произвольную точку М экрана приходят две
волны и возбуждают колебания
![]()
разность фаз
которых, согласно (2), равна
![]() (3)
(3)
где D = (r1 –
r2)
– разность хода лучей от источников до точки М. Амплитуда
результирующего колебания в точке М определяется выражением
![]()
а интенсивность
света в данной точке
![]()
(4)
где I0 – интенсивность от каждого из источников в
отдельности.
Таким
образом, результат интерференции зависит от величины cosd . При cosd = –1 интенсивность I = 0; совокупность таких точек на
экране образует ряд темных полос. При cosd = 1 интенсивность максимальна: I = I max = 4I0 – такие точки образуют светлые полосы.
Как
известно, cosd = 1 при d = 2kp и cosd = –1 при d = (2k + 1)p , где k Î Z. С учетом
выражения (3) получим условия наблюдения максимумов
D = kl
(5)
и минимумов
D = (2k + 1)×![]() (6)
(6)
Найдем положение соответствующих точек, т.е.
координаты светлых и темных полос на экране. Направим ось Oy
вертикально в плоскости экрана Э; начало координат совместим с центром
наблюдаемой картины (см. рис. 1). Воспользуемся теоремой Пифагора:

Вычитая
почленно первое уравнение из второго, получим
r12 – r12 = 2yd
или
(r2 + r1)( r2 – r1) = 2yd (7)
(здесь и в
дальнейшем индекс «М» у координаты исследуемой точки опущен).
Расстояние
между щелями d составляет менее 1 мм, а
расстояние от щелей до экрана D – несколько
десятков сантиметров. Поэтому можно с достаточной степенью точности положить
величину (r2 + r1) » 2D. Учитывая
также, что ( r2 – r1) = D, преобразуем (7) к виду
![]() (8)
(8)
Координаты
светлых полос найдем, подставляя (8) в условие максимума (5):
![]()
Ширина
интерференционной полосы Dy (расстояние
между соседними максимумами или минимумами) может быть определена как

![]()
Полученное
соотношение позволяет по известным расстояниям d, D и Dy найти длину волны излучения:
![]()
(9)
Примерный
вид интерференционной картины от двух щелей показан на рис. 2. Для
практического определения ширины интерференционной полосы необходимо измерить
рас-стояние LN , на котором
укладывается целое число N светлых полос. Ширина
полосы находится из очевидного соотношения
![]() (10)
(10)
(чем больше N, тем точнее будет определена величина Dy; в приведенном на
рис. 2 примере N = 7).
Таблица №1: таблица
исходных данных
|
Номер |
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
|
Номер |
||||||
|
1,3,5 |
1 |
2 |
3 |
4 |
5 |
6 |
|
2,4,6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1,4,7 |
13 |
14 |
15 |
16 |
17 |
18 |
|
1,3,6 |
19 |
20 |
21 |
22 |
23 |
24 |
Порядок
измерений и обработки результатов

1)
В блоке «Лазер» нажмите
кнопку «Сеть», между платинами появится ярко красное пятно.
2)
В блоке «Пластинка со
щелями» стрелками «вверх/вниз» установите пластинку с номером, рекомендованным
исходными данными. На экране появится интерференционная картина в виде хорошо
различимых красных и темных полос.
3)
В блоке «Экран» стрелками
«влево/вправо» добейтесь четкости картинки.
4)
Запишите в таблицу
значения D и d.
5)
Отсчитайте возможно
большее число красных полос N, занесите в таблицу.
6)
В блоке «Линейка» нажмите
кнопку «Приложить» и стрелками «влево/вправо» и «вверх/вниз» измерьте
расстояние LN (см. рис. 2) и результат занесите в таблицу.
7)
Повторите опыт с еще двумя
рекомендуемыми парами щелей.
8)
Для каждого из опытов
рассчитайте по формуле (10) ширину интерференционной полосы Dy, а
затем – длину волны излучения l по
формуле (9). Результаты расчетов запишите в таблицу, переведя значение l из мм в нм.
Таблица №2:
таблица результатов измерений и вычислений
|
Номер опыта |
d, мм |
D, мм |
N |
LN , мм |
Dy, мм |
l , нм |
|
1 |
||||||
|
2 |
||||||
|
3 |
Оценка погрешности вычислений
Определите
среднее значение
![]()
Вычислите
среднеквадратичную ошибку среднего арифметического:

где ![]() – число измерений,
– число измерений, ![]() –
–
число степеней свободы.
Абсолютную
ошибку измерения ![]() определите как произведение
определите как произведение
среднеквадратического отклонения ![]() на коэффициент
на коэффициент
Стьюдента ![]() , который при надежности
, который при надежности ![]() , равен 4,3:
, равен 4,3:
![]()
Окончательный
результат запишите в таком виде:
![]()
Относительную
погрешность вычислите по формуле:
![]()
Контрольные вопросы
1.
Дайте определение
интерференции световых волн.
2.
Дайте определение
когерентных источников света и расскажите о методах их получения.
3.
Физический смысл понятия оптической
разности хода лучей.
4.
Сформулируйте условия
наблюдения минимумов и максимумов при интерференции.
5.
Опишите опыт Юнга.
6.
Расчет интерференционной
картины от двух источников.
7.
Расскажите о практическом
применении явления интерференции.
Работа 5.2
ИЗУЧЕНИЕ ДИФРАКЦИИ СВЕТА НА ОДИНОЧНОЙ
ЩЕЛИ
И ДИФРАКЦИОННОЙ РЕШЕТКЕ
Цель работы: 1) наблюдение
картины дифракции Фраунгофера от одиночной щели и дифракционной решетки в
монохро-матическом свете;
2) экспериментальное определение шири-ны щели и периода
дифракционной решетки
Схема экспериментальной установки
 |
 1, 2, 3 – штативы, 4, 5
1, 2, 3 – штативы, 4, 5
– регулировочные винты, Л – газовый лазер, БП – блок питания
лазера, Щ – пластинка со щелью,
ДР
– дифракционная решетка, Э – экран
Описание
установки и методики измерений
Установка
для изучения дифракции света аналогична той, которая используется для
наблюдения интерференционной картины в работе 5.1. Различие между ними
заключается в том, что вместо пластинки П с горизонтальными щелями
используется пластинка Щ с одной вертикальной щелью (упражнение 1) и
дифракционная решетка ДР (упражнение 2). Их увеличенное схематическое
изображение дано на схеме установки справа.
Рассмотрим
прохождение через щель шириной b нормально падающей
на нее плоской световой волны (на рис. 3 показан «вид сверху»). Согласно
принципу Гюйгенса-Френеля каждая точка фронта волны (следовательно, каждая
точка плоскости щели) является источником вторичных волн, распространяющихся во
всех направлениях и заходящих в область геометрической тени. Так как эти
вторичные волны когерентны, при наложении друг на друга они дают на экране Э
картину интерференции. Сложность анализа этой картины заключается в
необходимости учета бесконечного множества источников когерентных волн.

Рис. 3
Выясним
результат наложения лучей в произвольной точке экрана М, расположенной
на расстоянии xM от центра картины (ось Ох
направлена горизонтально в плоскости экрана). Если ширина щели b и расстояние xM малы по
сравнению с расстоянием D от щели до экрана (b << D и xM << D), то попадающие в точку
М лучи практически параллельны друг другу и составляют с первоначальным
направлением распространения некоторый малый угол j . Результат интерференции вторичных волн зависит от величины этого
угла, и интенсивность света в точке М определяется выражением

(1)
где
![]()
(2)
I 0 – интенсивность света, идущего от всей щели в направлении первичного
пучка; l – длина волны света.
Из (2)
следует, что F(0) = 0; учитывая первый замечательный предел
![]()
получим, что при j = 0 (в
центре картины) имеет место максимум освещенности: Iщ(0) = I 0 .
Функция
(1) обращается в нуль при условии F(j) = ± p × m, где m Î N. Подставляя в это условие выражение (2), получим уравнение,
позволяющее определить углы, при которых наблюдаются минимумы освещенности
(темные полосы):
![]()
(3)
Условие
(3) можно также получить, воспользовавшись методом зон Френеля. Разобьем
фронт волны (плоскость щели) на участки, разность хода от которых до точки М
равна половине длины волны; так как соответствующая разность фаз равна ± p , волны от двух таких соседних зон при наложении гасят друг друга. Таким
образом, если для данной точки открыто четное число зон Френеля, то в ней
наблюдается минимум интенсивности. Число зон можно найти, разделив разность
хода крайних лучей D (см. рис. 3) на половину длины волны. Учитывая, что ![]() и положив количество зон равным четному
и положив количество зон равным четному
числу 2m, придем к условию (3).
Между
определяемыми этим условием минимумами наблюдаются слабо выраженные максимумы.
На рис. 4 показан график зависимости интенсивности от синуса угла
дифракции и соответствующая ему дифракционная картина на экране.
 Рис.4
Рис.4
Как
видно из рис. 3, координата х точки М на экране (индекс «М»
при х здесь и в дальнейшем опустим) связана с углом j простым
соотношением x = D×tgj . Поскольку угол j мал, имеем
![]() (4)
(4)
Подставляя
данное соотношение в условие (3), найдем координаты точек xm , в которых имеет место m-й по счету,
начиная от центра, минимум освещенности. Ограничившись положительной полуосью (x > 0), получим:
![]()
(5)
Координату
m-го минимума можно найти экспериментально путем
обработки дифракционной картины (рис. 4). Для этого необходимо отметить по
обе стороны от центрального максимума минимумы одного и того же порядка m (в примере на рисунке m = 3) и
измерить расстояние между ними Lm ;
расстояние от центра картины до m-го минимума
находится из очевидного соотношения
![]() .
.
(6)
Если
известна длина волны лазерного излучения l и расстояние от щели до
экрана D, то с помощью выражения (5) можно
определить ширину щели b:
![]() .
.
(7)
Дифракционная
решетка (ДР) представляет собой пластинку с множеством параллельных
узких щелей одинаковой ширины b, находящихся на
расстоянии d друг от друга (рис. 5).
Расстояние между центрами соседних щелей d
называется постоянной (или периодом) дифракционной решетки.
При
прохождении через решетку нормально падающей на нее плоской световой волны (см.
рис. 5) происходят следующие явления: 1) интерференция вторичных
волн, создаваемых точками в плоскости каждой из щелей (это явление подробно
рассмотрено выше); 2) интерференция световых пучков от различных щелей.
 |
Рис. 5
В
результате наложения этих явлений на экране наблюдается дифракционная картина,
имеющая довольно сложный характер. Так же, как и при дифракции от одиночной
щели, интенсивность света в точке М экрана зависит от угла дифракции j ; в случае решетки она определяется выражением
 (8)
(8)
где
![]()
(9)
N – общее
число щелей (штрихов) решетки, накрываемых падающей световой волной; Iщ(j ) – функция, определяемая выражениями (1)-(2).
Благодаря
множителю Iщ(j) выражение (8)
обращается в нуль при углах дифракции, определяемых условием (3); применительно
к решетке оно является условием наблюдения главных минимумов.
Найдем
значение I (j) при Y(j) = p × k, где k Î Z . Раскрыв неопределенность в фигурных скобках выражения (8), вычислим
предел:
![]()
Интенсивность
света при этом будет равна N 2Iщ . Условие Y(j) = p × k с учетом выражения (9) имеет вид
![]() (10)
(10)
и определяет углы,
под которыми наблюдаются главные максимумы освещенности. Число k называется порядком главного максимума. В частности, при k = 0 и, следовательно, j = 0 (в центре
картины) имеет место наиболее яркий центральный максимум интенсивностью Imax = N 2I0 . Все остальные главные
максимумы имеют меньшую интенсивность, зависящую от множителя Iщ(j).
Дробь
в фигурных скобках выражения (8) обращается в нуль при ![]() где
где
l – целое число, не равное kN. Поэтому в промежутках между соседними главными максимумами
наблюдается по (N – 1) вторичных минимумов, чередующихся со
слабо выраженными вторичными максимумами. При большом числе щелей N интенсивность самого яркого вторичного максимума составляет менее 5%
интенсивности ближайшего главного максимума. В условиях данной лабораторной
работы вторичные максимумы практически неразличимы и образуют бледную светлую
полосу, на фоне которой в виде ярких пятен наблюдаются главные максимумы.
На
рис. 6 показан график зависимости интенсивности I от sinj и соответствующая ему дифракционная картина на экране.

Рис. 6
Так же,
как и при дифракции на одиночной щели, в данном случае координата х на
экране и угол дифракции j связаны соотношением (4), с учетом которого условие (10) позволяет
определить координату k-го главного максимума:
![]()
(11)
Экспериментально
значение хk можно найти путем
обработки дифракционной картины. Для этого слева и справа от центрального
максимума нужно отметить положения главных максимумов одного и того же k-го порядка (в примере на рис. 6 k = 4)
и измерить расстояние между ними Lk , после чего определить координату xk как
![]() (12)
(12)
Зная xk , а также расстояние от решетки до экрана D
и длину волны света l , из выражения (11) можно найти
период дифракционной решетки:
![]()
(13)
Таблица №1: таблица
исходных данных
|
Номер |
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
|
Номер |
6 |
5 |
4 |
3 |
2 |
1 |
Порядок измерений и обработки
результатов
Упражнение № 1: Определение ширины щели

1)
В блоке «Лазер» нажмите
кнопку «Сеть», на экране появится ярко красное пятно.
2)
В блоке «Пластинка со
щелью» нажмите кнопку «Установить», на экране появится дифракционная картина.
3)
С помощью блока «Экран»
стрелками «влево/вправо» установите экран так, чтобы на нем наблюдалась четкая
дифракционная картина.
4)
Запишите значение D в
таблицу, выразив его в мм.
5)
Отсчитайте слева и справа
от центра картины одинаковое число m минимумов; измерьте линейкой расстояние между
ними Lm (см. рис. 4), нажав в блоке «Линейка»
кнопку «Приложить» и управляя стрелками «влево/вправо» и «вверх/вниз». Значения
m и Lm (в мм) занесите в таблицу.
6)
Изменяя расстояние D
между щелью и экраном, повторите опыт еще два раза.
7)
Для каждого опыта с
помощью соотношения (6) найдите координату m-го минимума xm . По формуле (7) рассчитайте ширину щели b;
последнюю выразите в мкм. Значения xm и
b занесите в таблицу.
8)
В блоках «Пластинка со
щелью» и «Линейка» нажмите кнопку «Убрать».
Таблица №2: таблица результатов измерений и вычислений
|
Номер опыта |
D, мм |
m |
Lm , мм |
хm , мм |
b, мкм |
|
1 |
|||||
|
2 |
|||||
|
3 |
Оценка погрешности измерений
Определите среднее
значение
![]()
Вычислите
среднеквадратичную ошибку среднего арифметического:

где ![]() – число измерений,
– число измерений, ![]() –
–
число степеней свободы.
Абсолютную
ошибку измерения ![]() определите как произведение
определите как произведение
среднеквадратического отклонения ![]() на коэффициент
на коэффициент
Стьюдента ![]() , который при надежности
, который при надежности ![]() , равен 4,3:
, равен 4,3:
![]()
Окончательный
результат запишите в таком виде:
![]()
Относительную
погрешность вычислите по формуле:
![]()
Упражнение №2: Определение периода дифракционной решетки

1)
В блоке «Дифракционная
решетка» нажмите кнопку «Установить», на экране появится дифракционная картина.
2)
С помощью блока «Экран»
стрелками «влево/вправо» установите экран так, чтобы на нем наблюдалась четкая
дифракционная картина.
3)
Запишите значение D в
таблицу, выразив его в мм.
4)
Отсчитайте от центра
картины (среднего из трех наиболее ярких максимумов) влево и вправо по
одинаковому количеству k главных максимумов (не считая центрального!);
измерьте расстояние между ними Lk ( см. рис. 6), нажав в блоке «Линейка» кнопку
«Приложить» и управляя стрелками «влево/вправо» и «вверх/вниз».. Значения k и
Lk занесите в таблицу.
5)
Изменяя расстояние D
между щелью и экраном, повторите опыт еще два раза.
Для каждого опыта
по формулам (12) и (13) рассчитайте координату k-го
максимума xk и период дифракционной решетки d.
Результаты расчетов занесите в табл. 2.
Таблица №2:
таблица результатов измерений и вычислений
|
Номер опыта |
D, мм |
k |
Lk , мм |
xk , мм |
d, мм |
|
1 |
|||||
|
2 |
|||||
|
3 |
Оценка погрешности измерений
Определите среднее
значение
![]()
Вычислите
среднеквадратичную ошибку среднего арифметического:

где ![]() – число измерений,
– число измерений, ![]() –
–
число степеней свободы.
Абсолютную
ошибку измерения ![]() определите как произведение
определите как произведение
среднеквадратического отклонения ![]() на коэффициент
на коэффициент
Стьюдента ![]() , который при надежности
, который при надежности ![]() , равен 4,3:
, равен 4,3:
![]()
Окончательный
результат запишите в таком виде:
![]()
Относительную
погрешность вычислите по формуле:
![]()
Контрольные вопросы
1.
Дайте определение
дифракции света.
2.
Сформулируйте принцип
Гюйгенса-Френеля.
3.
Объясните прямолинейно
распространение света на основе метода зон Френеля.
4.
Применение зон Френеля для
анализа дифракционной картины.
5.
Дайте понятие дифракции
Фраунгофера на одиночной щели. Условие наблюдения минимумов.
6.
Дайте определение
дифракционной решетки, периода решетки.
7.
Сформулируйте условия
наблюдения главных максимумов и минимумов.
8.
Дифракционная решетка как
спектральный прибор. Угловая дисперсия и разрешающая способность решетки.
Работа 5.3
ИЗУЧЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
С ПОМОЩЬЮ ЯРКОСТНОГО ПИРОМЕТРА
Цель работы:
1) ознакомление с принципом действия яркостного пирометра и практическое
измерение яркостной температуры нагретого тела;
2) применение закона Кирхгофа и формулы
Планка для определения истинной температуры тела;
3) экспериментальная проверка справед-ливости
закона Стефана-Больцмана.
Схема экспериментальной установки

Л –
исследуемая лампа, П – пирометр, Б – батарея питания,
1 –
нить накала лампы Л, 2 – защитный кожух, 3 – окно,
4 –
объектив, 5 – окуляр, 6 – кольцо потенциометра,
7 –
шкала, 8 – ввод/вывод нейтрального светофильтра.
Описание установки и методики измерений
 Объектом
Объектом
исследования в данной работе является раскаленная нить 1 лампы Л.
Лампа помещена в защитный кожух 2, в котором имеется прямоугольное окно 3.
Проходя через это окно, излучаемый лампой свет попадает на объектив 4 яркостного
пирометра П – специального прибора для бесконтактного (осуществляемого на
расстоянии) измерения высоких температур.
Схема питания лампы Л от выпрямителя В
изображена на рис. 7. Подаваемое на лампу напряжение регулируется с
помощью потенциометра Р1 (практически это осуществляется вращением
ручки на щите блока питания, в состав которого входит выпрямитель В) и
измеряется вольтметром V1 ; для
измерения силы тока, протекающего по нити накала 1, служит амперметр А.
 Основной частью пирометра П является
Основной частью пирометра П является
вмонтированная внутри прибора пирометрическая эталонная лампа Э.
Эталонная лампа питается от внешней аккумуляторной батареи Б по схеме,
изображенной на рис. 8. Цепь замыкается тумблером К, расположенным
у основания пирометра. Потенциометр Р2 служит для
регулирования подаваемого на лампу Э напряжения; на практике это
осуществляется вращением кольца 6 на корпусе прибора. Температура нити
накала эталонной лампы однозначно связана с подаваемым на нее напряжением;
поэтому шкала 7 измеряющего его вольтметра V2 проградуирована в градусах Цельсия.


Попадающий на объектив 4 свет от
исследуемой лампы Л проходит через систему линз оптической трубы
пирометра (рис. 9), позволяющую наблюдать в окуляр 5 совмещенные в
одной плоскости изображения нитей накала исследуемой (Л) и эталонной (Э)
ламп. Расположенный в оптической трубе красный светофильтр КФ пропускает
в окуляр практически монохроматический свет с длиной волны l = 660 нм; поэтому изображения
нитей имеют красную окраску.
Рис. 10
Изменяя напряжение, подаваемое на эталонную лампу,
можно добиться одинаковой яркости обеих нитей. Рис. 10 показывает
наблюдаемую в окуляр картину в случаях, когда яркость нити Э меньше (а),
больше (б) и равна (в) яркости нити Л. В последнем случае
эталонная нить становится незаметной на фоне исследуемой (поэтому приборы такого
типа называют пирометрами с исчезающей нитью).
При
высокой температуре лампы Л предусмотрено введение нейтрального
светофильтра НФ с помощью рычажка 8 на корпусе пирометра.
Нейтральный светофильтр уменьшает яркость изображения нити Л и позволяет
уравнять яркости наблюдаемых в окуляр нитей при меньшем напряжении на лампе Э.
При введенном светофильтре НФ показания пирометра снимаются с его нижней
шкалы, а при выведенном (низкие температуры) – с верхней.
В
отсутствие красного светофильтра КФ яркость изображения нити прямо
пропорциональна ее излучательности (энергетической светимости) R,
т.е. энергии, излучаемой за единицу времени с единицы площади поверхности тела
(нити) во всем диапазоне длин волн. Через светофильтр КФ проходит лишь
часть этой энергии DRl , соответствующая интервалу длин волн от l до l + Dl . Для достаточно узкого интервала Dl можно положить
![]()
(1)
где ![]() – спектральная плотность излучательности
– спектральная плотность излучательности
(испускательная способность) тела; Т – его абсолютная температура.
Проблема
градуировки пирометра заключается в том, что различные тела имеют разные
значения спектральной плотности излучательности при одних и тех же длине волны
и температуре. Открытые экспериментально и обоснованные теоретически законы
описывают тепловое излучение абсолютно черного тела (АЧТ).
Поэтому проградуированная соответствующим образом шкала пирометра показывает не
истинную температуру Т нити эталонной лампы Э, а так называемую яркостную
температуру Тя , т.е. температуру АЧТ, имеющего
такую же яркость. При выравнивании яркостей нитей Л и Э
значения DRl у них становятся одинаковыми. Учитывая (1),
можем записать
![]()
(2)
где ![]() – спектральная плотность излучательности
– спектральная плотность излучательности
абсолютно черного тела при температуре Тя .
Как
следует из закона Кирхгофа, спектральные плотности излучательности
реального тела r(l,Т)
и АЧТ r0(l,Т) связаны соотношением
![]()
(3)
где a(l,Т)
– коэффициент поглощения (степень черноты) тела. У многих тел, в частности, у
вольфрама, из которого изготовлена нить лампы Л, коэффициент поглощения
не очень сильно зависит от температуры (см. справочные данные в приложении).
Поэтому можно с достаточной степенью точности использовать для заданной длины
волны l осредненное в данном температурном диапазоне
значение al . Тогда последнее соотношение примет вид
![]() (4)
(4)
Приравнивая
друг другу правые части выражений (2) и (4), получим:
![]()
(5)
Зависимость
спектральной плотности излучательности АЧТ от длины волны и температуры
(универсальная функция Кирхгофа) r0(l,T) описывается формулой Планка

где h –
постоянная Планка; с – скорость света в вакууме; k –
постоянная Больцмана. При сравнительно низких температурах (T < 6000 К) единицей в квадратных
скобках можно пренебречь, и формула Планка примет вид

Подставляя
последнее выражение в (5), получим:

или, после
логарифмирования:
![]()
(6)
Уравнение
(6) связывает истинную температуру Т излучающего тела с его яркостной
температурой Тя . Решая его относительно Т,
находим:
 ,
,
(7)
где
![]() .
.
(8)
Как
известно, тепловое излучение тел имеет место при любой отличной от абсолютного
нуля температуре. Поэтому отключенная от источника питания нить лампы Л
излучает энергетический поток
![]()
(9)
где S –
площадь поверхности нити; R(T0) – ее излучательность при комнатной температуре Т0 .
После подключения лампы к сети питания ее нить разогревается за счет джоулева
тепла до температуры Т и излучает энергетический поток
![]()
(10)
превышающий F0
на величину потребляемой лампой мощности:
![]()
(11)
где h – кпд питающей цепи, учитывающий различные
энергопотери. Мощность Р легко рассчитать как
![]() ,
,
(12)
где U –
питающее напряжение; I – сила тока в цепи.
С
учетом (9) и (10) уравнение (11) можно переписать в виде
![]() (13)
(13)
Излучательность
R(T) определяется из интегрального соотношения

или, с учетом (3):

Считая
нить лампы Л серым телом, т.е. пренебрегая зависимостью ее
коэффициента поглощения от длины волны и заменив функцию a(l,Т)
ее осредненным во всем диапазоне длин волн значением aТ , получим:

где R0(T) – излучательность абсолютно черного тела.
Согласно закону Стефана-Больцмана зависимость R0(T) имеет вид
![]()
где s – постоянная Стефана-Больцмана.
С
учетом принятых допущений выражение (13) примет вид
![]() (14)
(14)
Значения
коэффициента поглощения ![]() (при температуре Т0) и aТ
(при температуре Т0) и aТ
(при температуре Т) составляют десятые доли единицы, т.е. являются
величинами одного порядка, в то время как абсолютная температура раскаленной
нити в четыре-пять раз превышает комнатную температуру Т0.
Таким образом, Т04 << Т 4 и вычитаемым в левой части уравнения (14) можно
пренебречь. Перепишем это уравнение в виде
![]()
(15)
где ![]() .
.
Логарифмируя
уравнение (15) и выражая из него величину lnT, получим
![]()
(16)
где С2 = 0,25 lnС1 .
Из
соотношения (16) следует, что график зависимости lnT от lnP
должен иметь характер, близкий к линейному с угловым коэффициентом, примерно
равным 0,25.
Таблица №1: таблица исходных данных
|
Номер установки |
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
|
Номер варианта |
6 |
5 |
4 |
3 |
2 |
1 |

Порядок измерений и обработки результатов
1)
В блоке «Потенциометр:
яркость лампы Л» стрелкой «вверх» увеличивайте подаваемое на эталонную лампу Э
напряжение до тех пор, пока в окуляр не будет видна нить этой лампы, имеющая
форму дуги.
2)
В блоке «Светофильтры»
введите красный светофильтр.
3)
С помощью блока
«Потенциометры: яркость лампы Л» стрелкой «вверх» установите рекомендованное
значение напряжения U.
4)
Снимите показания
амперметра А и выразив в амперах занесите значение силы тока в таблицу.
5)
В блоке «Потенциометры:
яркость лампы Э» стрелкой «вверх» вращая кольцо потенциометра Р2,
получите вторую дугу и добейтесь их одинаковой яркости (см. рис. 10).
6)
По верхней шкале пирометра
определите яркостную температуру нити и занесите ее значения (в °С) в
таблицу.
7)
Не глядя в окуляр, в блоке
«Потенциометры: яркость лампы Э» стрелкой «вниз» сбейте настройку пирометра.
8)
Повторите данный опыт с
этим же значением напряжения еще дважды. Рассчитайте и занесите в таблицу
среднее из трех значений температуры t. Переведите это значение из °С в
кельвины и заполните следующий столбец таблицы (Тя).
9)
Выполните опыт для каждого
из рекомендованных значений напряжения. Если при дальнейшем выполнении работы
показания пирометра будут близки к концу его верхней шкалы, на экране появится
сообщение «Для продолжения работы необходимо ввести нейтральный светофильтр;
использовать НИЖНЮЮ часть шкалы пирометра». Тогда в блоке «Светофильтры»
установите «нейтральный», при этом не убирая красного и в блоке «Потенциометры:
яркость лампы Э» добейтесь для заданного значения напряжения U
стрелкой «вниз» одинаковой яркости на обоих дугах. Далее считывайте значение
яркостной температуры с нижней шкалы пирометра.
10)
Используя справочные
данные о коэффициенте поглощения вольфрама, оцените его среднее в исследованном
температурном диапазоне значение al
при длине волны l = 660 нм.
Выразив величину l в метрах, по
формуле (8) вычислите константу С (в К –1).
11)
Для каждого опыта
рассчитайте по формуле (7) истинную температуру Т нити накала лампы Л,
а также величину lnТ. Занесите полученные значения в таблицу.
12)
Нанесите экспериментальные
точки на график зависимости lnT от lnP; проведите по ним сглаживающую прямую.
Оцените (с учетом масштаба!) угловой коэффициент этой прямой. Сделайте вывод о
применимости закона Стефана-Больцмана для данного объекта исследования.
Таблица №2:
таблица результатов измерений и вычислений
|
Номер опыта |
U, B |
I, A |
P, Вт |
lnP |
t, °C |
Тя , К |
Т, К |
lnT |
|
1 |
t1 |
|||||||
|
t2 |
||||||||
|
t3 = |
||||||||
|
t = |
||||||||
|
2 |
t1 |
|||||||
|
t2 |
||||||||
|
t3 = |
||||||||
|
t = |
||||||||
|
3 |
t1 |
|||||||
|
t2 |
||||||||
|
t3 = |
||||||||
|
t = |
||||||||
|
4 |
t1 |
|||||||
|
t2 |
||||||||
|
t3 = |
||||||||
|
t = |
||||||||
|
5 |
t1 |
|||||||
|
t2 |
||||||||
|
t3 = |
||||||||
|
t = |
||||||||
|
6 |
t1 |
|||||||
|
t2 |
||||||||
|
t3 = |
||||||||
|
t = |
Контрольные вопросы
1.
Тепловое излучение и его
характеристики: энергетический (световой) поток; излучательность
(энергетическая светимость); спектральная плотность излучательности
(испускательная способность).
2.
Запишите связь между
характеристиками теплового излучения.
3.
Поясните физический смысл
коэффициентов пропускания, отражения и поглощения. Серые тела. Абсолютно черное
тело (АЧТ).
4.
Сформулируйте закон
Кирхгофа. Универсальная функция Кирхгофа и ее физический смысл.
5.
Сформулируйте законы
излучения АЧТ: закон Стефана-Больцмана; законы Вина.
6.
Гипотеза Планка о
квантовом характере излучения. Формула Планка.
7.
Пирометры и их назначение.
Яркостный пирометр. Яркостная температура тела и ее связь с истинной
температурой.
Работа 5.4
ФОТОЭФФЕКТ
Цель работы:
1) снятие вольт-амперной характеристики (ВАХ) вакуумного фотоэлемента;
2) определение работы выхода
электронов и красной границы фотоэффекта.
Схема экспериментальной установки

ФЭ – вакуумный фотоэлемент: k –
катод, а – анод,
Л –
источник света, СФ – светофильтр, ИП – источник питания,
П –
переключатель, А – микроамперметр, V – вольтметр.
Описание установки и методики измерений
Для
исследования явления внешнего фотоэффекта в данной установке используется
вакуумный фотоэлемент ФЭ. Фотоэлемент представляет собой откачанный
стеклянный баллон, одна половина которого покрыта тонким слоем
светочувствительного вещества k, служащего катодом. В центре баллона
располагается анод а, выполненный
в виде кольца или
шарика. Корпус фотоэлемента снабжен специальным карманом, в который помещается
светофильтр СФ. Расходящийся пучок в света от источника (лампы Л,
помещенной в специальный кожух с отверстием и закрепленной на штативе) проходит
через светофильтр, благодаря которому на катод падает практически
монохроматическое излучение длиной волны l . Значение l определяется цветом
выбранного светофильтра. Величину светового потока F, падающего на катод, можно регулировать, изменяя
расстояние L между источником света и фотоэлементом.
Источник
питания ИП предназначен для подачи постоянного напряжения U
между катодом и анодом; величина U может быть измерена вольтметром V.
При замыкании переключателя П в положение 1 на катод подается
отрицательный потенциал, а на анод – положительный. В этом случае выбитые
светом электроны (фотоэлектроны) устремляются к аноду, и по цепи течет
ток (фототок) I, для измерения которого служит микроамперметр
А. Зависимость фототока I от напряжения U
называется вольт-амперной характеристикой (ВАХ) фотоэлемента.
Проанализируем вид этой зависимости исходя из теории явления фотоэффекта.
Согласно
современным квантовым представлениям, монохроматическую электромагнитную
(световую) волну можно рассматривать как поток особых частиц – фотонов,
энергия каждого из которых e ф зависит от частоты n (или от длины волны l) излучения:
![]()
(1)
где h –
постоянная Планка; с – скорость света в вакууме.
Внутри
металла, из которого изготовлен катод k фотоэлемента, имеется большое количество
свободных электронов. При падении света на катод определенная часть фотонов
взаимодействует с этими электронами, отдавая им свою энергию. Получив
дополнительную энергию e ф , электрон может совершить работу выхода Ав
и покинуть катод. Величина работы выхода постоянна для данного металла, поэтому
фотоэффект (выбивание электрона) возможен только при выполнении условия e ф > Aв . С учетом (1) это условие принимает вид
![]()
и позволяет найти
максимальную длину волны lкр , при которой еще возможен фотоэффект:
![]()
(2)
(значение lкр называют красной границей фотоэффекта).
Итак,
при выполнении сформулированного выше условия электрон может покинуть металл.
Разница между энергией фотона и энергией, затраченной на выход, сохраняется в
виде кинетической энергии Wk .
Максимальной кинетической энергией обладают те электроны, взаимодействие
которых с фотонами произошло непосредственно у поверхности металла. Превращение
энергии при фотоэффекте описывается известным уравнением Эйнштейна
![]()
(3)
 |
Рис.11
Множество
покинувших катод электронов движутся во всевозможных направлениях, и некоторые
из них попадают на анод. Поэтому даже при отсутствии напряжения между катодом и
анодом (U = 0) в цепи течет малый по
величине фототок I 0 (на рис. 11 показан примерный вид вольт-амперной характеристики
– ВАХ фотоэлемента).
Уменьшить
фототок I 0 можно путем подачи обратного напряжения («–» на анод, « + »
на катод), что осуществляется замыканием переключателя П в положение 2
(см. схему установки). Фототок будет полностью прекращен, если приложенное
таким образом электрическое поле будет тормозить («загонять» обратно в катод)
самые быстрые электроны. Соответствующее значение задерживающего (запирающего)
напряжения Uз
можно найти из условия, что работа сил электрического поля при этом полностью
затрачивается на «погашение» максимальной кинетической энергии электронов:
![]()
(4)
где e – элементарный электрический заряд.
С
учетом (4) и (1) уравнение (3) принимает вид
![]()
откуда можно найти
работу выхода электронов из металла Ав по известным значениям
длины волны излучения l и задерживающего напряжения Uз :
![]() .
.
(5)
Длина
волны излучения l, как уже отмечалось, определяется цветом используемого светофильтра СФ.
Для измерения задерживающего напряжения Uз необходимо замкнуть переключатель П в положение 2 и
увеличивать подаваемое обратное напряжение до тех пор, пока показания
микроамперметра А не обратятся в нуль; соответствующее показание
вольтметра V и будет представлять собой величину Uз.
Продолжим
анализ характера зависимости I(U). Подача напряжения в прямом направлении (« + »
на анод, « – » на катод) путем установки переключателя П в положение 1
заставляет фотоэлектроны двигаться к аноду. Увеличение напряжения вовлекает в
этот процесс все больше выбитых электронов, вследствие чего ток I возрастает (см. рис. 11). При некотором значении U = Uн все фотоэлектроны попадают на анод, и дальнейшее повышение напряжения
не приводит к увеличению фототока (наступает насыщение ВАХ). Величина
фототока насыщения Iн прямо пропорциональна общему числу выбитых электронов, а
следовательно, количеству падающих на катод фотонов. Количество фотонов, в свою
очередь, определяется величиной светового потока F. Таким образом, квантовая
теория объясняет один из экспериментально открытых А.Г.Столетовым законов
фотоэффекта: фототок насыщения прямо пропорционален освещенности катода. Для
проверки справедливости этого закона в данной работе предусмотрено снятие ВАХ
при двух значениях светового потока F и F¢ < F (уменьшение освещенности катода осуществляется
путем увеличения расстояния L между источником
света и фотоэлементом).
Таблица №1: таблица исходных данных
|
Номер установки |
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
|
Номер варианта |
6 |
5 |
4 |
3 |
2 |
1 |

Порядок
измерений и обработки результатов
Упражнение №1: Снятие ВАХ фотоэлемента
1)
В блоке «Перемещение лампы
Л» стрелками «влево/вправо» установите расстояние L,
согласно исходным данным. Значение L запишите в левую часть таблицы.
2)
В блоке «Светофильтры» установите
светофильтр, рекомендованный исходными данными.
3)
В блоке «Переключатель П»
установите положение 1.
4)
Увеличивая согласно
рекомендациям подаваемое на фотоэлемент напряжение, заносите показания
вольтметра (U) и микроамперметра (I ) в
таблицу до тех пор, пока не будет достигнуто насыщение (при дальнейшем
повышении напряжения фототок практически не будет изменяться).
5)
С помощью блока
«Потенциометр Р» и стрелкой «вниз» установите источник питания на нуль.
6)
Измените в соответствии с
рекомендациями расстояние L и запишите его значение в правую часть таблицы.
7)
По результатам проделанных
измерений постройте на одном графике обе вольт-амперные характеристики.
Сделайте соответствующие выводы.
Таблица №2:
таблица результатов измерений и вычислений
|
L = см |
L = см |
||
|
U, |
I, |
U, |
I, |
|
0 |
0 |
||
|
2 |
2 |
||
|
4 |
4 |
||
|
6 |
6 |
||
|
8 |
8 |
||
|
10 |
10 |
||
|
15 |
15 |
||
|
20 |
20 |
||
|
25 |
25 |
||
|
30 |
30 |
||
|
40 |
40 |
||
|
50 |
50 |
||
|
60 |
60 |
||
|
70 |
70 |
||
|
80 |
80 |
Упражнение № 2. Определение работы выхода электронов
1)
В блоке «Перемещение дампы Л» стрелками
«влево/вправо» установите рекомендованное исходными данными расстояние L.
2)
В блоке «потенциометр Р» и стрелкой «вниз»
установите источник питания на нуль.
3)
В блоке «Светофильтры» установите первый (синий 1).
4)
В блоке «Переключатель П» установите положение 2.
5)
Увеличивайте подаваемое на фотоэлемент напряжение
до тех пор, пока показания микроамперметра не обратятся в нуль. Занесите в
таблицу значение задерживающего напряжения Uз . Уменьшите показания вольтметра до нуля.
6)
Повторите опыт, меняя светофильтры в порядке их
перечисления в таблице.
7)
Используя справочные материалы и выражая длину
волны l в метрах, по формуле (5) рассчитайте для каждого опыта работу выхода
электрона Ав. Переведите полученное значение из джоулей в
электрон-вольты и занесите его в таблицу.
8)
Используя среднее значение ![]() , по формуле (2) найдите
, по формуле (2) найдите
длину волны красной границы фотоэффекта lкр .
Таблица №3:
таблица результатов измерений и вычислений
|
Номер опыта |
Светофильтр |
l, мкм |
Uз , В |
Ав , эВ |
|
1 |
Синий 1 |
0,43 |
||
|
2 |
Синий 2 |
0,46 |
||
|
3 |
Зеленый |
0,50 |
||
|
4 |
Желтый |
0,51 |
||
|
5 |
Оранжевый |
0,52 |
||
|
6 |
Красный |
0,57 |
Контрольные вопросы
1.
Сформулируйте понятие
внешнего фотоэффекта и его основные закономерности.
2.
Сформулируйте условие
наблюдения фотоэффекта (красная граница).
3.
Квантовая теория фотоэффекта.
Фотоны.
4.
Запишите уравнение
Эйнштейна и поясните его физический смысл. Работа выхода.
5.
Вольт-амперные
характеристики фотоэлемента и их объяснение с позиций квантовой теории.
Литература
Основная:
1.
Грабовский Р.И. Курс физики: Учебное пособие для
с.-х. институтов – 6-е изд., перераб. и доп. – М: Высшая школа, 2002 – 607с.
2.
Трофимова Т.И. Курс физики: Учебное пособие для
технических вузов – 2-е издан. М: Высшая школа, 2001. – 478с.
Дополнительная:
3.
Грибов Л.А., Прокофьева Н.И. Основы физики: Учебник
для с.-х. и биологических спец. вузов. – М: Высшая школа, 1992 – 430с.
4.
Ремизов А.Н. Медицинская и биологическая физика:
Учебное пособие для медицинских, сельскохозяйственных и биологических
специальностей. – М: Высшая школа, 1992 – 616с.
5.
Хитун В.А., Скляревич В.В. Практикум по физике для
медицинских вузов. Изд.2-е, доп. Учебное пособие для институтов, М: Высшая
школа, 1972 – 360с.
Программное обеспечение:
1.
Виртуальная лаборатория физики 2.0 (Тверской
государственный технический университет (ТГТУ), Тверь, 2006 год)
Содержание
Введение 4
Работа 5.1
«Интерференция света. Опыт Юнга» 5
Работа 5.2 «Изучение
дифракции света на одиночной
щели и дифракционной решетке» 12
Работа 5.3 «Изучение
законов теплового излучения с
помощью яркостного пирометра» 26
Работа 5.4
«Фотоэффект» 37
Литература 46
Елена Георгиевна Баленко
Татьяна Юрьевна Тарусова
Оптика.
Часть 5: Методические указания к выполнению лабораторных работ на
интерактивной доске для студентов сельскохозяйственного
ВУЗа. – пос. Персиановский, ДонГАУ, 2012 – 48 с.
Учебно –
методическое издание
Под
редакцией Е.Г. Баленко
Компьютерная
верстка: Тарусова Т. Ю.
Донской
государственный аграрный университет
346493,
пос. Персиановский, Октябрьский район, Ростовская обл.
