Содержание
- Как по координатам найти расстояние между точками земли
- Как измерить расстояние между координатами*
- Способы измерения
- Сложности вычисления расстояния между точками
- Итог
- Как по координатам найти расстояние между точками земли
- Географические координаты
- Формула гаверсинуса
- Пример вычисления расстояния
- Вывод
- Как по координатам найти расстояние между точками земли
- Координаты широты и долготы
- Формула Гаверсинуса
- Пример расчета расстояния
- Общий итог
Как по координатам найти расстояние между точками земли
При изучении географии, астрономии, навигации или любой другой науке, связанной с земными координатами, одним из самых важных элементов является знание того, как измерить расстояние между двумя точками на поверхности Земли.
В этой статье мы рассмотрим, как можно вычислить расстояние между двумя точками, заданными географическими координатами. Мы также рассмотрим некоторые ключевые особенности процесса расчета дистанции между точками и поговорим о возможных трудностях, с которыми вы можете столкнуться при выполнении этих вычислений.
Как измерить расстояние между координатами*
Самый простой способ вычисления расстояния между двумя точками заключается в использовании расстояния по прямой линии, также известного как «великий круг». Это расстояние измеряется в градусах и зависит от широты и долготы каждой из точек.
Для вычисления расстояния между двумя точками на поверхности Земли, вы можете использовать следующую формулу:
расстояние = 6371 * acos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(long2 – long1))
Здесь 6371 представляет собой радиус Земли в километрах, а lat1, lat2, long1 и long2 представляют собой широту и долготу каждой из двух точек, заданных в радианах. Формула работает, если заданы координаты точек в радианах. Если заданы в градусах, то их нужно преобразовать в радианы, умножив на pi / 180.
Способы измерения
Существует несколько способов измерения расстояния между точками на поверхности Земли. Один из самых популярных методов — это использование GPS (Global Positioning System).
GPS — это система спутникового навигационного определения местоположения, разработанная для использования военными и предназначенная для определения местоположения, скорости и времени в любой точке на земном шаре.
Сегодня GPS — это наиболее точный и универсальный способ определения местоположения и расстояния между точками на поверхности Земли. Если у вас есть доступ к GPS, то вы можете легко определить координаты двух точек и использовать эти координаты для вычисления расстояния между ними.
Однако GPS не всегда доступен или не всегда практичен для использования, поэтому существуют и другие способы расчета расстояния между точками.
Еще один способ — это использование профессиональных картографических инструментов, например, Google Maps или ArcGIS. Эти инструменты могут предоставлять дополнительную информацию о местоположении точек, такую как высота над уровнем моря, скорость и т.д., что может быть полезно при расчете точного расстояния между ними.
Сложности вычисления расстояния между точками
Вычисление расстояния между двумя точками на поверхности Земли — это сложный процесс, который может включать в себя множество факторов, включая атмосферные условия, изменения уровня моря и другие внешние факторы.
Кроме того, вычисление дистанции между точками может быть трудной задачей, если вам не хватает определенных навыков работы с координатами или математическими формулами. В таких случаях может быть полезно обратиться за помощью к опытному специалисту, который сможет помочь вам с проблемой вычисления расстояния между точками.
Итог
Вычисление расстояния между двумя точками — это важный аспект множества научных дисциплин, но это может быть сложной задачей с учетом многих факторов. Тем не менее, если вы знакомы с основами географии, математики и обретете некоторый опыт работы с координатами, вы сможете успешно рассчитать расстояние между точками на поверхности Земли.
Вы можете использовать различные способы измерения расстояния между точками, включая GPS, картографические инструменты или математические формулы. Вы также можете обратиться за помощью, если у вас возникнут трудности в процессе вычисления расстояния между точками на поверхности Земли.
* Вы можете найти еще много других методов или формул для измерения расстояния между точками. В этой статье мы рассмотрели самый простой способ и наиболее распространенную формулу.
Как по координатам найти расстояние между точками земли
Определение расстояния между двумя точками на земле может быть полезным в различных областях, включая науку, инженерию, геодезию и навигацию. В этой статье мы рассмотрим, как вычислить расстояние между двумя точками на земле, используя географические координаты.
Географические координаты
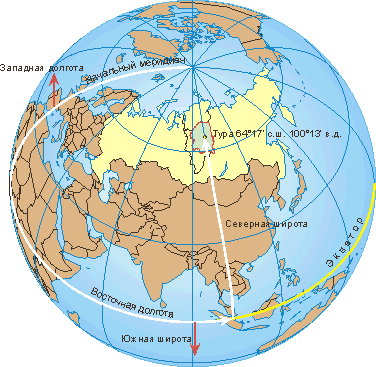
Географические координаты — это система определения местоположения на плоскости Земли. Она основана на градусах широты и долготы, которые описываются в градусах, минутах и секундах.
Широта — это угол между точкой на поверхности Земли и экватором. Экватор имеет широту 0 градусов, полюса имеют широты 90 градусов северной или южной широты. Широта может быть отрицательной для точек, расположенных южнее экватора.
Долгота — это угол между точкой на поверхности Земли и точкой пересечения Гринвичского меридиана. Гринвичский меридиан имеет долготу 0 градусов, причем долгота увеличивается на востоке и уменьшается на западе до 180 градусов. Долгота может быть отрицательной для точек, расположенных на западе этой линии.
Формула гаверсинуса
Одним из методов определения расстояния между двумя точками на плоскости Земли является формула гаверсинуса. В этой формуле расстояние между точками определяется по формуле:
d = 2r * arcsin(sqrt(sin^2((lat2 — lat1) / 2) + cos(lat1) * cos(lat2) * sin^2((lon2 — lon1) / 2)))
где:
- d — расстояние между точками;
- r — радиус Земли (в метрах);
- lat1, lon1 — широта и долгота первой точки;
- lat2, lon2 — широта и долгота второй точки.
Эта формула работает только для небольших расстояний, которые могут быть измерены в метрах или километрах. Если расстояние между точками значительно, то формула может дать неточный результат, так как форма Земли не является точно сферической.
Пример вычисления расстояния
Для примера вычислим расстояние между двумя городами — Москва и Нью-Йорк. Координаты этих городов можно найти в Интернете. Согласно Google Earth, координаты Москвы — 55.7558° северной широты, 37.6173° восточной долготы. Координаты Нью-Йорка — 40.7128° северной широты, 74.0060° западной долготы.
Применяя формулу гаверсинуса, расстояние между этими двумя городами составляет около 7 832 км. Это примерный результат, который может отличаться в зависимости от выбранного радиуса Земли и других факторов.
Вывод
Определение расстояния между точками на земле может быть полезно в различных областях, от науки до навигации. Для вычисления расстояния можно использовать географические координаты и формулу гаверсинуса. Однако важно помнить, что эта формула может дать неточный результат для больших расстояний, так как форма земли не является точно сферической. Используйте результаты с осторожностью и проверяйте их в нескольких источниках.
Как по координатам найти расстояние между точками земли
Координаты широты и долготы являются важной информацией для многих профессиональных и любительских деятелей, особенно для специалистов в области географии и навигации. Одним из наиболее распространенных вопросов, связанных с координатами, является «Как по координатам найти расстояние между точками земли?». В этой статье мы подробно разберем этот вопрос и покажем, как рассчитать расстояние между двумя точками на поверхности Земли.
Координаты широты и долготы
Широта и долгота — это координаты, используемые для указания точного местоположения на поверхности Земли. Широта измеряется в градусах от экватора до полюса, а долгота измеряется в градусах от Гринвичского меридиана на восток или на запад.
Координаты могут быть записаны в различных форматах, в зависимости от того, что требуется. Например, координаты можно записать в градусах, минутах и секундах (DMS), как мы видим на картах и навигационных приборах. Но при работе с координатами широты и долготы на компьютере или в Интернете чаще всего используется формат десятичных градусов (DD).
Формула Гаверсинуса
Формула Гаверсинуса является одним из наиболее распространенных способов рассчитать расстояние между точками на поверхности Земли по их координатам широты и долготы. Формула основана на геометрическом принципе сферы и предполагает, что Земля является идеальной сферой. Таким образом, в реальности могут быть маленькие отклонения от результатов, полученных с помощью формулы Гаверсинуса.
Формула Гаверсинуса выглядит так:
d = 2r * asin(sqrt(sin²((lat2 — lat1)/2) + cos(lat1) * cos(lat2) * sin²((lon2 — lon1)/2)))
Где:
- d — расстояние между точками в километрах
- r — радиус Земли в километрах (приблизительно 6,371 км)
- lat1, lat2 — широта первой и второй точек в радианах
- lon1, lon2 — долгота первой и второй точек в радианах
Пример расчета расстояния
Давайте рассмотрим пример, чтобы проиллюстрировать, как использовать формулу Гаверсинуса для рассчета расстояния между двумя точками на поверхности Земли.
Для этого мы будем использовать следующие координаты:
- Точка 1: широта 37.7749, долгота -122.4194
- Точка 2: широта 40.7128, долгота -74.0060
Первым шагом мы переводим десятичные координаты в радианы:
- lat1 = 0.6599660530304349
- lon1 = -2.134210930027159
- lat2 = 0.7101745809840069
- lon2 = -1.29171492961996
Далее мы используем эти значения в формуле Гаверсинуса, чтобы рассчитать расстояние между точками:
d = 2 * 6371 * asin(sqrt(sin²((0.7101745809840069 — 0.6599660530304349)/2) + cos(0.6599660530304349) * cos(0.7101745809840069) * sin²((-1.29171492961996 — -2.134210930027159)/2)))
После решения уравнения, мы получаем расстояние между точками 4 138,19 км. Таким образом, мы можем утверждать, что расстояние между Сан-Франциско и Нью-Йорком примерно 4 138 км.
Общий итог
Рассчитывать расстояние между точками на поверхности Земли по их координатам широты и долготы довольно просто, если знать формулу Гаверсинуса. Несмотря на то, что формула основана на предположении, что Земля идеально круглая, результаты все равно довольно точны и объективны. Все, что нужно для рассчета расстояния, — это знание координат двух точек и небольшой математический расчет. Надеемся, что этот материал был полезен для вас, и поможет вам быстро рассчитать расстояние между точками на поверхности Земли.
Содержание
- Расстояние между точками на земле по географическим координатам
- GIS-LAB
- Вычисление расстояния и начального азимута между двумя точками на сфере
- Содержание
- [править] Введение
- [править] Формулы
- [править] Сферическая теорема косинусов
- [править] Формула гаверсинусов
- [править] Модификация для антиподов
- [править] Реализация на Avenue
- [править] Реализация на языке Python
- [править] Реализация в Excel
- [править] Проверочный набор данных
- [править] Ссылки по теме
Расстояние между точками на земле по географическим координатам


Определение расстояний на поверхности Земли
Размеры и форма Земли
Форма Земли отличается от шара и имеет несколько сплющенную форму, близкую к сфероиду (эллипсоиду вращения), но истинная фигура Земли отличается и от сфероида, и от трехосного эллипсоида и не может быть представлена ни одной из известных математических фигур.
Поэтому, говоря о фигуре Земли, имеют в виду не физическую форму земной поверхности, с океанами и материками, с их возвышенностями и впадинами, а так называемую поверхность геоида.
Поверхность, нормалями к которой в любой из ее точек являются отвесные линии, называется уровенной поверхностью, или поверхностью равновесия. Уровенных поверхностей, как внутри Земли, так и охватывающих земную поверхность, или пересекающихся с ней, можно провести бесчисленное множество.
Та поверхность равновесия, которая совпадает в открытом океане с поверхностью покоящейся свободной воды, называется геоидом.
Для решения многих задач навигации и составления карт мелкого масштаба Землю принимают за сферу (шар).
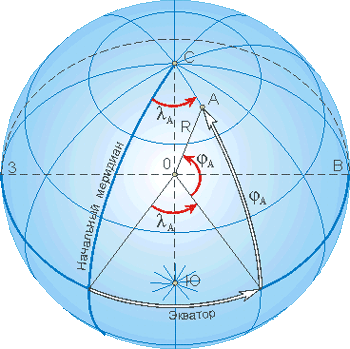
Положение точки па земной сфере определяется сферическими координатами: сферической широтой и сферической долготой (в картографии применяют термин «географические координаты«).
Сферическая широта точки А — угол φ А между плоскостью экватора и направлением R на данную точку из центра земной сферы.
Сферическая долгота точки А — угол λ А , заключенный между плоскостью нулевого (Гринвичского) меридиана и плоскостью меридиана данной точки.
Средний радиус Земли R = 6371210 м.
Экваториальный радиус Земли RЭ = 6378,245 м.
Полярный радиус Земли RП = 6356,830 м.
Длина дуги меридиана (дуги экватора, дуги окружности большого круга) в 1°, 1′ и 1″ равна соответственно:
111 197 м (111,2 км), 1852 м (1,852 км) и 30,9 м.
Законы сферической тригонометрии позволяют рассчитывать расстояния между точками, расположенными на сфере.
Кратчайшее расстояние между двумя точками на земной поверхности (если принять ее за сферу) определяется зависимостью:
где φ А и φ B — широты, λ А , λ B — долготы данных пунктов, d — расстояние между пунктами, измеряемое в радианах длиной дуги большого круга земного шара.
Расстояние между пунктами, измеряемое в километрах, определяется по формуле:
где R = 6371 км — средний радиус земного шара.
Таблица расстояний (с точностью 1 км), рассчитанными по этим формулам,
для пунктов Эвенкийского автономного округа (Эвенкийского муниципального района):
| уточнения внесены 25.03.2010 | Тура | Байкит | Ванавара |
| Красноярск | 1007 | 662 | 738 |
| Агата | 426 | ||
| Географический центр РФ, Виви | 364 | ||
| Ессей | 467 | ||
| Кислокан | 201 | ||
| Нидым | 21 | ||
| Ногинск | 439 | ||
| Тембенчи | 99 | ||
| Тура | 350 | 450 | |
| Тутончаны | 313 | ||
| Учами | 186 | ||
| Чиринда | 363 | ||
| Эконда | 293 | ||
| Юкта | 293 | ||
| Байкит | 350 | 352 | |
| Бурный | 197 | ||
| Кузьмовка | 236 | ||
| Куюмба | 82 | ||
| Мирюга | 220 | ||
| Ошарово | 177 | ||
| Полигус | 101 | ||
| Суломай | 274 | ||
| Суринда | 114 | ||
| Таимба | 203 | ||
| Усть-Камо | 121 | ||
| Ванавара | 450 | 352 | |
| Кербо | 242 | ||
| Муторай | 147 | ||
| Оскоба | 100 | ||
| Стрелка-Чуня | 159 | ||
| Тунгусский метеорит (эпицентр) | 64 | ||
| Чемдальск | 102 |
Для расчета расстояния между пунктами, расположенными в разных полушариях (северное-южное, восточное-западное), знаки (±) у соответствующих параметров (широт или долгот) должны быть разными.
Пример: (см. таблицу ниже)
для вычисления расстояния между Турой и Сиднеем (Австралия) применяем формулу:
cos(d) = sin(φ А )·sin(−φ B ) + cos(φ А )·cos(−φ B )·cos(λ А − λ B ) = −0,27462.
d = 1,848988
Расстояние L = d·R = 11 779,9 км.
для вычисления расстояния между Турой и Нью-Йорком (США) применяем формулу:
cos(d) = sin(φ А )·sin(φ B ) + cos(φ А )·cos(φ B )·cos(λ А + λ B ) = 0,259532.
Расстояние L = d·R = 8 334,92 км.
В таблице расстояния определены с точностью 1 км.
Источник
GIS-LAB
Географические информационные системы и дистанционное зондирование
Вычисление расстояния и начального азимута между двумя точками на сфере
Измерение расстояния и начального азимута между точками без проекционных преобразований
Содержание
[править] Введение
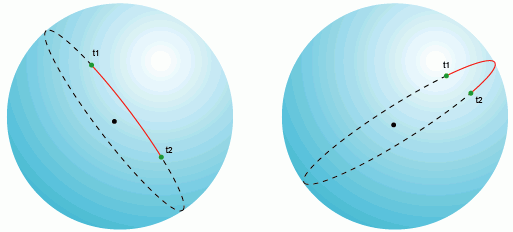
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут [angles-rhumb.html отличен от постоянного], следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.
Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.
На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.
Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.
Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.
Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.
[править] Формулы
Существует три способа расчета сферического расстояния большого круга (подробнее).
[править] Сферическая теорема косинусов
В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением. Графическое изображение формул здесь и далее — из Википедии.
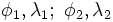
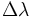
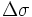
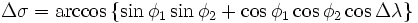
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).
[править] Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.
[править] Модификация для антиподов
Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.
[править] Реализация на Avenue
На языке Avenue, используя последнюю формулу для вычисления расстояния большого круга между двумя точками, можно использовать следующий код. Точки для вычисления передаются другим скриптом, либо добавляются в начало данного в виде pnt = point.make(long, lat) (скачать скрипт):
Для вызова процедуры расчета длин приведенной выше, можно также воспользоваться следующим скриптом, результатом его работы будет расчет длин между точкой testpont до всех точек активной темы вида и запись результата в поле Newdist атрибутивной таблицы этой темы:
[править] Реализация на языке Python
Реализует полный вариант расчета через atan2(), более универсальнее, чем вариант для Avenue. (скачать скрипт)
[править] Реализация в Excel
Скачать пример расчета расстояния большого круга и начального азимута в Excel. Демонстрирует расчеты через закон косинусов, гаверсинус, полное уравнение и полное уравнение через atan2().
Можно также воспользоваться следующей функцией:
[править] Проверочный набор данных
Если все считается правильно, должны быть получены следующие результаты (координаты точек даны как широта/долгота, расстояние в метрах, начальный угол в десятичных градусах):
| # | Точка 1 | Точка 2 | Расстояние | Угол |
| 1 | 77.1539/-139.398 | -77.1804/-139.55 | 17166029 | 180.077867811 |
| 2 | 77.1539/120.398 | 77.1804/129.55 | 225883 | 84.7925159033 |
| 3 | 77.1539/-120.398 | 77.1804/129.55 | 2332669 | 324.384112704 |
[править] Ссылки по теме
Последнее обновление: 2014-05-14 23:41
Дата создания: 06.06.2006
Автор(ы): Максим Дубинин
Источник
From Wikipedia, the free encyclopedia
Geographical distance or geodetic distance is the distance measured along the surface of the earth. The formulae in this article calculate distances between points which are defined by geographical coordinates in terms of latitude and longitude. This distance is an element in solving the second (inverse) geodetic problem.
Introduction[edit]
Calculating the distance between geographical coordinates is based on some level of abstraction; it does not provide an exact distance, which is unattainable if one attempted to account for every irregularity in the surface of the earth.[1] Common abstractions for the surface between two geographic points are:
- Flat surface;
- Spherical surface;
- Ellipsoidal surface.
All abstractions above ignore changes in elevation. Calculation of distances which account for changes in elevation relative to the idealized surface are not discussed in this article.
Nomenclature[edit]
Distance, 





Latitude and longitude coordinates on maps are usually expressed in degrees. In the given forms of the formulae below, one or more values must be expressed in the specified units to obtain the correct result. Where geographic coordinates are used as the argument of a trigonometric function, the values may be expressed in any angular units compatible with the method used to determine the value of the trigonometric function. Many electronic calculators allow calculations of trigonometric functions in either degrees or radians. The calculator mode must be compatible with the units used for geometric coordinates.
Differences in latitude and longitude are labeled and calculated as follows:
It is not important whether the result is positive or negative when used in the formulae below.
“Mean latitude” is labeled and calculated as follows:
Colatitude is labeled and calculated as follows:
- For latitudes expressed in radians:
- For latitudes expressed in degrees:
Unless specified otherwise, the radius of the earth for the calculations below is:
= 6,371.009 kilometers = 3,958.761 statute miles = 3,440.069 nautical miles.

Singularities and discontinuity of latitude/longitude[edit]
Longitude has singularities at the Poles (longitude is undefined) and a discontinuity at the ±180° meridian. Also, planar projections of the circles of constant latitude are highly curved near the Poles. Hence, the above equations for delta latitude/longitude (










If a calculation based on latitude/longitude should be valid for all Earth positions, it should be verified that the discontinuity and the Poles are handled correctly. Another solution is to use n-vector instead of latitude/longitude, since this representation does not have discontinuities or singularities.
Flat-surface formulae[edit]
A planar approximation for the surface of the earth may be useful over small distances. The accuracy of distance calculations using this approximation become increasingly inaccurate as:
- The separation between the points becomes greater;
- A point becomes closer to a geographic pole.
The shortest distance between two points in plane is a straight line. The Pythagorean theorem is used to calculate the distance between points in a plane.
Even over short distances, the accuracy of geographic distance calculations which assume a flat Earth depend on the method by which the latitude and longitude coordinates have been projected onto the plane. The projection of latitude and longitude coordinates onto a plane is the realm of cartography.
The formulae presented in this section provide varying degrees of accuracy.
Spherical Earth projected to a plane[edit]
This formula takes into account the variation in distance between meridians with latitude:
- where:
and
are in radians;
must be in units compatible with the method used for determining
- To convert latitude or longitude to radians use
This approximation is very fast and produces fairly accurate result for small distances[citation needed]. Also, when ordering locations by distance, such as in a database query, it is faster to order by squared distance, eliminating the need for computing the square root.
Ellipsoidal Earth projected to a plane[edit]
The FCC prescribes the following formulae for distances not exceeding 475 kilometres (295 mi):[2]
- where
= Distance in kilometers;
and
are in degrees;
must be in units compatible with the method used for determining
- Where
and
are in units of kilometers per degree. It may be interesting to note that:
= kilometers per degree of latitude difference;
= kilometers per degree of longitude difference;
- where
and
are the meridional and its perpendicular, or “normal“, radii of curvature (the expressions in the FCC formula are derived from the binomial series expansion form of
and
, set to the Clarke 1866 reference ellipsoid).
For a more computationally efficient implementation of the formula above, multiple applications of cosine can be replaced with a single application and use of recurrence relation for Chebyshev polynomials.
Polar coordinate flat-Earth formula[edit]
- where the colatitude values are in radians. For a latitude measured in degrees, the colatitude in radians may be calculated as follows:
Spherical-surface formulae[edit]
If one is willing to accept a possible error of 0.5%, one can use formulas of spherical trigonometry on the sphere that best approximates the surface of the earth.
The shortest distance along the surface of a sphere between two points on the surface is along the great-circle which contains the two points.
The great-circle distance article gives the formula for calculating the distance along a great-circle on a sphere about the size of the Earth. That article includes an example of the calculation.
Tunnel distance[edit]
A tunnel between points on Earth is defined by a line through three-dimensional space between the points of interest.
The great circle chord length may be calculated as follows for the corresponding unit sphere:
The tunnel distance between points on the surface of a spherical Earth is



Ellipsoidal-surface formulae[edit]
Geodesic on an oblate ellipsoid
An ellipsoid approximates the surface of the earth much better than a
sphere or a flat surface does. The shortest distance along the surface
of an ellipsoid between two points on the surface is along the
geodesic. Geodesics follow more complicated paths than great
circles and in particular, they usually don’t return to their starting
positions after one circuit of the earth. This is illustrated in the
figure on the right where f is taken to be 1/50 to accentuate the
effect. Finding the geodesic between two points on the earth, the
so-called inverse geodetic problem, was the focus of many
mathematicians and geodesists over the course of the 18th and 19th
centuries with major contributions by
Clairaut,[3]
Legendre,[4]
Bessel,[5]
and Helmert.[6]
Rapp[7]
provides a good summary of this work.
Methods for computing the geodesic distance are widely available in
geographical information systems, software libraries, standalone
utilities, and online tools. The most widely used algorithm is by
Vincenty,[8]
who uses a series which is accurate to third order in the flattening of
the ellipsoid, i.e., about 0.5 mm; however, the algorithm fails to
converge for points that are nearly antipodal. (For
details, see Vincenty’s formulae.) This defect is cured in the
algorithm given by
Karney,[9]
who employs series which are accurate to sixth order in the flattening.
This results in an algorithm which is accurate to full double precision
and which converges for arbitrary pairs of points on the earth. This
algorithm is implemented in GeographicLib.[10]
The exact methods above are feasible when carrying out calculations on a
computer. They are intended to give millimeter accuracy on lines of any
length; one can use simpler formulas if one doesn’t need millimeter
accuracy, or if one does need millimeter accuracy but the line is short.
Rapp,[11] Chap. 6, describes the Puissant method,
the Gauss mid-latitude method, and the Bowring method.[12]
Lambert’s formula for long lines[edit]
Lambert’s formulae[13]
give accuracy on the order of 10 meters over thousands of kilometers. First convert the latitudes 



where 
Then calculate the central angle 





where 
On the GRS 80 spheroid Lambert’s formula is off by
- 0 North 0 West to 40 North 120 West, 12.6 meters
- 0N 0W to 40N 60W, 6.6 meters
- 40N 0W to 40N 60W, 0.85 meter
Bowring’s method for short lines[edit]
Bowring maps the points to a sphere of radius R′, with latitude and longitude represented as φ′ and λ′. Define
where the second eccentricity squared is
The spherical radius is
(The Gaussian curvature of the ellipsoid at φ1 is 1/R′2.)
The spherical coordinates are given by
where 



Altitude correction[edit]
The variation in altitude from the topographical or ground level down to the sphere’s or ellipsoid’s surface, also changes the scale of distance measurements.[14]
The slant distance s (chord length) between two points can be reduced to the arc length on the ellipsoid surface S as:[15]
where R is evaluated from Earth’s azimuthal radius of curvature and h are ellipsoidal heights are each point.
The first term on the right-hand side of the equation accounts for the mean elevation and the second term for the inclination.
A further reduction of the above Earth normal section length to the ellipsoidal geodesic length is often negligible.[15]
See also[edit]
- Arc measurement
- Earth radius
- Spherical Earth
- Great-circle distance
- Great-circle navigation
- Ground sample distance
- Vincenty’s formulae
- Meridian arc
- Scale (map)
References[edit]
- ^ “The British Cartographic Society > How long is the UK coastline?”. Archived from the original on 2012-05-22. Retrieved 2008-12-06.
- ^ “Reference points and distance computations” (PDF). Code of Federal Regulations (Annual Edition). Title 47: Telecommunication. 73 (208). October 1, 2016. Retrieved 8 November 2017.
- ^
Clairaut, A. C. (1735). “Détermination géometrique de la perpendiculaire à la méridienne tracée par M. Cassini” [Geometrical determination of the perpendicular to the meridian drawn by Jacques Cassini]. Mémoires de l’Académie Royale des Sciences de Paris 1733 (in French): 406–416. - ^
Legendre, A. M. (1806). “Analyse des triangles tracées sur la surface d’un sphéroïde” [Analysis of spheroidal triangles]. Mémoires de l’Institut National de France (in French) (1st semester): 130–161. - ^
Bessel, F. W. (2010) [1825]. . Translated by C. F. F. Karney & R. E. Deakin. “The calculation of longitude and latitude from geodesic measurements”. Astronomische Nachrichten. 331 (8): 852–861. arXiv:0908.1824. Bibcode:2010AN….331..852K. doi:10.1002/asna.201011352. S2CID 118760590. English translation of Astron. Nachr. 4, 241–254 (1825). Errata. CS1 maint: postscript (link) - ^
Helmert, F. R. (1964) [1880]. Mathematical and Physical Theories of Higher Geodesy. Vol. 1. St. Louis: Aeronautical Chart and Information Center. English translation of Die Mathematischen und Physikalischen Theorieen der Höheren Geodäsie, Vol. 1 (Teubner, Leipzig, 1880). CS1 maint: postscript (link) - ^
Rapp, R. H. (March 1993). Geometric Geodesy, Part II (Technical report). Ohio State University. Retrieved 2011-08-01. - ^
Vincenty, T. (April 1975). “Direct and Inverse Solutions of Geodesics on the Ellipsoid with application of nested equations” (PDF). Survey Review. 23 (176): 88–93. doi:10.1179/sre.1975.23.176.88. Retrieved 2009-07-11. Addendum: Survey Review 23 (180): 294 (1976).{{cite journal}}: CS1 maint: postscript (link) - ^
Karney, C. F. F. (2013). “Algorithms for geodesics”. Journal of Geodesy. 87 (1): 43–55. arXiv:1109.4448. Bibcode:2013JGeod..87…43K. doi:10.1007/s00190-012-0578-z. S2CID 119310141(open access). Addenda. CS1 maint: postscript (link) - ^
Karney, C. F. F. (2013). “GeographicLib”. 1.32. - ^ a b
Rapp, R, H (1991). Geometric Geodesy, Part I (Report). Ohio Start Univ. hdl:1811/24333. - ^ a b
Bowring, B. R. (1981). “The direct and inverse problems for short geodesics lines on the ellipsoid”. Surveying and Mapping. 41 (2): 135–141. - ^
Lambert, W. D (1942). “The distance between two widely separated points on the surface of the earth”. J. Washington Academy of Sciences. 32 (5): 125–130. - ^ “Archived copy” (PDF). Archived from the original (PDF) on 2014-08-27. Retrieved 2014-08-26.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ a b Torge & Müller (2012) Geodesy, De Gruyter, p.249
External links[edit]
- An online geodesic calculator (based on GeographicLib).
- An online geodesic bibliography.
Задача простая. Нужно вычислить расстояние между двумя точками на карте, при этом известны только их географические координаты, то есть широта и долгота. Для примера вычислим расстояние между Москвой и Питером, но данная методика, конечно же, будет применима и к другим двум точкам местности. В наше время у многих людей есть такие компасы, например при смартфонах, которые показывают не только направление, но и географические координаты.
Итак, задача: вычислить расстояние между двумя городами. Известно только одно – географические координаты, то есть широта и долгота. Посмотрим эти данные в справочнике, ну или в Википедии.
Итак, что нам известно: координаты Москвы:
55,7522 град. с.ш., 37.6156 град. в.д.
Координаты Петербурга:
59,89444 град. с.ш., 30,26417 град. в.д.
Построим с помощью Excel трапецию:
Итак, у нас есть трапеция ABCD. На ней точка D – это Москва, точка B – это Петербург. Отрезок AB проходит по меридиану Петербурга, BC – по параллели Петербурга, CD – по меридиану Москвы и AD – по параллели Москвы.
Что нам известно? Во-первых известны все географические координаты каждой из точек:
A: 55,7522, 30,26417;
B: 59,89444, 30,26417;
C: 59,89444, 37,6156;
D: 55,7522, 37,6156.
Вычислить AB и CD достаточно просто. На меридианах в градусе примерно одинаковое число километров. Это расстояние можно взять из справочных данных, и оно составляет примерно 111,1 км в каждом градусе.
Нужная нам разница в градусах – это 59,89444-55,7522, или 4,14224. А это значит, что разница в километрах – это 4,14224*111,1=460,2029 км.
Что же касается оснований трапеции, там тоже все достаточно просто. Экватор – это ноль градусов северной широты, и длина каждого градуса на экваторе около 111,3 км. Поскольку косинус ноля – это единица, то для любой параллели верна следующая формула: длина каждого градуса равна произведению 111,3 на косинус того угла, который числится в градусах северной широты (ну или южной, если это происходит южнее экватора).
Итак, с помощью Excel вычислим нужные нам косинусы:
- cos(55.7522) = 0,562773
- cos(59.89444) = 0,501595
Это значит, что 1 градус в верхнем основании нашей трапеции =111,3*0,501595=55,82749 км, а один градус в нижнем основании трапеции =111,3*0,562773=62,6366 км. Поскольку число градусов одинаково как в верхнем, так и в нижнем основаниях трапеции и составляет 37,6156-30,26417, то есть 7,35143 градуса. Но число километров в верхнем и нижнем основаниях трапеции не одинаковое.
Рассчитаем эти расстояния в километрах. BC=7,35143*55,82749=410,4119 км.
AD=7,35143*62,6366=460,469 км.
Теперь проведем высоту BH в нашей трапеции:
В прямоугольном треугольнике ABH нам известно, что гипотенуза равна 460,2029 км, малый катет тоже известен (это половина разницы между длинами оснований трапеции, то есть 0,5*[460,469-410,4119], то есть 0,5*50,05711, или 25,02856 км).
Итак, найдем высоту трапеции ABCD, ее можно вычислить с помощью теоремы Пифагора. Напомню, что мы знаем и длину гипотенузы, и длину наименьшего из катетов.
- Квадрат гипотенузы: 211786,7
- Квадрат известного катета: 626,4
- Разность между этими числами: 211160,2
Корень из этой разности – 459,5218 км. Это и есть наша высота трапеции, то есть BH.
Задача почти решена. Для нахождения расстояния между Москвой и Питером нам нужно вычислить диагональ трапеции, то есть BD. Нарисуем эту линию:
Итак, у нас есть треугольник BHD. BH мы только что вычислили (459,5218 км), HD тоже известно (нужно от большего основания трапеции отнять AH. 460,469-25,02856=435,4404).
Два катета известны, нужно найти гипотенузу. По той же теореме Пифагора, и мы увидим, что гипотенуза будет равна 633,0629 км. Это и есть расстояние от Питера до Москвы.
Проверим наши вычисления, спросив у Яндекса, сколько составляет расстояние от Питера до Москвы.
Мы увидим ответ – 634 км. При вычислениях по нашей методике получилось чуть больше, чем 633 км. Это значит, что погрешность при данном виде вычислений достаточна мала. Но если учесть, что крупные города – это не маленькие точки, а большие расстояния с севера на юг и с запада на восток, то можно сказать, что мы вычислили все правильно.
А на этом пока всё, подписывайтесь на мой канал и до новых встреч!
Расчет расстояний между точками по их координатам на плоскости элементарен, на поверхности Земли — немного посложнее: мы рассмотрим измерение расстояния и начального азимута между точками без проекционных преобразований.
Для начала разберемся в терминологии.
Введение
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения.
Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут отличен от постоянного, следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.

Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или π*R, где R – радиус сферы.

На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.

Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.
Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.
Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.
Формулы
Существует три способа расчета сферического расстояния большого круга.
1. Сферическая теорема косинусов
В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением.
φ1, λ1; φ2, λ2 — широта и долгота двух точек в радианах
Δλ — разница координат по долготе
Δδ — угловая разница
Δδ = arccos {sin φ1 sin φ2 + cos φ1 cos φ2 cos Δλ}
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).
2. Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.
3. Модификация для антиподов
Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.
Моя реализация на РНР
// Радиус земли
define('EARTH_RADIUS', 6372795);
/*
* Расстояние между двумя точками
* $φA, $λA - широта, долгота 1-й точки,
* $φB, $λB - широта, долгота 2-й точки
* Написано по мотивам http://gis-lab.info/qa/great-circles.html
* Михаил Кобзарев <mikhail@kobzarev.com>
*
*/
function calculateTheDistance ($φA, $λA, $φB, $λB) {
// перевести координаты в радианы
$lat1 = $φA * M_PI / 180;
$lat2 = $φB * M_PI / 180;
$long1 = $λA * M_PI / 180;
$long2 = $λB * M_PI / 180;
// косинусы и синусы широт и разницы долгот
$cl1 = cos($lat1);
$cl2 = cos($lat2);
$sl1 = sin($lat1);
$sl2 = sin($lat2);
$delta = $long2 - $long1;
$cdelta = cos($delta);
$sdelta = sin($delta);
// вычисления длины большого круга
$y = sqrt(pow($cl2 * $sdelta, 2) + pow($cl1 * $sl2 - $sl1 * $cl2 * $cdelta, 2));
$x = $sl1 * $sl2 + $cl1 * $cl2 * $cdelta;
//
$ad = atan2($y, $x);
$dist = $ad * EARTH_RADIUS;
return $dist;
}
Пример вызова функции:
$lat1 = 77.1539; $long1 = -139.398; $lat2 = -77.1804; $long2 = -139.55; echo calculateTheDistance($lat1, $long1, $lat2, $long2) . " метров"; // Вернет "17166029 метров"
Статья взята с сайта gis-lab.info Автор: Максим Дубинин
Ссылки
- Вычисление расстояния и начального азимута между двумя точками на сфере(официальный источник)
- Haversine formula
- Способы расчета сферического расстояния большого круга
- Сферическая система координат
- Сферические координаты
- Calculate distance, bearing and more between Latitude/Longitude points
coordinates distance PHP tips tricks










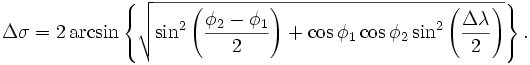
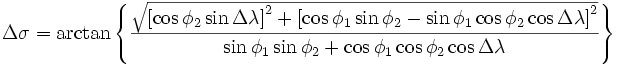
































![begin{align}
tanphi_1' &= frac{tanphi}B,\
Deltaphi' &= frac{Delta phi}{B}biggl[1 + frac{3 e'^2 }{4 B^2}(Delta phi) sin (2 phi_1 + tfrac23 Delta phi )biggr],\
Deltalambda' &= ADeltalambda,
end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7718f268ebe1f627fa63ebfceabc20f8e847b431)



