Как найти расстояние между точками определение - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Представьте расстояние между двумя точками в виде отрезка прямой линии, соединяющего эти точки. Длину этого отрезка можно найти по формуле: √ $(x2-x1)^{2}+(y2-y1)^{2}$ .

Шаги

1
Определите координаты двух точек, расстояние между которыми вы хотите вычислить. Обозначим их Точка 1 (x1,y1) и Точка 2 (x2,y2). Неважно, как именно вы обозначите точки, главное, не перепутать их координаты при расчетах.^[1]
- x1 − это горизонтальная координата (вдоль оси x) Точки 1, а x2 − горизонтальная координата Точки 2. Соответственно, y1 − вертикальная координата (вдоль оси y) Точки 1, и y2 − вертикальная координата Точки 2.
- Возьмем, например, точки (3,2) и (7,8). Если мы примем, что (3,2) − это (x1,y1), тогда (7,8) − это (x2,y2).
2

Ознакомьтесь с формулой для вычисления расстояния. Эта формула позволяет найти длину прямого отрезка, соединяющего две точки, Точку 1 и Точку 2. Длина этого отрезка равна квадратному корню от суммы квадратов расстояний между точками по горизонтали и вертикали. Проще говоря, это квадратный корень из $(x2-x1)^{2}+(y2-y1)^{2}$ .^[2]
3
Найдите, чему равны расстояния между точками по горизонтали и вертикали. Расстояние по вертикали найдем в виде разности y2 – y1. Соответственно, расстояние по горизонтали составит x2 – x1. Не волнуйтесь, если в результате вычитания вы получите отрицательное значение. Следующим шагом будет возведение найденных расстояний в квадрат, что в любом случае даст положительное целое число.^[3]
- Найдите расстояние вдоль оси y. Для нашего примера с точками (3,2) и (7,8), где координаты (3,2) соответствуют Точке 1, а координаты (7,8) − Точке 2, находим: (y2 – y1) = 8 – 2 = 6. Это значит, что расстояние между нашими точками по оси y равно шести единицам длины.
- Найдите расстояние вдоль оси x. Для нашего примера с точками (3,2) и (7,8) получаем: (x2 – x1) = 7 – 3 = 4. Это значит, что по оси x наши точки разделяет расстояние, равное четырем единицам длины.
4
Возведите оба значения в квадрат. Необходимо по отдельности возвести в квадрат расстояние вдоль оси x, равное (x2 – x1), и расстояние вдоль оси y, составляющее (y2 – y1):
- $6^{2}=36$
- $4^{2}=16$
5

Сложите полученные значения. В результате вы найдете квадрат диагонали, то есть расстояния между двумя точками. В нашем примере для точек с координатами (3,2) и (7,8) находим: (7 – 3) в квадрате равно 36, и (8 – 2) в квадрате равно 16. Складывая, получаем 36 + 16 = 52.
6
Извлеките квадратный корень из найденной величины. Это последний шаг. Расстояние между двумя точками равно квадратному корню от суммы квадратов расстояний вдоль оси x и вдоль оси y.^[4]
- Для нашего примера находим: расстояние между точками (3,2) и (7,8) равно корню квадратному из 52, то есть примерно 7,21 единицы длины.
Реклама

Советы

Не страшно, если в результате вычитания y2 – y1 или x2 – x1 у вас получилось отрицательное значение. Поскольку затем разность возводится в квадрат, расстояние все равно будет равно положительному числу.

Об этой статье

Эту страницу просматривали 89 362 раза.

Была ли эта статья полезной?

Источник

Решение задач по математике у учащихся часто сопровождается многими трудностями. Помочь учащемуся справиться с этими трудности, а так же научить применять имеющиеся у него теоретические знания при решении конкретных задач по всем разделам курса предмета «Математика» – основное назначение нашего сайта.

Приступая к решению задач по теме «Расстояние между двумя точками на плоскости», учащиеся должны уметь строить точку на плоскости по ее координатам, а так же находить координаты заданной точки.

Вычисление расстояния между взятыми на плоскости двумя точками А(х_А; у_А) и В(х_В; у_В), выполняется по формуле d = √((х_А – х_В)² + (у_А – у_В)²), где d – длина отрезка, который соединяет эти точки на плоскости.

Если один из концов отрезка совпадает с началом координат, а другой имеет координаты М(х_М; у_М), то формула для вычисления d примет вид ОМ = √(х_М² + у_М²).

1. Вычисление расстояния между двумя точками по данным координатам этих точек

Пример 1.

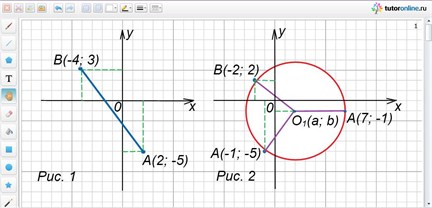
Найти длину отрезка, который соединяет на координатной плоскости точки А(2; -5) и В(-4; 3) (рис. 1).

Решение.

В условии задачи дано: х_А = 2; х_В = -4; у_А = -5 и у_В = 3. Найти d.

Применив формулу d = √((х_А – х_В)² + (у_А – у_В)²), получим:

d = АВ = √((2 – (-4))² + (-5 – 3)²) = 10.

2. Вычисление координат точки, которая равноудалена от трех заданных точек

Пример 2.

Найти координаты точки О₁, которая равноудалена от трех точек А(7; -1) и В(-2; 2) и С(-1; -5).

Решение.

Из формулировки условия задачи следует, что О₁А = О₁В = О₁С. Пусть искомая точка О₁ имеет координаты (а; b). По формуле d = √((х_А – х_В)² + (у_А – у_В)²) найдем:

О₁А = √((а – 7)² + (b + 1)²);

О₁В = √((а + 2)² + (b – 2)²);

О₁С = √((а + 1)² + (b + 5)²).

Составим систему из двух уравнений:

{√((а – 7)² + (b + 1)²) = √((а + 2)² + (b – 2)²),
{√((а – 7)² + (b + 1)²) = √((а + 1)² + (b + 5)²).

После возведения в квадрат левой и правой частей уравнений запишем:

{(а – 7)² + (b + 1)² = (а + 2)² + (b – 2)²,
{(а – 7)² + (b + 1)² = (а + 1)² + (b + 5)².

Упростив, запишем

{-3а + b + 7 = 0,
{-2а – b + 3 = 0.

Решив систему, получим: а = 2; b = -1.

Точка О₁(2; -1) равноудалена от трех заданных в условии точек, которые не лежат на одной прямой. Эта точка – есть центр окружности, проходящей через три заданные точки (рис. 2).

3. Вычисление абсциссы (ординаты) точки, которая лежит на оси абсцисс (ординат) и находится на заданном расстоянии от данной точки

Пример 3.

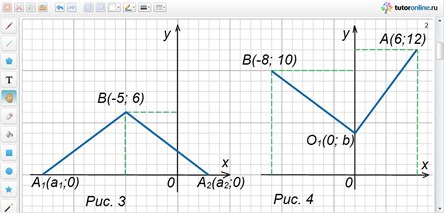
Расстояние от точки В(-5; 6) до точки А, лежащей на оси Ох равно 10. Найти точку А.

Решение.

Из формулировки условия задачи следует, что ордината точки А равна нулю и АВ = 10.

Обозначив абсциссу точки А через а, запишем А(а; 0).

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) находим:

АВ = √((а + 5)² + (0 – 6)²) = √((а + 5)² + 36).

Получаем уравнение √((а + 5)² + 36) = 10. Упростив его, имеем

а² + 10а – 39 = 0.

Корни этого уравнения а₁ = -13; а₂ = 3.

Получаем две точки А₁(-13; 0) и А₂(3; 0).

Проверка:

А₁В = √((-13 + 5)² + (0 – 6)²) = 10.

А₂В = √((3 + 5)² + (0 – 6)²) = 10.

Обе полученные точки подходят по условию задачи (рис. 3).

4. Вычисление абсциссы (ординаты) точки, которая лежит на оси абсцисс (ординат) и находится на одинаковом расстоянии от двух заданных точек

Пример 4.

Найти на оси Оу точку, которая находится на одинаковом расстоянии от точек А(6; 12) и В(-8; 10).

Решение.

Пусть координаты нужной по условию задачи точки, лежащей на оси Оу, будут О₁(0; b) (у точки, лежащей на оси Оу, абсцисса равна нулю). Из условия следует, что О₁А = О₁В.

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) находим:

О₁А = √((0 – 6)² + (b – 12)²) = √(36 + (b – 12)²);

О₁В = √((а + 8)² + (b – 10)²) = √(64 + (b – 10)²).

Имеем уравнение √(36 + (b – 12)²) = √(64 + (b – 10)²) или 36 + (b – 12)² = 64 + (b – 10)².

После упрощения получим: b – 4 = 0, b = 4.

Необходимая по условию задачи точка О₁(0; 4) (рис. 4).

5. Вычисление координат точки, которая находится на одинаковом расстоянии от осей координат и некоторой заданной точки

Пример 5.

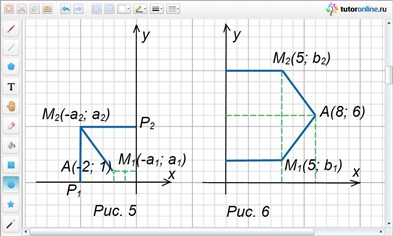
Найти точку М, расположенную на координатной плоскости на одинаковом расстоянии от осей координат и от точки А(-2; 1).

Решение.

Необходимая точка М, как и точка А(-2; 1), располагается во втором координатном углу, так как она равноудалена от точек А, Р₁ и Р₂ (рис. 5). Расстояния точки М от осей координат одинаковые, следовательно, ее координатами будут (-a; a), где а > 0.

Из условия задачи следует, что МА = МР₁ = МР₂, МР₁ = а; МР₂ = |-a|,

т.е. |-a| = а.

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) находим:

МА = √((-а + 2)² + (а – 1)²).

Составим уравнение:

√((-а + 2)² + (а – 1)²) = а.

После возведения в квадрат и упрощения имеем: а² – 6а + 5 = 0. Решим уравнение, найдем а₁ = 1; а₂ = 5.

Получаем две точки М₁(-1; 1) и М₂(-5; 5), удовлетворяющие условию задачи.

6. Вычисление координат точки, которая находится на одинаковом заданном расстоянии от оси абсцисс (ординат) и от данной точки

Пример 6.

Найти точку М такую, что расстояние ее от оси ординат и от точки А(8; 6) будет равно 5.

Решение.

Из условия задачи следует, что МА = 5 и абсцисса точки М равна 5. Пусть ордината точки М равна b, тогда М(5; b) (рис. 6).

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) имеем:

МА = √((5 – 8)² + (b – 6)²).

Составим уравнение:

√((5 – 8)² + (b – 6)²) = 5. Упростив его, получим: b² – 12b + 20 = 0. Корни этого уравнения b₁ = 2; b₂ = 10. Следовательно, есть две точки, удовлетворяющие условию задачи: М₁(5; 2) и М₂(5; 10).

Известно, что многие учащиеся при самостоятельном решении задач нуждаются в постоянных консультациях по приемам и методам их решения. Зачастую, найти путь к решению задачи без помощи преподавателя учащемуся не под силу. Необходимые консультации по решению задач учащийся и может получить на нашем сайте.

Остались вопросы? Не знаете, как найти расстояние между двумя точками на плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

Источник

На этой странице находится все необходимое, чтобы найти расстояние между двумя точками. Просто введите координаты точек и получите ответ и подробное решение с помощью наших онлайн-калькуляторов. Кроме того на сайте можно найти координаты середины отрезка.

Расстояние между двумя точками – это длина отрезка, соединяющего эти точки.

Формула расстояния между двумя точками на плоскости:

d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}}

x_a и y_a – координаты первой точки A,

x_b и y_b – координаты второй точки B

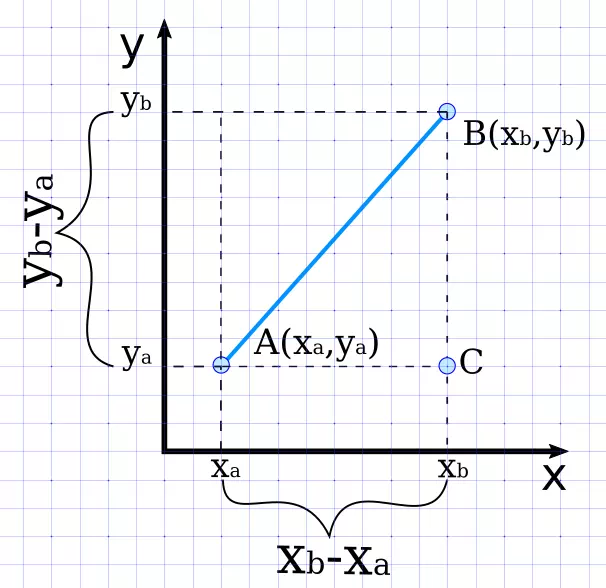
Нахождение расстояния между двумя точками на плоскости сводится к решению треугольника, а точнее – нахождению его гипотенузы. Для этого используется теорема Пифагора. Посмотрите на рисунок.

Соединив отрезком точки A и B, а также опустив перпендикуляры на оси мы получим треугольник ABC. В этом треугольнике стороны AC и BC являются катетами прямоугольного треугольника, а AB – его гипотенузой. Длины катетов AC и BC найти довольно просто:

AC = x_b – x_a

BC = y_b – y_a

Осталось применить теорему Пифагора и получить сторону AB, которая является гипотенузой прямоугольного треугольника и расстоянием между точками A и B:

AB=sqrt{{AC}^2 + {BC^2}}

Подставив вместо отрезков AC и BC их длины, получим итоговую формулу расстояния между двумя точками:

AB=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}} или d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}}

Формула расстояния между двумя точками в пространстве:

{d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2} + {(z_b – z_a)^2}}}

x_a, y_a и z_a – координаты первой точки A,

x_b, y_b и z_b – координаты второй точки B

Примеры задач на вычисление середины отрезка

Задача 1

Найдите расстояние между точками А и В, если А(2; 7), В(-2; 7).

Решение

Подставим координаты точек в формулу расстояния между двумя точками на плоскости и вычислим результат:

d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}} = sqrt{{(-2 – 2)}^2 + {(7 – 7)^2}} = sqrt{{-4}^2 + {0^2}} = sqrt{16 + 0} = sqrt{16} = 4

Мы получили расстояние между точками и оно равно 4.

Ответ: 4.

Проверим результат с помощью калькулятора .

Источник

Здесь будет калькулятор

Расстояние между двумя точками на прямой

Рассмотрим координатную прямую, на которой отмечены 2 точки: AA и BB. Чтобы найти расстояние между этими точками, нужно найти длину отрезка ABAB. Это делается при помощи следующей формулы:

Расстояние между двумя точками на прямой

AB=∣a−b∣AB=|a-b|,

где a,ba, b — координаты этих точек на прямой (координатной прямой).

Ввиду того, что в формуле присутствует модуль, при решении не принципиально, из какой координаты какую вычитать (так как берется абсолютная величина этой разности).

То есть:

∣a−b∣=∣b−a∣|a-b|=|b-a|

Разберем пример, чтобы лучше понять решение подобных задач.

Пример 1

На координатной прямой отмечены точка AA, координата которой равна 99 и точка BB с координатой −1-1. Нужно найти расстояние между этими двумя точками.

Решение

Здесь a=9,b=−1a=9, b=-1

Пользуемся формулой и подставляем значения:

AB=∣a−b∣=∣9−(−1)∣=∣10∣=10AB=|a-b|=|9-(-1)|=|10|=10

Ответ

Расстояние между двумя точками на плоскости

Рассмотрим две точки, заданные на плоскости. Из каждой отмеченной на плоскости точки нужно опустить по два перпендикуляра: На ось OXOX и на ось OYOY. Затем рассматривается треугольник ABCABC. Так как он является прямоугольным (BCBC перпендикулярно ACAC), то найти отрезок ABAB, он же является и расстоянием между точками, можно с помощью теоремы Пифагора. Имеем:

AB2=AC2+BC2AB^2=AC^2+BC^2

Но, исходя из того, что длина ACAC равна xB−xAx_B-x_A, а длина BCBC равна yB−yAy_B-y_A, эту формулу можно переписать в следующем виде:

Расстояние между двумя точками на плоскости

AB=(xB−xA)2+(yB−yA)2AB=sqrt{(x_B-x_A)^2+(y_B-y_A)^2},

где xA,yAx_A, y_A и xB,yBx_B, y_B — координаты точек AA и BB соответственно.

Пример 2

Необходимо найти расстояние между точками CC и FF, если координаты первой (8;−1)(8;-1), а второй — (4;2)(4;2).

Решение

xC=8x_C=8
yC=−1y_C=-1
xF=4x_F=4
yF=2y_F=2

CF=(xF−xC)2+(yF−yC)2=(4−8)2+(2−(−1))2=16+9=25=5CF=sqrt{(x_F-x_C)^2+(y_F-y_C)^2}=sqrt{(4-8)^2+(2-(-1))^2}=sqrt{16+9}=sqrt{25}=5

Ответ

Расстояние между двумя точками в пространстве

Нахождение расстояния между двумя точками в этом случае происходит аналогично предыдущему за исключением того, что координаты точки в пространстве задаются тремя числами, соответственно, в формулу нужно добавить еще и координату оси аппликат. Формула примет такой вид:

Расстояние между двумя точками в пространстве

AB=(xB−xA)2+(yB−yA)2+(zB−zA)2AB=sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}

Пример 3

Найти длину отрезка FKFK в пространстве, если координаты точек его концов таковы: (−1;−1;8)(-1;-1;8) и (−3;6;0)(-3;6;0). Ответ округлить до целого числа.

Решение

F=(−1;−1;8)F=(-1;-1;8)
K=(−3;6;0)K=(-3;6;0)

FK=(xK−xF)2+(yK−yF)2+(zK−zF)2=(−3−(−1))2+(6−(−1))2+(0−8)2=117≈10.8FK=sqrt{(x_K-x_F)^2+(y_K-y_F)^2+(z_K-z_F)^2}=sqrt{(-3-(-1))^2+(6-(-1))^2+(0-8)^2}=sqrt{117}approx10.8

По условию задачи нам нужно округлить ответ до целого числа.

Ответ

Источник

В данной публикации мы рассмотрим, чему равно расстояние между двумя точками, и по какой формуле оно считается (на плоскости и в пространстве). Также разберем примеры решения задач по этой теме.