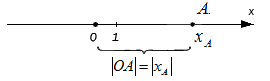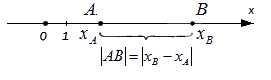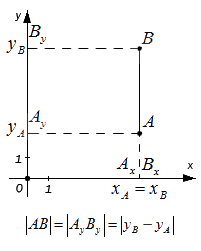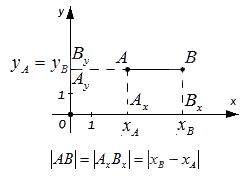Пересечение двух окружностей
Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай – окружности совпадают (это одна и та же окружность) | ||
| Окружности не касаются друг друга | r1 + r2″ /> | |
| Одна окружность содержится внутри другой и не касается ее | ||
| Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше | |
| Окружности соприкасаются в одной точке | Частный случай предыдущего |
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
Сначала калькулятор находит отрезок a
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
Всё про окружность и круг
Окружность – это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол – это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Расстояние между двумя точками онлайн
С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку “Решить”. Теоретическую часть смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между двумя точками на прямой
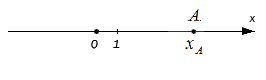
Пусть заданы на оси OX точки A с координатой xa и B с координатой xb (Рис.1). Найдем расстояние между точками A и B.
Расстояние между точками A и В равно:
| ( small AB=OB-OA. ) | (1) |
Поскольку расстояние от O до В равна xb, а расстояние от O до A равна xa, получим:
| ( small AB=x_b-x_a . ) | (2) |
На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:
| ( small AB=OB+OA. ) | (3) |
Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:
| ( small AB=x_b+|x_a|=x_b-x_a . ) | (4) |
На рисунке 3 точки A и В находятся c левой стороны начала координат O.
B этом случае рассояние между точками A и B равно:
| ( small AB=OA-OB. ) | (5) |
Координаты точек A и B отрицательны. Тогда , то (5) можно записать так:
| ( small AB=|x_a|-|x_b|=x_b-x_a . ) | (6) |
Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).
Формулы (2),(4),(6) можно записать и так:
| ( small AB=|x_b-x_a|= |x_a-x_b| . ) | (7) |
Пример 1. на оси Ox заданы точки ( small A(x_a)=A(-4) ) и ( small B(x_b)=B(7) ) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):
| ( small AB=|x_b-x_a|= |7-(-4)|=11 . ) | (7) |
Расстояние между двумя точками на плоскости
Пусть на плоскости задана декартова прямоугольная система координат XOY и пусть на плоскости заданы точки A и B, где A имеет координаты (xa,ya), а B имеет координаты (xb,yb) (Рис.4).
Учитывая результаты предыдующего параграфа, можем найти расстояние между точками A и M, а также расстояние между точками B и M:
| ( small AM=x_b-x_a,;; BM=y_b-y_a. ) | (8) |
ABM является прямоугольным треугольником, где AB гипотенуза, а AM и BM катеты. Тогда, исходя из теоремы Пифагора, имеем:
( small AB^2=AM^2+BM^2. )
Тогда, учитывая (8), получим:
( small AB^2=AM^2+BM^2=(x_b-x_a)^2+(y_b-y_a)^2. )
| ( small AB=sqrt <(x_b-x_a)^2+(y_b-y_a)^2>. ) | (9) |
Пример 2. На плоскости, в декартовой прямоугольной системе координат XOY заданы точки ( small A(x_a; y_a)=A(-6;3) ) и ( small B(x_b, y_b)=B(11,-4). ) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек A и B в формулу (9), получим:
Ответ: .
Расстояние между двумя точками в пространстве
Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (xa,ya,za), а B имеет координаты (xb,yb,zb) (Рис.5).
AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника. Тогда, по теореме Пифагора, имеем:
| ( small AB^2=AM^2+BM^2. ) | (10) |
Учитывая, что BM равно разности третьих координат точек B и A, получим:
Из предыдующего параграфа следует, что:
| ( small A’B’^2=(x_b-x_a)^2+(y_b-y_a)^2. ) | (11) |
Но AM=A’B’. Тогда из (10) и (11) следует:
( small AB^2=AM^2+BM^2=A’B’^2+BM^2 ) ( small =(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2. )
| ( small AB= sqrt<(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2>. ) | (12) |
Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки ( small A(x_a; y_a ; z_a)=A(5;1;0) ) и ( small B(x_b, y_b, z_b)=B(-8,-4;21). ) Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:
Ответ: .
[spoiler title=”источники:”]
http://www.stranamam.ru/post/8974384/
http://matworld.ru/analytic-geometry/rasstoyanie-mezhdu-dvumya-tochkami.php
[/spoiler]
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Точность вычисления
Знаков после запятой: 2
Проверка расстояния между окружностями
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай – окружности совпадают (это одна и та же окружность) | ||
 |
Окружности не касаются друг друга | |
 |
Одна окружность содержится внутри другой и не касается ее | |
  |
Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше |
  |
Окружности соприкасаются в одной точке | Частный случай предыдущего |
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
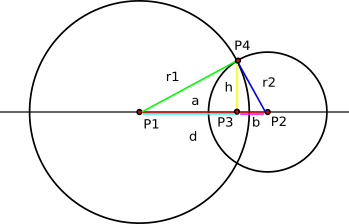
Сначала калькулятор находит отрезок a
и затем отрезок h
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Вторая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
Как найти расстояние между точками на окружности
Содержание
- Расстояние между точками на координатной прямой
- Расстояние между точками на плоскости
- Расстояние между точками в пространстве
- Примеры решения задач на нахождение расстояния между точками
- Содержание
- Общие определения
- Касательная к окружности
- Углы в окружности
- Вписанная окружность
- Описанная окружность
- Теорема Птолемея
Имеем окружность (радиус не имеет значения, например 1), на которой расположены некие точки, полученные при пересечении этой окружности лучом, исходящим из центра окружности под произвольным углом. Как реализовать алгоритм нахождения ближайшей из точек А, В, С, Д и тд N (доступных по варианту) к точке X, являющейся известной заранее. Пробовал по формуле нахождения минимальной хорды и минимального угла — получаю неверный результат. Реализовать мне это нужно в Excel.
Alex Nikush: Итак, решение я нашел: =МИН(ABS(ЕСЛИ($C$2:$C$4-$E$2 19 Ноября в 15:42 и в 19:10 .
“Шапка” табл.1 (Объект/Луч/Субъект/Код) — A1:D1
Данные табл.1 A2:C6
“Шапка” табл.2 (Субъект/Код/Луч) — A9:C9
Данные табл.2 A10:C15
В D2 формула массива:
Протянуть формулу по строкам (D2:D6)
Формула тяжелая, облегчение возможно, но нужно “щупать” живой файл.
Без файла Excel воспроизведение решения трудоемкое.
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
Исходные данные: координатная прямая O x и лежащая на ней произвольная точка А . Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число х A , оно же – координата точки А .
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.
К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О , необходимо будет отложить три единичных отрезка. Если точка А имеет координату — 4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние О А равно 3 ; во втором случае О А = 4 .
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О ) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4 111 .
Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна 11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то O A = x A (число принимается за расстояние); если координата меньше нуля, то O A = — x A . В общем, эти утверждения справедливы для любого действительного числа x A .
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
- 0, если точка совпадает с началом координат;
- x A , если x A > 0 ;
- — x A , если x A 0 .
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B , лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты x A и x B : A B = x B — x A .
Расстояние между точками на плоскости
Исходные данные: точки A и B , лежащие на плоскости в прямоугольной системе координат O x y с заданными координатами: A ( x A , y A ) и B ( x B , y B ) .
Проведем через точки А и B перпендикуляры к осям координат O x и O y и получим в результате точки проекции: A x , A y , B x , B y . Исходя из расположения точек А и B далее возможны следующие варианты:
— если точки А и В совпадают, то расстояние между ними равно нулю;
— если точки А и В лежат на прямой, перпендикулярной оси O x (оси абсцисс), то точки и совпадают, а | А В | = | А y B y | . Поскольку, расстояние между точками равно модулю разности их координат, то A y B y = y B — y A , а, следовательно A B = A y B y = y B — y A .
— если точки A и B лежат на прямой, перпендикулярной оси O y (оси ординат) – по аналогии с предыдущим пунктом: A B = A x B x = x B — x A
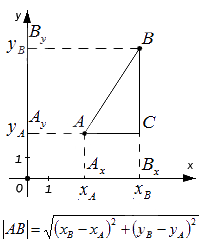
— если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
Мы видим, что треугольник А В С является прямоугольным по построению. При этом A C = A x B x и B C = A y B y . Используя теорему Пифагора, составим равенство: A B 2 = A C 2 + B C 2 ⇔ A B 2 = A x B x 2 + A y B y 2 , а затем преобразуем его: A B = A x B x 2 + A y B y 2 = x B — x A 2 + y B — y A 2 = ( x B — x A ) 2 + ( y B — y A ) 2
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
A B = ( x B — x A ) 2 + ( y B — y A ) 2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: A B = ( x B — x A ) 2 + ( y B — y A ) 2 = 0 2 + 0 2 = 0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
A B = ( x B — x A ) 2 + ( y B — y A ) 2 = 0 2 + ( y B — y A ) 2 = y B — y A
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
A B = ( x B — x A ) 2 + ( y B — y A ) 2 = ( x B — x A ) 2 + 0 2 = x B — x A
Расстояние между точками в пространстве
Исходные данные: прямоугольная система координат O x y z с лежащими на ней произвольными точками с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить расстояние между этими точками.
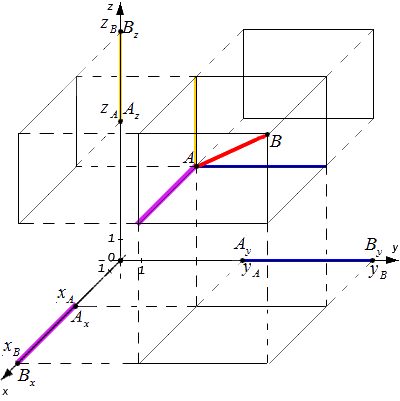
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: A x , A y , A z , B x , B y , B z
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: A x B x , A y B y и A z B z
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2
Используя полученные ранее выводы, запишем следующее:
A x B x = x B — x A , A y B y = y B — y A , A z B z = z B — z A
A B 2 = A x B x 2 + A y B y 2 + A z B z 2 = x B — x A 2 + y B — y A 2 + z B — z A 2 = = ( x B — x A ) 2 + ( y B — y A ) 2 + z B — z A 2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
A B = x B — x A 2 + y B — y A 2 + ( z B — z A ) 2
Полученная формула действительна также для случаев, когда:
— лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A ( 1 — 2 ) и B ( 11 + 2 ) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B .
Решение
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно O A = 1 — 2 = 2 — 1
- Расстояние между точками A и B определим как модуль разности координат этих точек: A B = 11 + 2 — ( 1 — 2 ) = 10 + 2 2
Ответ: O A = 2 — 1 , A B = 10 + 2 2
Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A ( 1 , — 1 ) и B ( λ + 1 , 3 ) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние А В будет равно 5 .
Решение
Чтобы найти расстояние между точками A и B , необходимо использовать формулу A B = ( x B — x A ) 2 + y B — y A 2
Подставив реальные значения координат, получим: A B = ( λ + 1 — 1 ) 2 + ( 3 — ( — 1 ) ) 2 = λ 2 + 16
А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:
λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3
Ответ: А В = 5 , если λ = ± 3 .
Исходные данные: задано трехмерное пространство в прямоугольной системе координат O x y z и лежащие в нем точки A ( 1 , 2 , 3 ) и B — 7 , — 2 , 4 .
Решение
Для решения задачи используем формулу A B = x B — x A 2 + y B — y A 2 + ( z B — z A ) 2
Подставив реальные значения, получим: A B = ( — 7 — 1 ) 2 + ( — 2 — 2 ) 2 + ( 4 — 3 ) 2 = 81 = 9
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
Содержание
Общие определения
Окружность — это множество точек, которое располагается на одинаковом расстоянии от ее центра, представленного точкой.
Для любой точки L , лежащей на окружности, действует равенство OL=R . (Длина отрезка OL равняется радиусу окружности).
Отрезок, который соединяет две точки окружности, является ее хордой.
Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D) . Диаметр можно вычислить по формуле: D=2R
Длина окружности вычисляется по формуле: C=2pi R
Площадь круга: S=pi R^
Дугой окружности называется та ее часть, которая располагается между двух ее точек. Эти две точки и определяют две дуги окружности. Хорда CD стягивает две дуги: CMD и CLD . Одинаковые хорды стягивают одинаковые дуги.
Центральным углом называется такой угол, который находится между двух радиусов.
Длину дуги можно найти по формуле:
- Используя градусную меру: CD = frac<pi R alpha ^<circ>><180^<circ>>
- Используя радианную меру: CD = alpha R
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
ANcdot NB = CN cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей.
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.
Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть.
AC cdot BC = EC cdot DC
Углы в окружности
Градусные меры центрального угла и дуги, на которую тот опирается, равны.
angle COD = cup CD = alpha ^
Вписанный угол — это угол, вершина которого находится на окружности, а стороны содержат хорды.
Вычислить его можно, узнав величину дуги, так как он равен половине этой дуги.
angle AOB = 2 angle ADB
Опирающийся на диаметр, вписанный угол, прямой.
angle CBD = angle CED = angle CAD = 90^
Вписанные углы, которые опираются на одну дугу, тождественны.
angle ADB = angle AEB = angle AFB
Опирающиеся на одну хорду вписанные углы тождественны или их сумма равняется 180^ <circ>.
angle ADB + angle AKB = 180^
angle ADB = angle AEB = angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
angle DMC = angle ADM + angle DAM = frac<1> <2>left ( cup DmC + cup AlB
ight )
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
angle M = angle CBD — angle ACB = frac<1> <2>left ( cup DmC — cup AlB
ight )
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника.
В точке пересечения серединных перпендикуляров сторон этой фигуры будет находиться центр описанной окружности.
Радиус можно найти, вычислив его как радиус окружности, которая описана около треугольника, определенного любыми 3 -мя вершинами многоугольника.
Есть следующее условие: окружность возможно описать около четырехугольника только, если сумма его противоположных углов равна 180^ < circ>.
angle A + angle C = angle B + angle D = 180^
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
16. Задачи по планиметрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи с окружностями
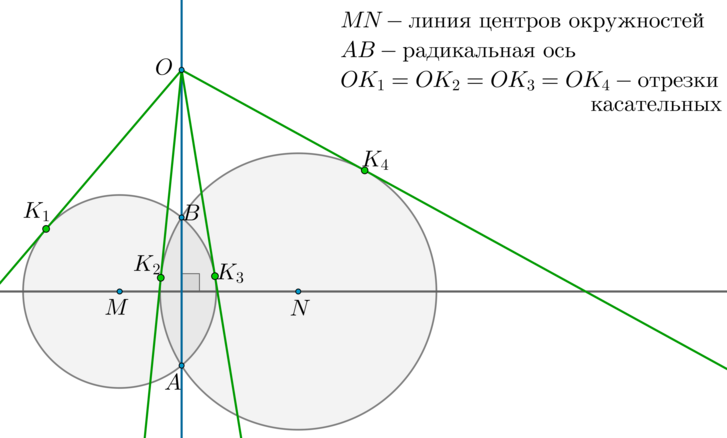
(blacktriangleright) Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.
Радикальная ось перпендикулярна линии центров окружностей. Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.
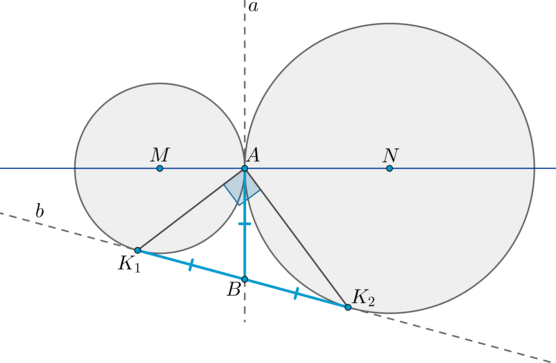
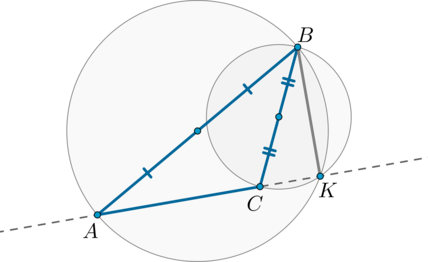
(blacktriangleright) Пусть две окружности с центрами (M) и (N) касаются внешним образом в точке (A). Две общие касательные (внутренняя и внешняя) (a) и (b) этих окружностей пересекаются в точке (B). Точки касания — точки (A, K_1, K_2). Тогда [{large{K_1B=AB=K_2B}}] [{large{angle K_1AK_2=90^circ}}]
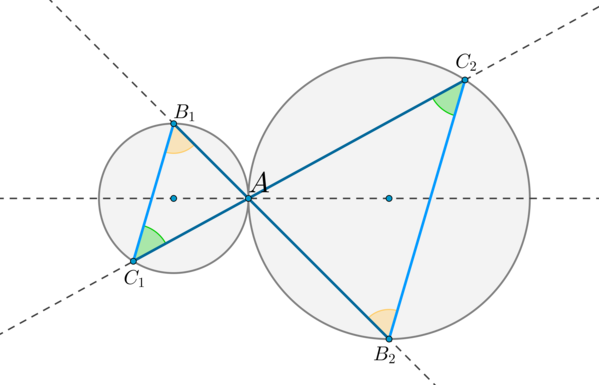
(blacktriangleright) Пусть две окружности касаются внешним образом в точке (A). Через точку (A) проведены две прямые (B_1B_2) и (C_1C_2), пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: [{large{triangle AB_1C_1 sim triangle
AB_2C_2}}] [{large{B_1C_1parallel B_2C_2}}]
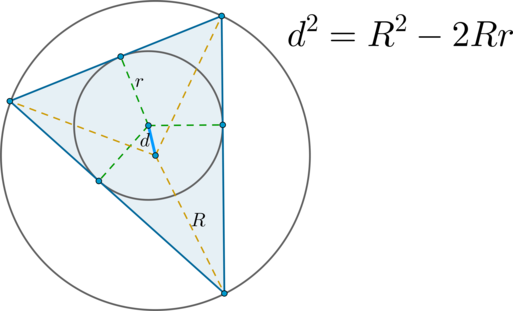
(blacktriangleright) Формула Эйлера: Пусть (R) — радиус описанной около треугольника окружности, (r) — радиус вписанной окружности. Тогда расстояние между центрами этих окружностей вычисляется по формуле:
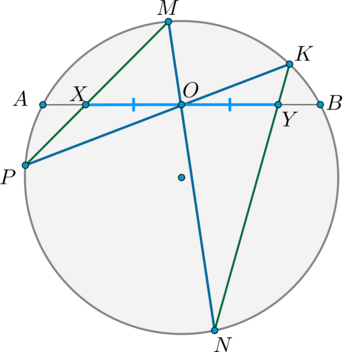
(blacktriangleright) Теорема о бабочке: Пусть через середину хорды (AB) — точку (O), проведены две хорды (MN) и (KP). Пусть (MPcap AB=X, KNcap AB=Y). Тогда [{large{OX=OY}}]
Задание
1
#2378
Уровень задания: Легче ЕГЭ
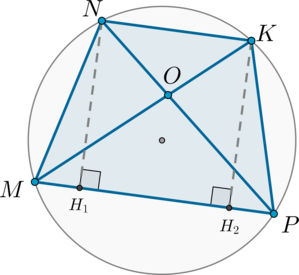
В окружность вписан четырехугольник (MNKP), причем площади треугольников (MNP) и (MKP) равны.
Докажите, что треугольник (NOK) – равнобедренный, где (O) – точка пересечения отрезков (MK) и (NP).
Т.к. (S_{triangle MNP}=S_{triangle MKP}) и эти треугольники имеют общее основание (MP), то [frac12cdot MPcdot NH_1=frac12cdot MPcdot KH_2 quad Rightarrow quad
NH_1=KH_2]
Таким образом, точки (N) и (K) находятся на одинаковом расстоянии от прямой (MP), следовательно, (NKparallel MP). Таким образом, (MNKP) – трапеция, вписанная в окружность. Т.к. параллельные прямые отсекают от окружности равные дуги, то меньшие полуокружности дуги (buildrelsmileover{MN}=buildrelsmileover{KP}). Т.к. равные дуги стягиваются равными хордами, то отрезки (MN) и (KP) равны. Следовательно, трапеция (MNKP) является равнобедренной.
В равнобедренной трапеции (triangle MOP) и (triangle NOK) являются равнобедренными, чтд.
Действительно, вписанные углы (angle NKM) и (angle KNP) равны, т.к. опираются на равные дуги, следовательно, (triangle NOK) – равнобедренный.
Ответ:
Доказательство
Задание
2
#2379
Уровень задания: Легче ЕГЭ
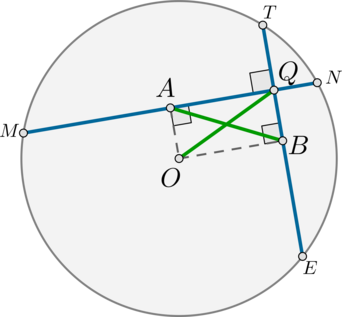
Две хорды окружности взаимно перпендикулярны. Найдите расстояние от точки их пересечения до центра окружности, если расстояние между их серединами равно (2).
Пусть (Q) – точка пересечения взаимно перпендикулярных хорд (MN) и (TE), (O) – центр окружности. Тогда необходимо найти (OQ).
Пусть (A) и (B) – середины этих хорд, то есть (AB=2). Тогда (OA) и (OB) – перпендикуляры к этим хордам.
Действительно, (triangle MON) – равнобедренный ((OM=ON) – радиусы), поэтому медиана (OA) в нем является и высотой. Аналогично доказывается, что (OBperp TE).
Таким образом, в четырехугольнике (OAQB) три угла – прямые ((angle
A=angle Q=angle B=90^circ)), следовательно, этот четырехугольник по признаку является прямоугольником. Т.к. в прямоугольнике диагонали равны, то (AB=OQ=2).
Ответ: 2
Задание
3
#2380
Уровень задания: Легче ЕГЭ
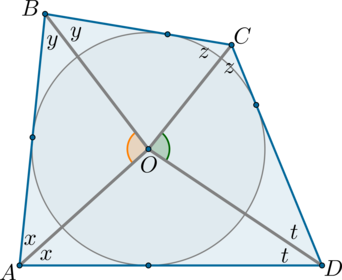
Четырехугольник (ABCD) описан около окружности с центром (O). Докажите, что (angle AOB+angle COD=180^circ).
Если окружность вписана в многоугольник, то ее центр лежит на пересечении биссектрис углов этого многоугольника. Действительно, окружность вписана в угол (A), следовательно, центр окружности лежит на биссектрисе этого угла. Аналогично можно сказать и про остальные углы.
Введем обозначения: (angle A=2x, angle B=2y, angle C=2z, angle
D=2t). Сумма углов четырехугольника равна (360^circ), следовательно, [2x+2y+2z+2t=360^circ quad Rightarrow quad
x+y+z+t=180^circ.] Из (triangle AOB): (angle AOB=180^circ-x-y);
из (triangle
COD): (angle COD=180^circ-z-t).
Таким образом, [angle AOB+angle COD=180^circ-x-y+180^circ-z-t=
360^circ-(x+y+z+t)=360^circ-180^circ=180^circ.]
Ответ:
Доказательство
Задание
4
#2381
Уровень задания: Легче ЕГЭ
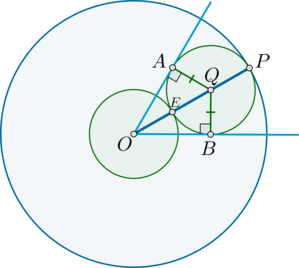
Даны две концентрические окружности радиусов (1) и (3) с общим центром (O). Третья окружность касается их обеих. Найдите угол между касательными к третьей окружности, проведенными из точки (O).
Если две окружности касаются, то их центры и точка касания лежат на одной прямой. Таким образом, для первой и третьей окружности точки (O), (Q) и (P) лежат на одной прямой, для второй и третьей — точки (O), (Q) и (E) лежат на одной прямой. Таким образом, все эти четыре точки лежат на одной прямой.
Значит, (OP=3), (OE=1), следовательно, (EP=3-1=2) — диаметр третьей окружности, следовательно, ее радиус (EQ=1).
Пусть касательные к третьей окружности касаются ее в точках (A) и (B). Тогда радиусы (QA) и (QB) перпендикулярны к касательным (OA) и (OB) соответственно. Таким образом, (triangle AOQ=triangle BOQ) по катету и гипотенузе, следовательно, (angle AOQ=angle BOQ).
Найдем (angle AOQ). Заметим, что в (triangle AOQ) катет (AQ=1), гипотенуза (OQ=2). Следовательно, (angle AOQ=30^circ) как угол, лежащий против катета, равного половине гипотенузы.
А значит весь (angle AOB=30^circ+30^circ=60^circ).
Ответ:
(60^circ)
Задание
5
#2382
Уровень задания: Легче ЕГЭ
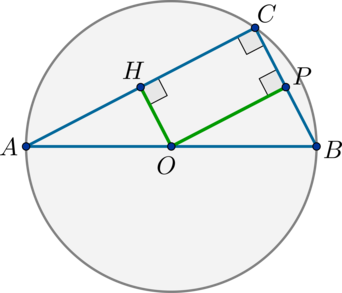
Через концы диаметра окружности проведены две хорды, пересекающиеся на окружности, сумма длин которых равна (14). Найдите сумму длин расстояний от центра окружности до этих хорд.
Пусть (AB) – диаметр, (O) – центр окружности, (AC) и (BC) – хорды, (AC+BC=14).
Т.к. (angle ACB) – вписанный и опирающийся на диаметр, то (angle
ACB=90^circ). Проведем (OHperp AC, OPperp BC). В четырехугольнике (OHCP) три угла прямые, следовательно, по признаку он является прямоугольником. Таким образом, (OH=CP), (OP=HC).
Заметим, что т.к. радиус, перпендикулярный к хорде, делит ее пополам, то (AH=HC), (CP=PB). Таким образом, [OH+OP=CP+HC=frac12BC+frac12AC=dfrac12left(BC+ACright)=
frac12cdot 14=7.]
Ответ: 7
Задание
6
#2383
Уровень задания: Легче ЕГЭ
Докажите, что отличная от (B) точка пересечения окружностей, построенных на сторонах (BA) и (BC) треугольника (ABC) как на диаметрах, лежит на прямой (AC).
Пусть (K) – вторая точка пересечения окружностей.
(angle AKB=90^circ) как вписанный угол, опирающийся на диаметр (AB). Аналогично (angle CKB=90^circ) как вписанный угол, опирающийся на диаметр (BC). Таким образом, через точку (K) к прямой (BK) проведены две прямые (AK) и (CK), перпендикулярные (BK). Следовательно, эти прямые либо совпадают, либо параллельны. Но т.к. они имеют общую точку (K), то они не могут быть параллельны, то есть они совпадают. Значит, точки (A, C) и (K) лежат на одной прямой, чтд.
Ответ:
Доказательство
Задание
7
#2385
Уровень задания: Легче ЕГЭ
Катеты прямоугольного треугольника равны (a) и (b), а гипотенуза равна (c). Докажите, что радиус вписанной окружности равен [dfrac{a+b-c}2]
1 способ
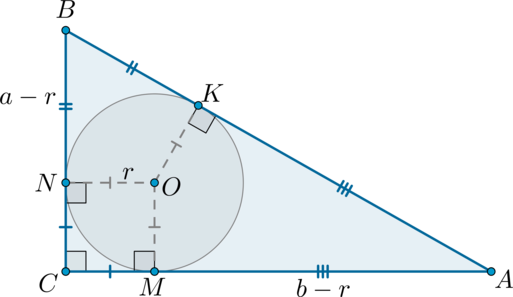
Рассмотрим прямоугольный (triangle ABC), пусть (BC=a, AC=b, AB=c). Проведем радиусы (ON, OK, OM) в точки касания. Обозначим также радиус (ON=r).
Рассмотрим четырехугольник (CNOM). У него 3 угла прямые, следовательно, по признаку он является прямоугольником. Также соседние стороны ((ON=OM=r)) у него равны. Следовательно, все его стороны равны (r) (то есть это квадрат). Таким образом, (CN=CM=r).
Значит, (BN=a-r), (AM=b-r). Т.к. отрезки касательных, проведенные из одной точки к окружности, равны, то (BK=BN=a-r), (AK=AM=b-r).
Таким образом, гипотенуза (AB=a-r+b-r=a+b-2r). Но с другой стороны гипотенуза равна (c). Таким образом, [a+b-2r=c quad Rightarrow
quad r=dfrac{a+b-c}2]
2 способ
Как известно, площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. Т.к. (S=frac12ab), (p=frac12left(a+b+cright)), то
[frac12ab=frac12left(a+b+cright)cdot r quad Rightarrow quad
r=dfrac{ab}{a+b+c}]
По теореме Пифагора (a^2+b^2=c^2), следовательно, (a^2+b^2-c^2=0). Сделаем преобразования:
(r=dfrac{ab}{a+b+c}=dfrac{ab(a+b-c)}{(a+b+c)(a+b-c)}=
dfrac{ab(a+b-c)}{(a+b)^2-c^2}=)
(=dfrac{ab(a+b+c)}{a^2+2ab+b^2-c^2}=
dfrac{ab(a+b-c)}{2ab}=dfrac{a+b-c}2.)
Ответ:
Доказательство
Планиметрические задачи с окружностями в ЕГЭ по математике традиционно встречаются из года в год. Находить правильное решение в подобных заданиях нужно уметь каждому ученику вне зависимости от того, базовый или профильный уровень экзамена ему предстоит сдавать. Освоив задачи по теме «Геометрия окружности», учащиеся смогут успешно выполнить ЕГЭ по математике и рассчитывать на получение достойных баллов по итогам прохождения аттестационного испытания.
Готовьтесь к экзамену вместе с образовательным порталом «Школково»
Приступая к решению задач с окружностями в ЕГЭ, рекомендуем освежить в памяти параметры и свойства вписанных и описанных фигур. Кроме того, в некоторых заданиях понадобится применить базовые теоремы.
Всю необходимую теоретическую информацию, которая поможет вам в решении задач на окружность в ЕГЭ по математике, вы найдете на образовательном портале «Школково». Наши специалисты подготовили материал и представили его в максимально доступной форме. Ознакомиться с ним можно в разделе «Теоретическая справка».
Закрепить полученные знания и отточить навык выполнения задач на окружности при подготовке к ЕГЭ вам помогут соответствующие упражнения. Подборка простых и более сложных заданий представлена в блоке «Каталог». Раздел регулярно обновляется и дополняется.
Попрактиковаться в решении задач по планиметрии с окружностями, подобным тем, которые встречаются в ЕГЭ математике, можно в режиме онлайн, находясь в Москве или любом другом городе России.

УСТАЛ? Просто отдохни