Пусть
даны две прямые l1
и l2
на плоскости:
![]() .
.
Чтобы
определить их взаимное расположение,
достаточно решить систему уравнений:
 (3.8)
(3.8)
Если
эта система имеет единственное решение
(х0,
у0),
то прямые l1
и l2,
пересекается в точке М0(х0,
у0).
Если система (3.8) не имеет решений, то
прямые l1
и l2
не пересекаются, следовательно, l1
|| l2.
Если система (3.8) имеет бесконечное
множество решений, то l1
и l2
совпадают.
Однако
решить вопрос о взаимном расположении
l1
и l2
можно и не решая системы (3.3). Действительно,
из общего уравнения прямой l1,
находим, что ее нормальный вектор
![]() имеет координатыА1
имеет координатыА1
и В1
, т.е.
![]() = {А1,
= {А1,
В1},
а прямая l2
имеет нормальный вектор
![]() = {А2,
= {А2,
В2}.
Если векторы
![]() ,
,![]() коллинеарны, то прямыеl1
коллинеарны, то прямыеl1
и l2
либо параллельны, либо совпадают. Если
![]() ,
,![]() неколлинеарны, то прямые пересекаются.
неколлинеарны, то прямые пересекаются.
Зная, что коллинеарные векторы (и только
они) имеют пропорциональные координаты,
получаем: если![]() ,
,
то прямыеl1
и l2
пересекаются; если
![]() то
то
прямыеl1
и l2
параллельны;
если
![]() то
то
прямыеl1
и l2
совпадают.
Используя
нормальные векторы
![]() ,
,![]() можно также найти угол между прямыми,
можно также найти угол между прямыми,
так как угол между нормальными векторами
равен одному из углов![]() между прямымиl1
между прямымиl1
и l2
(рис. 3.9).
И з
з
определения скалярного произведения
векторов получаем:![]() ,
,
поэтому![]() .
.
Пусть
на плоскости заданы прямая
![]() и точкаМ0(х0,
и точкаМ0(х0,
у0).
Найдем расстояние d
от точки М0(х0,
у0)
до прямой l
(рис. 3.10). Пусть М1(х1,
у1)
– точка пересечения прямой l
и прямой, проходящей через точку М0
перпендикулярно l.
Так как М1
лежит на l,
то ее
координаты удовлетворяют уравнению
этой прямой, таким образом, имеем
тождество:
![]() .
.
(3.9)
Рассмотрим
вектор
![]() .
.
Этот вектор коллинеарен нормальному
вектору![]() = {А1,
= {А1,
В1}
прямой l
и
![]() ,
,
поэтому косинус угла между векторами![]() и
и![]() равен либо 1, либо -1. Следовательно,
равен либо 1, либо -1. Следовательно,![]() ,
,
откуда
![]() .
.
Учитывая
тождество (3.9) получаем:
![]() .
.
(3.10)
Пример
3.3. Найти
расстояние от точки пересечения прямых
ll
и l2
до прямой l3.
Определить взаимное расположение пар
прямых l1,
l3
и l2,
l3,
если прямые заданы общими уравнениями:
![]()
Решение.Решим систему уравнений:

Получим:
х0
= 1, у0
= 2
– единственное
решение. Следовательно, прямые l1
и l2
пересекается
в точке М0(1,
2). Используя формулу (3.10), найдем расстояние
d
от М0
до l3:
![]()
Нормальные
векторы прямых l1,
l2
и l3
соответственно будут
![]() = {3, –2},
= {3, –2},![]() = {1, 1},
= {1, 1},![]() = {–6, 4}. Так как координаты
= {–6, 4}. Так как координаты![]() и
и![]() пропорциональны 3/( – 6) = –2/3 и –2/4
пропорциональны 3/( – 6) = –2/3 и –2/4![]() 1/(
1/(
–3), тоl1
|| l3.
Для
![]() и
и![]()
имеем:
1/(–6)![]() 1/4,
1/4,
следовательно,l2
и l3
пересекаются.
3.3. Плоскость в пространстве
П усть
усть
в пространстве задана прямоугольная
система координат: 0 – начало координат,![]() – единичные направляющие векторы осей
– единичные направляющие векторы осей
координат, соответственно 0х,
0у
и 0z.
Рассмотрим в пространстве произвольную
плоскость
![]() .
.
Выведем уравнение этой плоскости, т.е.
уравнение, содержащее переменныех,
у,
z,
которому удовлетворяют координаты
любой точки, лежащей на плоскости
![]() и не удовлетворяют координаты никакой
и не удовлетворяют координаты никакой
точки, не лежащей
на этой
плоскости.
Пусть
задана точка М1(х1,
у1,
z1)![]() и вектор
и вектор![]() ={А,
={А,
В,
C}
перпендикулярный плоскости
![]() (нормальный вектор плоскости). ПустьM(x,
(нормальный вектор плоскости). ПустьM(x,
у,
z)
– произвольная точка, принадлежащая
плоскости
![]() .
.
Тогда вектор
![]()
перпендикулярен
вектору
![]() (рис. 3.11), а поэтому
(рис. 3.11), а поэтому![]()
![]() =
=
0 (условие перпендикулярности векторов
(см. разд. 2.4)) или
![]() .
.
(3.11)
Итак,
координаты любой точки М,
лежащей в плоскости
![]() ,
,
удовлетворяют этому уравнению
и,
легко видеть, что координаты точки, не
лежащей в плоскости
![]() ,
,
не удовлетворяют уравнению (3.11).
Следовательно, уравнение (3.11) является
уравнением плоскости и называется
уравнением плоскостипо
точке и нормальному вектору.
Уравнение
(3.11) является уравнением первой степени
относительно текущих координат х,
у,
z.
Можно показать (аналогично тому, как
это было сделано в разд. 3.1), что всякое
уравнение первой степени относительно
x,
у,
z
![]()
(3.12)
является
уравнением некоторой плоскости (оно
называется общим
уравнением плоскости), причем вектор
![]() ={А,
={А,
В,
C},
является нормальным вектором плоскости.
Если
в уравнении (3.12) D
= 0, то этому
уравнению удовлетворяет тройка чисел
(0, 0, 0), т.е. соответствующая плоскость
проходит через начало координат. Нетрудно
видеть, что плоскость 0ху
имеет уравнение
![]() ,
,
плоскость 0xz
– уравнение
![]() ,
,
a плоскость 0yz
задается уравнением
![]() .
.
Известно,
что плоскость однозначно определяется
тремя точками, не лежащими на одной
прямой. Пусть
![]() иМ(х,
иМ(х,
у,
z)
– произвольная точка плоскости
![]() (рис. 3.12). Рассмотрим векторы
(рис. 3.12). Рассмотрим векторы
![]()
они
компланарны, поэтому
их смешанное
произведение равно 0, т.е.

(3.13)
Это
уравнение называется уравнением
плоскости по
трем точкам.
Пусть
плоскость
![]() пересекает оси координат в точках:М1(а,
пересекает оси координат в точках:М1(а,
0, 0), М2(0,
b,
0), M3(0,
0, с).
Подставляя
их координаты
в уравнение (3.13), находим:
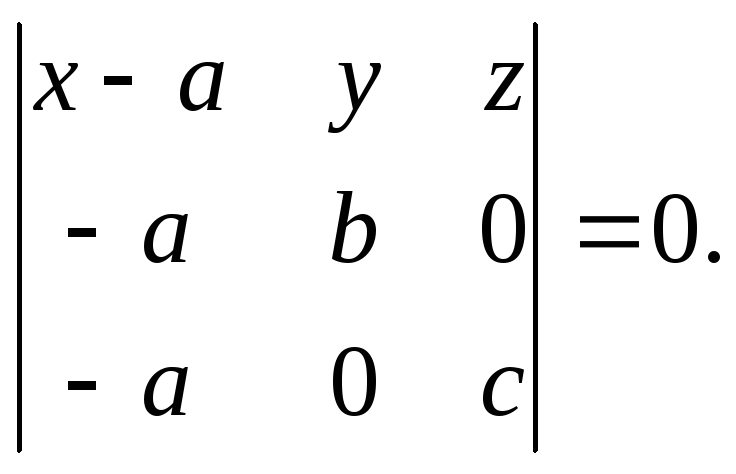
Вычислив определитель,
получим:
![]() ,
,
откуда
![]()
Это
уравнение называется уравнением
плоскости в
отрезках.
Пример
3.4. Построить
плоскость, заданную общим уравнением:
![]() .
.
Решение.
Преобразуем данное уравнение в уравнение
в отрезках
![]()
В
M1
 идим,
идим,
что плоскость отсекает на осях 0x,
0y, 0z, соответственно отрезки 3,
2, 1. Следовательно, она проходит через
точки
М1(3,
0, 0), М2(0
2, 0), М3(0,
0, 1).
По этим данным легко
построить плоскость (рис. 3.13).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
���������: 3- ������: 8,9 |
�������� ����������� |
�������
������� ���������� ����� ������ A(1, 7) � ������
����������� ������ x – y – 1 = 0 � x + 3y – 12 = 0.
�������
����� �������, ���ģ� ����� B(15/4, 11/4) ����������� ������ ������. �� ������� ��� ���������� ����� ����� �������
AB2 = (15/4 – 1)2 + (11/4 – 1)2 = (11/4)2 + (17/4)2 = 1/16 + (121 + 289) = 410/16.
�����
.
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 4221 |
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 66753 3. Найти расстояние от точки пересечения…
Условие
![]()
6369509f4ce58c1f3e23acb6
08.11.2022 18:31:57
3. Найти расстояние от точки пересечения прямых, заданных уравнениями
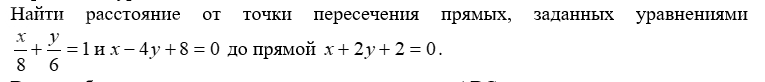
математика ВУЗ
253
Решение
![]()
5f3ea7e3faf909182968ddd9
08.11.2022 18:54:58
★
Находим координаты точки пересечения прямых
Решаем систему уравнений:
{(x/8)+(y/6)=1
{x-4y+8=0
{3x+4y-24=0
{x-4y+8=0
4x-16=0
x=4
y=3
Расстояние от точки (4;3) до прямой х+2у+2=0 находим по формуле.

Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 декабря 2022 года; проверки требует 1 правка.
- В данной статье рассматриваются две параллельные прямые на плоскости. Для параллельных прямых, расположенных не в одной плоскости, смотрите Скрещивающиеся прямые#расстояние.
Расстояние между двумя прямыми линиями на плоскости — это наименьшее расстояние между любыми двумя точками, лежащими на этих прямых. В случае пересекающихся линий расстояние между ними равно нулю, потому что минимальное расстояние между ними равно нулю (в точке пересечения), в то время как в случае двух параллельных линий это перпендикуляр — расстояние от точки на одной прямой к другой прямой.
Формулы и доказательства[править | править код]
Если линии параллельны, то расстояние между ними — это постоянная величина, так что не важно, какая точка выбрана, чтобы измерить расстояние. Даны уравнения двух параллельных линий
расстояние между двумя параллельными прямыми — это расстояние между двумя точками пересечения этих линий с перпендикуляром
Это расстояние может быть найдено при решении системы линейных уравнений
и
чтобы получить координаты точек пересечения. Определяем координаты точки пересечения
и
Расстояние между точками
которое можно сократить, как
Если известны уравнения прямых в декартовой системе координат, то можно их записать:
где расстояние между прямыми можно записать так
См. также[править | править код]
- Расстояние от точки до линии
- Скрещивающиеся прямые#расстояние
Найдите правильный ответ на вопрос ✅ «Найти расстояние между точкой пересечения прямых х-у=4 и 3 у=12 и точкой М (1; 7) …» по предмету 📘 Геометрия, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Дано треугольник OBS угол B=90 градусов угол S=45 градусов OB=1008 СМ Найти SB
Ответы (1)
Дано abcd-параллелограмм, BCA=31 градусов, BAC=25 градусов
Ответы (1)
Один угол параллелограмма в 4 разОдин угол параллелограмма в 4 раза больше другого. Найдите больший угол. Ответ дайте в градусах. а больше другого. Найдите больший угол.
Ответы (1)
NK на 19 см. больше MN, MK = 81 см. Найти : MK, NK
Ответы (1)
Начертите угол AOB и лучи ОК и ОМ, проходящие между сторонами этого угла, так, чтобы угол AOB = 90, AOK = 40, MOB = 30, Найдите KOM
Ответы (1)
Главная » Геометрия » Найти расстояние между точкой пересечения прямых х-у=4 и 3 у=12 и точкой М (1; 7)












