Диагональ AC параллелограмма ABCD равна 9 см.
Найдите расстояние между основаниями перпендикуляров , опущенных из точек A и C на прямые BC и AD соответственно.
На этой странице находится вопрос Диагональ AC параллелограмма ABCD равна 9 см?. Здесь же – ответы на него,
и похожие вопросы в категории Геометрия, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 5 – 9 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.
География,
вопрос задал tsabirova,
8 лет назад
как найти расстояние между двумя точками одной параллели ?
Ответы на вопрос
Ответил KatrinGray
0
Нужно измерить расстояние между двумя точками и умножить его на масштаб(тогда получится расстояние на местности).
Ответил KatrinGray
0
Если поставить кому-нибудь “лучшее решение”,25% баллов вернется к вам.
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Алгебра,
5 лет назад
Упростите выражения.
Пожалуйста напишите с решением подробно.
Биология,
5 лет назад
Сообщества живых организмов , находящиеся в определенных условиях с неживой природой это * 1 балл вещество экосистема планета материк К естественным экосистемам относят * 1 балл огород, пшеничное…
Геометрия,
8 лет назад
Задачку,пожалуйста .
Тело массой 2 кг свободно падает с высота 80 м…
Математика,
8 лет назад
найдите периметр равностороннего треугольика со стороной 12 сантиметров…
Геометрия,
8 лет назад
Помогите пожалуйста! В параллелограмме стороны равны 4 и 8. Высота ВН, проведенная к большей стороне,равна 3. Найдите высоту CG, проведенную к меньшей стороне параллелограмма. Спасибо за помощь.
Математика,
8 лет назад
в два супермаркета привезли 1800 кг картофеля, расфасованного в одинаковые сетки. в первый супермаркет привезли 540 сеток картофеля. во второй- 360 сеток. сколько килограммов картофеля привезли в…
Светило науки – 7292 ответа – 165986 раз оказано помощи
Центр описанной вокруг треугольника окружности находится в точке пересечения срединных перпендикуляров треугольника.
Треугольники АВD и BCD равны, т.к. параллелограмм делится диагональю ВD на два равных треугольника.
Радиусы описанных вокруг этих треугольников окружностей равны.
Проведем срединные перпендикуляры и найдем центры О и О1 описанных окружностей.
Соединив центры О и О1 с вершинами В и D параллелограмма, получим ромб
ВОDО1, т.к. его стороны – радиусы равных описанных окружностей, и диагонали пересекаются под прямым углом.
Его диагональ ОО1- искомое расстояние между центрами окружностей.
Угол ВОD центральный ( находится между двумя радиусами окружности с центром О) и равен удвоенному углу α, который является вписанным в эту окружность.
Сторона ромба = R
R=a:2 sin α
где а – диагональ BD параллелограмма
α — угол ромба, лежащий против стороны BD.
Ход решения:
1. Найти ВD по теореме косинусов
Найти сторону ОВ=R
Найти ОО1, диагональ ромба, – искомое расстояние – по формуле
d=a√(2-2·cos α)=a√(2+2·cosβ)

В параллелограмме ABCD известны стороны AB = a, BC = b и ∠BAD= α Найдите расстояние между центрами окружностей, описанных
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,921
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
В параллелограмме ABCD известны стороны AB = a, BC = b и угол BAD = Найдите расстояние между центрами окружностей, описанных около треугольников BCD и DAB?
Геометрия | 10 – 11 классы
В параллелограмме ABCD известны стороны AB = a, BC = b и угол BAD = Найдите расстояние между центрами окружностей, описанных около треугольников BCD и DAB.

Центр описанной вокруг треугольника окружности находится в точке пересечения срединных перпендикуляров треугольника.
Треугольники АВD и BCD равны, т.
К. параллелограмм делится диагональю ВD на два равных треугольника.
Радиусы описанных вокруг этих треугольников окружностей равны.
Проведем срединные перпендикуляры и найдем центры О и О1 описанных окружностей.
Соединив центры О и О1 с вершинами В и D параллелограмма, получим ромб
К. его стороны – радиусы равных описанных окружностей, и диагонали пересекаются под прямым углом.
Его диагональ ОО1 – искомое расстояние между центрами окружностей.
Угол ВОD центральный ( находится между двумя радиусами окружности с центром О) и равен удвоенному углу α, который является вписанным в эту окружность.
Сторона ромба = R
где а – диагональ BD параллелограмма
α — угол ромба, лежащий против стороны BD.
Найти ВD по теореме косинусов
Найти сторону ОВ = R
Найти ОО1, диагональ ромба, – искомое расстояние – по формуле
d = a√(2 – 2·cos α) = a√(2 + 2·cosβ).


Определите угол между диагоналями параллелограмма если известно что этот параллелограмм описан около окружности?
Определите угол между диагоналями параллелограмма если известно что этот параллелограмм описан около окружности.

Периметр параллелограмма ABCD равен 42 см, угол DAB = Углу ABD?
Периметр параллелограмма ABCD равен 42 см, угол DAB = Углу ABD.
Найдите стороны паралеллограмма если периметр треугольника BCD = 30 см.

В окружности с центром в точке O проведены диаметры AD и BC?
В окружности с центром в точке O проведены диаметры AD и BC.
Найдите угол DAB.

Сторона АС треугольника АВС проходит через центр описанной около него окружности?
Сторона АС треугольника АВС проходит через центр описанной около него окружности.
Найдите угол С, если угол А = 75 градусов.

Сторона АС треугольника АВС проходит через центр описанной около него окружности?
Сторона АС треугольника АВС проходит через центр описанной около него окружности.
Найдите угол С, если уголА = 44.

Найдите радиус окружности, описанной около треугольника ABC, если расстояние от центра окружности до стороны BC равно 1, 5, а угол BAC = 60?
Найдите радиус окружности, описанной около треугольника ABC, если расстояние от центра окружности до стороны BC равно 1, 5, а угол BAC = 60.

Сторона AC треугольника ABC проходит через центр описанной около него окружности?
Сторона AC треугольника ABC проходит через центр описанной около него окружности.
Найдите угол C, если угол А = 53 градуса.

Сторона ас треугольника авс проходит через центр описанной около него окружности найдите угол с, если угол а = 24?
Сторона ас треугольника авс проходит через центр описанной около него окружности найдите угол с, если угол а = 24.

Сторона AC треугольника ABC проходит через центр описанной около него окружности?
Сторона AC треугольника ABC проходит через центр описанной около него окружности.
Найдите угол С, если А = 75.

Известно, что ABCD – параллелограмм, BD = 2, угол ACB равен 45о?
Известно, что ABCD – параллелограмм, BD = 2, угол ACB равен 45о.
Прямая CD касается окружности, описанной около треугольника ABD.
Найдите площадь параллелограмма ABCD.
Вы перешли к вопросу В параллелограмме ABCD известны стороны AB = a, BC = b и угол BAD = Найдите расстояние между центрами окружностей, описанных около треугольников BCD и DAB?. Он относится к категории Геометрия, для 10 – 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

По теореме Пифагора, CB² = AB² – AC² = 225 – 29 = 196 условных единиц длины⇒CB = √196 = 14 условных единиц длины.

S = 2(3 * 2 + 2 * 5 + 3 * 5) = 62 v = 3 * 2 * 5 = 30 .

5) вм = ма / тг60 = (8√3) / 3 ав = ма / син60 = (16√3) / 3 Площадь(авм) = ам * вм * 1 / 2 = (32√3) / 3 Высота, проведенная с точки м : мн = 2 * площадь / ав = (64√3) / 3 * 3 / (16√3) = 4. 10) напротив угла в 30 градусов лежит катет вдвое меньший гип..

Не понятно какая точка равноудалена : Е или Р, и где находится точка Р тогда. Расстояние от точки до прямой это перпендикуляр, значит PB перпендикулярна ВС, РМ перпендикулярна AD, PK перпендикулярна CD и надо доказать что PB = PM = PK. 1. Рассмотри..

Ответ : 90°, 270°. Решение прилагаю.

Решение задачи во вложенном файле. Тангенс угла равен отношению противолежащего катета к прилежащему катету. (Гипотенуза “не участвует”).
Задача про две окружности в параллелограмме
а) В параллелограмме (ABCD) расположены две равные непересекающиеся окружности. Первая касается сторон (AD), (AB) и (BC), вторая сторон (AD), (CD) и (BC).
б) Пусть (ABCD) – прямоугольник, а прямая (l) касается окружностей в точках (M) и (N). Найдите площадь четырёхугольника с вершинами в точках (M), (N) и в центрах окружностей, если (AD=36), а расстояние между центрами окружностей равно (20).
а) В параллелограмме (ABCD) расположены две равные непересекающиеся окружности. Первая касается сторон (AD), (AB) и (BC), вторая сторон (AD), (CD) и (BC).
1) У параллелограмма точка пересечения диагоналей – это точка, в которой диагонали делятся пополам.
2) Диагональ и касательная (l) обязательно пересекаются в какой-то точке, поскольку очевидно не параллельны. Значит, если доказать, что касательная делит диагональ пополам, то можно говорить о том, что касательная проходит через точку пересечения диагоналей.
3) Как же доказать, что (AK=KC)? Один из самых популярных способов доказать, что отрезки равны – доказать равенство треугольников, в которых эти отрезки являются, например, сторонами. В нашем случае это (∆AKF) и (∆EKC).
4) Как доказать, что (∆AKF=∆EKC)? С углами всё хорошо – все три пары углов в этих треугольниках равны либо как вертикальные, либо как накрест лежащие. А вот со сторонами сложнее. Нужно доказать либо (EK=KF), либо (AF=EC).
5) Есть ощущение, что (AH_1=H_2 C) и (EH_2=H_1 F). Но ощущений маловато, нужно что-то посерьезнее… Вспомним, что это отрезки касательных, а где есть касание, там зачастую правильным действием будет провести радиус в точку касания. И соединим еще центры окружностей с (F) и (E), чтоб получились треугольники.
6) Можно ли доказать, что (∆O_1 FH_1=∆O_2 EH_2)? Есть прямые углы между радиусами и сторонами параллелограмма (ведь эти стороны – касательные к окружности). Есть радиусы, и они равны, так как по условию задачи окружности равные. Нужно равенство еще одной пары сторон или углов.
7) Попробуем доказать, что (∠H_1FO_1=∠H_2 EO_2).
Заметим, что (∠AFE=∠FEC) как накрест лежащие. При этом окружность с центром (O_1) вписана в угол (AFE), то есть (FO_1) – биссектриса. И с (EO_2) аналогично! Тогда получается, то (∠H_1 FO_1=∠H_2 EO_2) как половинки от равных углов (∠AFE=∠FEC)!
8) Супер! Последний кусочек найден, теперь можно собирать весь паззл.
(∆O_1 FH_1=∆O_2 EH_2) по катету и острому углу: (∠H_1 FO_1=∠H_2 EO_2), (O_1 H=O_2 H) как радиусы. Значит (H_1 F=EH_2).
9) Аналогично можно доказать равенство (∆O_1 H_1 A=∆O_2 H_2 C) из которого сделать вывод (AH_1=H_2 C).
10) (AF=AH_1+H_1 F=H_2 C+EH_2=EC),
(∠KAF=∠KCE) (как накрест лежащие),
(∠KFA=∠KEC) (аналогично).
Следовательно, (∆AKF=∆EKC), а значит и (AK=KC).
11) Получается касательная проходит через середину диагонали, а значит и через точку пересечения диагоналей.
1) Обозначим точку пересечения касательной (l) и диагонали (AC) как (K), точки касания окружностями сторон параллелограмма – (H_1) и (H_2), точки пересечения касательной и сторон параллелограмма – (E) и (F).
2) (∠H_1 FO_1=∠H_2 EO_2): (∠AFE=∠FEC) как накрестлежащие, (FO_1) и (EO_2) – биссектрисы по свойству вписанной окружности, значит (∠H_1 FO_1=frac<1><2>∠AFE=frac<1><2>∠FEC=∠H_2 EO_2).
3) Радиусы двух окружностей равны, так как окружности равные по условию задачи.
4) (∆O_1 FH_1=∆O_2 EH_2) по катету и острому углу: (∠H_1 FO_1=∠H_2 EO_2), (O_1 H_1=O_2 H_2) (как радиусы), (∠O_1 H_1 F=∠O_2 H_2 E=90^°) (как углы между касательными и радиусами, проведенными в точку касания). Значит (H_1 F=EH_2).
5) Аналогично можно доказать равенство (∆O_1 H_1 A=∆O_2 H_2 C) из которого сделать вывод (AH_1=H_2 C).
6) Таким образом имеем: (AF=AH_1+H_1 F=H_2 C+EH_2=EC), (∠KAF=∠KCE), (∠KFA=∠KEC) (как накрест лежащие). Следовательно, (∆AKF=∆EKC), а значит (AK=KC).
7) Точка пересечения диагоналей параллелограмма – это их общая середина, а т.к. касательная (l) проходит через середину (AC), то она проходит и через точку пересечения диагоналей.
Что и требовалось доказать.
б) Пусть (ABCD) – прямоугольник, а прямая (l) касается окружностей в точках (M) и (N). Найдите площадь четырёхугольника с вершинами в точках (M), (N) и в центрах окружностей, если (AD=36), а расстояние между центрами окружностей равно (20).
1) (MN) – касательная, (O_1 M) – радиус. Значит угол между ними – (90^°). Получается (∆MNO_1) прямоугольный. Треугольник (∆MNO_2) точно такой же, и если найти его площадь, то можно будет умножить её на (2) и найти площадь всего четырехугольника.
2) Давайте проведем радиусы к нижней стороне и к боковым сторонам прямоугольника.
3) Очевидно, что получилось два равных квадрата и их стороны можно найти: (AT=LD=frac<2>=frac<36-20><2>=8). Тогда радиус тоже равен (8).
4) Заметим, что (O_2 N∥O_1 M) (ведь они оба перпендикулярны одной и той же прямой MN) и (O_2 N=O_1 M), следовательно (O_1 MO_2 N) – параллелограмм. А значит диагонали точкой пересечения делятся пополам и (O_2 K=frac<1><2>O_1 O_2=10).
5) Получается (KN=sqrt<100-64>=6), а (MN=6cdot 2=12).
6) (S_=frac<1> <2>MNcdot MO_1=frac<1><2>cdot 12cdot 8=48).
1) (O_2 N⊥MN) и (O_1 M⊥MN) как радиусы, проведенные в точку касания. Значит (O_2 N∥O_1 M). К тому же, (O_2 N=O_1 M) как радиусы равных окружностей. Следовательно, (O_1 MO_2 N) – параллелограмм.
2) (O_1 O_2) и (MN) – диагонали в параллелограмме, то есть они точкой пересечения делятся пополам. Значит (O_1 K=KO_2=frac<1> <2>O_1 O_2=10).
3) Проведем из центров окружностей четвре радиуса к сторонам прямоугольника в точки касания, получились два четырехугольника: (VO_1 TA) и (O_2 SDL). (∠O_1 VA=∠ATO_1=∠VAT=90^°) и (VO_1=O_1 T) (как радиусы), следовательно, (VO_1 TA) квадрат. Аналогично доказывается, что (O_2 SDL) квадрат, причем (VO_1 TA=O_2 SDL), так как стороны их равны радиусам.
4) (O_1 O_2 LT) – прямоугольник: (O_1 T=O_2 L) (радиусы) и (∠O_1 TL=∠O_2 LT=90^°), следовательно, (O_1 T∥O_2 L). Значит (TL=O_1 O_2=20).
5) (AD=AT+TL+LD),
(AT=LD) (стороны равных квадратов).
Тогда (AT=LD=frac<2>=frac<36-20><2>=8).
Следовательно, радиусы окружностей тоже равны (8).
6) Рассмотрим (∆O_2 KN) – прямоугольный.
(KN=sqrt=sqrt<100-64>=6).
(MK=KN), т.к. (K) – точка пересечения диагоналей.
(MN=2KN=12).
7) (∆O_1 MN=∆O_2 MN) (т.к. (O_1 MO_2 N) – параллелограмм), следовательно, (S_=S_), а значит (S_=2S_).
(∆O_1 MN) – прямоугольный ((∠O_1 MN=90^°)), значит (S_=frac<1> <2>MNcdot MO_1=frac<1><2>cdot 12cdot 8=48).
(S_=2S_=96).
[spoiler title=”источники:”]
http://geometria.my-dict.ru/q/900902_v-parallelogramme-abcd-izvestny-storony-ab/
http://cos-cos.ru/ege/zadacha216/373/
[/spoiler]
На этой странице находится все необходимое, чтобы найти расстояние между двумя точками. Просто введите координаты точек и получите ответ и подробное решение с помощью наших онлайн-калькуляторов. Кроме того на сайте можно найти координаты середины отрезка.
Расстояние между двумя точками – это длина отрезка, соединяющего эти точки.
Формула расстояния между двумя точками на плоскости:
d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}}
xa и ya – координаты первой точки A,
xb и yb – координаты второй точки B
Нахождение расстояния между двумя точками на плоскости сводится к решению треугольника, а точнее – нахождению его гипотенузы. Для этого используется теорема Пифагора. Посмотрите на рисунок.
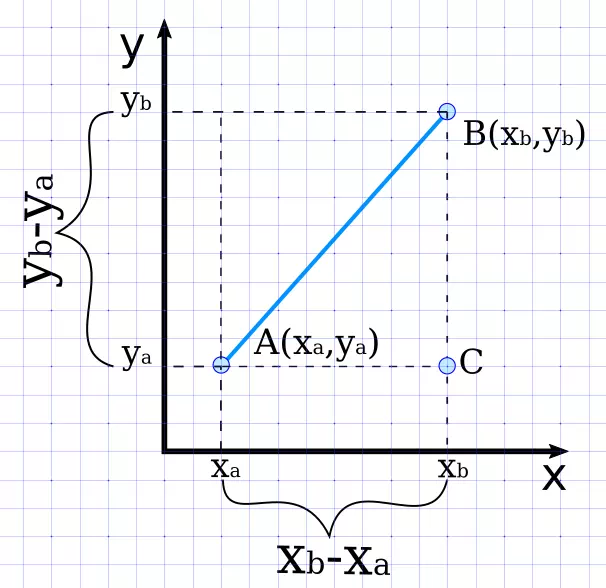
Соединив отрезком точки A и B, а также опустив перпендикуляры на оси мы получим треугольник ABC. В этом треугольнике стороны AC и BC являются катетами прямоугольного треугольника, а AB – его гипотенузой. Длины катетов AC и BC найти довольно просто:
AC = xb – xa
BC = yb – ya
Осталось применить теорему Пифагора и получить сторону AB, которая является гипотенузой прямоугольного треугольника и расстоянием между точками A и B:
AB=sqrt{{AC}^2 + {BC^2}}
Подставив вместо отрезков AC и BC их длины, получим итоговую формулу расстояния между двумя точками:
AB=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}} или d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}}
Формула расстояния между двумя точками в пространстве:
{d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2} + {(z_b – z_a)^2}}}
xa, ya и za – координаты первой точки A,
xb, yb и zb – координаты второй точки B
Примеры задач на вычисление середины отрезка
Задача 1
Найдите расстояние между точками А и В, если А(2; 7), В(-2; 7).
Решение
Подставим координаты точек в формулу расстояния между двумя точками на плоскости и вычислим результат:
d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}} = sqrt{{(-2 – 2)}^2 + {(7 – 7)^2}} = sqrt{{-4}^2 + {0^2}} = sqrt{16 + 0} = sqrt{16} = 4
Мы получили расстояние между точками и оно равно 4.
Ответ: 4.
Проверим результат с помощью калькулятора .
